ОБРАБОТКА И ВИЗУАЛЬНЫЙ АНАЛИЗ МНОГОМЕРНЫХ ДАННЫХ
А.Е. Бондарев, В.А. Галактионов, Л.З. Шапиро
bond@keldysh.ru, vlgal@gin.keldysh.ru, pls@gin.keldysh.ru
Институт прикладной математики им. М.В.Келдыша РАН, Москва, Россия
Содержание
3. Примеры построения упругих карт
Аннотация
В работе рассматриваются задачи визуального анализа многомерных наборов данных. Для визуального анализа применяется известный подход построения упругих карт, описанный в работах [1-3]. Упругие карты используются в качестве методов отображения исходных точек данных во вложенные многообразия меньшей размерности для последующего анализа кластерных структур в исходном объеме данных. Уменьшая параметры упругости, можно проектировать поверхность карты, которая намного лучше аппроксимирует многомерный набор данных. Точки исследуемого объема данных проецируются на карту. Развертка карты на плоскость вкупе с отображением в пространство первых главных компонент позволяет получить представление о кластерной структуре многомерного набора данных. Построение упругих карт не требует априорной информации о данных и не зависит от характера данных, происхождения данных и т. д., что является важным преимуществом этого метода. В работе приведены результаты применения упругих карт для визуального анализа многомерных наборов данных различного происхождения. В частности, рассматривается задача анализа текстовой информации, представленной в виде многомерного массива частот совместного употребления глаголов и существительных. Описаны приемы обработки данных, позволяющие улучшить полученные результаты. Так, например, применение метода «квази-зум» позволяет существенно улучшить результаты в области сгущения точек изучаемого многомерного пространства.
Ключевые слова: многомерные данные, визуальный анализ, упругие карты, кластерные структуры.
1. Введение
В анализе многомерных данных особое место занимают задачи классификации. При классификации объема многомерных данных может решаться как задача разделения исследуемой совокупности явлений на классы, так и отнесения одного или нескольких явлений к уже существующим классам. Для решения подобных задач используются методы кластерного анализа. Методов и алгоритмов кластерного анализа на современном этапе существует очень много, они постоянно развиваются и отличаются большим разнообразием. Многообразие алгоритмов кластерного анализа обусловлено множеством различных критериев, выражающих те или иные аспекты качества автоматического группирования. При решении задач классификации весьма полезными оказываются подходы визуальной аналитики, являющиеся синтезом нескольких алгоритмов понижения размерности и визуального представления многомерных данных во вложенных в исходный объем многообразиях меньшей размерности.
К таким алгоритмам можно отнести отображение исходного многомерного объема в упругих картах (Elastic Maps) [1-3] с разными свойствами упругости или эластичности. Эти методы позволяют тем или иным образом выделить из исходного многомерного объема данных содержащуюся в нем кластерную структуру. Авторами подхода [1-3] разработан программный комплекс ViDaExpert [4], позволяющий проводить построение и визуальное представление упругих карт. Основные функциональные особенности данного программного комплекса подробно описаны в [1].
Следует заметить, что интерес к упругим картам появился у нас при разработке вычислительной технологии для построения, обработки, анализа и визуального представления многомерных параметрических решений задач газовой динамики. Вычислительная технология реализована как единая технологическая цепочка алгоритмов производства, обработки, визуализации и анализа многомерных данных. Такая технологическая цепочка может рассматриваться как прототип обобщенного вычислительного эксперимента для нестационарных задач вычислительной газовой динамики. Схема реализации подобного обобщенного вычислительного эксперимента представлена на рисунке 1.
Подобный обобщенный вычислительный эксперимент неявно предполагает наличие надежной математической модели, численного метода для ее решения и набор экспериментальных результатов для верификации. В процессе вычислений необходимо реализовать организацию постоянного сравнения с экспериментальными данными при наличии такой возможности. Набор используемых методов должен включать в себя решение обратных и оптимизационных задач. Будучи реализованными с помощью описанных ранее параллельных интерфейсов, эти методы позволят получать решения задач параметрического исследования и оптимизационного анализа в виде многомерных объемов данных.
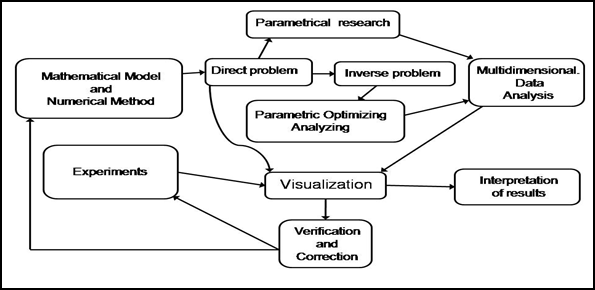
Рис. 1. Схема организации обобщенного вычислительного эксперимента.
Для обработки этих объемов и выявления скрытых взаимозависимостей между изучаемыми в объеме параметрами необходимо интегрировать в общий набор алгоритмов методы анализа многомерных данных и их визуального представления. В итоге подобный обобщенный вычислительный эксперимент позволит получать решение не одной, отдельно взятой, задачи, а решение для целого класса задач, задаваемого диапазонами изменения определяющих параметров. Также следует отметить универсальность подобного обобщенного вычислительного эксперимента. Он может быть применен к широкому кругу задач математического моделирования нестационарных процессов. Практическая реализация подобного обобщенного эксперимента может обеспечивать организацию крупномасштабных промышленных расчетов. Описание элементов реализованной вычислительной технологии приведено в работах [5,6].
На практике упругие карты оказались полезным и достаточно универсальным инструментом, что позволило применять их к многомерным объемам данных разного типа. Например, данный подход был применен к задачам анализа текстовой информации, где в качестве числовых характеристик выступали частоты употребления слов [7].
2. Построение упругих карт
Идеология и алгоритмы реализации построения упругих карт подробно представлены в работах [1,2]. Подобная карта представляет собой систему упругих пружин, вложенную в многомерное пространство данных. Этот подход основывается на аналогии с задачами механики: главное многообразие, проходящее через «середину» данных, может быть представлено как упругая мембрана или пластинка. Метод упругих карт формулируется как оптимизационная задача, предполагающая оптимизацию заданного функционала от взаимного расположения карты и данных.
Согласно [1] основой для построения упругой карты является двумерная прямоугольная сетка G, вложенная в многомерное пространство, которая аппроксимирует данные и обладает регулируемыми свойствами упругости по отношению к растяжению и изгибу. Расположение узлов сетки ищется в результате решения оптимизационной задачи на нахождение минимума функционала:
![]() ,
,
где │X│- число точек в многомерном объеме данных X; m - число узлов сетки, λ, μ - коэффициенты упругости, отвечающие за растяжение и изогнутость сетки соответственно; D1, D2, D3 - слагаемые, отвечающие за свойства сетки, где D1 является мерой близости расположения узлов сетки к данным, D2 представляет меру растянутости сетки, а D3 представляет меру изогнутости (кривизны) сетки.
Варьирование параметров упругости заключается в построении упругих карт с последовательным уменьшением коэффициентов упругости, в силу чего карта становится более мягкой и гибкой, наиболее оптимальным образом подстраиваясь к точкам исходного многомерного объема данных. После построения упругую карту можно развернуть в плоскость для наблюдения кластерной структуры в изучаемом объеме данных. Применение упругих карт позволяет более точно и четко определять кластерную структуру изучаемых многомерных объемов данных.
Следует отметить, что при построении упругих карт в многомерном облаке данных, состоящем из сгущений и отдельных отдаленных точек, возникает проблема масштабируемости. Упругая карта будет пытаться подстроиться под рассматриваемый объем в целом – как к отдаленным точкам, так и к областям сгущения, что, естественно, не может получиться одинаково хорошо. Для того чтобы решить эту проблему и обеспечить четкое представление о данных в области сгущений в работе [7] был предложен подход, названный «квази-зум» (quasi-Zoom), заключающийся в вырезании области сгущения из рассматриваемого облака многомерных данных и построения для вырезанной области упругой карты заново.
3. Примеры построения упругих карт
Рассмотрим пример построения упругих карт для объема многомерных данных представляющих собой описание характеристик полезных ископаемых, а именно, трех сортов угля из месторождений Польши [8].
Рассматриваются многомерные данные, представляющие собой точки в многомерном пространстве признаков (характеристик образцов угля). Пространство признаков состоит из следующих характеристик образцов угля – плотность, масса, удельная теплота сгорания, зольность, содержание серы, содержание летучих компонент, содержание влаги.
Таким образом, мы имеем набор точек в 7-мерном пространстве, соответствующих различным образцам угля. В наборе данных отображены три сорта угля. Рассматривается визуальный анализ с помощью применения упругих карт и главных компонент с целью изучения кластеризации многомерного облака данных и разделения сортов угля. Здесь и далее построение и визуальное представление упругих карт реализовано с помощью программного комплекса ViDaExpert [4], подробно описанного в [1].
Для исходного объема строится «мягкая» упругая карта, отображаемая в пространстве, образованном первыми тремя главными компонентами. Красные, зеленые и синие точки соответствуют трем типам угля (Рис.2).
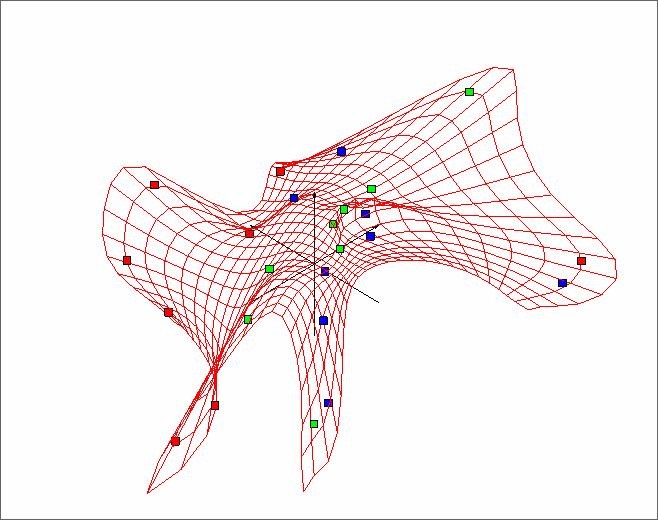
Рис. 2. Построение «мягкой» упругой карты, представляющей три сорта угля.
Далее представляем развертку построенной карты (Рис.3) на плоскость, образованную двумя первыми главными компонентами.
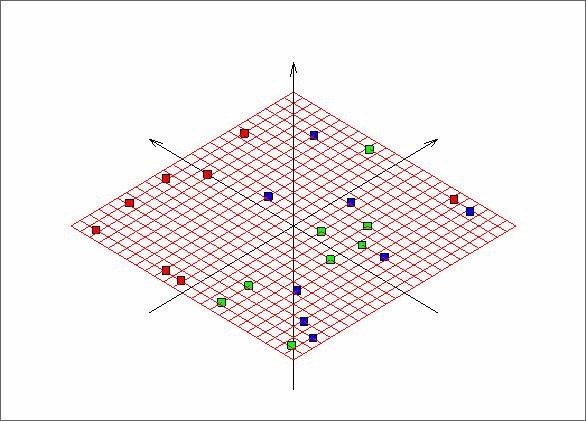
Рис. 3. Развертка «мягкой» упругой карты, представленной на предыдущем рисунке.
По развертке видно, что красные точки образуют отделившийся кластер, за исключением точки в правой части рисунка. Зеленые и синие точки перемешаны.
Для дальнейшего улучшения разделения применим фильтрацию исходного объема данных. Следует отметить, что для некоторых точек в исходном массиве представлены неполные данные, то есть для некоторых образцов информация по ряду характеристик отсутствует, или находится в широком диапазоне вариации, а не представлена точно. В частности, данные по размерам образцов представлены либо неопределенной величиной меньше некоторого или больше некоторого предела (огромные куски или пыль). Попробуем провести фильтрацию данных, то есть убрать все точки, данные по которым представлены нечетким или неполным образом.
Удаление подобных точек из исходного объема приводит к следующим результатам (Рис.4).
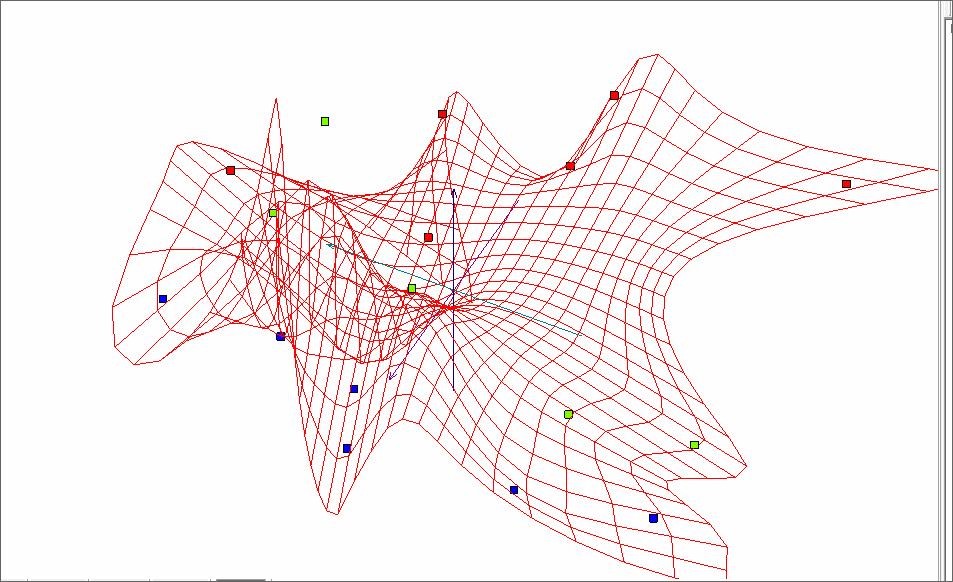
Рис. 4. Построение «мягкой» упругой карты после фильтрации данных.
На рисунке 4 представлена «мягкая» упругая карта для измененного объема данных. Ниже представлена развертка этой упругой карты.
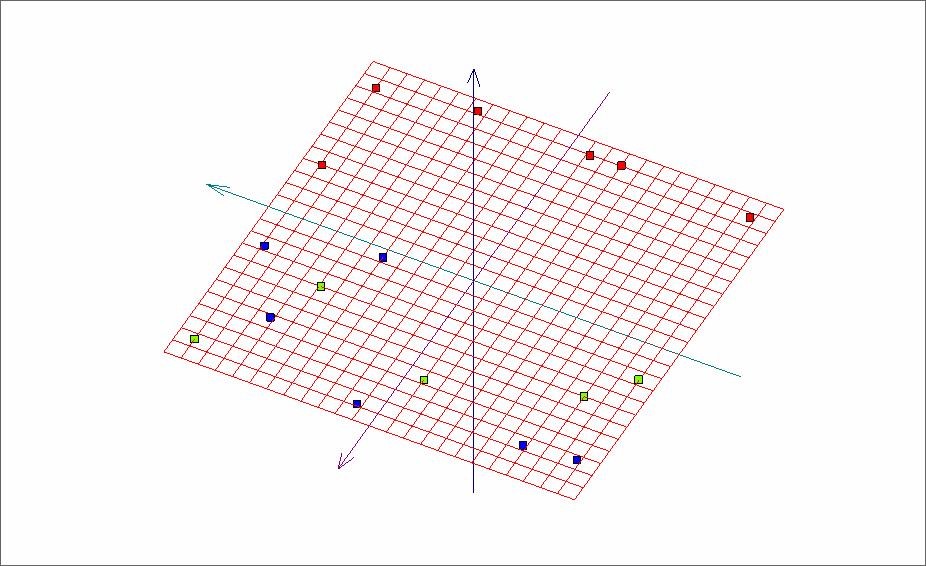
Рис. 5. Развертка «мягкой» упругой карты после фильтрации данных.
Сорт угля, представленный точками красного цвета, полностью отделился после процедуры удаления из исходного объема данных точек с нечетко определенными координатами в 7-мерном пространстве.
Сорта, представленные синими и зелеными точками, остались смешанными. Попробуем еще раз провести ту же процедуру удаления точек из данных. Однако на этот раз исключим из рассматриваемого объема красные точки целиком. Назовем эту процедуру флотацией (от английского термина flotation) аналогично термину, применяющемуся при очистке горных пород, когда более легкие фракции всплывают на поверхность и удаляются.
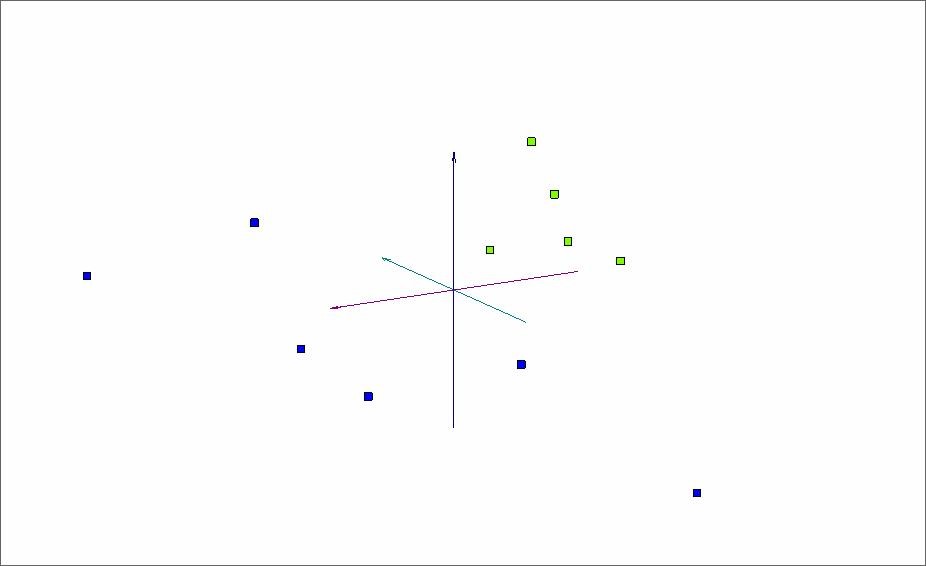
Рис. 6. Оставшиеся точки в пространстве трех первых главных компонент после флотации (удаления отделившегося полностью класса).
Теперь для четкого разделения двух оставшихся сортов достаточно отобразить точки нового объема данных в пространстве трех первых главных компонент (Рис.6).
Итак, комбинируя построение упругих карт, отображение на вложенные в исходное пространство главные 2D и 3D многообразия и операции удаления нечетких точек и отделившихся классов (фильтрация и флотация данных), можно полностью провести разделение заданных в исходном объеме образцов на три класса, соответствующие трем сортам угля.
Эти же приемы обработки исходных данных послужили основой для разработки приема quasi-Zoom при анализе текстовой информации в работе [7]. В данной работе основное внимание уделялось изучению возможности применения методов упругих карт и t-SNE для анализа тематической близости слов русского языка.
Основой предлагаемого метода является анализ непосредственного окружения слов. Основная гипотеза состоит в том, что близкие по смыслу слова должны встречаться в примерно одинаковом контексте. В связи с этим в пространстве признаков они будут находиться на относительно близком расстоянии друг от друга, тогда как отличающиеся слова будут находиться на более удаленном друг от друга расстоянии.
Рассмотрим результаты построения упругих карт для тестового объема [7]. Для первичных тестов было отобрано около 100 глаголов со 155 наиболее связанными с ними существительными. Полученные таким образом данные далее рассматривались как многомерный объем данных, представляющий собой 100 точек в 155-мерном пространстве. Числовые значения получающейся в результате матрицы определяются как частоты совместного употребления. Рассмотрим применение упругих карт к изображению данного объема. На рис.7 представлен изучаемый многомерный объем в пространстве трех первых главных компонент.

Рис.7. Представление многомерного объема в пространстве главных компонент [7].
Здесь видно, что изучаемый объем данных, содержит область высокой плотности данных и точки, достаточно далеко отстоящие от этой области.
На рисунке 8 представлена развертка «мягкой» упругой карты для данного объема.
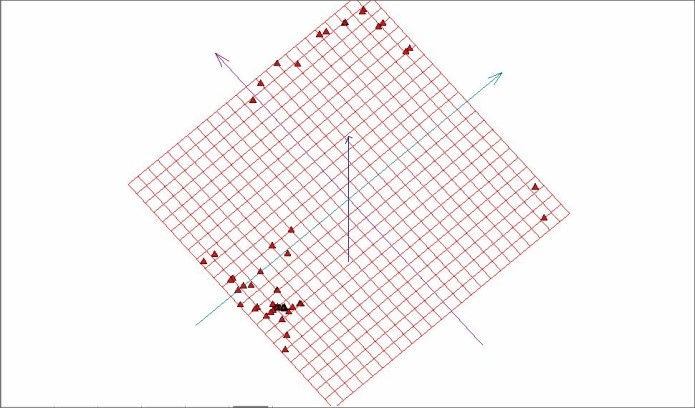
Рис. 8. Построение развертки «мягкой» упругой карты на плоскость первых двух главных компонент [7].
На рисунках 7,8 видно, что изучаемый объем данных, содержит область высокой плотности данных и точки, достаточно далеко отстоящие от этой области.
Именно в таких случаях возникает проблема масштабируемости, описанная ранее. Для решения этой проблемы был разработан подход «квази-зум» (quasi-Zoom), представленный в работе [7]. При исследовании объема частот совместного употребления глаголов и существительных в работе [7] практическая задача ставилась следующим образом. Нужно было максимально разделить «слипшиеся» точки. Для этой цели был разработан подход «quasi-Zoom», который позволил решить эту задачу. Суть этого технологического приема заключается в том, что для более тонкой подстройки необходимо выделять большие кластеры в исследуемом объеме многомерных данных и проводить построение упругих карт для выделенных кластеров отдельно, организуя тем самым эффект, подобный функции «zoom» в современной фототехнике. Это позволит избежать проблем с масштабируемостью, когда упругая карта должна описывать как области сгущения, так и сильно удаленные отдельные точки. Этот прием сродни проиллюстрированным ранее фильтрации и флотации, однако он отличается от них тем, что имеет четкую последовательность применения. Рассмотрим, как работает этот прием.
На рисунке 9 представлены те же результаты, что и на рисунке 8, но с аннотациями соответствующих глаголов для точек исследуемого объема.
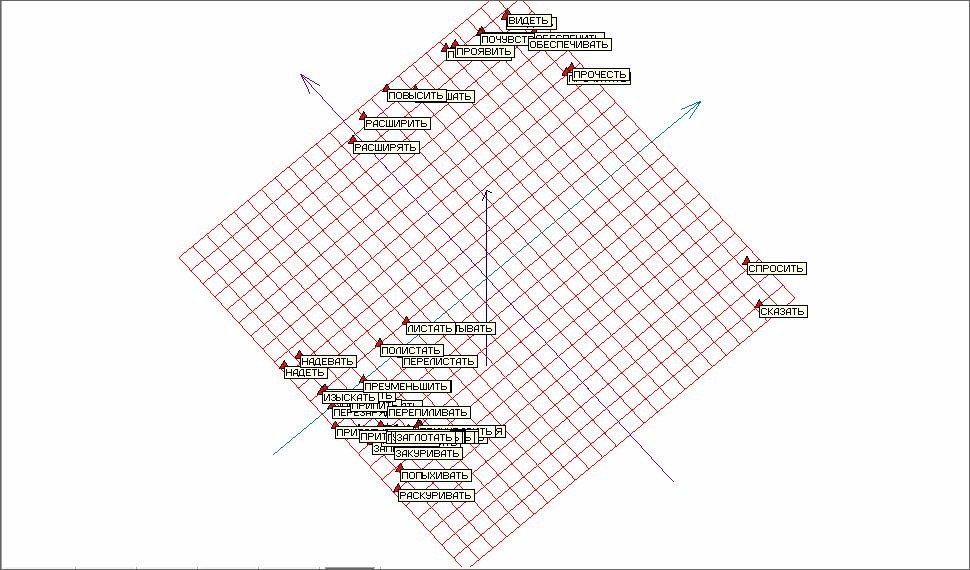
Рис. 9. Развертка «мягкой» упругой карты с аннотациями.
Видно, что пары схожих глаголов несовершенной и совершенной формы лежат достаточно близко друг к другу, что дополнительно свидетельствует о применимости и работоспособности метода упругих карт применительно к задачам анализа текстовой информации.
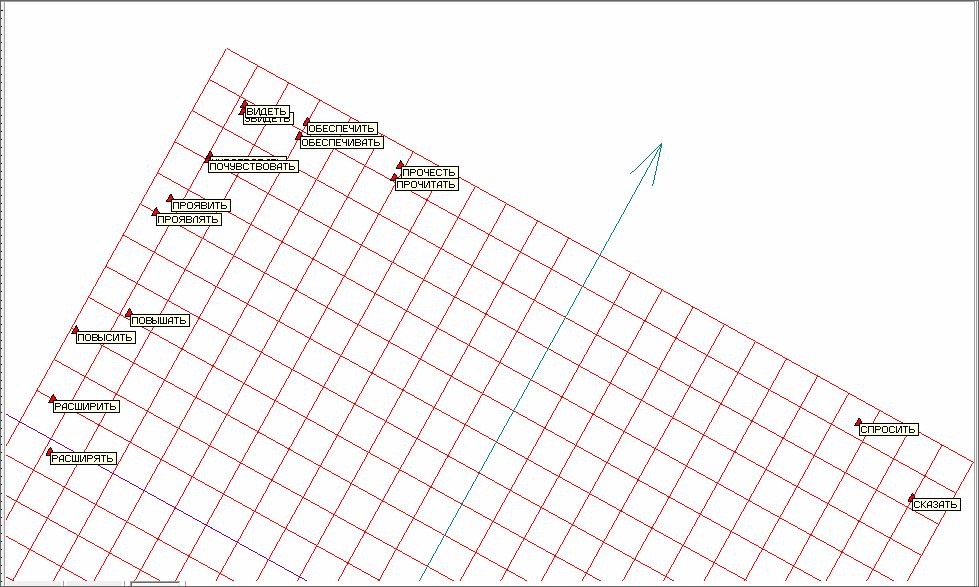
Рис. 10. Верхняя часть развертки «мягкой» упругой карты с аннотациями.
Для улучшения разделения в области сгущения применим подход «quasi-Zoom». Из исходного многомерного объема данных вырежем отделившиеся точки верхней части развертки (рисунок 10). К получившемуся в результате этой процедуры новому объему многомерных данных заново применим построение упругой карты. При этом упругую карту будем строить сразу максимально мягкой.
На рисунке 11 представлена получившаяся в результате развертка упругой карты после первого применения подхода «quasi-Zoom». Разделение точек удалось значительно улучшить. Однако под точкой, соответствующей наивысшей плотности данных скрываются еще 37 «слипшихся» слов – глаголов, приведенных на рисунке.
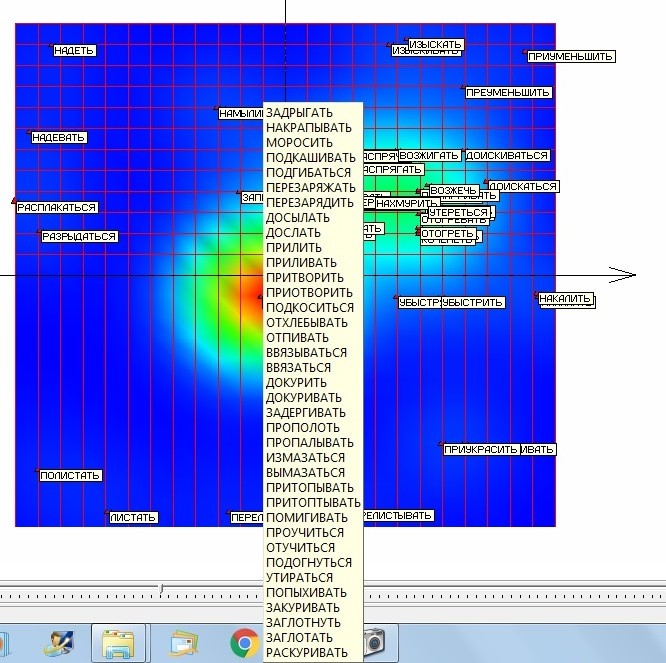
Рис. 11. Список «слипшихся» глаголов в точке наивысшей плотности данных после первого применения подхода «quasi-Zoom».
Для того, чтобы обеспечить разделение оставшихся 37 глаголов в точке наивысшей плотности данных, применим прием «quasi-Zoom» еще раз. Снова вырезаются отделившиеся точки таким образом, чтобы в результирующем многомерном объеме данных остались только 37 «слипшихся точек».
Повторно проводим для получившегося нового многомерного объема данных из 37 точек построение максимально мягкой упругой карты из сетки с таким же количеством узлов, как и на предыдущем этапе. Результаты представлены на рисунке 12, где изображена развертка упругой карты с раскраской по плотности и списком «слипщихся» слов после вторичного применения приема «квази-зум». Большую часть точек удалось разделить, однако в зоне наивысшей плотности данных осталось еще 17 «слипшихся» точек.
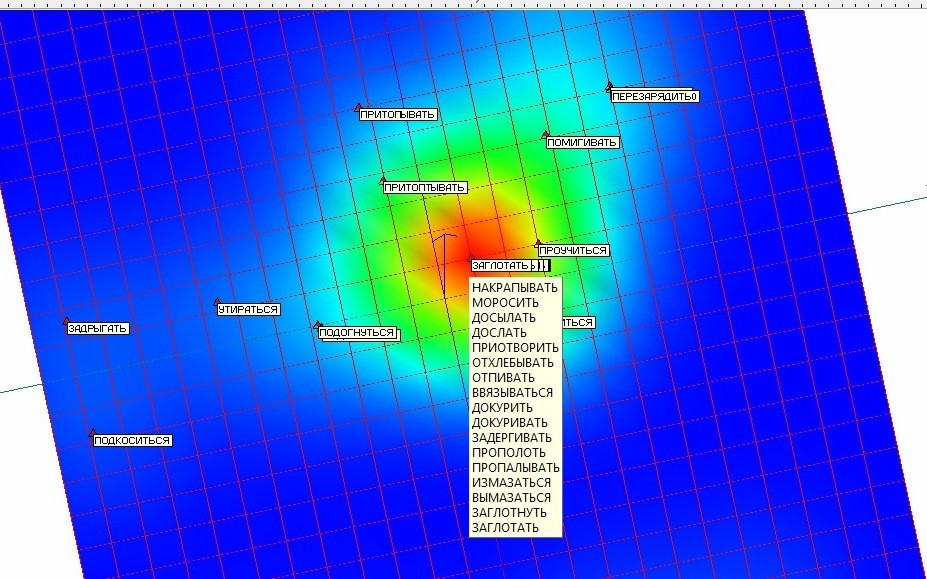
Рис. 12. Развертка упругой карты со списком «слипщихся» слов после вторичного применения приема «quasi-Zoom».
Проводим процедуру «квази-зум» в третий раз для оставшихся 17 точек. Результаты представлены на рисунке 13. В результате третьего применения процедуры удалось отделить еще 4 точки. Непосредственный анализ частот встречаемости для оставшихся 13 точек показал, что все они имеют одинаковые координаты по всем измерениям равные нулю. Следовательно, их разделение невозможно в принципе.
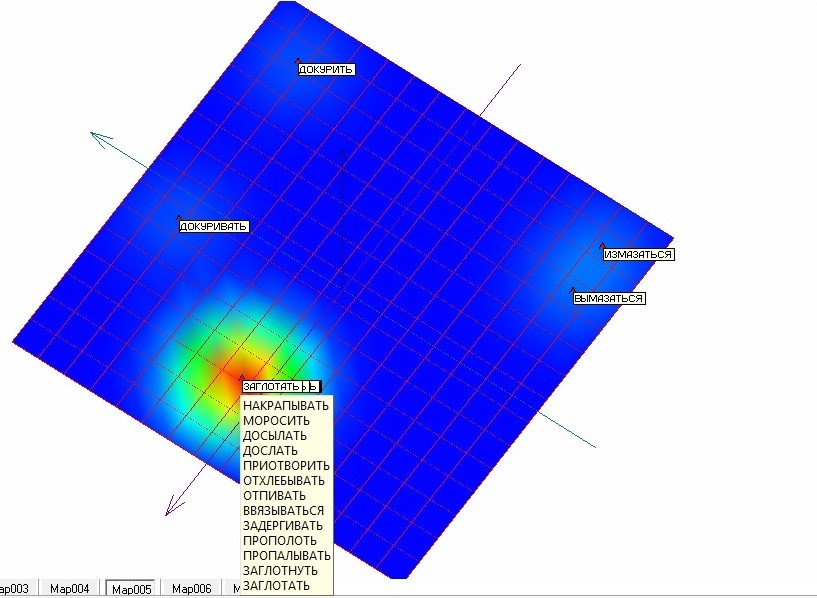
Рис. 13. Развертка упругой карты с раскраской по плотности после третьего применения процедуры «квази-зум» [7].
Таким образом, процесс разделения точек в тестовом многомерном объеме данных с помощью построения упругих карт и применения процедуры «квази-зум» завершен полностью и успешно. Удалось разделить все точки многомерного объема данных, имеющие различные и отличающиеся от нуля координаты. Апробация приема quasi-Zoom, проведенная в работе [7] показала эффективность разработанного подхода. При этом результаты показали необходимость проведения фильтрации данных на предварительном этапе с целью удаления точек с полностью нулевыми или полностью одинаковыми координатами. Для этой цели был построен автоматический фильтр в виде программного модуля, позволяющий проводить фильтрацию по указанному признаку. Для полного разделения точек рассматриваемого объема потребовалось только два раза последовательно применить quasi-Zoom. На рисунке 14 представлена развертка упругой карты после вторичного применения quasi-Zoom для массива с отфильтрованными данными.
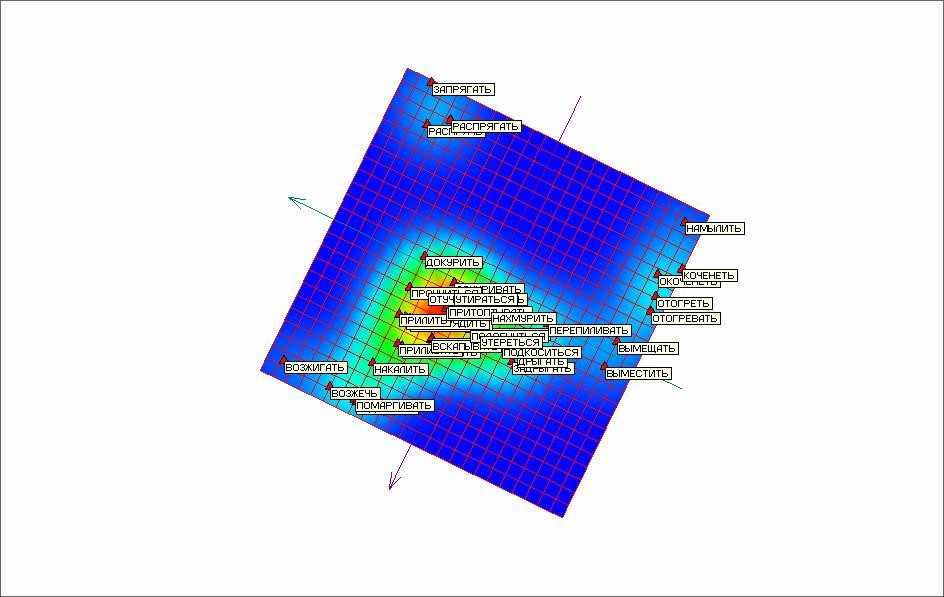
Рис. 14. Развертка упругой карты для фильтрованного набора данных после второго применения quasi-Zoom.
Повторное применение quasi-Zoom уже не оставляет слипшихся точек. Таким образом можно сделать вывод, что предварительная очистка данных путем фильтрации существенно ускоряет обработку многомерного массива и улучшает качество обработки.
Следующим интересующим нас вопросом являлся вопрос влияния на результат транспонирования рассматриваемого многомерного массива данных. Что будет, если поменять существительные и глаголы местами? Теперь рассмотрим 155 точек, характеризующих существительные, а в качестве измерений у нас будут служить 100 глаголов (87 после фильтрации).
Соответственно многомерный массив будет также состоять из частот совместного употребления существительных и глаголов, и мы сможем посмотреть и оценить, насколько схожие в понятийном смысле слова будут близки на развертке упругой карты. Общий вид развертки упругой карты представлен на рисунке 15.
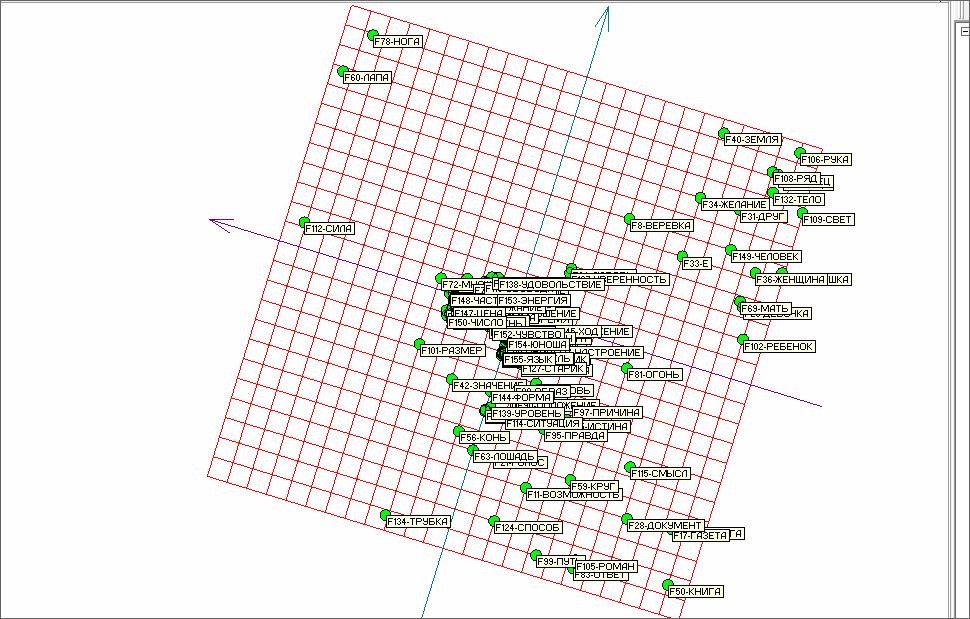
Рис. 15. Развертка упругой карты для транспонированного массива.
Здесь в отличие от предыдущего случая нет парных глаголов, а есть слова, близкие в понятийном смысле. Рассмотрим их крупным планом.
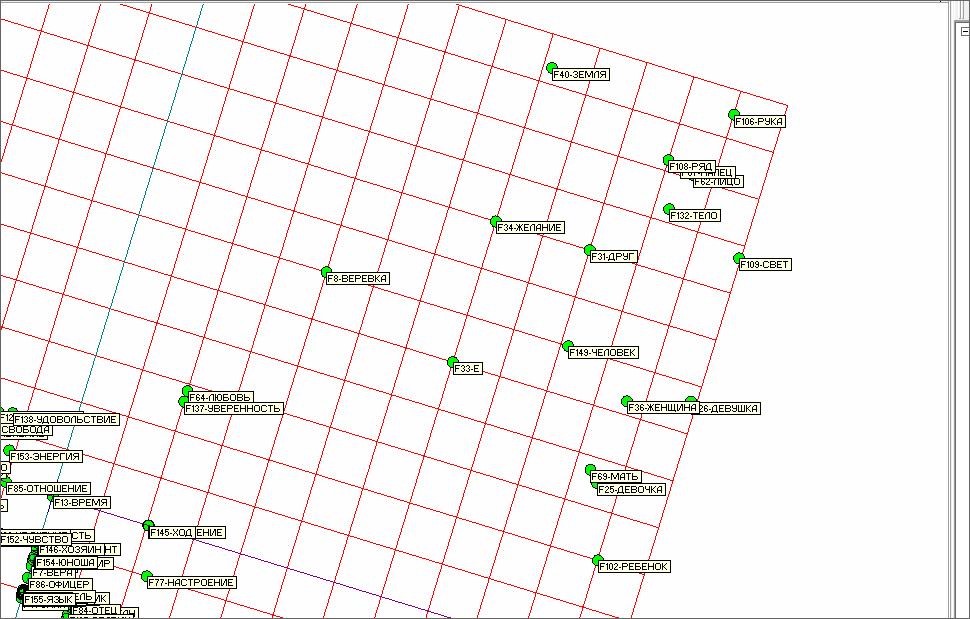
Рис. 16. Верхняя правая часть рисунка 15.
На рисунке 16 представлена верхняя правая часть рисунка 15. На этом рисунке можно видеть достаточно четко выделенный понятийный кластер – ЧЕЛОВЕК, ЖЕНЩИНА, ДЕВОЧКА, ДЕВУШКА, МАТЬ, РЕБЕНОК. Чуть выше менее четко просматривается смысловой кластер – РУКА, ПАЛЕЦ, ЛИЦО, ТЕЛО.
На рисунке 17 представлена нижняя правая часть рисунка 15. Здесь также просматривается кластер понятий – СМЫСЛ, ДОКУМЕНТ БУМАГА, ГАЗЕТА, КНИГА, РОМАН, ОТВЕТ.
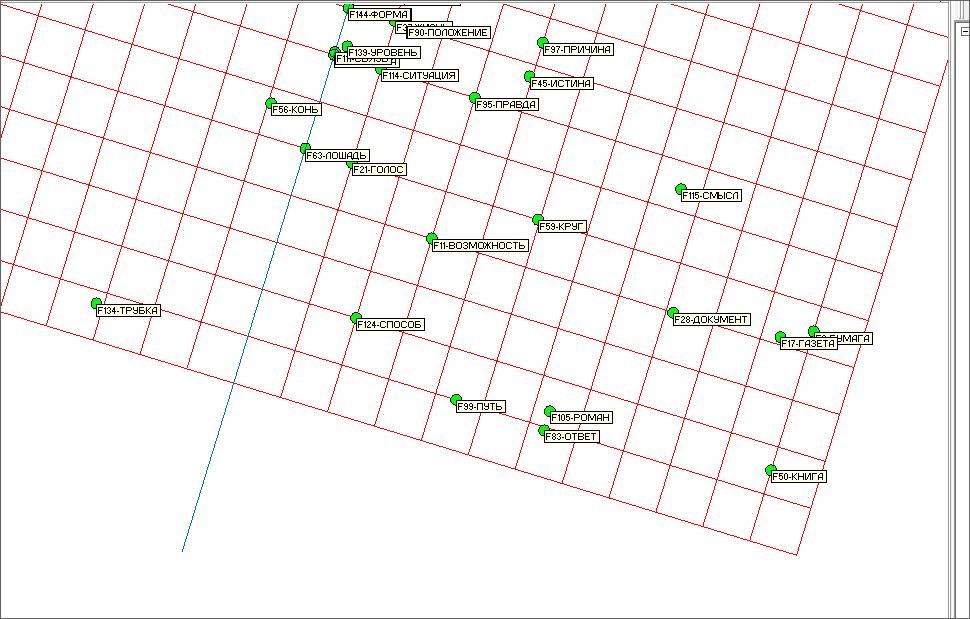
Рис. 17. Нижняя правая часть рисунка 15.
Это открывает широкие возможности по анализу и трактовке смысловых группировок для специалистов в этой области. Для более тщательного анализа и трактовки смысловой близости следует развивать данные подходы с точки зрения анализа расстояний между точками многомерного массива для различного задания метрики. Также интересной и важной задачей в этом плане должно стать выяснение влияния выбора метрики.
Применение технологий построения упругих карт для решения задач кластерного анализа не предполагает никакой априорной информации об изучаемых данных. Это дает возможность применять их к анализу данных самого различного типа вне зависимости от природы их происхождения. Подобное абстрагирование метода от типа и происхождения данных делает используемый подход построения упругих карт в достаточной степени универсальным инструментом анализа многомерных объемов данных.
Приведем пример применения построения упругих карт к анализу биомедицинских данных. Для этой цели были использованы данные работы [9]. Этот набор данных содержит значения шести биомеханических признаков, используемых для классификации ортопедических пациентов на 2 класса (нормальный «normal», или с отклонением от нормы «abnormal»). Каждый пациент представлен в наборе данных шестью биомеханическими признаками, полученными из формы и ориентации таза и поясничного отдела позвоночника: тазовое опускание, тазовый наклон, угол поясничного лордоза, крестцовый наклон, радиус таза и степень спондилолистеза.
Набор данных содержит 310 точек в 6-мерном пространстве. Рассматривая данный набор как многомерный объем в 6-мерном пространстве признаков, можно применять подход построения упругих карт, варьировать коэффициенты упругости карты для достижения наилучшего результата, далее проецировать точки многомерного объема на полученную карту и строить ее развертку в плоскости двух первых главных компонент.
На рисунке 18 представлена развернутая карта с раскраской по плотности данных. Зеленые точки соответствуют категории «normal», красные точки соответствуют категории «abnormal».
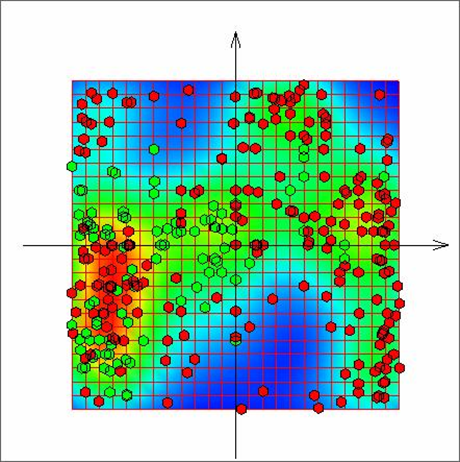
Рис. 18. Развертка упругой карты для биомедицинских данных [9].
Полученные результаты дают возможность получить представление о взаимном расположении основных классов в изучаемом многомерном объеме. Однако на рисунке 18 видна область смешения данных из двух категорий. Для улучшения разделения необходимо в дальнейшем усовершенствовать алгоритм построения упругих карт за счет возможности сгущения исходной сетки карты в областях повышенной плотности данных. Подобная возможность широко используется в задачах математического моделирования сплошных сред. Автоматическое сгущение сетки в области высоких градиентов в вычислительной механике жидкости и газа является отдельным направлением, где реализовано большое количество эффективных и апробированных на практике алгоритмов.
4. Заключение
Для анализа кластерных структур в многомерных объемах данных использованы технологии построения упругих карт, представляющие собой методы отображения точек исходного многомерного пространства на вложенные многообразия меньшей размерности. Варьируя поверхность упругой карты за счет последовательного уменьшения коэффициентов упругости, можно добиться лучшего соответствия подстройки карты под многомерное облако данных. Рассмотрен ряд приемов обработки данных, позволяющих улучшить результаты – предварительная фильтрация данных, удаление отделившихся кластеров (флотация). Для решения проблемы масштабируемости, когда упругая карта подстраивается как под область сгущения точек данных, так и к отдельно расположенным точкам облака данных, применяется подход «квази-зум» (quasi-Zoom). Суть подхода заключается в том, что для более тонкой подстройки в многомерном облаке данных выделяются большие кластеры, после чего проводится отдельное построение упругих карт для выделенных кластеров. Приведены примеры построения упругих карт для многомерных данных различного происхождения.
Благодарности
Данная работа выполнена при поддержке грантов Российского фонда фундаментальных исследований (проекты 16-01-00553а и 17-01-00444а).
Литература
[1] Зиновьев А. Ю., Визуализация многомерных данных, Красноярск, Изд. КГТУ, 2000. 180 с.
[2] A. Gorban, B. Kegl, D. Wunsch, A. Zinovyev (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58, Springer, Berlin – Heidelberg – New York, 2007.
[3] Gorban A. N., Zinovyev A. Principal manifolds and graphs in practice: from molecular biology to dynamical systems International Journal of Neural Systems, Vol. 20, No. 3 (2010) 219–232.
[4] http://bioinfo.curie.fr/projects/vidaexpert/
[5] Bondarev A.E., Galaktionov V.A. Analysis of Space-Time Structures Appearance for Non-Stationary CFD Problems // Proceedings of 15-th International Conference On Computational Science ICCS 2015 Rejkjavik, Iceland, June 01-03 2015, Procedia Computer Science, Volume 51, 2015, Pages 1801–1810.
[6] Bondarev A.E., Galaktionov V.A. Multidimensional data analysis and visualization for time-dependent CFD problems // Programming and Computer Software, 2015, Vol. 41, No. 5, pp. 247–252, DOI: 10.1134/S0361768815050023.
[7] Бондарев А.Е., Бондаренко А.В., Галактионов В.А., Клышинский Э.К. Визуальный анализ кластерных структур в многомерных объемах текстовой информации / Научная визуализация, Т.8, № 3, 2016, с. 1-24. http://sv-journal.org/2016-3/01.php?lang=ru
[8] Niedoba T., Multi-parameter data visualization by means of principal component analysis (PCA) in qualitative evaluation of various coal types, Physicochemical Problems of Mineral Processing, vol. 50, iss. 2, pp. 575-589, 2014.
[9] Rocha Neto A., Barreto G., 2009. On the Application of Ensembles of Classifiers to the Diagnosis of Pathologies of the Vertebral Column: A Comparative Analysis, IEEE Latin America Transactions, 7(4):487-496.
PROCESSING AND VISUAL ANALYSIS OF MULTIDIMENSIONAL DATA
A.E. Bondarev, V.A. Galaktionov, L.Z. Shapiro
bond@keldysh.ru, vlgal@gin.keldysh.ru, pls@gin.keldysh.ru
Keldysh Institute of Applied Mathematics RAS, Moscow, Russian Federation
Abstract
The paper considers the problems of visual analysis of multidimensional data sets. For visual analysis, the known approach of constructing elastic maps, described in [1-3], is used. Elastic maps are used as methods of mapping the initial data points of original data points mapping to enclosed manifolds having less dimensionality for the subsequent analysis of cluster structures in the original data volume. Diminishing the elasticity parameters, one can design map surface which approximates the multidimensional dataset in question much better. The points of dataset in question are projected onto the map. The extension of designed map to a flat plane with mapping into the space of the first three main components allows one to get an insight about the cluster structure of multidimensional dataset. The design of elastic cards does not require a priori information about the data and does not depend on the nature of the data, the origin of the data, etc., which is an important advantage of this method. The paper presents the results of applying elastic maps for the visual analysis of multidimensional data sets of various origins. In particular, the problem of the analysis of textual information represented in the form of a multidimensional array of frequencies of joint use of verbs and nouns is considered. Data processing techniques are described that allow improving the results obtained. For example, the application of the "quasi-Zoom" method makes it possible to significantly improve the results in the region of condensation of the points of the multidimensional space under study.
Keywords: multidimensional data, visual analysis, elastic maps, cluster structures.
References
1. Zinovyev A. Vizualizacija mnogomernyh dannyh [Visualization of multidimensional data]. Krasnoyarsk, publ. NGTU. 2000. 180 p. [In Russian]
2. Gorban A. et al. Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58, Springer, Berlin – Heidelberg – New York, 2007.
3. Gorban A., Zinovyev A. Principal manifolds and graphs in practice: from molecular biology to dynamical systems International Journal of Neural Systems, Vol. 20, No. 3 (2010) 219–232.
4. http://bioinfo.curie.fr/projects/vidaexpert/
5. Bondarev A.E., Galaktionov V.A. Analysis of Space-Time Structures Appearance for Non-Stationary CFD Problems // Proceedings of 15-th International Conference On Computational Science ICCS 2015 Rejkjavik, Iceland, June 01-03 2015, Procedia Computer Science, Volume 51, 2015, Pages 1801–1810.
6. Bondarev A.E., Galaktionov V.A. Multidimensional data analysis and visualization for time-dependent CFD problems // Programming and Computer Software, 2015, Vol. 41, No. 5, pp. 247–252, DOI: 10.1134/S0361768815050023.
7. Bondarev A.E., Bondarenko A.V., Galaktionov V.A., Klyshinsky E.S. Visual analysis of clusters for a multidimensional textual dataset / Scientific Visualization. V.8, № 3, pp.1-24, 2016, URL: http://sv-journal.org/2016-3/index.php?lang=en
8. Niedoba T., Multi-parameter data visualization by means of principal component analysis (PCA) in qualitative evaluation of various coal types, Physicochemical Problems of Mineral Processing, vol. 50, iss. 2, pp. 575-589, 2014.
9. Rocha Neto A., Barreto G., 2009. On the Application of Ensembles of Classifiers to the Diagnosis of Pathologies of the Vertebral Column: A Comparative Analysis, IEEE Latin America Transactions, 7(4):487-496.