ИСПОЛЬЗОВАНИЕ ВИЗУАЛИЗАЦИИ ПРИ РЕШЕНИИ ЗАДАЧ МНОГОКРИТЕРИАЛЬНОГО ВЫБОРА
А.П. Нелюбин1, Т.П. Галкин2, А.А. Галаев2, Д.Д. Попов2, С.Ю. Мисюрин2, В.В. Пилюгин2
1Институт машиноведения им. А.А. Благонравова Российской академии наук, Россия
2Национальный исследовательский ядерный университет «МИФИ», Россия
email: nelubin@gmail.com
Содержание
2. Классификация методов решения многокритериальных задач выбора
3. Визуализация в методах прямого сравнения вариантов по предпочтительности
4. Визуализация в методах свертки критериев
5. Визуализация в методах построения отношения предпочтения
6. Визуализация в методах анализа решений в пространстве критериев
Аннотация
В статье рассматриваются особенности процесса решения задач многокритериального выбора, связанные с необходимостью моделирования предпочтений лица, принимающего решение. Приведена общая классификация методов решения таких задач. В описании методов упор делается на используемые в них средства визуализации. Рассматриваются подходы к визуальному анализу чувствительности решения в методах свертки критериев, к визуализации частичного отношения предпочтения на множестве альтернатив, к визуальному исследованию множества допустимых решений в пространстве критериев. Визуальный анализ в многокритериальных задачах играет существенную роль и является неотъемлемой составляющей интерактивных методов их решения. Интерактивный подход к организации процесса принятия решения позволяет более точно выявить реальные предпочтения лица, принимающего решение, и осуществить наилучший выбор.
Ключевые слова: Многокритериальный анализ, важность критериев, интерактивные процедуры решения задачи выбора, системы поддержки принятия решений.
1. Введение
Большинство сложных задач управления, требующих принятия решений, являются многокритериальными. Например, при выборе места строительства потенциально опасного или вредного промышленного объекта (скажем, аэродрома или химического комбината) необходимо учитывать, помимо «ресурсных» критериев, еще и воздействие функционирующего объекта на окружающую среду, социальные, а иногда и политические последствия принимаемого решения.
Задача выбора в общем случае заключается в поиске и выделении среди множества возможных альтернатив некоторого подмножества наиболее подходящих альтернатив. Чаще всего на практике требуется выбрать одну или несколько альтернатив. Исходное множество альтернатив может быть конечным или бесконечным. Конечное множество альтернатив может быть небольшим, а может быть таким большим, что все альтернативы не перебрать за разумное время даже численными методами. Бесконечное множество альтернатив чаще всего является континуальным, при этом сами альтернативы задаются набором параметров, которые могут принимать значения из определенного диапазона, интервала. В таких задачах выбора необходимо предварительно произвести поиск допустимых альтернатив, удовлетворяющих всем ограничениям.
Если определен единый критерий выбора – функция, которая ставит в соответствие каждой альтернативе степень того, насколько она подходит для выбора, – то задача выбора решается численными методами оптимизации. В многокритериальных задачах выбора каждая альтернатива характеризуется вектором значений функций каждого критерия. Такие векторные оценки альтернатив могут оказаться несравнимы между собой. Поэтому для осуществления выбора в многокритериальных задачах требуется произвести дополнительный анализ критериев и альтернатив.
Этот анализ должен производится с участием лица, принимающего решение (ЛПР), особенно в сложных стратегических задачах выбора [1-4]. В качестве ЛПР может выступать группа людей, экспертов в данной области. ЛПР заинтересовано в осуществлении наилучшего для него выбора, поэтому является носителем информации о предпочтениях. Проблема состоит в том, что эти предпочтения обычно не могут быть сразу сформулированы в явном виде, тем более в виде количественных соотношений. Принятие ответственного решения является особым процессом, которому свойственна протяженность во времени и активная мыслительная деятельность. В начале этого процесса ЛПР имеет лишь примерное представление о своих предпочтениях. В ходе анализа задачи эти предпочтения могут проясняться, уточняться и даже меняться.
В этом процессе особую роль играют средства представления данных: об альтернативах, о критериях, о предпочтениях. Визуальное представление таких данных является наиболее естественным для человека, поскольку оно затрагивает и логическое, и образное мышление. Известно, что человек может держать в голове одновременно не более 5-7 факторов (вариантов, оценок) [1-2]. Графический образ позволяет агрегировать больший объем информации об анализируемом объекте. Поэтому для решения задач многокритериального выбора целесообразно применение интерактивных графических методов. В процессе диалога с компьютерной системой поддержки принятия многокритериальных решений ЛПР и эксперты глубже понимают задачу, возможности достижения поставленных целей, уточняют свои предпочтения [4].
Работа выполнена при финансовой поддержке РФФИ (гранты № 15-08-05493, № 16-29-04401, № 16-01-00404).
2. Классификация методов решения многокритериальных задач выбора
Существует множество подходов к решению многокритериальных задач выбора. Эти подходы различаются по тому, какая модель используется для описания предпочтений ЛПР и как организован сам процесс принятия решения.
В наиболее общем случае предпочтения ЛПР описываются функцией выбора [3], которая произвольному множеству альтернатив ставит в соответствие его подмножество, соответствующее постановке задачи выбора. Построить такую функцию выбора непосредственно можно лишь в задачах небольшой размерности. Поэтому на практике принимают упрощающие допущения о виде этой функции. Чаще всего все критерии агрегируют в один обобщенный критерий, позволяющий ранжировать по предпочтительности произвольный набор альтернатив. Среди таких методов:
- выделение одного главного критерия;
- лексикографическое упорядочение критериев по важности;
- свертка критериев с использованием весов их относительной важности;
- построение функции полезности.
Такие методы решения многокритериальных задач выбора называют априорными, поскольку полностью восстановленная функция выбора позволяет осуществить выбор на произвольном множестве альтернатив.
С другой стороны, для решения единичных задач выбора полностью восстанавливать функцию выбора не требуется. Методы, в которых предпочтения ЛПР устанавливаются при изучении имеющегося множества альтернатив, называют апостериорными. Среди таких методов:
- построение отношений предпочтения на множестве вариантов;
- анализ вариантов в пространстве критериев: исследование границы Парето, наложение ограничений и допусков.
По способу организации процесса решения задачи выбора методы можно разделить на одношаговые и многошаговые (итеративные). Под шагом понимается цикл, состоящий из двух этапов:
1. Выяснение информации о предпочтениях ЛПР в соответствии с используемой моделью;
2. Формирование выводов и рекомендаций по осуществлению выбора на основе полученной информации о предпочтениях.
Для решения сложных и ответственных задач многокритериального выбора лучше подходят многошаговые интерактивные методы. К интерактивным методам решения многокритериальных задач часто необоснованно относят простые итеративные процедуры, в которых этапы построения модели предпочтений ЛПР чередуется с этапами формальных вычислений [5]. Помимо наличия нескольких шагов, эти методы должны обеспечивать обратную связь для ЛПР, то есть формируемые рекомендации на каждом шаге должны сопровождаться некоторым обоснованием [6], чтобы их можно было проанализировать и скорректировать предпочтения на следующем шаге решения задачи. На этой стадии анализа задачи существенную роль играют средства визуализации, позволяющие донести до ЛПР в виде образа информацию о текущем решении и как оно зависит от указанных параметров предпочтений.
3. Визуализация в методах прямого сравнения вариантов по предпочтительности
При небольшом числе альтернатив и критериев иногда можно попытаться сравнить альтернативы по предпочтительности, не делая каких-либо допущений о взаимосвязи критериев между собой. Для этих целей разработано множество различных графических представлений альтернатив, позволяющих ЛПР визуально сопоставить выигрыши и потери по разным критериям для сравниваемых альтернатив. Рассмотрим лишь некоторые примеры таких представлений.
На рис. 1 изображена диаграмма профилей эффективности альтернатив. Каждая альтернатива представлена в виде двумерного графика зависимости значения критерия от номера критерия. Чем выше в целом расположен такой профиль эффективности альтернативы, тем предпочтительнее должна быть сама альтернатива.
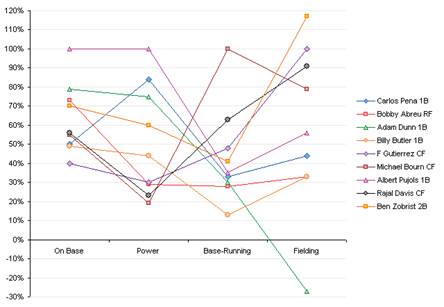
Рис. 1. Диаграмма профилей эффективности: 4 критерия, 9 альтернатив.
На рис. 2 изображена радарная диаграмма. Критерии расположены по кругу. Каждая альтернатива на диаграмме представлена в виде звезды, длина лучей которой равна значению по соответствующему критерию. Чем больше звезда, тем предпочтительней должна быть соответствующая альтернатива.
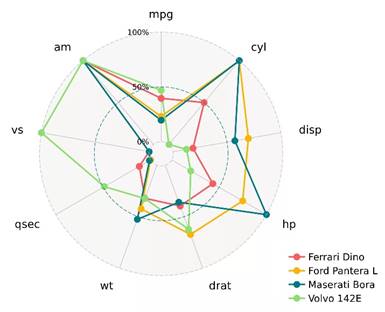
Рис. 2. Радарная диаграмма: 9 критериев, 4 альтернативы.
Разумеется, при большем числе критериев или альтернатив использование таких методов будет затруднительным.
4. Визуализация в методах свертки критериев
Среди априорных методов решения многокритериальных задач выбора рассмотрим один из самых распространенных, заключающийся в построении обобщенного критерия с использованием весов относительной важности критериев. Чаще всего в виде такого обобщенного критерия выступает линейная свертка критериев. Она используется в таких методах, как SMART [7], Analytical Hierarchy Process [8-9] и др.
Визуализация применяется в таких методах на разных этапах выяснения информации о предпочтениях ЛПР и представления результатов. Но особое значение визуализация имеет для анализа чувствительности (устойчивости) решения к изменению параметров предпочтений [10-11]. Просто потому, что без визуализации этот анализ был бы сильно затруднен и имел бы значительно меньшую эффективность.
Анализ чувствительности позволяет выявить параметры предпочтений, от которых в большей или меньшей степени зависит результат выбора. Этот анализ, как правило, производится локально и позволяет понять, изменится ли результат при небольших отклонениях, введенных данных. Поэтому его ещё иногда называют анализом устойчивости результата выбора.
В анализе чувствительности визуализация служит для представления зависимости результата выбора (формируемых рекомендаций) от введенных параметров предпочтений, в частности, весов относительной важности критериев. Также могут быть использованы средства интерактивного взаимодействия с ЛПР. На рис. 3 и 4 представлены иллюстрации анализа чувствительности в системе Expert Choice [10]. В первом примере (рис. 3) анализируется зависимость результата выбора от значения веса важности одного из критериев. По каждой альтернативе представлен график зависимости значения свертки критериев от значения веса рассматриваемого критерия. При этом делается довольно сильное допущение, что веса остальных критериев изменяются пропорционально.
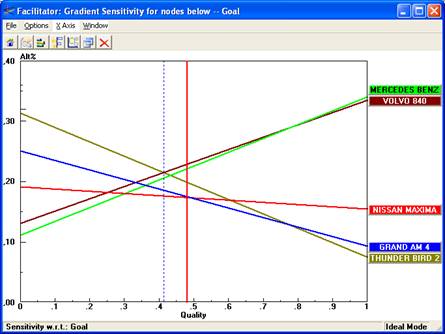
Рис. 3. Анализ чувствительности по одному из критериев.
Во втором примере (рис. 4) анализируется зависимость результата выбора от совокупности значений весов всех критериев. При этом альтернативы представлены в виде профилей эффективности, а веса критериев в виде столбиковых диаграмм.
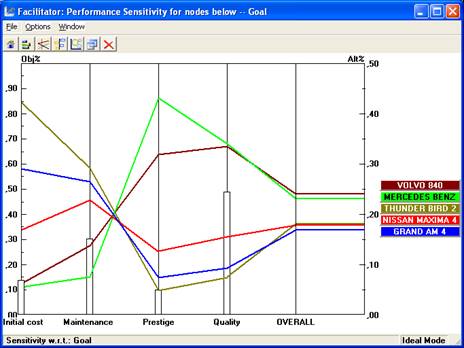
Рис. 4. Анализ чувствительности по совокупности критериев.
Наличие инструмента визуального анализа чувствительности переводит априорный метод в разряд многошаговых и интерактивных.
5. Визуализация в методах построения отношения предпочтения
Отношения предпочтения на множестве вариантов строится в таких методах, как outranking (системы ELECTRE и др.) [12], Теория важности критериев (система DASS) [13-15]. Визуализация при этом может использоваться для представления отношений предпочтения в виде ориентированных графов. В вершинах графа расположены варианты, а ребра соединяют их в направлении доминирования (предпочтения).
Теория важности критериев позволяет работать с неполной и неточной информацией о предпочтениях. При этом отношение предпочтения также может оказаться неполным, то есть не все альтернативы сравнимы между собой. Тогда соответствующий ориентированный граф будет несвязным. Для решения задачи многокритериального выбора используется итеративно-фрагментарный подход, который состоит в последовательном усложнении и непротиворечивом уточнении информации о предпочтениях ЛПР, вследствие чего отношение предпочтения постепенно пополняется новыми связями. На рис. 5 показан пример из трёх шагов такого процесса.
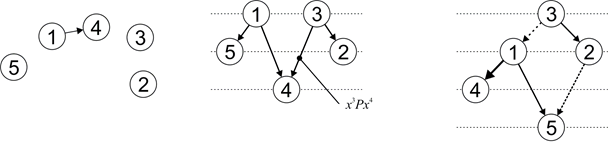
Рис. 5. Процесс пополнения графа частичного упорядочения альтернатив.
Средства визуализации способствуют превращению данного итеративного подхода в интерактивный. ЛПР удобно видеть перед собой общую картину взаимосвязей между альтернативами. При этом важно также то, как граф отображен на плоскости [16]. Имеет смысл расположить альтернативы сверху вниз по степени их доминируемости, так что сразу видны наиболее предпочтительные из них. Визуализация также сопровождает методы обоснования решения и поиска дальнейшего направления процесса решения задачи выбора [17].
6. Визуализация в методах анализа решений в пространстве критериев
Рассмотрим общий случай задачи многокритериальной оптимизации, когда множество альтернатив задается с помощью набора из n параметров, непрерывных или дискретных, которые могут принимать значения из n-мерного пространства решений X. На значение каждого параметра накладывается свое ограничение, обычно в виде интервала. Модель оптимизируемого объекта или процесса может быть как аналитической, так и имитационной. В этой модели могут быть наложены дополнительные ограничения на совокупность значений параметров, то есть возможно, что не все решения из X являются допустимыми. Помимо этого, модель позволяет вычислить для каждого допустимого решения x значения по каждому из критериев оптимизации K1, K2, … Km. Такое отображение пространства параметров X в m-мерное пространство критериев Y схематично показано на рис. 6 на примере двух критериев (m = 2).
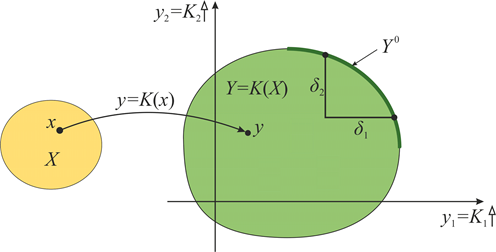
Рис. 6. Отображение пространства параметров в пространство критериев.
На данной схеме предполагается, что значения по обоим критериям требуется максимизировать. Поэтому наилучшие решения расположены справа и сверху в области допустимых решений Y(X) в пространстве критериев. На этой границе расположены оптимальные по Парето решения Y0. При выборе одного наилучшего решения искать его следует именно среди оптимальных по Парето [18]. Апостериорные методы решения задачи выбора в такой постановке построены на основе исследования этой границы Парето с применением средств визуализации и интерактивных инструментов для визуального анализа решений. Например, визуально можно сопоставить выигрыш δ1 по первому критерию с потерей δ2 по второму критерию при переходе от одного решения на границе Парето к другому (см. рис. 6).
Авторы работ [19-21] развивают Метод достижимых целей (МДЦ) – Feasible Goal Method (FGM) – интерактивный графический метод поиска предпочтительных решений многокритериальных задач выбора. Множество достижимых целей представляется в виде оболочки Эджворта-Парето (Edgeworth-Pareto Hull) этого множества, поскольку для решения задачи многокритериального выбора одной наилучшей альтернативы нас интересуют в первую очередь оптимальные по Парето решения. Для построения оболочки Эджворта-Парето используют различные методы аппроксимации на основе упрощенных, интегральных моделей анализируемой задачи.
Визуализация оболочки Эджворта-Парето осуществляется при помощи Диалоговых карт решений (ДКР) – Interactive Decision Maps (IDM) [20]. Карта решений – это набор двумерных сечений оболочки Эджворта-Парето по двум критериям для нескольких значений третьего критерия. Двухкритериальные сечения, соответствующие разным значениям третьего критерия, могут накладываться одно на другое на одном изображении, при этом цветовой градиент обозначает изменение значений третьего критерия (см. рис. 7).
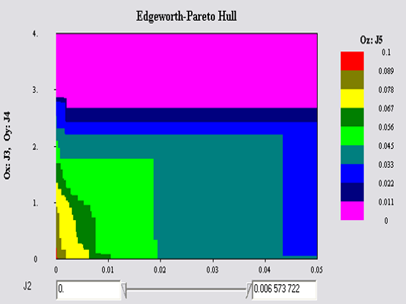
Рис. 7. Диалоговые карты решений.
С помощью диалоговых карт решений производится визуальный анализ совокупности достижимых целей. Интерактивное перемещение между картами решений для разных значений остальных критериев может осуществляться при помощи бегунка (slidebar) (см. рис. 7). С помощью такого интерактивного визуального анализа производится выбор наиболее предпочтительной (компромиссной) достижимой цели.
Другой подход к визуализации границы Парето состоит в переборе достаточно большого числа решений в области X и генерации соответствующих точек в пространстве критериев. Такой перебор можно осуществлять методами направленного поиска решений, например, генетическими алгоритмами [1, 5], методами случайного поиска, а также перебором равномерно распределенных точек в области X [22].
В системе MOVI [23] используется метод исследования пространства параметров путем генерации равномерно распределенной последовательности точек [22]. Отображаются двумерные проекции множеств допустимых решений и решений, оптимальных по Парето (см. рис. 8).
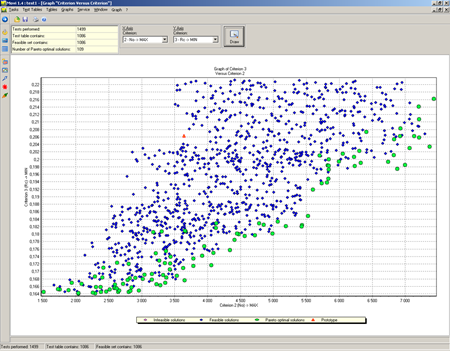
Рис. 8. Анализ решений в двумерной проекции по двум критериям в системе MOVI.
Помимо этого, в системе MOVI можно визуально проанализировать зависимости критериев от параметров, а также области сосредоточения допустимых и наилучших решений в пространстве параметров с целью осуществить углубленный поиск решений в этих областях на следующих шагах интерактивной процедуры решения задачи. Пример решения инженерной задачи многокритериальной оптимизации данным методом можно найти в [24].
В лаборатории научной визуализации МИФИ проводятся исследования по созданию новой системы визуального анализа решений в пространстве критериев и параметров. При этом используются современные технологии работы с трехмерными сценами (см. рис. 9).
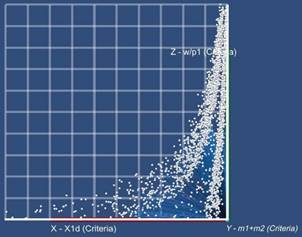

Рис. 9. Анализ решений в двумерных и трехмерных проекциях пространства критериев в новой системе Visual Analytics Tool.
Преимущества данного подхода:
- Возможность анализировать 3-хмерные подпространства критериев и параметров.
- Интерактивность в смысле активного анализа изображения – возможность вращать сцену, изменять масштаб и другие параметры визуализации.
- Интерактивность в смысле постановки задачи – возможность менять исходные данные и ограничения, наблюдая при этом за соответствующим изменением результатов.
Это позволяет:
- Иметь перед глазами общую картину достижимости целей.
- Сравнивать варианты решений не попарно, а в совокупности: сопоставлять масштаб относительных выигрышей/потерь, выявлять особенные «выступы» и «провалы» на границе оптимальных по Парето решений.
- Находить сложные зависимости критериев от (совокупности) параметров оптимизации, незаметные на 2-мерных проекциях.
- Выявлять кластеры решений, близких по значениям критериев и/или параметров.
- Исследовать пространство параметров: выявлять перспективные для поиска решений области; выявлять области неустойчивости, в которых близкие по значениям параметров решения сильно отличаются по значениям критериев.
- Исследовать влияние ограничений на решение: выявлять ограничения, к изменению которых решение чувствительно; выявлять ограничения, мало влияющие на решение; понять, какие ограничения целесообразно ослабить, а какие можно усилить без существенного ухудшения результатов.
7. Заключение
В данной работе было показано, как средства визуализации могут использоваться в совершенно разных подходах к решению задачи многокритериального выбора. Особую роль визуальный анализ играет в интерактивных методах принятия решений. Он является неотъемлемой составляющей этого интерактивного процесса и определяет качество принимаемых решений.
Графический образ способствует целостному восприятию большего количества комплексной информации. Средства визуализации в составе интерактивной процедуры способствуют тому, что ЛПР может прочувствовать решаемую задачу, видеть и контролировать ход ее решения. Визуальное представление множества вариантов решения задачи многокритериального выбора позволяет выявить имеющиеся между ними взаимосвязи, сопоставить разности в значениях критериев, выделить компромиссное решение.
Список литературы
1. Trends in multiple criteria decision analysis / M. Ehrgott, J. Figuera, S. Greco (eds.). – New York: Springer, 2010.
2. Ларичев О.И. Теория и методы принятия решений / Учебник. М.: Логос. 2002.
3. Айзерман М.А., Алескеров Ф.Т. Выбор вариантов. Основы теории. М.: Наука. 1990.
4. Подиновский В.В. Анализ задач многокритериального выбора методами теории важности критериев при помощи компьютерных систем поддержки принятия решений // Известия АН. Теория и системы управления. 2008. № 2. С. 64 – 68.
5. K. Miettinen, F. Ruiz, A.P. Wierzbicki Introduction to Multiobjective Optimization: Interactive Approaches. In: Multiobjective Optimization. Interactive and Evolutionary Approaches, Lecture Notes in Computer Science, V. 5252, Springer, 2008. P. 27 – 57.
6. Ф. Хейес-Рот, Д. Уотерман, Д. Ленат Построение экспертных систем. Пер. с англ. – М: Мир, 1987. – 441 с.
7. Edwards W., Barron F.H. SMARTS and SMARTER: improved simple methods for multiattribute utility measurement // Organization Behavior and Human Processes. 1994. Vol. 60. P. 306 – 325.
8. Saaty T.L. The Analytic Hierarchy Process. – N-Y: McGraw-Hill. 1980.
9. Saaty T.L. Decision Making with Dependence and Feedback. The Analytic Network Process. Pittsburg: University of Pittsburg. 2001.
10. Insua D.A., French S. A framework for sensitivity analysis in discrete multi-objective decision-making // European Journal of Operational Research. - 1991. - Vol. 54. - P. 176-190.
11. Ishizaka Alessio, Labib Ashraf, Analytic Hierarchy Process and Expert Choice: Benefits and Limitations // ORInsight, 2009, 22(4), pp. 201–220.
12. Roy B. The outranking approach and the foundations of ELECTRE methods. In: C. Bana e Costa (ed.). Reading in Multiple Criteria Decision Aids. Berlin: Springer. 1990. P. 155 – 183.
13. Подиновский В.В. Введение в теорию важности критериев в многокритериальных задачах принятия решений: Учебное пособие. – М.: Физматлит, 2007. – 64 с.
14. Подиновский В.В., Потапов М.А. Важность критериев в многокритериальных задачах принятия решений: теория, методы, софт и приложения // Открытое образование. 2012. № 2. С. 55 – 61.
15. http://mcodm.ru/soft/dass/
16. Сергеев М.А., Нелюбин А.П. Методы визуализации логики выбора при решении многокритериальных задач // Материалы XLI Международной конференции “Информационные технологии в науке, образовании, телекоммуникации и бизнесе IT+SE'2013”. Приложение к журналу «Открытое образование». 2013. С. 64 – 66.
17. Нелюбин А.П. Технология интерактивного решения многокритериальных задач // Материалы XLI Международной конференции “Информационные технологии в науке, образовании, телекоммуникации и бизнесе IT+SE'2013”. Приложение к журналу «Открытое образование». 2013. С. 61 – 63.
18. Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. – М.: Физматлит, 1982. 254 с. – Изд. второе, испр. и доп. 2007. 256 с.
19. Лотов А.В., Бушенков В.А., Каменев Г.К., Черных О.Л. Компьютер и поиск компромисса. Метод достижимых целей. – М.: Наука, 1997 – 240 с.
20. A.V.Lotov, V.A.Bushenkov, and G.K.Kamenev Interactive Decision Maps. Approximation and Visualization of Pareto Frontier. Kluwer Academic Publishers, Boston Hardbound, ISBN 1-4020-7631-2. February 2004, 336 pp.
21. http://www.ccas.ru/mmes/mmeda/soft/
22. Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями. М.: Наука, 1981. – 110 с.
23. http://www.psi-movi.com/
24. Ивлев В.И., Бозров В.М., Мисюрин С.Ю., Нелюбин А.П. Выбор параметров пневмомотора на основе методов многокритериальной оптимизации и поддержки принятия решений // Проблемы машиностроения и надежности машин, 2013, № 5. С. 12 – 18.
USAGE OF VISUALIZATION IN THE SOLUTION OF MULTICRITERIA CHOICE PROBLEMS
A.P. Nelyubin1, T.P. Galkin2, A.A. Galaev2, D.D. Popov2, S.Yu Misyurin2, V.V. Pilyugin2
1Mechanical Engineering Research Institute of the Russian Academy of Sciences, Russian Federation
2National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Russian Federation
email: nelubin@gmail.com
Abstract
The article discusses the features of the process of solving multicriteria choice problems associated with the need for modeling preferences of decision makers. A general classification of methods of solving such problems is given. The visualization tools involved in these methods are described. We consider approaches to the visual sensitivity analysis of the solution in the criteria aggregation methods, visualization of partial preference relations on the set of alternatives, and visual investigation methods of the set of feasible solutions in the criteria space. Visual analysis plays a significant role in multicriteria problems and is an essential part of interactive methods of solving such problems. Interactive approach to the organization of the decision-making process allows us to more accurately reveal the actual preferences of decision makers, and to make the best possible choice.
Keywords: Multicriteria analysis, criteria importance, interactive approaches to solution of choice problem, decision support systems.
References
1. Trends in multiple criteria decision analysis / M. Ehrgott, J. Figuera, S. Greco (eds.). – New York: Springer, 2010.
2. Larichev O.I. Theory an methods of decision making. – Moscow: Logos. 2002. (in Russian)
3. Aizerman M.A., Aleskerov F.T. Choice of variants. Theory foundations. – Moscow: Nauka. 1990. (in Russian)
4. Podinovski V.V. Analysis of Multicriteria Choice Problems by Methods of the Theory of Criteria Importance, Based on Computer Systems of Decision-Making Support // Journal of Computer and Systems Sciences International. 2008, Vol. 47, No. 2, pp. 221–225.
5. K. Miettinen, F. Ruiz, A.P. Wierzbicki Introduction to Multiobjective Optimization: Interactive Approaches. In: Multiobjective Optimization. Interactive and Evolutionary Approaches, Lecture Notes in Computer Science, V. 5252, Springer, 2008. P. 27 – 57.
6. Hayes-Roth F., Waterman D.A., Lenat D.B. Building Expert Systems. In: The Teknowledge Series in Knowledge Engineering. Reading, PA: Addison-Wesley, 1983.
7. Edwards W., Barron F.H. SMARTS and SMARTER: improved simple methods for multiattribute utility measurement // Organization Behavior and Human Processes. 1994. Vol. 60. P. 306 – 325.
8. Saaty T.L. The Analytic Hierarchy Process. – N-Y: McGraw-Hill. 1980.
9. Saaty T.L. Decision Making with Dependence and Feedback. The Analytic Network Process. Pittsburg: University of Pittsburg. 2001.
10. Insua D.A., French S. A framework for sensitivity analysis in discrete multi-objective decision-making // European Journal of Operational Research. - 1991. - Vol. 54. - P. 176-190.
11. Ishizaka Alessio, Labib Ashraf, Analytic Hierarchy Process and Expert Choice: Benefits and Limitations // ORInsight, 2009, 22(4), pp. 201–220.
12. Roy B. The outranking approach and the foundations of ELECTRE methods. In: C. Bana e Costa (ed.). Reading in Multiple Criteria Decision Aids. Berlin: Springer. 1990. P. 155 – 183.
13. Podinovski V.V. Introduction into criteria importance theory in multicriteria decision making problems. – Moscow: PhysMatLit, 2007. – 64 с. (in Russian)
14. Podinovski V.V., Potapov M.A. Criteria importance in multicriteria decision making problems: theory, methods, soft, and applications // Otkrytoye obrazovanie. 2012. No. 2. pp. 55 – 61. (in Russian)
15. http://mcodm.ru/soft/dass/
16. Sergeev M.A., Nelyubin A.P. Methods of visualization of choice logic in multicriteria problems // Proceedings of XLI International conference Information technologies in science, education, telecommunication, and business IT+SE'2013. pp. 64 – 66. (in Russian)
17. Nelyubin A.P. Technology of interactive solution of multicriteria problems // Proceedings of XLI International conference Information technologies in science, education, telecommunication, and business IT+SE'2013. pp. 61 – 63. (in Russian)
18. Podinovski V.V., Nogin V.D. Pareto-optimal solutions of multicriteria problems. – Moscow: PhysMatLit, 1982. 254 pp. – The second edition 2007. 256 pp. (in Russian)
19. Lotov A.V., Bushenkov V.A., Kamenev G.K., Chernykh O.L. Computer and searching for compromise. The feasible goal method. – Moscow: Nauka, 1997 – 240 pp. (in Russian)
20. Lotov A.V., Bushenkov V.A., and Kamenev G.K. Interactive Decision Maps. Approximation and Visualization of Pareto Frontier. Kluwer Academic Publishers, Boston Hardbound, ISBN 1-4020-7631-2. February 2004, 336 pp.
21. http://www.ccas.ru/mmes/mmeda/soft/
22. Sobol I.M., Statnikov R.B. Optimal parameters choice in the problems with multiple criteria. Moscow: Nauka, 1981. – 110 pp. (in Russian)
23. http://www.psi-movi.com/
24. Ivlev V.I., Bozrov V.M., Misyurin S.Yu., and Nelyubin A.P. Parameterization of an Air Motor Based on Multiobjective Optimization and Decision Support // Journal of Machinery Manufacture and Reliability, 2013, Vol. 42, No. 5, pp. 353-358.