In this work, we present and compare three methods for edge detection applied to range images based on deformable models. We will apply a classic active contour, level sets then an adaptive active contour. Despite the good experimental results on the simple objects, we note that the adaptive and classical snake methods have a few limitations. The adaptive and classical snake cannot detect discontinuities in curvatures and some items do not always converge. The level set method is very efficient for segmenting range images with curvature and with complex forms. Finally, we propose a multi-agent system approach for segmenting range images.

Keywords: Range image, segmentation, multi-agent system, active contour, snake, level set.

1. Introduction

There are several methods of segmentation for a range image into regions [1], which subsequently can be analyzed according to their shapes, sizes, relative positions and other characteristics, and there is several possible classifications for techniques of range segmentation. The range segmentation generally suffers from the lack of results and comparative methods. The range image contains not only information [2] related to the color and intensity of a pixel as the intensity image, but in addition, it contains a vector associated to the depth of that pixel « called RANGEL». It provides the geometrical information about the object regardless of the position, orientation and intensity of the light sources illuminating the scene [3], or reflectance properties of the object. Segmentation of range images has been the subject of much research in the computer vision field for nearly 30 years. During this period, several partial results have found their place in many industrial applications [4] such as geometric inspection, reverse engineering or autonomous navigation systems. However, in the same way that the spectral image segmentation, range image segmentation is still unsatisfactory. Our first objective in this work is to apply deformable models to segment range images, we will use three active contour (classical active contour, a classic improved active contour will be called "adaptive active contour" and the Level set method). We want through this application see the behavior of active contours on range images, we will try later to analyze the segmentation results to see which is the most suitable algorithm to these images. Our second and final objective is to propose a multi-agent approach to perform segmentation by region of a range image. We would use the flexibility and autonomy offered by multi-agent systems on their distribution picture by independent entities. The remainder of the paper is organized as follows: Section 2 describes the range image and some examples of range sensors. In Section 3, an overview of the used adaptive contour and level set methods is presented. The experimental results are discussed in Section 4. In section 5 we will propose a method for range of image segmentation by adopting a multi-agent approach, and finally, conclusions from the work are drawn and further research work is suggested.

2. Range image

2.1. Definition

A range image is a two-dimensional array of 3D positions [5] checking the spatial coherence property, each component of this matrix represents the distance between a reference point (the sensor) and a point in the field of vision of the sensor (camera, video camera), it is the equivalent of a video image wherein the gray level of each pixel (x, y) would be replaced by an altitude z (2.5D is an intermediate case between the 2D and 3D not a fractal dimensions). The feature of this type of data thus lies essentially in its grid structure (x, y) and in its ability to describe the scene graph as a function z = f (x, y). The term rangel (range picture element) refers to an element of the array. Range images provide geometric information about the object independent of the position, direction and intensity of light sources illuminating the scene or of reflectance properties of the object. For these reasons range images play a very important role in image understanding, three-dimensional object reconstruction, autonomous navigation, medical diagnosis, etc.


(a)	(b)

Fig. 1. Range image example. (a) Original intensity image. (b) Correspondent range image.

2.2. Depth of a range image

The depth is the distance between the visible surface of an object in a scene and the camera, it is a useful indicator for the calculation of the point’s coordinates belonging to this surface in a three-dimensional space reference, many methods have been developed [6] to obtain 3D coordinates of objects using range images, all exploit changes acquisition parameters of the system taken, these parameters acquisition system or light environment provides information essential to establish a relationship between the image and the actual scene.

2.3. Range image sensor

Range imaging sensors collect 3-D coordinate data from reflective surfaces of objects in a scene. They (range imaging sensors) may be classified as being either active or passive [7]. Active sensors project energy onto a scene and measure the portion of the energy that is reflected. Radar, sonar and laser ranging systems are examples of active sensors. Passive sensors operate using existing environmental conditions. Laser ranging digital cameras have emerged as premier devices useful in a broad class of 3-D computer vision applications due to their spatial accuracy, resolution, cost/performance. Recently, range image sensors are evolving continuously, allowing nowadays digitizing a full scene with high resolution in a short time. Thus, algorithms and techniques developed to process range images have to evolve with the same dynamism to enforce the processing of whole information rapidly.

2.3.1. Flying Laser Range Sensor

The FLRS was developed to measure large-scale objects from the air by using a balloon as a base rather than constructing scaffolds. With respect to the measurement principle, the passive stereopsis method could capture images « Fig.2 » without the influence of balloon motion. The laser radar method [8] is suitable for outdoor measurement of large objects.


(a)	(b)

Fig. 2. FLRS result. (a) The object for the experiment. (b) The range data obtained.

2.3.2 Imaging radar

A second method for range imaging is the imaging radar [9]. In a time-of-flight pulsed radar, the distance to the object is computed by calculating the time difference between the transmitted and received electromagnetic pulse, the depth information is obtained by detecting the phase difference between the transmitted and received waves. Several commercial laser beam imaging systems are built using these principles. The figure 3 shows an example a range image aquired by a time-of-flight pulsed radar.

Fig. 3 Range image aquired by a time-of-flight pulsed radar.

2.3.3. Stereo camera

A stereo camera [10] is a type of camera with two or more lenses with a separate image sensor or film frame for each lens. This technique allows the camera to simulate human binocular vision, and gives it the ability to capture three-dimensional images (Fig 4). The stereo cameras may be used for making 3D pictures for movies and for range imaging. The stereo cameras are sometimes mounted in cars to detect the lane's width and the proximity of an object on the road.

Fig. 4 Range image aquired by a stereo camera.

3. Developments

The proposed algorithms are implemented with Java NetBeans 7.21 which is a RAD (Rapid Application Development), an open-source Integrated Development Environment for software developers designed by Sun for creating applications and a GUI with all the tools needed to create professional desktop, enterprise, web, and mobile applications with the Java language. NetBeans IDE is easy to install and use straight out of the box and runs on many platforms including Windows, Linux, Mac OS X and Solaris.

3.1. Pre-Processing

The contour of objects in a scene is affected by noisy pixels which are caused by detector noise, quantization and calibration errors and which often lead to unreliable image segmentation results [11]. Range images with noise will hamper the recognition and positioning of the target. In this study, to alleviate the effects of any noise present, the image is filtered by the Floyd & Steinberg filter which improves the overall perception of a range image and to avoid the exclusion of the low intensity areas as in Fig5(a).


(a)	(b)

Fig. 5. Segmented image. (a) Without dithering. (b) Using Floyd & Steinberg dithering.

The Floyd-Steinberg dithering algorithm [12] is based on error dispersion. For each point in the image we find the closest color available. We calculate the difference between the value in the image and the color we have, then we divide these error values and distribute them over the neighboring pixels which have not been visited yet. When we get to these later pixels, we just add the errors distributed from the earlier ones and clip the values to the allowed range if needed. We start our experiment with Sobel, Canny and Prewitt dithering which are traditionally used in range segmentation, but as can be seen in Fig.6 these three filters are not adequate for our segmentation method (Snake).


(a)	(b)	(c)	(d)

Fig. 6. Segmented image. (a) Canny. (b) Sobel. (c) Prewitt. (d) Floyd & Steinberg.

3.2. The classic snake method

The classic snake we use is a parametric curve “C” will be attracted to areas with strong gradients (Where the norm of the gradient of a point will be very high). The principle is to place in the image an initial contour which is then deformed under the action of several energies. This maneuver needs two energies, internal energy and external energy

· An internal energy: The internal energy will depend on the derivatives of the first and second order of the parametric curve representing the snake. This energy corresponds to the shape and curve characteristics such as curvature and length.

· The external energy relates to the image and its properties and characteristics, such as the presence of edges or noise. It ensures that the snake is on the edges of the image by maximizing the amount of the standard gradient throughout the curve and thus minimizing its opposite.

The initial contour is first placed in the center of the image in a circle, movement and evolution of this model is through the iteration of the algorithm to minimize the total energy. For each point P of the active contour energy function E is calculated for every point n belonging to the neighborhood of P.
The point P0 characterized by minimum energy E0 is then chosen to replace P if E> E0, Otherwise, the contour point P is not changed. This mechanism is repeated until convergence (when the contour obtained in iteration t is identical to that obtained in iteration t + 1).

3.3. The Level Set method

The Level Set technique is an important category of modern image segmentation techniques based on partial differential equations (PDE). Progressive evaluation of the differences among neighboring pixels to find object boundaries, ideally, the algorithm will converge at the boundary of the object where the differences are the highest. The outstanding characteristic of level set methods is that contours can split or merge as the topology of the level set function changes. This method [13] can detect more than one boundary simultaneously by placing multiple initial contours, but the convergence speed will be slower than other segmentation methods.

The idea is to start with a closed curve and allows it to move perpendicular to itself at a prescribed speed, we describe this curve by using an explicit parametric form (as used in snakes), but it causes difficulties when the curves have to undergo splitting or merging. To address this difficulty during the evolution to the desired shape, the implicit active contour takes the original interface and embeds it in higher dimensional scalar function, defined over the entire image. The interface is represented implicitly as the zero-th level set (or contour) of this scalar function over the rest of the image space. This level set function is a signed distance function from the zero-th level set. This given a closed curve C0, if the pixel lies on the curve the function will be zero, otherwise, it’s the signed minimum distance from the pixel to the curve (the distance is negative for pixels inside C0 and positive for pixels outside C0). The function “Formula1” varies with time and space and is evolved using a partial differential equation (PDE) containing terms that are either hyperbolic or parabolic .

The evolution of our function can be written as:

Where F is the speed in the direct n normal to the curve, we consider the evolution of the function as it evolves in a direction normal to itself with a known speed F.

This speed F “Formula2” is composed of three terms, a term constant (similar to the force of inflation used in the deformable models), a term dependent on the curvature local at each point and a term dependent on the image (in our case, the edges of the image).

Where U_n is the function defining the area or object to be searched, K the local curvature at each, K₁ stopping criterion.

A key challenge in the level set is the placement of the initial contour. Since the contour moves either inward or outward, the segmentation obtained is dependent on the initial placement of the contour points. We start with an initial contour centered on the image, the sign of the called « balloon force » is changed to generate the necessary outward propagation of the initial contour. Then the signed distance function is calculated (the minimum distance from each pixel in the image to the prescribed initial contour). It is done by solving the Eikonal equation. The signed distance function can often lose the distance property. When the curve stops evolving near an edge and the zero level set is not exactly at the edge, the distance function is re-initialized.

3.4. Adaptive active contours

The technique of active contours [14] is based upon the utilization of deformable contours which conform to various object shapes and motions. Snakes provide an accurate location of the edges only if the initial contour is given sufficiently near the edges, because they only use the local information along the contour and estimating a proper position of initial contours without prior knowledge is a difficult problem. The adaptive active contour mixes two classical approaches of deformable models, deformable curves and classical active contours. In the deformable curves formulation, a curve is submitted to a deformation vector field and only the normal component of the deformation vector acts on the shape of the curve. This method, based on deformation along normals, makes the model attracted to the nearest edges found perpendicularly to the model, which in the case of infoldings are located inside cavities. As shown in the figure 7 the final displacement results from a compromise between the complete displacement towards the nearest contour along the normal and the satisfaction of the geometrical constraints incorporated into the internal energy. The snake is a list of points and each point is attracted towards the nearest edge along the normal of that point. The Canny-Deriche operator is used to detect the edges. Starting from the position of a point we search along the normal for the nearest pixel having a gradient magnitude above a specified threshold. Segmentation of an image by adaptive snake operates through energy functional controlling the deformation of an initial contour curve under the influence of internal and external forces achieving a minimum energy state at high-gradient locations. The energy functional for active contour models is expressed as:

The first two terms (α, β) control the rigidity and elasticity of the contour (defining the internal energy of the deformable object) while the last term attracts the model to high-gradient locations in the image (defining the external energy of the model). We denote by C (s) = (x (s), y (s)) (the arc length s ∈ [0, 1]) the current point of the contour C.

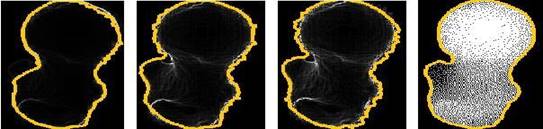
Fig. 7. Adaptive snake algorithm.

We define this snake model as closed 2D contour elements. We associate with these nodes time varying consisting of a set of nodes connected in series. We initialize the snake with a position and a shape that significantly differ from that of the structure of interest. Initially, regularization parameters are given high values to guarantee model smoothness and to capture the overall shape of the object, at each step, the average point displacement is calculated. If the displacement is stable or increasing the regularization parameters are decreased for the next iteration (its allows the snake to progressively enter small infoldings).

4. Experimental results

In this section we describe the results of our experiments of segmentation using the adaptive snake and level set methods, then, the segmentation results obtained will be compared with the results of our previous classic snake algorithm. We are interested in understanding what benefits are obtained by the level set and deformable curves approach. The performance analysis has been conducted on a standard PC with an Intel(R), 2.20GHz Processor, and 1GB RAM, in order to evaluate the quality of the proposed methods we have used about 82 real range images from the Stuttgart database. This database contains a collection of synthetic range images taken from high-resolution polygonal models available on the web. Six of these models (07_Deoflach, 08_Deorund, 15_Mole, 24_Kroete, 28_Ente, 29_Schwein) were reconstructed from real range scans in the Stuttgart lab (they can also be downloaded from http://range.informatik.uni-stuttgart.de/htdocs/html/). To illustrate the experimental results, we present a set of images and a Table. We differentiate between two categories of image (simple images and images with curvature). Fig.8 shows the segmentation results using the implicit active contour, the adaptive snake and level set approach on the simple images.

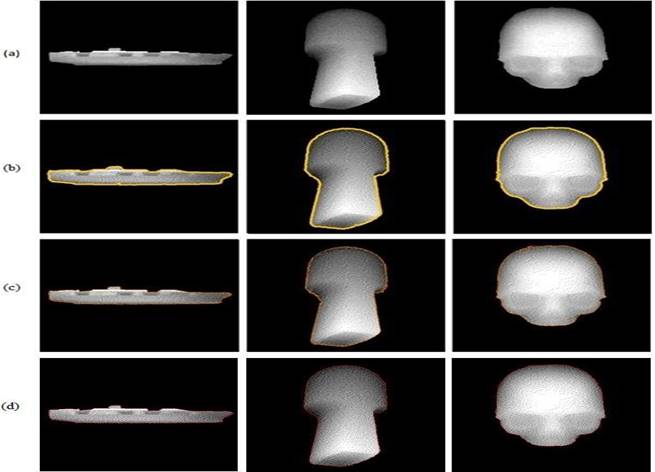
Fig. 8. Simple range image segmentation: (a) The range image. (b) Segmentation obtained by applying the classic snake algorithm. (c) Segmentation results using the Level Set method. (d) Segmentation obtained using adaptive snake algorithm.

As we can see in Fig.8 the classic snake algorithm and the adaptive snake offer a perfect segmentation for the simple images, however, the results of segmentations obtained for range images with cavities are not complete for the adaptive and classic snakes. The two snakes methods can’t segment very thin and complex structures such as the ones present in Fig.9 and does not enter into cavities. The limitations of edge-based energy terms are well-known. The models often either fail to lock on to weak edges, or become distracted from the feature of interest by stronger but less interesting edges.

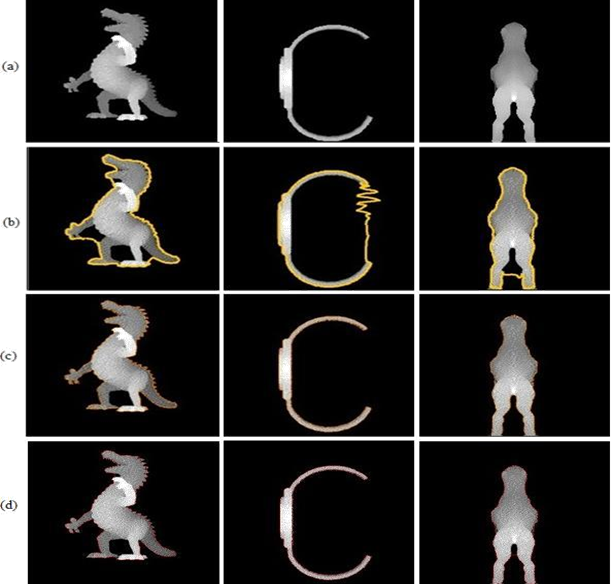
Fig. 9. Range image with curvature segmentation: (a) The range image. (b) Segmentation obtained using classic snake algorithm. (c) Segmentation results using Level Set method. (d) Segmentation obtained using adaptive snake algorithm.

Fig.9 shows the segmentation results using the implicit active contour and level set approach on the range images with cavity and as we can see the level set algorithm offers a better segmentation results than the classic snake and adaptive snake algorithms. In order to evaluate the three different segmentation methods, we have segmented the range images manually and developed a framework in C++ Builder that compares the contour point’s position obtained using the three methods with the position of the contour points in the reference segmentation. Then we calculate the percentage of pixels in right places. As we can see in the figure 10, the framework provides the sum of all misplaced pixels and the sum of all well placed pixels.

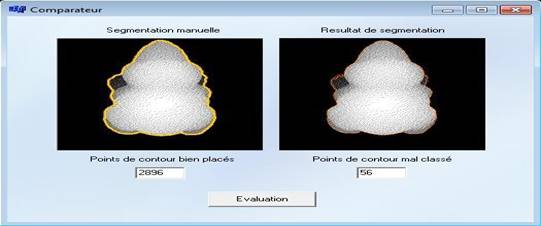
Fig. 10. Framework developed for the comparison.

This operation is repeated to the 82 test images and the overall result (average) is 96.01% of good detection for the level set algorithm and 95.17% for the adaptive active contour, however, the result of correct detection for the classic snake is 82.60 (which is considerably less than the results obtained by the two other approaches). We selected eight of these 82 result images where the gap is superior to 3% and as we can see, the result in Table1 confirms our visual comparison for the images with cavities. The worst result obtained by the level set algorithm is 'Pitt4’ with 92.17% of good detection. Unlike the classical snake that gives very bad results for images with cavities as can be seen in the images ‘Dinopet3’, 76.48% and 'Watch1' 54.55% which is a significant gap compared to the results obtained by the level set (respectively 96.16% and 97.05%) and the adaptive snake (respectively 94.67 % and 85.21 %).

Table 1. Percentage of good detection for Snake, level set and adaptive actives contours methods.

	Fighter5	Agfa3	Pitbull3	Manta2	Dinopet3	Watch1	Pitt4	Kroete2
Snake	98.57 %	99.19 %	80.74 %	89.96 %	76.48 %	54.55 %	76.16 %	85.18 %
Level set	95.12 %	95.18 %	98.07 %	97.44 %	96.16 %	97.05 %	92.17 %	95.01 %
Adaptive	94.24 %	98.70 %	92.36 %	96.05 %	94.67 %	85.21 %	81.21 %	97.89 %

The rate of good segmentation was calculated for the 82 segmented images and those of the three techniques (Level set, Adaptive and Snake Classic Snake). The overall result (on average) is 96.01% of correct detection for images segmented via the algorithm Level sets, followed by adaptive active contour algorithm "Fig.11" with a rate of 95 17% . The classical active contour algorithm offers 82, 60% of correct detection (which is much less than the results obtained by the two other approaches).

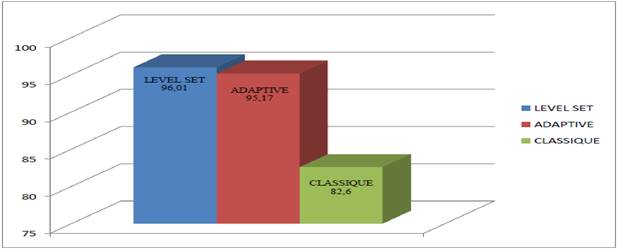
Fig. 11. Rate of good segmentation for each algorithm.

We then analyzed separately good segmentation rate for the simple images (without cavities) and complex images having cavities and those for the three applied algorithms. We note that for simple images, the traditional active contour provides very good results with 98% of good segmentation “Fig.12” more that the adaptive active contours and the level set respectively 94% and 96%. However, for images with deep cavities we note that Level set and the adaptive snake provides good segmentation results (96% and 95.69%) in contrast to classical snake “Fig.13” that accounts only 67% of good segmentation.

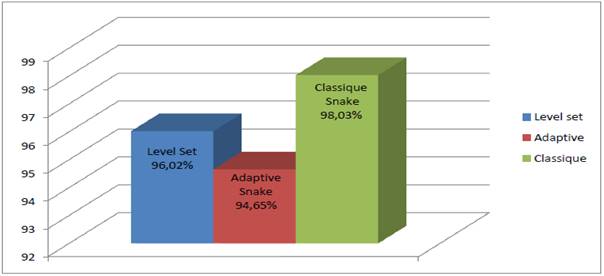
Fig. 12. Rate of good segmentation for the simple images.

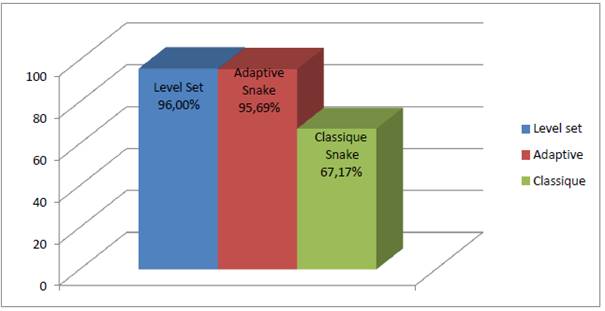
Fig. 13. Rate of good segmentation for the complex images.

5. Proposal for a multi-agent approach for range images segmentation

Traditional methods image segmentation using a sequential approach of treating the image after rangel rangel. However there are other approaches such as multi-agent systems that processed the image of a non-sequential manner. A multi-agent system consists of a number of agents that interact. An agent is able to perceive its environment, autonomously interacts with other agents, to learn from experience and adapt to its environment.

The method we propose in what follows is an extension of the traditional regions growing method where we introduced a multi-agent architecture to perform segmentation. In this architecture we have two types of agents:

· Control Agent: The controlling agent can be defined as a super agent, which will handle the creation and launch the execution of other agents.

· Growth Agents: Who will be the agents whose main task is the execution of the region growing. Their creation is requested by the controller.

An agent has a limited life, with a beginning and an end, it will be created at the beginning by the agent controller and can be also destroyed at any time. During its lifetime an agent will have three possible states, it will be "active" when it will execute the treatment he will be responsible, the agent can enter the status "Suspended" when it is waiting for information to be produced by another agent. When the agent is stopped in its treatment by the stop condition, he will be "Inactive".

5.1. Initialization process

First, there will be an initialization phase of the agents and their initialization in the range image. This selection process will be crucial, for it is all selected rangels depends potential choice of algorithm and generally what one might call the "field of vision" of the construction method. This initialization will be an automatic way and will be performed on the gradient image of the local minima while maintaining a certain distance between two agents for not too neighboring agents.

5.2. Segmentation process

During the second phase, "the implementation phase of segmentation", each agent moves in the image of the current point to that of its neighborhood. Each agent has a set of points (neighborhood) representatives to explore the next. Similarly, each agent also updates statistics on the already aggregated rangels enabling it to calculate the average at any time and the standard deviation of gray levels of owns rangels. The criterion chosen is one that favors rangels whose intensity is closest to the average. All Associate rangel is marked as belonging to the agent that the brand and it will thus become its owner.

5.3. Communication process

A marking conflict occur when an agent will realize that he wants to score a rangel who is already taken by another agent. In this case, the two agents must negotiate. We will have two modes of communication, indirect communication which is a communication signals via the environment and direct communication conducting an exchange of messages between agents. The first mode will be provided by the marking of rangel allowing an agent to know that rangel is already taken. Direct communication would be used in the negotiation phase of a dispute rangel. We will have three messages:

· A message "Discussion": It will be prepared and sent by any agent who wants to score a rangel. Any agent that wants to score a rangel must ensure that it is free. Otherwise it must negotiate with its current owner. He then has the responsibility to initiate the discussion. If an agent A wants to send a discussion message to an agent B which is the owner of rangel R which is the subject of the claim, it must ensure that (A-R) <(B-R). A is the value assigned to the agent A and B the value given to the agent B. Each message includes such information as a point representing the rangel to which the discussion the given value of the two agents, the reference, the sender agent of the request and the reference of the destination agent of the message.

· The message "Given Rangel": Following receipt of a discussion message, an agent must first check that it is the owner of rangel to which the discussion. If this is the case, it reassesses its value and compares it with that contained in the message. It must give rangel if its revalued amount is lower than that received in the message. In this case, it must also make updates to remove this rangel its aggregated rangels. He then has the responsibility to change the marking rangel considered by positioning the other agent as the new owner. Finally, to inform the other agent that he is the new owner of rangel, it must prepare and send a message of type "RangelDonné" so that it can consider this rangel as its own and continue his exploration by taking into account this fact. Any message of this type comprises information as the references of the transmitter and the receiver.

· The message "Free": This message is prepared and sent by any agent that receives a discussion message type and realizes that he is no longer the owner of rangel to which the discussion. This can happen for example if two agents A and B send a chat message to a third another agent on the same rangel. If this third agent processes the first message from A and bequeath his rangel, when processing the query B he will realize he is no longer the owner of rangel. As the message " Given Rangel " any type of message "Free" any message of this type comprises information as the references of the transmitter and the receiver.

Before integration rangel, the agent must verify that this is possible. If appropriate, the statistical data are updated. The value of rangel is evaluated and is rangel marked as belonging to the agent. One will then set the value of this threshold will limit the spread area of growth and will also ensure that the aggregated rangels end of growth are not bad. Generally, rangels won in the final moments of the region growing process among those who most helps to increase the standard deviation of the rangels in the region. An agent stops after five consecutive rangels yield which would mean that the area he represents can no longer increase "Fig.14". When all agents will stop, no increase will be possible and we will have the final segmentation.

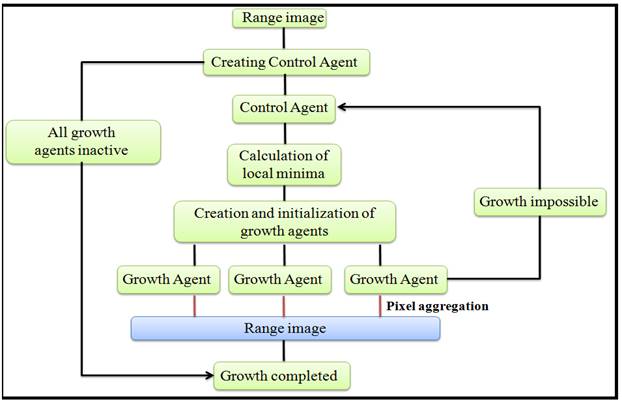
Fig. 14. A multi-agent approach for range images segmentation.

After implementation, the results of this approach could be compared with the multi-agent approach for range image segmentation proposed by Smain Mazouzi in [15]. Their approach consists in using a population of autonomous agents to segment a range image in its planar regions. The agents adapt to the regions on which they move, then perform cooperative and competitive actions allowing a collective segmentation of the image.

6. Conclusions

This paper considered the use of a deformable model for an important low-level computer vision problem, namely, range image segmentation. We have presented and compared two new methods for edge detection applied to range images based on deformable models. As mentioned in the introduction, the motivation of our work was to apply two deformable models (Snake) which never been done before in range segmentation. Despite the good experimental results on the simple object, the first method (adaptive snake) proposed in this paper has a few limitations and cannot detect discontinuities in curvatures. Adaptive active contours are very relevant to isolate regular convex shapes; however, they have some disadvantages. First, the function is not intrinsic and depends on the parameterization of the contour (choice of constants is difficult). The snake provides an accurate location of the edges only if the initial contour is given sufficiently near the edges because it uses only the local information along the contour (estimating a proper position of initial contours without prior knowledge is a difficult problem). The geometry of the object to be detected is not taken into account. Finally, minimization of its functional shows terms that require the calculation of derivatives of order 4, which poses problems discretization and numerical instabilities. We propose in this paper a multi-agent architecture for segmenting range images using the method of increasing regions. By their definition, the use of agents provides flexibility in the segmentation compared to sequential approaches. Indeed, distribute agents on the surface of an image can be beneficial. However, as a software agent acts autonomously component depending on the implementation of its behavior. In the future, we plan to extend this work by including the geodesic and geometric active contour to our work and evaluate them on real range images. We are also considering implementing the proposed segmentation (with multi-agent system) we could compare the results obtained with those of the deformable model.

References

1. Amine Khaldi, Hayet Merouani, An active contour for range image segmentation, Signal & Image Processing: An International Journal, Vol 03, No 03, pp 17–29, 2012

2. P. Merchan, A.S. Vaszquez, A. Adan, S. Salamanca, 3D scene analysis from a single range image through occlusion graphs, Pattern Recognition Letters, Vol 29, pp 1105–1116, 2008

3. Xiaoming Peng, Mohammed Bennamoun, Ajmal S.Mian, A training-free nose tip detection method from face range images, Pattern Recognition, Vol 44, No3, pp 544-558, 2011

4. Katsuaki Mishima, Tomohiro Yamada, Asuka Ohura, Toshio Sugahara, Production of a range image for facial motion analysis: A method for analyzing lip motion, Computerized Medical Imaging and Graphics, Vol 30, pp. 53–59, 2006

5. Sonya A. Coleman, Shanmugalingam Suganthan, Bryan W. Scotney, Gradient operators for feature extraction and characterization in range images, Pattern Recognition Letters, Vol 31, pp. 1028–1040, 2010

6. Jorge Hernández, Beatriz Marcotegui, Point cloud segmentation towards urban ground modeling, 5th workshop on remote sensing and data fusion over urban areas, Shangai, China, 2009.

7. Peter Kohlhepp, Daniel Fischer, Ekkehard Hoffmann, Intrinsic line features and contour metric for locating 3-D objects in sparse, segmented range images, Image and Vision Computing, Vol 17, pp. 403–417, 2009

8. Banno, T. Masuda, T. Oishi, K. Ikeuchi, Flying Laser Range Sensor for Large-Scale Site-Modeling and Its Applications in Bayon Digital Archival Project, International Journal of Computer Vision, Vol 78, pp. 207–222, 2008

9. Hansard Miles, Lee Seungkyu, Cho Ouk, Horaud Radu, Time-of-flight cameras: Principles, Methods and Applications. Springer Briefs in Computer Science, ISBN 978-1-4471-4657-5, 2012

10. Dong-Joong Kanga, Sung-Jo Lima, Jong-Eun Hab, Mun-Ho Jeongc, A detection cell using multiple points of a rotating triangle to find local planar regions from stereo depth data, Pattern Recognition Letters, Vol 30, No 5, pp 486–493, 2009

11. Qi Wang, Qi Li, Zhe Chen, Jianfeng Sun, Rui Yao, Range image noise suppression in laser imaging system, Optics & Laser Technology, Vol 41, pp.140– 147, 2009

12. Anuja Dagar, Archana, Deepak Nandal, High performance Computing Algorithm Applied in Floyd Steinberg Dithering, International Journal of Computer Applications, Vol 43– No.23, pp. 0975 – 8887, April 2012

13. Danping Peng, Barry Merriman, Stanley Osher, Hongkai Zhao and Myungjoo Kang, A PDE-Based Fast Local Level Set Method, Journal of Computational Physics, No 155, pp. 410–438, 1999

14. S.K. Weeratunga, C. Kamath, An Investigation of Implicit Active Contours for Scientific Image Segmentation, Visual Communications and Image Processing Conference, San Jose, CA, January 18-22, 2004.

15. S. Mazouzi, Z. Guessoum, F. Michel, M. Batouche, An Agent-Based Approach for Range Image Segmentation, International Conference on Autonomous Agents and Multiagent Systems, Honolulu, HI, USA, 2007