АЛГОРИТМЫ ИДЕНТИФИКАЦИИ ГРАНИЦЫ И ВИЗУАЛИЗАЦИЯ РЕШЕНИЯ ЗАДАЧИ ПЛАТО В СРЕДЕ BLENDER
Е.Г. Григорьева, А.А. Клячин, В.А. Клячин
Волгоградский государственный университет, Волгоград, Россия
e_grigoreva@volsu.ru, klyachin-aa@yandex.ru, klyachin.va@volsu.ru
Содержание
2. Идентификация граничных точек
4. Визуализация решения задачи Плато
5. Расчет и 3D-моделирование поверхностей минимальной площади с заданным перекрываемым объемом.
Аннотация
В настоящей работе рассматривается задача численного расчета и построения поверхности, имеющей минимально возможную площадь с заданным краем (задача Плато) и с возможно дополнительным ограничением в виде заданной величины объёма области, которую данная поверхность перекрывает. Подобные задачи известны из практики проектирования современных архитектурных сооружений, где в качестве покрытий или ограждений часто используются тонкие оболочки. Поэтому приходится обращаться к решению задачи: как при наименьшей площади оболочки покрыть объем, имеющий фиксированное или максимальное значение. В своей работе мы математически формулируем данную вариационную задачу и представляем алгоритм ее решения, использующий решения уравнения постоянной средней кривизны. В статье даётся описание программной реализации этого алгоритма, приводятся рисунки вычисленных поверхностей с различными расчётными областями и краевыми условиями. Точность вычислений в среднем составила 0.01%.
Для численного решения классической задачи Плато построена математическая модель, позволяющая свести задачу минимизации соответствующего функционала типа функционала площади к конечно мерному случаю. С целью визуализации строящихся решений рассматривается возможность конструирования граничных контуров непосредственно в среде моделирования Blender. При этом, в статье демонстрируются два алгоритма идентификации таких контуров для многогранной поверхности произвольного топологического строения. Реализация упомянутых алгоритмов в среде моделирования позволяет расчет поверхности с минимальным значением функционала выполнять в интерактивном режиме, а результат расчёта сохранять в любом удобном 3D формате. В настоящее время, встроенный модуль размещён в открытом доступе на сервере GitHub и включает в себя реализацию алгоритмов расчёта минимальных поверхностей, капиллярных поверхностей и поверхностей постоянной средней кривизны.
Ключевые слова: поверхность минимальной площади, пространственная триангуляция, кусочно-линейная поверхность, аппроксимация функционала площади, поверхность постоянной средней кривизны, капиллярная поверхность.
1. Введение
В практике проектирования современных сооружений в качестве покрытий или ограждений часто используются тонкие оболочки [10], [11]. В связи с этим актуальной является задача, как при наименьшей площади оболочки покрыть объем, имеющий фиксированное или максимальное значение. Решение ее позволяет минимизировать расход материала и вес оболочки при максимальной кубатуре сооружения. Как отмечено в работе [10], "природа конструирует в виде мыльной пленки единственно возможную при заданной внешней нагрузке равнонапряженную равновесную форму с фиксированным подоболочечным объемом и минимальной площадью поверхности. Относительные геометрические параметры форм поверхностей мыльных пленок могут быть приняты в качестве оптимальных параметров, которые следует учитывать при проектировании реальных пневмооболочек воздухоопорного типа". К тому же добавим, что минимальные поверхности сами по себе имею привлекательный внешний вид. Решение описанной задачи мы разбиваем на два основных случая: случай параметрических поверхностей произвольного топологического строения и случай непараметрических поверхностей, заданных графиком подходящей функции. В первом случае минимизацию функционала типа площади мы осуществляем с применением метода градиентного спуска в классе кусочно-линейных поверхностей с фиксированным краем, представляющем собой пространственную ломаную. Частным случаем решаемой задачи является классическая задача Плато [3],[4] для минимальных поверхностей. Топология искомой поверхности задается визуально посредством построения ее модели в 3D редакторе. Это требует решения задачи об определении граничных вершин, чтобы можно было построить граничную пространственную ломаную. В нашей работе мы описываем два алгоритма решения этой задачи. Минимизация функционалов для построения равновесных поверхностей иллюстрируется на примере классов минимальных поверхностей, поверхностей постоянной средней кривизны, тентовх и капиллярных поверхностей. Отметим ряд работ, посвященных программному моделированию минимальных поверхностей различного топологического строения [16], [17], [18].
Для графиков задача сводится к отысканию решений уравнения постоянной средней кривизны. Задача Дирихле для данного уравнения исследовалась многими математиками. Одними из первых работ, в которых были получены теоремы существования и единственности решений этой задачи, являются работы [14], [15]. Для поиска приближенных решений мы используем вариационный метод, предполагающий минимизацию некоторого интегрального функционала в классе кусочно-линейных функций. В своей статье мы описываем алгоритм и его программную реализацию расчета таких поверхностей на основе соответствующей математической модели.
В статье рассматривается задача построения поверхности, имеющей минимально возможную площадь при условии, что такая поверхность перекрывает объем фиксированного значения. Разработаны несколько программных модулей, позволяющих рассчитывать такие поверхности и обрабатывать полученные данные для построения ее трехмерной модели.
2. Идентификация граничных точек
При решении вычислительных задач в областях сложной формы
(например, в задачах расчета формы равновесных поверхностей [1],
[2]) инициализация краевых условий становится особенно трудоемкой, если
соответствующая вычислительная сетка имеет достаточно большое количество узлов.
Заметим, что моделирование таких областей и поверхностей не составляет большого
труда, если воспользоваться редактором геометрических моделей. В частности,
пакет Blender предоставляет возможность сконструировать модель расчетной
области и поверхности произвольной формы. Однако определение граничных вершин
модели возможно только для каждой компоненты связности границы в ручном режиме.
В настоящей статье мы представляем некоторые алгоритмы решения такой
задачи. Дадим ее формальное описание. Пусть ![]() -- произвольная многогранная
поверхность в трехмерном пространстве. Такая поверхность может быть определена
с помощью двух конечных множеств (массивов). Во-первых, это множество V
вершин поверхности M. Соответствующий массив имеет вид
-- произвольная многогранная
поверхность в трехмерном пространстве. Такая поверхность может быть определена
с помощью двух конечных множеств (массивов). Во-первых, это множество V
вершин поверхности M. Соответствующий массив имеет вид
![]()
Во-вторых, это множество T треугольных граней многогранной поверхности, которое может быть задано массивом, имеющим вид
![]()
В этом массиве числа являются номерами точек из массива V,
являющимися вершинами соответствующего треугольника. Задача ставится как задача
определения массива B номеров тех вершин из V, которые являются
граничными точками в смысле обычной топологии непрерывных поверхностей в![]() . Каждый
рассматриваемый нами алгоритм на первом своем шаге строит триангуляцию каждой
грани многогранной поверхности и вспомогательный массив NT вида
. Каждый
рассматриваемый нами алгоритм на первом своем шаге строит триангуляцию каждой
грани многогранной поверхности и вспомогательный массив NT вида
![]() ,
,
в котором NT[k] представляет собой массив номеров
треугольников из массива T, у которых точка V[k] является
вершиной. Другими словами, для каждой вершины ![]() находится список треугольников, инцидентных
данной вершине. Первый из рассматриваемых алгоритмов ведет подсчет числа f(k)
граней и числа e(k) ребер, инцидентных рассматриваемой вершине
находится список треугольников, инцидентных
данной вершине. Первый из рассматриваемых алгоритмов ведет подсчет числа f(k)
граней и числа e(k) ребер, инцидентных рассматриваемой вершине ![]() . Если через | |
обозначить мощность множества, то указанные величины определяются следующим
образом f(k)=|NT[k]|, e(k)=|E(k)|, где
. Если через | |
обозначить мощность множества, то указанные величины определяются следующим
образом f(k)=|NT[k]|, e(k)=|E(k)|, где ![]() . Тогда условие e(k)=f(k)
необходимо и достаточно для того, чтобы вершина
. Тогда условие e(k)=f(k)
необходимо и достаточно для того, чтобы вершина ![]() не была граничной. Второй алгоритм
основан на подсчете числа вхождений вершин в треугольники, инцидентные данной
вершине. С этой целью для каждой вершины
не была граничной. Второй алгоритм
основан на подсчете числа вхождений вершин в треугольники, инцидентные данной
вершине. С этой целью для каждой вершины ![]() строится совокупность (предполагается
множественность вхождения элементов)
строится совокупность (предполагается
множественность вхождения элементов)
![]()
Условие граничности точки, в этом случае, эквивалентно тому,
что, хотя бы один номер в ![]() будет уникальным.
будет уникальным.
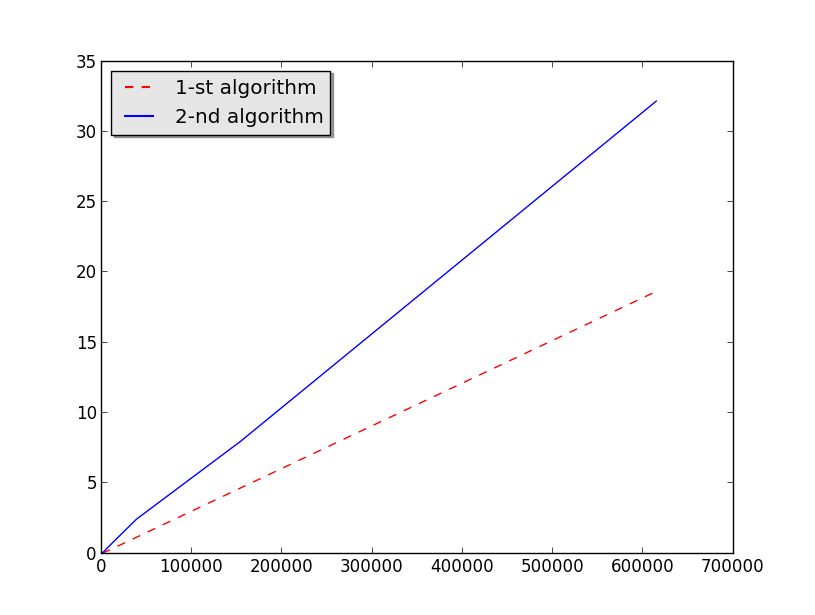
Рис. 1. Сравнение алгоритмов идентификации граничных точек.
Алгоритмы реализованы в виде встраиваемого модуля в программную среду Blender 2.77 на языке программирования Python 3. Данный модуль позволяет вычислить границу произвольной полигональной модели, расположенной в окне 3D вида, используя интерфейс, сгенерированный этим модулем и встроенный в среду программы Blender. Результат расчета можно сохранить в виде файла стандартного формата для пространственных моделей, который свою очередь может быть использован для инициализации краевых условий. На приведенном графике показаны экспериментальные данные времени выполнения реализаций, указанных выше алгоритмов. По горизонтальной оси отмечены количества граней рассматриваемых моделей, а по вертикальной оси -- время вычисления границы в секундах. Сравнение показывает, что первый алгоритм приблизительно в 1,5 раза выполняется быстрее второго.
Далее, мы демонстрируем использование полученного алгоритма в численном решении классической задачи Плато о поиске поверхности минимальной площади, затягивающий заданный контур в пространстве.
3. Задача Плато
Классической краевой задачей геометрии является так
называемая задача Плато. Эта задача заключается в построении поверхности
минимальной площади с заданным краем. В двумерном случае существование
решение задачи Плато было доказано Дугласом и Радо [3],[4].
Мы рассмотрим численное решение этой задачи методом градиентного спуска в
специальном построенном пространстве. Пусть как и выше многогранная поверхность
![]() задается
набором V точек и массивом треугольников T. По каждому целому N
и массиву T можно построить линейное пространство
задается
набором V точек и массивом треугольников T. По каждому целому N
и массиву T можно построить линейное пространство ![]() элементами которого будут
многогранные поверхности с N вершинами и гранями, определяемыми массивом
T. Операции сложения и умножения на число в
элементами которого будут
многогранные поверхности с N вершинами и гранями, определяемыми массивом
T. Операции сложения и умножения на число в ![]() вводятся естественным образом как
векторные операции над массивом точек V. При этом сохраняется массив T,
по которому определяются грани поверхности. Точки такого пространства будем
обозначать заглавной латинской буквой, а соответствующие вершины поверхности –
прописными
вводятся естественным образом как
векторные операции над массивом точек V. При этом сохраняется массив T,
по которому определяются грани поверхности. Точки такого пространства будем
обозначать заглавной латинской буквой, а соответствующие вершины поверхности –
прописными ![]() .
Обозначим через
.
Обозначим через ![]() множество
треугольников соответствующей многогранной поверхности. Рассмотрим функционал
множество
треугольников соответствующей многогранной поверхности. Рассмотрим функционал
![]() ,
,
где суммирование идет по всем треугольникам ![]() , а f(S) – некоторая
положительная функция на множестве всех треугольников. В работе [5]
рассматривался функционал, построенный по функции
, а f(S) – некоторая
положительная функция на множестве всех треугольников. В работе [5]
рассматривался функционал, построенный по функции ![]() , где
, где ![]() – положительная, однородная степени 1,
выпуклая вниз функция, а
– положительная, однородная степени 1,
выпуклая вниз функция, а ![]() – нормаль к плоскости треугольника
– нормаль к плоскости треугольника ![]() . При этом
предполагалось, что
. При этом
предполагалось, что ![]() , что означает независимость значения
функционала F от ориентации поверхности. Тем не менее, будем считать,
что рассматриваемые поверхности ориентированны. Для такого функционала в [5]
был вычислен градиент
, что означает независимость значения
функционала F от ориентации поверхности. Тем не менее, будем считать,
что рассматриваемые поверхности ориентированны. Для такого функционала в [5]
был вычислен градиент
![]() ,
,
где суммирование ведется по всем треугольникам S, инцидентным
вершине ![]() ,
, ![]() – вектор,
соединяющий вершины треугольника S, не совпадающие с вершиной
– вектор,
соединяющий вершины треугольника S, не совпадающие с вершиной ![]() . При этом обход
треугольников осуществляется в соответствии с положительной ориентацией
поверхности. Заметим, что вектор
. При этом обход
треугольников осуществляется в соответствии с положительной ориентацией
поверхности. Заметим, что вектор ![]() формально можно считать вектором пространства
формально можно считать вектором пространства ![]() . Поэтому для
отыскания минимума функционала F воспользуемся методом градиентного спуска.
Этот метод представляет собой итерационный процесс вида
. Поэтому для
отыскания минимума функционала F воспользуемся методом градиентного спуска.
Этот метод представляет собой итерационный процесс вида
![]() ,
,
где величина смещения ![]() может быть подобрана экспериментально. При этом
необходимо задать
может быть подобрана экспериментально. При этом
необходимо задать ![]() . Эта точка будет задавать начальную форму
поверхности, а в процессе вычислений ее край должен быть зафиксирован. Это
достигается за счет вычисления градиента
. Эта точка будет задавать начальную форму
поверхности, а в процессе вычислений ее край должен быть зафиксирован. Это
достигается за счет вычисления градиента ![]() по вышеприведенной формуле во всех точках, за
исключением граничных, в которых значение
по вышеприведенной формуле во всех точках, за
исключением граничных, в которых значение ![]() полагается равным нулю. В настоящей работе мы
рассматриваем случай
полагается равным нулю. В настоящей работе мы
рассматриваем случай ![]() , который соответствует кусочно-линейным
минимальным поверхностям. В таком случае
, который соответствует кусочно-линейным
минимальным поверхностям. В таком случае
![]() .
.
4. Визуализация решения задачи Плато
Для визуализации решения задачи Плато разработан
встраиваемый модуль в среду Blender 2.7. Этот модуль представляет собой пакет
состоящий из программных модулей на языке программирования Python. Структура
пакета включает в себя пять файлов. Файлы geometry.py и triangulation.py
содержат классы для вычисления геометрических характеристик треугольников и
кусочно-линейных поверхнстей в ![]() . В файле ndimvar.py релизован
обобщенный алгоритм градиентного спуска. Файл minsquare.py
содержит вычисления градиента функционала площади для кусочно-линейных
поверхностей в
. В файле ndimvar.py релизован
обобщенный алгоритм градиентного спуска. Файл minsquare.py
содержит вычисления градиента функционала площади для кусочно-линейных
поверхностей в ![]() .
Все классы геометрических данных основаны на массивах NumPy. Этот пакет стал
доступен в среде Blender, начиная с версии 2.7. Последний файл пакета
panel_addon.py реализует интерфейс для пользователя программы. Интерфейс
предлагает три функциональности:
.
Все классы геометрических данных основаны на массивах NumPy. Этот пакет стал
доступен в среде Blender, начиная с версии 2.7. Последний файл пакета
panel_addon.py реализует интерфейс для пользователя программы. Интерфейс
предлагает три функциональности:
1. Построение границы выделенного объекта в окне 3D вида.
2. Настройка числа итераций и шага ![]() метода градиентного спуска.
метода градиентного спуска.
3. Вычисление поверхности, полученной применением заданного количества итераций к выделенному объекту.
При этом в качестве контура в соответствующей задаче Плато выбирается граница этого выделенного объекта. Для использования пакета необходимо поместить файлы в каталог /scripts/addons в каталоге установки программы Blender. При очередной загрузке программы пакет будет добавлен в список доступных встраиваемых модулей, которые пользователь может увидеть через основное меню программы File->User Preference->Addons->3D View.
Рис. 2. Отображение информации о подключенном модуле в среде Blender.
После отметки данного модуля он становится доступным для использования через сконструированный интерфейс.
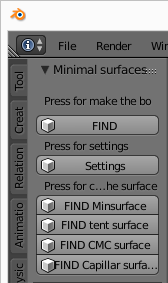
Рис. 3. Графический интерфейс предоставляемый встроенным модулем.
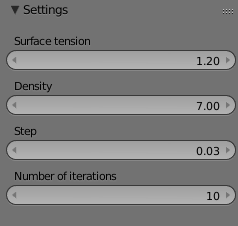
Рис. 4. Настройка параметров модуля.
В модуле реализованы алгоритмы расчета не только минимальных поверхностей, но и поверхностей с постоянной средней кривизной (Constant Mean Curvature surfaces), тентовых поверхностей (минимизирующих потенциальную энергию тяжелой упругой поверхности) и капиллярной поверхности. Для расчета пользовательский интерфейс встроенный в программу Blender позволяет определять такие параметры как плотность жидкой среды, ее коэффициент поверхностного натяжения, величину, определяющую шаг итерации градиентного спуска и число итераций алгоритма.
Ниже представлен результат работы поиска граничных ребер поверхности, смоделированной в окне 3D вида программы Blender.
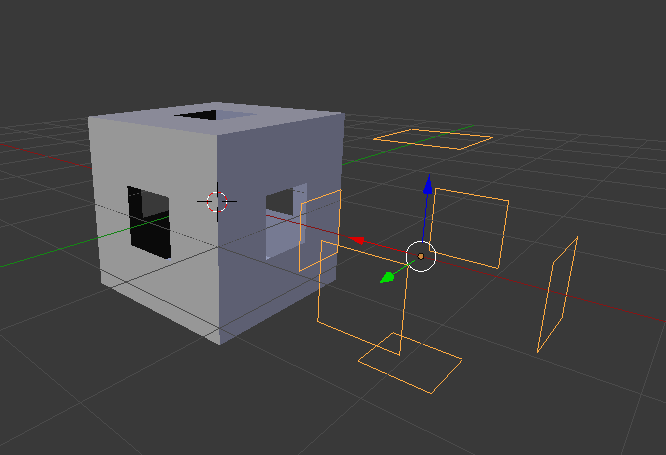
Рис. 5. Результат работы алгоритма идентификации границы.
Для решения вариационной задачи предварительно необходимо построить расчетную сетку на поверхности. Эту операцию можно выполнить в режиме редактирования с помощью инструмента Subdivide программы Blender. Триангуляция сетки так же выполняется стандартными средствами Blender с использованием модификатора Triangulation.
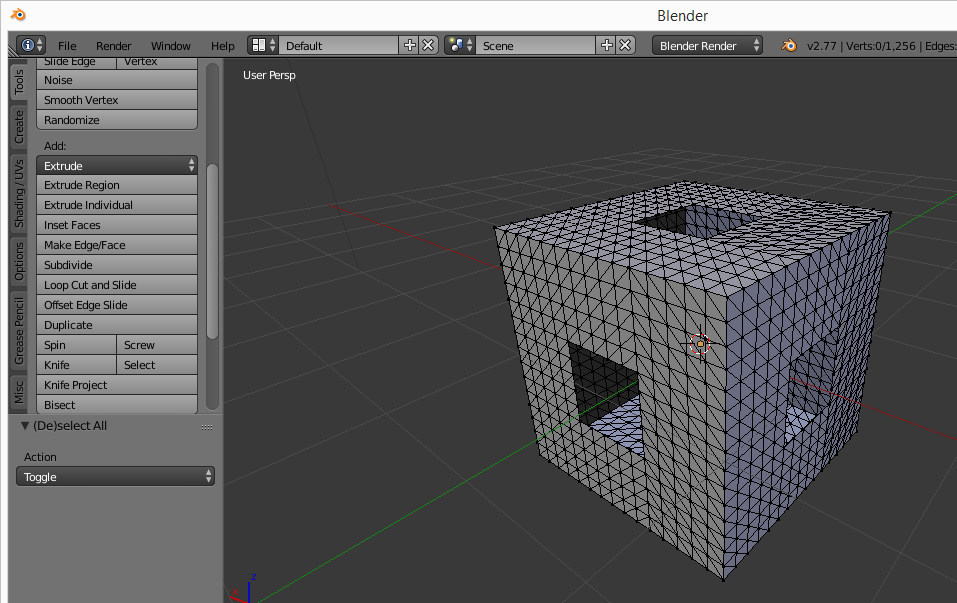
Рис. 6. Триангуляция поверхности модели.
Ниже представлена визуализация процесса минимизации площади поверхности методом градиентного спуска. Всего было выполнено750 итераций. Каждый GIF кадр создавался после 50 итераций. Из рисунка 7 видно, что итерационный процесс сглаживает углы куба, как точки выпуклости начальной поверхности. Этот факт согласуется с теоретическими выводами о, том, что каждая точка минимальной поверхности является седловой или гиперболической точкой с гауссовой кривизной K<0.

Рис. 7. Визуализация процесса градиентного спуска.
На следующей GIF анимации показана ситуация, когда цилиндр стягивается в отрезок, соединяющий центры двух окружностей, находящихся в двух параллельных плоскостях на достаточном расстоянии. Это объясняется тем, что соответствующая задача Плато в данном случае не имеет решения в классе поверхностей вращения. Теоретические обоснования данного эффекта даны в работах [6]--[9].

Рис. 8. Сохраняя топологический тип поверхности процесс минимизации стремится получить два диска.
Приведем еще несколько минимальные поверхностей с граничным контуром, имеющим сложное геометрическое строение и расчитанных с применением разработанного нами модуля. Следует отметить, что для получения устоявшейся формы поверхности было задействовано, как и выше, 750 итераций метода градиентного спуска.

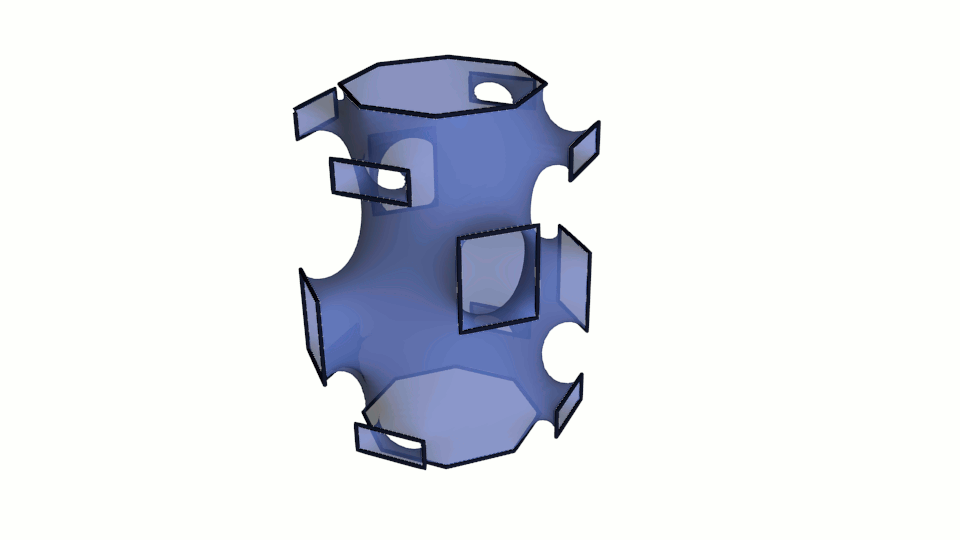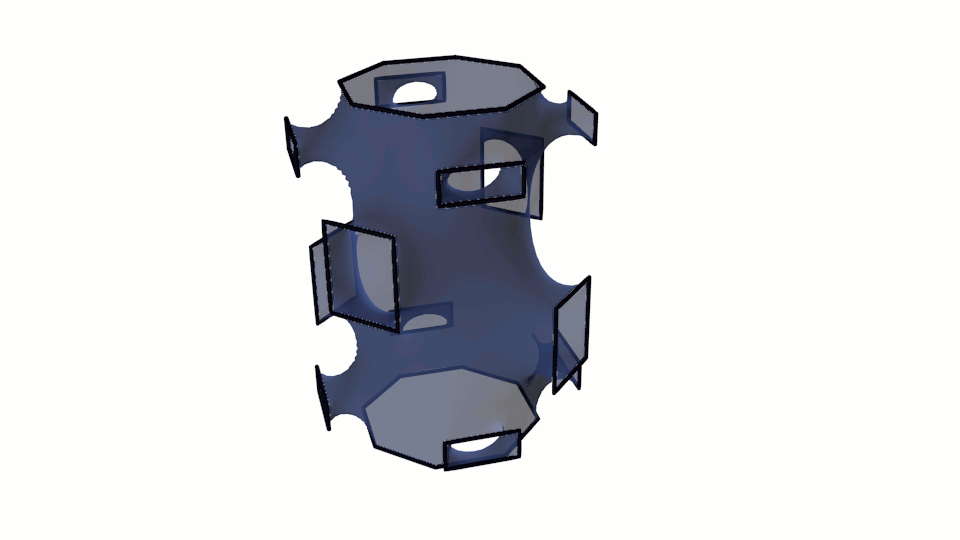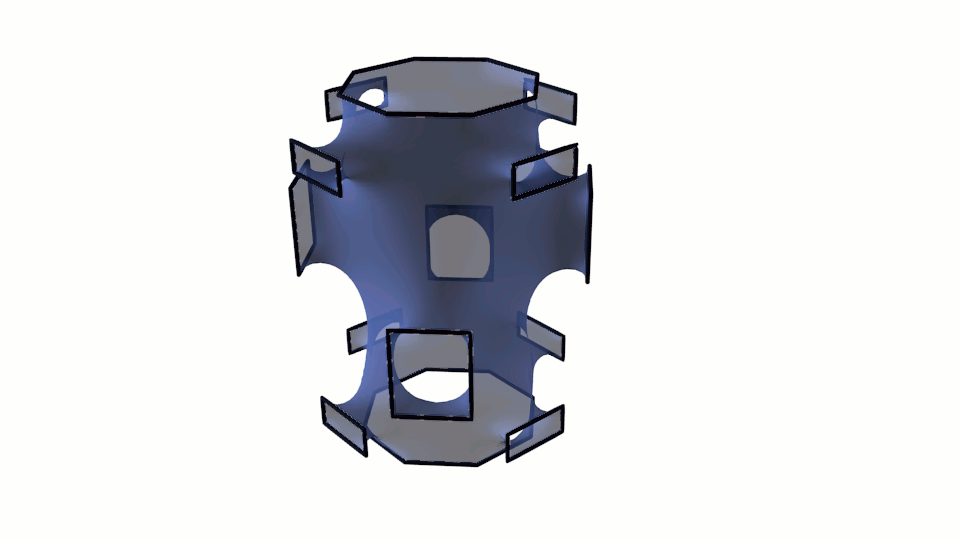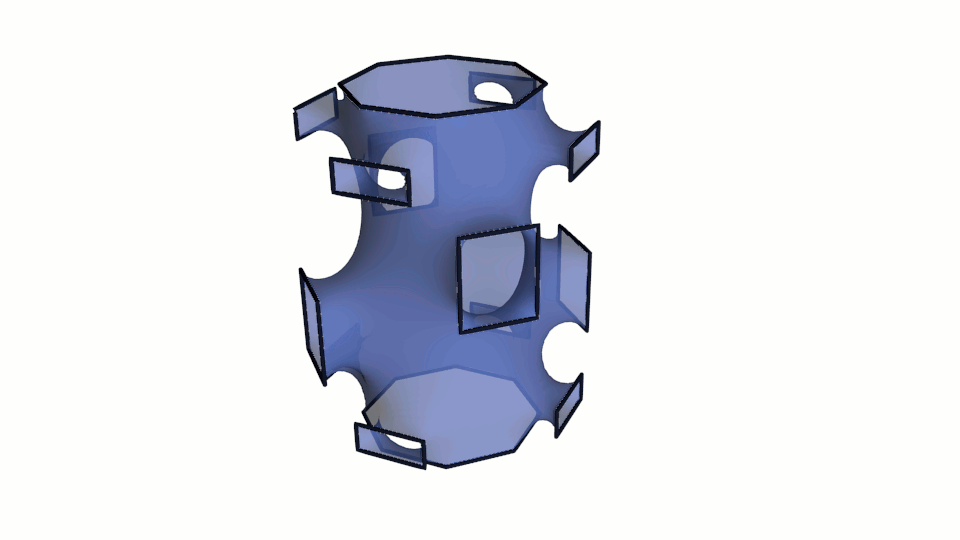
Рис. 9. Визуализация минимальных поверхностей расчитанных методом градиентного спуска.
Ниже на рисунке 10 приведена визуализация результата расчета почти периодических минимальных поверхностей. Первая модель получена с применением принципа симметрии, который позволяет распространить поверхность неограниченно во все пространство.


Рис. 10. Пример визуализации фрагмента периодических минимальных поверхностей.
Результат моделирования капиллярной поверхности представлен на следующей GIF анимации (см. рисунок 11). Здесь можно наблюдать процесс формирования формы капли жидкости в поле силы тяжести.

Рис. 11. Процесс моделирования капли.
Модуль, разработанный нами свободно доступен на сайте github.com по адресу:
https://github.com/KlyachinVA/MinimalSurface
Для его подключения в среду Blender необходимо скачать zip-архив c указанного адреса, и его содержимое распаковать в каталог scripts/addons/boundary в каталоге установки пакета Blender.
5. Расчет и 3D-моделирование поверхностей минимальной площади с заданным перекрываемым объемом.
В данном разделе статьи мы рассматриваем задачу отыскания
поверхности, имеющей минимально возможную площадь при заданном значении
перекрываемого ею объема. Математически обозначенная задача формулируется
следующим образом. Пусть на плоскости ![]() с декартовыми координатами
с декартовыми координатами ![]() задана ограниченная
область
задана ограниченная
область ![]() и
и ![]() – непрерывная функция, заданная в
замыкании этой области. Требуется для фиксированного положительного числа
– непрерывная функция, заданная в
замыкании этой области. Требуется для фиксированного положительного числа
![]() определить функцию
определить функцию ![]() , такую, что
, такую, что
при этом
В нашей работе мы эту задачу решаем в классе кусочно-линейных поверхностей, т. е. поверхностей, составленных из треугольников, примыкающих друг к другу. Известно, что решение данной вариационная задачи будет удовлетворять нелинейному дифференциальному уравнению с частными производными
с краевым условием
Постоянная величина H, которая равна средней кривизне графика f(x,y), определяется значением перекрываемого объема. Чаще всего найти точное решение данной краевой задачи не представляется возможным. В настоящей работе мы используем подход, предусматривающий построение приближенных решений уравнения (3) над произвольной областью с заданной в ней триангуляцией. Для расчета таких поверхностей и дальнейшей обработки полученных данных, нами была разработана вычислительная программа приближенного решения вариационных краевых задач для функционала общего вида
![]()
Для нашей задачи мы взяли ![]() . С ее помощью были рассчитаны поверхности
минимальной площади с заданным значением перекрываемого ими объема и с
различными краевыми условиями. Для построения поверхностей и их
изображения мы сохранили результаты вычислений в текстовом файле формата
STL и воспользовались программой Blender 2.67b. В настоящей работе
приводим изображения некоторых из построенных поверхностей. Отметим, что
разработанная программа позволяет находить приближенно нужную поверхность над
областью достаточно сложной формы. Это достигнуто за счет того, что
основным условием для проведения вычислений является наличие трех входных
файлов, которые содержат перечень вершин и треугольников триангуляции, а также
значения граничной функции. Этим достигается универсальность программы и
независимость ее от строения используемой расчетной сетки. Отметим, что в
работах [12],
аналогичным образом решалась задача построения минимальных поверхностей
без дополнительного условия на объем.
. С ее помощью были рассчитаны поверхности
минимальной площади с заданным значением перекрываемого ими объема и с
различными краевыми условиями. Для построения поверхностей и их
изображения мы сохранили результаты вычислений в текстовом файле формата
STL и воспользовались программой Blender 2.67b. В настоящей работе
приводим изображения некоторых из построенных поверхностей. Отметим, что
разработанная программа позволяет находить приближенно нужную поверхность над
областью достаточно сложной формы. Это достигнуто за счет того, что
основным условием для проведения вычислений является наличие трех входных
файлов, которые содержат перечень вершин и треугольников триангуляции, а также
значения граничной функции. Этим достигается универсальность программы и
независимость ее от строения используемой расчетной сетки. Отметим, что в
работах [12],
аналогичным образом решалась задача построения минимальных поверхностей
без дополнительного условия на объем.
Для решения задачи (1),
(2)
мы для заданного значения средней кривизны H решаем краевую задачу (3), (4).
Для этого мы используем вариационный метод для отыскания такой функции ![]() , на которой
достигает своего минимального значения функционал
, на которой
достигает своего минимального значения функционал
![]()
среди всех функций ![]() таких, что
таких, что ![]() Далее мы будем предполагать, что область
Далее мы будем предполагать, что область ![]() представляет
собой многоугольник на плоскости. Рассмотрим некоторое разбиение этого
многоугольника на невырожденные треугольники
представляет
собой многоугольник на плоскости. Рассмотрим некоторое разбиение этого
многоугольника на невырожденные треугольники ![]() . Пусть
. Пусть ![]() -- все вершины этих треугольников. Будем
предполагать, что ни одна из точек
-- все вершины этих треугольников. Будем
предполагать, что ни одна из точек ![]() не является внутренней точкой ни одной стороны
треугольников. Данную конструкцию будем называть триангуляцией области
не является внутренней точкой ни одной стороны
треугольников. Данную конструкцию будем называть триангуляцией области ![]() и обозначать
и обозначать
![]() . Далее
будем мелкостью разбиения называть величину
. Далее
будем мелкостью разбиения называть величину ![]()
Для произвольного набора числовых значений ![]() определим кусочно --
линейную функцию
определим кусочно --
линейную функцию ![]() так, что
так, что ![]() и функция
и функция ![]() на каждом треугольнике
на каждом треугольнике ![]() . Данная функция будет непрерывной
в
. Данная функция будет непрерывной
в ![]() и в каждом треугольнике
и в каждом треугольнике ![]() определен ее градиент
определен ее градиент ![]() . Поэтому можно вычислит
значение функционала
. Поэтому можно вычислит
значение функционала ![]() для кусочно-линейной функции
для кусочно-линейной функции ![]()
![]()
где ![]() -- площадь треугольника
-- площадь треугольника ![]() и
и ![]() -- среднее арифметическое значений функции
-- среднее арифметическое значений функции
![]() в вершинах
треугольника
в вершинах
треугольника ![]() . Значения переменных
. Значения переменных ![]() выражаются линейно через
переменные
выражаются линейно через
переменные ![]() .
Тогда найдутся такие числа
.
Тогда найдутся такие числа ![]() и
и ![]() , что
, что
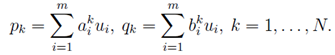
Коэффициенты ![]() и
и ![]() однозначно определяются разбиением области
однозначно определяются разбиением области ![]() на
треугольники
на
треугольники ![]() .
Поэтому
.
Поэтому
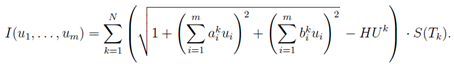
Поставим задачу нахождения такой кусочно-линейной
функции ![]() ,
на которой достигается минимум функционала
,
на которой достигается минимум функционала ![]() , т. е. задачу
, т. е. задачу
![]()
где минимум ищется среди всех наборов ![]() , для которых
, для которых ![]() .
.
Для решения задачи (3)
- (4)
мы воспользовались простым градиентным методом для поиска точек минимума
функций конечного числа переменных. Для этого нами разработана основная
процедура минимизации minimum_func_mix() и несколько вспомогательных, нужных
для подготовки расчетов. Кратко опишем их работу. Отметим вначале, что
координаты узлов триангуляции ![]() хранятся в отдельном файле, имеющем простую
структуру: первые 8 байт отводятся под количество этих точек, а дальше каждая
точка занимает 20 байт - две координаты по 8 байт и информация о принадлежности
границе и типе граничного условия (еще 4 байта). Отметим также, что в функции
minimum_func_mix() реализована возможность задания как краевых условий Дирихле,
т. е. значений искомого решения на границе области, так и смешанных
краевых условий, содержащих условия на производные этого решения. Вот в
этих 4-х байтах мы указываем тип точки: 0 -- внутренняя точка области
хранятся в отдельном файле, имеющем простую
структуру: первые 8 байт отводятся под количество этих точек, а дальше каждая
точка занимает 20 байт - две координаты по 8 байт и информация о принадлежности
границе и типе граничного условия (еще 4 байта). Отметим также, что в функции
minimum_func_mix() реализована возможность задания как краевых условий Дирихле,
т. е. значений искомого решения на границе области, так и смешанных
краевых условий, содержащих условия на производные этого решения. Вот в
этих 4-х байтах мы указываем тип точки: 0 -- внутренняя точка области ![]() , 1 --
граничная точка с условием Дирихле, 2 -- граничная точка, в которой задается
условие на производные решения.
, 1 --
граничная точка с условием Дирихле, 2 -- граничная точка, в которой задается
условие на производные решения.
Треугольники используемой триангуляции также включаются в отдельный файл, который устроен похожим образом: вначале 8 байт отводится под общее число треугольников, затем идут номера точек, составляющих описываемый треугольник. Таким образом на каждый треугольник мы отводим 24 байта (три номера точек по 8 байт).
Как было сказано выше, мы решаем задачу в классе
кусочно-линейных функций. Любая такая функция, определенная над областью ![]() однозначно
определяется значениями ее в узлах триангуляции. Поэтому кусочно-линейную
функцию мы храним в файлах, в которых первые 8 байт заняты под количество точек
триангуляции, а далее последовательно идут значения функции в соответствующих
вершинах.
однозначно
определяется значениями ее в узлах триангуляции. Поэтому кусочно-линейную
функцию мы храним в файлах, в которых первые 8 байт заняты под количество точек
триангуляции, а далее последовательно идут значения функции в соответствующих
вершинах.
Градиентный метод предполагает вычисление производных ![]() для тех значений индекса i, для
которых точка
для тех значений индекса i, для
которых точка ![]() является внутренней для области
является внутренней для области ![]() . Тогда понятно,
что после дифференцирования выражения I по
. Тогда понятно,
что после дифференцирования выражения I по ![]() в соответствующей сумме
остаются слагаемые только по тем треугольникам, которые содержат точку
в соответствующей сумме
остаются слагаемые только по тем треугольникам, которые содержат точку ![]() в качестве своей
вершины. Поэтому, для повышения скорости работы программы, мы создаем
структуру, в которой для каждого узла триангуляции заносится набор таких
соседних для этой точки треугольников.
в качестве своей
вершины. Поэтому, для повышения скорости работы программы, мы создаем
структуру, в которой для каждого узла триангуляции заносится набор таких
соседних для этой точки треугольников.
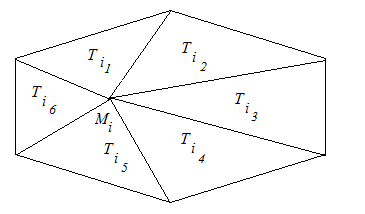
Рис. 12. Соседние треугольники для вершины ![]()
Тогда, после вполне естественных преобразований,
вычислительная схема будет выглядеть так. Если индексом ![]() будем обозначать номер
итерации, то на шаге
будем обозначать номер
итерации, то на шаге ![]() значения во внутренних узлах
значения во внутренних узлах ![]() триангуляции пересчитываются
по формуле
триангуляции пересчитываются
по формуле
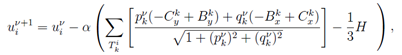
где суммирование берется по треугольникам ![]() , у которых точка
, у которых точка ![]() является вершиной,
а
является вершиной,
а ![]() и
и ![]() две другие точки
треугольника
две другие точки
треугольника ![]() ,
, ![]() -- шаг градиентного спуска.
-- шаг градиентного спуска.
Таким образом мы для каждого значения H находим
приближенное решение краевой задачи (3), (4)
в виде значений ![]() в
узла триангуляции
в
узла триангуляции ![]() . Эти значения однозначно определяют
кусочно-линейную функцию
. Эти значения однозначно определяют
кусочно-линейную функцию ![]() . Если теперь вычислить интеграл
. Если теперь вычислить интеграл
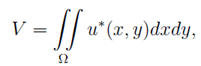
то будет определена непрерывная функция V=V(H). Для
решения исходной задачи (1)-(2)
при заданном ![]() достаточно найти
такое
достаточно найти
такое![]() , что
, что ![]() . Для этого будем
действовать по следующему алгоритму:
. Для этого будем
действовать по следующему алгоритму:
1) находим отрезок ![]() такой, что число
такой, что число ![]() попадает между значениями
попадает между значениями ![]() и
и ![]() ;
;
2) пусть ![]() . Тогда, если
. Тогда, если ![]() , то рассматриваем отрезок
, то рассматриваем отрезок ![]() и далее полагаем
и далее полагаем ![]() . Если
. Если![]() , то рассматриваем
отрезок
, то рассматриваем
отрезок ![]() и далее
полагаем
и далее
полагаем ![]() . Если
же
. Если
же ![]() , то искомая
точка нашлась и мы полагаем
, то искомая
точка нашлась и мы полагаем ![]() ;
;
3) далее действуем в соответствии с методом деления отрезка
пополам, повторяя шаг 2), и с необходимой точностью находим ![]() .
.
Результатами вычисления являются найденные приближенные
значения ![]() ,
соответствующие точке минимума функции I. Эти значения заносятся в
отдельный файл, описание которого мы дали выше. Нами написана также процедура
окончательной обработки результатов вычисления, которая преобразует их в
два типа файлов. Один из них текстовый файл, каждая строка которого
хранит трехмерные координаты одной точки модели. Три подряд идущие
строки задают один треугольник в триангуляции поверхности. Другой файл
является файлом стандартного формата 3D графики stl для хранения такой
поверхности.
,
соответствующие точке минимума функции I. Эти значения заносятся в
отдельный файл, описание которого мы дали выше. Нами написана также процедура
окончательной обработки результатов вычисления, которая преобразует их в
два типа файлов. Один из них текстовый файл, каждая строка которого
хранит трехмерные координаты одной точки модели. Три подряд идущие
строки задают один треугольник в триангуляции поверхности. Другой файл
является файлом стандартного формата 3D графики stl для хранения такой
поверхности.
В начале мы провели проверку точности расчета на примере построения кругового цилиндра над прямоугольной областью. Известно, что такая поверхность имеет постоянную среднюю кривизну, равную обратной величине радиуса основания цилиндра. Поэтому, зная это точное решение, не сложно оценить степень погрешности расчетов.

Рис. 13. Цилиндрическая поверхность.
Для 2500 узлов триангуляции точность вычислений оказалась
порядка 0,1%. Отметим, что сходимость применяемого метода была ранее
изучена в работах [2],
[12]
и для уравнения минимальной поверхности и уравнения равновесной
капиллярной поверхности. Для уравнения постоянной средней кривизны,
которое мы используем для расчета наших поверхностей, теми же методами можно
доказать аналогичное свойство сходимости.
Далее проводилась серия экспериментов с различными значениями величины H
и граничными функциями ![]() . Например, чтобы проследить как меняется форма
поверхности в зависимости от средней кривизны, а значит и перекрываемого
объема, расчеты были сделаны для следующих значений H: от 0 до 1.9 с
шагом 0.1. Изображение четырех из получившихся поверхностей приводим на рисунке
11.
. Например, чтобы проследить как меняется форма
поверхности в зависимости от средней кривизны, а значит и перекрываемого
объема, расчеты были сделаны для следующих значений H: от 0 до 1.9 с
шагом 0.1. Изображение четырех из получившихся поверхностей приводим на рисунке
11.

Рис. 14. Динамика изменения формы поверхности, в зависимости от значения средней кривизны.
На следующих рисунках мы поместили изображения некоторых из рассчитанных поверхностей над прямоугольной и восьмиугольной областями. Для них использовалась триангуляция, описание и исследование качества которой дано в работе [13].

Рис. 15. Поверхность с параболическим граничным каркасом над прямоугольной областью (H=1.0).

Рис. 16. Поверхность, построенная над восьмиугольником.
6. Заключение
В настящей работе рассматривалась задача расчета и построения поверхности, имеющей минимально возможную площадь с заданным краем и значением объема области, которую данная поверхность перекрывает и другие похожие задачи. Математически сформулирована данная вариационная задача и представлен алгоритм ее решения, использующий решения уравнения постоянной средней кривизны для случая поверхностей заданных графиком функции и метод градиентного спуска для параметрических поверхностей произвольного топологического строения в классе кусочно-линейных поверхностей. В результате получен модуль на языке программирования Python, который встраивается в среду 3D моделирования Blender. Этот модуль позволяет в интерактивном режиме задавать краевые условия для решения задачи Плато и задавать топологический тип искомой поверхности, а также осуществлять расчет поверхности и ее визуализацию непосредственно в окне 3D вида программы Blender. Результат расчета в виде полигональной поверхности можно сохранить в виде 3D модели в одном из стандартных форматов файлов векторной 3D графики.
Кроме этого, в статье дается описание программной реализации алгоритма расчета поверхностей минимизирующих функционал типа пощади в классе поверхностей, заданных графиком функции, приводятся рисунки вычисленных поверхностей с различными расчетыми областями и краевыми условиями. Точность вычислений в среднем составила 0.01%.
Работа поддержана грантом РФФИ № 15-41-02517
Список литературы
[1] Клячин А.А., Клячин В.А., Григорьева Е.Г. Визуализация расчета формы поверхностей минимальной площади. Научная визуализация. 2014, Т.6, №2. с. 34-42.
[2] Клячин А.А. О равномерной сходимости кусочно-линейных решений уравнения равновесной капиллярной поверхности. Сиб. журн. индустр. матем., 18:2 (2015), c. 52–62.
[3] Douglas J. Solution of the problem of Plateau. Trans. Amer. Math. Soc. 33 (1931), p. 263-321.
[4] Radó T. On Plateau's problem. The Annals of Mathematics, Vol. 31, No. 3 p. 457–469.
[5] Клячин А.А., Клячин В.А., Григорьева Е.Г. Визуализация устойчивости и расчета формы равновесной капиллярной поверхности. Научная визуализация. 2016, Т.8, №2. с. 37-52.
[6] Веденяпин А. Д., Миклюков В. М. Внешние размеры трубчатых минимальных гиперповерхностей. Матем. сб., 131(173):2(10) (1986), с. 240–250.
[7] Миклюков В. М., Ткачëв В. Г., Некоторые свойства трубчатых минимальных поверхностей произвольной коразмерности. Матем. сб., 180:9 (1989), 1278–1295.
[8] Ткачëв В. Г. Теорема о радиусе просвета для минимальных поверхностей. Матем. заметки, 59:6 (1996).
[9] Клячин В. А. Оценка протяженности трубчатых минимальных поверхностей произвольной коразмерности. Сиб. мат. ж. Т. 33. 1992. N. 5. С.~201–206.
[10] Михайленко В.Е., Ковалев С.Н., Конструирование форм современных архитектурных сооружений. Киев:Будiвельник, 1978. 138 с.
[11] Абдюшев А.А., Мифтахутдинов И.Х., Осипов П.П. Проектирование непологих оболочек минимальной поверхности. Известия КазГАСУ, Строительные конструкции, здания и сооружения, 2009, № 2 (12).
[12] Гацунаев М.А., Клячин А.А. О равномерной сходимости кусочно-линейных решений уравнения минимальной поверхности. Уфимский математический журнал. Том 6, № 3 (2014), с. 3-16.
[13] Клячин А.А. Равномерная триангуляция плоских областей. Вестник ВолГУ. Серия 1, Мат Физ. 2011. №2(15). 7 с.
[14] Serrin J. Gradient estimates for solutions of nonlinear elliptic differential equations. Acta Math., 1964, V. 111, p. 247-302.
[15] Giaquinta M. On the Dirichlet problem for surfaces of prescribed mean curvature. Manuscripta Math., 1974, V. 12, p. 73-86.
[16] Капустина Т.В. Минимальные поверхности в среде Mathematica. Международная научно-практическая конференция "Информационные технологии в образовании и науке - ИТОН-2014", IV Международный научный семинар по математическому моделированию в системах компьютерной математики -KAZCAS-2014" - материалы конференции и труды семинара. - Казань: Фолиант, 2014. - C. 216-219.
[17] Бельченко Ю.М., Шумун Н.М. Моделирование 3-ткани для минимальных поверхностей. Инженерный Вестник Дона. 2015. №4-1 С. 127.
[18] Киселев А.В. О минимальных поверхностях, связанных с неполиномиальными контактными симметриями. Фундаментальная и прикладная математика, 2006, том 12, № 7, с. 93—100.
BOUNDARY IDENTIFICATION ALGORITHMS AND VISUALIZATION OF THE SOLUTION OF THE PLATEAU PROBLEM IN A BLENDER ENVIRONMENT
E.G. Grigorieva, A.A. Klyachin, V.A. Klyachin
Volgograd State University, Volgograd, Russia
e_grigoreva@volsu.ru, klyachin-aa@yandex.ru, klyachin.va@volsu.ru
Abstract
In this paper we consider the calculation and construction of the surface having the lowest possible area with the specified edge and the value of the volume of domain that covers this surface. This problem is known from the practice of modern design constructions in which thin shell are often used as coatings or protections. Therefore, one has to solve the problem: How to cover the volume, having a fixed or maximum value, for the minimum area of the its surface. In our work we mathematically formulate this variational problem and present a solution algorithm, using the solutions of the equation of constant mean curvature. The article gives a description of the software implementation of this algorithm, the images calculated surfaces with different computational domain and the boundary conditions. Accuracy of calculations on the average was 0.01%.
For the numerical solution of the classical Plateau problem it was built a mathematical model that allows to reduce the problem of minimizing the corresponding functional of the functional area type to the finite-dimensional case. In order to visualize resulting solutions, we consider the possibility of constructing the boundary contours directly in Blender modeling environment. At the same time, the article demonstrates two algorithms for the identification of such circuits for multi-faceted surfaces of an arbitrary topological structure. The implementation of the mentioned algorithms in the simulation environment allows us to calculate of the surface with a minimum value of the functional in interactive mode, and the calculation results are stored in a convenient 3D format. Currently, the built-in module is placed in the public domain on GitHub server and includes the implementation of algorithms for the calculation of minimal surfaces, the capillary surfaces and surfaces of constant mean curvature.
Keywords: surface of minimal area, space triangulation, piecewise linear surface, approximation of the area functional, constant mean curvature surface, capillar surface.
References
[1]Klyachin A.A., Klyachin V.A., Grigorieva E.G., Visulization of calculation of minimal area surfaces. Scientific visualization. Electronic Journal . 2014,V .6, N 2, pp. 34-42.
[2] Klyachin A.A. On the uniform covergence of piecewise linear solutions of an equilibrium capillary surface equation. Journal of Applied and Industrial Mathematics, 2015, 9(3), pp. 381-391
[3] Douglas J. Solution of the problem of Plateau. Trans. Amer. Math. Soc. 33 (1931), p. 263-321.
[4] Radó T. On Plateau's problem. The Annals of Mathematics, Vol. 31, No. 3 p. 457–469.
[5] Klyachin A.A., Klyachin V.A., Grigorieva E.G. Visualization of stability and calculation of the shape of the capillary equilibrium surface. Scientific visualization. Electronic Journal . 2016, V.8, №2. pp. 37-52.
[6] Vedenyapin A. D., Miklyukov V.M. Extrinsic dimensions of tubular minimal hypersurfaces. Math. USSR-Sb., V.59, №1 (1988) , p.237-245.
[7] Miklyukov V. M., Tkachev V. G. Some properties of the tubular minimal surfaces of arbitrary codimension. Math. USSR-Sb, 68:1(1991), p.133-150 .
[8] Tkachev V. G. On the bore radius for minimal surfaces. Math. Notes, 59:6 (1996), p.657-660.
[9] Klyachin V. A. An estimation of spread for tubular minimal surfaces of arbitrary codimension. Sib. Math. J. V. 33. 1992. N. 5. p.~201–206.
[10] Mikhaylenko V.E., Kovalev S.N. Designing forms of modern architecture.Kiev Budivelnik, 1978. 138 .
[11] Abdyushev A.A., Miftahutdinov I.H., Osipov P.P.Design of shallow shells of minimal surface. News KSUAE, Building construction, building, 2009, N2 (12).
[12] Gatsunaev M. A., Klyachin A.A.On uniform convergence of piecewise linear solutions to minimal surface. Ufa Mathematical Journal. V. 6, N3 (2014), pp. 3-16.
[13] Klyachin A.A. Uniform triangulation of planar domains . Science Journal of VolSU. Mathematics. Phisics. 2011.N2(15).
[14] Serrin J. Gradient estimates for solutions of nonlinear elliptic differential equations. Acta Math., 1964, V.111, p. 247-302.
[15] Giaquinta M. On the Dirichlet problem for surfaces of prescribed mean curvature. Manuscripta Math., 1974, V.12, p. 73-86.
[16] Kapustina T.V. Minimal surfaces in Mathematica enviroment. International scientific-practical conference "Information Technologies in Education and Science-ITON 2014", IV International sciemtific seminar on mathematical modeling in systems of computer mathematics -"KAZCAS-2014"-conference materials and works of the seminar-Kazan. "Foliant", 2014.-P.216-219.
[17] Belchenko Yu. M., Shumun N.M. Simulation of 3-tissue for minimal surfaces. Ingenernyi Vestnik Dona. 2015. N 4-1, p.127.
[18] Kiselev A.V. Minimal surfaces associated with nonpolynomial contact symmetries. Fundamentalnaya i Prikladnaya Matematika, 2006, V. 12, N 7, p. 93-100.
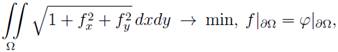 (1)
(1)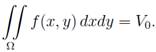 (2)
(2)