ПОВЫШЕНИЕ КАЧЕСТВА ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЯ ПРИ ОБРАТНОМ ПРЕОБРАЗОВАНИИ РАДОНА

К.Я. Кудрявцев

Национальный исследовательский ядерный университет «МИФИ», Россия

Содержание

1. Введение

2. Основные соотношения

2.1. Описание алгоритма

2.2. Алгоритм увеличения размерности матрицы преобразования Радона.

3. Оценка эффективности

4. Заключение

Список литературы

Приложение. Скрипт вычисления аппроксимационной матрицы преобразования Радона

Аннотация

Построение изображения внутреннего содержимого объекта без его физического разрушения, применяемое в медицине, металлургии, кристаллографии основано на просвечивании его рентгеновским излучением с последующей математической обработкой полученных данных. При просвечивании объекта интенсивность луча на выходе равна интегралу функции распределения плотности вещества вдоль траектории луча. Регистрируя излучение, выполняемое под различными углами, получают исходные данные, используемые для восстановления изображения. Данные представляются в виде матрицы, каждый элемент которой является результатом вычисления интеграла вдоль заданной прямой. Чем больше размерность матрицы, т.е. чем больше имеется экспериментальных данных, тем точнее будет восстановлено изображение. Однако количество экспериментов часто бывает ограничено медицинскими, техническими, экономическими и др. причинами. В качестве математического аппарата для восстановления изображения поперечного сечения объекта используется прямое и обратное преобразование Радона. В данной работе предлагается алгоритм повышение качества восстановления изображения из матрицы преобразования Радона путем добавления дополнительных столбцов содержащих преобразование Радона в промежуточных углах поворота, вычисленных по выведенным формулам аппроксимации. Двукратное увеличение количества столбцов матрицы интегрального преобразования Радона позволяет значительно повысить качество восстановления изображения при обратном преобразовании Радона.

Ключевые слова: интегральное преобразование Радона, обратное преобразование Радона, восстановление изображения.

1. Введение

При просвечивании объекта интенсивность луча на выходе зависит от плотности исследуемого объекта и равна интегралу функции распределения плотности вещества вдоль траектории луча. Регистрируемое излучение (радоновский образ или проекция), измеренное для набора параллельных лучей при различных углах поворота, представляется в виде матрицы размерности , каждый столбец которой соответствуе определнному углу поворота, а количество строк определяется количеством излучателей-детекторов. Собственно, восстановление изображения осуществляется с помощью операции обратного преобразования Радона (метода обратной проекции [5]), исходными данными для которого выступают значения матрицы .

Чем больше размерность матрицы , т.е. чем более подробно проведено сканирование объекта, тем точнее будет восстановлено изображение. Однако обеспечение высокой размерности матрицы сопряжено с рядом технических, медицинских и экономических ограничений. Поэтому желательно иметь алгоритмический метод вычисления дополнительных значений матрицы R на основе имеющихся экспериментальных данных, т.е. возникает задача «восстановления» отсутствующих данных. На самом деле данные не отсутствуют. Для повышения качества восстановления изображения желательно увеличить количество стобцов матрицы R, тем самым как бы уменшив шаг дискретизации угла поворота линейки излучателей.

В работе [6] дано сравнение различных методов [7-13] для восстановления отсутствующих данных, а именно:

· заполнение общим средним,

· заполнения с подбором,

· заполнение по регрессии,

· методы сплайн-интерполяции,

· заполнение по методу максимального правдоподобия,

· методы факторного анализа,

· методы кластерного анализа,

· алгоритмы семейства Zet (Wanga),

· методы использование нейросетей.

Результаты сравнительного анализа [6] позволяют сделать вывод, что лучшие результаты восстановления среди всех методов показал метод восстановления пропущенного значения сплайн-интерполяцией по присутствующим элементам.

Таким образом, для вычисления значений элементов дополнительных столбцов матрицы R целесообразно использовать подход, основанный на методах аппроксимации.

В данной статье предлагается алгоритм повышение качества восстановления изображения за счет добавления дополнительных столбцов, содержащих преобразование Радона в промежуточных углах поворота, вычисленных по выведенным формулам аппроксимации. Двукратное увеличение количества столбцов матрицы интегрального преобразования Радона позволяет значительно повысить качество восстановления изображения при обратном преобразовании Радона.

2. Основные соотношения

Основная идея предлагаемого подхода ранее была изложена автором в работе [14]. Здесь предлагается более подробное и строгое обоснование математических соотношений.

Пусть имеется преобразование Радона некоторого изображения I. Как правило, преобразование Радона представляется в виде матрицы размерности .

- определяется размером изображения I и шагом дискретизации τ проведения прямых, вдоль которых вычисляется интегральное преобразование Радона.

- определяется количеством углов поворота с шагом (в диапазоне от 0 до 180 градусов) вращающейся системы координат, внутри которой проводятся прямые для вычисления преобразования Радона.

Элемент матрицы соответствует интегралу, вычисленному вдоль прямой перпендикулярной оси абсцисс вращающейся системы координат и находяейся на расстоянии от начала координат. Угол поворота равен

где - шаг поворота подвижной системы координат. Уравнение прямой задается выражением [1]

Как показано в [5], в соответствии с формулой Шеннона-Котельникова для восстановления изображения с приемлемым качеством должно выполняться соотношение:

В связи с этим особый интерес представляет увеличение (удвоение) размерности , т.е. уменьшение шага угла поворота вращающейся системы координат.

Наиболее простой способ получения матрицы размерности заключается в добавлении между столбцами матрицы по одному столбцу и вычислению элементов по формулам линейной аппроксимации:

Однако, как будет показано ниже, такой подход не приводит к повышению качества восстановления изображения и поэтому требуется разработать специальный алгоритм, увеличивающий размерность в два раза. Другими словами, если исходное преобразование Радона размерности выполнено с шагом угла поворота , то в результате работы алгоритма необходимо получить матрицу преобразования Радона размерности , т.е. получить преобразование Радона, выполненное с шагом угла поворота .

2.1. Описание алгоритма

Рассмотрим системы координат x₁Oy₁ и x₂Oy₂, центр которых связан с центром исследуемого объекта и повернутых относительно друг друга на угол (см рис.1).

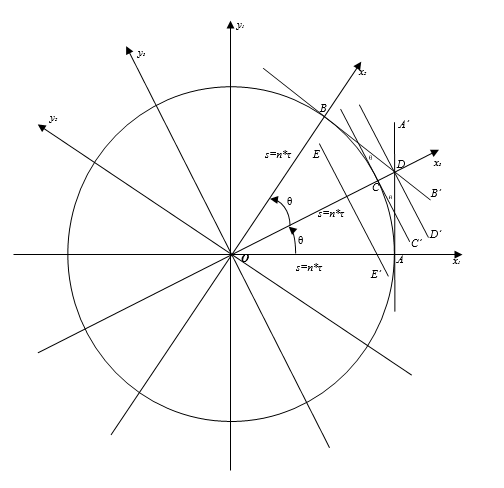
Рис. 1. Системы координат x₁Oy₁ и x₂Oy₂ повернутых относительно друг друга на угол 2θ

В системе координат x₁Oy₁интеграл вычисляется вдоль прямой AA’ находяейся на расстоянии s=nτ от начала координат. В системе координат x₂Oy₂,повернутой на угол относительно x₁Oy₁ интеграл вычисляется вдоль прямой BB’ также находяейся на расстоянии s=nτ от начала координат. Рассмотрим систему координат x₃Oy₃повернутую на угол относительно x₁Oy₁. Заметим, что система координат x₂Oy₂повернута на угол относительно x₃Oy₃.

Требуется оценить значение интеграла вдоль прямой CC’ перпендикулярной оси Ox₃ и находяейся на расстоянии s=nτ от начала координат, т.е. вычислить преобразование Радона с шагом угла поворота в два раза меньшим исходного .

Обозначим значение интеграла вдоль прямых AA’, BB’, CC’ через R_AA’ ; R_BB’ ; R_CC’ соответственно. Оценка интеграла R_CC’ по формуле

является некорректной, т.к. прямая CC’ проходит в значительной своей части вне секторов BDA’ и ADB’. Такое усреднение правильней отнести к оценке интеграла R_DD’, т.е. интеграла вдоль прямой DD’, проходящей между прямыми AA’ и BB’ и полностью лежащей внутри секторов BDA’ и ADB’.

Таким образом будем считать

Расстояние от начала координат на котором проходит прямая DD’ равно

Для дальнейших преобразований введем следующие обозначания:

где . Здесь первый аргумент функции обозначает расстояние от начала координат, а второй угол поворота. Так, например, означает, что ингерал вычислен вдоль прямой перпендикулярной оси Ox₁, повернутой на угол равный нулю и находящейся на расстоянии от начала координат.

Для расстояния можно написать аналогичные соотношения и в частности для прямой EE’

Если вычислены значения и , то значение , может быть вычислено с помощью линейной аппроксимации, при условии, что прямая CC’ находится между прямыми EE’ и DD’.

Для этого должно выполняться соотношение

или

Если правое неравенство выполняется всегда, то для левого можно записать

или

Максимальное значение равно . Тогда

или

Таким образом получаем ограничение на угол поворота , который связан со значением .

Считая, что последнее неравенство на угол поворота выполнено, получим с помощью линейной аппроксимации выражение для

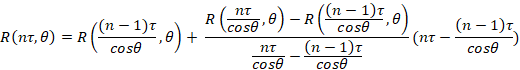
Упрощая данное выражение получим

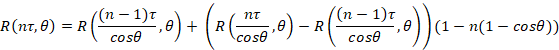
И наконец, учитывая, что

Окончательно получим

Полученное выражение является довольно интересным. В нем присутствует слагаемое

которое можно рассматривать как обычную линейную аппроксимацию вида и некоторая поправка (поправка Кудрявцева)

учитывающая расположение прямой вдоль которой должно выполняться интегрирование относительно прямых используемых для вычисления аппроксимации.

Следует отметить, что при

т.е. поправка не учитывается, т.к. прямая прямая CC’ целиком располагается внутри секторов BDA’ и ADB’ и делит их пополам.

2.2. Алгоритм увеличения размерности матрицы преобразования Радона.

Исходные данные: Матрица преобразования Радона размерности . Шаг угла поворота равен , т.е. вычисление интегралов выполняется для углов: , причем .

Требуется: вычислить матрицу преобразования Радона размерности с шагом угла поворота .

Представим данный алгоритм в виде последовательности нескольких этапов.

Этап 1. Создаем матрицу размерности и заполняем ее нулями.

Этап 2. Присваиваем нечетные столбцы матрицы , соответствующим столбцам матрицы

Этап 3. Вычисляем значения четных столбцов матрицы для по формулам:

где

Этап 4. Вычисляем значения столбца матрицы для по формулам:

где

Этап 5. Вычисляем значения четных столбцов матрицы для по формулам:

где

Этап 6. Вычисляем значения столбца матрицы для по формулам:

где

3. Оценка эффективности

Оценку эффективности предложенного алгоритма будем выпонять в среде MatLab 7.0. В качестве тестового изображения выберем так называемого изображения фантома (см. рис.2) размерности 256 х 256 пикселей.

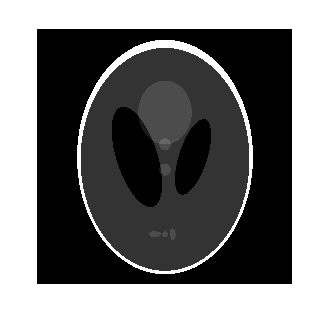
Рис. 2. Исходное изображение фантома

Выберем в качестве шага угла поворота и вычислим матрицу преобразования Радона с помощью функции radon из MatLab 7.0. Результатом данного вычисления является матрица размерности . Здесь .

Выполняя обратное преобразование Радона с помощью функции iradon получим восстановленное изображение (см. рис.3)

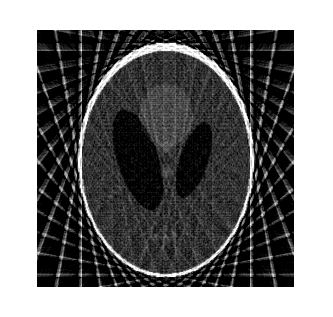
Рис. 3. Восстановленное изображение фантома (шаг угла поворота )

Как видно качество восстановленного изображения не очень высокое, т.к. шаг угла поворота в оказывается довольно большим.

Если в качестве шага угла поворота взять , вычислить матрицу преобразования Радона размерности и затем выполнить обратное преобразование Радона то получим более качественное восстановленное изображение (см. рис.4)

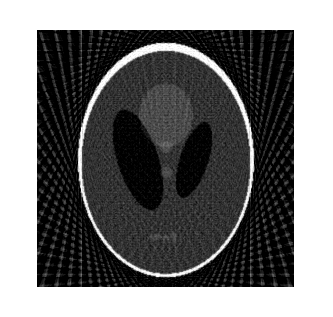
Рис. 4. Восстановленное изображение фантома (шаг угла поворота )

Используя в качестве исходных данных матрицу размерности , построим в соответствии с описанным алгоритмом по формулам (1)-(5) матрицу преобразования Радона размерности . Выполняя обратное преобразование Радона, получим изображение, представленное на рис. 5.

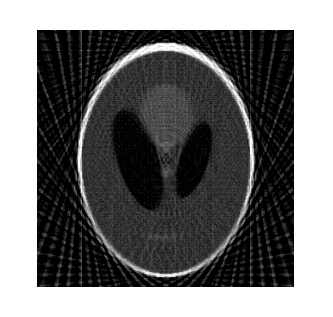
Рис. 5. Изображение фантома, восстановленное из аппроксимационной матрицы

Сравнивая рисунки 3, 4 и 5 можно сделать вывод, что предложенный алгоритм улучшает качество восстанавливаемого изображения. Рис. 5 визуально является менее четким по сравнению с рис. 4, но превосходит изображение на рис. 3.

Для того чтобы подчеркнуть значимость предложенной аппроксимационной поправки (поправки Кудрявцева), построим аппроксимационную матрицу преобразования Радона без поправки и восстановим изображение (см. рис.6)

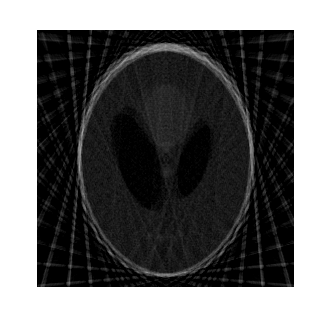
Рис. 6. Изображение, восстановленное из аппроксимационной матрицы без учета аппроксимационной поправки.

Как видно игнорирование аппроксимационной поправки не приводит к улучшению качества изображения.

Кроме субъективной, визуальной оценки эффективности предложенного алгоритма найдем среднее абсолютное отклонение вычисленных аппроксимационных значений от точных значений. В качестве точных значений возьмем матрицу преобразования Радона размерности с шагом угла поворота . Оценка вычисляется по формуле

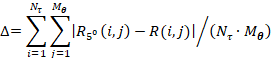
где - элементы матрицы преобразования Радона с шагом угла поворота ,

- элементы аппроксимационной матрицы преобразования вычисленные в соответствии с описанным алгоритмом по формулам (1)-(5).

В результате вычислений получено, что . Для сравнения, если аппроксимационную матрицу строить без поправок, то среднее абсолютное отклонение составило . Как видно из таблицы 1, при использовании меньших шагов углов поворота () значение становится еще меньше.

Таблица 1. Сравнение точности вычислений матриц аппроксимации


11.2847	0.3261	34.6
11.2554	0.2969	37.9
11.1721	0.2138	52.25
11.1182	0.1598	69.57
11.0718	0.113	97.98

Таким образом предложенная аппроксимационная поправка улучшает качество аппроксимации более чем на порядок, что является весьма существенным результатом.

Реализация описанного алгоритма представлена в приложении в виде скрипта на языке MatLab 7.0.

4. Заключение

В данной работе предложен алгоритм повышение качества восстановления изображения из матрицы преобразования Радона путем добавления дополнительных столбцов, содержащих преобразование Радона в промежуточных углах поворота, вычисленных по выведенным формулам аппроксимации.

Предложенный алгоритм состоит из шести этапов:

- на первом этапе создается матрица с удвоенным количеством столбцов и заполняется нулями;

- на втором этапе нечетные столбцы матрицы , присваиваются соответствующим столбцам исходной матрицы;

- на последующих этапах вычисляются значения элементов матрицы по формулам (2)-(5).

Экспериментальная проверка показала, что предложенный алгоритм позволяет существенно улучшить качество восстановления изображений с помощью обратного преобразования Радона.

Все полученные соотношения прошли экспериментальную проверку в системе MatLab 7.0, которая подтвердила их полную корректность.

Список литературы

1. Natterer F. The Mathematics of Computerized Tomography (Classics in Applied Mathematics, 32), Philadelphia, PA: Society for Industrial and Applied Mathematics, 2001 ISBN 0-89871-493-1

2. The Physics of Medical Imaging. Edited by Steve Webb Adam Hilger, Bristol and Philadelphia, 1991. ISBN 0-885274-367-0

3. Kudryavtsev K.Ya., Mikhaylov D.M. Radon integral transform on sparse rectangular grid. International Journal of Tomography and Simulation ISSN 2319-33362015, V. 28, N. 1, p. 89-104

4. Грузман И.С., Киричук В.С., Косых В.П., Перетягин Г.И., Спектор А.А. Цифровая обработка изображений в информационных системах: Учебное пособие.- Новосибисрк: Изд-во НГТУ, 2002. - 352 c.

5. Kak A.C., Slaney M. Principles of computerized tomographic imaginng (Classics in Applied Mathematics, 33), Philadelphia, PA 19104-2688: Society for Industrial and Applied Mathematics, ISBN 0-89871-494-X

6. Абраменкова И.В., Круглов В.В. Методы восстановления пропусков в массивах данных. Программные продукты и системы, 2005, №2, с.18-22

7. Литтл Р.Дж.А., Рубин Д.Б. Статистический анализ данных с пропусками. Финансы и статистика, 1990.

8. Загоруйко Н.Г. Прикладные методы анализа данных и знаний. Изд-во ин-та математики, 1999.

9. Загоруйко Н.Г., Елкина В.Н., Тимеркаев В.С. Алгоритм заполнения пропусков в эмпирических таблицах (алгоритм Zet). Эмпирическое предсказание и распознавание образов. Новосибирск, 1975. Вып. 61: Вычислительные системы. - С. 3-27.

10. Россиев А.А. Моделирование данных при помощи кривых для восстановления пробелов в таблицах. Методы нейроинформатики. Под. ред. А.Н. Горбаня. Красноярск: КГТУ, 1998.

11. Демиденко Е.З. Линейная и нелинейная регрессия. Финансы и статистика, 1981.

12. Двоенко С.Д. Неиерархический дивизимный алгоритм кластеризации. Автоматика и телемеханика. 1999. № 4. С. 117-124.

13. Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. Горячая линия. Телеком, 2002.

14. Kudryavtsev K.Ya. Rising the Quality of Restor-ing Image with Radon Inverse Transform Basing on Spectral Approximation Formulas.- International Journal of Tomography and Simulation ISSN 2319-3336 2016, Том 29, Выпуск 2, с. 50-61

Приложение. Скрипт вычисления аппроксимационной матрицы преобразования Радона

P=phantom(256);

imshow(P);

dtheta=10;

theta1=0:dtheta:(180-dtheta);

[R1, xp] = radon(P, theta1);

theta2=0:dtheta/2:(180-dtheta/2);

[R2, xp] = radon(P, theta2);

I1=iradon(R1,dtheta);

I2=iradon(R2,dtheta/2);

Ntau=size(R1, 1);

NZero=(Ntau+1)/2;

Ntheta=size(R1, 2);

Ntheta2=2*Ntheta;

R1Appr = zeros(Ntau,Ntheta2);

R1ApprSimple = zeros(Ntau,Ntheta2);

Nel=size(R1Appr, 1) * size(R1Appr, 2);

Ktheta=(1-cos(pi*dtheta/360))/2;

for i=1:Ntheta

R1Appr(:,2*i-1)=R1(:,i);

end

for i=1:Ntheta

for n=1:NZero

j=NZero+n-1;

I0Nt=R1Appr(j,2*i-1);

I0Nt1=R1Appr(j-1,2*i-1);

if i < Ntheta

I2Nt=R1Appr(j,2*i+1);

I2Nt1=R1Appr(j-1,2*i+1);

else

I2Nt=R1Appr(j,1);

I2Nt1=R1Appr(j-1,1);

end

R1Appr(j,2*i)=(I0Nt+I2Nt)/2-(I0Nt-I0Nt1+I2Nt-I2Nt1)*(n-1)*Ktheta;

R1ApprSimple(j,2*i)=(I0Nt+I2Nt)/2;

end

for i=1:Ntheta

for n=1:NZero

j=NZero-n+1;

I0Nt=R1Appr(j,2*i-1);

I0Nt1=R1Appr(j+1,2*i-1);

if i < Ntheta

I2Nt=R1Appr(j,2*i+1);

I2Nt1=R1Appr(j+1,2*i+1);

else

I2Nt=R1Appr(j,1);

I2Nt1=R1Appr(j+1,1);

end

R1Appr(j,2*i)=(I0Nt+I2Nt)/2-(I0Nt-I0Nt1+I2Nt-I2Nt1)*(n-1)*Ktheta;

R1ApprSimple(j,2*i)=(I0Nt+I2Nt)/2;

end

Pogr=sum(sum(abs(R1Appr-R2)))/Nel

PogrSimple=sum(sum(abs(R1ApprSimple-R2)))/Nel

% xp - вектор значений смещений по оси x [-183, +183]

IAppr=iradon(R1Appr,dtheta/2);

IApprSimple=iradon(R1ApprSimple,dtheta/2);

figure,imshow(I1);

figure, imshow(I2);

figure, imshow(IAppr);

figure, imshow(IApprSimple);

IMPROVEMENT OF THE QUALITY OF RESTORING IMAGE WITH RADON INVERSE TRANSFORM

K.Ya. Kudryavtsev

National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Russian Federation

KYKudryavtsev@mephi.ru

Abstract

The creation of the image of internal contents of object without its physical corrupting applied in medicine, metallurgy and crystallography is based on X-ray radiation with the subsequent mathematical processing of received data. When the object is being scanned, the output ray intensity is equal to density distribution function along the ray path. Registration of emission calculated at different angles allows to obtain the original data used to reconstruct the image. Data used for image reconstruction has the form of matrix, each element of which is the result of integral evaluation along the determined line. The bigger matrix is, i.e. the more experimental data is available, the more exact image reconstruction will be possible. However, the number of experiments is often limited by medical, technical, economic and other reasons. As a mathematical tool for the reconstruction of the cross-sectional image of an object, a direct and inverse Radon transform is used. This paper proposes the algorithm of rising the quality of reconstructed image from Radon transform matrix by adding additional colums containing Radon transform in interjacent angle turn calculated with the help of developed approximation formulas. Doubling the number of Radon integral transformation matrix colums helps to significantly rise the quality of image being reconstructed with Radon inverse transformation.

Keywords: integral Radon transformation, Radon inverse transformation, image reconstruction

References

1. Natterer F. The Mathematics of Computerized Tomography (Classics in Applied Mathematics, 32), Philadelphia, PA: Society for Industrial and Applied Mathematics, 2001 ISBN 0-89871-493-1

2. The Physics of Medical Imaging. Edited by Steve Webb Adam Hilger, Bristol and Philadelphia, 1991. ISBN 0-885274-367-0

3. Kudryavtsev K.Ya., Mikhaylov D.M. Radon integral transform on sparse rectangular grid. International Journal of Tomography and Simulation ISSN 2319-33362015, V. 28, N. 1, p. 89-104

4. Gruzman I.S., Kirichuk V.S., Kosyh V.P., Peretjagin G.I., Spektor A.A. Digital image processing in information systems: Textbook. NSTU, 2002. 352 p.

5. Kak A.C, Slaney M. Principles of computerized tomographic imaginng (Classics in Applied Mathematics, 33), Philadelphia, PA 19104-2688: Society for Industrial and Applied Mathematics, ISBN 0-89871-494-X

6. Abramenkova I.V., Kruglov V.V. Methods for recovering gaps in data sets. - Software products and systems, 2005, №2, p.18-22

7. Little R.J.A., Rubin D.B. Statistical analysis of data with omissions. - Moscow: Finance and Statistics, 1990.

8. Zagoruiko N.G. Applied methods of data and knowledge analysis. - Novosibirsk: Publishing house of the Institute of Mathematics, 1999.

9. Zagoruiko NG, Elkina VN, Timerkaev VS An algorithm for filling out blanks in empirical tables (Zet algorithm). Empirical prediction and pattern recognition. Novosibirsk, 1975. Issue. 61: Computing systems. p. 3-27.

10. Rossiev AA Modeling data using curves to restore gaps in tables. Methods of Neuroinformatics. Krasnoyarsk: KSTU, 1998.

11. Demidenko E.Z. Linear and nonlinear regression. Finance and Statistics, 1981.

12. Dvienko S.D. Non-hierarchical divisible clustering algorithm. Automation and telemechanics. 1999. № 4. P. 117-124.

13. Kruglov VV, Borisov VV Artificial neural networks. Theory and practice. M .: Hot line - Telecom, 2002.

14. Kudryavtsev K.Ya. Rising the Quality of Restor-ing Image with Radon Inverse Transform Basing on Spectral Approximation Formulas. International Journal of Tomography and Simulation ISSN 2319-3336 2016, V. 29, N. 2, p. 50-61.