ВИЗУАЛИЗАЦИЯ ФАЗОВОЙ СТРУКТУРЫ ТЕРМОГРАВИТАЦИОННОЙ СТРУИ С РЕКОНСТРУКЦИЕЙ ТЕМПЕРАТУРНОГО ПОЛЯ
В.А. Арбузов1, 2, Э.В. Арбузов2, 3, Ю.Н. Дубнищев1, 2, В.С. Бердников1, 2, О.С. Мелёхина2
1 Институт теплофизики им. С.С. Кутателадзе Сибирского отделения Российской академии наук.
2 Новосибирский государственный технический университет.
3 Институт математики им. С.Л. Соболева Сибирского отделения Российской академии наук.
E-mail: dubnistchev@itp.nsc.ru
Содержание
2. Визуализация фазовой структуры плюма
Аннотация
Методами гильберт-оптики и интерферометрии визуализирована фазовая структура термогравитационной струи, индуцированной внезапно включенным тепловым источником в сильновязкой жидкости. С использованием полиномов Берштейна и кривых Безье выполнена аппроксимация фазовых изолиний, реконструированы поля скоростей и температуры. Приведены результаты сравнения сдвиговой интерферограммы, синтезированной из реконструированного температурного поля струи, с экспериментально полученной интерферограммой. Термогравитационные струи (плюмы) представляют научный интерес как модели подъёмного течения в задачах геодинамики, связанных с поведением земной мантии на больших глубинах и в зонах спрединга.
Ключевые слова: оптическая визуализация потоков; гильберт-оптика; интерференция; термогравитационная конвекция; физическое моделирование геодинамических процессов.
1. Введение
Методы оптической диагностики широко используются в экспериментальной гидро- и газодинамике, теплофизике, биологии, медицине, а также в промышленных технологиях, связанных с необходимостью исключения возмущающего воздействия на исследуемую среду при контроле и измерениях [1–5]. Методы интерферометрии и гильберт-оптики позволяют с высокой чувствительностью визуализировать поля фазовой оптической плотности в газах и жидкостях [6–8]. В геодинамике одной из важнейших проблем является изучение и физическое моделирование поведения мантии Земли на больших глубинах, мантийных плюмов и подводных течений в зоне спрединга [9, 10]. Плюмы или термогравитационные плавучие струи – это конвективные течения разогретого вещества, возникающие на границе ядро–мантия в гравитационном поле Земли. В работе [11] измерялась скорость движения ламинарного плюма при различных параметрах среды. Плюм визуализировался методом дифференциальной интерферометрии. Методом голографической интерферометрии [12] и визуализации трассеров [13] исследовалось развитие свободно-конвективной струи жидкости над линейным тепловым источником и источником, близким к точечному.
В работе [14] методами гильберт-оптики и сдвиговой интерферометрии визуализировалась фазовая структура и температурное поле плюма, индуцированного в сильновязкой жидкости внезапно включенным линейным тепловым источником. Достоверность проверялась путём гильберт-преобразования реконструированного температурного поля и сравнения восстановленного гильберт-образа с экспериментально полученным гильберт-образом плюма. Одной из проблем является исследование возможности реконструкции температурного поля и поля скоростей теплового потока плюма по сдвиговой интерферограмме. Настоящая работа мотивирована необходимостью решения этой задачи.
2. Визуализация фазовой структуры плюма
Эскизная схема экспериментальной установки показана на рис. 1. Схема содержит линейный световой источник 1 и объектив 2, формирующие зондирующее световое поле в исследуемой среде 3, которая представляет собой слой сильновязкой жидкости ПЭС–5, помещённой в прямоугольную полость 4 с прозрачными стенками оптического качества. Внутренние размеры полости 60×100×540 мм. В центральном по длине полости сечении находится константановая проволочка 5, ориентированная параллельно оси оптической системы и плоскости дна. Управляемый нагрев проволочки осуществляется постоянным током от стабилизированного источника питания 6. В двух заданных точках исследуемой среды температура контролируется термопарами 7. В качестве светового источника используются лазерный диод, излучающий на длине волны 0,64 мкм или галогенная лампа. Объектив 8 формирует в частотной плоскости фурье-спектр возмущённого исследуемой средой светового поля и изображение светового источника. В фурье-плоскости объектива помещён квадрантный гильберт-фильтр 9, согласованный с ориентацией изображения источника. Объектив 10 выполняет обратное фурье-преобразование фильтрованного оптического сигнала и формирует гильберт-изображение визуализированной фазовой структуры плюма, регистрируемое камкордером 11. Выходы цифровой камеры 11 и термопар 7 подключены к компьютеру 12. Оптический комплекс реализован на базе серийного прибора ИАБ–463М с модифицированным осветительным модулем, узлами фильтрации оптического сигнала и регистрации изображения.
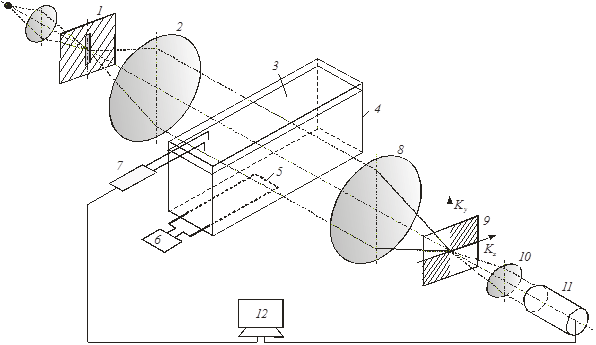
Рис. 1. Схема экспериментальной установки.
Сравнительные исследования термогравитационных струй в одних и тех же режимах выполнялись с применением методов гильберт-оптики и интерферометрии. Для этого использовалась модифицированная приставка РП–452, выполненная по схеме зеркального интерферометра сдвига (рис. 2) [3].
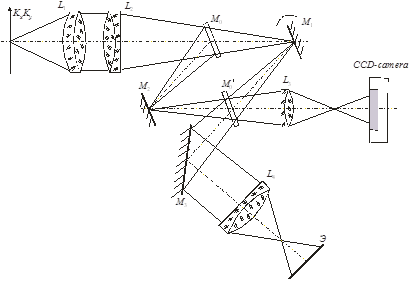
Рис. 2. Схема интерферометра.
Интерференционная приставка при проведении эксперимента
помещается позади частотной плоскости вместо модуля, осуществляющего
фильтрацию, обратное фурье-преобразование фильтрованного сигнала и его
регистрацию. Зондирующее поле, сформированное фурье-объективом 2 от
светового источника 1, проходит через исследуемую среду 3, в
которой тепловым источником 5 индуцируется термогравитационное течение в
виде плавучей струи. Объектив 8 формирует в частотной плоскости
фурье-спектр ![]() фазовых
возмущений зондирующего поля, вызванных исследуемой средой. При
гильберт-визуализации фильтрация выполняется квадрантным фурье-фильтром 10,
когерентная передаточная функция которого:
фазовых
возмущений зондирующего поля, вызванных исследуемой средой. При
гильберт-визуализации фильтрация выполняется квадрантным фурье-фильтром 10,
когерентная передаточная функция которого:
![]()
![]() , (1)
, (1)
где ![]() – пространственные частоты,
– пространственные частоты, ![]() и
и ![]() – функции включения:
– функции включения: ![]() , где
, где ![]() – знаковая функция.
Непосредственно за фильтром формируется фурье–спектр фильтрованного оптического
сигнала, выражение для которого с учётом (1) имеет вид:
– знаковая функция.
Непосредственно за фильтром формируется фурье–спектр фильтрованного оптического
сигнала, выражение для которого с учётом (1) имеет вид:
![]()
![]() , (2)
, (2)
где ![]() – фурье–спектр одномерного
гильберт–преобразования фазового возмущения
– фурье–спектр одномерного
гильберт–преобразования фазового возмущения ![]() . Пространственно–частотная ось Kх
в фурье–плоскости ортогональна направлению оси Kу, задаваемой
изображением щелевого источника. Объектив 10 выполняет обратное
фурье–преобразование фильтрованного фурье–спектра (2).
. Пространственно–частотная ось Kх
в фурье–плоскости ортогональна направлению оси Kу, задаваемой
изображением щелевого источника. Объектив 10 выполняет обратное
фурье–преобразование фильтрованного фурье–спектра (2).
Восстановленный сигнал представляет собой сумму изображений
фазового возмущения и его одномерного гильберт–образа с весовыми коэффициентами
![]() и
и ![]() :
:
![]() . (3)
. (3)
Фазовый сдвиг j
зависит от длины волны зондирующего поля, ![]() . Как следует из (3), при
. Как следует из (3), при ![]() выполняется одномерное
преобразование Гильберта. В этом случае на фотоматрице камеры 11 формируется
изображение одномерного гильберт–образа фазовых возмущений зондирующего поля,
индуцированных исследуемой средой,
выполняется одномерное
преобразование Гильберта. В этом случае на фотоматрице камеры 11 формируется
изображение одномерного гильберт–образа фазовых возмущений зондирующего поля,
индуцированных исследуемой средой, ![]() . В эксперименте используется
пространственно-частотный фильтр, обеспечивающий на длине волны
. В эксперименте используется
пространственно-частотный фильтр, обеспечивающий на длине волны ![]() = 0,63 мкм фазовый сдвиг
= 0,63 мкм фазовый сдвиг ![]() .
.
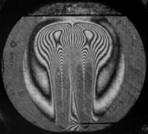
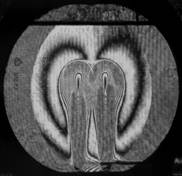
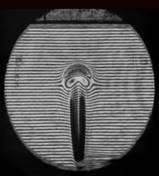
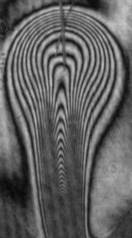
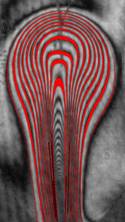
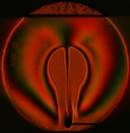
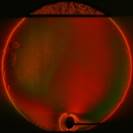
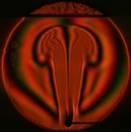
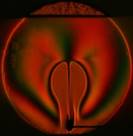
На рис. 3 показаны примеры гильберт-изображений и сдвиговых интерферограмм плюма. Нумерация указывает последовательность кадров.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3. Гильберт-изображения и сдвиговые интерферограммы плюма.
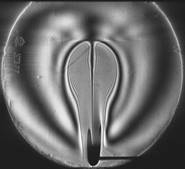
Плюм индуцировался в жидкости ПЭС–5 (силиконовое масло) внезапно включенным линейным тепловым источником при скачкообразном изменении тока от 0 до 0,5 А. Диаметр поля зрения составляет 110 мм. Визуализация выполнялась с применением оптического комплекса, упрощённая схема которого показана на рис. 1. На рис. 4 показаны примеры фазовых структур термогравитационной струи, визуализированных методами сдвиговой интерферометрии (а–е) и гильберт-оптики (f).
|
|
|
|
|
|
Δx > L, Δy = 0, a = 0, b=0. a) |
0 < Δx < L, Δy = 0, a = 0, b=0. b) |
Δx = 0, Δy >0, a = 0, b > 0. c) |
|
|
|
|
|
|
|
0 < Δx < L, Δy = 0, a = 0, b > 0. d) |
Δx = 0, Δy >0, a > 0, b = 0. e) |
f) |
|
Рис. 4. Сдвиговые интерферограммы и гильберт-изображение термогравитационного течения:
L – ширина плюма; ∆x – величина сдвига по горизонтали; ∆y – величина сдвига по вертикали;
a, b – параметры настройки интерферометра на полосы конечной ширины.
Представленные примеры интерферограмм показывают, что
непосредственное восстановление фазовой функции по изображению, полученному с
помощью интерферометра Маха–Цендера (сдвиг ![]() ), возможно только на ограниченном временном
интервале эволюции плюма. Настройка интерферометра на горизонтальный сдвиг
сужает область восстановления поля в верхней части. Применение настроек
интерферометра на полосы конечной ширины позволяет идентифицировать
интерференционные полосы в меньшей пространственной области по сравнению с
настройкой на полосу бесконечной ширины.
), возможно только на ограниченном временном
интервале эволюции плюма. Настройка интерферометра на горизонтальный сдвиг
сужает область восстановления поля в верхней части. Применение настроек
интерферометра на полосы конечной ширины позволяет идентифицировать
интерференционные полосы в меньшей пространственной области по сравнению с
настройкой на полосу бесконечной ширины.
Фазовая структура сдвиговой интерферограммы описывается семейством кривых, удовлетворяющих уравнению:
![]() ,
,
где ![]() ,
, ![]() , и
, и ![]() – фазы взаимно совмещённых интерферирующих
полей, a и b – постоянные, характеризующие настройку
интерферометра.
– фазы взаимно совмещённых интерферирующих
полей, a и b – постоянные, характеризующие настройку
интерферометра.
В случае малых фазовых сдвигов ![]() аппроксимируется через частные
производные:
аппроксимируется через частные
производные:
![]() . (4)
. (4)
Фазовая функция восстанавливается интегрированием её
дифференциального представления (4) на пространственных масштабах, определяемой
величиной сдвига. При сдвигах, малых по сравнению с масштабами исследуемой
неоднородности, на масштабах, достаточных для дифференциальной аппроксимации
(4), восстановление ![]() возможно по методике, описанной в [15].
возможно по методике, описанной в [15].
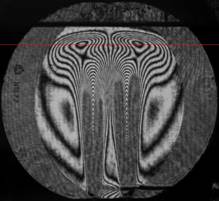
В ситуации, когда величина сдвига превосходит масштабы фазовых неоднородностей, для интерполяции интерференционной структуры, полученной на интерферометре сдвига, настроенном на бесконечно широкую полосу, можно воспользоваться полиномами Берштейна. При этом каждая интерференционная полоса аппроксимируется кривой Безье по выбранному числу точек. Пример такой аппроксимации показан на рис. 5.
|
a |
b |
Рис.5. Исходная интерференционная картина (a) и её аппроксимация кривыми Безье (b).
Фазовая структура плюма определяется пространственно-временными возмущениями коэффициента преломления среды, индуцированными тепловым источником. При известной температурной зависимости коэффициента преломления (рис. 6) визуализированная методами сдвиговой интерферометрии или гильберт-оптики фазовая структура позволяет реконструировать температурное поле плюма. Поскольку в фазовой структуре плюма интерференционные полосы, являясь линиями равных фаз, отображают изотермы, для этого достаточно контролировать с помощью термопар разность температур (δТ) в паре соседних интерференционных полос (изотерм) и измерять температуру (Т0) среды в начале эксперимента. Зависимость коэффициента преломления жидкости ПЭС–5 от температуры – линейная, что существенно упрощает процедуру реконструкции температурного поля. В процессе реконструкции строится равномерная сетка, в каждой точке которой температура определяется как отсчёт («высота») в направлении, ортогональном плоскости сетки в соответствии с формулой
![]() ,
,
где ![]() – номер линии. Аппроксимация фазовых изолиний
полиномами Берштейна позволяет строить сетку, адаптирующуюся к деформации
интерференционных полос.
– номер линии. Аппроксимация фазовых изолиний
полиномами Берштейна позволяет строить сетку, адаптирующуюся к деформации
интерференционных полос.
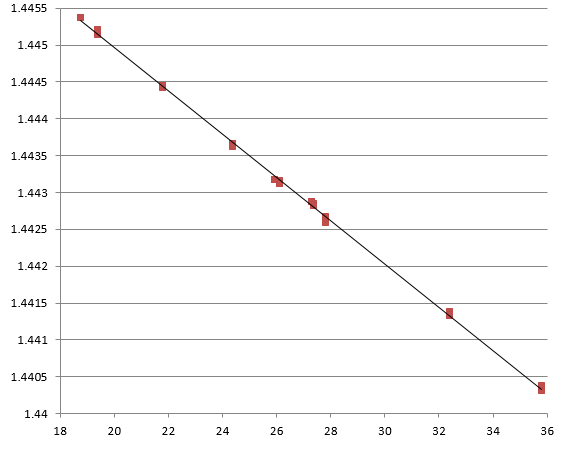
Рис. 6. График зависимости показателя преломления жидкости ПЭС–5 от температуры в интервале +18 °С – +36 °С.
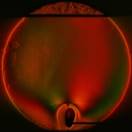
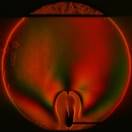
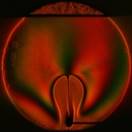
По полученной сетке производится двумерная сплайн-интерполяция и восстанавливается температурное поле. На рис. 7 показано реконструированное температурное поле плюма, полученное при δТ=0,046°С и Т0=20,5°С. В качестве проверки для реконструированного температурного поля вычислялась интерферограмма сдвига в предположении настройки интерферометра на бесконечно широкую полосу.
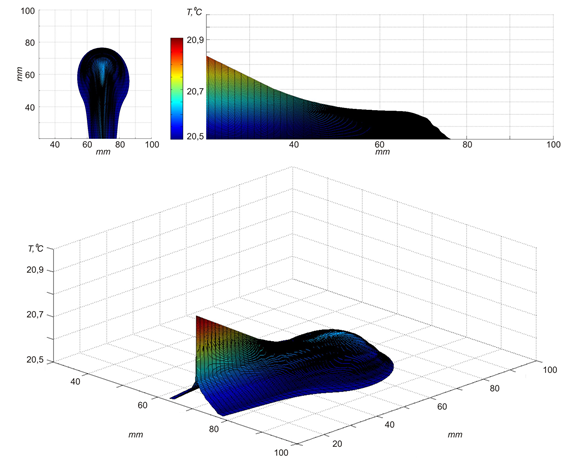
Рис. 7. Температурное поле плюма, реконструированное по сдвиговой интерферограмме.
На рис. 8 приведены экспериментальная и смоделированная по реконструированному температурному полю интерферограммы сдвига и их функция корреляции. Схожесть интерферограмм вполне удовлетворительная.
|
a |
b |
c |
Рис. 8. Исходная (a), смоделированная (b) интерферограммы и их функция корреляции (c).
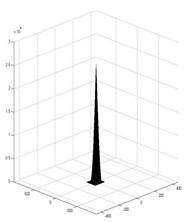
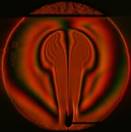
При достижении верхней границы слоя жидкости плюм деформируется. В этом случае восстановление фазовых структур производится на наборе сечений, а затем выполняется двумерная сплайн-интерполяция. Двумерная сплайн-интерполяция выполняется по точкам, которые определяют центры интерференционных полос в заданном сечении. При этом интерференционные полосы предварительно аппроксимируются кривыми Безье. Пример реконструированного температурного поля плюма (рис. 8а), деформированного верхней границей слоя жидкости, показан на рис. 9.
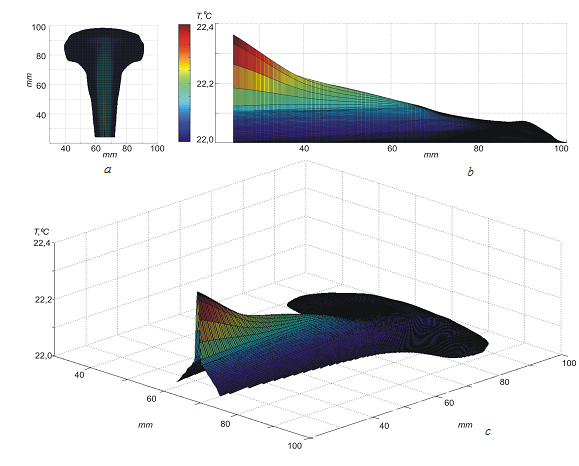
Рис. 9. Температурное поле плюма, реконструированное по интерферограммам сдвига: а – плюм; b – реконструированное температурное поле в плоской проекции; c – в аксонометрической проекции.
В качестве верификации результатов по реконструированному температурному полю (рис. 9b) при заданной надстройке интерферометра моделировалась интерферограмма сдвига. Рис. 10 иллюстрирует схожесть исходной и реконструированной интерферограмм.
|
a |
b |
Рис. 10. Исходная (a) и смоделированная (b) интерферограммы сдвига.
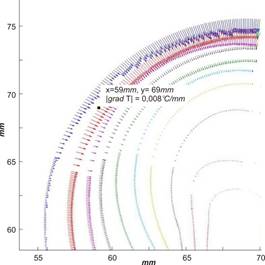
Рис. 11. Градиенты температурного поля, реконструированные по интерферограмме сдвига.
Градиенты поля оптической фазовой плотности плюма, индуцированного в жидкости внезапно включенным источником тепла, отображают градиенты температурного поля в заданных точках на изотермах, отображаемых линиями постоянной фазы. Это показано на рис. 11. Параметрическое задание интерференционных полос полиномами Берштейна и аппроксимация их кривыми Безье позволяет реконструировать температурное поле термогравитационных струй в жидкости по сдвиговым интерферограммам при известной зависимости коэффициента преломления исследуемой среды от температуры.
3. Заключение
На примере исследования термогравитационных струй в жидкости с известной зависимостью коэффициента преломления от температуры показана возможность реконструкции температурных полей путём сочетания методов сдвиговой интерферометрии с параметрическим заданием интерференционных полос полиномами Берштейна и аппроксимацией изотерм кривыми Безье. Выбор термогравитационных струй в качестве объекта исследований связан с проблемой моделирования геодинамических процессов в мантии Земли на больших глубинах. Методы реконструкции температурных полей по распределению оптической фазовой плотности могут быть полезны при исследовании самых разнообразных конвективных течений, имеющих место, например, в системе вода–лёд или при выращивании кристаллов.
Авторы выражают благодарность Н.С. Буфетову за помощь в работе.
Работа выполнена при частичной поддержке Российского фонда фундаментальных исследований (проект № 14–08–00818) и (проект 15–08–07991).
Список литературы
1. Settles G.S. Schlieren and shadowgraph techniques: Visualising Phenomena in Transparent Media. Springer. 2001. 376 p.
2. Smits A.J., and Lim T.T. Flow Visualization. Techniques and Examples. 2000, Imperial College Press. 396 p.
3. Белозёров А.Ф. Оптические методы визуализации газовых потоков. Казань: изд-во Казанского гос. техн. унив-та. 2007. 747 с.
4. Дубнищев Ю.Н., Арбузов В.А., Белоусов П.П., Белоусов П.Я. Оптические методы исследования потоков. Новосибирск: Сиб. унив. изд-во. 2003. 418 с.
5. Евтихиева О.А., Расковская И.А., Ринкевичюс Б.С. Лазерная рефрактография. М.: Физматлит. 2008. 176 с.
6. Malacara D., Servin M., Malacara Z. Interferogramm analysis for optical testing. Taylor & Fransis Group. 2005.
7. Арбузов В.А., Арбузов Э.В., Дворников Н.А., Дубнищев Ю.Н., Нечаев В.Г., Шлапакова Е.О. Оптическая диагностика взаимодействия кольцевых вихрей с пламенем. Автометрия. 2016. Т. 52, № 2. С. 66–72.
8. Арбузов В.А., Арбузов Э.В., Буфетов Н.С., Шлапакова Е.О. Гильберт–диагностика рэлей–бенаровской конвекции в жидкости. Автометрия. 2012. Т. 48, № 3. С. 61–67.
9. Wilson J.T. A Possible Origin of the Hawaiian Islands. Canadian Journal of Physics. 1969. V. 41. No 6. P. 863–870.
10. Добрецов Н.Л., Кирдяшкин А.Г., Кирдяшкин А.А. Глубинная геодинамика. Новосибирск: изд-во СО РАН «ГЕО». 2001. 409 с.
11. Kaminski E., Jaupart C. Laminar starting plumes in high–Prandtl–number fluids. J. Fluid Mech. 2003. 478. P. 287–298.
12. Ганжерли Н.М., Мауреч И.А., Черных Д.Ф. Исследование свободно-конвективной струи методом голографической интерферометрии. ЖТФ. 2002. Т. 72, № 2. С. 42–46.
13. Антонов П.В., Арбузов В.А., Бердников В.С., Гришков В.А., Новосёлова О.Н., Тихоненко В.В. Экспериментальные и численные исследования нестационарных плавучих струй. Автометрия. 2013. Т. 48, № 3. С. 90–100.
14. Арбузов В.А., Арбузов Э.В., Бердников В.С., Буфетов Н.С., Дубнищев Ю.Н., Шлапакова Е.О. Оптическая диагностика структуры и эволюции плавучих струй в сильновязкой жидкости. Автометрия. 2014. Т. 50, № 5. С. 47–55.
15. Комиссарук В.А. Элементы прикладной теории интерферометров. Оптические методы исследований в баллистическом эксперименте. Наука. 1979. С. 40–41.
VISUALIZATION OF PHASE STRUCTURE OF THE THERMOGRAVITATIONAL JET WITH THE RECONSTRUCTION OF TEMPERATURE FLUID
V.A. Arbuzov1, 2, E.V. Arbuzov2,3, Yu.N. Dubnishchev1, 2, V.S. Berdnikov1, 2, O.S. Melekhina2
1 Institute of Thermophysics, Siberian Branch, Russian Academy of Sciences, Russian Federation
2 Novosibirsk State Technical University, Russian Federation
3 Institute of Mathematics, Siberian Branch, Russian Academy of Sciences, Russian Federation
E-mail: dubnistchev@itp.nsc.ru
Abstract
The structure and evolution of thermogravitational buoyant jets in a high-viscosity liquid above a linear source of heat suddenly switched on are studied by methods of the Hilbert optics and shear interferometry. Based on the interferogram structure, reconstruction of the temperature field in the jet is performed with using approximation by Bernstein polinomials and Bezier curves. Recovery the phase function and the temperature of the plume was carried out on the interferogram using spline interpolation. Reliability of the results was tested by simulating shear interferogram of the reconstructed field and comparing it with the experimentally obtained fringe pattern. Such jets can be considered as a model of an upward flow in the spreading zone in geodynamic problems associated with the behavior of the Earth’s mantle at large depths.
Keywords: optical diagnostics of the flow, Hilbert optics, interferometry, thermogravitational convection, buoyant jets, physical modeling of geodynamic processes.
References
1. Settles G.S. Schlieren and shadowgraph techniques: Visualising Phenomena in Transparent Media. Springer. 2001. 376 p.
2. Smits A.J., and Lim T.T. Flow Visualization. Techniques and Examples. 2000, Imperial College Press. 396 p.
3. Belozjorov A.F. Opticheskie metody vizualizacii gazovyh potokov [Optical methods of the visualization of gas flows]. Kazan State Technical University publish house. 2007. 747 p. [In Russian]
4. Dubnishhev Ju.N., Arbuzov V.A., Belousov P.P., Belousov P.Ja. Opticheskie metody issledovanija potokov [Optical methods for studying flows]. Siberian University publish house. 2003. 418 p. [In Russian]
5. Evtihieva O.A., Raskovskaja I.A., Rinkevichjus B.S. Lazernaja refraktografija. Fizmatlit. 2008. 176 p. [In Russian]
6. Malacara D., Servin M., Malacara Z. Interferogramm analysis for optical testing. Taylor & Fransis Group. 2005.
7. Arbuzov V.A., Arbuzov Je.V., Dvornikov N.A., Dubnishhev Ju.N., Nechaev V.G., Shlapakova E.O. Opticheskaja diagnostika vzaimodejstvija kol'cevyh vihrej s plamenem [Optical diagnostics of ring vortices interact with the flame]. Avtometrija. 2016. Vol. 52, No 2. pp. 66–72. [In Russian]
8. Arbuzov V.A., Arbuzov Je.V., Bufetov N.S., Shlapakova E.O. Gil'bert–diagnostika rjelej–benarovskoj konvekcii v zhidkosti [Gilbert diagnostics Rayleigh-benarovskoy convection in the fluid]. Avtometrija. 2012. vol. 48, no. 3. pp. 61–67. [In Russian]
9. Wilson J.T. A Possible Origin of the Hawaiian Islands. Canadian Journal of Physics. 1969. V. 41. No 6. P. 863–870.
10. Dobrecov N.L., Kirdjashkin A.G., Kirdjashkin A.A. Glubinnaja geodinamika [Deep geodynamics]. SO RAN «GEO». 2001. 409 p. [In Russian]
11. Kaminski E., Jaupart C. Laminar starting plumes in high–Prandtl–number fluids. J. Fluid Mech. 2003. vol. 478. P. 287–298.
12. Ganzherli N.M., Maurech I.A., Chernyh D.F. Issledovanie svobodno-konvektivnoj strui metodom golograficheskoj interferometrii [The study of free-convection jet method holographic interferometry]. Technical Physics. 2002. vol. 72, no. 2. pp. 42–46. [In Russian]
13. Antonov P.V., Arbuzov V.A., Berdnikov V.S., Grishkov V.A., Novosjolova O.N., Tihonenko V.V. Jeksperimental'nye i chislennye issledovanija nestacionarnyh plavuchih struj [Experimental and numerical study of unsteady buoyant jets]. Avtometrija. 2013. vol. 48, no. 3. pp. 90–100. [In Russian]
14. Arbuzov V.A., Arbuzov Je.V., Berdnikov V.S., Bufetov N.S., Dubnishhev Ju.N., Shlapakova E.O. Opticheskaja diagnostika struktury i jevoljucii plavuchih struj v sil'novjazkoj zhidkosti [Optical diagnostics of the structure and evolution of the buoyant jets in high-viscosity liquids]. Avtometrija. 2014. vol. 50, no. 5. pp. 47–55. [In Russian]
15. Komissaruk V.A. Jelementy prikladnoj teorii interferometrov. Opticheskie metody issledovanij v ballisticheskom jeksperimente [Elements Applied interferometers theory. Optical research methods in a ballistic experiment]. Science. 1979. pp. 40–41. [In Russian]
 1
1 
 7
7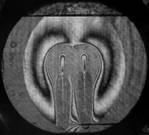
 2
2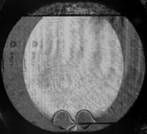
 8
8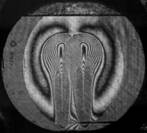
 3
3
 9
9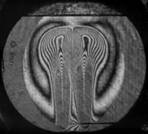
 4
4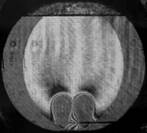
 10
10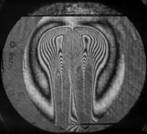
 5
5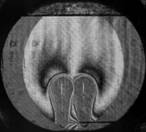
 11
11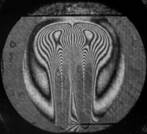
 6
6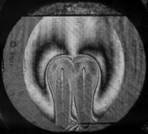
 12
12