ОБРАБОТКА ДАННЫХ В СИСТЕМАХ МОДЕЛИРОВАНИЯ И 3D-ВИЗУАЛИЗАЦИИ ТЕПЛООБМЕННЫХ ПРОЦЕССОВ В ТВЕРДЫХ МНОГОСЛОЙНЫХ ОБЪЕКТАХ
М.Н. Аралов, В.Ф. Барабанов, А.Д. Данилов, С.Л. Подвальный
Воронежский государственный технический университет, Россия
aralow@mail.ru, bvf@list.ru, danilov-ad@yandex.ru
Оглавление
2. Математические методы расчета тепловых параметров
4. Результаты работы программного комплекса
Аннотация
Данная статья посвящена проблемам моделирования тепловых процессов, протекающих внутри твердых многослойных объектов. Для моделирования таких процессов предлагается использовать специальное программное обеспечение с возможностью сопряжения с распространенными графическими системами и средствами разработки. Предложен комплекс математических методов для эффективного расчета тепловых параметров многослойного объекта с последующей их визуализацией. Приведена сравнительная характеристика результатов расчета тепловых параметров, полученных при помощи различных математических методов. Даны рекомендации для повышения эффективности и надежности процесса обработки данных при использовании разработанного программного обеспечения для моделирования и 3D-визуализации тепловых полей многослойных объектов. Представлена структура программного комплекса для моделирования и 3D-визуализации тепловых полей многослойных объектов. Разработанный программный комплекс позволяет производить расчет, корректировку и верификацию тепловых параметров, а также визуализацию тепловой модели многослойного объекта. В заключении приведены результаты работы программного комплекса.
Ключевые слова: многослойный объект, тепловое моделирование, термограмма, обработка данных, 3D-визуализация.
1. Введение
В современной промышленности нередко возникает необходимость моделирования физических свойств многослойных объектов. К таким объектам можно отнести сложные электронные компоненты, стены современных зданий, теплообменные аппараты, вулканические породы, препреги и пр. Важное значение имеет расчет тепловых параметров многослойных материалов при воздействии различных факторов и визуализация теплового поля (формирование термограммы объекта). Тепловая модель – массив, содержащий распределение температуры внутри объекта, рассчитанный на основе математических методов. Визуализация тепловой модели – процесс, при котором температуре каждой точки объекта ставится в соответствие определенный цвет. Полученное изображение называется термограммой.
Для целей моделирования и 3D-визуализации тепловых полей многослойных объектов, как правило, используют универсальные программные средства, не учитывающие однородности параметров внутри отдельного слоя. Методы и алгоритмы таких программных средств не позволяют оперативно менять порядок слоев, добавлять или удалять новые слои в существующий объект. После таких операций процесс моделирования необходимо начинать с нуля, что требует больших ресурсов вычислительной системы. Это отрицательно сказывается на эффективности и надежности процессов обработки и передачи данных. Примером универсальных средств моделирования служат пакеты Ansys, SolidAge, SolidWorks и пр.
Решением данной проблемы является создание специального математического и программного обеспечения, позволяющего производить моделирование и 3D-визуализацию тепловых параметров определенных классов объектов. Для снижения временных издержек, такие программы должны использовать высокоэффективные алгоритмы и методы расчета, обладать удобным человеко-машинным интерфейсом с возможностью трехмерной визуализации, а также иметь возможность сопряжения с распространенными программными средствами [1].
2. Математические методы расчета тепловых параметров
Процесс теплопроводности в декартовой системе координат описывается уравнением Фурье-Кирхгофа:
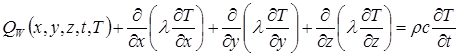 . (1)
. (1)
Это уравнение связывает временные и пространственные изменения температуры в любой точке тела. Здесь ρ – плотность, с – удельная теплоемкость, λ – коэффициент теплопроводности, QW – мощность внутренних источников тепла.
При расчете тепловых параметров многослойных объектов, целесообразно рассчитывать отдельно тепловые параметры каждого слоя и влияние соседних слоев друг на друга. Такой подход позволит оперативно пересчитывать тепловые параметры объекта при изменении порядка слоев, добавлении или удалении слоя из модели многослойного объекта.
В ряде решаемых задач слои моделируемого объекта достаточно тонкие для дискретизации по высоте [2]. В этом случае слой представляется как плоский объект единичной толщины. Уравнение (1) при расчете параметров i-го слоя примет следующий вид:
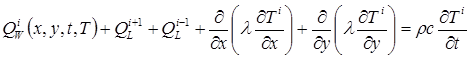 . (2)
. (2)
Здесь ![]() и
и ![]() – мощность теплопередачи от соседних слоев.
Наглядно процесс теплопередачи в многослойном объекте показан на рисунке 1.
– мощность теплопередачи от соседних слоев.
Наглядно процесс теплопередачи в многослойном объекте показан на рисунке 1.
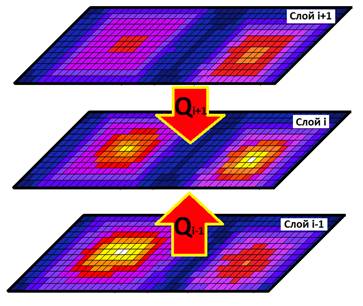
Рис. 1. Воздействие соседних слоев на распределение температуры слоя i в многослойном объекте
Условия однозначности уравнений (1) и (2) содержат геометрические, физические, начальные и граничные условия, характерные для многослойных объектов.
Геометрические условия определяют форму и размеры тела, в котором протекает моделируемый процесс. Физические условия определяют характеристики тела ρ, с, λ. Начальные условия содержат распределение температуры на начальный момент времени: t = 0: T = f(x,y,z) – в общем виде. При равномерном распределении температуры в определенном слое начальное условие упрощается: t = 0: T = T0 = const. Граничные условия определяют особенности протекания процесса на поверхности и могут быть заданы несколькими способами.
Граничные условия первого рода задают распределение температуры на внешних границах слоя для каждого момента времени:
![]() ,
,
где ![]() – температура границы слоя. Часто в условиях
решаемой задачи
– температура границы слоя. Часто в условиях
решаемой задачи
![]() = const.
= const.
Граничные условия второго рода задают значение теплового потока для каждой точки поверхности слоя в любой момент времени:
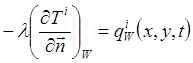 ,
,
где ![]() – нормаль к
поверхности слоя. Наиболее часто задается граничное условие
– нормаль к
поверхности слоя. Наиболее часто задается граничное условие ![]() = const.
= const.
Граничные условия третьего рода задают взаимосвязь между потоком тепла за счет теплопроводности твердой стенки и тепловым потоком из окружающей среды за счет температурного напора (закон Ньютона - Рихмана):
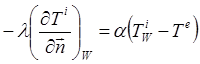 ,
,
где α – коэффициент теплообмена.
Граничные условия четвертого рода определяют тепловое взаимодействие между слоями, имеющими различные теплофизические характеристики, и задают равенства температур и тепловых потоков по обе стороны теплового раздела:
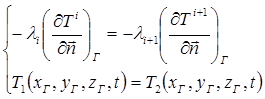
где xГ, yГ, zГ – координаты раздела сред, T1, T2 – температуры соприкасающихся сред. Это условие чаще всего применяется при решении задач теплопроводности многослойных объектов.
Дифференциальное уравнение (2) вместе с условиями однозначности дает полную математическую формулировку краевой задачи теплопроводности для тонкого слоя многослойного объекта.
В общем случае отдельный слой в свою очередь дискретизируется на ячейки равномерно в x, y, и z направлениях, δx, δy и δz – размеры стороны каждой ячейки. Смежные элементы взаимодействуют через диффузию тепла. Каждый элемент достаточно маленький, чтобы выражать его температуру как дифференциальное уравнение, рассматривать его материальные характеристики, рассеяние мощности и температуры его соседних элементов. Каждой ячейке присвоена удельная теплоемкость. Если вторая сетка будет сформирована путём присоединения к центрам смежных ячеек, то каждое ребро этой сетки пересечет точно одну грань основной сетки. Теплопроводность присвоена краю второй сетки. Если эти две ячейки по обе стороны от поверхности принадлежат одному и тому же материалу, присвоенная теплопроводность – теплопроводность материала (рис. 2).
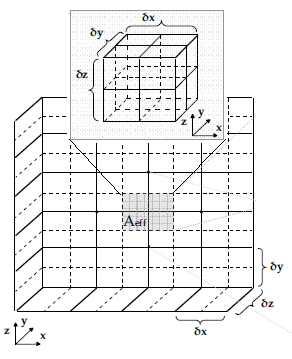
Рис. 2. Дискретизация объекта
В пределах тонкого слоя первоначально трехмерная модель упрощается до двух активных координат. Собственные тепловые параметры каждого слоя могут рассчитываться отдельно и использоваться для перерасчетов параметров моделируемого объекта при изменении порядка слоев.
Анализ современных математических методов расчета тепловых параметров выявил основные методы, наиболее подходящие для моделирования и 3D-визуализации тепловых полей многослойных объектов [2]. Эти методы характеризуются различным уровнем точности результатов и различными требованиями к вычислительной системе. В таблице 1 приведены результаты расчета тепловых параметров, полученных различными математическими методами, а также рассчитанными в среде Ansys. Расчет производился для моделей различной сложности, в качестве эталона для сравнения точности результатов расчета использованы температурные параметры, полученные при помощи тепловизионной съемки реального объекта.
Таблица 1. Сравнение различных математических методов для расчета тепловых параметров многослойного тела
|
Метод расчета |
Время моделирования (минут) для объектов различной сложности (количество элементов) |
Среднее отклонение результатов (%) |
||||
|
10 тыс. эл. |
100 тыс. эл. |
1 млн. эл. |
10 млн. эл. |
100 млн. эл. |
||
|
Функция Грина |
Менее 1 |
2.5 |
83 |
747 |
нет данных |
8 |
|
Разрывный метод Галеркина |
3 |
9 |
47 |
93 |
638 |
2 |
|
Комбинированный метод |
2.7 |
8 |
40 |
84 |
604 |
5 |
|
Ansys |
2 |
6 |
58 |
130 |
698 |
4 |
На рисунке 3 приведена примерная зависимость времени расчета тепловых параметров многослойного объекта от детализации моделируемого объекта при использовании различных математических методов.
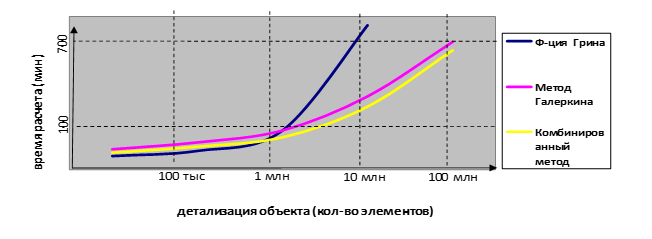
Рис. 3. Эффективность математических методов для различной детализации моделируемого объекта
Часто моделирование тепловых полей используется только для выявления критического перегрева, и детализация полной тепловой картины не играет решающей роли. В этом случае в процессе моделирования теплового поля многослойного объекта целесообразно менять математические методы расчета тепловых параметров по мере изменения температуры. Это значит, что для слоев с низкой температурой целесообразно использовать грубые методы расчета тепловых параметров и переходить к более точным методам только по мере приближения максимальной температуры слоя к заданному пользователем критическому уровню (Ткр). Изменение алгоритмов расчета происходит во время достижения пороговых уровней температуры (Тп1 и Тп2), которые рассчитываются автоматически, в зависимости от динамики изменения максимальной температуры.
Такой подход позволяет сократить время моделирования при соблюдении приемлемой точности расчетов. Порядок изменения метода расчета для слоя с детализацией менее 1 млн. элементов отображен на рисунке 4. Для более сложных объектов использование метода на основе функции Грина не рационально.
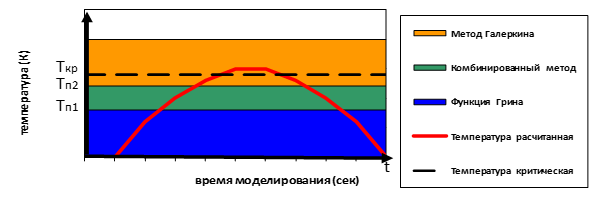
Рис. 4. Изменение метода расчета тепловых параметров слоя
Для системы моделирования и 3D-визуализации тепловых полей многослойных объектов целесообразно использование всех математических методов, описанных в [2], что даст широкие возможности рационализации по качественным и временным параметрам при решении конкретных задач.
3. Структура программных компонентов моделирования и 3D-визуализации тепловых полей многослойных объектов
Взаимосвязь программных модулей моделирования и 3D-визуализации теплового поля многослойного объекта показана на рисунке 5. Связующим звеном между этими программными модулями является специальная база данных тепловых параметров обрабатываемого объекта (далее БДТП). Поля БДТП содержат исходные и рассчитанные тепловые характеристики каждого элемента обрабатываемого объекта. К исходным характеристикам относятся теплоемкость, теплопроводность, плотность, а также геометрические параметры. К рассчитанным характеристикам относится распределение температуры в определенный момент времени.
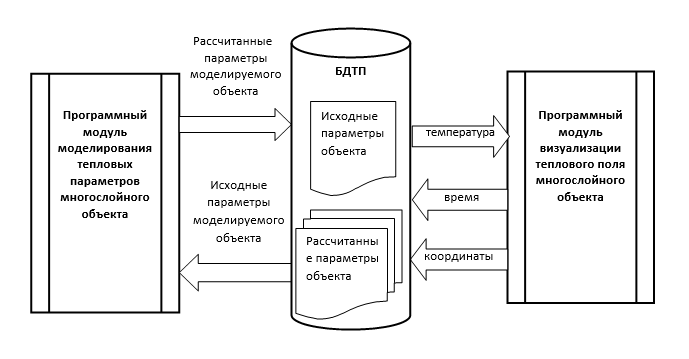
Рис. 5. Схема взаимосвязи модуля моделирования и модуля 3D-визуализации тепловых параметров многослойного объекта
Разработанный программный модуль 3D-визуализации теплового поля многослойного объекта имеет следующие возможности [3]:
- построение трехмерного изображения распределения температуры внутри моделируемого объекта;
- построение двухмерного изображения распределения температуры внутри выбранного слоя;
- отображение фактической температуры выбранной точки;
- вывод матрицы температур слоя и настройка степени дискретизации этой матрицы;
- широкий диапазон настройки соответствия температура-цвет;
- сохранение изображения в графическом формате.
Разработанный программный модуль 3D-визуализации теплового поля многослойного объекта состоит из трех основных частей – пользовательского интерфейса, системы визуализации, компонента обработки цветовых параметров и набора графических библиотек (рис. 6) .
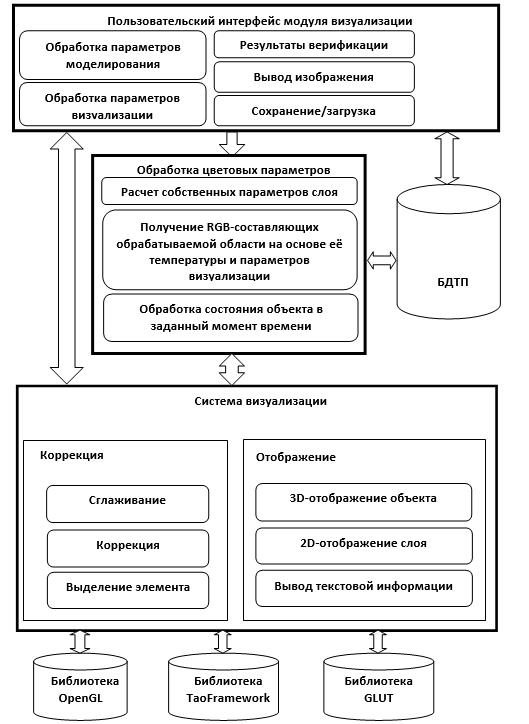
Рис. 6. Структура программного модуля 3D-визуализации теплового поля многослойного объекта
Компонент пользовательского интерфейса отображает исходный объект как в виде текста, так и в виде термограммы, а также позволяет осуществлять ввод граничных значений температур, подробнее о которых ниже. В этом модуле предусмотрены функции выбора исходного объекта и сохранения термограммы в графическом формате.
В компоненте визуализации происходит инициализация библиотеки стандарта OpenGL и отображение тепловой модели многослойного объекта в графическом виде. Этот модуль получает RGB-параметры цвета, соответствующего температуре обрабатываемого элемента. На основе цветовых параметров каждого элемента обрабатываемого объекта строится цветовой градиент, который и является термограммой.
Модуль расчета цвета определяет RGB-составляющие цвета, который соответствует входному параметру температуры. Верхняя и нижняя границы температуры определяют интервал, на котором будет происходить визуализация. Температуре, выходящей за нижнюю границу, соответствует черный цвет. Температуре, выходящей за верхнюю границу, соответствует белый цвет. Внутри интервала цветовой градиент меняется по возрастанию температуры в такой последовательности: черный, синий, фиолетовый, красный, оранжевый, желтый, белый как показано на рисунке 7.
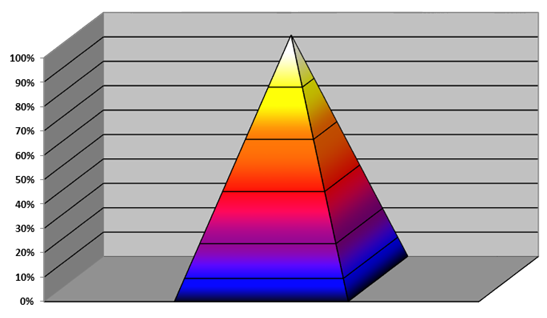
Рис. 7. Цветовой градиент для отображения температуры
Разработанный программный модуль моделирования теплового поля многослойного объекта имеет следующие возможности:
- редактирование полей БДТП;
- ввод начальных условий и параметров моделирования;
- послойная корректировка объекта;
- расчет тепловых параметров многослойного объекта при помощи различных математических алгоритмов;
- верификация объекта и динамический контроль температуры;
- выбор оптимального математического алгоритма для разных слоев и разных температурных диапазонов.
Разработанный программный модуль моделирования теплового поля многослойного объекта (см. рис. 8) состоит из четырех основных частей – пользовательского интерфейса, системы корректировки объекта, системы контроля и верификации и блока расчета тепловых параметров многослойного объекта [4, 5].
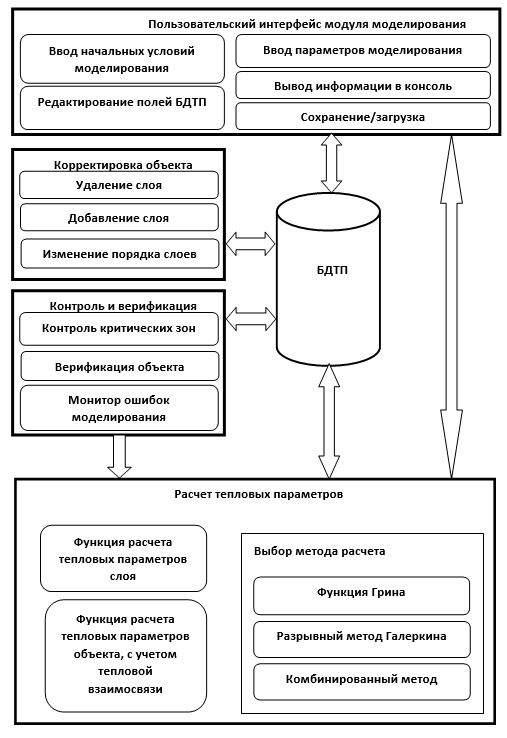
Рис. 8. Структура программного модуля моделирования теплового поля многослойного объекта
Пользовательский интерфейс разработанного программного модуля моделирования тепловых полей многослойных объектов обеспечивает возможность выбора обрабатываемого объекта, оперативного изменения параметров моделирования (шага и времени моделирования), редактирования полей выбранной БДТП и вывода статусной информации о текущем состоянии процесса моделирования.
Компонент корректировки объекта позволяет вносить изменения в порядок слоев обрабатываемого объекта, удалять и добавлять новые слои.
Компонент контроля и верификации осуществляет динамический мониторинг процесса моделирования, что позволяет выявлять критические ситуации и определять пороговые значения температур для динамического изменения алгоритма расчета. Этот компонент позволяет провести верификацию рассчитанных параметров обрабатываемого объекта, выявить зоны критического перегрева, составить отчет верификации и предложить варианты решения выявленных проблем.
Блок расчета тепловых параметров многослойного объекта проводит расчет температурного распределения на основе исходных данных БДТП. Выбор используемого математического алгоритма осуществляется с учетом пользовательских настроек и информации из компонента контроля и верификации.
4. Результаты работы программного комплекса
Представленные структурные схемы были реализованы в виде программного комплекса, позволяющего производить моделирование и визуализацию тепловых полей многослойных объектов. Данный программный комплекс был апробирован при расчете тепловых параметров микроконтроллера [2]. Для оценки результатов работы программного комплекса использовалась тепловизионная съемка процесса включения питания данного микроконтроллера. Термограмма, полученная при помощи тепловизора, приведена на рисунке 9. Окружностью выделен участок с зонами локального перегрева.

Рис. 9. Термограмма реального объекта
На рисунке 10 приведена термограмма модели микроконтроллера, полученная при помощи разработанного программного комплекса.
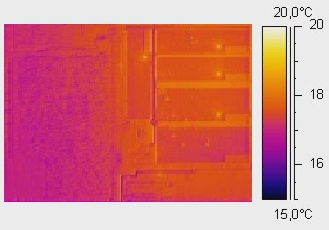
Рис. 10. Термограмма модели микроконтроллера с диапазоном отображаемых температур от 15ОС до 20ОС
Представленные термограммы идентичны. Наличие зон локального перегрева и их расположение выявлены. Таким образом, при помощи разработанного программного комплекса получена адекватная тепловая модель реального объекта.
Список литературы
1. Аралов М.Н., Барабанов В.Ф. Математические и программные средства моделирования теплового поля твердого тела слоистой структуры. Системы управления и информационные технологии. 2015. №2 (60). С. 4–8.
2. Аралов М.Н., Ачкасов А.В., Барабанов В.Ф., Подвальный С.Л. Программная реализация многовариантного математического моделирования тепловых полей. Вестник ВГТУ. 2015. Том 11, №1. С. 32–34.
3. Аралов М.Н., Барабанов А.В., Гребенникова Н.И. Визуализация тепловых полей с использованием библиотек OpenGL и TaoFramework. Вестник ВГТУ. 2015. Том 11, №1. С. 39–41.
4. Барабанов В.Ф., Аралов М.Н., Гребенникова Н.И. Математические методы моделирования тепловых полей в трехмерной сборке интегральных схем Вестник ВГТУ. 2013. Том 9, №6-3. С. 55–57.
5. Барабанов В.Ф., Подвальный С.Л., Ачкасов А.В., Аралов М.Н. Методы и алгоритмы моделирования тепловых полей в трехмерной сборке интегральных схем. Радиотехника. 2014. №6. С. 82–87.
DATA PROCESSING IN SYSTEMS OF MODEL OPERATION AND 3D-VIZUALIZATION OF HEAT EXCHANGE PROCESSES IN STRONG MULTILAYER OBJECTS
M.N. Aralov, V.F. Barabanov, A.D. Danilov, S.L. Podvalny
Voronezh state technical university, Russian Federation
aralow@mail.ru, bvf@list.ru, danilov-ad@yandex.ru
Abstract
This article is devoted to problems of model operation of the thermal processes proceeding in strong multilayer objects. For model operation of such processes it is offered to use the express software with a possibility of interface to widespread graphic systems and development tools. The complex of mathematical methods for efficient calculation of heat parameters of multilayer object with the subsequent their visualization is offered. The comparative characteristic of results of calculation of the heat parameters received by means of various mathematical methods is provided. Recommendations for increase of effectiveness and reliability of processing of data are made, when using of the developed software for model operation and 3D - visualization of thermal fields of multilayer objects. The structure of a program complex for model operation and 3D - visualization of thermal fields of multilayer objects is presented. The developed program complex allows to make calculation, adjustment and verification of heat parameters, and also visualization of thermal model of multilayer object. Results of work of a program complex are given in the conclusion.
Keywords: multilayer object, thermal model operation, thermogram, data processing, 3D - visualization.
References
1. Aralov M.N., Barabanov V.F. Matematicheskie i programmnye sredstva modelirovanija teplovogo polja tverdogo tela sloistoj struktury [Mathematical and software simulation of the thermal field of a solid layered structure]. Control Systems and Information Technology. 2015. No. 2 (60). Pp. 4–8. [In Russian]
2. Aralov M.N., Achkasov A.V., Barabanov V.F., Podval'nyj S.L. Programmnaja realizacija mnogovariantnogo matematicheskogo modelirovanija teplovyh polej [Program realization of multivariant mathematical model operation of thermal fields]. VGTU Bulletin. 2015. Vol. 11, No. 1. Pp. 32–34. [In Russian]
3. Aralov M.N., Barabanov A.V., Grebennikova N.I. Vizualizacija teplovyh polej s ispol'zovaniem bibliotek OpenGL i TaoFramework [Visualization of thermal fields with use of OpenGL and TaoFramework libraries]. VGTU Bulletin. 2015. Vol. 11, No. 1. Pp. 39–41. [In Russian]
4. Barabanov V.F., Aralov M.N., Grebennikova N.I. Matematicheskie metody modelirovanija teplovyh polej v trehmernoj sborke integral'nyh shem [Mathematical methods of model operation of thermal fields in three-dimensional assembly of chips]. VGTU Bulletin. 2013. Vol. 9, No. 6-3. Pp. 55–57. [In Russian]
5. Barabanov V.F., Podval'nyj S.L., Achkasov A.V., Aralov M.N. Metody i algoritmy modelirovanija teplovyh polej v trehmernoj sborke integral'nyh shem [Methods and algorithms of model operation of thermal fields in three-dimensional assembly of chips]. Radio engineering . 2014. No. 6. Pp. 82–87. [In Russian]