ВИЗУАЛИЗАЦИЯ ДИСКРЕТНОГО МНОЖЕСТВА ТОЧЕК ПРИ ПОМОЩИ ПЛАВНЫХ КРИВЫХ БЕЗ ЛОЖНЫХ ЭКСТРЕМУМОВ
К.В. Рябинин
Пермский государственный национальный исследовательский университет, Пермь, Россия
Содержание
2. Критерии качества плавной кривой
4. Построение плавных кривых в популярном программном обеспечении
5. Наиболее распространённые способы построения плавных кривых
6. Построение плавной кривой без ложных экстремумов на основе кривых Безье
Статья посвящена вопросу визуализации дискретного множества точек, соединённых плавной кривой, при условии, что недопустимыми являются ложные экстремумы (экстремумы кривой в точках, не принадлежащих входному набору), ложные самопересечения (самопересечения кривой в случае, когда ломаная, соединяющая точки исходного набора, самопересечений не имеет) и осцилляции (существенные отклонения кривой от ломаной, соединяющей точки исходного набора). Такие условия могут возникать, например, в задачах визуальной аналитики репрезентативных выборок измерений каких-либо параметров (например, эконометрических показателей или физических величин), являясь при этом критичными с точки зрения правильной интерпретации результатов визуализации.
В статье проанализированы средства в составе популярного программного обеспечения, позволяющие отображать дискретные множества точек при помощи плавных кривых, и сделан вывод, что далеко не везде поддерживаются режимы, адекватные описанной задаче. Кроме того, рассмотрены наиболее распространённые на практике способы интерполяции плавными кривыми и выяснено, что большинство из них в классическом виде также оказываются непригодными для решения данной задачи.
В связи с этим актуальной является разработка нового способа, позволяющего строить плавные кривые без ложных экстремумов, ложных самопересечений и осцилляций, по заданным наборам точек.
Приводится авторское решение данной задачи для двумерного случая. Предлагаемый способ основан на построении по входному набору точек кусочно-заданной параметрической кривой, сегментами которой являются кубические кривые Безье. Концевые точки каждой из них берутся из входного набора, а промежуточные контрольные точки рассчитываются таким образом, чтобы удовлетворить заявленным требованиям. Данный способ по визуальному качеству результата не уступает известным решениям, и, в отличие от большинства из них, может быть гибко сконфигурирован для адаптации к специализированным задачам.
По результатам проведённых исследований был реализован алгоритм построения плавных кривых, интегрированный в разрабатываемую и поддерживаемую автором библиотеку NChart3D и систему научной визуализации SciVi.
Ключевые слова: гладкая интерполяция, кривая Безье, ложные экстремумы, плавная кривая, построение графиков, визуальная аналитика.
1. Введение
Один из самых распространённых способов визуализации дискретного множества точек – построение линии, интерполирующей это множество. Такой способ используется в визуальной аналитике, когда необходимо показать некоторый потенциально непрерывный процесс или явление, основываясь на дискретном множестве состояний.
В данной статье будет рассматриваться случай, когда входные данные представлены лишь множеством из n точек, и никакой дополнительной информации о характере визуализируемого процесса или явления нет. Такой случай является наиболее общим и допускает различные подходы к интерполяции заданных точек в зависимости от преследуемых целей визуализации, но безотносительно природы самих точек.
Самым простым вариантом интерполяции является линейная – в этом случае результат визуализации представляет собой ломаную, проходящую через заданные точки. Однако ломаная не всегда оказывается адекватной задачам наглядного представления данных: в целях большей привлекательности итогового изображения и лучшей читаемости графика часто предпочтительнее оказывается построить гладкую кривую, то есть кривую, имеющую непрерывные производные до k-го порядка включительно, где k – порядок гладкости.
На практике наиболее популярным способом гладкой интерполяции являются сплайны степени m – кусочно-заданные функции, состоящие из полиномов степени m. Разность между степенью сплайна и порядком последней непрерывной его производной называется дефектом этого сплайна.
Часто для построения гладких кривых используется кубический сплайн дефекта 1 [1] (обладающий, соответственно, гладкостью второго порядка). Однако особенностью этого способа, как и многих других способов построения гладких кривых по дискретному множеству точек, являются возникающие в результате интерполяции ложные экстремумы (т. н. выбросы) – экстремумы, не принадлежащие исходному множеству точек. Данная ситуация продемонстрирована на рис. 1.
В ряде случаев ложные экстремумы могут оказаться серьёзным недостатком с точки зрения визуализации. Например, если предположить, что на оси абсцисс графика на рис. 1 отложено время, на оси ординат – доходы (и убытки) некоторого предприятия, а точки 1–17 соответствуют значениям доходов/убытков в конце отчётных периодов, то линейная интерполяция будет соответствовать динамике финансовой эффективности предприятия, тогда как кубический сплайн дефекта 1 сформирует у зрителя абсолютно ложное представление о положении дел на этом предприятии.
В большинстве современных систем визуализации данных и визуальной аналитики, в частности, в популярных коммерческих программных продуктах, присутствует возможность использования гладких интерполяций при визуализации дискретного множества точек, однако проблема ложных экстремумов решена далеко не везде.
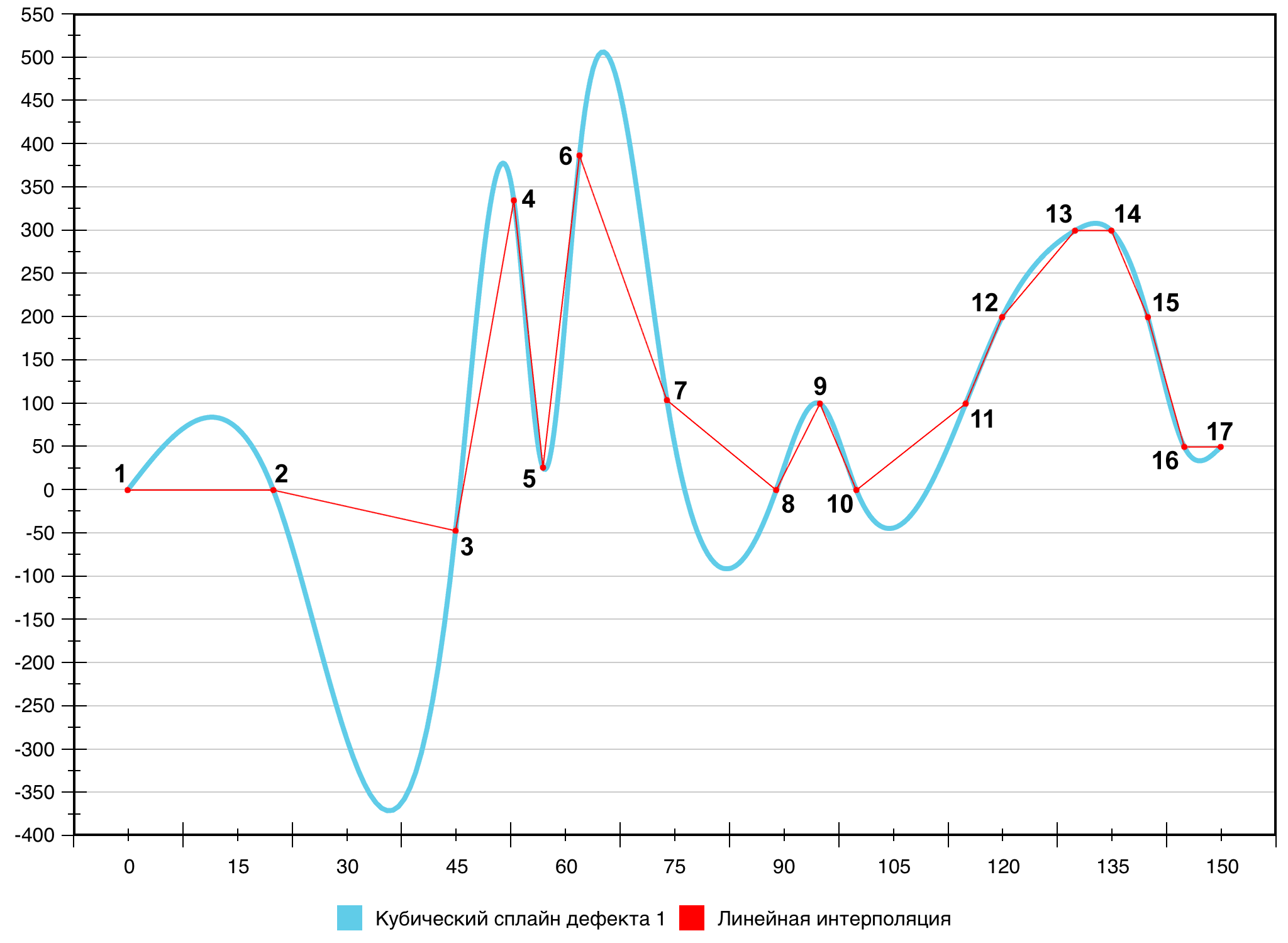
Рис. 1. Сравнение кубического сплайна дефекта 1 и линейной интерполяции
Важно отметить, что для обеспечения высокого визуального качества результата и удобства читаемости графика требуется скорее не математически строгая гладкость итоговой кривой, а её визуальная плавность – отсутствие заметных изломов. Далее в тексте под плавной кривой будет пониматься кривая, визуально не имеющая изломов, то есть кажущаяся гладкой (при этом не обязательно имеющая непрерывные производные на области своего определения), а под плавной интерполяцией – способ построения такой кривой по заданному дискретному множеству точек.
Актуальной задачей является разработка способов построения плавных кривых, обладающих высоким визуальным качеством (наглядно демонстрирующих исходное множество, по возможности не допускающих неоднозначностей в интерпретации и эстетично смотрящихся), интерполирующих заданное множество точек и не порождающих при этом ложных экстремумов. Целью данной работы является решение такой задачи для двумерного случая.
Созданный в рамках данной работы способ интерполяции дискретного множества точек был использован в библиотеке визуализации данных NChart3D [2] и в системе научной визуализации SciVi [3].
2. Критерии качества плавной кривой
Оценка визуального качества изображений, как правило, является субъективной. С точки зрения визуальной аналитики главная задача визуализации – быть наглядной и непротиворечивой, чтобы помочь зрителю сделать правильные выводы относительно анализируемых процессов и явлений. Наглядность и непротиворечивость, в свою очередь, уже более объективные требования, которые в зависимости от конкретного класса задач могут быть достаточно точно сформулированы, а иногда даже строго формализованы.
Авторами предлагается следующих список требований, которым
должна удовлетворять кривая, интерполирующая дискретное множество точек ![]() :
:
1. Плавность: на кривой не должно быть заметных изломов, либо их число должно быть минимальным.
2. Отсутствие
ложных экстремумов: минимум и максимум кривой на отрезке ![]() ,
, ![]() должны
достигаться лишь в граничных точках, кроме того, кривая должна быть монотонна
на каждом из этих отрезков.
должны
достигаться лишь в граничных точках, кроме того, кривая должна быть монотонна
на каждом из этих отрезков.
3. Отсутствие самопересечений, если таковых не имеет ломаная, полученная в результате линейной интерполяции.
4. Отсутствие
существенных колебаний вдоль оси абсцисс: отсутствие пересечения кривой на
отрезке ![]() ,
, ![]() и
прямых, проходящих через точки
и
прямых, проходящих через точки ![]() ,
, ![]() ,
перпендикулярных оси абсцисс, а также отсутствие осцилляций вдоль оси абсцисс у
кривой на каждом из сегментов
,
перпендикулярных оси абсцисс, а также отсутствие осцилляций вдоль оси абсцисс у
кривой на каждом из сегментов ![]() .
.
5. Наличие эффективных алгоритмов построения.
Следует отметить, что данные требования не являются универсальными и в зависимости от конкретных прикладных задач визуализации могут корректироваться. Однако в данной статье рассматривается класс задач наглядного отображения дискретного множества точек, при интерполяции которого ложные экстремумы недопустимы. К этому классу относятся, например, задачи отображения результатов каких-либо достаточно частых измерений: при достаточно частом измерении все пики скорее всего будут отражены в известных результатах. Причём объект измерений в данном случае не имеет значения: ложные экстремумы (такие, например, как на сегменте 1–2 на рис. 1) будут одинаково негативно сказываться на интерпретации результатов финансовой отчётности предприятия, температуры воздуха, демографической ситуации и т. д.
Первое требование относится к визуальному качеству и является скорее субъективным. Как уже отмечалось выше, в некоторых случаях линейная интерполяция неадекватна задаче отображения данных, так как требуется получить такой график, вдоль которого скользил бы взгляд. Кроме того, плавность кривой часто способна придать определённую презентабельность итоговому изображению, так как психологически плавный график воспринимается как более точный (как будто бы построенный по большему числу опорных значений), что часто применяется, например, в рекламных презентациях. В этом случае критичной оказывается минимизация ложной информации, сообщаемой через изображение зрителю.
Второе требование следует из самой постановки задачи. Если предположить, что исходный набор значений анализируемого параметра репрезентативен (в противном случае анализ несостоятелен), логичным будет и предположение о монотонности переходов от одного известного значения к другому (в условиях отсутствия дополнительной информации о природе изменения параметра), что, в свою очередь, означает отсутствие экстремумов, не принадлежащих входному множеству точек.
Третье требование относится к однозначности интерпретации полученного графика. Если, например, на оси абсцисс отложено время (как это часто бывает при отображении результатов различных измерений), кривая с петлями может быть неверно трактована зрителем.
Четвёртое требование имеет такой же смысл, как второе и третье, по сути дополняя и усиливая их.
Пятое требование предъявляется уже не к самой кривой, а к алгоритму её построения: при создании систем визуализации скорость обработки данных и требуемый для этого объём памяти часто оказываются весьма значимыми характеристиками используемых алгоритмов. Поэтому чем меньше накладных расходов будет иметь программная реализация построения плавной кривой по заданным точкам, тем лучше.
3. Тестовый набор точек
В зависимости от конкретного способа интерполяции ложные экстремумы и колебания вдоль оси абсцисс могут проявляться в различных ситуациях взаимного расположения исходных точек.
В таблице 1 авторами предлагается набор двумерных точек для выяснения особенностей способов построения плавных кривых в популярном программном обеспечении, сравнения известных способов интерполяции и тестирования разработанного в рамках данного исследования алгоритма.
Таблица 1. Множество точек для тестирования плавной интерполяции
|
№ |
X |
Y |
|
1 |
0 |
0 |
|
2 |
20 |
0 |
|
3 |
45 |
–47 |
|
4 |
53 |
335 |
|
5 |
57 |
26 |
|
6 |
62 |
387 |
|
7 |
74 |
104 |
|
8 |
89 |
0 |
|
9 |
95 |
100 |
|
10 |
100 |
0 |
|
11 |
115 |
100 |
|
12 |
120 |
200 |
|
13 |
130 |
300 |
|
14 |
135 |
300 |
|
15 |
140 |
200 |
|
16 |
145 |
50 |
|
17 |
150 |
50 |
Приведённый набор покрывает большинство практически значимых случаев взаимного расположения точек: «плато» (равенство ординат подряд идущих точек, отрезки 1–2, 13–14, 16–17), «остроугольный пик» (например, отрезок 3–5), «тупоугольный пик» (отрезки 7–9 и 9–11), «выпуклый скат» (отрезки 11–13 и 14–16), «вогнутый скат» (отрезки 6–8 и 10–12) и т. п. Благодаря этому на основе данного набора становится возможным оценивать качество интерполяции и определять её особенности. Так, например, именно этот набор точек был использован для построения графика, изображённого на рис. 1. Этот же набор использовался и для других тестов, описанных в данной статье.
4. Построение плавных кривых в популярном программном обеспечении
Как отмечалось выше, возможность визуализации дискретного множества точек в виде плавной кривой поддерживается во многих популярных программных продуктах, доступных как конечным пользователям (системы научной визуализации и визуальной аналитики), так и программистам (библиотеки визуализации данных).
Одними из самых базовых, и, в то же время, самых популярных средств визуальной аналитики являются табличные процессоры Microsoft Excel [4] и OpenOffice Calc [5]. Эти программы просты в использовании и обладают достаточно широкой функциональностью для обработки и визуализации числовых данных. В частности, в них поддерживается и построение плавных кривых.
Результат такого построения по приведённому в таблице 1 набору точек в Microsoft Excel представлен на рис. 2. В данной программе поддерживается лишь один способ построения плавной кривой, который, как можно видеть на рис. 2, даёт достаточно много ложных экстремумов (на отрезках 1–2, 2–3, 13–14, 16–17).
OpenOffice Calc предоставляет возможность строить плавные кривые двумя разными способами – при помощи кривой Безье [6] (рис. 3) и B-сплайна [6] (рис. 4). В первом случае ложных экстремумов оказывается даже больше, чем на графике, построенном в Microsoft Excel. Во втором случае ложные экстремумы, хотя и присутствуют (например, в окрестности точки 8), но значительно менее заметны. При этом, однако, на графике образуются колебания вдоль оси абсцисс и самопересечения (отрезки 1–4, 11–16).
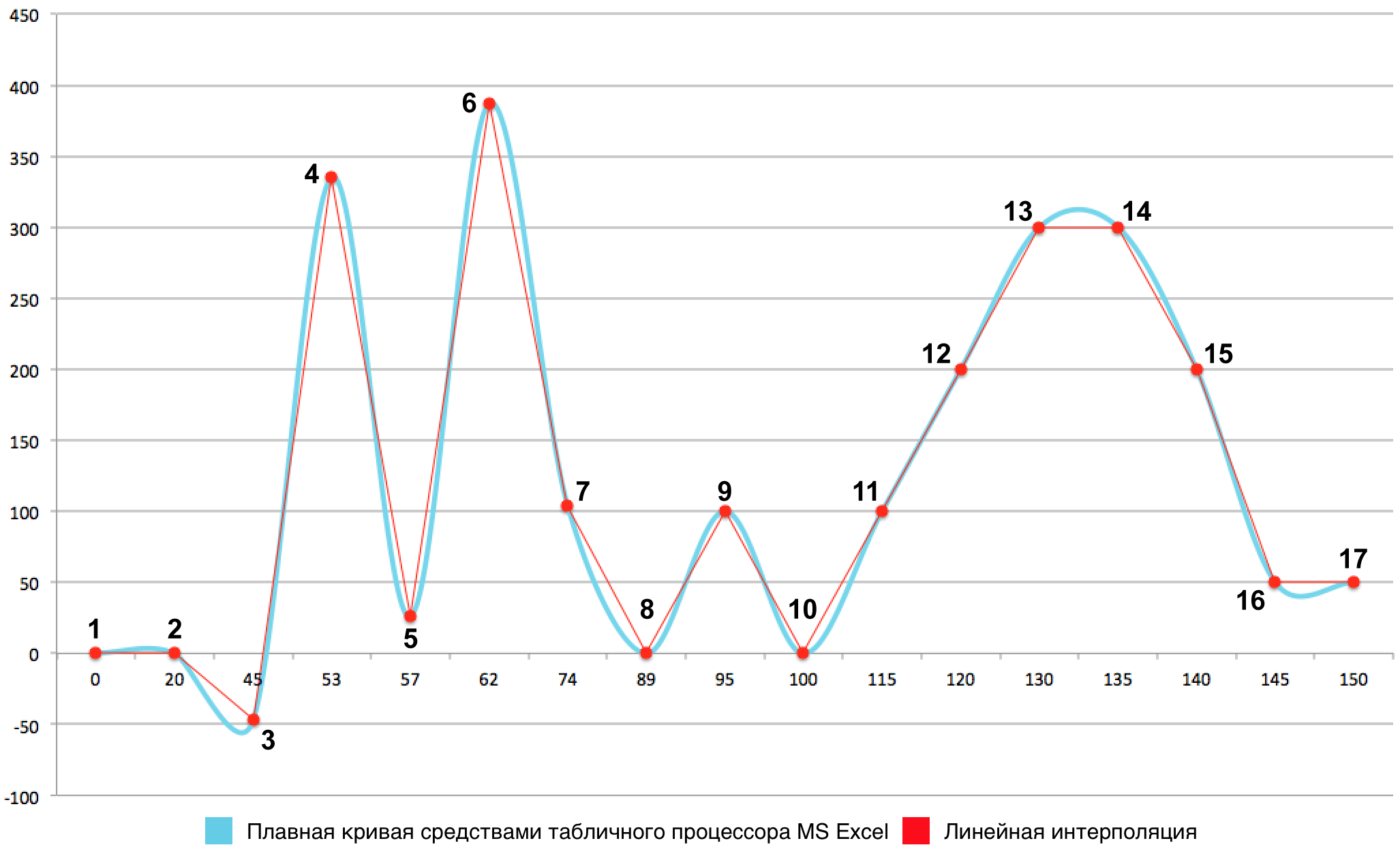
Рис. 2. Сравнение плавной кривой, построенной средствами табличного процессора Microsoft Excel, с линейной интерполяцией
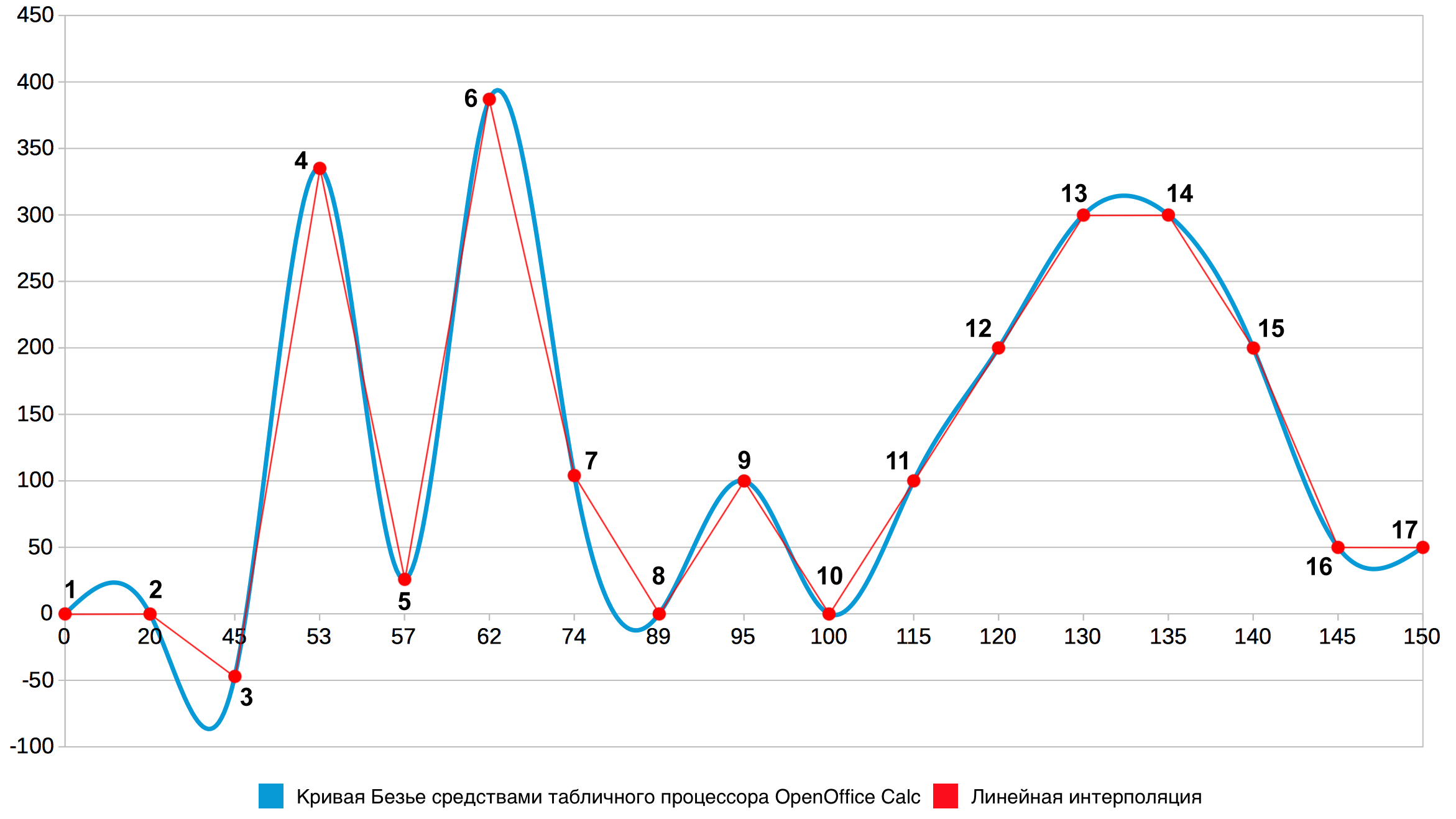
Рис. 3. Сравнение кривой Безье, построенной средствами табличного процессора OpenOffice Calc, с линейной интерполяцией
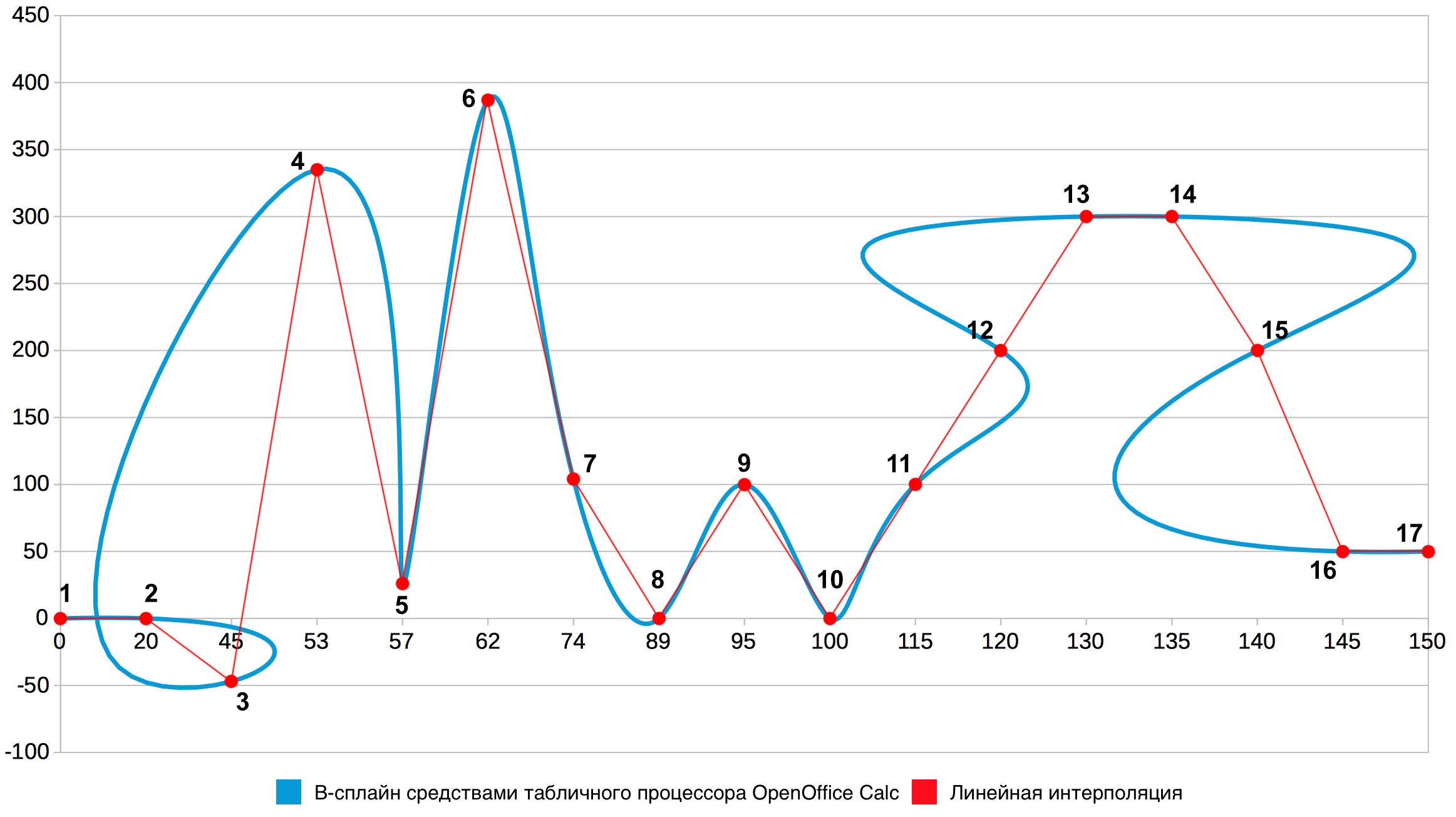
Рис. 4. Сравнение B-сплайна, построенного средствами табличного процессора OpenOffice Calc, с линейной интерполяцией
Одними из самых популярных на сегодняшний день библиотек визуализации данных, поддерживающих построение плавных кривых, являются Highcharts [7] (для создания Web-приложений), amCharts [8] (также для создания Web-приложений), CorePlot [9] (для создания мобильных приложений под iOS и настольных приложений под macOS) и AChartEngine [10] (для создания мобильных приложений под Android).
Результат использования библиотеки Highcharts для визуализации множества точек из таблицы 1 представлен на рис. 5. Как можно видеть, проблема ложных экстремумов в данном случае полностью решена, причём сохранено высокое визуальное качество и наглядность результирующей кривой.
Результат построения плавной кривой по тестовым данным при помощи библиотеки amCharts представлен на рис. 6. Полученная кривая очень похожа на построенную в Microsoft Excel (рис. 2) и имеет ложные экстремумы в тех же местах.
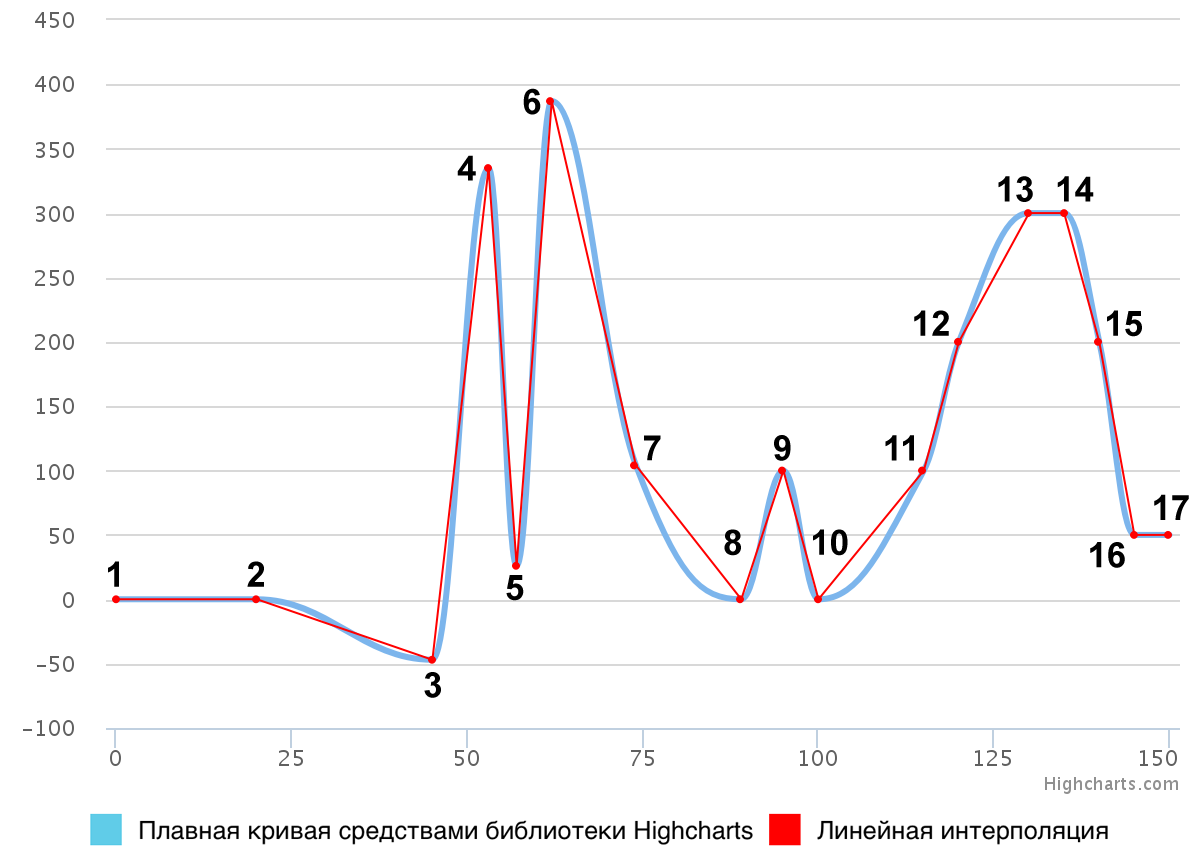
Рис. 5. Сравнение плавной кривой, построенной средствами библиотеки Highcharts, с линейной интерполяцией
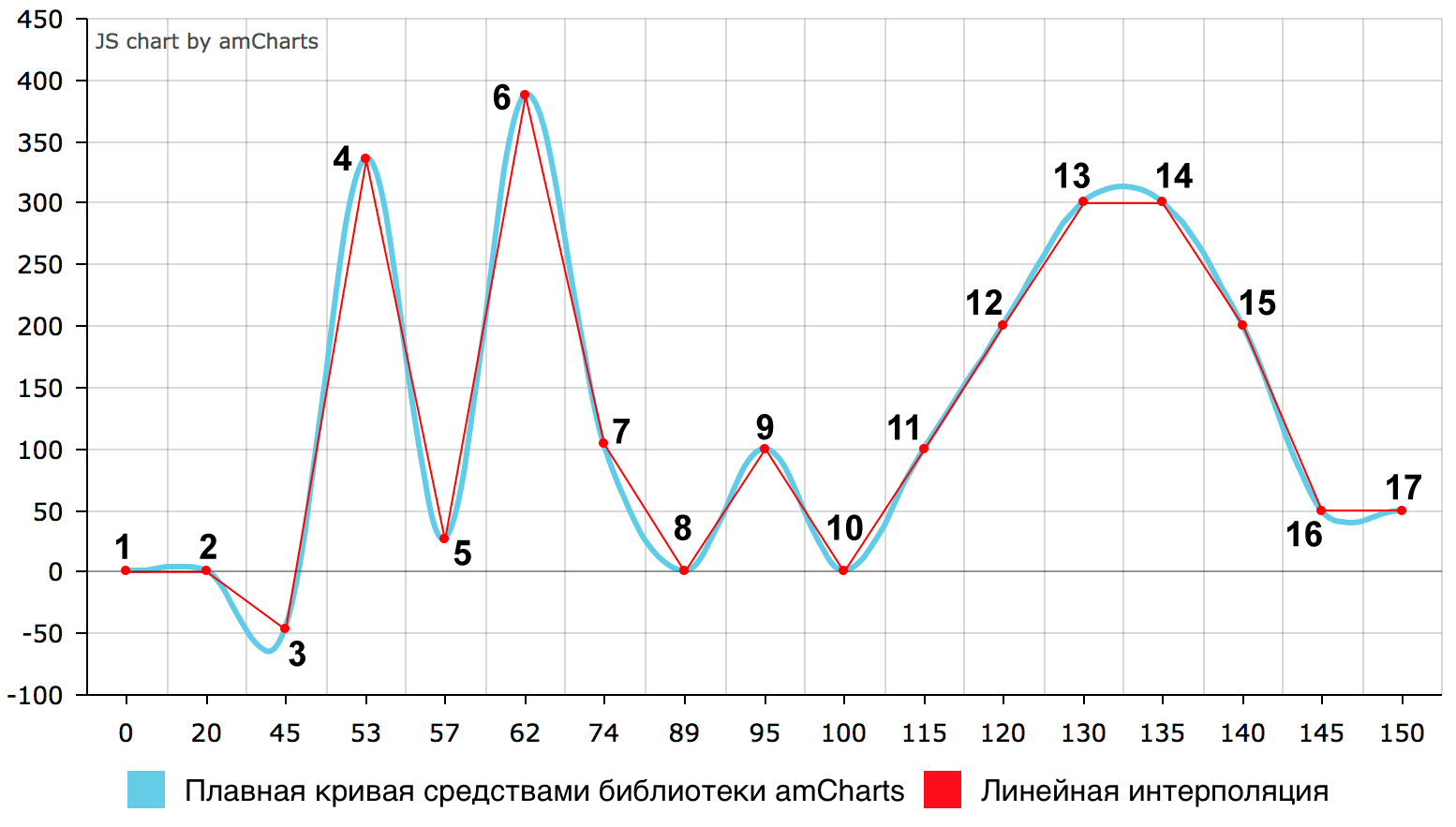
Рис. 6. Сравнение плавной кривой, построенной средствами библиотеки amCharts, с линейной интерполяцией
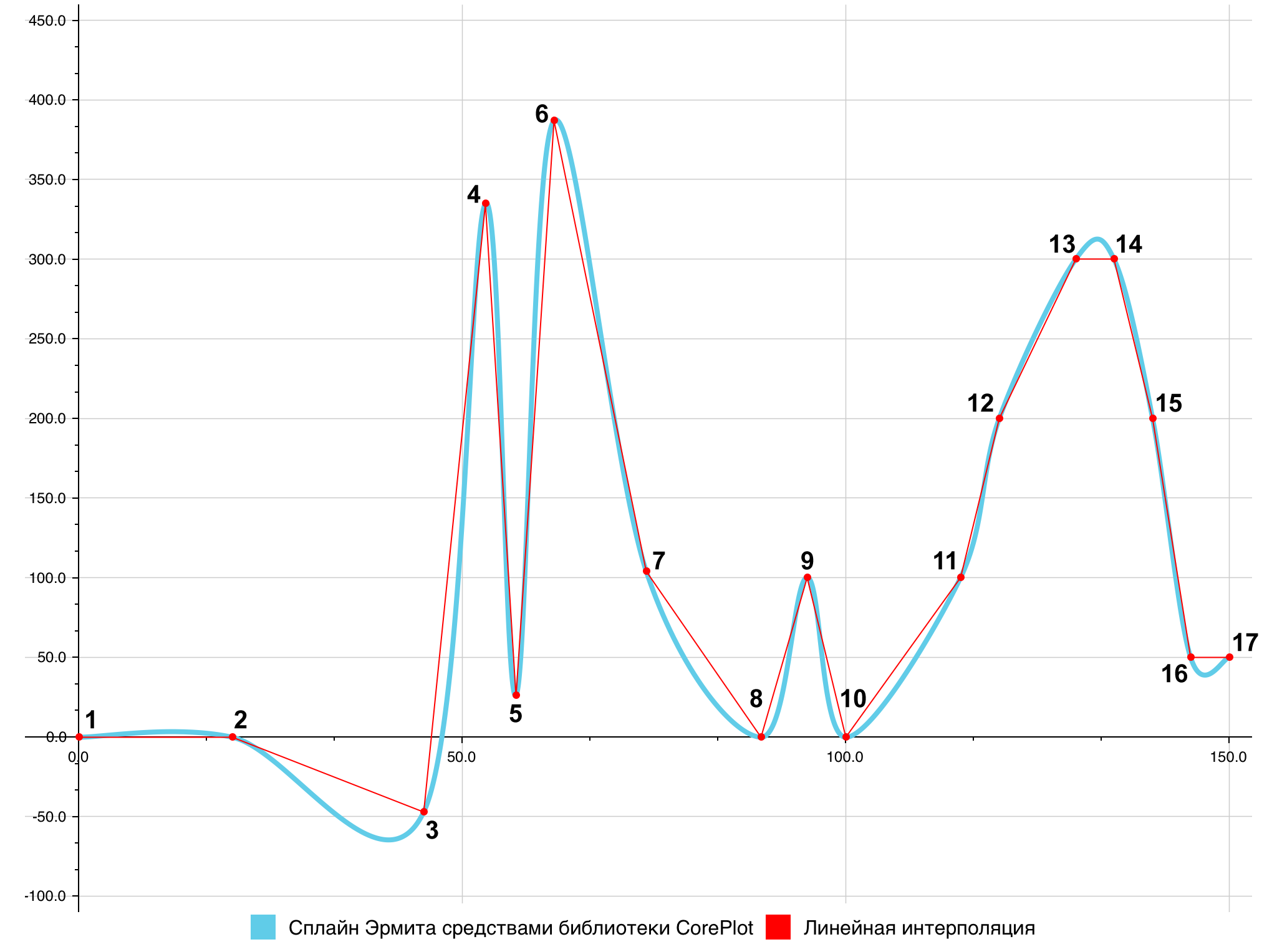
Библиотека CorePlot на данный момент поддерживает три различных способа построения плавных кривых: кривая Безье (рис. 7), сплайн Эрмита [11] (рис. 8) и сплайн Катмулла-Рома [12] (в частности, в библиотеке есть три выделенных разновидности этого сплайна – равномерный, центростремительный и хордальный; рис. 9).
Как можно видеть, все варианты порождают ложные экстремумы, хотя в случае хордального сплайна Катмулла-Рома они почти не заметны, присутствуя лишь на отрезках с совпавшими ординатами: 1–2, 13–14, 16–17. Но данный сплайн, в свою очередь, содержит самопересечение на отрезке 3–5.
В публичный API библиотеки CorePlot для сплайна Катмулла-Рома вынесен параметр, влияющий на кривизну его сегментов. Однако даже подбором этого параметра невозможно полностью избавиться от возникновения ложных экстремумов. Так, например, три представленных на рис. 9 сплайна различаются, по сути, лишь значениями этого параметра, а наличие у них специальных названий свидетельствует только о частоте практического применения данных выделенных значений.
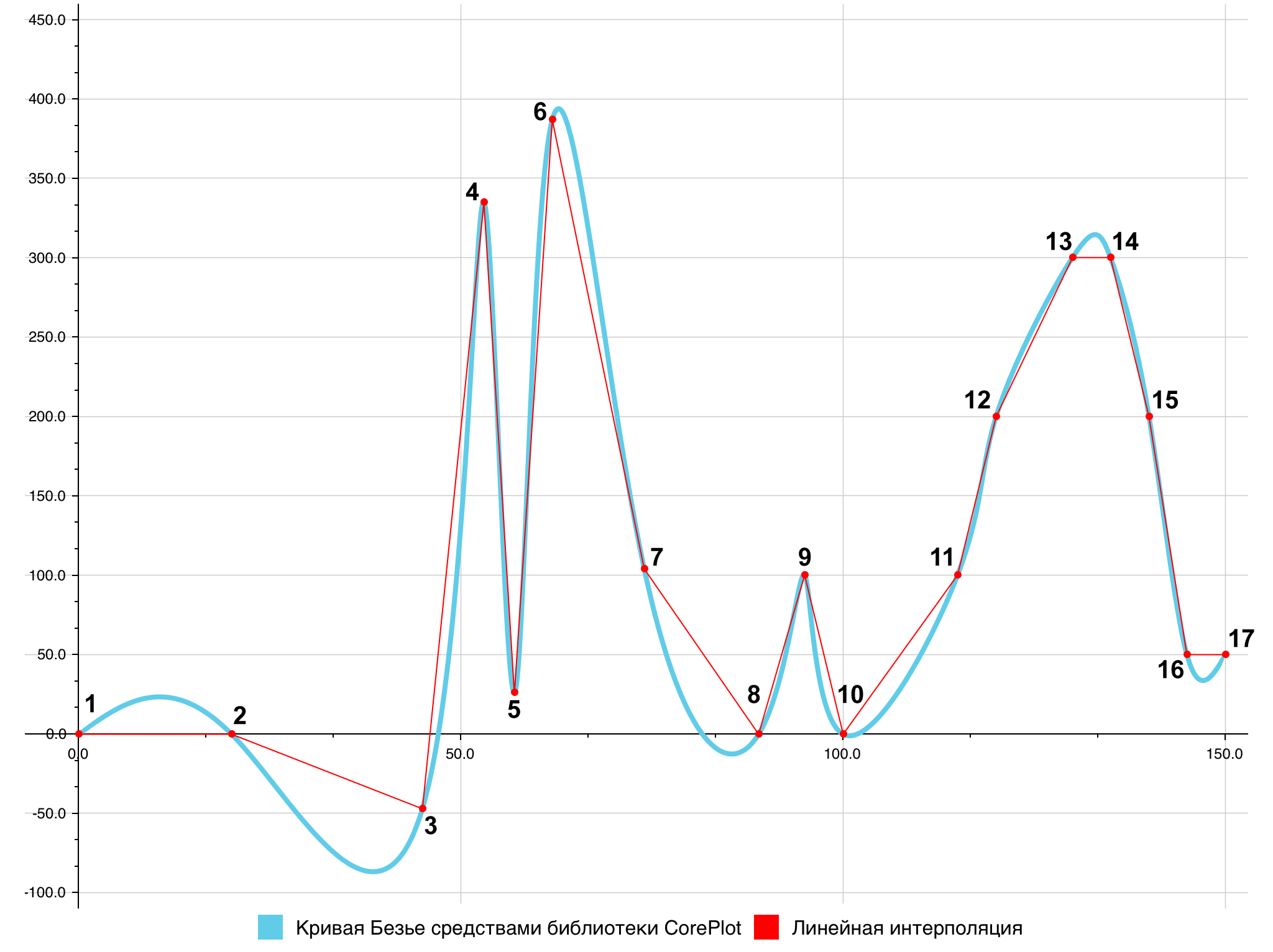
Рис. 7. Сравнение кривой Безье, построенной средствами библиотеки CorePlot, с линейной интерполяцией
Нетрудно заметить, что полученная средствами библиотеки CorePlot кривая Безье выглядит так же, как и кривая Безье, построенная в OpenOffice Calc (и имеет ложные экстремумы в тех же местах), что говорит об одинаковых подходах к построению этого типа кривых в указанном программном обеспечении.
Примечательно также, что полученный средствами библиотеки CorePlot сплайн Эрмита очень похож на плавные кривые, построенные в Microsoft Excel и amCharts. Из этого можно сделать предположение, что Microsoft Excel и amCharts используют именно сплайн Эрмита как способ гладкой интерполяции дискретного множества точек, хотя и не сообщают об этом ни на уровне графического интерфейса, ни в своей документации (исходный код же этих продуктов закрыт).
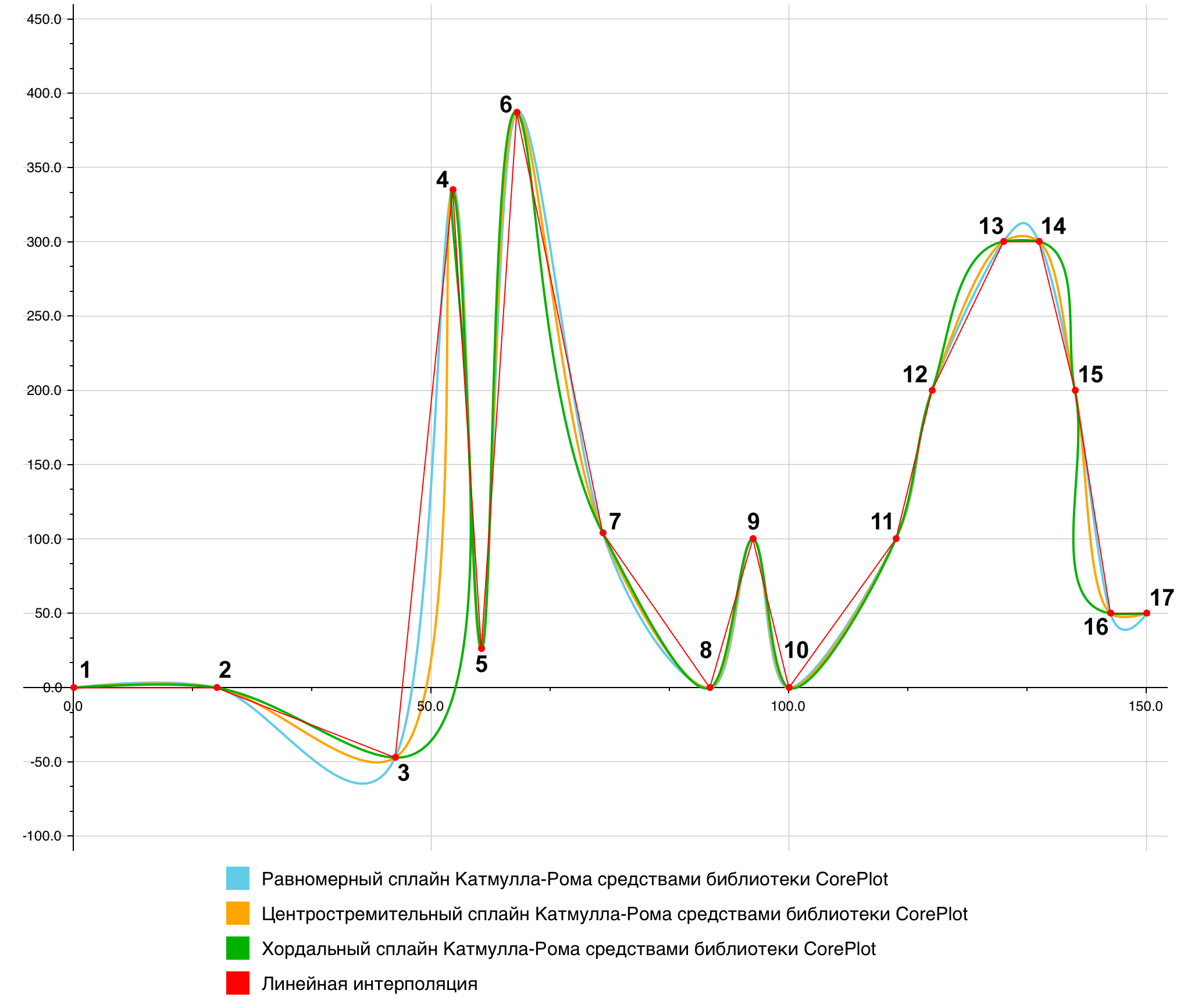
Рис. 9. Сравнение равномерного, центростремительного, хордального сплайнов Катмулла-Рома, построенных средствами библиотеки CorePlot, с линейной интерполяцией
Результат построения плавной кривой средствами библиотеки AChartEngine представлен на рис. 10. В отличие от предыдущих рассмотренных способов, значение ординаты в ложных экстремумах здесь по модулю меньше, а не больше соответствующих ординат точек из исходного множества, а полученная кривая не удовлетворяет условию интерполяции (не проходит через все заданные точки).
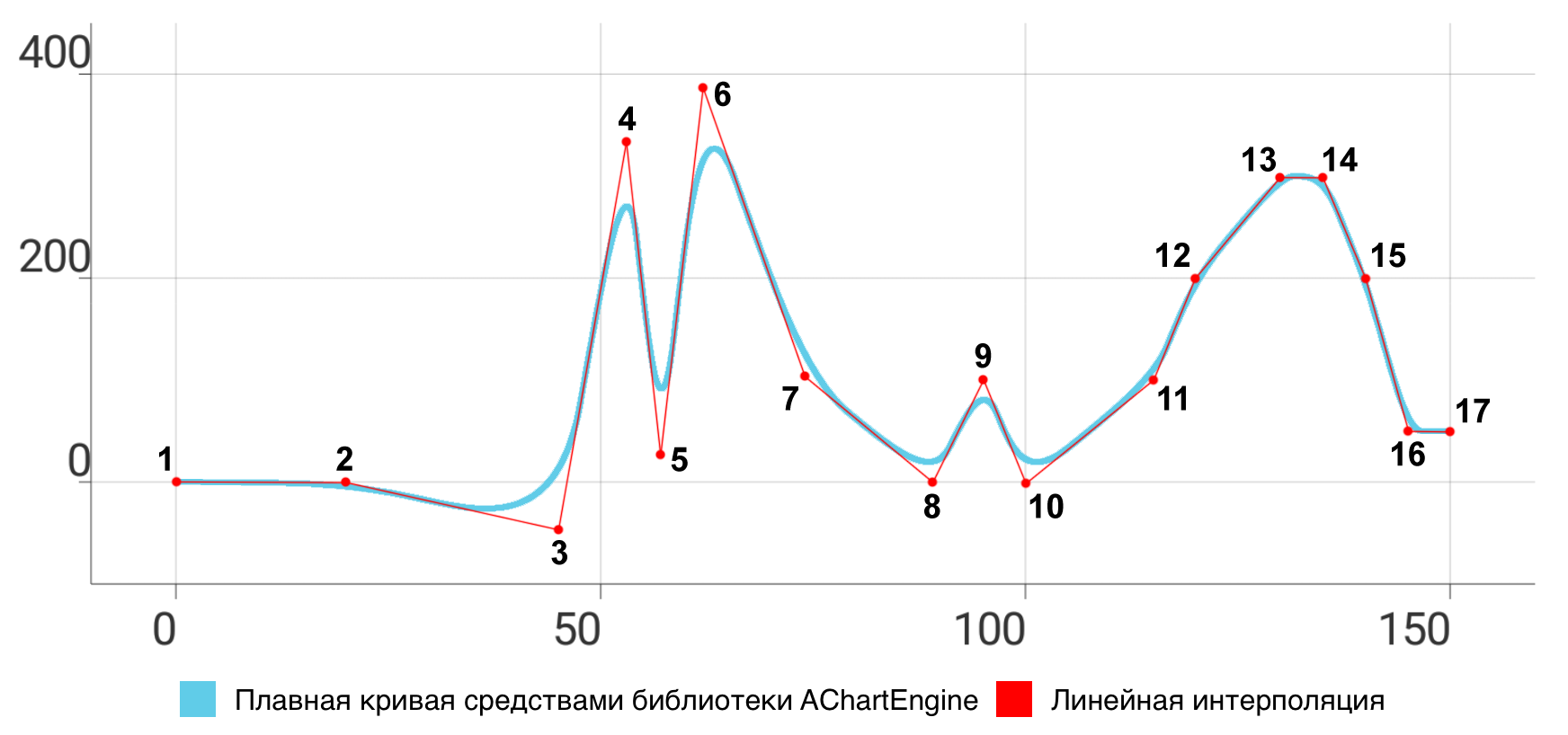
Рис. 10. Сравнение плавной кривой, построенной средствами библиотеки AChartEngine, с линейной интерполяцией
На основе приведённых выше результатов сравнения различных программных продуктов можно сделать вывод о том, что наиболее качественную с точки зрения рассматриваемых в данной статье критериев визуализацию дискретного множества точек в виде плавной кривой обеспечивает библиотека Highcharts. При этом исходный код этой библиотеки закрыт, а в документации ничего не сказано об используемых для такого рода визуализации способах.
В процессе разработки библиотеки визуализации данных NChart3D и базирующейся на ней системы научной визуализации SciVi автором было принято решение также поддержать функциональность построения плавных кривых по дискретному множеству точек. Для обеспечения конкурентоспособности этих продуктов наравне с популярными аналогами, было решено реализовать несколько способов интерполяции, чтобы у пользователя появилась возможность выбора в зависимости от решаемой прикладной задачи. Среди этих способов, помимо классических (таких, например, как кривая Безье или сплайн Эрмита, порождающих ложные экстремумы), необходимо было реализовать и такой, который бы гарантировал отсутствие на результирующей кривой ложных экстремумов, существенных колебаний вдоль оси абсцисс и самопересечений. При этом визуальное качество такой кривой должно быть, как минимум не ниже, чем в библиотеке Highcharts.
5. Наиболее распространённые способы построения плавных кривых
На сегодняшний день существует достаточно много различных способов получения плавных (в частности – гладких, то есть имеющих непрерывные производные на всей своей области определения) кривых. Чтобы разработать способ, удовлетворяющий требованиям из раздела 2, было решено идти по пути адаптации существующих.
Наиболее популярными способами построения плавных кривых являются:
1. Кубический сплайн дефекта 1.
2. Сплайн Эрмита.
3. Сплайн Катмулла-Рома.
4. Сплайн Акимы [13].
5. Полином Лагранжа [14].
6. Кривая Безье.
Кубический сплайн дефекта 1, как было продемонстрировано на
рис. 1, порождает ложные экстремумы, причём в ряде случаев очень сильно
отличающиеся от заданных интерполируемых значений. Этот сплайн в алгоритме
своего построения не содержит никаких параметров, которые могли бы быть
настроены, а также известно, что для заданного множества точек ![]() ,
, ![]() при
условии свободных концов (равенства нулю вторых производных сплайна в точках
при
условии свободных концов (равенства нулю вторых производных сплайна в точках ![]() и
и ![]() ) его
построение единственно. Следовательно, он не может быть модифицирован и
непригоден для решения поставленной в данной работе задачи.
) его
построение единственно. Следовательно, он не может быть модифицирован и
непригоден для решения поставленной в данной работе задачи.
Сплайн Эрмита (кубический), продемонстрированный на
рис. 8, в своём каноническом виде также может содержать ложные экстремумы.
Однако в ходе построения он требует знание касательных векторов к кривой в
точках ![]() , ,
, , ![]() , и
его конкретный вид зависит от способа вычисления этих векторов. Так, например,
на рис. 8 изображён сплайн Эрмита, касательные векторы к которому
вычислены по простой конечно-разностной схеме. При выборе другого способа
вычисления касательных векторов будут получаться другие результирующие кривые.
Следовательно, сплайн Эрмита можно рассматривать как потенциальную основу для
решения поставленной в данной работе задачи.
, и
его конкретный вид зависит от способа вычисления этих векторов. Так, например,
на рис. 8 изображён сплайн Эрмита, касательные векторы к которому
вычислены по простой конечно-разностной схеме. При выборе другого способа
вычисления касательных векторов будут получаться другие результирующие кривые.
Следовательно, сплайн Эрмита можно рассматривать как потенциальную основу для
решения поставленной в данной работе задачи.
Следует отметить, что сплайн Эрмита выступает обобщением для
некоторых других способов интерполяции, например, для сплайна Катмулла-Рома.
Сплайн Катмулла-Рома параметризуется числом ![]() ,
отвечающим за кривизну его сегментов. При
,
отвечающим за кривизну его сегментов. При ![]() он
носит название равномерного, при
он
носит название равномерного, при ![]() – центростремительного, при
– центростремительного, при ![]() – хордального. Эти
частные случаи представлены на рис. 9. Как уже отмечалось выше, при любом
значении параметра
– хордального. Эти
частные случаи представлены на рис. 9. Как уже отмечалось выше, при любом
значении параметра ![]() на графике присутствуют ложные
экстремумы, а иногда и самопересечения кривой. Следовательно, сплайн
Катмулла-Рома не может быть использован для решения поставленной в данной
работе задачи.
на графике присутствуют ложные
экстремумы, а иногда и самопересечения кривой. Следовательно, сплайн
Катмулла-Рома не может быть использован для решения поставленной в данной
работе задачи.
Сплайн Акимы создавался как способ гладкой интерполяции, устойчивый к выбросам, то есть не порождающий ложных экстремумов, а также не имеющий самопересечений и колебаний вдоль оси абсцисс. Результат построения этого сплайна представлен на рис. 11 (для построения использован инструмент aspline [15], входящий в набор пакетов для Debian GNU/Linux).
Как можно видеть, ложные экстремумы всё-таки присутствуют на результирующей кривой, однако только на отрезках-«плато» (1–2, 13–14, 16–17). Тривиальным решением этой проблемы может быть разбиение сплайна Акимы на части, не содержащие подряд идущих точек с равными ординатами, и соединение этих частей отрезками прямых. Однако такой способ ввиду неединообразности представления итоговой кривой может требовать более сложных структур данных для её хранения. Кроме того, сплайн Акимы не имеет параметризации кривизны сегментов: например, нет способа «вручную» (подбором какого-либо параметра) увеличить кривизну в окрестности точек 3 или 6. С позиций визуального качества кривая в этих точках выглядит излишне «заострённой», тогда как, например, на рис. 5 она изгибается более плавно, но при этом также не содержит ложных экстремумов. В связи с этим в рамках данной работы было решено отказаться от использования сплайна Акимы.
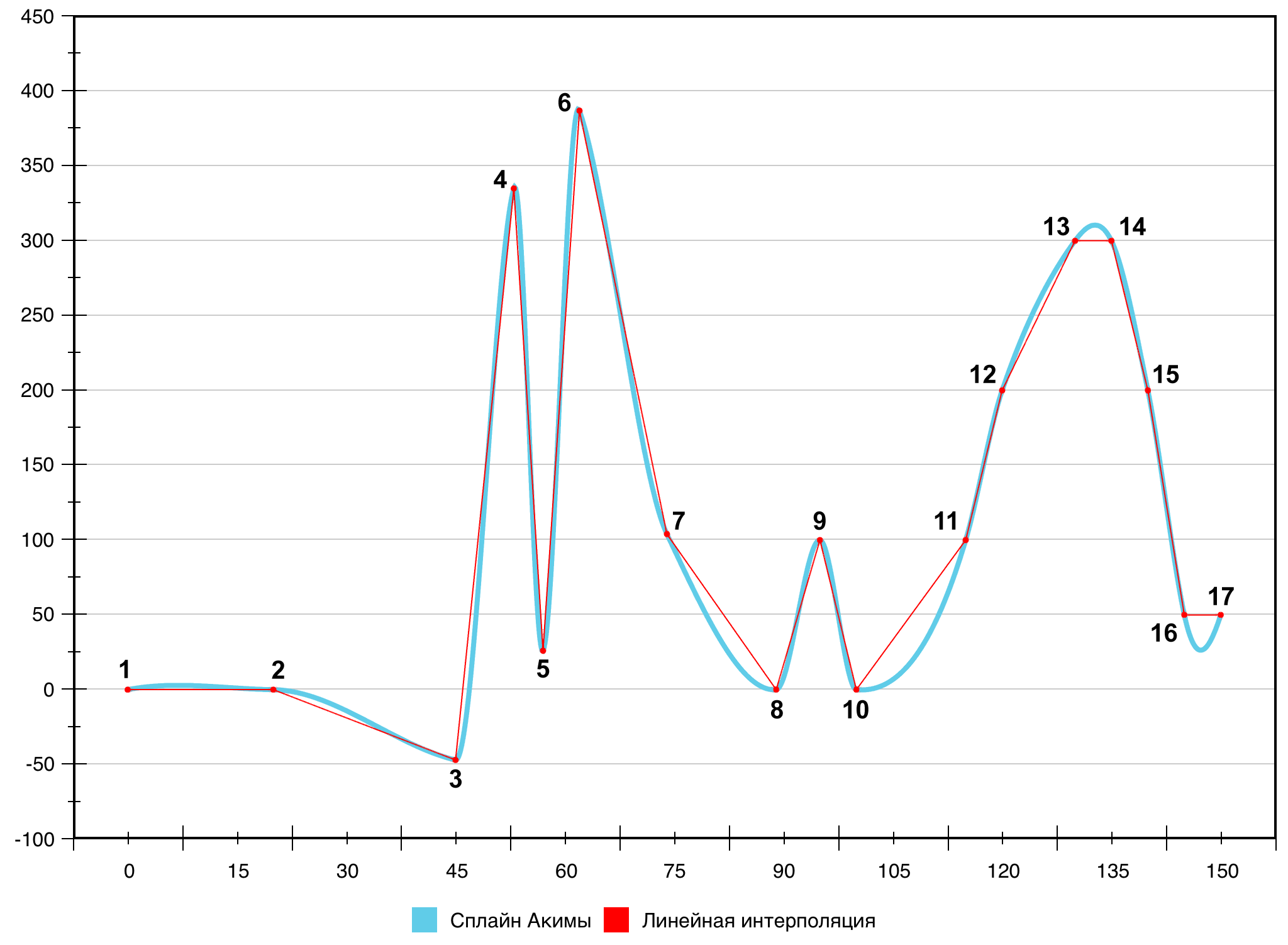
Рис. 11. Сравнение сплайна Акимы с линейной интерполяцией
Полином Лагранжа в классическом виде интерполирует n заданных точек при помощи единственного полинома степени не выше n, корнями которого являются исходные точки. Результат построения кривой, соответствующей интерполяционному полиному Лагранжа, по тестовому набору точек представлен на рис. 12.
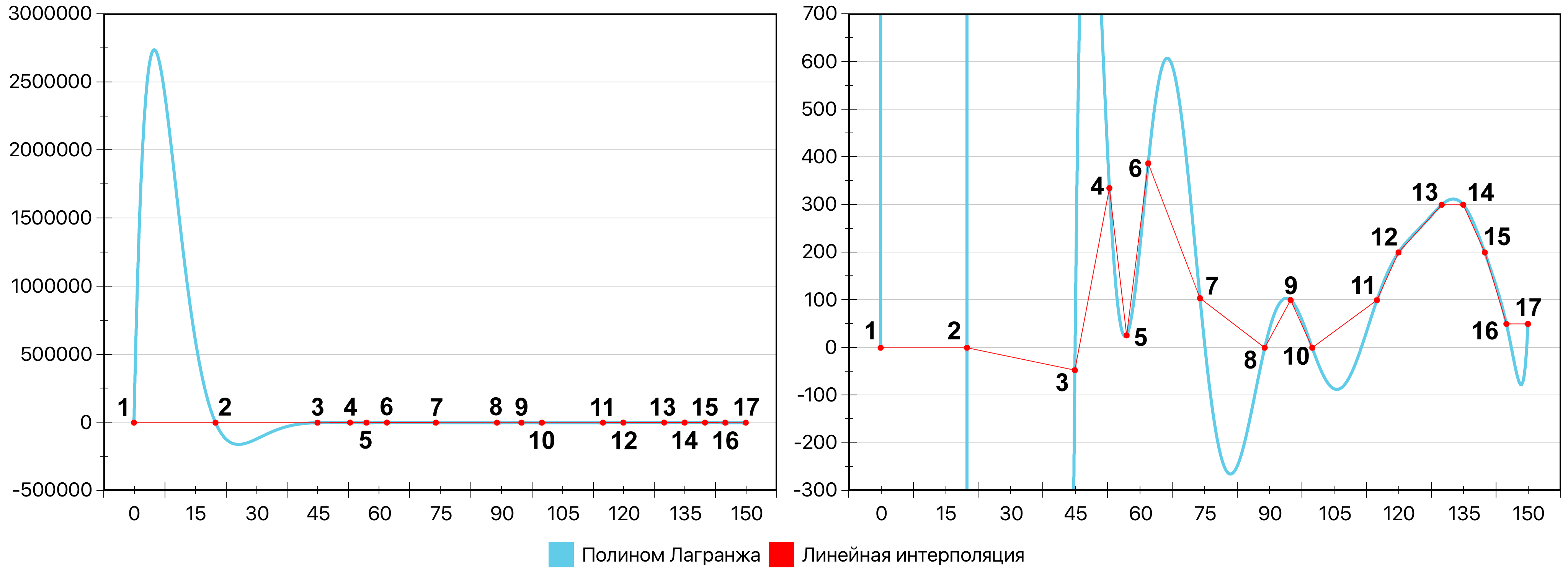
Рис. 12. Сравнение полинома Лагранжа с линейной интерполяцией. Полный график (слева) и увеличенная область интереса (справа)
Как можно видеть, данный способ интерполяции порождает ложные экстремумы, в некоторых случаях отличающиеся от реальных на несколько порядков, в результате чего применимость этого способа в общем случае оказывается очень ограниченной. Кроме того, у классического алгоритма построения кривой, соответствующей интерполяции полиномом Лагранжа, кубическая сложность, а коэффициенты по своим численным значениям могут превышать n!, что, в свою очередь, может привести к переполнению базовых типов данных и потребовать использования длинной арифметики.
Для любого набора заданных точек соответствующий им полином Лагранжа единствен и в классическом виде не имеет никаких настраиваемых параметров, в связи с чем не может быть использован для решения поставленной в данной работе задачи.
Кривая Безье – очень распространённый математический
инструмент в компьютерной графике, благодаря своей гибкости используемый в
широком спектре задач хранения и отображения различных объектов, например,
контуров в векторной графике, шрифтов, профилей тел вращения в трёхмерной
графике, кривых интерполяции состояний объектов при анимации и т. д.
Кривая Безье представляет собой параметрическую функцию, выраженную полиномом
степени k, в который в качестве переменной входит параметр t, а
коэффициенты вычисляются на основе ![]() контрольных точек. Число k
называется степенью кривой Безье. Взаимное расположение контрольных точек
управляет кривизной итоговой кривой, однако эта кривая не является для них
интерполирующей, так как проходит только через первую и последнюю, а к
промежуточным лишь стремится. В связи с этим напрямую невозможно использовать
аппарат кривых Безье для интерполяции заданного множества точек
контрольных точек. Число k
называется степенью кривой Безье. Взаимное расположение контрольных точек
управляет кривизной итоговой кривой, однако эта кривая не является для них
интерполирующей, так как проходит только через первую и последнюю, а к
промежуточным лишь стремится. В связи с этим напрямую невозможно использовать
аппарат кривых Безье для интерполяции заданного множества точек ![]() ,
, ![]() . Но
для каждого отрезка
. Но
для каждого отрезка ![]() ,
, ![]() можно
построить отдельную кривую Безье степени k, для которой
можно
построить отдельную кривую Безье степени k, для которой ![]() ,
, ![]() будут
являться первой и последней контрольными точками, а оставшиеся
будут
являться первой и последней контрольными точками, а оставшиеся ![]() контрольных точек
вычислены по некоторому алгоритму. В результате будет получена кусочно-заданная
параметрическая кривая, интерполирующая исходное множество точек.
контрольных точек
вычислены по некоторому алгоритму. В результате будет получена кусочно-заданная
параметрическая кривая, интерполирующая исходное множество точек.
Промежуточные контрольные точки на каждом из отрезков ![]() обычно
вычисляют из соображений обеспечения у итоговой кривой гладкости заданного
порядка: в интервале
обычно
вычисляют из соображений обеспечения у итоговой кривой гладкости заданного
порядка: в интервале ![]() кривая
имеет гладкость порядка
кривая
имеет гладкость порядка ![]() (так как, по сути, представлена
полиномом степени k и, следовательно, имеет непрерывные производные до
порядка
(так как, по сути, представлена
полиномом степени k и, следовательно, имеет непрерывные производные до
порядка ![]() включительно), однако в точках
включительно), однако в точках ![]() ,
, ![]() на
кривой могут быть изломы (производные общей кусочно-заданной функции могут
терпеть разрывы первого рода).
на
кривой могут быть изломы (производные общей кусочно-заданной функции могут
терпеть разрывы первого рода).
Чаще всего в компьютерной графике используются кривые Безье третьей степени (кубические), так как они, с одной стороны, допускают удобную и точную настройку кривизны (достаточную для решения большинства практических задач), а с другой – не требуют сложных вычислений и ограничиваются лишь 4 контрольными точками. При решении задачи интерполяции это означает, что для построения итоговой кривой необходимо вычислить по 2 дополнительных контрольных точки на каждый отрезок.
Интерполяция кубическими кривыми Безье очень популярна и реализована во многих программных средствах. Пример такой интерполяции представлен на рис. 7 (промежуточные контрольные точки выбраны так, чтобы итоговая кривая имела гладкость второго порядка). Итоговая кривая в приведённом примере содержит ложные экстремумы. Однако алгоритм её построения имеет большой потенциал для модификаций, заключённый в способе вычисления промежуточных контрольных точек, управляющих кривизной сегментов.
Следует отметить, что с математической точки зрения кубическая кривая Безье и кубический сплайн Эрмита эквивалентны: промежуточные контрольные точки кривой Безье задают, по сути, касательные векторы, необходимые для построения сплайна Эрмита. В данной работе было принято решение взять за основу именно эти способы и модифицировать их так, чтобы итоговая кривая удовлетворила сформулированным требованиям. Обрабатывать и хранить интерполирующую функцию было решено в виде кривой Безье, так как этот вид является стандартом де-факто в компьютерной графике (в частности, он поддерживается многими библиотеками визуализации, что делает предложенный способ легко переносимым в другое программное окружение).
6. Построение плавной кривой без ложных экстремумов на основе кривых Безье
Кривая Безье ![]() имеет
следующий общий вид:
имеет
следующий общий вид:
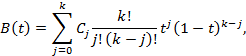
где k – степень кривой Безье,
![]() –
контрольные точки,
–
контрольные точки,
t – параметр, ![]() .
.
Кубическая кривая Безье, соответственно, имеет вид:
![]()
Для интерполяции дискретного множества точек ![]() ,
, ![]() , как
было сказано выше, может быть использована кусочно-заданная кривая, каждый
сегмент
, как
было сказано выше, может быть использована кусочно-заданная кривая, каждый
сегмент ![]() которой
представляет собой кубическую кривую Безье вида:
которой
представляет собой кубическую кривую Безье вида:
![]()
Данная идея продемонстрирована на рис. 13.
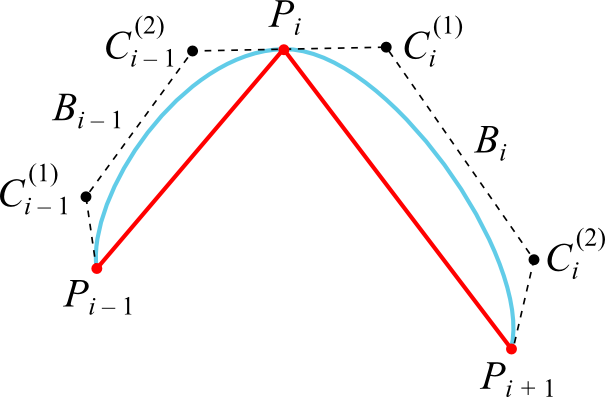
Рис. 13. Построение интерполяции при помощи кривых Безье
Как отмечалось выше, различные способы интерполяции при
помощи кривых Безье фактически отличаются лишь способом вычисления положений
контрольных точек ![]() и
и ![]() .
.
При условии достижения итоговой кривой гладкости второго
порядка (непрерывность первой и второй производных итоговой функции на отрезке ![]() ) и
условии свободных концов (равенства нулю вторых производных итоговой функции в
точках
) и
условии свободных концов (равенства нулю вторых производных итоговой функции в
точках ![]() и
и ![]() )
промежуточные контрольные точки вычисляются единственным образом, однако
итоговая кривая имеет ложные экстремумы (как показано на рис. 7). На
практике гладкость второго порядка зачастую оказывается избыточной: для
визуальной плавности кривой достаточно бывает гладкости первого порядка.
)
промежуточные контрольные точки вычисляются единственным образом, однако
итоговая кривая имеет ложные экстремумы (как показано на рис. 7). На
практике гладкость второго порядка зачастую оказывается избыточной: для
визуальной плавности кривой достаточно бывает гладкости первого порядка.
Нетрудно показать, что для достижения итоговой кривой
гладкости первого порядка (непрерывности первой производной итоговой функции на
отрезке ![]() )
необходимо и достаточно, чтобы точки
)
необходимо и достаточно, чтобы точки ![]() ,
, ![]() и
и ![]() лежали
на одной прямой, а также
лежали
на одной прямой, а также ![]() ,
, ![]() . В
этом случае неоднозначность заключается в определении векторов
. В
этом случае неоднозначность заключается в определении векторов ![]() и
точек
и
точек ![]() и
и ![]() .
.
Исходя из принципа построения кривой Безье ![]() ,
векторы
,
векторы ![]() и
и ![]() задают
касательные. Для сохранения монотонности кривой
задают
касательные. Для сохранения монотонности кривой ![]() ,
, ![]() на
отрезке
на
отрезке ![]() и
отсутствия пересечений этой кривой с прямыми
и
отсутствия пересечений этой кривой с прямыми ![]() и
и ![]() ,
, ![]() ,
достаточно, чтобы точки
,
достаточно, чтобы точки ![]() и
и ![]() лежали
в пределах прямоугольных областей
лежали
в пределах прямоугольных областей ![]() и
и ![]() ,
показанных на рис. 14.
,
показанных на рис. 14.
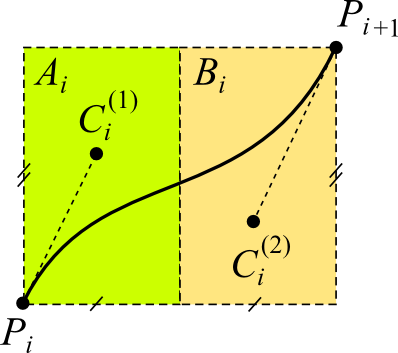
Рис. 14. Зоны для расположения промежуточных контрольных точек кривой Безье
Это свойство можно использовать для защиты от ложных
экстремумов и осцилляций: если в качестве касательных к кривым ![]() брать
касательные к углам ломаной
брать
касательные к углам ломаной ![]() и при
этом соответствующим образом ограничивать длины векторов
и при
этом соответствующим образом ограничивать длины векторов ![]() и
и ![]() ,
итоговая кривая окажется «зажатой» между этими касательными, на каждом отрезке
,
итоговая кривая окажется «зажатой» между этими касательными, на каждом отрезке ![]() будет
монотонной, а её минимум и максимум будут достигаться в граничных точках.
будет
монотонной, а её минимум и максимум будут достигаться в граничных точках.
Введём обозначения:
![]()
Нормированный касательный вектор может быть вычислен по формуле:
![]()
Формула вычисления итоговых касательных векторов, в свою очередь, может быть записана так:
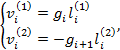
где ![]() ,
, ![]() –
длины касательных векторов.
–
длины касательных векторов.
Существует, однако, специальный случай, когда касательные
должны быть вычислены иначе: если у двух подряд идущих точек совпадают абсциссы
либо ординаты, на графике на соответствующем отрезке должны сформироваться
«плато» либо «вертикаль». Для этого соответствующие сегменты итоговой кривой
должны быть представлены, по сути, отрезками прямых, а касательные к кривой на
таких сегментах должны совпадать с этими прямыми. В этом случае, если
обозначить за ![]() ,
, ![]() координаты
вектора
координаты
вектора ![]() ,
формула (1) примет следующий вид:
,
формула (1) примет следующий вид:
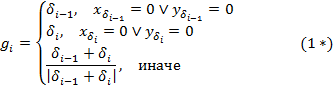
Описанный вариант вычисления касательных векторов предполагает исключение совпавших точек из входного множества.
Для определения точек ![]() и
и ![]() длины
касательных векторов на концах кривой по аналогии с условием свободных концов
могут быть положены равными нулю:
длины
касательных векторов на концах кривой по аналогии с условием свободных концов
могут быть положены равными нулю:
![]()
Для определения длин касательных векторов в промежуточных
точках введём обозначения: ![]() ,
, ![]() –
координаты вектора
–
координаты вектора ![]() ,
вычисленного в соответствии с (1*), то есть нормированного направляющего
вектора касательной в точке
,
вычисленного в соответствии с (1*), то есть нормированного направляющего
вектора касательной в точке ![]() ;
; ![]() ,
, ![]() –
координаты вектора
–
координаты вектора ![]() .
Тогда в соответствии с рис. 14 ограничение длин касательных векторов к
кривой может быть записано так:
.
Тогда в соответствии с рис. 14 ограничение длин касательных векторов к
кривой может быть записано так:

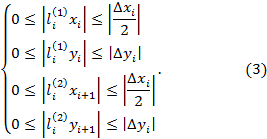
Для достижения гладкости первого порядка должно также удовлетворяться ограничение:
![]()
При выполнении ограничений (2), (3) и (4) в независимости от конкретного способа вычисления длин касательных формально будут выполняться все требования, предъявляемые к кривой, сформулированные в разделе 2. В частности, выполняться будет и требование плавности, так как итоговая кривая будет иметь гладкость первого порядка. Однако конкретный способ вычисления длин касательных векторов влияет на внешний вид плавной кривой. Таким образом, в предлагаемом концептуальном решении остаётся свобода для адаптации к конкретной задаче и субъективным предпочтениям пользователя.
Следует отметить, что ограничения (2), (3) и (4) формально
не могут быть выполнены одновременно в ситуации, когда во входном множестве
присутствуют три подряд идущих точки ![]() ,
, ![]() ,
, ![]() ,
образующие прямой угол (две подряд идущих точки совпадают по абсциссе и
различаются по ординате, две других подряд идущих точки совпадают по ординате и
различаются по абсциссе). Выполнение ограничений (3) и (4) в этом случае
возможно лишь если
,
образующие прямой угол (две подряд идущих точки совпадают по абсциссе и
различаются по ординате, две других подряд идущих точки совпадают по ординате и
различаются по абсциссе). Выполнение ограничений (3) и (4) в этом случае
возможно лишь если ![]() , то
есть не выполняется ограничение (2). Это, однако, приведёт к нарушению
гладкости, так как в вершине прямого угла левый и правый пределы производной
интерполяционной функции будут различаться, а, следовательно, нарушится
непрерывность этой производной.
, то
есть не выполняется ограничение (2). Это, однако, приведёт к нарушению
гладкости, так как в вершине прямого угла левый и правый пределы производной
интерполяционной функции будут различаться, а, следовательно, нарушится
непрерывность этой производной.
С точки зрения достоверной визуализации нарушение гладкости в описанной ситуации является неизбежным, так как в противном случае возникнут ложные экстремумы. Поэтому при построении итоговой кривой ограничение (2) учитывать не нужно.
Сложность алгоритма подготовки данных для построения кривой
(определения промежуточных контрольных точек кривой Безье) – ![]() , где n
– число входных точек, так как всё необходимое вычисляется за один проход по
входному множеству точек. Сложность построения кривой Безье по известным
параметрам –
, где n
– число входных точек, так как всё необходимое вычисляется за один проход по
входному множеству точек. Сложность построения кривой Безье по известным
параметрам – ![]() , где m
– число интервалов дискретизации кривой при отображении. Таким образом,
сложность итогового алгоритма оказывается линейной, что вполне удовлетворяет
требованию эффективности, выдвинутому в разделе
2.
, где m
– число интервалов дискретизации кривой при отображении. Таким образом,
сложность итогового алгоритма оказывается линейной, что вполне удовлетворяет
требованию эффективности, выдвинутому в разделе
2.
В листинге 1 приведён псевдокод алгоритма вычисления длин касательных векторов, реализованного в рамках данной работы:
Листинг 1. Псевдокод алгоритма вычисления длин касательных векторов
1. ![]() ,
, ![]() =
координаты вектора
=
координаты вектора ![]() ,
вычисленного в соответствии с (1*).
,
вычисленного в соответствии с (1*).
2. ![]() ,
, ![]() = координаты
вектора
= координаты
вектора ![]() ,
вычисленного в соответствии с (1*).
,
вычисленного в соответствии с (1*).
3. ![]() ,
, ![]() =
координаты вектора
=
координаты вектора ![]() .
.
4. ![]() ,
, ![]() = координаты вектора
= координаты вектора ![]() .
.
5. ![]() ,
, ![]() =
координаты вектора
=
координаты вектора ![]() .
.
6. Если
![]() , То
, То ![]() .
.
7. Если
![]() , То
, То ![]() .
.
8. Если
![]() , То
, То ![]() .
.
9. Если
![]() , То
, То ![]() .
.
10. ![]() .
.
11. Если ![]() , То
, То ![]() ,
Иначе
,
Иначе ![]() .
.
12. Если ![]() , То
, То ![]() ,
Иначе
,
Иначе ![]() .
.
13. Если ![]() , То
, То
13.1. Если
![]() , То
, То ![]() ,
Иначе
,
Иначе ![]() .
.
14. Если ![]() , То
, То
14.1. Если
![]() , То
, То ![]() ,
Иначе
,
Иначе ![]() .
.
Параметр ![]() отвечает за размер зон
отвечает за размер зон ![]() и
и ![]() (показанных
на рис. 14). Чем этот параметр больше, тем, соответственно, меньше
оказываются указанные зоны и тем более кривая похожа на ломаную. Нижняя граница
значений параметра обусловлена ограничением (1).
(показанных
на рис. 14). Чем этот параметр больше, тем, соответственно, меньше
оказываются указанные зоны и тем более кривая похожа на ломаную. Нижняя граница
значений параметра обусловлена ограничением (1).
Для обеспечения гладкости порядка 1 данный алгоритм предполагает, что во входном множестве точек нет подряд идущих совпадающих точек и троек, образующих прямые углы. В случае возникновения указанных ситуаций алгоритм продолжает порождать визуально плавные кривые, однако гладкость интерполяции может нарушаться в местах дублирования точек и гарантированно будет нарушаться на прямых углах.
Результат построения кривой, касательные к которой вычислены в соответствии с приведённым в листинге 1 алгоритмом, представлен на рис. 15.
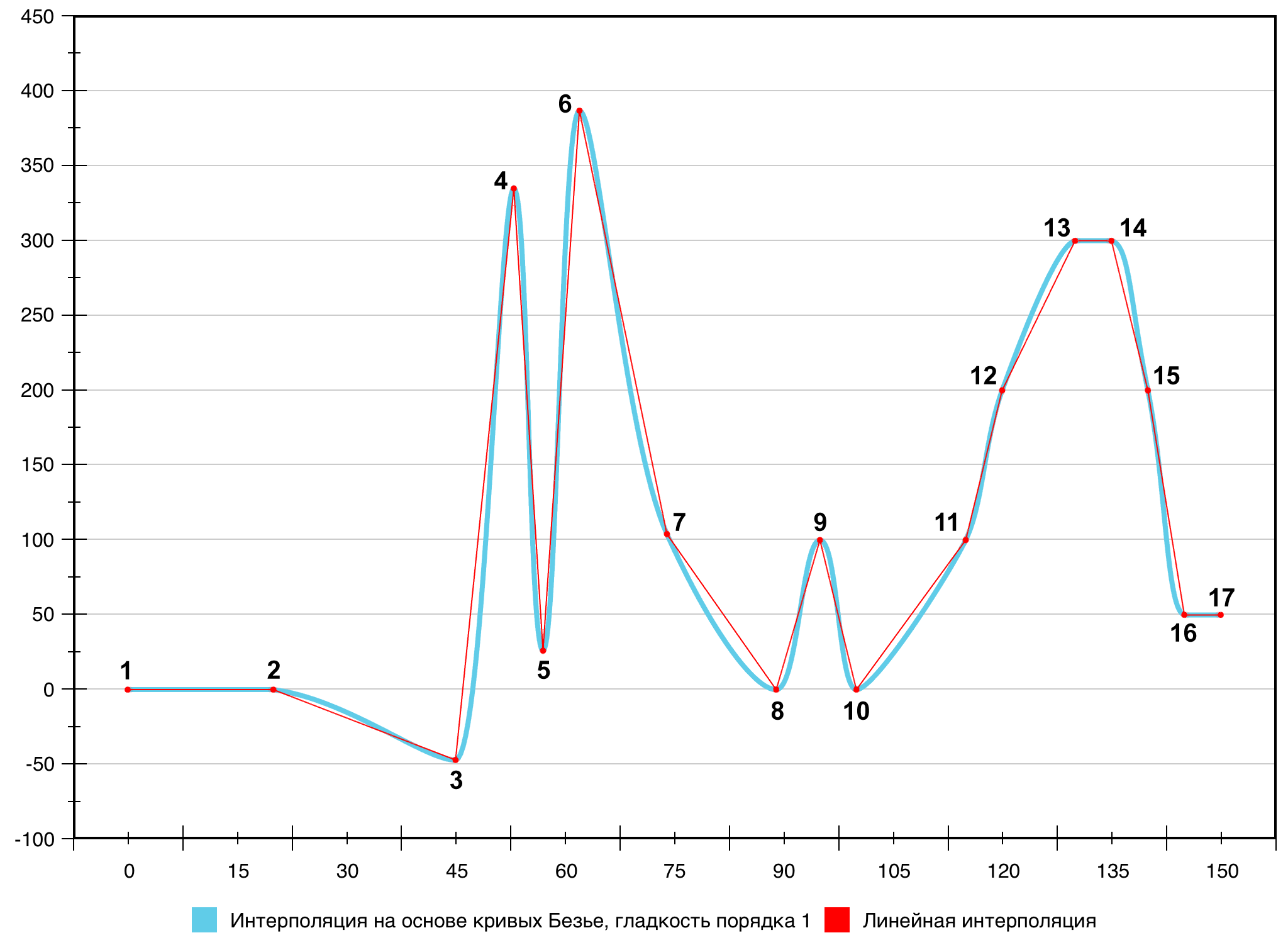
Рис. 15. Сравнение интерполяции на основе кривых Безье (гладкость порядка 1) с линейной интерполяцией
Данный результат уже можно считать решением поставленной в
работе задачи. Тем не менее, на основании обсуждения визуального качества
итоговой кривой со специалистами по дизайну автором был скорректирован её
внешний вид с целью увеличения «покатости» сегментов. Для этого пришлось
отказаться от ограничения (4). Формально после этого кривая перестаёт быть
гладкой (первая производная в точках ![]() может
терпеть разрыв), однако поскольку контрольные точки
может
терпеть разрыв), однако поскольку контрольные точки ![]() ,
, ![]() и
и ![]() кривых
Безье, составляющих итоговую кривую, по-прежнему лежат на одной прямой,
визуальная плавность сохраняется.
кривых
Безье, составляющих итоговую кривую, по-прежнему лежат на одной прямой,
визуальная плавность сохраняется.
По сути для перехода к новому способу вычисления в шагах
(6)–(9) алгоритма, приведённого в листинге 1, условия были заменены на
тождественную истину. При этом, соответственно, шаги (3) и (5), как и
переменные, объявленные в них, оказываются не нужны, и весь дальнейший алгоритм
оперирует лишь координатами вектора ![]() .
.
Результирующая кривая, полученная в этом случае, представлена на рис. 16.
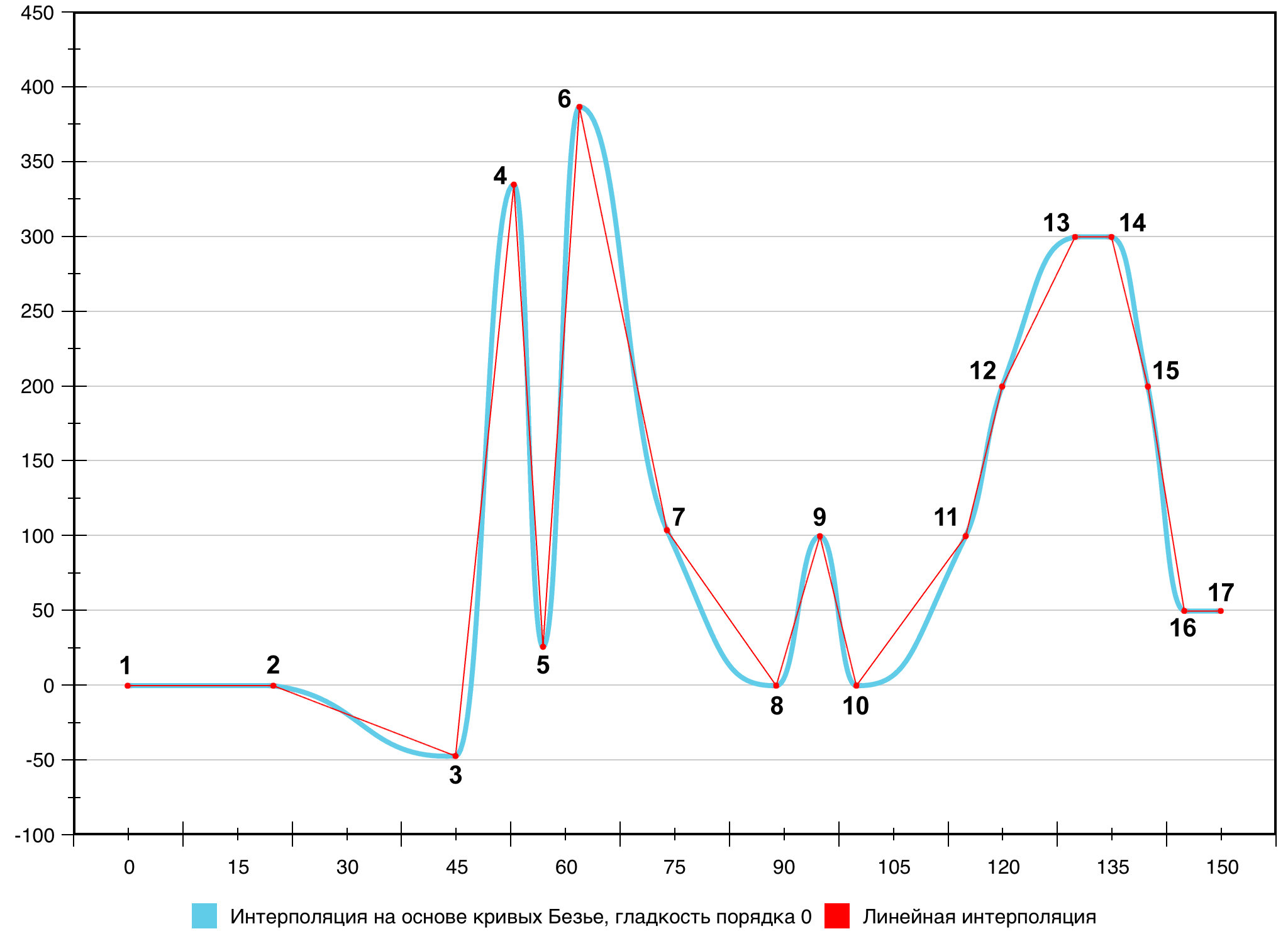
Рис. 16. Сравнение интерполяции на основе кривых Безье (гладкость порядка 0) с линейной интерполяцией
Как можно видеть, кривая не имеет острых углов, «покатость»
сегментов увеличилась, однако общее эстетическое качество упало: кривая стала
смотреться «помятой». Для устранения этого эффекта в алгоритм вычисления была
введена эвристика: если абсцисса точки пересечения касательных в точках ![]() и
и ![]() лежит
в отрезке
лежит
в отрезке ![]() , где
, где ![]() ,
, ![]() –
абсциссы точек
–
абсциссы точек ![]() и
и ![]() соответственно,
то максимальное из
соответственно,
то максимальное из ![]() и
и ![]() зануляется.
Результирующая кривая представлена на рис. 17.
зануляется.
Результирующая кривая представлена на рис. 17.
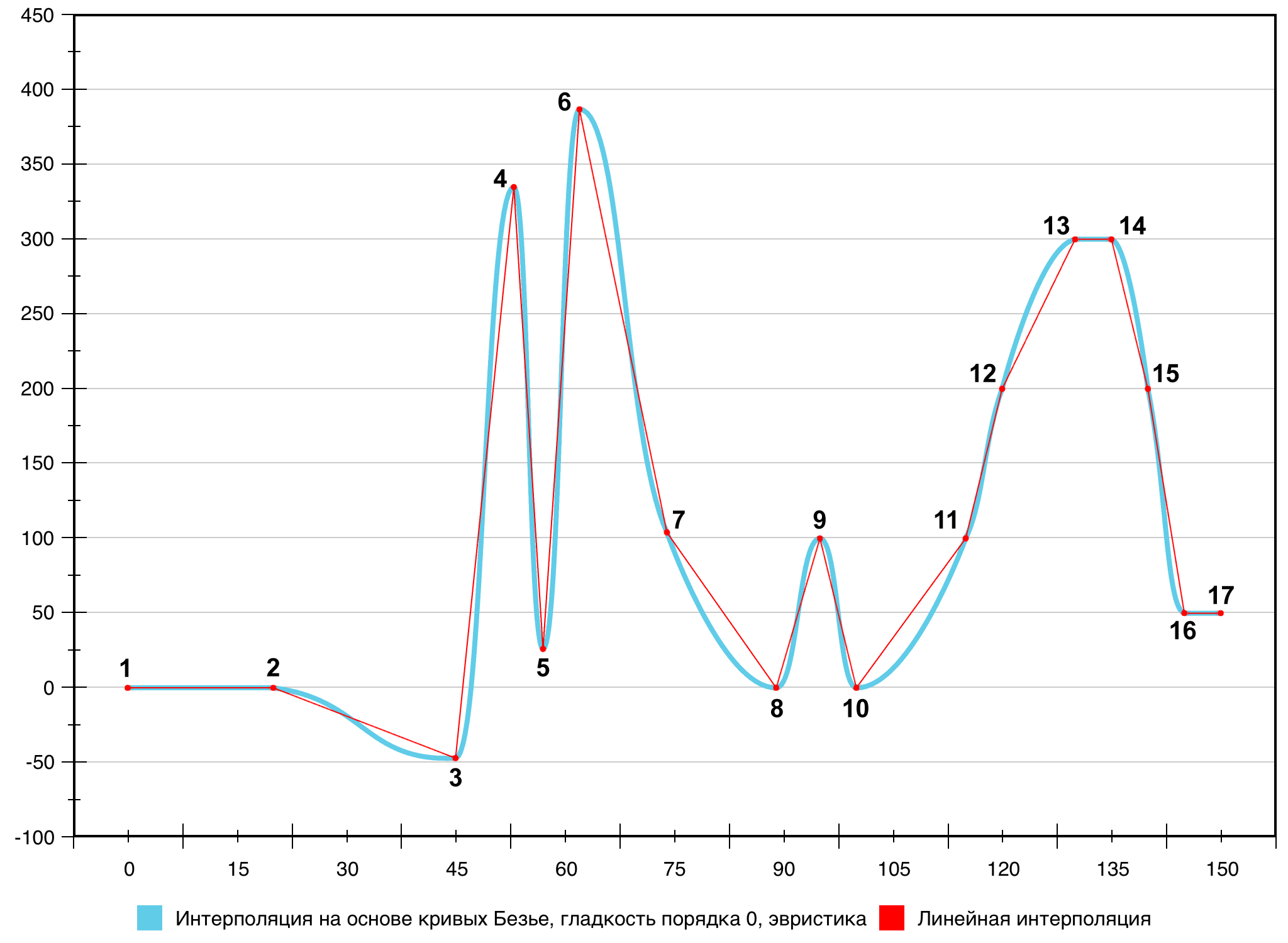
Рис. 17. Сравнение интерполяции на основе кривых Безье (гладкость порядка 0, использование эвристики для укорачивания касательных векторов) с линейной интерполяцией
Данный результат был сочтён удовлетворительным с точки зрения визуального качества. Следует, однако, подчеркнуть, что эта модификация (отказ от выполнения ограничения (4)) имеет смысл в основном для создания различных презентационных и рекламных иллюстраций. В условиях научной визуализации и визуальной аналитики на взгляд автора предпочтительнее использовать изначальный вариант алгоритма (с ограничением (4)), так как итоговая кривая, получаемая с его помощью, оказывается ближе к линейной интерполяции: точки оказываются соединены по пути, близкому к кратчайшему. Это, в свою очередь, в большей степени соответствует предположению о репрезентативности входного множества точек (содержания в нём всей необходимой для анализа информации об изучаемом процессе или явлении): факт их соединения по пути, близкому к кратчайшему, вносит минимум дополнительной информации о поведении описываемого точками процесса или явления, и тем самым минимизирует «ложные» сведения, сообщаемые зрителю (сильные изгибы кривой не отвлекают зрителя от точек, в которых, по сути, и заключается вся достоверно известная информация об изучаемом процессе или явлении). Следуя этой логике, наилучшим вариантом интерполяции в такой ситуации является линейная (либо же, если порядок точек не важен – отображение точек не связанными между собой вообще). Однако, как уже отмечалось выше, в ряде случаев возникает требование плавности с целью увеличения комфорта восприятия и визуальной привлекательности иллюстрации. В этих случаях предложенный способ в своём изначальном варианте является разумным компромиссом между требованиями достоверности и визуальной привлекательности.
Сравнение вариантов интерполяции при помощи кривых Безье с порядками гладкости итоговых кривых 2, 1, 0 и 0 с эвристическим укорачиванием касательных векторов представлено в виде анимационной последовательности на рис. 18.
Сравнение разработанного способа со способом, реализованным в библиотеке построения диаграмм и графиков Highcharts, а также со сплайном Акимы, представлено в виде анимационной последовательности на рис. 19.
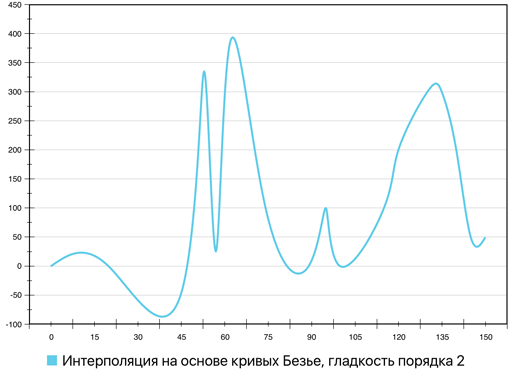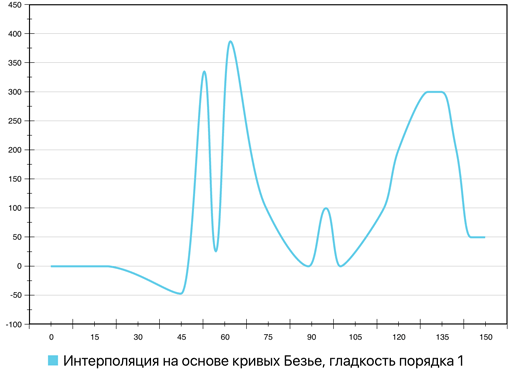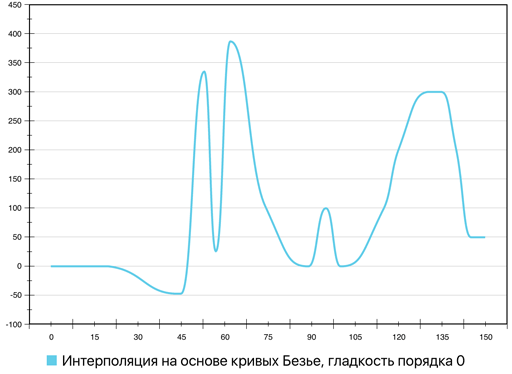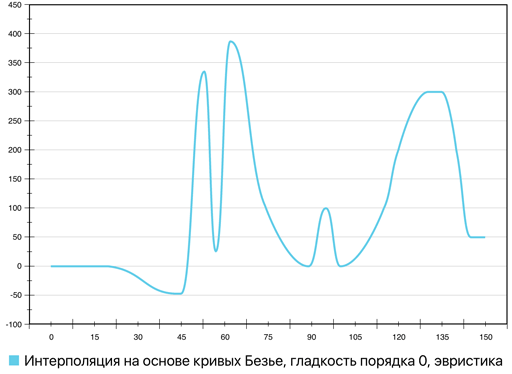
Рис. 18. Сравнение различных вариантов интерполяции при помощи кривых Безье
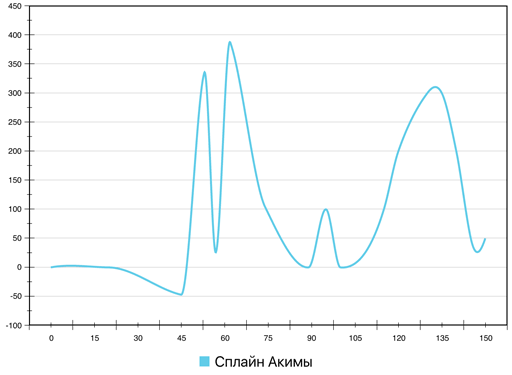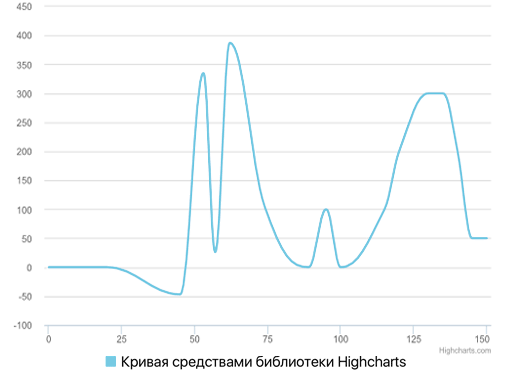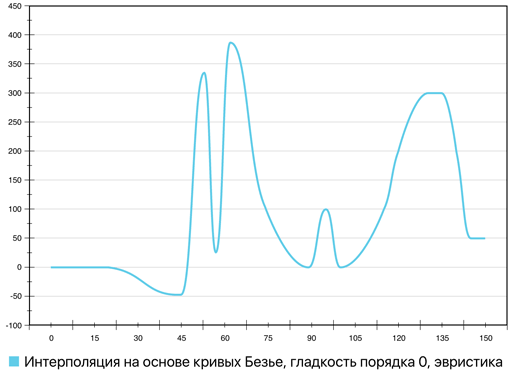
Рис. 19. Сравнение разработанного способа плавной интерполяции с известными
7. Заключение
Разработанный способ построения плавной интерполяции дискретного множества точек при помощи кривых Безье удовлетворяет всем требованиям, описанным в разделе 2 данной статьи, и может быть использован для построения графиков в ситуациях, когда наличие ложных экстремумов нежелательно или недопустимо.
По визуальному качеству итоговых кривых предложенный способ не уступает общеизвестным решениям (например, сплайну Акимы) и решениям, реализованным в коммерческом программном обеспечении (например, в библиотеке Highcharts). В отличие от этих решений предлагаемый способ является настраиваемым: в авторской реализации имеется параметр, отвечающий за кривизну сегментов. Кроме того, описанные в данной работе ограничения дают возможность создавать на базе предложенного способа другие алгоритмы интерполяции, отвечающие сформулированным требованиям и по визуальным характеристикам результирующих кривых подходящие для решения специализированных задач научной визуализации.
Следует также отметить, что предложенный способ (в отличие от многих основанных на разностных схемах способов интерполяции) позволяет без модификаций алгоритма обрабатывать подряд идущие точки, совпавшие как по ординатам, так и по абсциссам (так и по обеим координатам одновременно).
Этот способ был реализован в ядре мультиплатформенной библиотеки визуализации данных NChart3D (распространяющейся на коммерческой основе компанией ООО «Ньюлана»), а также внедрён в систему научной визуализации SciVi (построенную, в частности, на основе библиотеки NChart3D).
В процессе настройки визуальных свойств графика в системе SciVi пользователь может переключаться между двумя описанными в статье модификациями предложенного алгоритма – с учётом и без учёта ограничения (4), сформулированного в разделе 6. Но по умолчанию предлагается модификация с учётом указанного ограничения, так как этот вариант на взгляд автора в большей степени соответствует большинству задач научной визуализации.
Авторская реализация разработанного способа на языке С++ доступна на GitHub и распространяется по лицензии MIT [16]: https://github.com/icosaeder/tbezier. В репозитории имеется как вариант построения кривой с порядком гладкости 1, так и вариант с описанной в статье эвристикой.
Список литературы
1. Волков Е.А. Численные методы. Учеб. пособие для вузов. 2-е изд., испр. Наука, 1987. С. 63–68.
4. Табличный процессор Microsoft Excel [Электронный ресурс]. URL: https://products.office.com/ru-ru/excel (дата обращения: 11.07.2016).
5. Табличный процессор OpenOffice Calc [Электронный ресурс]. URL: https://www.openoffice.org/product/calc.html (дата обращения: 11.07.2016).
7. Библиотека построения диаграмм и графиков Highcharts [Электронный ресурс]. URL: http://www.highcharts.com/ (дата обращения: 11.06.2016).
8. Библиотека построения диаграмм и графиков amCharts [Электронный ресурс]. URL: https://www.amcharts.com/ (дата обращения: 11.06.2016).
9. Библиотека построения диаграмм и графиков CorePlot [Электронный ресурс]. URL: https://github.com/core-plot/core-plot (дата обращения: 11.06.2016).
10. Библиотека построения диаграмм и графиков AChartEngine [Электронный ресурс]. URL: https://github.com/ddanny/achartengine (дата обращения: 11.06.2016).
14. Hazewinkel M. Lagrange interpolation formula [Электронный ресурс] 2001. – URL: https://www.encyclopediaofmath.org/index.php/Lagrange_interpolation_formula (дата обращения: 11.07.2016).
15. Frey D. Akima spline interpolation program [Электронный ресурс] URL: http://homepage.hispeed.ch/david.frey/ (дата обращения: 11.07.2016).
16. The MIT License [Электронный ресурс]. URL: https://opensource.org/licenses/MIT (дата обращения: 11.07.2016).
VISUALIZATION OF SMOOTH CURVES WITHOUT MISPLACED EXTREMES BASED ON DISCRETE POINT SET
K.V. Ryabinin
Perm State University, Perm, Russian Federation
Abstract
The paper is devoted to the visualization of discrete point set as a smooth curve that should have no misplaced extremes (extremes not belonging to the input point set), awry self-intersections (self-intersections of the interpolation curve while the polygonal line connecting the input points has no self-intersections) and oscillations (essential divergence of the interpolation curve from the polygonal line connecting the input points). Such requirements are critical in some visual analytics tasks, for example while analysing the representative measurement results (in econometrics, physics, etc.), because they help to interpret the input data properly and uniquely.
Popular visualization software products that are able to render smooth curves based on discrete point sets and popular smooth interpolation algorithms are examined. It is found out that only a few of them meet the mentioned requirements. Therefore the development of a new smooth interpolation approach ensuring absence of misplaced extremes, awry self-intersections and oscillations is a challenging task.
The original solution of this task for 2D-case is described. The proposed solution is based on the piecewise parametric curve constructed of cubic Bezier curves. The endpoints of each Bezier curve belong to the input data set while the intermediate control points are calculated to make the result curve meet the declared requirements.
The proposed interpolation method can be easily configured for solving scientific visualization problems with the special requirements of visual features. In common case the visual quality of the result curve is competitive with the known methods and software means. The implementation of the described interpolation algorithm is integrated in the data visualization library NChart3D and in the scientific visualization system SciVi.
Keywords: smooth interpolation, Bezier curve, misplaced extremes, smooth curve, charts rendering, visual analytics.
References
1. Volkov E.A. Chislennye metody. Ucheb. posobie dlja vuzov. 2-e izd., ispr [Numerical methods. Textbook for high schools. 2nd ed., corr]. Nauka, 1987. Pp. 63–68.
2. Rjabinin K.V. Razrabotka mul'tiplatformennoj biblioteki postroenija i vizualizacii diagramm [Development of Multiplatform Charting Library]. Scientific Visualization. 2014. Vol. 6, No. 1. Pp. 51–67.
3. Ryabinin K., Chuprina S. Development of Ontology-Based Multiplatform Adaptive Scientific Visualization System. Journal of Computational Science. 2015. Vol. 10. Pp. 370–381.
4. Microsoft Excel . URL: https://products.office.com/ru-ru/excel (Access date: 11.07.2016).
5. Tablichnyj processor OpenOffice Calc. URL: https://www.openoffice.org/product/calc.html (Access date: 11.07.2016).
6. Rogers D., Adams J. Matematicheskie osnovy mashinnoj grafiki [Matematical Elements for Computer Graphics]. Textbook, Russian translation by P.A. Monakhova, G.V. Olokhtonova, D.V. Volkov, edited by Y.M. Bayakovsky, V.A. Galaktionov, V.V. Martynuk. Mir 2001. 604 p.
7. Library for constructing diagrams and graphs Highcharts. URL: http://www.highcharts.com/ (Access date: 11.06.2016).
8. Library for constructing diagrams and graphs amCharts. URL: https://www.amcharts.com/ (Access date: 11.06.2016).
9. Library for constructing diagrams and graphs CorePlot. URL: https://github.com/core-plot/core-plot (Access date: 11.06.2016).
10. Library for constructing diagrams and graphs AChartEngine. URL: https://github.com/ddanny/achartengine (Access date: 11.06.2016).
11. Spitzbart A. A Generalization of Hermite's Interpolation Formula. The American Mathematical Monthly. Vol. 67, No. 1. 1960. P. 42–46.
12. Catmull E., Rom R. A class of local interpolating splines. Computer Aided Geometric Design. Academic Press, 1974. P. 317–326.
13. Akima H. A New Method of Interpolation and Smooth Curve Fitting Based on Local Procedures. Journal of the ACM. Vol. 17, Iss. 4. 1970. P. 589–602.
14. Hazewinkel M. Lagrange interpolation formula 2001. URL: https://www.encyclopediaofmath.org/index.php/Lagrange_interpolation_formula (Access date: 11.07.2016).
15. Frey D. Akima spline interpolation program URL: http://homepage.hispeed.ch/david.frey/ (Access date: 11.07.2016).
16. The MIT License. URL: https://opensource.org/licenses/MIT (Access date: 11.07.2016).