ВИЗУАЛИЗАЦИЯ СВЕРХЗВУКОВОГО ДВИЖЕНИЯ СФЕРЫ В ВОЗДУХЕ И В ВОДЕ

С.И. Герасимов^1,2,3,4,5, В.А. Кикеев^1,3, К.В. Тотышев², А.П.Фомкин², Б.А. Яненко⁴

¹Нижегородский государственный технический университет им. Р.Е.Алексеева, Россия

²Российский федеральный ядерный центр - Всероссийский научно-исследовательский институт экспериментальной физики, Саров, Россия

³ Институт проблем машиностроения РАН, Нижний Новгород, Россия

⁴Саровский физико-технический институт НИЯУ МИФИ, Саров, Россия

⁵Национальный исследовательский ядерный университет «МИФИ», Москва, Россия

E-mail: s.i.gerasimov@mail.ru, vkikeev@mail.ru

Содержание

1. Введение

2. Постановка экспериментов

3. Движение в воде

4. Численные расчеты

5. Заключение

Литература

Аннотация

Среди различных диагностических методик, применяемых в баллистических экспериментах, оптические методы визуализации играют определяющую роль из-за отсутствия ограничений характерных для контактных методов. Cовременные трассы должны оснащаться средствами регистрации движения объекта, включая визуализацию его спектров обтекания. Регистрация положений метаемого объекта дает информацию о его траектории полета. На основе теневой картины можно судить о сопутствующих движению газодинамических и физических процессах, например, образовании ударных волн, характере пограничного слоя, положении и образовании зон отрыва, течений основного потока и в следе. Выполнен ряд экспериментов с целью оценки возможности и методической отработки проведения аэробаллистических испытаний при сверхзвуковых скоростях обтекания. Показаны возможности методов оптико-рентгенографической регистрации при сверх- и гиперзвуковых скоростях полета и взаимодействиях с преградой. Объектом исследований являлись металлические шары, изготовленные из различных материалов. Показан характер обтекания, получены зависимости коэффициента аэродинамического сопротивления, изменение радиуса кривизны ударной волны вблизи критической точки шара от числа Маха. Проведено численное моделирование. Впервые приведены экспериментальные картины движения ударной волны в воде при горизонтальном движении шара с начальной сверхзвуковой скоростью входа.

Ключевые слова: аэробаллистическое испытание, визуализация, теневая и силуэтная регистрация, численное моделирование, коэффициент сопротивления.

1. Введение

Движению сферы в идеальной жидкости было посвящено большое количество теоретических и экспериментальных исследований в силу практической и учебной ценности сопровождающих это движение явлений [1-30]. Шар, как тело простой формы, теоретически хорошо изученное аэродинамиками, используется в аэробаллистическом эксперименте ВНИИЭФ для юстировочных работ при наладке измерительного оборудования, используемого в фотограмметрических методиках измерений маркированных моделей для определения их аэродинамических характеристик [31-33]. Как метаемый объект это наиболее экономичная модель для отработки режимов метания и совершенствования узлов пороховых и легкогазовых баллистических установок[34-35]. При исследовании соударений испытываемых образцов с поражающими элементами, шар удобен как с точки зрения моделирования осколка, так и с позиции обеспечения заданных скорости и точки встречи при сравнительно легкой отсечке элементов поддона, используемого для разгона метаемого объекта в стволе баллистической установки. В исследованиях поведения различных материалов в свободном полете при гиперзвуковых скоростях (аэротермомеханический унос) шаровая модель более выгодна, чем удлиненная из соображений прочности и устойчивости [36]. При этом большая часть известных экспериментальных работ по изучению характеристик шара проведена для режимов с числом Маха не более 5. Опыты с большими скоростями, как правило, проводились отстрелом шара навстречу сверхзвуковому потоку в аэродинамической трубе [37,38]. При такой постановке не моделируются аэротермомеханические процессы, сопровождающие движение объекта, движущегося с гиперзвуковыми скоростями в неподвижном воздухе атмосферного давления. В реальном полете идет интенсивный прогрев и унос материала движущегося объекта, в том числе и шаровой формы [36]. При изменении обводов меняется и коэффициент сопротивления исходного шара на траектории. Кроме того, в отличие от экспериментов на ударных трубах, где коэффициент сопротивления считается постоянным на измерительном участке [23], в экспериментах с отстрелом моделей в невозмущенную атмосферу по внешнетраекторным данным можно высчитывать реальные значения Cx(M), описываемые нелинейными зависимостями [39,40]. Ниже приводятся схемы регистрации, применяемые в прямых аэробаллистических экспериментах, когда шар находится в свободном полете  в невозмущенной среде при атмосферном давления. Полученные с помощью данных схем результаты могут применяться для тестирования известных и вновь разрабатываемых численных методик, а также применяемых в них моделей и уравнений состояний. Также впервые в истории научной визуализации приводятся фотографии ударной волны в воде комнатной температуры при горизонтальном движении в ней шара с начальной сверхзвуковой (относительно воды) скоростью входа.

2. Постановка экспериментов

В состав типовой баллистической установки для аэродинамических исследований входят следующие основные системы:

1. Метательная система порохового, пневматического или легкогазового типа.

2. Камера отсечки ускоряющего газа и отделения поддона, с помощью которого исследуемая модель ведется по стволу в процессе ускорения.

3. Измерительный участок.

4. Системы оптической, рентгеновской регистрации движения объекта и состояния газа в ударной среде.

5. Система синхронизации регистрирующего оборудования, включающая датчики пролета объекта через сечения регистрации и электронную аппаратуру, формирующую управляющие сигналы и обеспечивающую хронометрирование движения объекта.

6. Устройство для улавливания высокоскоростного объекта в конце трассы или в ее промежуточных сечениях, либо объект испытания.

Существенное преимущество разгона метаемого объекта баллистической установкой состоит в том, что в процессе "плавного" разгона, в отличие от часто используемых взрывных метательных установках, практически не изменяется его термодинамическое состояние. Для разгона шаров в большом диапазоне размеров и скоростей использовались пороховая (ПБУ) и легкогазовая (ЛГУ) пушки, внешний вид которых приведен на рисунках 1,2.

Рис. 1. Пороховая пушка ПБУ, вид спереди – сверху

Рис. 2. Легкогазовая  пушка ЛГУ, вид спереди – сверху

С помощью данных средств разгонялись шары, установленные в поддоне диаметром от 8 до 85 мм, до скоростей 7 км/с.

Конструкции метаемых объектов (МО) разрабатывались с учетом реализации требуемых скоростей метания, соударения ударника и мишени, прочности метаемого объекта на этапе его разгона в стволе установки и надежной обтюрации метающих газов. Используемые для исследований метаемые объекты представляли собой шары из алюминиевых сплавов Д16 и АД1, размещаемых в поддонах из полиэтилена 170  (см. рис. 3).

а)

б)

в)

Рис. 3. Метаемые объекты для пороховой (а,б) и легкогазовой (в) пушек

Все модели, отстреливаемые из пороховой баллистической установки, имели гладкую боковую поверхность, покрашенную матовой эмалью белого цвета и оснащенную системой реперных марок, предназначенных для получения внешнетраекторных измерений.

Для получения теневых спектров обтекания моделей в полете использовался стенд прямотеневого теневого фотографирования (СТФ). В качестве источников света для регистрации моделей во время свободного полета на измерительной трассе аэробаллистической установки использовались точечные газоразрядные источники света длительностью 0,2 мкс.

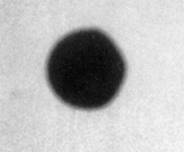
На рис.4 приведен спектр обтекания сферы (здесь - шар диаметром 80 мм, М~2,5). Интерес к этой простой классической форме заключается в возможности получения «идеального» симметричного обтекающего потока, поскольку при отсутствии вращения (или при наличии вращения вокруг оси, совпадающей с вектором скорости) сфера не испытывает ни подъемной, ни поперечной силы, что, в частности, используется в тестовых опытах для юстировки и настройки оборудования, задействованного для получения информации, необходимой для проведения внешнетраекторных измерений в баллистическом эксперименте. (Поперечная сила по отношению к направлению движения сферы возникает вследствие эффекта Магнуса и максимальна, если сфера вращается вокруг оси, перпендикулярной направлению полета).

По мере увеличения расстояния от критической точки - точки, в которой скорость воздуха равна нулю, - увеличивается скорость газа и в определенной точке на поверхности сферы она достигает значения местной скорости звука. Эта точка располагается не далее, чем первые видимые линии возмущения, отходящие от поверхности сферы в виде веера темных полос. Причиной появления этих линий может быть и шероховатость поверхности сферы, но необходимым условием их появления является сверхзвуковой поток возле поверхности сферы. Пограничный слой с наветренной стороны поверхности сферы неразличим вплоть до точки отрыва потока за экватором. Отрыв слоя сопровождается значительным увеличением его толщины, что вызывает поворот потока перед линией отрыва. Поворот потока приводит к появлению волн сжатия, которые формируют косую (краевую) ударную волну сразу за зоной отрыва. На подветренной стороне формируется донное течение – расширение и нагревание газа, обладающего малой скоростью. По мере увеличения расстояния вдоль оси потока ширина оторвавшегося потока уменьшается, достигая минимума в «горле» следа. Далее вниз по потоку течение слегка расширяется, образуя зону так называемого «горячего» следа. Сжатие сверхзвукового течения в окрестности «горла» турбулентного следа вызывает образование второй («хвостовой») ударной волны. Эта волна формируется постепенно из серии слабых скачков, вызванных сжатием потока в следе.

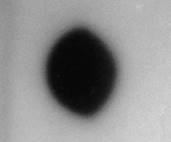
На рис.5 показано характерное обтекание сферы (шар диаметром 23 мм) при большей скорости (М~4). Изображение сферы искажено за счет сильной рефракции света в ударном слое перед ней, в отличие от донной кромки. Эти искажения практически неизменны для всех соответствующих постов регистрации вдоль небольшого отрезка траектории, где скорость шара меняется незначительно, что, в конечном итоге, не сказывается на точности измерений координат. Видно, что отрыв пограничного слоя происходит непосредственно за экватором, что сопровождается генерируемой ударной волной.

Рис. 4. Спектр обтекания сферы, Ø=80 мм, М~2,5

Рис. 5. Спектр обтекания сферы, Ø=23 мм, М~4

Прямотеневой способ, имея максимально возможное разрешение на уровне 0,05-0,1 мм, в ряде случаев может быть заменен схемой комбинированного поста (рис.6), имеющего меньшее разрешения за счет использовании оптических деталей, но позволяющего одновременно получать фотографию в отраженном свете и  теневое изображение. Примеры опытов с шаром с необработанной поверхностью представлены на рис.7.

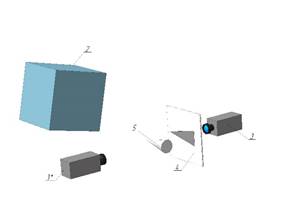
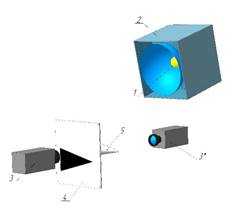
Рис. 6. Состав комбинированного поста регистрации

1. точечный излучатель

2. газоразрядный накопитель

3. камера с затвором с ЭОП

4. полупрозрачный экран

5. регистрируемый объект исследования

а)

б)

Рис. 7. Одновременно полученные теневая фотография (а) и снимок в отраженном свете (б) полета шара (М =4,52)

При гиперзвуковых скоростях полета прямотеневая съемка невозможна из-за фонового излучения ионизированного воздуха и теневые снимки были получены в схеме комбинированного поста (рис.8-10). При этом одновременно при срабатывании точечного источника света строится теневое изображение летящего тела на полупрозрачном экране (а), регистрируемое одной камерой с электронно-оптическим затвором и производится фотографирование в отраженном свете другой (б) [42,43]. Снимки в отраженном свете –свечение ионизованного газа, обтекающего с гиперзвуковой скоростью шар- отличаются в зависимости от условий опыта, скорости и материала шара. На рис. 8 (б) (шар из сплава ВР-27 (вольфрам – 73 %, рений – 27 %)- ярко светящаяся лобовая поверхность объекта испытания с ореолом, сильное свечение ближнего следа; разрушение отсутствует. На рис.9 (б) (шар из прессованного вольфрама с добавкой 0,2 % никеля) - яркое свечение как самого объекта, так ближнего и дальнего следа; полет объекта испытания сопровождается разлетом мелких частиц материала, по-видимому, вольфрама, след имеет форму "хвоста кометы";трек яркий с выбросом отдельных частиц вперед по потоку, как и при аэротермомеханическом разрушении объектов из ВНЖ [36]. На рис.10 (б) (шар из сплава ВР-27  %, рений – 27 %) - ярко светящаяся лобовая поверхность объекта испытания с ореолом, сильное свечение ближнего и дальнего следа; летящие в следе и за его границами светящиеся частицы – фрагменты контактного датчика для запуска рентгеновского аппарата; лобовая поверхность данного материала при высоких скоростях приобретает "метеоритную" форму (а).

а)

б)

Рис. 8. Одновременно полученные теневая фотография (а) и снимок в отраженном свете (б) полета шара (М =14,23)

а)

б)

Рис. 9. Одновременно полученные теневая фотография (а) и снимок в отраженном свете (б) полета шара (М =15,44)

а)

б)

Рис. 10. Одновременно полученные теневая фотография (а) и снимок в отраженном свете (б) полета шара (М =15,92)

1) (A=0,838; B=1,33722; C=2,35146)

2)  (A=-1,23517; B=0,08081; C=0,054)

3)    (A=-0,94393; B=0,26575; C=-0,61788)

Рис. 11. Аппроксимационные зависимости по результатам экспериментальных исследований полета тел сферической формы

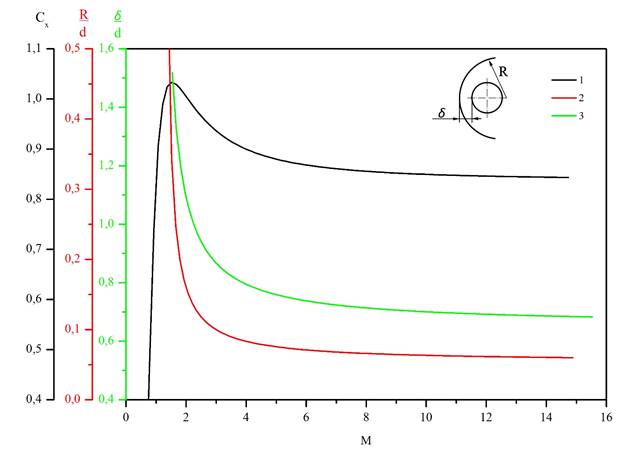
Ударная волна около шара, движущегося со сверхзвуковой скоростью визуально описывается: отходом ударной волны вблизи критической точки; радиусом кривизны ударной волны в области критической точки [41], см. рис.11. Проведенные аэробаллистические исследования свободного полета шара в воздухе атмосферного давления суммированы в виде экспериментальных зависимостей коэффициента сопротивления от числа Маха C_x(M), величины отхода ударной волны вблизи критической точки δ/d (M) (d – диаметр шара), радиусом кривизны ударной волны вблизи критической точки R/d (M) и представлены на рис.11. Приведенные аппроксимационные зависимости используются в оценках до наступления режима  разрушения шара вследствие уноса.

Представленные данные с пятипроцентной точностью совпадают с известными данными для сферы до чисел Маха ≈10. При больших скоростях данные по коэффициенту сопротивления могут значительно отличаться от кривой 1 на рис.11. Причиной является аэротермомеханический унос с поверхности шара (см.  рис. 9), имеющий разный механизм в зависимости от материала.

Для оптимальных методов визуализации при этих условиях применяется метод импульсного рентгенографирования. Разрешение снимка при этом дополнительно падает на порядок и нет возможности регистрировать оптические неоднородности при обтекании шара, но появляется возможность получения мгновенного (времена экспонирования составляют несколько наносекунд) силуэтного изображения в увеличенном масштабе.

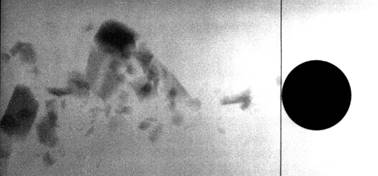
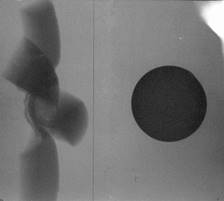
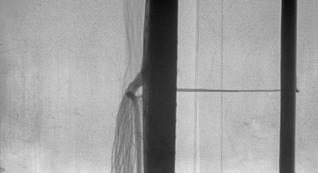
Примеры регистрации состояния шара перед соударением и при взаимодействии с преградой с помощью одноракурсной рентгеновской регистрации показаны на рис.12 (движение здесь идет слева направо).

а)

б)

в)

г)

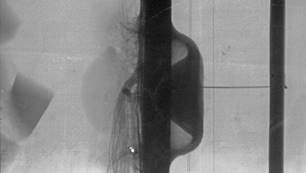
д)

Рис. 12. Результаты регистрации шара в полете и при взаимодействии с преградой: а), б) последовательные положения стального шарика Ø36,5 мм выстреливаемого из ЛГУ с дульной скоростью 10,87М (вертикальные линии – отвесы, расположенные в сечениях в соответствии с расчетной скоростью движения шара), в) летящий алюминиевый полый шар массой 206 г, диаметром Ø80мм (расчетная дульная скорость – 10,15М), г), д) преграда до и во время встречи с шаром (г)

Визуализация поведения шаров из различных конструкционных материалов (сплавы, композитные материалы, материалы порошковой металлургии) к воздействию гиперзвукового потока показала, что:

- шарики из высокопрочного сплава ВР-27 (вольфрам – 73 %, рений – 27 %): в диапазоне начальных скоростей до 15,31М стойки к аэротермомеханическому разрушению,

- при скоростях 15,92М полета зафиксирован унос материала с лобовой поверхности ОИ, сопровождающийся изменением геометрии и массы объекта (рис.13).

- шарики из псевдосплава ВНЖ-97,5 (W – 97,5 %, Ni-Fe – 2,5 %):

- при начальной скорости полета ОИ  17,7М км/с  зафиксировано интенсивное разрушение материала с вылетом частиц вперед по потоку (рис.14), аналогичная картина наблюдалась в экспериментах, проведенных ранее с шариками такого же диаметра, изготовленными из ВНЖ-90, при начальных скоростях полета более 12.7М .

Шарики из материала порошковой металлургии "вольфрам + 0,2 % никеля":

- при начальной скорости полета около 15.43М зафиксировано разрушение материала с выбросом материала частиц вперед по потоку.

Шарики из чистого прессованного порошкового вольфрама:

- при начальной скорости полета 14.27М разрушения материала не зафиксировано;

- при начальной скорости полета 17.64М и выше зафиксирован процесс  аэротермомеханического разрушения материала с вылетом его частиц вперед по  потоку.

Зависимости коэффициента силы лобового сопротивления  от числа Маха для шаров, изготовленных из разных конструкционных материалов, представлены на рисунках 15, 16. Зависимость коэффициента силы лобового сопротивления  для сферы при отсутствии уноса материала ОИ соответствуют "классическим"  представлениям и практически постоянна  в пределах погрешности эксперимента  во всем реализованном скоростном диапазоне. В отдельных опытах (кривые №4 (рис.15) и №3 (рис.16)) зависимости  имеют больший градиент, что является косвенным доказательством наличия аэротермомеханического разрушения конструкционных материалов объектов испытаний, сопровождающегося существенными изменениями геометрии и массы (~ 10-15 %) – см. также рентгенограммы этих экспериментов.

РА1 – Х ≈ 6 м, М ≈ 15,56	РА2 – Х ≈ 90 м, М ≈ 10,73
РА3 – Х ≈ 126 м, М ≈ 8,82	РА4 – Х ≈ 144 м, М ≈ 5,92

Рис. 13. Результаты последовательного рентгенографирования полета шара, изготовленного из сплава ВР и метаемого с начальной скоростью М ≈ 16

РА1 – Х ≈ 6 м, М ≈  17,4

РА2 – Х ≈ 90 м, М≈12,76

Рис. 14. Результаты последовательного рентгенографирования полета шара, изготовленного из сплава ВНЖ и метаемого с начальной скоростью М ≈  17,7

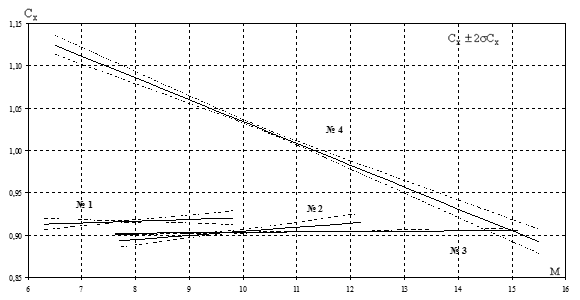
Рис. 15. Зависимость коэффициента силы лобового сопротивления от числа Маха для шарика из сплава ВР

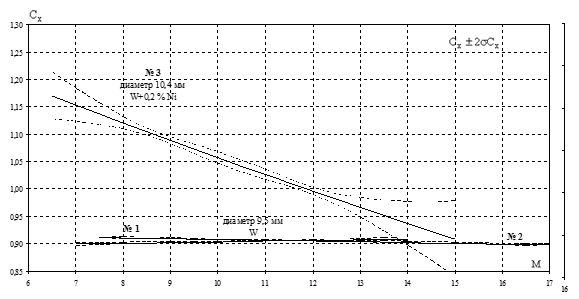
Рис. 16. Зависимость коэффициента силы лобового сопротивления от числа Маха для шарика из тугоплавкого материала

3. Движение в воде

Интерес к изучению гидродинамических свойств воды вызван потребностью разработки методов расчёта гидродинамических характеристик сверхскоростных технических средств, взаимодействующих с водной средой, например, спускаемые космические аппараты.

При движении со сверхзвуковой скоростью перед телом движется скачок уплотнения, форма и относительное положение которого определяются числом  и геометрией носовой оконечности тела. Ниже представлены результаты регистрации поведения стального шара диаметром 13,5 мм, выпущенного из пороховой метательной установки со скоростью примерно 1500 м/с в водопроводную воду комнатной температуры.

Схема оптической регистрации предусматривала получение информации в проходящем свете на фоне «светящегося экрана» с помощью скоростной камеры «ВИДЕОСПРИНТ» (скорость съемки 8065 к/с, время экспозиции 2 мкс, прореживание 4, диафрагма 4), а также видеокамерой Sony DR 170P, снимающей общий вид хода опыта.

Запуск источника импульсного источника света (ИИС) производился без задержки от срабатывания контактного датчика, находящегося на расстоянии 160 см от торца резервуара с водой. ИИС располагался на расстоянии 155 см от боковой стенки резервуара.

Размеры резервуара составляли 60×30×50 см; боковые стенки сделаны из оргстекла толщиной 0,5 см; дно, передняя и задняя стенки закрыты плёнкой из полиэтилена. На боковой стенке аквариума закреплена лавсановая плёнка. Высота воды в аквариуме составляла 20 см (объём ~36 литров).

Шар прошёл в воде по прямолинейной траектории (рис.17). На раскадровке записи виден движущийся в каверне элемент поддона. За резервуаром располагались уловители — два мешка длиной 60 см, наполненных сырыми опилками. Шар прошёл через первый уловитель, пробил картонную перегородку и прекратил движение во втором уловителе. В ходе эксперимента шар не претерпел видимых деформаций. На рис. 18-20 приведены результаты измерений.

Рис. 17. Раскадровка записи с камеры «ВИДЕОСПРИНТ»

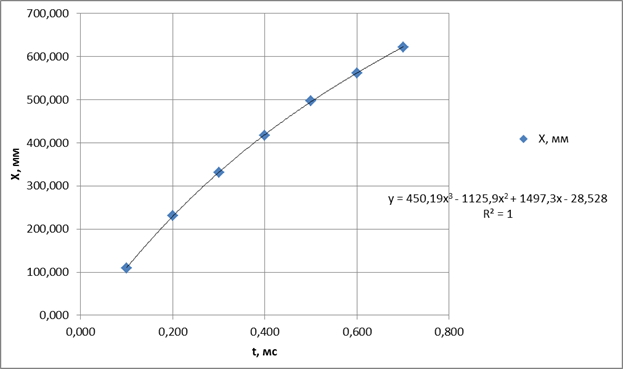
Рис. 18. Диаграмма перемещения ОИ в воде

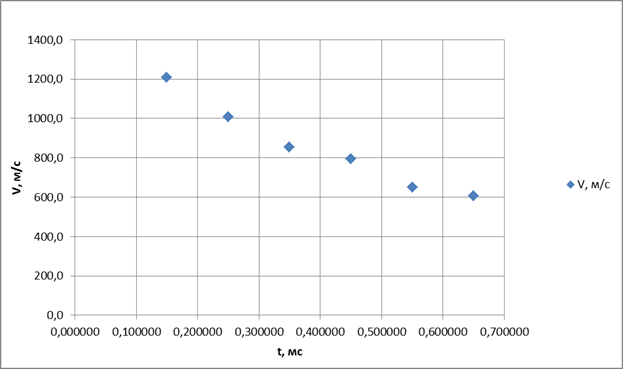
Рис. 19. Экспериментальная зависимость скорости движения ОИ в воде

Рис. 20. Ударная волна (R_УВ/d≈20)

4. Численные расчеты

Для отработки методик расчета с помощью современных инженерных методов компьютерного моделирования процесса гиперзвукового обтекания произведен расчет моделей при различных скоростях обтекания.

В качестве метода моделирования выбран метод численного решения осредненных по Рейнольдсу уравнений Навье-Стокса, дополненных k-ε - моделью турбулентности.

Кинетическая энергия турбулентности k и диссипация этой энергии ε определяются в результате решения следующих уравнений:

где: , , ,

(1) (2)

где t – время, ρ – плотность текучей среды, P – давление текучей среды,  - дельта функция Кронекера,  - составляющая гравитационного ускорения в координатном направлении ,, =1 при  и =0 при ,,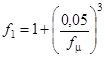,,,, , - коэффициент динамической вязкости, - коэффициент турбулентной вязкости.

 Этот метод реализован в современном инженерном программном пакете SolidWorks Flow Simulation [44]. Пакет представляет собой комбинацию полной версии системы как графической среды и гидрогазодинамического решателя, препроцессор которого позволяет реализовывать автоматизированный или ручной метод блочного построения расчетной сетки и ее последующей адаптации в зонах больших градиентов параметров потока. Данный пакет позволяет рассчитывать широкий круг различных течений: двумерные и трехмерные, ламинарные, турбулентные и переходные, несжимаемые, сжимаемые, с до-, транс- и сверхзвуковыми областями, стационарные и нестационарные течения многокомпонентных текучих сред в каналах и/или вокруг тел, с учетом гравитации, пограничного слоя, в том числе с учетом шероховатости стенок, с конвективным теплообменом между текучей средой и твердым телом, которое, в свою очередь, может состоять из нескольких материалов; с одновременным расчетом теплопередачи в твердых телах, т. е. с решением задачи сопряженного теплообмена, в том числе с учетом радиационного теплообмена между поверхностями; течения газовых смесей с равновесной конденсацией содержащегося в них водяного пара; течения воды с равновесной кавитацией или равновесным кипением; течения через пористые среды как через рассредоточенные сопротивления; ламинарные течения неньютоновских жидкостей; течения сжимаемых жидкостей; двухфазные течения как движение жидких или твердых частиц в потоке текучей среды.

В качестве граничных условий, помимо обычных условий непротекания и прилипания на стенке, тепловых условий на стенке, контактирующей с текучей средой (температура поверхности или тепловой поток между стенкой и текучей средой) — если не рассчитывается теплопередача внутри стенки, или если теплопередача внутри стенки рассчитывается, то тепловых условий на внешней поверхности тела на границе расчетной области, параметров текучей среды на входных и выходных отверстиях модели (в том числе с возможным моделированием приточных или вытяжных вентиляторов) во внутренних и внешних задачах или на границах расчетной области во внешних задачах, могут быть заданы также вращательные и/или поступательные движения поверхности стенки, не меняющие геометрию стенки, или вращение тела в выделенной осесимметричной подобласти расчетной области. Возможно задание объемных источников тепла в текучей среде и/или в теле (если рассчитывается теплопередача в твердых телах), поверхностных источников тепла на поверхности твердого тела. В результате решения определяются аэродинамические силы и моменты, действующие на обтекаемую поверхность объекта, получены параметры обтекающего газа в расчетном объеме - поля давлений, плотностей, температур, скоростей. Полученные результаты могут выводиться в виде контурных распределений параметров течения в объеме и на поверхности тела и в виде соответствующих графиков для любого выбранного сечения.

Для дискретизации дифференциальных уравнений в SolidWorks Flow Simulation используется метод конечных объемов. Соответственно, собственно дискретизация непрерывной математической модели состоит в том, что значения физических переменных рассчитываются (и хранятся) только в центрах расчетных ячеек, а на гранях этих ячеек рассчитываются потоки массы, импульса, энергии, необходимые для расчета этих значений. При этом пространственные производные аппроксимируются с помощью неявных разностных операторов второго порядка точности. А именно, полученные из уравнений (1,2) интегрированием по поверхности и объему ячейки расчетной сетки интегральные уравнения

                               (3)

где U — вектор физических параметров (независимых переменных), V — объем ячейки, F — потоки, S — площадь поверхности (граней) ячейки, Q — массовые силы, преобразуются к дискретной форме:

                           (4)

Потоки F рассчитываются с использованием их аппроксимации вперед второго порядка точности, основанной на модифицированных неявных QUICK- аппроксимациях Леонарда [45] и методе минимизации полной вариации TVD [46]. Специальные аппроксимации применяются для конвективных членов, операторов div и grad.

В частичных, т. е. пересеченных поверхностью твердого тела на границе с текучей средой, расчетных ячейках вводятся дополнительные внутренние грани, аппроксимирующие попавшую в эти ячейки поверхность твердого тела, и используется специальная процедура для расчета условий на этих гранях.

Чтобы выполнить дискретизацию по времени, для каждой ячейки расчетной сетки в расчетной области из условия Куранта определяется допустимый максимальный шаг по времени, зависящий как от значений физических величин, так и от шага дискретизации по пространству в этой ячейке. Если решается нестационарная задача, то затем определяется минимальный из определенных таким образом шагов по времени по всем ячейкам расчетной сетки в расчетной области и с этим шагом, одинаковым для всех ячеек, выполняется переход (т. е. расчет параметров) к следующему моменту времени. Если решается стационарная задача, то для ускорения установления решения по времени шаги по времени в разных ячейках расчетной сетки в расчетной области разные, а именно определяются из условия Куранта в зависимости от значений физических величин и шага дискретизации по пространству в ячейке.

При дискретизации по времени используется метод расщепления операторов для более эффективного расчета давления и скорости. В соответствии с методом типа SIMPLE [47], давление рассчитывается в результате решения дискретного эллиптического уравнения, полученного алгебраическими преобразованиями дискретных уравнений сохранения массы и импульса с учетом граничных условий для скорости.

Для повышения устойчивости и ускорения сходимости используется также процедура сглаживания получаемого решения [48].

С точки зрения проверки возможностей данного численного метода с автоматической адаптацией расчетной сетки, задача обтекания шара гиперзвуковым потоком газа выглядит крайне актуальной и целесообразной в связи с наличием экспериментального материала.

В качестве объекта моделирования выбран шар 10,4 мм. Для определения влияния размеров расчетного домена на характер обтекания шара и коэффициент лобового сопротивления рассматривались несколько доменов различных размеров при одной начальной скорости обтекания (M = 6). Исходя из условий симметрии, была взята лишь четвертая часть полного, окружающего весь шар домена. Расчетный домен, используемый в дальнейших исследованиях влияния начальной скорости потока на коэффициент лобового сопротивления и на характер обтекания шара, имеет размеры 90×50×50 мм.

а)	б)
в)

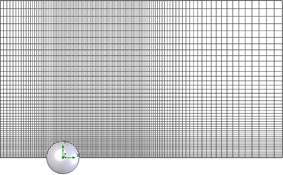
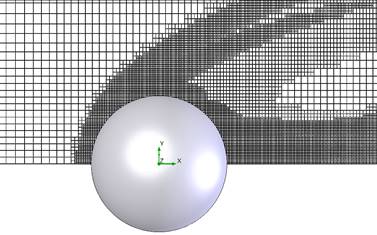
Рис. 21. Исходная а) и адаптированная б) расчетная сетка при M = 7, в) – фрагмент адаптированной сетки шара

На рисунках 21(а,б) приведена исходная счетная сетка для расчетов обтекания модели, а также показана, дважды адаптированная после 1380 и 2070 итераций, сетка для условий обтекания с начальной скоростью М = 7. Исходная сетка состояла из 234963 ячеек, а адаптированная сетка из 381676, 801067.

На рисунке 21в фрагмент адаптированной сетки для условий обтекания с начальной скоростью М = 7 показан в увеличенном масштабе.

Трехмерный расчет процесса внешнего обтекания шара сверхзвуковым потоком сжимаемого газа проводился с учетом соответствующих граничных условий на поверхности шара и на стенках расчетного домена. Решались полные, осредненные по Рейнольдсу уравнения Навье-Стокса, дополненные двухпараметрической моделью турбулентности. Диапазон рассмотренных начальных скоростей обтекания составлял 6 – 15 M. Для воздуха использовалось уравнение состояния совершенного газа. В процессе расчета определялись полные в объеме домена поля для всех параметров обтекающего газа, определялось значение коэффициента лобового сопротивления шара. Характер обтекания шара при начальной скорости М = 7 показан на рисунках 22-25.

Рисунки представляют из себя контурные отображения распределения полей давлений, температур, плотностей и суммарных векторов скоростей в потоке газа, обтекающего шар. Данные контурные отображения построены с помощью штатных возможностей постпроцессора программного комплекса SolidWorks Flow Simulation. Постпроцессор позволяет в различных сечениях расчетного домена строить линии тока, вектора, изолинии и контура параметров потока (до 255 различных контуров). Контурное отображение имеет возможность градации по 21 различной цветовой схеме. В данном случае приведены рисунки, выполненные в монохроматической цветовой схеме, что обусловлено наличием областей (головная ударная волна перед шаром) высоких значений градиента параметров потока газа (например, давления). Применение классической цветной гаммы делает подобные рисунки менее информативными из-за сложности визуального опознания различных областей потока, имеющих меньший градиент параметров газа.

Из рисунков можно заметить, что характер обтекания в целом соответствуют классическим представлениям об обтекании шара сверх- и гиперзвуковым потоком газа  – наличие головной ударной волны перед шаром; образование донного течения с подветренной стороны за телом – расширение и нагревание газа, обладающего малой скоростью; наличие «хвостовой» ударной волны.

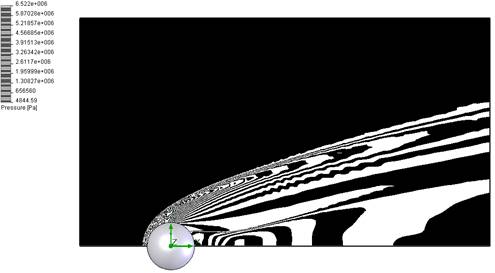
Рис. 22. Распределение полей давлений (Па) в потоке при обтекании шара с начальной скоростью M = 7

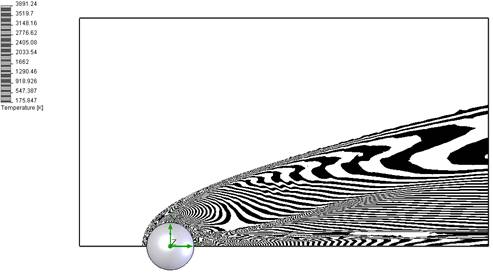
Рис. 23. Распределение полей температур (K) в потоке при обтекании шара с начальной скоростью M = 7

Рис. 24. Распределение полей плотностей (кг/м³) в потоке при обтекании шара с начальной скоростью M = 7

Рис. 25. Распределение полей суммарных векторов скоростей (м/с) в потоке при обтекании шара с начальной скоростью M = 7

Вычисленные значения коэффициента сопротивления в зависимости от чисел Маха (рисунок 26) достаточно близки к экспериментальным (в пределах примерно 5%) в опытах, где не наблюдалось разрушение шара.

Рис. 26. Зависимость коэффициента силы лобового сопротивления () от числа Маха () для шаров из различных конструкционных материалов

Расчеты с начальными скоростями более М = 10 показали, что при данных скоростях обтекания происходит нарушение алгоритма автоматической адаптации расчетной сетки. Видимо, данное явление связано с крайне высоким значением градиента параметров потока в реализованном численном методе, что приводит к неестественным изменениям расчетной сетки. Возникают значительные осцилляции вычисляемых параметров, что не позволяет говорить о сходимости решения даже спустя достаточно большое количество расчетных итераций. Также, при столь высоких скоростях обтекания возможен процесс аэротермомеханического разрушения шара, сопровождающий процесс обтекания, характеризующийся наличием химических реакций, уноса материала и изменением формы шара, ионизацией. Наличие вышеописанных явлений требует существенной корректировки математической модели. Тем не менее, анализ полученных результатов численного моделирования до скорости не выше М = 10 и экспериментальных данных, позволяет сделать вывод о возможности использования данной математической модели в определенном скоростном диапазоне.

Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта № 16-38-60125 мол_а_дк "Разработка методов повышения точности определения аэродинамических характеристик и внешнетракторных данных в аэробаллистических экспериментах» и программы повышения конкурентноспособности НИЯУ МИФИ.

5. Заключение

В работе приведены теневые фотографии сверхзвукового движения шара в воздухе и в воде. Приведены силуэтные рентгеновские снимки гиперзвукового движения шаров из различных материалов в условиях аэротермомеханического разрушения. Получены экспериментальные данные, характеризующие движение головных ударных волн в воздухе и в воде при сверхзвуковом движении шара в этих средах. Представлены экспериментальные и численные результаты определения коэффициента силы лобового сопротивления.

Литература

1. Lunnon R. G. Fluid Resistance to Moving Sphere. Proceedings of the Royal Society of London, Ser. A, Vol. 118, April 2, 1928, pp. 680-694

2. Eisner F. Das Widerstandsproblem. Proceedings of the Third International Congress on Applied Mechanics, Stockholm, 1931.

3. Charters A., Thomas R. The Aerodynamic Performance of Small Spheres from Subsonic to High Supersonic Velocities. Journal of the Aeronautical Sciences, Vol. 12, No. 4, Oct. 1945, pp. 468-476.

4. Clark A. G. J., Harris F. T. Free-Flight Air Drag Measurement Techniques. Journal of the Aeronautical Sciences, Vol. 19, No. 6, June 1952, pp. 385-390

5. May A., Witt A. Free-Flight Determinations of the Drag Coefficients of Spheres. Journal of the Aeronautical Sciences, Vol. 20, No. 9, Sept. 1953, pp. 635-638.

6. Naumann A. Aerodynamische Gesichtspunkte der Wind-kanalentwucklung. Jahrbuch 1954, Der Wissenschaftlichen Gesell-schaft für Luftfahrt E.V. (WGL), Herausgegeben von Hermann Blenk , Friedr. Vieweg & Sohn Braunschweig.

7. Hodges A. J. The Drag Coefficient of Very High Velocity Spheres. Journal of the Aeronautical Sciences, Vol. 24, No. 10, Oct. 1957. pp. 755-758.

8. Красильщиков А.П. Об определении коэффициента сопротивления при отстрелах моделей в аэродинамических трубах. Труды ЦАГИ, № 765, 1959

9. Wegener P., Ashkenas H. Wind Tunnel Measurements of Sphere Drag at Supersonic Speeds and Low Reynold Numbers. Journal of Fluid Mechanics, VoL 4, No. 10, 1961, pp. 550-561

10. Мишин Г.И. Исследование коэффициента сопротивления сферы при сверхзвуковых скоростях в газах с различным отношением удельных теплоемкостей. Журнал технической физики. т. 31, № 4, 1961.

11. Hoglund R.F. Recent Advances in Gas-Particle Nozzle Flows. ARS Journal, Vol. 32, No. 5, May 1962, pp. 662-671

12. Белоцерковскии О.М. Симметричное обтекание затупленных тел сверхзвуковым потоком совершенного и реального газа, Журнал вычислительной математики и математической физики, т. 2, № 6, 1962.

13. Heinrich H.G., Niccum R.J., Haak E. L. The Drag Coefficient of a Sphere Corresponding to a One Meter ROBIN Sphere Descending from 260,000 ft Altitude (Reynolds Nos. 789 to 23,448, Mach Nos. 0.056 to 0.90. Research and Development of ROBIN Meteorological Rocket Balloon, Vol. II, Contract AF 19(604)-8034 (AD480309), Univ. of Minnesota, Minneapolis, Minn., May 1963

14. Галинский С.М., Теленин Г.Ф., Тиняков Г.П. Методы расчета сверхзвукового обтекания затупленных тел с отошедшей ударной волной. Известия АН СССР, Механика и машиностроение № 4, 1964

15. Bailey A.B., Koch K.E. Launching of Foamed Plastic Models with a Two-Stage Light-Gas Gun. AEDC-TR-66-60 (AD632925), May 1966, Arnold Engineering Development Center, Arnold Air Force Station, Tenn

16. Bailey A.B. Sphere Drag Measurements in an Aeroballistics Range at High Velocities and Low Reynolds Numbers. AEDC-TR-66-59 (AD633278), May 1966, Arnold Engineering Development Center, Arnold Air Force Station, Tenn.

17. Мишин Г.И. Простой метод расчета коэффициента сопротивления по данным пространственно-временной зависимости. Cборник «Аэрофизические исследования сверхзвуковых течений». Наука. 1967.

18. Масленников В.Г. О форме отошедшей ударной волны, образующейся при сверхзвуковом движении полусферы и цилиндрического торца в различных газах. Сб. «Аэрофизические исследования сверхзвуковых течений», М.—Л., «Наука», 1967, стр. 256

19. Lawrence W.R. Free-Flight Range Measurements of Sphere Drag at Low Reynolds Numbers and Low Mach Numbers. AEDC-TR-67-218 (AD660545), Nov. 1967, Arnold Engineering Development Center, Arnold Air Force Station, Tenn.

20. Красильщиков А.П., Подобии В.П. Экспериментальное исследование аэродинамических характеристик шара в свободном полете. Изв. АН СССР, МЖГ № 4, 1968.

21. Status of Passive Inflatable Falling-Sphere Technology for Atmospheric Sensing to 100 Km. NASA SP-219, 1969

22. Kussoy M.I., Stewart A., Horstman С.С. Sphere Drag in Near Free-Molecule Hypersonic Flow, АIАА Journal, No. 11, pp. 2104 — 2105,  1970.

23. Гурьяшкин Л.П., Красильщиков А.П., Подобии В.П. Аэробаллистическая труба для измерения сопротивления моделей в свободном полете при гиперзвуковых скоростях. Ученые записки ЦАГИ, т.1, № 2, 1970.

24. Roos, Frederick W. and Willmarth, William W. Experimental Results on Sphere and Disk Drag. AIAA Journal. Vol. 9, No. 2, Feb. 1971. pp. 285-291

25. Bailey A.B., Hiatt J. Free-Flight Measurements of Sphere Drag at Subsonic, Transonic, and Supersonic and Hypersonic Speeds for Continuum, Transition and Near-Free-Molecular Flow Conditions. AEDC-TR-70-291, March 1971, Arnold Engineering Development Center, Arnold Air Force Station, Tenn.

26. Оптические методы исследований в баллистическом эксперименте, под ред. Мишина Г.И. Наука, 1979.

27. Физико-газодинамические баллистические исследования, под ред. Мишина Г.И. Изд. Наука, 1980

28. Андреев А.А., Холодов А.С. О сверхзвуковом пространственном обтекании затупленных тел с учетом интерференции. Ж. вычисл. матем. и матем. физ. 1989. Т. 29, № 1. С. 142-147.

29. Azovskii A.N., Shuvalov V.V. The influence of geometric shape on the motion of fragments of a dissociated meteoroid. Solar System Research. 2002. Vol. 36, No 4. P. 334¬340.

30. Лабунцов Д.А., Ягов В.В. Механика двухфазных систем: учебное пособие для вузов – 2-е изд., перер. и доп.- М. Издательский дом МЭИ, 2007 – 384с

31. Герасимов С.И., Файков Ю.И., Холин С.А. Кумулятивные источники света, РФЯЦ-ВНИИЭФ, Саров, 2011

32. Герасимов С.И., Калмыков П.Н., Костин В.И. Получение внешнетраекторных данных в аэробаллистическом эксперименте. Сборник статей ХХ Юбилейной Всероссийской научно-технической школы-семинара «Обработка, передача и отображение информации о быстропротекающих процессах», Москва РПА «АПР», 2009, с.153

33. Герасимов С.И., Смирнов И.Ю., Лысенков В.Е. Аэробаллистический тир ВНИИЭФ. Методика проведения экспериментов, результаты испытаний Сборник докладов «Оптические методы исследования потоков»,

Москва, МЭИ, 2007, с.386

34. Герасимов С.И., Ерофеев В.И., Каныгин И., Cальников А.В. Визуализация дульного выхлопа при выстреле из легкогазовой пушки. Научная визуализация, т.6, №2, 2014

35 Методы исследования свойств материалов при интенсивных динамических нагрузках /Под ред. Жерноклетова М.В. ФГУП РФЯЦ-ВНИИЭФ, Саров, 2005г.

36. Герасимов С.И., Ерофеев В.И., Кикеев В.А., Фомкин А.П. Различные механизмы разрушения тел в гиперзвуковом потоке, выявленных с помощью рентгенографической регистрации. Научная визуализация. т.7, №1, 2015, с. 38-44

37. Златин H.A., Красильщиков А.П., Мишин Г.И., Попов H.H. Баллистические установки и их применение в экспериментальных исследованиях. М.: Наука. 1974.

38. Лыжин О.В., Красильщиков А.П., Пассова З.Г. Гиперзвуковая аэродинамическая труба Т-123 ЦАГИ. Труды ЦАГИ. вып. 2374. М. 1988

39. Chapman G.T., Kirk D.B. A Method for Extracting Aerodynamic Coefficients from Free-Flight Data. AIAA Journal, No. 4, pp. 753—758, 1970

40. Герасимов С.И., Костин В,И.,Сперанский А.В., Менде Н.П. Алгоритмы определения внешнетраекторных параметров и аэродинамических характеристик движения тела вращения: - пособие для студентов вузов. СарФти НИЯУ МИФИ, 2013, 44с.

41. Масленников В.Г. О форме отошедшей ударной волны, образующейся при сверхзвуковом движении полусферы и цилиндрического торца в различных газах. Сб. «Аэрофизические исследования сверхзвуковых течений», М.—Л., «Наука», 1967

42. Герасимов С.И., Тотышев К.В. Комбинированный фотопост для оптической регистрации быстропротекающих процессов 2010, Бюл. №34 Патент РФ №100313

43. Герасимов С.И., Вашурков А.С. Лень А.В Газоразрядный импульсный источник света Бюл. №4 2003 Патент РФ №27739

44. https://www.solidworks.com/sw/resources/videos/flow-simulation.htm

45. Roache P.J. fundamentals of computational fluid dynamics. Hermosa Publishers, Albuquerque, New Mexico, USA, 1998.

46. Patankar S.V. Numerical heat transfer and fluid flow. Hemisphere, Washington, 1980.

47. Hirsh C. Numerical computation of internal end external flows. John Wiley & Sons, Chichester, 1988.

48. Алямовский А.А. SolidWorks 2007/2008. Компьютерное моделирование в инженерной практике. СПб.: БХВ-Петербург, 2008. 1040 с.

---

VISUALIZATION OF SUPERSONIC MOTION OF A SPHERE IN AIR AND IN WATER

S. I. Gerasimov^1,2,3,4,5, V. A. Kikeev^1,3, K.V. Totyshev², A.P. Fomkin², B.A. Yanenko⁴

¹Nizhny Novgorod State Technical University n.a. R.E. Alekseev, 603950 Russia

²Russian Federal Nuclear Center – All-Russia Research Institute of Experimental Physics, 607188 Sarov, Nizhny Novgorod region, Russia

³ Institute of Mechanical Engineering Problems,  607350  Nizhny Novgorod , Russia

⁴Sarov Physics and Technical Institute of National Research Nuclear University «MEPHI», 607186 Nizhny Novgorod region, Russia

⁵ National Research Nuclear University «MEPHI», 115409 Moscow, Russia

E-mail: s.i.gerasimov@mail.ru, vkikeev@mail.ru

Annotation

Among various diagnostic techniques applied in ballistic experiment optical ones play foremost part inasmuch as use of contact methods in this case is extremely restricted. A modern ballistic range should be equipped with means for observation of projectile motion and visualization of flow about the projectile. Registration of projectile position in the course of the flight gives information about the projectile trajectory. On the basis of the flow pattern one makes conclusions on fundamental gasdynamic and physical phenomena following the projectile motion, such as shock wave formations, viscous flow regimes, boundary layer conditions, location of flow separation points and configuration of separation zones, base flow, and body wake. Serious tests for estimating possibilities of supersonic aeroballisic setting up have been performed. Experimental optic and x-ray images at super-and-hypersound velocities of flight and collision are demonstrated. Moving spheres of different materials have been studied. Flows around model, dependences of drug coefficient, shock curvature versus Mach number are presented. Numerical simulation has been performed. For the first time visualization of head shock in water at horizontal entrance of supersonic sphere has been recorded.

Keywords: aeroballistic test, shadow and silhouette recording, numerical simulation, drag coefficient.

References

1. Lunnon R. G. Fluid Resistance to Moving Sphere. Proceedings of the Royal Society of London, Ser. A, Vol. 118, April 2, 1928, pp. 680-694

2. Eisner F. Das Widerstandsproblem. Proceedings of the Third International Congress on Applied Mechanics, Stockholm, 1931.

3. Charters A., Thomas R. The Aerodynamic Performance of Small Spheres from Subsonic to High Supersonic Velocities. Journal of the Aeronautical Sciences, Vol. 12, No. 4, Oct. 1945, pp. 468-476.

4. Clark A. G. J., Harris F. T. Free-Flight Air Drag Measurement Techniques. Journal of the Aeronautical Sciences, Vol. 19, No. 6, June 1952, pp. 385-390

5. May A., Witt A. Free-Flight Determinations of the Drag Coefficients of Spheres. Journal of the Aeronautical Sciences, Vol. 20, No. 9, Sept. 1953, pp. 635-638.

6. Naumann A. Aerodynamische Gesichtspunkte der Wind-kanalentwucklung. Jahrbuch 1954, Der Wissenschaftlichen Gesell-schaft für Luftfahrt E.V. (WGL), Herausgegeben von Hermann Blenk , Friedr. Vieweg & Sohn Braunschweig.

7. Hodges A. J. The Drag Coefficient of Very High Velocity Spheres. Journal of the Aeronautical Sciences, Vol. 24, No. 10, Oct. 1957. pp. 755-758.

8. Krasil'shhikov A.P. Ob opredelenii kojefficienta soprotivlenija pri otstrelah modelej v ajerodinamicheskih trubah [On the determination of the coefficient of resistance in the shooting of models in wind tunnels]. Proceedings of TsAGI, No. 765, 1959 [In Russian]

9. Wegener P., Ashkenas H. Wind Tunnel Measurements of Sphere Drag at Supersonic Speeds and Low Reynold Numbers. Journal of Fluid Mechanics, VoL 4, No. 10, 1961, pp. 550-561

10. Mishin G.I. Issledovanie kojefficienta soprotivlenija sfery pri sverhzvukovyh skorostjah v gazah s razlichnym otnosheniem udel'nyh teploemkostej [Research of the sphere resistance coefficient at supersonic speeds in gases with different ratio of specific heats]. Journal of Technical Physics, Vol. 31, No. 4, 1961. [In Russian]

11. Hoglund R.F. Recent Advances in Gas-Particle Nozzle Flows. ARS Journal, Vol. 32, No. 5, May 1962, pp. 662-671

12. Belocerkovskii O.M. Simmetrichnoe obtekanie zatuplennyh tel sverhzvukovym potokom sovershennogo i real'nogo gaza [Symmetric flow of blunt bodies over supersonic flow of perfect and real gas]. Journal of Computational Mathematics and Mathematical Physics. Vol. 2, No. 6, 1962. [In Russian]

13. Heinrich H.G., Niccum R.J., Haak E. L. The Drag Coefficient of a Sphere Corresponding to a One Meter ROBIN Sphere Descending from 260,000 ft Altitude (Reynolds Nos. 789 to 23,448, Mach Nos. 0.056 to 0.90. Research and Development of ROBIN Meteorological Rocket Balloon, Vol. II, Contract AF 19(604)-8034 (AD480309), Univ. of Minnesota, Minneapolis, Minn., May 1963

14. Galinskij S.M., Telenin G.F., Tinjakov G.P. Metody rascheta sverhzvukovogo obtekanija zatuplennyh tel s otoshedshej udarnoj volnoj [Methods for calculating the supersonic flow past blunt bodies with a retreating shock wave]. Proceedings of the Academy of Sciences of the USSR, Mechanics and Mechanical Engineering. No. 4, 1964 [In Russian]

15. Bailey A.B., Koch K.E. Launching of Foamed Plastic Models with a Two-Stage Light-Gas Gun. AEDC-TR-66-60 (AD632925), May 1966, Arnold Engineering Development Center, Arnold Air Force Station, Tenn

16. Bailey A.B. Sphere Drag Measurements in an Aeroballistics Range at High Velocities and Low Reynolds Numbers. AEDC-TR-66-59 (AD633278), May 1966, Arnold Engineering Development Center, Arnold Air Force Station, Tenn.

17. Mishin G.I.  Moskva, 1967. [In Russian]

18. Maslennikov V.G. O forme otoshedshej udarnoj volny, obrazujushhejsja pri sverhzvukovom dvizhenii polusfery i cilindricheskogo torca v razlichnyh gazah [A simple method of calculating the coefficient of resistance from the data of space-time dependence]. Collection of Aerophysical Research of supersonic flows. Science. 1967, 256 p. [In Russian]

19. Lawrence W.R. Free-Flight Range Measurements of Sphere Drag at Low Reynolds Numbers and Low Mach Numbers. AEDC-TR-67-218 (AD660545), Nov. 1967, Arnold Engineering Development Center, Arnold Air Force Station, Tenn.

20. Krasil'shhikov A.P., Podobii V.P. Jeksperimental'noe issledovanie ajerodinamicheskih harakteristik shara v svobodnom polete [Experimental study of aerodynamic characteristics of a ball in free flight]. Izv. AN SSSR, MZHG. No. 4, 1968. [In Russian]

21. Status of Passive Inflatable Falling-Sphere Technology for Atmospheric Sensing to 100 Km. NASA SP-219, 1969

22. Kussoy M.I., Stewart A., Horstman S.S. Sphere Drag in Near Free-Molecule Hypersonic Flow, AIAA Journal, No. 11, pp. 2104 — 2105,  1970.

23. Gur'jashkin L.P., Krasil'shhikov A.P., Podobii V.P. Ajeroballisticheskaja truba dlja izmerenija soprotivlenija modelej v svobodnom polete pri giperzvukovyh skorostjah [Aeroballistic pipe for measuring the resistance of models in free flight at hypersonic speeds]. TsAGI scientific notes, vol. 1, no. 2, 1970. [In Russian]

24. Roos, Frederick W. and Willmarth, William W. Experimental Results on Sphere and Disk Drag. AIAA Journal. Vol. 9, No. 2, Feb. 1971. pp. 285-291

25. Bailey A.B., Hiatt J. Free-Flight Measurements of Sphere Drag at Subsonic, Transonic, and Supersonic and Hypersonic Speeds for Continuum, Transition and Near-Free-Molecular Flow Conditions. AEDC-TR-70-291, March 1971, Arnold Engineering Development Center, Arnold Air Force Station, Tenn.

26. Opticheskie metody issledovanij v ballisticheskom jeksperimente [Optical methods of research in the ballistic experiment]. ed. Mishina G.I. Science, 1979.  [In Russian]

27. Fiziko-gazodinamicheskie ballisticheskie issledovanija [Physico-gas dynamic ballistic studies]. ed. Mishina G.I. Science, 1980 [In Russian]

28. Andreev A.A., Holodov A.S. O sverhzvukovom prostranstvennom obtekanii zatuplennyh tel s uchetom interferencii [About supersonic spatial flow around blunt bodies in view of the interference]. Journal of computed Math. And Math. Phys. 1989. Vol. 29, No. 1. Pp. 142-147. [In Russian]

29. Azovskii A.N., Shuvalov V.V. The influence of geometric shape on the motion of fragments of a dissociated meteoroid. Solar System Research. 2002. Vol. 36, No 4. P. 334¬340.

30. Labuncov D.A., Jagov V.V. Mehanika dvuhfaznyh sistem: uchebnoe posobie dlja vuzov [Mechanics of two-phase systems: a textbook for high schools]. Publishing house MPEI, 2007. 384 p. [In Russian]

31. Gerasimov S.I., Fajkov Ju.I., Holin S.A. Kumuljativnye istochniki sveta [Cumulative light sources]. RFNC-VNIIEF, 2011 [In Russian]

32. Gerasimov S.I.,  Kalmykov P.N., Kostin V.I. Poluchenie vneshnetraektornyh dannyh v ajeroballisticheskom jeksperimente [Obtaining external-data data in an aeroballistic experiment]. Collection of articles of the twentieth Anniversary of All-Russian scientific-technical workshop "Treatment, transmission and display of information about the fast processes", 2009, 153 p. [In Russian]

33. Gerasimov S.I.,  Smirnov I.Ju., Lysenkov V.E. Ajeroballisticheskij tir VNIIJeF. Metodika provedenija jeksperimentov. rezul'taty ispytanij. [Aerial ballistic shooting range of VNIIEF. Methods of conducting experiments]. Test results Collection of reports "Optical methods of flow studies", 2007, 386 p. [In Russian]

34. Gerasimov S.I. , Erofeev V.I., Kanygin I., Cal'nikov A.V. Vizualizacija dul'nogo vyhlopa pri vystrele iz legkogazovoj pushki [Visualization of Muzzle Exhaust Following the Light Gas Gun Shot]. Scientific visualization, Vol. 6, No. 2, 2014 [In Russian]

35 Metody issledovanija svojstv materialov pri intensivnyh dinamicheskih nagruzkah [Methods for studying the properties of materials under intense dynamic loads]. Ed. Zhernokletova M.V. FSUE RFNC-VNIIEF, 2005. [In Russian]

36. Gerasimov S.I., Erofeev V.I., Kikeev V.A.,  Fomkin A.P. Razlichnye mehanizmy razrushenija tel v giperzvukovom potoke, vyjavlennyh s pomoshh'ju rentgenograficheskoj registracii [Various mechanisms of aerothermomechanical destruction of objects in hypersonic flow recorded with optical and x-ray techniques]. Scientific visualization. Vol. 7, No. 1, 2015, pp. 38-44 [In Russian]

37. Zlatin H.A., Krasil'shhikov A.P., Mishin G.I., Popov H.H. Ballisticheskie ustanovki i ih primenenie v jeksperimental'nyh issledovanijah [Ballistic installations and their application in experimental studies]. Science. 1974. [In Russian]

38. Lyzhin O.V., Krasil'shhikov A.P., Passova Z.G. Giperzvukovaja ajerodinamicheskaja truba T-123 CAGI [Hypersonic wind tunnel T-123 TsAGI]. Proceedings of TsAGI. No. 2374. 1988 [In Russian]

39. Chapman G.T., Kirk D.B.. A Method for Extracting Aerodynamic Coefficients from Free-Flight Data. AIAA Journal, No. 4, pp. 753—758, 1970

40. Gerasimov S.I., Kostin V,I.,Speranskij A.V., Mende N.P. Algoritmy opredelenija vneshnetraektornyh parametrov i ajerodinamicheskih harakteristik dvizhenija tela vrashhenija: - posobie dlja studentov vuzov [Algorithms for determining the external parameters and aerodynamic characteristics of the motion of the body of revolution: - A manual for university students]. Sarov Physics and Technical Institute of National Research Nuclear University «MEPHI», 2013, 44 p. [In Russian]

41. Maslennikov V.G. O forme otoshedshej udarnoj volny, obrazujushhejsja pri sverhzvukovom dvizhenii polusfery i cilindricheskogo torca v razlichnyh gazah [On the form of a shock wave that is formed during supersonic motion of a hemisphere and a cylindrical butt in various gases]. Coll. "Aerophysical studies of supersonic flows". Science, 1967 [In Russian]

42. Gerasimov S.I., Totyshev K.V. Combined photostate for optical recording of fast processes 2010, Patent of the Russian Federation No. 100313 [In Russian]

43. Gerasimov S.I., Vashurkov A.S. Len' A.V Gas-discharge pulse light source. 2003 Patent of the Russian Federation No. 27739 [In Russian]

44. https://www.solidworks.com/sw/resources/videos/flow-simulation.htm

45. Roache P.J. fundamentals of computational fluid dynamics. Hermosa Publishers, Albuquerque, New Mexico, USA, 1998.

46. Patankar S.V. Numerical heat transfer and fluid flow. Hemisphere, Washington, 1980.

47. Hirsh C. Numerical computation of internal end external flows. John Wiley & Sons, Chichester, 1988.

48. Aljamovskij A.A. SolidWorks 2007/2008. Komp'juternoe modelirovanie v inzhenernoj praktike [Computer modeling in engineering practice]. 2008. 1040 p. [In Russian]
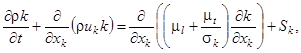
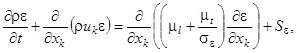
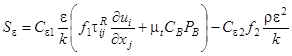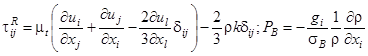