КРИПТОГРАФИЧЕСКИЙ СПОСОБ ДОКУМЕНТИРОВАНИЯ ПОКАДРОВЫХ ИЗОБРАЖЕНИЙ

Д.А. Мельников, А.А. Абрамов, В.С. Горбатов, А.П. Дураковский, Р.Д. Махмутов

Национальный исследовательский ядерный университет «МИФИ», Россия

DAMelnikov@mephi.ru, mvpcvp@gmail.com, VSGorbatov@mephi.ru, APDurakovskiy@mephi.ru, infmaxx@gmail.com

Содержание

1. Введение

2. Демонстрация способа геометрического перемежения

3. Способы геометрического перемежения ПТИ

4. Усложнение перемежения: разнонаправленная контурная ротация

5. Некоторые аспекты практической реализации

6. Заключение

Список литературы

Аннотация

Сегодня одним из направлений развития сферы информационных технологий является визуализация, т.е. представление чего-либо - физического процесса, явления и т.п. в форме, удобной для наблюдения [1]. Визуализация получила широкое распространение во многих практических областях, одной из которых является цифровая криминалистика. В последней стали активно использоваться визуальные доказательства. Визуальное доказательство любых правонарушений является основой реализации принципа неотвратимости наказания. Вместе с тем, визуальные доказательства являются цифровой формой вещественных доказательств и поэтому требуют специфической защиты от разного рода модификаций. В некоторых случаях может потребоваться защита конфиденциальности визуального доказательства, если оно содержит сведения, составляющие государственную или коммерческую тайну, или персональные данные.

С другой стороны, визуальное доказательство должно быть таким, чтобы исключить любые попытки правонарушителя отказаться от какого-либо действия или бездействия, подтверждающего факт нарушения законодательства. В таком случае, судья может затребовать визуальное доказательство и по нему определить, произошло или нет нарушение законодательства.

В работе рассмотрены основные идеи и подходы к практической реализации криптографического способа обеспечения целостности и конфиденциальности покадровых изображений (визуального доказательства) - “способа Мельникова-Джонса” [2]. Кроме того, этот способ может использоваться при формировании и защите визуального доказательства при разрешении юридических споров (обеспечение неотказуемости). Данный способ основан на предварительном скремблировании и нескольких последующих геометрических перестановках пикселей изображения путём его разбиения с использованием треугольной решётки, что практически исключает возможность его злоумышленного искажения, т.е. любая попытка модификации визуального документа будет обнаружена.

Ключевые слова: визуальное доказательство, цифровая криминалистика, треугольная решетка, геометрическая перестановка, шестигранник, угол поворота, перестановка, скремблирование, криптография, шифрование, целостность, модификация.

1. Введение

В настоящее время наблюдается расширение использования мультимедийных средств для сбора визуальных (документальных) доказательств в практике правового разрешения конфликтных ситуаций. При этом одним из основных требований является наличие определенных гарантий целостности представленного доказательства, что достигается тем или иным средством защиты от подделки.

Одним из направлений развития способов защиты визуальных доказательств является применение цифровых водяных знаков (ЦВЗ, digital watermark), которые относятся к стеганографическим методам защиты данных [3,4]. Главными недостатками таких ЦВЗ-систем являются: во-первых, их прямое воздействие на защищаемое визуальное доказательство, т.е. его искажение, что, с точки зрения получения и хранения вещественных доказательств не допустимо. И, во-вторых, стойкость ЦВЗ весьма слабая, т.е. они легко вскрываются (например, с помощью вставки монохромного кадра) и могут быть модифицированы.

Ещё одним способом защиты визуальных доказательств является применение электронных подписей (ЭП), которые позволяют защитить доказательство от модификации и установить автора самой ЭП [5]. Однако ЭП не позволяет защитить конфиденциальность доказательства, если оно содержит сведения, составляющие служебную или коммерческую тайну.

В настоящей статье рассмотрен один из криптографических способов обеспечения защиты целостности и конфиденциальности (визуализации документирования) статического изображения (кадра), основанного на процедуре скремблирования исходной последовательности точек изображения (ПТИ) и ее геометрического перемежения.

Любое статическое изображение представляет собой последовательность точек (пиксел), каждая из которых имеет свой цвет. Диапазон цветовой гаммы может быть различным и зависит от конкретного типа кодирования цвета. Ввиду того, что любое изображение обладает большой информационной избыточностью, то, как правило, оно подвергается процедуре сжатия (в соответствии с выбранным алгоритмом сжатия) и уже в этом виде, либо хранится в памяти того или иного устройства на электронном носителе информации, либо передается по каналам связи.

Одним из надежных способов защиты покадровых изображений является использование процедуры зашифрования, реализуемой следующим образом. Последовательность точек изображения, представленная, в двоичной форме, складывается по mod 2 с выходной последовательностью генератора шифра. При этом необходимо отметить важную особенность результирующей последовательности: она полностью сохраняет исходную ПТИ.

В [2,6] показано, что для создания надёжного алгоритма защиты покадровых изображений необходимо решить две задачи:

1. исключить какие-либо корреляционные (статистические) связи между соседними и близлежащими точками изображения [7];

2. исключить какие-либо рекуррентные свойства поточного (блочного) шифра [5].

Для решения первой задачи можно использовать линейный или нелинейный скремблер на основе конечного автомата (генератора шифра), который обладает хорошими статистическими свойствами [5].

Рис. 1. Изображение (пиксели) с нанесённой на него треугольной решеткой (пиксели в форме квадратной решётки)

Процедура скремблирования устраняет корреляционные связи между ТИ. Однако, ввиду того, что скремблер представляет собой конечный автомат, проскремблированная исходная ПТИ будет обладать рекуррентными свойствами, которые определяются генераторным полиномом автомата.

Кроме этого, измененная в ходе процедуры скремблирования ПТИ будет сохранять естественный порядок следования ТИ, что также снижает стойкость предложенного способа защиты покадровых изображений.

Следовательно, на втором этапе необходимо исключить указанные рекуррентные свойства измененной ПТИ, а также естественный порядок следования в ней ТИ. Эти условия могут быть выполнены путем геометрического перемежения проскремблированной исходной ПТИ.

2. Демонстрация способа геометрического перемежения

Для решения второй задачи предлагается вообще исключить применение каких-либо алгебраических структур, а использовать только геометрические приёмы для перемежения ПТИ. Для этого, в начале, нанесем на квадратное изображение пикселей треугольную решетку (рис.1).

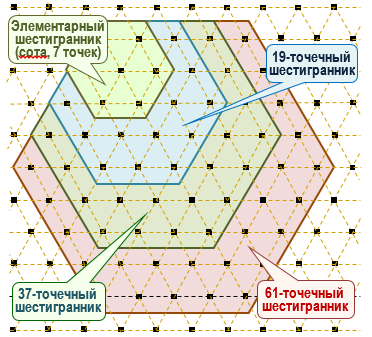
Рис. 2. Элементарный (7-точечный), 19-, 37- и 61-точечный шестигранники (пиксели структурированы в форме треугольной решётки)

На рис. 2 представлены различные разбиения ТИ, расположенных в узлах треугольной решётки [8]. В приведённом случае разбиение и/или группирование ТИ происходит на основе выбора шестигранника H_n со стороной n ТИ, то есть с выбранной длиной стороны шестигранника, измеряемой в ТИ. На рис. 2 показаны четыре таких шестигранника H₂, H₃, H₄ и H₅. Каждый из этих шестигранников включает 7, 19, 37 и 61 ТИ. Рассмотрим величину S_n, определяемую как число ТИ, входящих в H_n, которая определяется по следующей формуле:

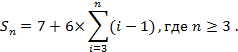
Например, для шестигранника со стороной 7 ТИ общее число ТИ, входящих в этот шестигранник, будет равно:

Для нахождения числа ТИ входящих в шестигранник со стороной n ТИ можно воспользоваться и другой формулой. Например, для шестигранника со стороной 7 ТИ можно записать последовательность чисел: 7 8 9 10 11 12 13 12 11 10 9 8 7. Каждое из чисел указывает на число ТИ в каждой строке (число строк равно 2n – 1) указанного шестигранника. Тогда формула вычисления числа ТИ в шестиграннике будет иметь вид:

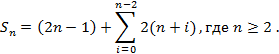
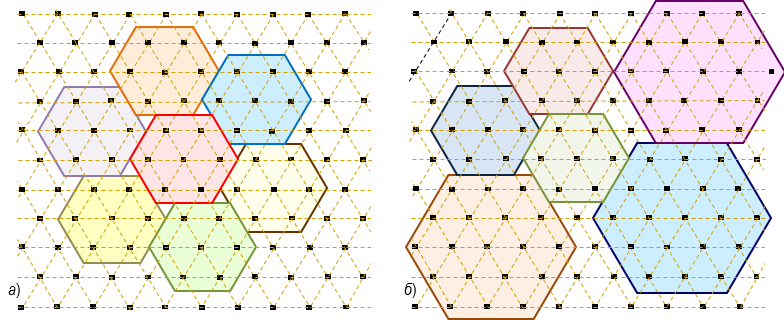
Рис. 3. Примеры двух различных мозаичных фигур (матриц): а) симметричной; б) несимметричной

Вместе с тем, существует и более общая формула для определения числа ТИ вписанных в шестигранник со стороной n ТИ:

С помощью таких шестигранников можно построить достаточно большое количество всевозможных мозаичных фигур или “матриц” с разными рисунками (рис. 3, а). Необходимо отметить, что матрицы могут быть основаны на шестигранниках различного размера и иметь несимметричные рисунки (рис. 3, б).

В простейшем случае, для перемежения исходной ПТИ впишем её, например, в H₄ (S₄ = 37 ТИ, рис. 4) и затем повернём его на различные допустимые углы (60^о, 120^о, 180^о, 240^о, 300^о). После поворота шестигранника считываем вновь получившуюся ПТИ. Результирующие последовательности для различных вариантов поворота представлены на рис. 4. Следует заметить, что повороты на 60° и 240°, а также на 120° и 300° являются дуальными, то есть вновь сформированные ПТИ в каждой паре поворотов имеют обратный порядок следования.

Таким образом, всю исходную ПТИ (защищаемое изображение) можно “пропустить” через выбранный шестигранник и повторить такую процедуру несколько раз с различными шестигранниками.

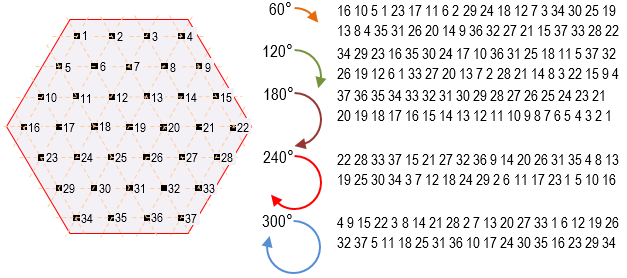
Рис. 4. Пример шестигранника H4 и результирующие последовательности после ротации шестигранника

Очевидно, что приведённый пример перемежения исходной ПТИ на основе только одного шестигранника H₄ является весьма упрощённым и предназначен только лишь для демонстрации процедуры перемежения. В реальных системах могут использоваться самые разнообразные по своему мозаичному рисунку матрицы на основе различных шестигранников с точки зрения их размера. Такие матрицы, естественно, по числу охвата точек будут превышать реальное число ТИ. При этом порядок записи исходной ПТИ в матрицу, порядок считывания точек из матрицы после выполнения её ротации (поворота шестигранников), углы поворота шестигранников в матрице, число используемых матриц, а также порядок их следования при перемежении ПТИ могут быть различными и зависят от конкретной реализации рассматриваемого способа.

Когда процедура перемежения ТИ с использованием всех матриц завершена, то в результате получим итоговую последовательность, которая может выступать в роли таблицы отображения (ТО) начальной ПТИ в новую перемеженную последовательность.

3. Способы геометрического перемежения ПТИ

Варианты перемежения ПТИ могут быть самыми различными, но, тем не менее, все возможности базируются на следующих способах.

1. ТИ представляются в виде прямоугольной матрицы (решётки) и в ней выбираются элементы в виде шестигранника и затем осуществляется перестановка этих элементов в виде поворота шестигранника (рис. 1).

2. ТИ могут быть представлены в виде треугольной матрицы (решётки), в которой выбираются элементы в виде внутренних шестигранников. Затем осуществляется перестановка этих элементов в виде поворота каждого внутреннего шестигранника (рис. 2 и рис. 4).

3. ТИ рассматриваются в виде строки, в которой осуществляется перестановка эквивалентная перестановке поворота шестигранника для подряд идущих элементов.

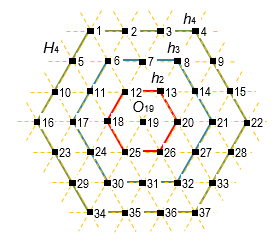
Рис. 5. Примеры контурных шестигранников h4, h3 и h2

4. ТИ рассматриваются в виде кольца, в котором осуществляется перестановка эквивалентная перестановке поворота шестигранника для подряд идущих элементов.

Прежде чем провести сравнительный анализ указанных способов перемежения, рассмотрим шестигранник H₄ на рис. 5. Назовём контурным шестигранником h_n размерности n такие ТИ, которые принадлежат грани шестигранника H_n, состоящего из S_n ТИ. То есть шестигранник H₄ на рис. 5 состоит из трёх контурных шестигранников h₄, h₃ и h₂ и центрального элемента O₁₉. Тогда количество ТИ в h_n вычисляется по формуле 6(n – 1) и, соответственно, минимальный контурный шестигранник – это h₂.

Ротация шестигранника возможна только на допустимые углы, кратные 60°, так как грани шестигранника состоят из ТИ с фиксированными позициями. Другими словами, поворот на произвольный угол невозможен, так как определение новых позиций ТИ, в таком случае, будет крайне затруднительным, в частности, при использовании квадратной решётки.

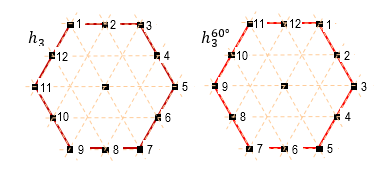
Рис. 6. Поворот контурного шестигранника h₃

Теперь проанализируем поворот контурного шестигранника h₃ на 60°, представленного на рис. 6. Записав ТИ в строку, получаем: 1 2 3 4 5 6 7 8 9 10 11 12, после поворота имеем 11 12 1 2 3 4 5 6 7 8 9 10 (). Представленная процедура соответствует циклическому сдвигу (n–1) ТИ, где n – число ТИ в грани h_n. Таким образом, поворот шестигранника H_n представляет сдвиг на m–1 ТИ каждого из n–1 контурных шестигранников размерности m, где , а m – целое число. То есть перестановка (поворот) шестигранника H_n может быть разложена в композицию перестановок (поворот) контурных шестигранников, входящих в состав шестигранника H_n.

Первый и второй способы перемежения отличаются по форме организации данных: в первом случает это квадратная матрица, а во втором – это треугольная. Преимущество формы организации данных в треугольной решётке заключается в том, что гарантировано отсутствие неподвижных ТИ. В случае с квадратной решёткой, четыре ТИ, которые находятся в углах матрицы, гарантировано неподвижны, так как не существует такого шестигранника, в который бы они были включены. В остальном эти подходы одинаковы и требуют использования лишь двух простых операций для осуществления поворота:

· выбор ТИ, которые принадлежат шестиграннику H_n с центром в точке O_n;

· перестановка выбранных ТИ в соответствии с нужным углом поворота шестигранника.

Рассмотрим третий способ перемежения ТИ. Если рассматривать ПТИ как строку, то первая ТИ будет неподвижна и так, как она не участвует в перестановке, а лишь определяет начало строки (ПТИ), то её можно упразднить. Тогда количество элементов в шестиграннике будет: где n – число ТИ в грани шестигранника.

Пусть m – количество точек в изображении, x – максимальное целое удовлетворяющее условию: . Для шестигранника, состоящего из ТИ существует m – k различных позиций в ПТИ, в каждой из которых он может быть повёрнут на 6 различных углов (в том числе и на 0°), т.е. для первого шестигранника размерности n существует состояний, для второго и так далее. Таким образом, число возможных состояний только для шестигранников, состоящих из k ТИ:

Так как k может быть различным и можно использовать любую комбинацию неодинаковых шестигранников (даже с одним центром), то всего комбинаций:

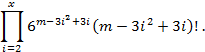
Пусть в битовом представлении изображения длиной y присутствует z нулей, тогда число различных изображений, которые можно получить из исходного изображения, будет не более, чем

Таким образом, количество различных изображений, которые будут получены в результате перестановки, зависит от самого исходного изображения. Максимум изображений будет при z = y/2. Очевидно, что число перестановок превосходит число различных изображений. Эту проблему можно решить, увеличив битовую длину ТИ в перестановке, это уменьшит количество перестановок и позволит сократить число перестановок, приводящих к одинаковому результату.

Теперь рассмотрим четвертый способ перемежения ТИ. По аналогии с предшествующим рассуждением получим, что число перестановок для шестигранников размером k на изображении размером m будет: , a всего перестановок , что ещё больше превышает число доступных состояний изображения. Данную проблему можно решить также путём увеличения битовой длины ТИ. Однако в случае реализации четвертого принципа перемежения неизбежны тождественные перестановки, что связано с представлением изображения в виде кольца.

Общим недостатком третьего и четвертого способов перемежения ТИ является то, что изображение плохо “перемешивается” по вертикали и хорошо по горизонтали. Это связано с представлением изображения в виде строки, что существенно упрощает процесс реализации, однако существенно сказывается на качестве результата процедуры перемежения. На основе вышесказанного рекомендуется использовать второй способ перемежения ТИ.

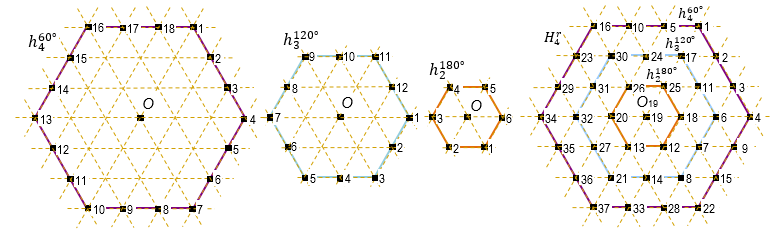
Результирующая ПТИ: 16 10 5 1 23 30 24 17 2 29 31 26 25 11 3 34 32 20 19 18 6 4 35 27 13 12 7 9 36 21 14 8 15 37 33 28 22

Рис. 7. Примеры контурных шестигранников h₄, h₃ и h₂, которые имеют разные углы поворота (60°, 120°, 180°; исходный H₄ представлен на рис.5)

4. Усложнение перемежения: разнонаправленная контурная ротация

Декомпозиция любого шестигранника H_n на совокупность контурных шестигранников h_m () позволяет усложнить процедуру ротации исходного шестигранника, то есть процедуру перемежения исходной ПТИ.

На рис. 7 представлен пример разнонаправленной контурной ротации шестигранника H₄. Все контурные шестигранники h₄, h₃ и h₂, входящие в состав шестигранника H₄, имеют различные углы поворота: и . В данном примере каждый угол поворота, кратный 60°, возрастает последовательно по мере уменьшения стороны контурного шестигранника.

Очевидно, что если шестигранник H_n будет иметь сторону n >> 4, и соответственно, число входящих в его состав контурных шестигранников будет n >> 3, то углы поворота каждого контурного шестигранника h_n могут выбираться произвольно по мере уменьшения его стороны. На рис. 8 представлен шестигранник H₈, включающий семь контурных шестигранников с соответствующими углами поворотов: и , а также результирующая ПТИ.

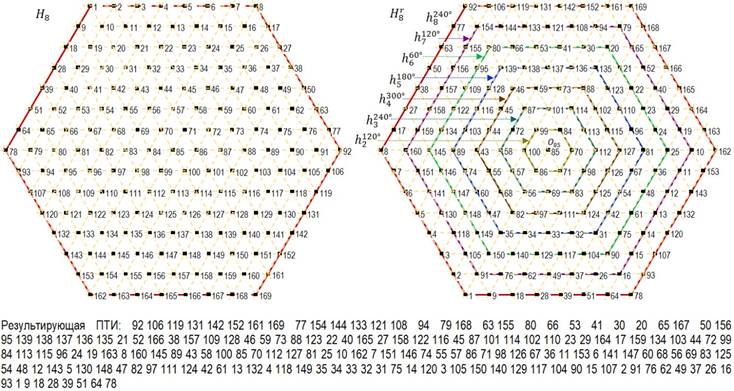
Рис. 8. Пример разнонаправленной ротации шестигранника H₈ и результирующая ПТИ

На рис. 9 представлены примеры перемежения пикселей реального изображения (рис. 9, а). При перемежении исходной ПТИ использовалось множество шестигранников:

, где

Для каждого варианта перемежения использовалось, соответственно, 50 (рис. 9, б), 100 (рис. 9, в), 200 (рис. 9, г) и 300 (рис. 9 , д), шестигранников. Кроме этого, во всех вариантах перемежения ТИ угол поворота, начальная точка и размер шестигранника (из множества H) выбирались случайным образом.

5. Некоторые аспекты практической реализации

Рассмотрим ещё один пример реализации предлагаемого способа защиты статических изображений (рис. 10). На рис. 10, а представлено исходное изображение, которое имеет следующую специфику: весь рисунок является чёрно-белым, за исключением глаз тигра.

На рис. 10, б представлен результат аддитивного скремблирования данного изображения исходной ПТИ, то есть сложения по mod 256 каждого октета пикселя в исходной ПТИ с псевдослучайным числом (октетом). В данном примере использовался линейный конгруэнтный генератор:

со следующими коэффициентами: m = 2³², a = 1664525, c = 1013904223. Очевидно, что может использоваться любой другой генератор псевдослучайных чисел, обладающий хорошими статистическими свойствами. Следует заметить, что на рис. 10, б всё же просматриваются очертания исходного изображения тигра, а именно контуры глаз.

а)

б)

в)

г)

д)

Рис. 9. Примеры перемежения ПТИ с использованием 50 (б), 100 (в), 200 (г) и 300 (д), шестигранников

На рис. 10, в представлено итоговое изображение, сформированное из результирующей ПТИ, которая была получена путём перемежения проскремблированной ПТИ. Необходимо отметить, что в результате перемежения, число итераций которого составило 20, расстояние между близлежащими ТИ исходного изображения увеличилось в среднем до 6682 позиций.

При перемежении проскремблированной ПТИ использовалось следующее множество шестигранников:

, где ,

что составляет 7351...18961 пиксель исходного изображения.

При практической реализации представленного здесь способа покадрового документирования в целях обеспечения надежного уровня безопасности целесообразно выполнять следующие рекомендации:

Рис. 10. Пример защиты статического изображения. Исходная (а), проскремблированная (б) и результирующая (в) ПТИ

1. Вектор начального заполнения (ВНЗ) скремблера и таблица отображения (ТО) относятся к данным, обладающим свойством конфиденциальности, то есть подлежащим защите от несанкционированного доступа (НСД).

2. Для формирования ТО необходимо использовать несколько мозаичных матриц (чем больше, тем лучше) с различными рисунками, различными по размеру шестигранниками и углами поворота последних, а также различные варианты вписывания ПТИ в матрицу и считывания ТИ из нее. Все исходные данные для формирования ТО также обладают свойством конфиденциальности и фактически являются основой алгоритма ее генерации.

3. При проектировании программно-аппаратного комплекса его необходимо разделить на два функциональных модуля:

1) модуль генерации (МГ) ТО и ВНЗ скремблера;

2) модуль засекречивания (МЗ) неподвижных изображений с использованием готовых ТО и ВНЗ.

4. Для каждой пары (для двух взаимодействующих пользователей) МЗ генерируется свой уникальный массив ТО и ВНЗ (для каждой ТО свой ВНЗ) в двух экземплярах, которые записываются на два электронных запоминающих устройства, по одному на каждого пользователя.

5. МГ должен располагаться в отдельном особо охраняемом помещении.

Выполнение указанных требований обеспечит пользователям высокий уровень защищенности статических изображений, даже если другая пара МЗ была скомпрометирована.

6. Заключение

Современное развитие технологий визуализации связано, в первую очередь, с ростом их практической значимости. В частности, технологии визуализации нашли своё широкое применение в цифровой криминалистике. Визуальное доказательство является основой реализации принципа неотвратимости наказания.

В статье рассмотрен способ криптографической защиты визуальных доказательств, который обеспечивает их целостность и конфиденциальность. Данный способ основан на предварительном скремблировании и нескольких последующих геометрических перестановках пикселей изображения путём его разбиения с использованием треугольной решётки.

Также в работе представлена предварительная оценка стойкости этого способа, которая показала хорошие результаты. То есть даже, если злоумышленник [9,10] обладает исходным кадром и его зашифрованным аналогом, то ему будет весьма затруднительно (с точки зрения вычислительных затрат) определить число и рисунки мозаичных матриц, используемых для зашифрования сообщений, то есть алгоритм формирования ТО, а, следовательно, исказить исходное изображение (визуальное доказательство) в противоправных целях.

Список литературы

1. Ballard D., Brown C. Computer Vision. Prentice Hall, Englewood Cliffs, NJ, 1982.

2. Melnikov D., Jones A. Static Image Data Hiding and Encryption Method. Proceedings of the 3rd European Conference on Information Warfare and Security. Royal Holloway University of London, UK. 28-29 June 2004. p. 279-284.

3. Osborne C., van Schyndel R., Tirkel A. A Digital Watermark. IEEE Intern. Conf. on Image Processing, 1994. P. 86-90.

4. Грибунин В.Г., Аграновский А.В., Балакин А.В. Стеганография, цифровые водяные знаки и стеганоанализ. Вузовская книга, Москва, 2009.

5. Алферов А.П., Зубов А.Ю., Кузьмин А.С., Черемушкин А.В. Основы криптографии. Гелиос-АРВ, Москва, 2002.

6. Мельников Д.А. Метод защиты неподвижных изображений. Информационные технологии управления в социально-экономических системах. 2010. №4. С. 130-139.

7. Бабаш А.В., Шанкин Г.П. Криптография. СОЛОН-Р, Москва, 2002.

8. Conway J.H., Sloane N.J.A. Sphere Packings, Lattices and Groupsю Springer-Verlag, New-York, 1988.

9. Kahn D. The Codebreakers. MacMillan. New-York, 1967.

10. Denning D. Cryptography and Data Security. Addison-Wesley, Reading, MA, 1982.

CRYPTOGRAPHIC METHOD OF THE PICTURES DOCUMENTING

D.A. Melnikov, A.A. Abramov, V.S. Gorbatov, A.P. Durakovskiy, R.D. Makhmutov

National Research Nuclear University "MEPhI" (Moscow Engineering Physics Institute), Moscow, Russian Federation

DAMelnikov@mephi.ru, mvpcvp@gmail.com, VSGorbatov@mephi.ru, APDurakovskiy@mephi.ru, infmaxx@gmail.com

Abstract

Today one of the directions of data technology development is a visualization, i.e., a representation of something - a physical process, a phenomenon, etc. in a form convenient for viewing. Visualization became widespread in many practical areas, one of which is the digital forensics. In the latter one began to use the visual evidences very actively. In case of any crime the visual evidence plays a vital role for a realization of the punishment inevitability principle. However, the visual evidences have a digital nature and therefore require specific protection measures to be applied to stand any kinds of its modifications. In some cases, one might need to protect privacy of the visual evidence, particularly, if it contains information constituting a state or commercial secret or personal data.

On the other hand, the visual evidence has to confirm the fact of violation while not allowing an offender to desist from any action or inactivity confirming this fact. In this case, the judge may ask for visual evidence to make her/his mind about the fact of violation of the law.

The paper discusses the major ideas and approaches to practical implementation of the cryptographic method to ensure the integrity and confidentiality of images (visual evidence) - so called the method of Melnikov-Jones. In addition, this method can be used for formation and protection of visual evidence in the resolution of legal disputes (to assure non-repudiation). This method is based on the preparatory scrambling and several subsequent geometric permutations of pixels of the image via its decomposition using a triangular lattice that virtually eliminates any possibility of malicious distortion. In other words, any attempted modification of the visual document will be detected.

Keywords: visual evidence; digital forensics; triangular lattice; geometrical permutation; hexahedron; angle of rotation; partition; scrambling; cryptography; enciphering; integrity; modification

References

1. Ballard D., Brown C. Computer Vision. Prentice Hall, Englewood Cliffs, NJ, 1982.

3. Osborne C., van Schyndel R., Tirkel A. A Digital Watermark. IEEE Intern. Conf. on Image Processing, 1994. P. 86-90.

4. Gribunin V.G., Agranovskij A.V., Balakin A.V. Steganografija, cifrovye vodjanye znaki i steganoanaliz [Steganography, digital watermarking and steganalysis]. Vuzovskaja kniga, 2009. [In Russian]

5. Alferov A.P., Zubov A.Ju., Kuz'min A.S., Cheremushkin A.V. Osnovy kriptografii [Basics of cryptography]. Gelios-ARV, 2002. [In Russian]

6. Mel'nikov D.A. Metod zashhity nepodvizhnyh izobrazhenij [The method of protection of still images]. Informacionnye tehnologii upravlenija v social'no-jekonomicheskih sistemah. 2010. No 4. pp. 130-139. [In Russian]

7. Babash A.V., Shankin G.P. Kriptografija [Cryptography]. SOLON-R, 2002. [In Russian]

8. Conway J.H., Sloane N.J.A. Sphere Packings, Lattices and Groupsju Springer-Verlag, New-York, 1988.

9. Kahn D. The Codebreakers. MacMillan. New-York, 1967.

10. Denning D. Cryptography and Data Security. Addison-Wesley, Reading, MA, 1982.