РЕШЕНИЕ ЗАДАЧИ АНАЛИЗА МНОГОМЕРНЫХ ДИНАМИЧЕСКИХ ДАННЫХ МЕТОДОМ ВИЗУАЛИЗАЦИИ
Д.Д. Попов1, И.Е. Мильман1, В.В. Пилюгин1, А.А. Пасько2
1Национальный исследовательский ядерный университет «МИФИ», Москва, Россия
2Британский национальный центр компьютерной анимации при университете Борнмута, Борнмут, Великобритания
dpopovmephi@gmail.com, igalush@gmail.com, VVPilyugin@mephi.ru, apasko@bournemouth.ac.uk
Содержание
2.1. Описание многомерных геометрических процессов
2.2. Формальное описание процесса решения рассматриваемой задачи анализа методом визуализации
2.3. Визуализация исходных данных
3. Описание алгоритма решения задачи
4. Описание прикладной программы для решения задачи анализа
4.1. Функции прикладной программы
4.2. Примеры использования программного средства
Аннотация
В данной статье описывается решение задачи анализа данных. Анализируются данные об изменении заданного множества многомерных объектов с течением времени. Для решения указанной задачи предлагается воспользоваться методом визуализации. Приведена формализация метода – математическое описание каждого этапа визуализации исходных данных.
Описывается разработанная интерактивная прикладная программа визуализации. В её основе лежат идеи и модели из теоретической части статьи.
Подчёркивается эффективность использования метода визуализации. Он позволяет строить суждения об образовании кластеров и сгустков из объектов, формализуемых в виде n-ок действительных чисел, а также находить объекты, стремящиеся оказаться в кластере или сгустке. Кроме того, приведены примеры использования программы для поиска инвариантов в изменении исходных данных.
Ключевые слова: многомерный анализ, анализ динамических данных, визуальный анализ, многомерный визуальный анализ.
1. Введение
В современном мире актуальной является задача обработки и анализа многомерных данных. Для её решения разрабатывается множество различных методов и средств, как автоматических, так и интерактивных. Среди методов решения задач анализа данных отдельное место занимают визуальные методы.
Однако, внимательное изучение литературы, посвящённой описанию конкретных приложений с применением визуальных методов, позволяет утверждать, что в реальности интерактивным системам работы с многомерными данными зачастую придаётся меньшее значение по сравнению с системами отображения результатов применения методов Data Analysis. В качестве примера можно привести такие системы, как система ситуационного оповещения AdAware [1], система визуального анализа в задачах самолётостроения [2], система визуального анализа текстовой информации VxInsight, программный комплекс SAS Visual Analytics [3], предназначенный для обработки и анализа больших объёмов финансовой и экономической информации. Все указанные системы носят промышленный характер, являются коммерческими, предоставляют пользователю огромное количество интерфейсов и возможностей визуального представления данных. Однако в то же время все эти системы, по сути, настроены на внутреннюю обработку этих многомерных данных и представление их пользователю в удобном для него виде, не предоставляя возможности пользователю непосредственно работать с облаком многомерных данных с использованием визуальных отображений этих данных[4,7].
В работе [5], на примере научных данных, были рассмотрены теоретические обобщения решения задач анализа произвольных исходных данных методом визуализации. Этот метод заключается в последовательном, в общем случае многократном, решении двух задач:
· задачи визуализации исходных данных;
и
· задачи анализа полученных графических изображений с последующей формулировкой суждений относительно исходных данных.
В работе [6] предложен оригинальный алгоритм решения задачи анализа многомерных геометрических данных с использованием данного метода визуализации. На основе разработанного алгоритма была построена программа интерактивного визуального анализа многомерных данных. Особенность данной программы заключается в предоставлении пользователю возможности непосредственной работы с исходными многомерными данными. При этом не выполняется изначальной численной обработки исходных многомерных данных, а производится целенаправленное непосредственное манипулирование аналитиком исходными данными и визуальный анализ получаемых результатов. В работе показано, что данная программа позволяет эффективно решать задачу анализа для многомерных статических исходных данных.
Однако на практике часто приходится сталкиваться с многомерными динамическими исходными данными: годовые или месячные отчёты организаций, состояния элементарных частиц в различные моменты времени и т.д. Эти данные несут информацию о развитии рассматриваемых объектов во времени. Аналитика интересуют суждения об этом развитии, т.е. суждения о многомерных динамических исходных данных. В данной статье рассматривается разработанные математические модели многомерных динамических исходных данных и интерактивная программа, позволяющая осуществлять анализ этих данных методом визуализации.
2. Постановка задачи
Динамические исходные данные – это некоторые значения
количественных характеристик рассматриваемых объектов, которые могут изменяться
с течением времени. В фиксированный момент времени каждый объект задаётся n-кой
действительных чисел. Будем считать n-ки действительных чисел точками
многомерного евклидового пространства ![]() с
заданным расстоянием. Таким образом, исходной задаче анализа изменения
заданного множества многомерных объектов с течением времени поставим в
соответствие геометрическую интерпретацию, то есть задачу анализа изменения
взаимного расположения точек в пространстве
с
заданным расстоянием. Таким образом, исходной задаче анализа изменения
заданного множества многомерных объектов с течением времени поставим в
соответствие геометрическую интерпретацию, то есть задачу анализа изменения
взаимного расположения точек в пространстве ![]() .
.
В этом пространстве могут быть выделены подмножества точек, представляющие собой сгустки и кластеры, данные подмножества описаны в [4]:
Кластер — подмножество, при заданном множестве точек, попарное расстояние между которыми не превышает заданное d, а расстояние между точками кластера и остальными точками не меньше заданного d.
Сгусток — подмножество точек, большая часть расстояний между которыми не превышает заданное d.
В частном случае подмножества могут состоять из одной точки, там же [4] дана классификация точек:
Удалённая (одиночная) точка — точка, удалённая от всех остальных точек исходного множества на расстояние, большее заданного d.
Квазиудалённая (Квазиодиночная) точка — точка, не являющаяся удалённой, но и не входящая в сгусток или кластер при заданном разбиении.
Выделение сгустков и квазиудалённых точек осуществляется человеком в процессе решения задачи анализа.
Заметим, что удалённая и квазиудалённая точки – частные случаи кластеров и сгустков соответственно.
Значения координат точек могут изменяться со временем. Точки с течением времени могут образовывать сгустки и кластеры или присоединяться к ним, так же возможны обратные процессы.
Основной целью работы является решение задачи анализа
изменения взаимного расположения заданного множества точек пространства ![]() методом
визуализации. При достижении этой цели будет решена исходная задача анализа
изменения заданного множества многомерных объектов с течением времени.
методом
визуализации. При достижении этой цели будет решена исходная задача анализа
изменения заданного множества многомерных объектов с течением времени.
Выполнение работы можно разбить на следующие этапы:
· Составление математического описания анализируемых объектов.
· Разработка алгоритма решения задачи анализа исходных многомерных динамических данных методом визуализации.
· Написание прикладной программы для решения задачи анализа.
Введём в рассмотрение следующие понятия, которые будут использоваться при изложении последующего материала.
Геометрический процесс – множество точек пространства, координаты которых зависят от времени.
Будем называть пространственным процессом переменную пространственную сцену, зависящую от времени. Другими словами, пространственный процесс – это динамическая пространственная сцена. Подробное описание этой сцены будет дано ниже (пункт Мэппинг).
2.1. Описание многомерных геометрических процессов
Исходным объектом анализа является некоторое множество
n-мерных точек ![]() ,
значение координат которых задано для нескольких моментов времени:
,
значение координат которых задано для нескольких моментов времени: ![]()
Точка задаётся n координатами:
![]()
для каждой пары точек определено расстояние между ними:
![]()
Таким образом, изначально задан некоторый дискретный
геометрический процесс ![]() ,
представляющий собой множество дискретных процессов
,
представляющий собой множество дискретных процессов ![]() –
динамические n-мерные точки, каждая из которых, в свою очередь, задаётся
совокупностью процессов
–
динамические n-мерные точки, каждая из которых, в свою очередь, задаётся
совокупностью процессов ![]() –
динамические координаты этих точек.
–
динамические координаты этих точек.
Заданный процесс ![]() представляет собой упорядоченный по
времени набор геометрических описаний известных состояний рассматриваемых
объектов. Сами объекты изменяются во времени непрерывно. Для получения описания
непрерывно изменяющихся объектов можем воспользоваться интерполяцией.
представляет собой упорядоченный по
времени набор геометрических описаний известных состояний рассматриваемых
объектов. Сами объекты изменяются во времени непрерывно. Для получения описания
непрерывно изменяющихся объектов можем воспользоваться интерполяцией.
Для интерполяции процесса ![]() будем
использовать кусочно-линейную интерполяцию. В этом случае искомая
интерполяционная функция для динамических координат точек
будем
использовать кусочно-линейную интерполяцию. В этом случае искомая
интерполяционная функция для динамических координат точек ![]() является
алгебраическим двучленом
является
алгебраическим двучленом ![]() на
каждом интервале
на
каждом интервале ![]() ,
, ![]() . В таком случае при
любом
. В таком случае при
любом ![]() ,
, ![]()
![]() будет
рассчитываться по формуле:
будет
рассчитываться по формуле:
![]()
Пусть ![]() – непрерывный геометрический процесс,
полученный в результате интерполяции. Тогда
– непрерывный геометрический процесс,
полученный в результате интерполяции. Тогда ![]() –
временное сечение,
–
временное сечение, ![]() принадлежит
области определения
принадлежит
области определения ![]() .
.
С помощью временных сечений, из ![]() можно построить
дискретный геометрический процесс. Для этого выберем моменты времени
можно построить
дискретный геометрический процесс. Для этого выберем моменты времени ![]() и
определим этот дискретный геометрический процесс как совокупность временных
сечений
и
определим этот дискретный геометрический процесс как совокупность временных
сечений ![]() .
. ![]() состоит
из
состоит
из ![]() временных сечений процесса
временных сечений процесса ![]()
2.2. Формальное описание процесса решения рассматриваемой задачи анализа методом визуализации
Для решения поставленной задачи используется метод визуализации [5]. Он подразумевает последовательное (в общем случае многократное) решение двух задач, представленных на рисунке:
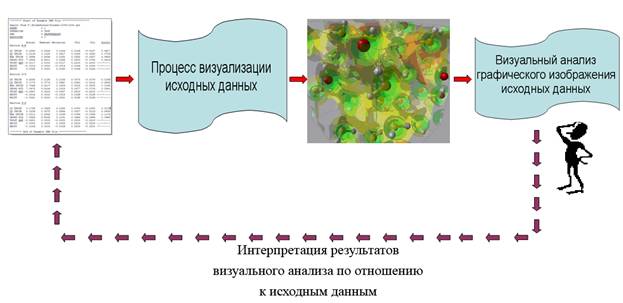
Рис. 1. Метод визуализации
Задание параметров визуализации и получение статических или анимационных графических изображений (т.е. временных последовательностей кадров) происходит до тех пор, пока аналитик не рассмотрит достаточное количество графических изображений для формирования некоторого суждения об изменении взаимного расположения заданного множества многомерных точек с течением времени. То есть решение задачи анализа исходных многомерных динамических данных методом визуализации является итеративным.
Прикладная программа визуализации должна обладать интерактивным пользовательским интерфейсом. Предоставленная аналитику возможность влиять на пространственную сцену и получаемые изображения позволяет эффективно решать поставленную задачу. Таким образом, решение рассматриваемой задачи анализа исходных многомерных динамических данных методом визуализации является итеративным и интерактивным.
Рассмотрим подробнее процесс визуализации исходных данных.
2.3. Визуализация исходных данных
Визуализация исходных данных представляет собой
последовательность следующих шагов, которую принято называть конвейером
визуализации (visualization pipeline):
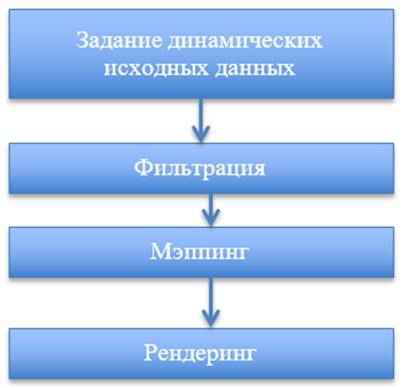
Рис. 2. Визуализация исходных данных
Задание динамических исходных данных
Задаётся дискретный геометрический процесс ![]() , для которого будет
проводиться визуализация.
, для которого будет
проводиться визуализация.
Фильтрация
На этом шаге исходные данные проходят предварительную обработку.
Для решения поставленной задачи исходный дискретный процесс ![]() интерполируется
линейно, как описано ранее. В результате фильтрации получается непрерывный
процесс
интерполируется
линейно, как описано ранее. В результате фильтрации получается непрерывный
процесс ![]() .
.
Мэппинг
Осуществляется выбор трёхмерного подпространства исходного
n-мерного пространства, которое будет использоваться для создания непрерывного
пространственного процесса.![]() номера
базисных векторов исходного n-мерного пространства, образующих базис
подпространства.
номера
базисных векторов исходного n-мерного пространства, образующих базис
подпространства.
Исходное множество точек проецируется на выбранное
подпространство. Пусть множество ![]() –
множество проекций точек на это подпространство, тогда
–
множество проекций точек на это подпространство, тогда ![]() .
.
n-мерным точкам ставятся
в соответствие сферы с центрами в точках ![]() . Далее, выбирается радиус сфер
. Далее, выбирается радиус сфер ![]() , их цвет
, их цвет ![]() и радиус цилиндров
и радиус цилиндров ![]() , соединяющих сферы, соответствующие точкам, расстояние между которыми
меньше заданного d.
, соединяющих сферы, соответствующие точкам, расстояние между которыми
меньше заданного d.
Поставим в соответствие непрерывному геометрическому
процессу![]() , полученному в результате интерполяции
исходного дискретного геометрического процесса
, полученному в результате интерполяции
исходного дискретного геометрического процесса ![]() , пространственную
сцену
, пространственную
сцену ![]() , где
, где ![]() –
описание геометрии сцены, а
–
описание геометрии сцены, а ![]() – описание оптических параметров сцены.
Смоделируем сцену как непрерывный пространственный процесс:
– описание оптических параметров сцены.
Смоделируем сцену как непрерывный пространственный процесс:
![]() .
.
Тогда, в каждый заданный момент ![]() ,
, ![]() будет
соответствовать
будет
соответствовать ![]() ,
, ![]() . Определим
. Определим![]() .
.
![]()
где ![]() сфера
с центром в точке
сфера
с центром в точке ![]() радиуса
радиуса
![]() ,
, ![]() –
цилиндр радиуса
–
цилиндр радиуса![]() ,
соединяющий 2 сферы,
,
соединяющий 2 сферы, ![]() .
.
![]()
где ![]() – цвета
сфер,
– цвета
сфер, ![]() –
цвета цилиндров.
–
цвета цилиндров.
Пусть ![]() – цвет
– цвет
![]() -ого
цилиндра, соединяющего сферы, соответствующие точкам
-ого
цилиндра, соединяющего сферы, соответствующие точкам ![]() , а
именно – значение цвета в RGB и непрозрачность:
, а
именно – значение цвета в RGB и непрозрачность:
![]()
![]()
![]()
![]()
![]()
![]()
где значение ![]() означает, что цилиндр абсолютно
прозрачен,
означает, что цилиндр абсолютно
прозрачен, ![]() % – абсолютно непрозрачен.
% – абсолютно непрозрачен.
Из полученного непрерывного пространственного процесса можно
получить дискретный пространственный процесс ![]() , как
было описано выше для непрерывного геометрического процесса
, как
было описано выше для непрерывного геометрического процесса ![]() .
.
Это может быть нужно, если аналитика интересуют лишь некоторые ключевые моменты, в которые, например, начинается образование сгустка или кластера, а не процесс в целом.
Рендеринг
Результатом рендеринга является проекционное графическое
изображение ![]() сцены
сцены ![]() . При рассмотрении
сцены как процесса:
. При рассмотрении
сцены как процесса: ![]() ,
каждому моменту времени
,
каждому моменту времени ![]() соответствует отдельная сцена, а,
следовательно, и отдельное проекционное изображение. Введём ещё один процесс
соответствует отдельная сцена, а,
следовательно, и отдельное проекционное изображение. Введём ещё один процесс ![]()
![]()
где ![]() –
атрибуты визуализации.
–
атрибуты визуализации.
К атрибутам визуализации относятся ![]() – камера,
освещение, физические характеристики среды, в которой находится сцена, размер
получаемого изображения и т.д. Атрибуты могут быть как статическими, так и
динамическими.
– камера,
освещение, физические характеристики среды, в которой находится сцена, размер
получаемого изображения и т.д. Атрибуты могут быть как статическими, так и
динамическими.
Под камерой будем подразумевать точку зрения для которой
строится проекционное изображение сцены ![]() .
. ![]() где
где ![]() фокус,
а
фокус,
а ![]() –
угол обзора камеры.
–
угол обзора камеры.
В результате рендеринга дискретного пространственного
процесса ![]() ,
получается последовательность кадров
,
получается последовательность кадров ![]() или
единственное графическое изображение в частном случае. Кадры
или
единственное графическое изображение в частном случае. Кадры ![]() могут
использоваться в качестве ключевых кадров для построения анимационного фильма.
могут
использоваться в качестве ключевых кадров для построения анимационного фильма.
3. Описание алгоритма решения задачи
Алгоритм решения задачи состоит из следующих этапов:
- ввод динамических исходных данных;
- их интерполяция и получение непрерывного геометрического процесса;
- задание d и статических параметров сцены: радиус сфер, радиус цилиндров, подпространство для проекции, цвет сфер;
- построение непрерывного пространственного процесса, соответствующего непрерывному геометрическому процессу, с использованием заданных статических параметров;
- построение временных сечений непрерывного пространственного процесса, то есть его дискретизация;
- задание камеры и других атрибутов визуализации для рендеринга;
- построение проекционных изображений дискретного пространственного процесса;
- дальнейшее сохранение проекционных изображений в галерею сечений или создание анимационного фильма;
В случае, если аналитик не может сделать интересующего его суждения относительно исходных данных по полученным проекционным изображениям, алгоритм предусматривает возвраты на этап задания модели сцены и этап задания атрибутов визуализации.
Вышеописанный алгоритм представлен на рисунке 3.
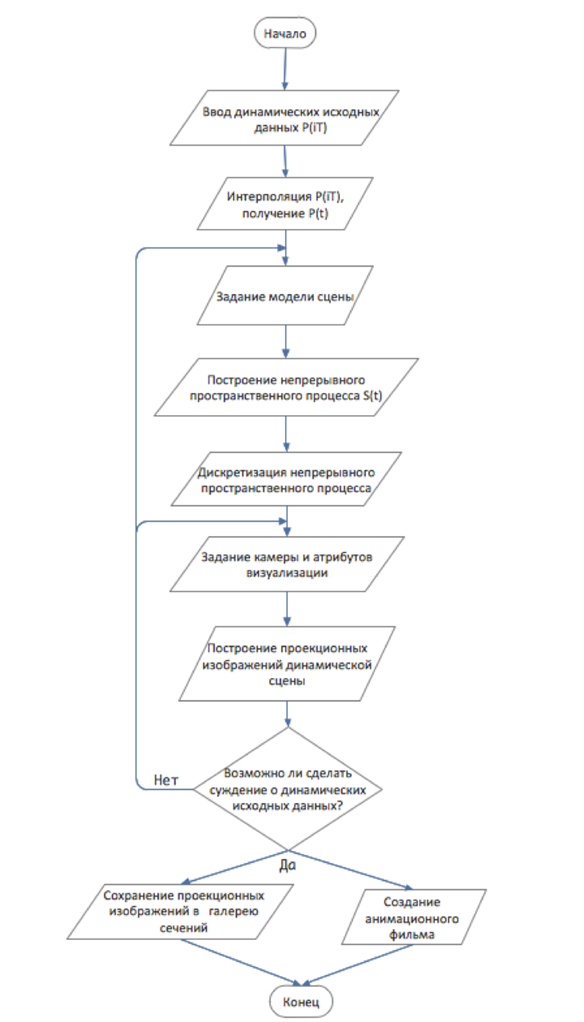
Рис. 3. Алгоритм решения задачи
4. Описание прикладной программы для решения задачи анализа
В ходе выполнения работы была разработана интерактивная прикладная программа визуализации, которая позволяет пользователю решать задачу анализа изменения взаимного расположения заданного множества точек, используя приведённый выше алгоритм.
4.1. Функции прикладной программы
Программа предоставляет аналитику следующие функции:
- Ввод динамических исходных данных путём чтения их из текстового файла со специальной структурой.
- Кусочно-линейная интерполяция дискретного геометрического процесса.
- Построение динамической сцены, соответствующей непрерывному геометрическому процессу.
- Задание атрибутов визуализации.
- Построение проекционных изображений дискретного пространственного процесса.
- Сохранение полученных проекционных изображений.
- Построение анимационного фильма.
Разработанная программа предоставляет пользователю удобный интерактивный визуальный интерфейс, позволяющий ему в процессе анализа непосредственно управлять визуализируемой пространственной сценой.
При разработке программы использовался программный продукт 3ds Max® с внутренним объектно-ориентированным языком программирования MAXScript.
4.2. Примеры использования программного средства
Данная программа была опробована на исходных данных, содержащих месячные отчёты кредитных организаций.
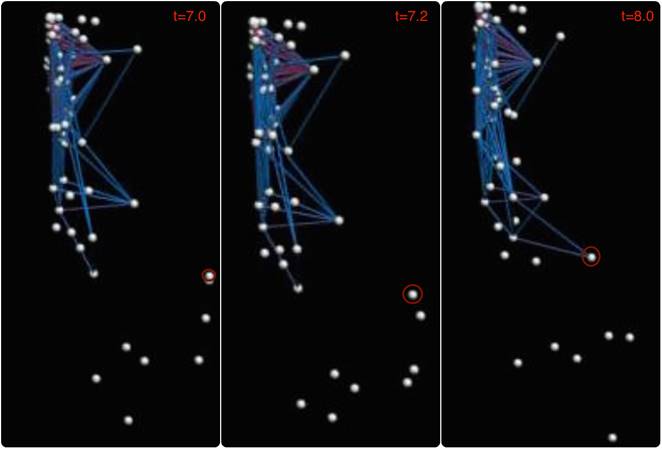
Рис. 4. Изображения из галереи сечений, полученные для данных по кредитным организациям.
В результате анализа графических изображений, представленных
на рисунке 4, был обнаружен момент присоединения удалённой точки к сгустку. То
есть, было сделано суждение о том, что за промежуток времени ![]() точка одного
подмножества стала точкой другого подмножества.
точка одного
подмножества стала точкой другого подмножества.
Изучив анимацию, представленную на рисунке 5, можем сделать интересное наблюдение.

Рис. 5. Анимация, полученная в результате рендеринга пространственного процесса
Все сферы, поставленные в соответствие исходным n-мерным точкам, располагаются примерно в одной плоскости.
Это наблюдение даёт возможность сделать следующее суждение.
Для координат точек ![]() ,
соответствующих выбранному подпространству, на промежутке
,
соответствующих выбранному подпространству, на промежутке ![]() справедливо равенство
справедливо равенство
![]() –
некоторые константы.
–
некоторые константы.
Используя исходные данные, были проведены расчёты методом наименьших квадратов и было получено следующее уравнение аппроксимирующей плоскости:
![]()
В рассмотренных примерах номера![]() соответствуют
координатам, значения которых отражают следующие финансовые показатели
кредитных организаций:
соответствуют
координатам, значения которых отражают следующие финансовые показатели
кредитных организаций:
- просроченная задолженность в кредитном портфеле;
- выпущенные облигации и векселя;
- активы нетто, выданные межбанковские кредиты (МБК).
Отметим, что схожие подходы, основанные на аппроксимации плоскостями в пространстве главных компонент, применялись в работах [8,9].
5. Заключение
Таким образом, в ходе выполнения данной работы было сделано следующее:
- Введён в рассмотрение ряд дискретных и непрерывных процессов, построено их математическое описание.
- Разработан алгоритм решения задачи анализа исходных динамических многомерных данных методом визуализации.
- Разработанный алгоритм реализован в интерактивной прикладной программе.
- Полученная прикладная программа была опробована на динамических данных о деятельности ряда кредитных организаций, содержащих ежемесячные финансовые показатели этих организаций.
- Получены суждения об этих данных.
Интерактивный пользовательский интерфейс позволяет успешно находить моменты времени, когда точки образуют кластеры и сгустки, когда покидают их. Разработанная прикладная программа предоставляет пользователю удобный интерактивный визуальный интерфейс, позволяющий ему в процессе анализа непосредственно управлять визуализируемой пространственной сценой.
Можем сказать, что разработанная прикладная программа осуществляет анимационную визуализацию многомерных динамических исходных данных. Эта программа автоматически создаёт описание ключевых пространственных сцен, которые впоследствии анимируются.
Кроме того, пользователю предоставлена возможность вырезать заинтересовавшую его часть процесса. Он может настроить скорость протекания этой части процесса в получаемом анимационном фильме. Эти опции доступны в интерактивном режиме.
Природа динамических исходных данных может требовать другого вида их интерполяции, поэтому в дальнейшем следует включить функцию выбора способа интерполяции в следующие версии программы. Ещё одним направлением развития работы по анализу многомерных динамических данных станет рассмотрение операторных преобразований геометрических и пространственных процессов.
Список литературы
1. Livnat Y., Agutter J., Moon S., Foresti S. Visual correlation for situational awareness. IEEE Symposium on Information Visualization. pp. 95-102, 2005.
2. Mavris D., Pinon O., Fullmer D.Jr. Systems design and modeling: A visual analytics approach. 27th Congress of International Council of the Aeronautical Sciences ICAS, 2010.
3. SAS the power to know. URL: http://www.sas.com/en_us/home.html. [Дата обращения: 26 1 2016].
4. Масленников О.П., Мильман И.Е., Сафиуллин А.Э., Бондарев А.Е., Низаметдинов Ш.У., Пилюгин В.В. Разработка системы интерактивного визуального анализа многомерных данных. Научная визуализация. 2014. том 6. №4. с. 30 – 49
5. Пилюгин В., Маликова Е., Пасько А., Аджиев В. Научная визуализация как метод анализа научных данных. Научная визуализация. 2012. том 4. №4. с. 56-70.
6. Мильман И.Е., Пахомов А.П., Пилюгин В.В., Писарчик Е.Е., Степанов А.А., Бекетнова Ю.М., Денисенко А.С., Фомин Я.А. Анализ данных о деятельности кредитных организаций с использованием программы интерактивного визуального анализа многомерных данных. Научная визуализация. 2015. том 7. №1. с. 45 – 64.
7. Масленников О.П., Мильман И.Е., Сафиуллин А.Э., Бондарев А.Е., Низаметдинов Ш.У., Пилюгин. В.В. Разработка и развитие системы интерактивного визуального анализа многомерных данных. Труды 25-й Международной Конференции по Компьютерной Графике и Зрению ГрафиКон'2015, Протвино, Россия, 22-25 сентября 2015 г. с. 227-231.
8. Bondarev A.E, Galaktionov V.A. Parametric Optimizing Analysis of Unsteady Structures and Visualization of Multidimensional Data. International Journal of Modeling, Simulation and Scientific Computing. 2013. V.04. N supp01. 13 p. DOI 10.1142/S1793962313410043.
9. Бондарев А.Е. Анализ многомерных данных в задачах вычислительной газовой динамики. Научная визуализация. Т.6, № 5, с.59-66, 2014.
A SOLUTION TO A MULTIDIMENSIONAL DYNAMIC DATA ANALYSIS PROBLEM BY THE VISUALIZATION METHOD
D.D. Popov1, I.E. Milman1, V.V. Pilyugin1, A.A. Pasko2
1National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Moscow, Russian Federation
2National Centre for Computer Animation, Bournemouth University, Bournemouth, United Kingdom
dpopovmephi@gmail.com, igalush@gmail.com, VVPilyugin@mephi.ru, apasko@bournemouth.ac.uk
Abstract
The article describes a solution of a data analysis problem. Data to be analyzed represent changes in a given set of multidimensional objects with time. We propose to apply the visualization method to solve this problem. A formalization of the method is presented with a mathematical description of each stage of the source data visualization.
A developed interactive visualization application program is described. It is based on the models of the theoretical part of the article.
We emphasize the efficiency of the visualization method. It allows one to make a judgment on the formation of bunches or clusters of objects formalized in the form of n-tuples of real numbers and to find the objects seeking to be in a cluster or a bunch. Additionally, examples of use of the developed program for searching for invariants in changing the source data are provided.
Keywords: multidimensional analysis, dynamic data analysis, visual analysis, multidimensional visual analysis.
References
1. Livnat Y., Agutter J., Moon S., Foresti S. Visual correlation for situational awareness. IEEE Symposium on Information Visualization. pp. 95-102, 2005.
2. Mavris D., Pinon O., Fullmer D.Jr. Systems design and modeling: A visual analytics approach. 27th Congress of International Council of the Aeronautical Sciences ICAS, 2010.
3. SAS the power to know. URL: http://www.sas.com/en_us/home.html. [Access date: 26 1 2016].
4. Maslennikov O.P., Milman I.E., Safiullin A.E., Bondarev A.E., Nizametdinov Sh.U., Pilyugin V.V. Razrabotka sistemy interaktivnogo vizualnogo analiza mnogomernykh dannykh [Development of a system for analyzing multidimensional data]. Scientific visualization. V.6, no. 4, p. 30-49, 2014. (in Russian)
5. Pilyugin V., Malikova E., Pasko A., Adzhiev V. Nauchnaja vizualizacija kak metod analiza nauchnyh dannyh [Scientific visualization as method of scientific data analysis]. Scientific Visualization. V. 4, no. 4, pp. 56-70, 2012 (in Russian)
6. Milman I.E., Pakhomov A.P., Pilyugin V.V., Pisarchik E.E., Stepanov A.A., Beketnova Yu.M., Denisenko A.S., Fomin Ya.A. Data analysis of credit organizations by means of interactive visual analysis of multidimensional data. Scientific Visualization. 2015. V. 7, no. 1, pp. 45 – 64
7. Maslennikov O.P., Milman I.E., Safiullin A.E., Bondarev A.E., Nizametdinov Sh.U., Pilyugin V.V. Interaktivny vizualny analiz mnogomernykh dannykh [Interactive visual analysis of multidimensional data]// GraphiKon'2014: 24th International conference on computer graphics and vision: Rostov-on-Don, the SFU Academy of architecture and arts, Conference materials. - p. 51-54 (in Russian)
8. Bondarev A.E, Galaktionov V.A. Parametric Optimizing Analysis of Unsteady Structures and Visualization of Multidimensional Data. International Journal of Modeling, Simulation and Scientific Computing. 2013. V.04. N supp01. 13 p. DOI 10.1142/S1793962313410043.
9. Bondarev A.E. Analiz mnogomernyh dannyh v zadachah vychislitel'noj gazovoj dinamiki [Multidimensional data analysis in cfd problems]. Scientific visualization. Vol. 6. No. 5. Pp. 61-68. 2014.