МОДЕЛИРОВАНИЕ И ВИЗУАЛИЗАЦИЯ НАНОСЕКУНДНОЙ ЛАЗЕРНОЙ АБЛЯЦИИ МЕТАЛЛОВ В ОКОЛОКРИТИЧЕСКОЙ ОБЛАСТИ

В. И. Мажукин^1,3, А. А. Самохин², А.В. Шапранов^1,3, М. М. Демин¹, П. А. Пивоваров^2,3

¹Институт прикладной математики им. М.В. Келдыша РАН, Москва, Россия

²Институт общей физики им. А.М. Прохорова РАН, Москва, Россия

³Национальный исследовательский ядерный университет «МИФИ», Москва, Россия

vim@modhef.ru, asam40@mail.ru, p_pivovvarov@hotmail.com

Содержание

1. Введение

2. Постановка задачи

3. Результаты и обсуждение

4. Заключение

Благодарность

Список литературы

Аннотация

Представлены теоретические результаты и их визуализация для случая молекулярно динамических расчетов наносекундной лазерной абляции жидкой металлической пленки при различных поглощаемых интенсивностях лазерного излучения G = 38.5, 44, 88, 154 MВт/см². Абляция толстой металлической пленки (толщина пленки 430 нм, начальное число частиц 5х10⁵), включающая докритические и закритические состояния, исследуется с помощью классического метода молекулярной динамики в сочетании с континуальным описанием подсистемы электронов проводимости. Поведение тонкой металлической пленки (48нм) также исследовано при интенсивностях G = 29 MВт/см² и G = 51 MВт/см² (соответственно скорости энерговклада 5 и 8,8К/пс). Результаты трехмерных вычислений представлены в виде двумерных мгновенных распределений плотности и одномерных распределений температуры, плотности, давления и скорости частиц. Также, как и для рассмотренного ранее случая тонких диэлектрических пленок для металлических пленок наблюдены четыре различных абляционных режима в зависимости от лазерной интенсивности: квазистационарное поверхностное испарение, взрывное (объемное) вскипание, спинодальный распад и режим расширения закритического флюида. Изменения в пространственно-временном поведении флуктуаций плотности в этих режимах явно видны из представленных визуализаций. Реализация взрывного вскипания заранее не очевидна из-за больших значений коэффициентов поглощения и теплопроводности, которые препятствуют проявлению этого процесса. Пульсации давления отдачи, обусловленные повторяющимися взрывными вскипаниями, могут быть использованы как экспериментальные маркеры приближения к области критических параметров, тогда как переход в закритическую область характеризуется исчезновением этих пульсаций давления.

Ключевые слова: лазерная абляция, молекулярная динамика, взрывное вскипание, спинодальный распад, закритический разлет

1. Введение

Исследования лазерной абляции металлов в околокритическом состоянии облучаемого вещества имеет весьма долгую историю (см., например, [1-25] и цитируемую там литературу), однако многие аспекты поведения вещества в этой области остаются недостаточно выясненными до настоящего времени. Это касается, например, перехода металл-диэлектрик [1,2,4-6,8,9,13] и даже самой возможности наблюдения критических особенностей при лазерной абляции. По этой причине и вследствие невозможности использовать статические методы определения критических параметров, их значения остаются плохо определенными. Процесс взрывного вскипания обсуждаемый во многих работах [3,6-8,23,25,26] также является недостаточно исследованным экспериментально и теоретически. В случае лазерной абляции металлов имеются различные заключения относительно влияния подповерхностного температурного максимума на проявление взрывного вскипания. В работах [23,25,26] утверждается, что этим влиянием можно пренебречь, в то время как в ранней работе [3] предполагается, что результатом этого влияния могут быть повторяющееся взрывные вскипания, генерирующие короткие (субнаносекундные) пики на основном фоне давления отдачи.

Поведение неравновесных процессов зависит от условий их реализации. При небольших перегревах в однородном жидком металле в результате флуктуаций плотности могут появляться такие неустойчивые пузырьки пара, которые способны к дальнейшему росту. При теоретическом рассмотрении этого процесса взаимодействие между такими отдельными пузырьками обычно не принимаются во внимание [27,28]. Это допущение перестает работать по мере приближения к температуре предельного перегрева (T_h), где скорость возникновения таких неустойчивых зародышей становится очень большой. Тем не менее, такое приближение в этом пределе используется во многих работах [25,26,29,30] где фактически нужны другие подходы. Метод молекулярно-динамического моделирования (МДМ) оказывается наиболее подходящим для анализа поведения сильно неравновесного состояния жидкой фазы вблизи границы предельного перегрева.

Поведение тонкой (48нм) жидкой диэлектрической пленки исследовалось в [31-35] вовремя и после выключения ее однородного нагрева при скоростях энерговклада q = 2-100 К/пс с помощью метода МДМ. Скорость энерговклада определялась с учетом идеальной теплоемкости материала 3k_Bn, где k_B – постоянная Больцмана, n – концентрация частиц в поглощающем материале. В отличие от случаев более коротких и интенсивных лазерных импульсов [11,15,24] в рассматриваемой ситуации относительно небольших скоростей нагрева эффект инерционного удержания не является существенным. В этом диапазоне более важным является эффект испарительного охлаждения, который приводит к формированию подповерхностного температурного максимума. Именно в области локализации этого максимума начинается процесс взрывного вскипания, который в итоге приводит к образованию двух практически одинаковых разлетающихся фрагментов [32-37]. Визуализация этого и других режимов поведения тонкой диэлектрической пленки при различных скоростях энерговклада представлена в [35].

В тонких металлических пленках температурный максимум во время их нагрева оказывается менее выраженным чем в диэлектрических пленках, в частности из-за больших значений коэффициента теплопроводности. Такой эффект температурного нивелирования может существенно изменить характер протекания процессов взрывного вскипания. Вместо одной образующейся полости в области слабовыраженного температурного максимума в пленке могут появляться множество отдельных неоднородностей. Однако, несмотря на почти выровненный температурный профиль, взрывное вскипание металлической пленки в некотором диапазоне поглощаемых интенсивностей также приводит к появлению двух разлетающихся фрагментов. Оказывается, что для более толстых по сравнению с длиной поглощения металлических пленок процесс взрывного вскипания при лазерной абляции характеризуется наличием последовательных вскипаний, а также соответствующих им отдельных пиков давления отдачи, как и предполагалось сорок лет назад [3].

В настоящей работе, которая является продолжением предыдущих исследований [31-40], представлены визуализации различных режимов лазерной абляции металлических (Al) пленок при различных толщинах и интенсивностях лазерного воздействия. Пространственно-временная визуализация процессов даёт наглядную картину достаточно сложного неравновесного поведения облучаемого вещества, которое включает четыре различных режима: квазистационарное поверхностное испарение, взрывное (объемное) вскипание, спинодальный распад и режим расширения закритического флюида.

2. Постановка задачи

Металлическая пленка рассматривается как совокупность двух взаимодействующих подсистем, состоящая соответственно из электронов проводимости и ионов решетки с энергообменом между ними [41-43]. Это означает, что подсистемы в общем случае не находятся в равновесии друг с другом, например, они могут иметь различные температуры в одной и той же точке пространства. Подобный подход был предложен ранее для описания спиновых систем в твердых телах [27], электронной и ионных подсистем в газовой плазме [44].

Лазерное излучение распространяется справа налево и падает нормально на свободную поверхность пленки. Часть излучения поглощается электронной компонентой, и в результате неупругих столкновений передается ионной подсистеме. С помощью периодических граничных условий в направлениях Y, Z задача эффективно сводится к одномерному приближению вдоль направления Х (для процессов переноса лазерного излучения и энергии в электронной подсистеме)

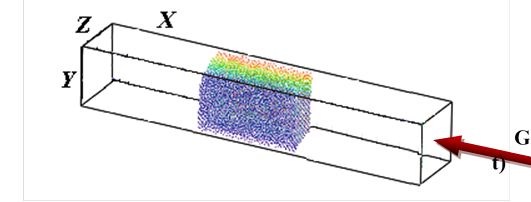
Схема вычислительного эксперимента в начальный момент времени.

Для описания процессов используется комбинированная модель ТТМ-МД [11].

Баланс энергии электронной подсистемы описывается континуальным уравнением энергии (1), дополненного уравнением переноса лазерного излучения (2):

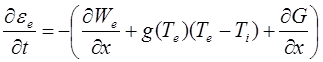(1)

(2)

Здесь – объемная плотность электронной энергии, – электронная и ионная температуры, – коэффициент электрон-ионного обмена энергией, G – плотность потока мощности лазерного излучения в среде, – коэффициент поглощения лазерного излучения, – тепловой поток, – коэффициент электронной теплопроводности.

Уравнение баланса энергии электронной подсистемы (1) решалось в пределах конденсированной среды конечно-разностным методом. В качестве граничных условий на поверхностях пленки и образующихся в процессе моделирования фрагментов задавался нулевой тепловой поток .

Связь электронных энергии и температуры получена с использованием аппроксимации интегралами Ферми [20]:

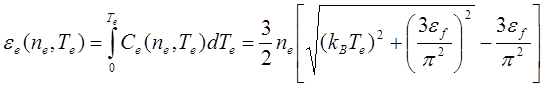(3)

Для описания движения ионов применяется 3D молекулярно динамическое моделирование:

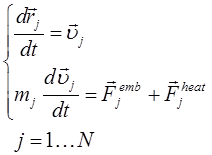(4)

Здесь – соответственно масса, радиус-вектор и скорость j-го иона, 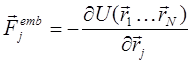– сила, действующая на j-й ион со стороны остальных, – потенциал взаимодействия, в качестве которого был выбран потенциал погруженного атома (EAM) [15], – дополнительная сила, учитывающая энергообмен между подсистемами.

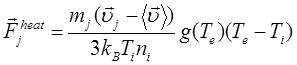, (5)

где – средняя скорость ионов в некоторой окрестности j-го иона.

В начальный момент времени t = 0 полагалось, что пленка нагрета до температуры 6400К, электронная и ионная подсистемы находятся в тепловом равновесии. Пленка расположена в средней по оси Х части расчетной области.

Критические параметры в рассматриваемой модели составляют соответственно T_c=7600K, r_c=0,48г/cм³ and p_c=1,4кбар.

3. Результаты и обсуждение

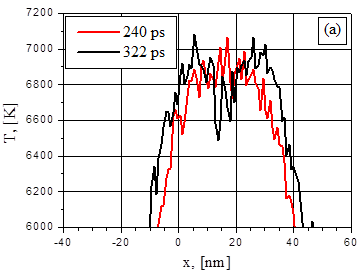
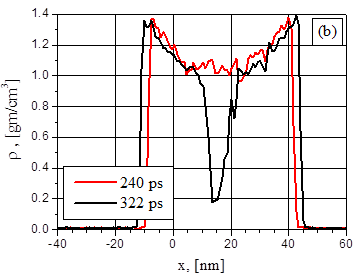
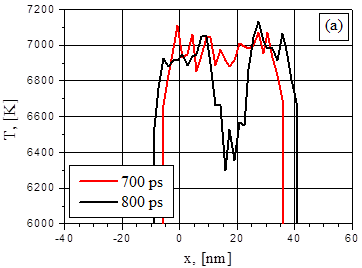
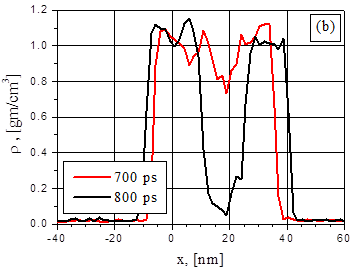
Прежде всего интересно сравнить распределение плотности и температуры в тонких (~ 48 нм) диэлектрической (рис.1) и металлической (рис.2) пленках при близких скоростях энерговклада: 4 К/пс и 5 К/пс соответственно. Эффективная скорость энерговклада q в металлической пленке связана с поглощаемой интенсивностью G соотношением q = GD/(3k_BnL), где D = 1-exp(-aL), n – плотность частиц, L – толщина пленки. Т.е. величинам q = 5 К/пс и 8.8 К/пс в тонкой металлической пленке соответствуют значения поглощаемых интенсивностей G= 29 МВт/см² и G = 51 МВт/см².

В случае металла распределения плотности и температуры не имели таких выраженных экстремумов до начала вскипания как в случае диэлектрической пленке.

Рис.1. Распределение температуры (a) и плотности (b) в диэлектрической пленке для двух моментов времени после начала нагрева с скоростью энерговклада 4 К/пс.

Рис.2. Распределение температуры (a) и плотности (b) в металлической пленке для двух моментов времени после начала нагрева со скоростью энерговклада 5 К/пс.

Тем не менее, в обоих случаях взрывные вскипания начинаются приблизительно в середине (по толщине) пленки. Распад пленки на два примерно одинаковых фрагмента отражает симметрию исследуемой задачи и тот факт, что металлическая пленка является термически тонкой, поскольку длина теплового влияния много больше ее толщины и длины поглощения излучения. В тоже время, различия в температурных распределениях приводит к различию в поведении на начальном этапе образования паровой полости. Это является демонстрацией упомянутой выше зависимости поведения неравновесного процесса от условий его реализации.

Начальная стадия формирования полости в металлической пленке в момент 826 пс, показанная на рис.3, является фрагментом всей картины визуализации демонстрирующей двумерное (усредненное по оси Z) поведение частиц в плоскости ХУ, а также одномерные распределения температуры, плотности, давления и скорости частиц вдоль оси Х, которая перпендикулярна поверхности пленки.

Металлическая пленка 5 К/пс

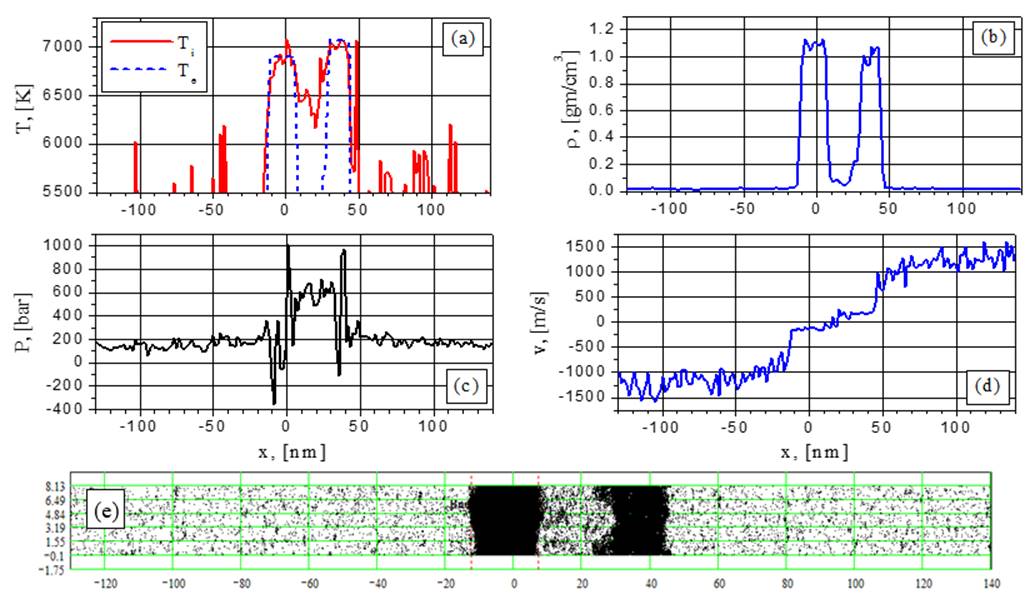
Рис.3. Момент t = 826 пс

Сравнение этих распределений показывает, что различия в поведении диэлектрических и металлических пленок проявляются еще до взрывного вскипания. Флуктуации плотности вблизи поверхности металлической пленки начинают расти до взрывного вскипания потому, что температура поверхности в этом случае меньше отличается от температурного максимума, чем для диэлектрической пленки. Такое температурное нивелирование приводит также к дополнительным флуктуациям поверхности паровой полости на начальном этапе ее формирования.

Подобные флуктуации поверхности полости становятся более выраженными при увеличении интенсивности до 8.8 К/пс (51 МВт/см²), как это видно из рис.4 и соответствующей визуализации. Вместо двух фрагментов в этом случае в самом начале процесса взрывного вскипания образуются сразу четыре фрагмента с сильно возмущенными поверхностями раздела. Эти возмущения затем становятся зародышами новых полостей с еще более размытыми границами.

Металлическая пленка 8.8 К/пс

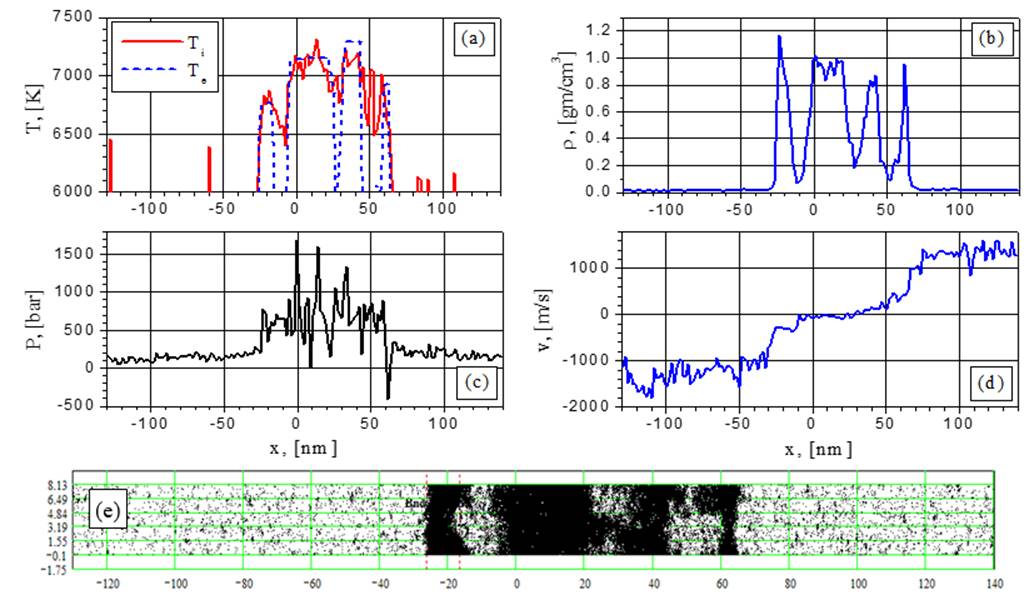
Рис.4. Момент t = 300 пс.

Для более толстых (417нм) металлических пленок процесс абляции отличается от случая тонких пленок, потому что температура обратной стороны пленки оказывается значительно ниже, чем температура ее облучаемой поверхности. Рис.5-22 (за исключением рис.9) дают одномерные распределения температур, плотностей, давлений и скоростей частиц, а также 2D-распределения частиц, которые представлены в такой же форме и на последующих визуализациях. Зависящие от времени распределения усреднены по временному интервалу 5пс.

На правой, облучаемой, поверхности пленки температура оказывается заметно выше, чем на левой стороне. Как это видно из рис.25 в пределе большой толщины пленки (неограниченное полупространство) локализация температурного максимума под поверхностью приблизительно совпадает с длиной поглощения , а разность пропорциональна параметру , где n и c обозначают скорость фронта испарения и коэффициент температуропроводности, - температура поверхности. Для металлов обычно d << 1 даже в околокритической области, если там еще не происходит переход металл-диэлектрик.

Однако, несмотря на эти мешающие факторы, наши вычисления (рис.5-12) ясно демонстрируют наличие повторяющихся взрывных вскипании, которые начинаются приблизительно в 1,04 нс, 1,44 нс, 1,64 нс и 2,34 нс для G= 38.5 МВт/cм² и 0,71 нс, 1,16 нс, 1,5 нс и 1,79 нс для 44 МВт/см² после включения облучения постоянной интенсивности в момент времени t=0. Во время этого процесса абляции очень тонкие фрагменты пленки отлетают последовательно от облучаемой поверхности. Начальная толщина отлетающих фрагментов приблизительно соответствует глубине проникновения излучения , которая почти в два раза меньше толщины фрагментов на рис.2-3.

Перед самым началом взрывного вскипания, например, в момент 1,04 нс, на рис.5b и соответствующей визуализации можно видеть нарастание флуктуации плотности и определенного рода конкуренцию между ними в ходе их эволюции под облучаемой поверхностью. В результате этой конкуренции из двух флуктуаций только одна, ближайшая к поверхности, продолжает развиваться, формируя растущую паровую полость, которая отделяет отлетающий фрагмент от остальной части пленки. Такая конкуренция флуктуаций наблюдается также при развитие взрывного вскипания в моменты 2 нс и 2,34 нс при G=38,5 МВт/cм²и при G=44 МВт/cм², но в более ранний момент времени (0,71 нс). Следует отметить, что при G=44 МВт/cм²подобная конкуренция становится менее эффективной на более поздних временах, начиная с 1,79нс (см. визуализацию), что приводит к практически одновременному образованию двух фрагментов (рис.12).

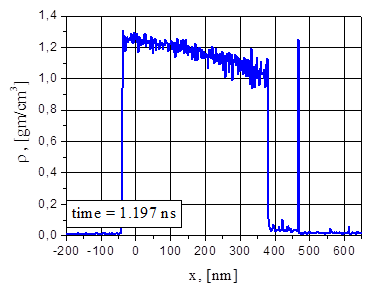
При небольших интенсивностях (38,5 МВт/cм²и 44 МВт/cм²) эволюция плотности отлетающих фрагментов не является монотонной по времени (рис.6b и 7b), причем плотность фрагмента достигает максимума, превосходящего плотность пленки на ее облучаемой поверхности. Это поведение более выразительно выглядит с использованием линейной шкалы для плотности (рис.9) и временного усреднения по интервалу 1 пс. Это свидетельствует об определенной стабилизации отлетающих от пленки фрагментов, которые обеспечивают заметные скачки в распределении плотности пара, давления и скоростей частиц в абляционном потоке (рис.7b, 7c, 7d).

Скорость пара демонстрирует скачок к положительным (правая поверхность пленки) или отрицательным (левая поверхность пленки) значениям, величина которого определяется кинетикой поверхностного испарения [5,45].

При больших интенсивностях (88 МВт/cм²и 154 МВт/cм²) не наблюдается никакого увеличения плотности фрагментов, границы которых становятся менее четкими, как это видно из рис.13b-20b и соответствующих визуализаций (88 МВт/cм²и 154 МВт/cм²). Такие режимы могут быть обозначены как спинодальный распад, который имеет место при докритических значениях давления и температуры с более размытыми фазовыми границами, чем в случае взрывного вскипания. Из-за больших скоростей нагрева при 88 МВт/cм²и 154 МВт/cм²не остается времени на развитие процессов взрывного вскипания, которые наблюдаются при меньших интенсивностях.

Толстая пленка G = 38.5 MВт/cм²

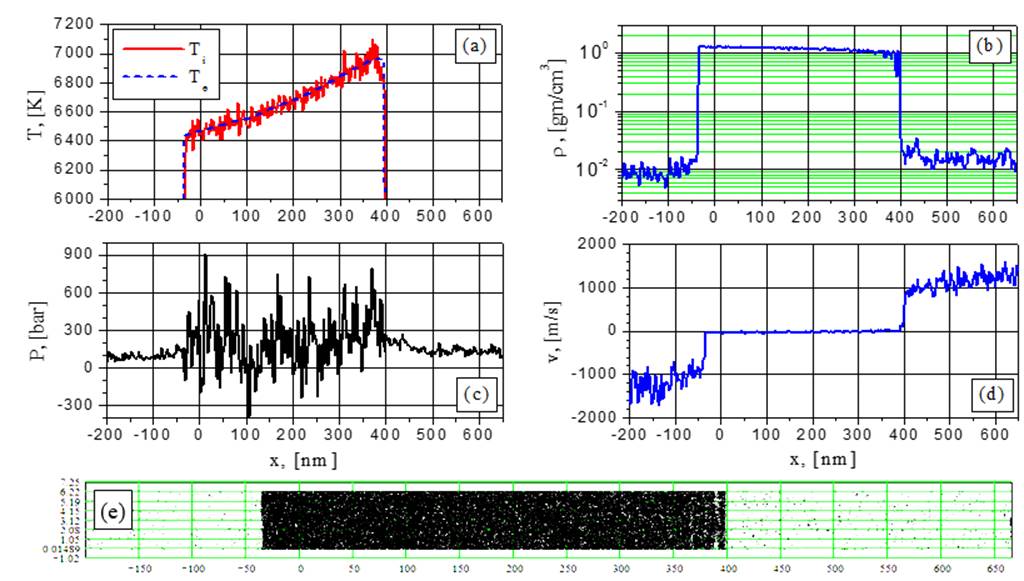
Рис.5. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G = 38.5 MВт/cм2 в момент времени t = 1.032 нс: начало взрывного вскипания

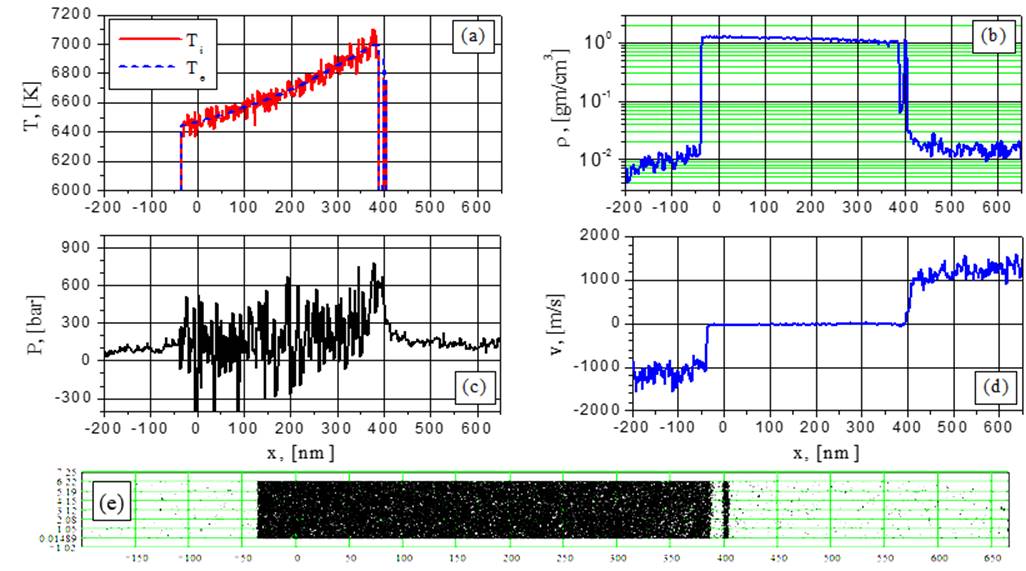
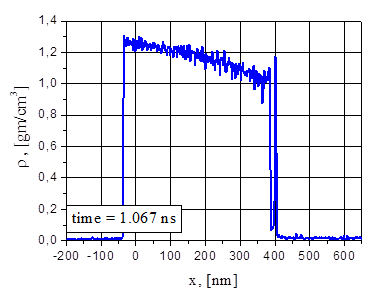
Рис.6. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D- распределение частиц (е) при G = 38.5 MВт/cм² в момент времени t = 1.067 нс: отделение первого фрагмента.

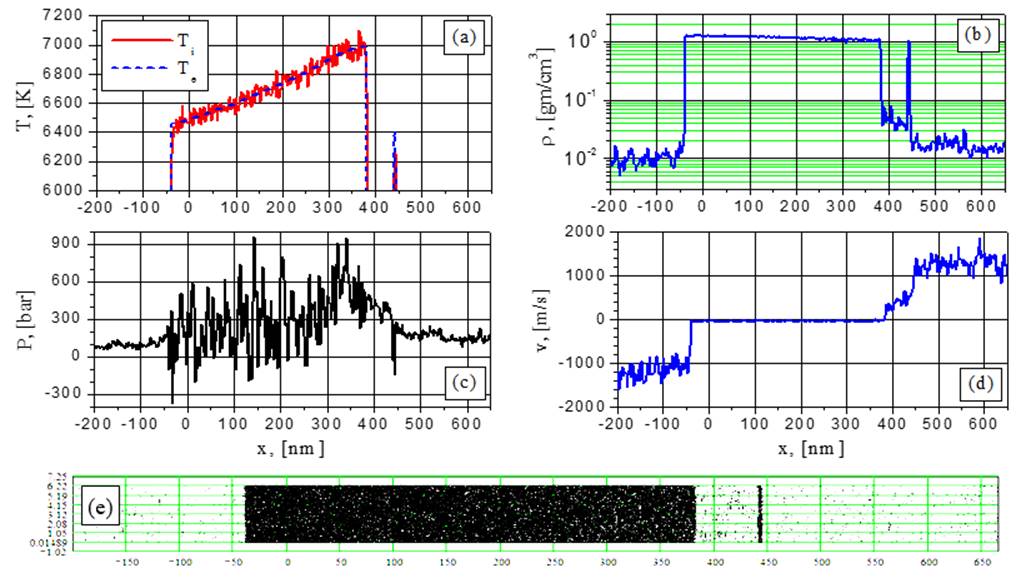
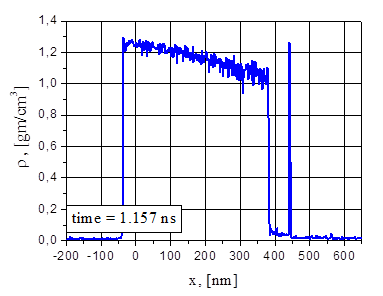
Рис.7. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G = 38.5 MВт/cм² в момент времени t = 1.157 нс: флуктуации скорости и плотности; рост плотности фрагмента.

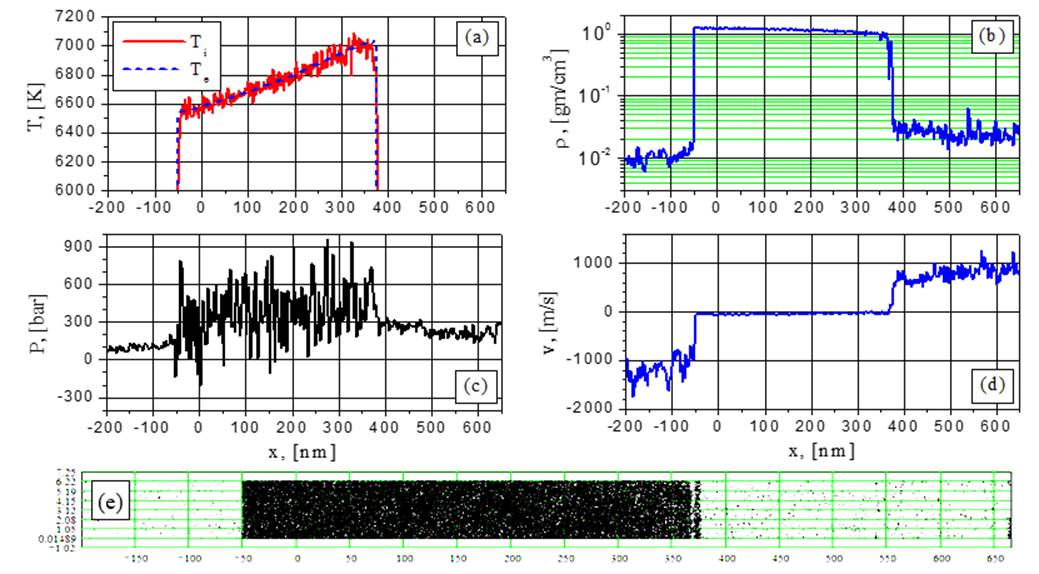
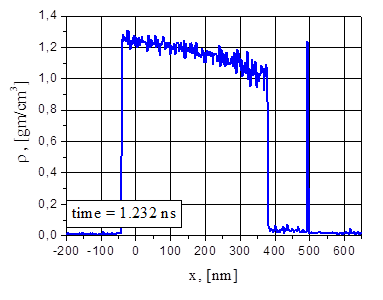
Рис.8. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G = 38.5 MВт/cм² в момент времени t = 1.447 нс: второе взрывное вскипание.

Рис.9. Эволюция распределения плотности (линейный масштаб, усреднение по времени – 1пс) после первого вскипания G = 38.5 MВт/cм²: рост плотности отлетающего фрагмента.

Толстая пленка G = 44 MВт/cм²

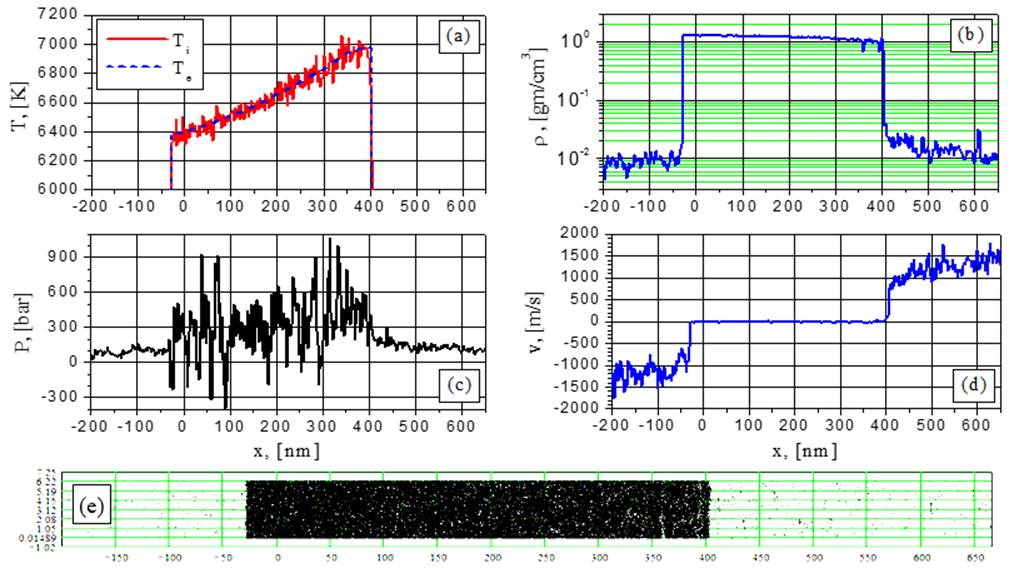
Рис.10. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G= 44 MВт/cм² в момент времени t = 0.6762 нс: “конкуренция” между растущими флуктуациями.

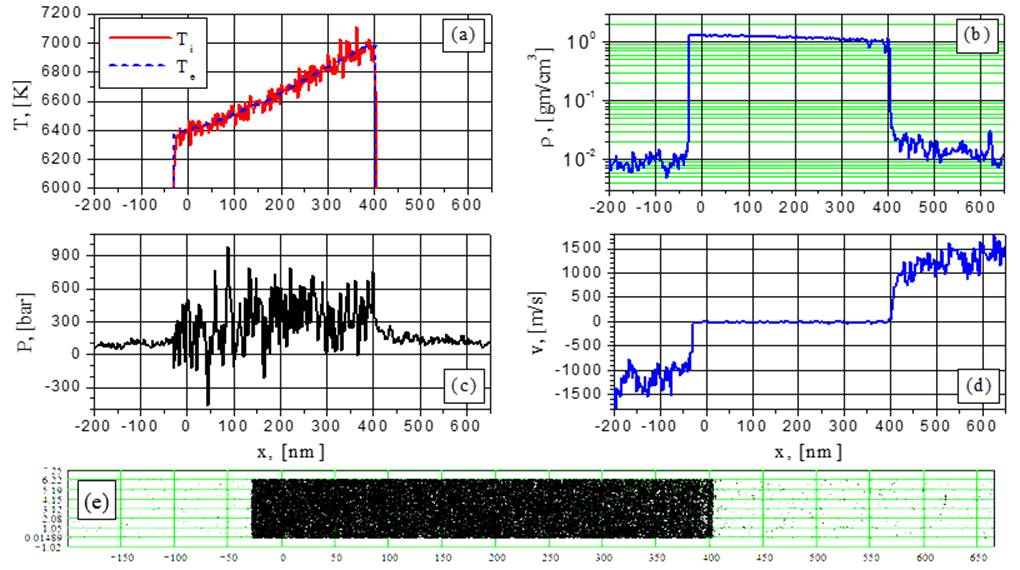
Рис.11. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G= 44 MВт/cм² в момент времени t = 0.6842 нс: “конкуренция” между растущими флуктуациями.

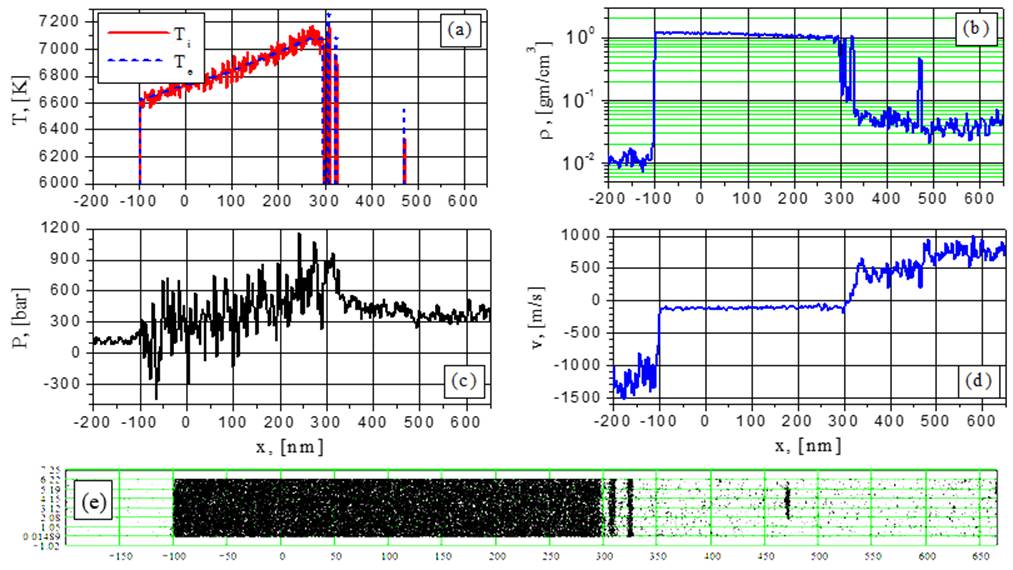
Рис.12. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G = 44 MВт/cм² в момент времени t = 1.8252 нс: продолжение нагрева – несколько последовательно отделившихся фрагментов, “конкуренция” между растущими флуктуациями.

Толстая пленка G = 88 MВт/cм²

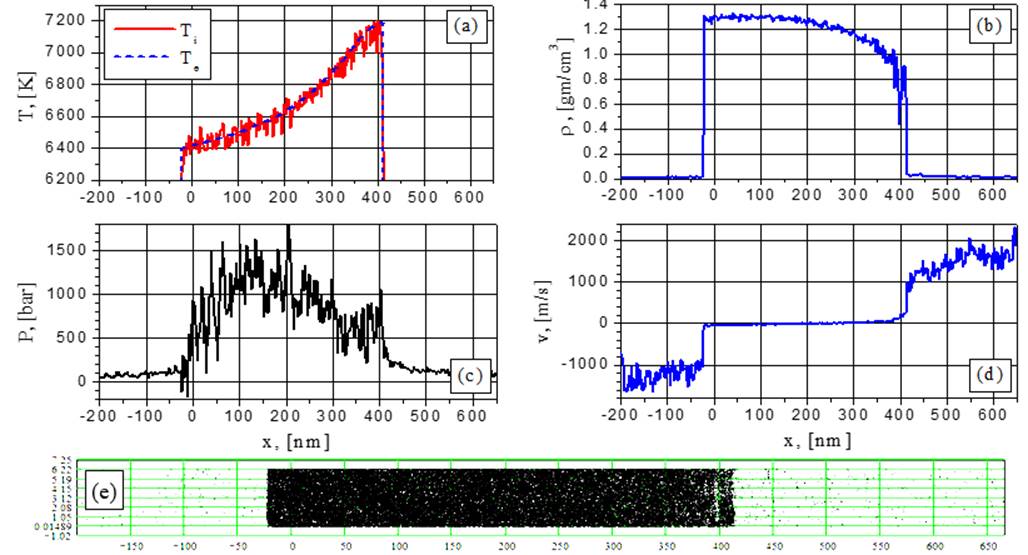
Рис.13. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G= 88 MВт/cм² в момент времени t = 0.2252 нс: переход от вскипания к спинодальному распаду.

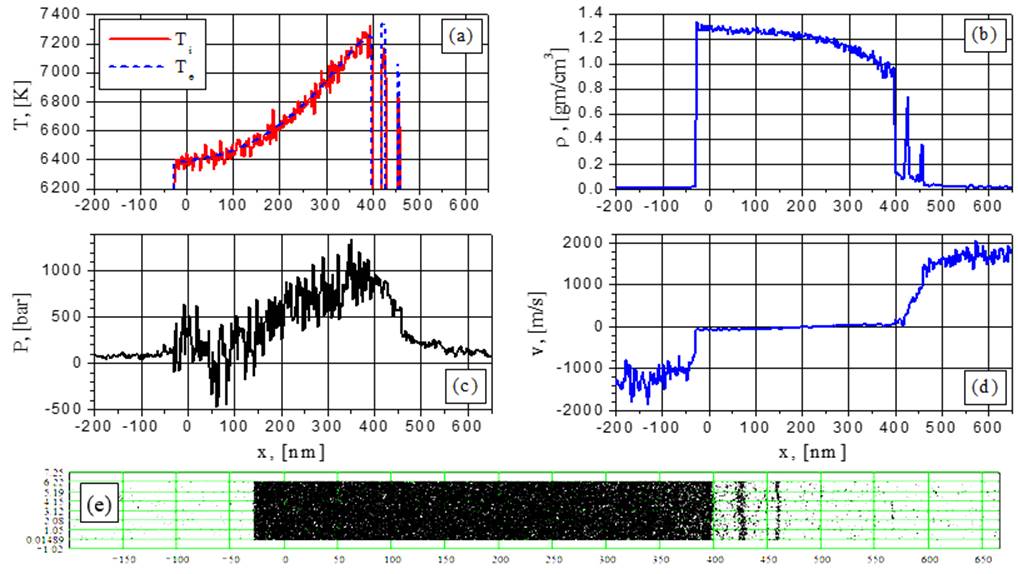
Рис.14. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G = 88 MВт/cм² в момент времени t = 0.3152 нс: переход от вскипания к спинодальному распаду.

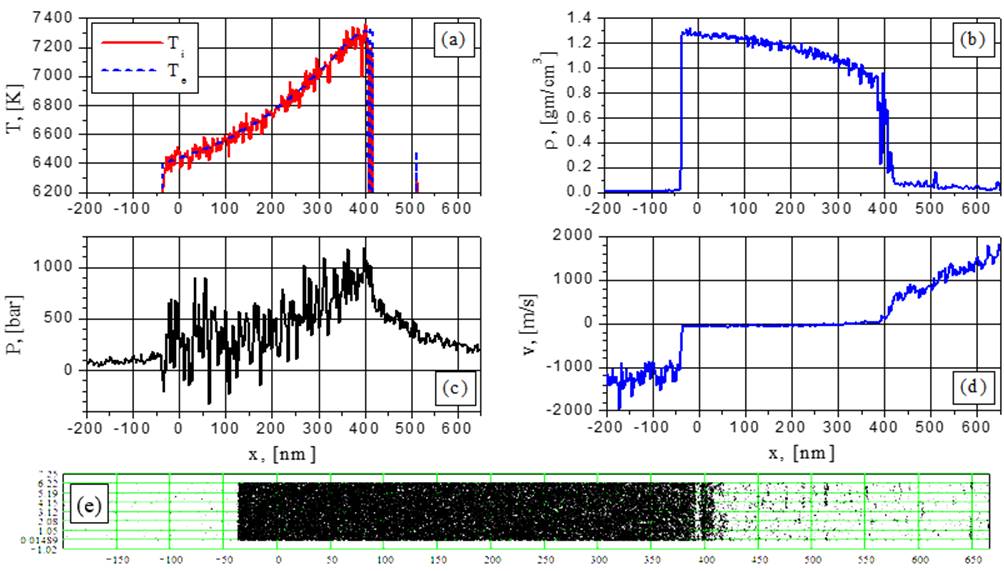
Рис.15. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G = 88 MВт/cм² в момент времени t = 0.4552 нс: переход от вскипания к спинодальному распаду.

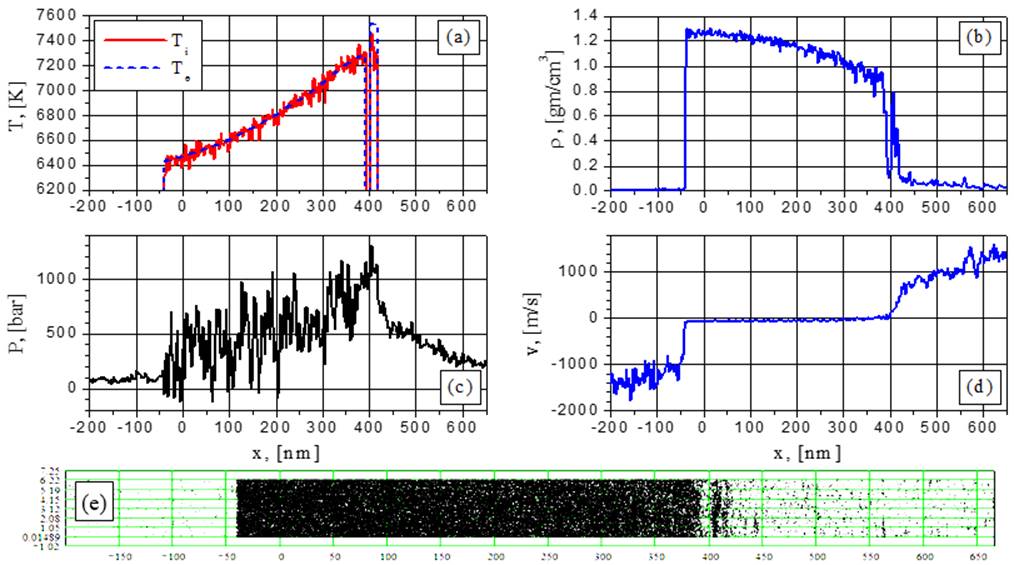
Рис.16. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G= 88 MВт/cм² в момент времени t = 0.5052 нс: переход от вскипания к спинодальному распаду.

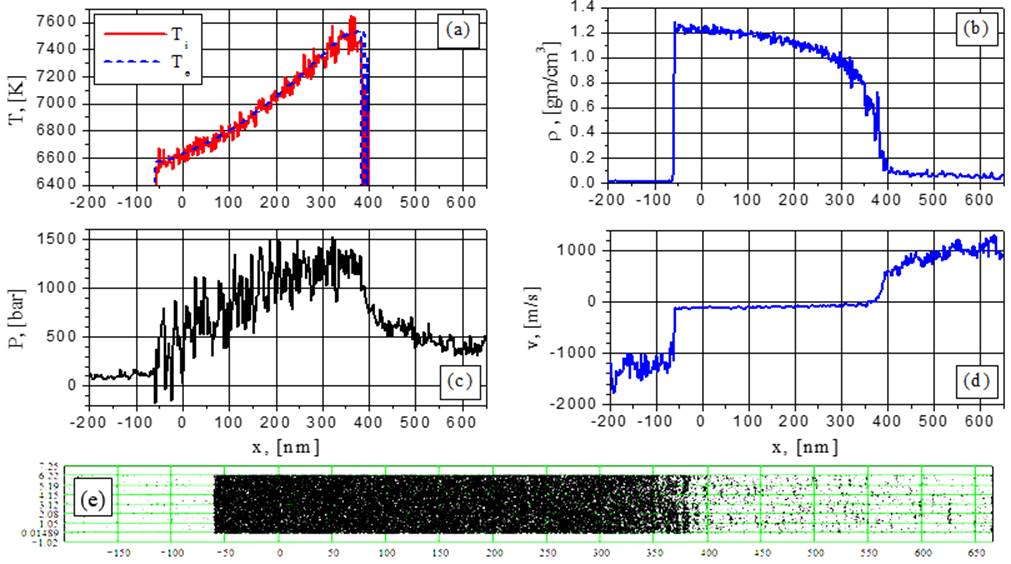
Рис.17. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G= 88 MВт/cм² в момент времени t = 0.7302 нс: спинодальной распад.

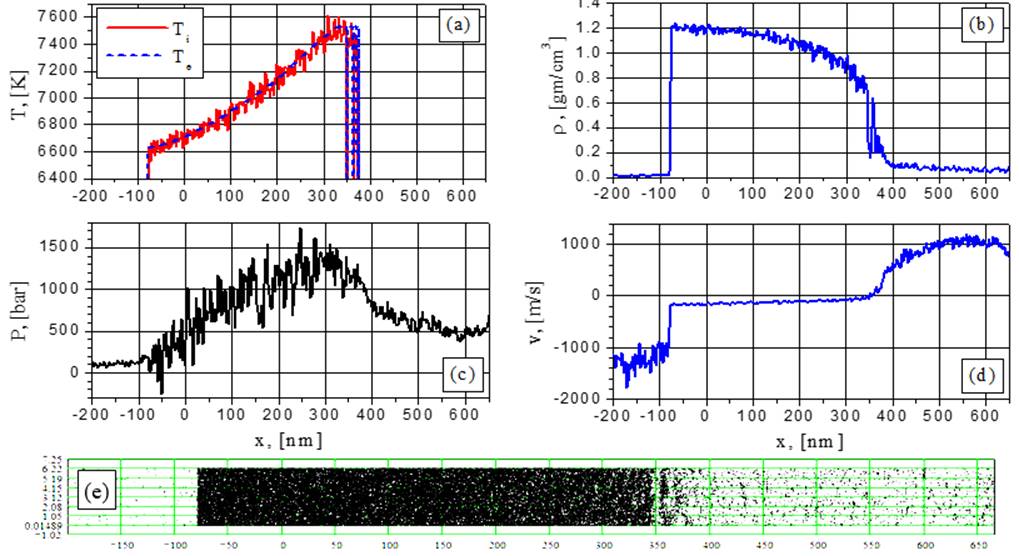
Рис.18. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G = 88 MВт/cм² в момент времени t = 0.8602 нс: спинодальной распад.

Толстая пленка G = 154 MВт/cм²

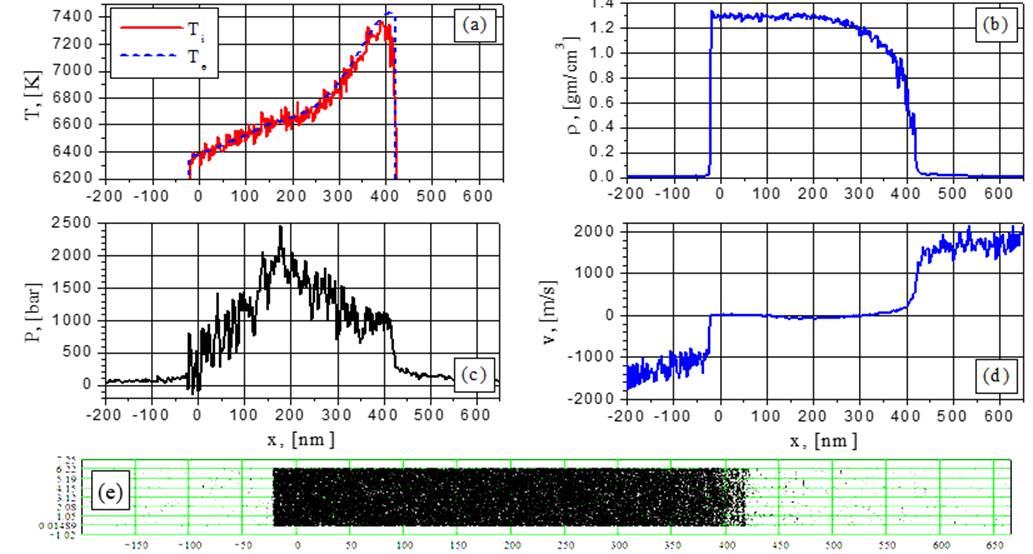
Рис.19. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G = 154 MВт/cм² в момент времени t = 0.1252 нс: спинодальной распад без взрывного вскипания.

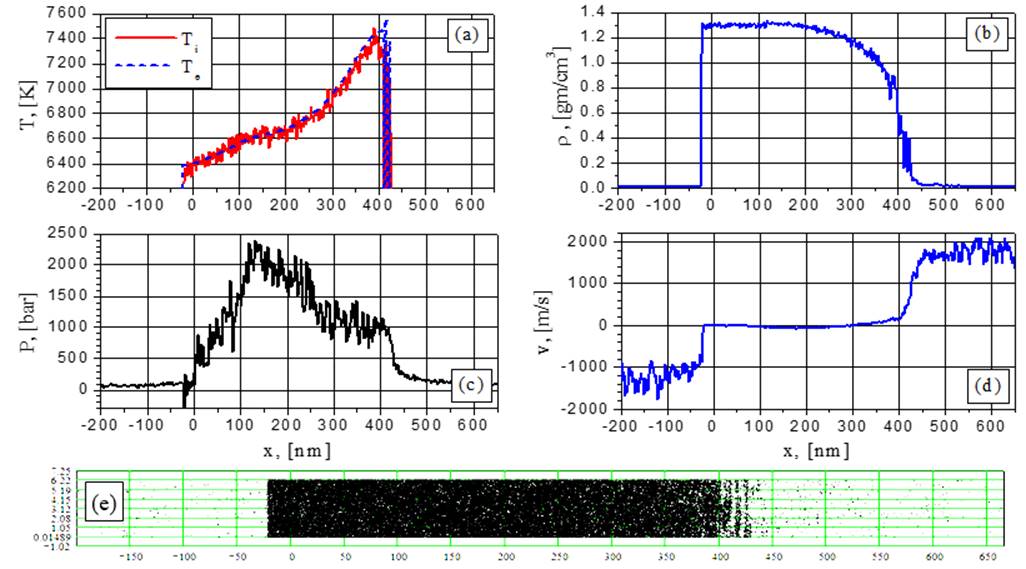
Рис.20. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G= 154 MВт/cм² в момент времени t = 0.1402 нс: спинодальной распад без взрывного вскипания.

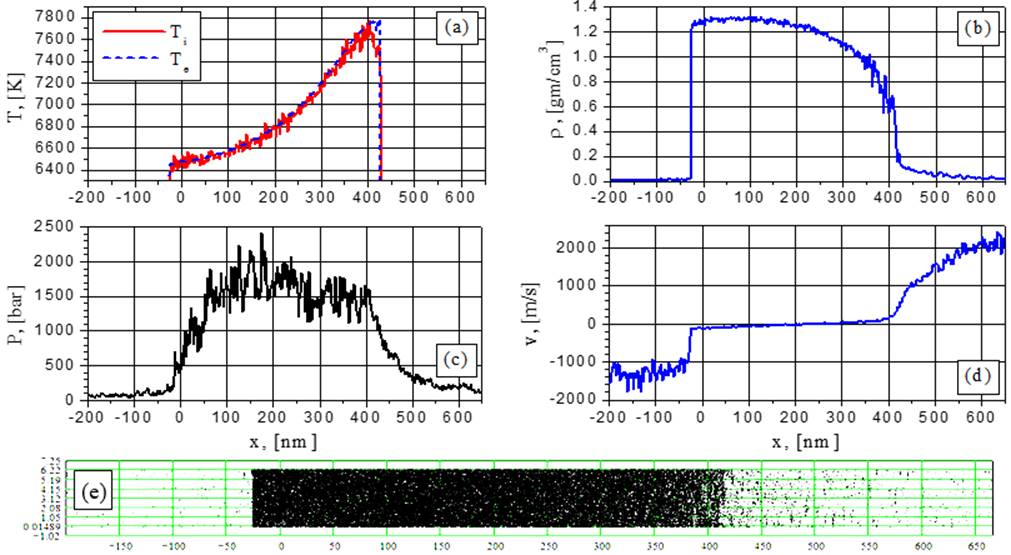
Рис.21. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G = 154 MВт/cм² в момент времени t = 0.2202 нс: переход от спинодального распада к закритической абляции.

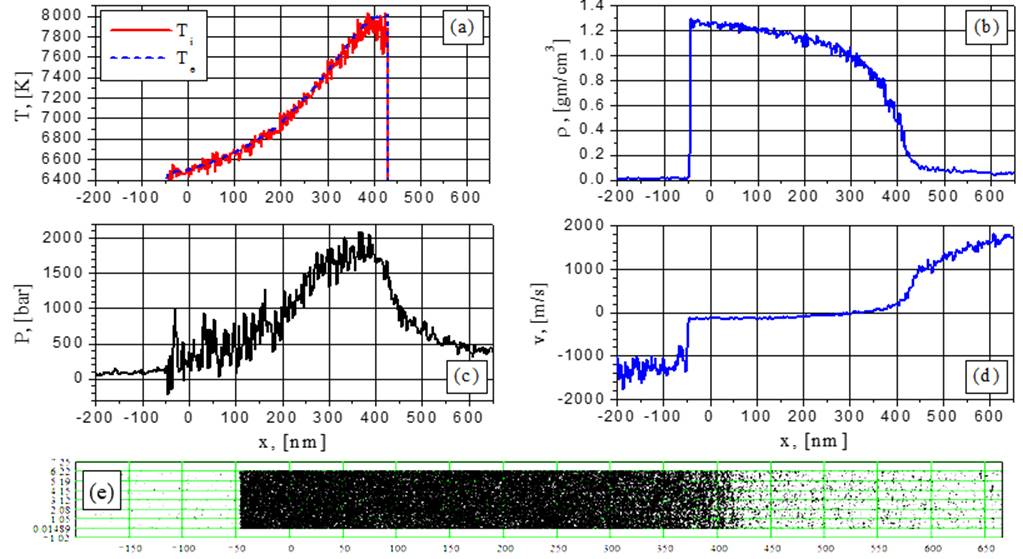
Рис.22. Электронная и ионная температуры (а), плотность (b), давление (с), скорость (d) и 2D-распределение частиц (е) при G = 154 MВт/cм² в момент времени t = 0.3752 нс: переход от спинодального распада к закритической абляции.

Режим спинодального распада виден также при G=154 МВт/cм²в моменты t =0,125 и 0,14 нс (рис.19-20 и визуализация). На более поздних временах (рис. 21-22) этот процесс трансформируется в режим разлета сверхкрититческого флюида с уменьшающимися флуктуациями плотности на правой стороне пленки, причем эти флуктуации становятся более плавными по сравнению со случаем докритической абляции (рис.5-20). Никаких эффектов взрывного вскипания при G=154 МВт/cм²не наблюдается даже в докритической области температур из-за большой скорости нагрева. Результаты нашего моделирования показывают, что эффект взрывного вскипания наиболее выражен при G=38,5 МВт/cм²и 44 МВт/cм².

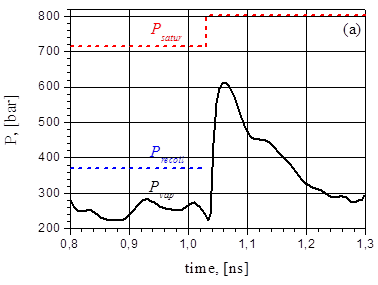
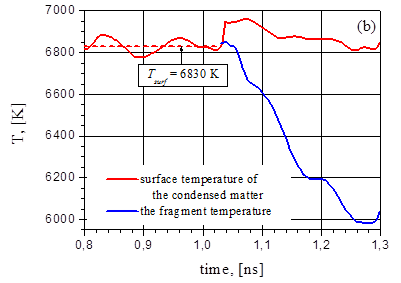
На рис.23 показаны поведение температуры и давления во время первого взрывного вскипания, которое происходит в интервале 0,8-1,3 нс после включения интенсивности с G=38,5 МВт/cм² . Кривые давления и температуры во время третьего взрывного вскипания в интервале 1,35-1,7 нс при интенсивности G=44 МВт/cм²показаны на рис.24.

На рис.23 кривая давления до момента t₁=1,04 нс обозначает давление P_vap в потоке пара около облучаемой поверхности, которое ниже, чем давление отдачи P_recoil ≥0.5P_satur(T_s) , где T_sозначает температуру облучаемой поверхности. При T_s=6830 K давление P_satur=714 бар_,тогда как вычисленное давление под поверхностью пленки (фактически равное давлению отдачи P_recoil) составляет примерно 370 бар. Во время взрывного вскипания давление отдачи увеличивается в 1,65 раза (до 610 бар), что несколько ниже, чем давление насыщения P_satur(T_m)=802 бар при T_m=6950 K. Температура T_m соответствует подповерхностному максимуму температуры, локализованному до момента взрывного вскипания на расстоянии длины поглощения излучения. Температурный скачок на рис.23b обусловлен смещением точки наблюдения от облучаемой поверхности в точку при , что примерно соответствует упоминаемому выше перепаду температур ().

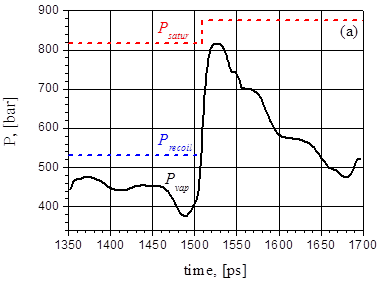
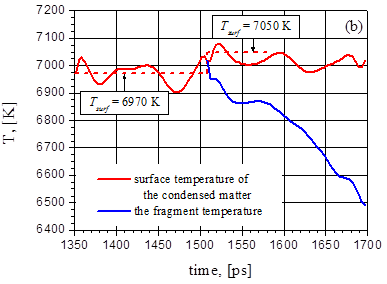
Для G= 44 МВт/cм²поведение давления и температуры при взрывном вскипании в интервале 1,35-1,7 нс подобно случаю c G= 38,5 МВт/cм²в интервале 0,8-1,3 нс при несколько увеличенных значениях p и T. В обоих случаях время нарастания давления составляет примерно 20 пс.

PvapSurf

TcondSurf

Рис.23. Эволюция давления (а) и температуры (b) на поверхности пленки (красная линия) и отлетающего фрагмента (синяя линия) для G = 38.5 MВт/cм2.

Рис.24. Эволюция давления (а) и температуры (b) на поверхности пленки (красная линия) и отлетающего фрагмента (синяя линия) для G= 44 MВт/cм².

Интересно отметить, что в эксперименте [14] наблюдаемое примерно двукратное увеличение давления отдачи в ударной волне над облучаемой поверхностью интерпретировалось как переход от нормального испарения к фазовому взрыву (взрывному вскипанию). В этом случае, однако, необходимо принимать во внимание эффекты, связанные с образованием плазмы, которые также могут приводить к увеличения давления над облучаемой поверхностью. Вопрос о роли плазмы в таких условиях требует дополнительного анализа.

Как уже упоминалось во введении, вопрос о влиянии подповерхностного перегрева на процесс взрывного вскипания в металлах не имел до последнего времени достаточно четкого ответа из-за больших значений коэффициентов поглощения и температуропроводности осложняющих проявление этого процесса. При контунаульном подходе [5] стационарный температурный профиль в облучаемом образце (лазерное излучение падает на образец слева направо) определяется уравнением температуропроводности, которое в системе координат, движущейся вместе с фронтом испарения x = 0 , имеет вид:

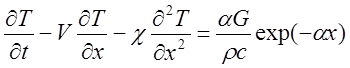(6)

где r-плотность, с - теплоемкость, χ – температуропроводность и коэффициент поглощения a для простоты приняты постоянными. Скорость испарения V и теплота испарения зависят от температуры поверхности.

Из решения задачи (6) следует выражение для стационарного распределения температуры

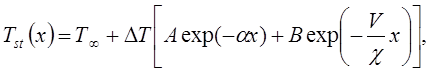(7)

где

(8)

Уравнение сохранения энергии (8) непосредственно следует из (6) и дает связь между поглощенной интенсивностью G, скоростью испарения V и теплофизическими параметрами облученного вещества. Скорость испарения зависит от температуры поверхности и числа Маха на внешней стороне кнудсеновского слоя [45]. В случае M=1 для V получаем:

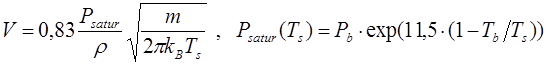(9)

где P_satur – давление насыщения при температуре поверхности T_s, T_b = 2792 K – температура кипения при нормальном давлении (P_b=1 бар), m - масса испаряемых частиц. В формуле (9) приняты во внимание свойства рассматриваемой модели нагретого вещества: r = 1 г/cм³, c = 0,8 cм²/с и m = 4,48∙10^-23 г.

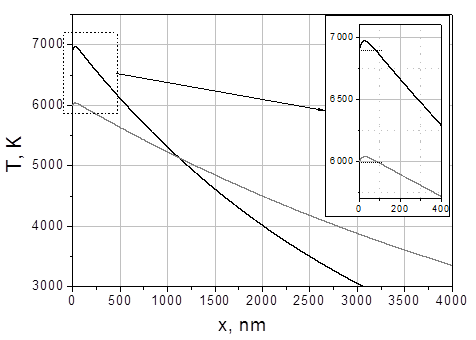
Рис.25. Распределение температур T(х) для двух интенсивностей: G = 19,5 MВт/cм² (серая линия), G = 38,5 MВт/cм² (черная линия),(лазерное излучение падает на образец слева направо).

Пределы применимости этого упрощенного подхода определяется также тем ограничением, что температура метастабильной жидкости должна быть ниже температуры предельного перегрева, поскольку в противном случае однородное существование жидкой фазы невозможно. Это ограничение является наиболее жестким в случае относительно небольших значений коэффициентов поглощения и температуропроводности, которые фактически исключают реализацию режима поверхностного испарения (7), в частности, из-за большого различия между величинами температуры поверхности T_s и величиной подповерхностного температурного максимума, где развивается взрывное вскипание.

Для металлов обычно c/V >>a^-1 и разность температур является малой так что модель (6)-(7) применима достаточно в широком диапазоне температур поверхности T_s значения которой может быть достаточно близким к температуре предельного перегрева T_h или спинодальной T_sp. Однако в этом случае возникает другой важный вопрос относительно возможного влияния на процесс лазерной абляции относительно малых значений подповерхностной разности температур T_m –T_s. В работе [3] предполагается, что, несмотря на относительно небольшую величину этого температурного перепада, может развиваться режим повторяющихся подповерхностных взрывных вскипаний, тогда как в работах [23,25,26] эта возможность считается не реализуемой. Результаты нашего математического моделирования дают вполне определенный ответ на этот вопрос.

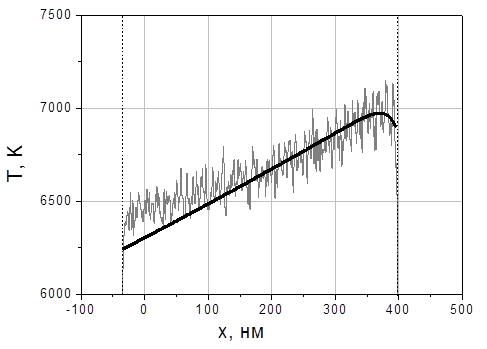
Рис.26. Аналитический (гладкая кривая) и численный (с флуктуациями) профили температуры в квазистационарном режиме перед началом взрывного вскипания. Излучение падает справа.

Рис.26 показывает распределение температуры (флуктуирующая кривая), полученное из МД вычислений при G=38,5 МВт/cм² и t=1,02нс как раз перед первым взрывным вскипанием и температурную кривую из рис.25, которые соответствуют одной и той же поверхностной температуре T_s = 6900 K.

Различия между этими кривыми на левой (обратной) стороне пленки обусловлено ее конечной толщиной которая в модели (6)-(7) предполагалась бесконечной. Толщина пленки сравнима с длиной температурного влияния c/V, поскольку в рассматриваемой модели c =0,8 cм²/с и скорость фронта испарения V=2764 cм/с в соответствии с уравнениями (8) и (9).

Несмотря на относительно малые значения подповерхностного температурного максимума T_m по сравнения с температурой поверхности T_s и весьма малому расстоянию между поверхностью и локализацией подповерхностного максимума T_m, результаты МД вычислений показывают, что процесс подповерхностного взрывного вскипания начинается именно в области локализации T_m . При малой толщине отлетающего фрагмента (порядка глубины проникновения излучения 10нм) он оказывается, тем не менее, достаточно плотным, чтобы обеспечить описанные выше перепады давления при взрывном вскипании (рис.23-24). Полезно напомнить, что подобные импульсы давления могут быть более выраженными, если в докритической области происходит переход металл-диэлектрик, который обсуждается во многих работах без пока еще окончательно подтверждающих его экспериментов (см. например [1,2,4-6,8,9,13] и цитируемую там литературу).

4. Заключение

Результаты нашего МД моделирования и их визуализация подтверждают обоснованность предложенного нами выделения четырех режимов наносекундной лазерной абляции металлов в зависимость от интенсивности облучения: поверхностное испарение, взрывное (объемное) вскипание, спинодальный распад и режим разлета закритического флюида. Эта общая картина наносекундной лазерной абляции отличается от других подходов [7,25,26,29] к описанию кинетики фазового перехода в рассматриваемых условиях

В частности, согласно нашим результатам, для металлов взрывное вскипание проявляется в виде повторяющихся субнаносекундных импульсов давления отдачи, которые с увеличением интенсивности становятся менее выраженными случае спинодального распада и полностью исчезают в режиме сверхкритического разлета облучаемого вещества. Такие особенности лазерной абляции металлов описаны в [3] сорок лет назад с предложением их использования для определения величины критического давления облучаемого материала.

Следует напомнить, что четко выраженное проявление взрывного вскипания происходит только при максимальном приближении к температуре предельного перегрева, где практически одновременно из неустойчивых флуктуаций плотности возникает большое количество зародышей паровой фазы. В этом пределе широко используемая теория нуклеция [25-30] неприменима, поскольку возникающие в этом случае в экстремально перегретой жидкости зародыши паровой фазы нельзя считать независимыми и даже предполагать их сферическую форму в случае сильной пространственной неоднородности температурного профиля или из-за больших флуктуаций.

Одновременное появление при температуре предельного перегрева жидкости множества растущих и сливающихся паровых зародышей приводит к увеличению эффективной теплоемкости метастабильной жидкости непосредственно перед моментом ее взрывного вскипания. Комбинирование молекулярно-динамического подходов в подобной ситуации позволяет получить новую информацию о сингулярном поведении теплофизических параметров при температуре предельного перегрева Т_h [46].

Динамика появления новой фазы наглядно демонстрируется на представленных визуализациях, которые показывают, что в рассматриваемых условиях вблизи Т_hвместо отдельных пузырьков фактически сразу формируется паровая полость, испарение в которую приводит к взрывному субнаносекундному всплеску давления отдачи. Очевидно, что появление отдельного критического зародыша или их совокупности в рамках континуальной модели само по себе не сопровождается ростом давления, т.е. для определения динамики нарастания давления должно учитываться взаимодействие и слияние таких зародышей.

В нашей модели жидкого алюминия при интенсивностях облучения меньших 35 МВт/cм² режим поверхностного испарения наблюдается в течении многих наносекунд после начала облучения, в то время как при 38,5 МВт/cм²и 44 МВт/cм²первые взрывные вскипания происходят соответственно при t = 1,04 и 0,71 нс. Подобные вскипания повторяются затем с субнаносекундными интервалами. Интервалы между вскипаниями не остаются неизменными из-за продолжающегося нагрева и флуктуационной природы инициирования взрывного вскипания.

Пульсации давления отдачи в режиме повторяющихся взрывных вскипаний могут быть использованы как признаки приближения к области критических параметров облучаемого вещества, а переход через критическую область характеризуется прекращением таких пульсаций. Как уже отмечалось во введении критические параметры для металлов до сих пор остаются плохо определенными [24,47]. Динамика отлетающих при взрывном вскипании фрагментов может регистрироваться также оптическими методами подобно тому, как это делалось в работе [48].

Благодарность

Работа выполнена при поддержке РНФ, грант № 15-11-30039

Список литературы

[1] Batanov V.A., Bunkin F.V., Prokhorov A.M., Fedorov V.B. Evaporation of metallic targets caused by intense optical radiation. Sov. Phys. JETP 36, 311 (1973). ЖЭТФ 63, 586 (1972).

[2] Карапетян Р.В., Самохин А.А. Влияние просветления на режим развитого испарения металлов под действием оптического излучения. Квантовая электроника. 1,2053 (1974). Sov. J. Quantum Electron., 4, 9, 1141 (1975)

[3] Samokhin A.A. Some aspects of the intense evaporation of condensed media by laser radiation. Sov. J. Quantum Electron., 4, 1144 (1975). Квантовая электроника 1, 2056, (1974).

[4] Zavecz T.E., Saifi M.A., Noits M., Metal reflectivity under high-intensity optical radiation. Appl. Phys. Lett. 26, 165 (1975).

[5] Samokhin A.A., First-order phase transitions induced by laser radiation in absorbing condensed matter. Proc. Institute of General Physics (USSR: Academy of Sciences), 13, p.1 (1988). Труды ИОФ РАН, 13, 3 (1988)

[6] Yoo J.H., Jeong S.H., Greif R., Russo R.E. Explosive change in crater properties during high power nanosecond laser ablation of silicon. Journal of Applied Physics 88, 1638 (2000)

[7] Bulgakova N.M., Bulgakov A.V. Pulsed laser ablation of solids: transition from normal vaporization to phase explosion. Appl. Phys. A, 73,199 (2001)

[8] Lu Q., Mao S., Mao X., Russo R. Delayed phase explosion during high-power nanosecond laser ablation of silicon. Appl. Phys. Lett., 80, 3072 (2002)

[9] Andreev S.N., Mazhukin V.I., Nikiforova N.M., Samokhin A.A., On possible manifestations of the induced transparency during laser evaporation of metals. Quantum Electron., 33, 771 (2003)

[10] Garrison B.J., Itina T.E., Zhigilei L.V., Limit of overheating and the threshold behaviour in laser ablation. Phys. Rev. B, 68, 041501 (2003)

[11] Ivanov D.S., Zhigilei L.V., Combined atomistic-continuum modeling of short-pulse laser melting and disintegration of metal films. Phys. Rev.B, 68, 064114 (2003)

[12] Pakhomov A.V., Thompson M.S., Gregory D.A. Laser-induced phase explosions in lead, tin and other elements: microsecond regime and UV emission. J. Phys. D: Appl. Phys. 36 2067 (2003)

[13] Porneala C., Willis D.A. Effect of the dielectric transition on laser-induced phase explosion in metals. Int. J. Heat Mass Transfer, 49, 1928 (2006)

[14] Porneala C., Willis D.A. Time-resolved dynamics of nanosecond laser-induced phase explosion. J. Phys. D: Appl. Phys., 42, 155503 (2009)

[15] Zhakhovskii V.V., Inogamov N.A., YPetrov u.V., Ashitkov S.I., Nishihara K. Two temperature relaxation and melting after absorption of femtosecond laser pulse. Appl. Surf. Sci., 255, 9592 (2009)

[16] Mazhukin V.I., Mazhukin V.A., Koroleva O.N. Optical properties of electron Fermi-gas of metals at arbitrary temperature and frequency. Laser Physics. 19, 1179 – 1186 (2009)

[17] Ionin A.A., Kudryashov S.I., Seleznev L.V., Sinitsyn D.V. Nonlinear regime of the excitation of a surface electromagnetic wave on the silicon surface by an intense femtosecond laser pulse. JETP Lett. 94, 753 (2011)

[18] Samokhin A.A., Il’ichev N.N., Klimentov S.M., Pivovarov P.A. Photoacoustic and laser-induced evaporation effects in liquids. Appl. Phys. B, 105, 551 (2011)

[19] Brown W.M., Wang P., Plimpton S.J., Tharrington A.N. Implementing molecular dynamics on hybrid high performance computers – short range forces. Comp. Phys. Commun., 182, 898 (2011)

[20] Mazhukin V.I. Kinetics and Dynamics of Phase Transformations in Metals Under Action of Ultra-Short High-Power Laser Pulses. Chapter 8, pp.219 -276. In “Laser Pulses – Theory, Technology, and Applications”, InTech. Ed. by I. Peshko., P 544, (2012).

[21] Ionin A.A., Kudryashov S.I., Seleznev L.V., Sinitsyn D.V., Bunkin A.F., Lednev V.N., Pershin S.M. Thermal melting and ablation of silicon by femtosecond laser radiation. JETP, 116, 347-362 (2013).

[22] Autrique D., Clair G., L'Hermite D., Alexiades V., Bogaerts A. The role of mass removal mechanisms in the onset of ns-laser induced plasma formation. J. Appl. Phys. 114, 023301 (2013)

[23] Adrian H. A. Lutey An improved model for nanosecond pulsed laser ablation of metals. J.of Appl. Phys. 114, 083108 (2013)

[24] Wu C., Zhigilei L.V. Microscopic mechanisms of laser spallation and ablation of metal targets from large-scale molecular dynamics simulations. Appl. Phys. A, 114, 11-32 (2014)

[25] Jiang M.Q., Wei Y.P., Wilde G., Dai L.H. Explosive boiling of a metallic glass superheated by nanosecond pulse laser ablation. Appl. Phys. Let. 106, 021904 (1-6), (2015).

[26] Miotello A., Kelly R. Critical assessment of thermal models for laser sputtering at high fluences. Appl. Phys. Lett. 67, 3535 (1995).

[27] Ландау Л.Д., Лифшиц Е.М. Статистическая физика. Часть 1. Издание 4-е. М.:Наука, 1995. («Теоретическая физика», том V)

[28] Скрипов В.П. Метастабильная жидкость. Москва: Наука, 1972. 312 с.

[29] Vogel A., Venugopalan V. Mechanisms of Pulsed Laser Ablation of Biological Tissues. Chem. Rev. 2003, 103, 577−644

[30] Autrique D., Clair G., L'Hermite D., Alexiades V., Bogaerts A., Rethfeld B. The role of mass removal mechanisms in the onset of ns-laser induced plasma formation. J. Appl. Phys. 114, 023301 (2013)

[31] Mazhukin V.I., Samokhin A.A., Shapranov A.V., Ivochkin A.Yu. Mathematical modeling of non-equilibrium phase transition in rapidly heated thin liquid film. Mathematica Montisnigri, 27, 65 (2013)

[32] Мажукин В.И., Шапранов А.В., Самохин А.А., Ивочкин А.Ю. Молекулярно-динамическое моделирование неравновесного перехода жидкость-пар при субнаносекундном однородном нагреве тонкой пленки. Прикладная физика и математика № 5, 3-17 (2013) стр.15, рис. 66

[33] Mazhukin V.I., Samokhin A.A., Shapranov A.V., Demin M.M. Modeling of thin film explosive boiling - surface evaporation and electron thermal conductivity effect. Mater. Res. Express 2 016402 (2015)

[34] Mazhukin V.I., Samokhin A.A., Shapranov A.V., Ivochkin A.Yu. Modelirovanie vzryvnogo vskipanija tonkoy plenki pri odnorodnom subnanosekundnom nagreve. Matematicheskoe Modelirovanie, 26, 125 (2014) (in Russian)

[35] Mazhukin V.I., Shapranov A.V., Samokhin A.A., Mazhukin A.V., Koroleva O.N. Visualization and analysis of the results of molecular-dynamic modeling of intensive evaporation of liquid in the near-critical region. Scientific Visualization, 6 (4) pp.72-95 (2014)

[36] Mazhukin V.I., Demin M.M., Shapranov A.V. Continuum modeling of pulsed laser fragmentation ja the metal with the homogeneous melting. 12th Int. Conf. On Laser Ablation (Cola 2013) Book of abstracts, 151 (2013)

[37] Mazhukin V.I., Samokhin A.A., Shapranov A.V., Ivochkin A.Yu. Modeling of thin film explosive boiling – surface evaporation effect. 12th Int. Conf. On Laser Ablation (Cola 2013) Book of abstracts, 152 (2013)

[38] Mazhukin V.I., Samokhin A.A., Shapranov A.V., Demin M.M. Vzryvnoe vskipanie metallov pod dejstviem nanosekundnogo lazernogo impul'sa. Kvantovaja Elektronika, 44 283 (2014) (in Russian)

[39] Mazhukin V.I., Samokhin A.A., Demin M.M., Shapranov A.V. Modeling of nanosecond laser vaporization and explosive boiling of metals. Mathem. Montisnigri. 29, 68 – 90. (2014).

[40] Mazhukin V.I., Samokhin A.A., Shapranov A.V., Demin M.M., Pivovarov P.A. On Different Regimes of Condensed Matter Ablation Depending on Intensity and Duration of Absorbed Electromagnetic Pulses. PIERS Proceedings, 2418 - 2421, July 6-9, Prague, 2015

[41] Каганов М.И., Лифшиц И.М., Танатаров Л.В. Релаксация между электронами и кристаллической решеткой. ЖЭТФ 31: 2(8)/232-237 (1956)

[42] Каганов М.И., Лифшиц И.М., Танатаров Л.В. К теории радиационных изменений в металлах. Атомная энергия 6/391-402 (1959)

[43] Anisimov S.I., Kapeliovich B.L., Perelman T.L. Electron emission from metal surfaces exposed to ultrashort laser pulses. Sov. Phys. JETP 39(2), 375-377 (1974) ЖЭТФ, 66 (2), 776-779 (1974)

[44] Гордеев Г.В. Низкочастотные колебания плазмы. ЖЭТФ 1(7) 19-23 (1954)

[45] Mazhukin V.I., Samokhin A.A. Boundary conditions for gas-dynamical modeling of evaporation processes. Mathem. Montisnigri. 24, 8-17 (2012)

[46] Samokhin A.A., Pivovarov P.A. On spinodal manifestation during fast heating and evaporation of thin liquid film. Mathem. Montisnigri. 33, 125- 128 (2015)

[47] Хомкин А.Л., Шумихин А.С. Критические точки паров металлов. ЖЭТФ, 148, 3(9), 597 (2015)

[48] Sokolowski-Tinten K., Bialkowski J., Cavalleri A., von der Linde D., Oparin A., Meyer-ter-Vehn J., Anisimov S.I. Transient States of Matter during Short Pulse Laser Ablation. Phys. Rev. Lett. 81, 224 (1998)

MODELING AND VISUALIZATION OF NANOSECOND LASER VAPORIZATION OF METALS IN NEAR CRITICAL REGION

V.I. Mazhukin^1,3, A.A. Samokhin², A.V. Shapranov^1,3, M.M. Demin¹, P.A. Pivovarov^2,3

¹Keldysh Institute of Applied Mathematics, RAS, Moscow, Russia

²A.M. Prokhorov General Physics Institute, RAS, Moscow, Russia

³National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Moscow, Russia

vim@modhef.ru, asam40@mail.ru, p_pivovvarov@hotmail.com

Abstract

Results and their visualizations are presented for the case of nanosecond laser ablation of a metal liquid film at different incident laser intensities G = 38.5, 44, 88 and 154 MW/cm². The ablation of an Al film (thickness 430nm, initial particle number 5×10⁵) including subcritical to supercritical states is investigated with the help of the classical molecular dynamic method and continual description of a conduction electron subsystem. Behavior of a thinner metal film (48nm) is also investigated at G = 29 MW/cm² and G = 51 MW/cm² (5 and 8,8 K/ps). 3D calculation results are given in the form of 2D particle distribution snapshots as well as temperature, density, pressure and particle velocity 1D distributions. As in the previously considered case of dielectric films for metal films four different ablation regimes are observed depending on the laser intensity: quasi-stationary surface evaporation, explosive (volume) boiling, spinodal decomposition and supercritical fluid expansion. Changes in space-time behavior of the density fluctuations in these regimes are clearly seen from the presented visualizations. Explosive boiling realization in metal ablation is not evident beforehand because of the high values of the thermal conductivity and absorption coefficients which can impede the manifestation of the process. Recoil pressure pulses that are caused by explosive boiling can be used as experimental markers of getting closer to the critical region while the critical region transition is characterized by the disappearance of the pressure pulsation.

Keywords: laser ablation, molecular dynamics, explosive boiling, spinodal decomposition, supercritical expansion.

References

[1] Batanov V.A., Bunkin F.V., Prokhorov A.M., Fedorov V.B. Evaporation of metallic targets caused by intense optical radiation. Sov. Phys. JETP 36, 311 (1973). ЖЭТФ 63, 586 (1972).

[2] Karapetjan R.V., Samohin A.A. Vlijanie prosvetlenija na rezhim razvitogo isparenija metallov pod dejstviem opticheskogo izluchenija [Effect of illumination on the mode of developed evaporation of metals under the influence of optical radiation]. Sov. J. Quantum Electron., 4, 9, 1141 (1975)