ИСПОЛЬЗОВАНИЕ СРЕДСТВ ВИЗУАЛИЗАЦИИ В ПРОГНОЗАХ ПОВРЕЖДЕНИЙ КОМПОЗИТНЫХ КОЛОНН С ЖЕСТКОЙ АРМАТУРОЙ

Г.Г. Кашеварова¹, А.С. Мартиросян², В.И. Травуш³

¹ Пермский Национальный Исследовательский Политехнический Университет (ПНИПУ), Пермь, Россия

² Пермский Национальный Исследовательский Политехнический Университет (ПНИПУ), Пермь, Россия

³ Российская Академия Архитектуры и Строительных Наук (РААСН), Москва, Россия

¹ggkash@mail.ru, ²anka_31@mail.ru, ³travush@mai.ru

 

Содержание

1. Введение

2. Модель колонны с линейными свойствами материалов

3. Модель, учитывающая нелинейные свойства бетона

4. Модель, учитывающая контактное взаимодействие на границе «жесткая арматура – бетон»

5. Модель колонны с учетом дополнительной гибкой арматуры

6. Выводы

Список литературы

 

Аннотация

Данная работа посвящена моделированию и  визуализации процесса деформирования и разрушения конструкции железобетонных колонн с жесткой арматурой.  Исследования дают возможность непосредственно увидеть распределение напряжений и деформаций на поверхности и внутри колонны, визуально представить зоны появления и распространения трещин при использовании разных расчетных моделей. Это необходимо при верификации результатов расчетов с натурными экспериментами.

Колонны нижних этажей многоэтажных высотных зданий воспринимают значительные нагрузки 10000 тонн и более. Эти нагрузки вызывают не только сжатие колонн, но и изгиб, вызванный случайными эксцентриситетами. Для армирования таких колонн целесообразно наряду с гибкой арматурой применять жесткую арматуру.

Традиционно совместная работа арматуры и бетона в конструкции обеспечивается за счет рифления на поверхности гибкой арматуры. На жесткой арматуре такое рифление отсутствует, поэтому требуется исследование о совместной работе этой арматуры с бетоном.

В статье рядом расчётных моделей проиллюстрировано использование средств визуализации для анализа процесса деформирования и разрушения конструкции колонны: 1 - модель колонны,  в которой учитывались только жесткая арматура и бетон с линейными свойствами обоих материалов; 2 - та же модель, но с учетом нелинейных свойств бетона (возможности растрескивания и раскрашивания); 3 - та же модель, но с учетом нелинейных свойств бетона  и контактного взаимодействия «металл – бетон»; 4 - нелинейная модель колонны с включением кроме жесткой, дополнительной гибкой арматуры.

Показано влияние на несущую способность  конструкции всех компонентов (жесткой и гибкой арматуры), нелинейных свойств материалов, учета контактного взаимодействия элементов. Указано на расхождение результатов расчета по различным моделям и возможность выбора на основании этого более адекватной расчетной модели.

 

Ключевые слова: численное моделирование, расчетная модель, железобетонная колонна с жесткой арматурой, контактное взаимодействие.

 

 

1. Введение

 

Тенденция развития мировой строительной индустрии обусловлена появлением большого количества высотных зданий со сложными несимметричными формами. Следуя мировым тенденциям высотного домостроения, в России в последние 20 лет были утверждены и реализуются следующие программы: строительство Московского международного делового центра «Москва-Сити»; проект строительства делового квартала «Лахта Центр» в Санкт-Петербурге. В других крупных городах России также проектируются и строятся высотные здания оригинальных архитектурных форм и конструктивных решений (гг. Екатеринбург, Владивосток, Казань, Тюмень, Пермь, Красноярск и др).

Колонны нижних этажей многоэтажных высотных зданий воспринимают значительные нагрузки, достигающие 10000-15000т, а иногда и более. Эти нагрузки вызывают не только сжатие колонн, но и изгиб, вызванный случайными эксцентриситетами. Для армирования таких колонн целесообразно наряду с гибкой арматурой применять жесткую арматуру, например, в виде двутавров, создавая, таким образом, композитную конструкцию.

Известно, что один из ключевых факторов, обеспечивающих совместную работу арматуры и бетона в конструкции и позволяющих работать двухкомпонентному железобетону как единому материалу, является сцепление арматуры с бетоном. Традиционно это обеспечивается за счет рифления на поверхности арматуры, что обеспечивает сопротивление бетона смятию и срезу [2, 3]. На жесткой арматуре такое рифление отсутствует, поэтому требуется исследование о совместной работе этой арматуры с бетоном.

Для выполнения расчетов и анализа реальная физическая модель исследуемого объекта заменяется некоторой аппроксимирующей моделью, которая должна отражать основные особенности поведения его под нагрузкой и позволять определять запасы прочности и (или) вероятность разрушения. Целесообразно рассматривать не одну модель, а систему аппроксимирующих моделей [4] для того, чтобы понять необходимость их усложнения, доступного современной вычислительной технике. Визуализация процесса деформирования и разрушения конструкции железобетонных колонн с жесткой арматурой позволяет непосредственно увидеть распределение напряжений и деформаций на поверхности и внутри колонны, визуально представить зоны появления и распространения трещин при использовании разных расчетных моделей. Такого рода вычислительные эксперименты с визуализацией позволяют определить, не является ли расхождение между расчетом и экспериментом следствием неудовлетворительной идеализации [5].

Далее рядом расчётных моделей проиллюстрировано использование средств визуализации для анализа процесса деформирования и разрушения конструкции колонны высотного здания с жесткой стальной арматурой из двух накрест расположенных двутавров и гибкой арматурой в виде вертикальных стержней и хомутов (рис.1).

Высота колонны – 8,4 м. На колонну действует вертикальная нагрузка Р = 14970 т, приложенная с эксцентриситетом, создающим моменты Мх = Му = 840 тм.

 

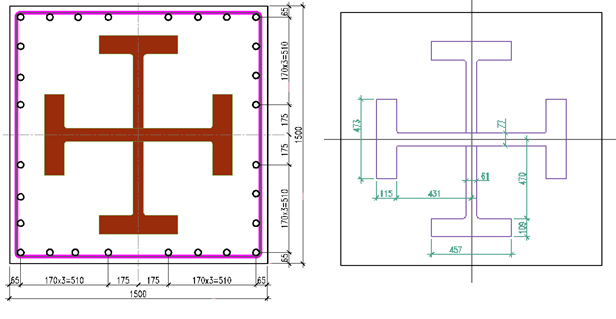
Рис.1. Геометрия колонны в плане

 

Математическая постановка краевой задачи определяется уравнениями равновесия, физическими и геометрическими соотношениями и граничными условиями. Для численной реализации краевой задачи использовался метод конечных элементов  и программный комплекс ANSYS [1], верифицированный в Российской академии архитектуры и строительных наук. Для создания моделей и расчета создавались макросы на языке APDL, встроенном в ПК  ANSYS.

Изучение процессов деформирования и разрушения конструкции в условиях сложного напряженного состояния с  учетом деформационного разупрочнения и структурного разрушения требует использования адекватных математических моделей механического поведения материалов и  высокой детализации компонентов конструкции. Это достаточно трудоемкая задача на этапе препроцессинга, и целесообразность такой детализации необходимо оценить.

В рамках данного исследования выполнено сравнение 4-х вариантов расчетных моделей колонны, приведенных ниже, в порядке усложнения реализации.

В расчетах использовались следующие значения основных констант, определяющих механические свойства материалов:

 

Таблица1. Механические свойства материалов

 

2. Модель колонны с линейными свойствами материалов

 

Решение краевой задачи с линейными определяющими соотношениями выполнялось методом конечных элементов в вариационной постановке. Предварительный линейный анализ способен показать наиболее опасные места расчетной модели, в которых возможно разрушение конструкции.

Для моделирования жесткой арматуры и бетона использовался пространственный конечный элемент SOLID45 (3-D 8-узловой элемент). Компьютерная модель колонны и конечно-элементные модели выделенных компонентов бетона и жесткой арматуры показаны на рис. 2. В данной модели сцепление арматуры с бетоном в области контакта считалось полным.

Граничные условия: нижняя грань закреплялась по всем координатам. На верхнюю грань прикладывалась нагрузка Р с эксцентриситетом. При этом узлы верхней грани объединялись по перемещениям в направлении z и углам поворота относительно осей x и y.

 

 

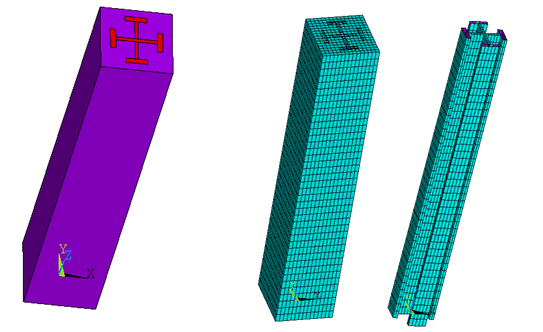
Рис.2. Компьютерная модель колонны и конечно-элементные модели выделенных компонентов бетона и жесткой арматуры

 

Результаты решения задачи представлены на рис. 3, 4. Показаны изополя напряжений  (SZ – обозначение в ПК ANSYS) и перемещений.

 

 

    

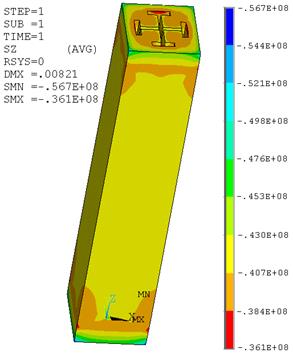
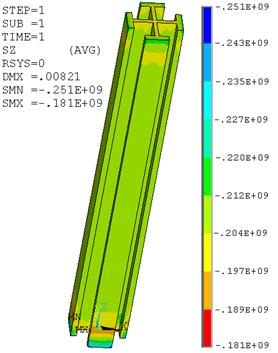
Рис. 3. Изополя напряжений (Па), в бетоне и жесткой арматуре

 

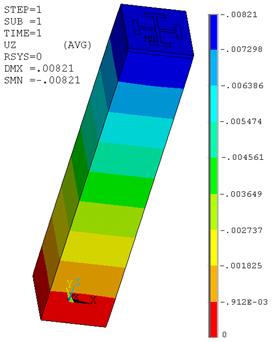
Рис. 4. Вертикальные перемещения  колонны

 

Для оценки сходимости расчеты выполнялись на двух сетках конечных элементов с общим числом степеней свободы 51660 и 312255. Практическая сходимость имеет место по перемещениям, погрешность по напряжениям находится в пределах 2-12%. Далее расчеты выполнялись на первой сетке, что дает большой выигрыш в скорости счета.

Результаты расчетов показали, что напряжения в бетоне превышают расчетный предел прочности.

 

3. Модель, учитывающая нелинейные свойства бетона

 

Известно, что бетон может работать в упругой области или проявлять нелинейные свойства (трещинообразование, пластичность, ползучесть), которые по-разному проявляются в разных конструкциях на разных этапах работы. Для конструкции, рассматриваемой в данной работе, мы исследовали возможность трещинообразования, и поэтому приняли математическую модель, ориентированную на описание упруго-хрупкого поведения бетона, разработанную K.J. Willam и E.D Warnke [6], учитывающую накопление структурных повреждений и деформационное разупрочнение, в которой предполагается, что изначально материал является изотропным, а разрушаясь, становится ортотропным. При этом коэффициенты жесткости  в определяющих соотношениях при появлении трещин изменяются скачком. «Трещина» - это образование в бесконечно малом элементе среды зоны со сниженными механическими характеристиками в результате накопления повреждений.

Появление «трещины» в плоскости, перпендикулярной одной из координатных осей x_i приводит к падению жесткости материала в данном направлении. Для каждой трещины  рассматривалось два состояния: трещина открыта или закрыта. Критерии открытия – закрытия трещины определяются в точке материала на поверхности трещины. Используя понятия о модулях упругости и коэффициентах Пуассона вместо упругой константы Е_i – вводится переменная величина , зависящая от уровня деформации, коэффициенты Пуассона приравниваются нулю. Кроме того, в соответствующие сдвиговые жесткости вводится понижающий коэффициент  (трещина открыта) или  (трещина закрыта), который косвенно учитывает трение по поверхностям трещины.

Раскрашивание (дробление) материала – это изменение структурной целостности материала, эквивалентное полной потере жесткости при одноосном, двухосном, или трехосном сжатии, при этом соответствующие коэффициенты жесткости .

В общем случае сложного напряженного состояния для упруго-хрупкого материала можно предположить, что разрушение происходит, когда интенсивность напряжений (второй инвариант тензора напряжений) достигает критического значения [7]. В этом случае материал теряет способность сопротивляться формоизменению и гидростатическому растяжению, сохраняя способность сопротивляться гидростатическому сжатию (если такой вид напряженного состояния возникнет после перераспределения напряжений и при дальнейшем деформировании).

При моделировании бетона использовался пространственный 8-узловой конечный элемент SOLID65, специально предназначенный для моделирования бетона и железобетона, способного к растрескиванию при растяжении и дроблению при сжатии.

Для численной реализации краевой задачи с нелинейными определяющими соотношениями использовался алгоритм пошагового решения. На каждом шаге для получения сходимости выполнялись равновесные итерации с помощью метода Ньютона – Рафсона. Проверка сходимости производилась с использованием евклидовой нормы для сил и перемещений по всем степеням свободы.

Вид деформированной колонны, полученный в результате расчета напряженно-деформированного состояния, свидетельствует о возможной потере устойчивости конструкции (рис. 5). На  рис. 6 показана картина распространения трещин в бетоне колонны.

 

Рис. 6. Картина трещин в колонне

 

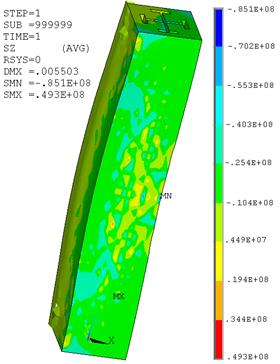
Рис. 5. Вид деформированной колонны и изополя напряжений

 

В данном случае при переходе конструкции в новое устойчивое состояние  при расчете возникли проблемы со сходимостью [1], и было выполнено уточнение модели деформирования бетона при сжатии.

В соответствии с рекомендациями свода правил СП 63.13330.2012 «Бетонные и железобетонные конструкции», в качестве рабочей диаграммы состояния тяжелого бетона, определяющей связь между напряжениями и относительными деформациями, была принята трехлинейная диаграмма. Для улучшения сходимости при реализации в ANSYS применялась модель CONCRETE с учетом кинематического упрочнения KINH, позволяющая учесть ниспадающую ветвь диаграммы деформирования (рис. 7).

Это соответствует реальному поведению бетонных конструкций, способных воспринимать внешнюю нагрузку при наличии систем трещин и разрывов. Наличие отдельных трещин – это еще не разрушение конструкции. Накапливаясь, трещины могут привести к потере несущей способности конструкции. Однако этот момент не является внезапным, а является результатом накопления повреждений на разных структурных уровнях [8]. Нелинейный расчет выполнялся методом Ньютона-Рафсона с использованием полной процедуры NROPT,FULL и автоматическим выбором шага. Для улучшения сходимости применена несимметричная схема хранения матриц.

 

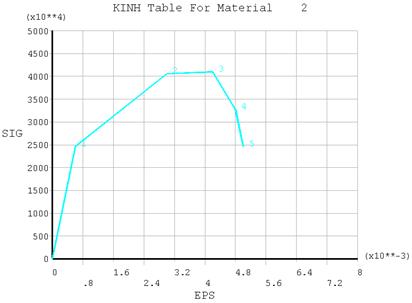
Рис.7. Диаграмма деформирования бетона при сжатии

 

В результате расчета изменился вид деформированного состояния колонны, потери устойчивости здесь не наблюдается (рис. 8).  Изменилось распределение напряжений  в колонне, а также картина трещин в бетоне.

 

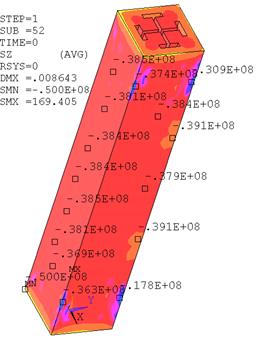
Рис. 8. Изополя напряжений в колонне (без учета гибкой арматуры)

 

На рис. 8 видно, что напряжения в бетоне превышают расчетный предел прочности лишь в отдельных зонах, в отличие от линейного расчета.

На рис. 9. показан пошаговый процесс развития трещин в зависимости от нагрузки.

 

            

Рис. 9. Процесс развития трещин в бетоне колонны без учета гибкой арматуры

 

4. Модель, учитывающая контактное взаимодействие на границе «жесткая арматура – бетон»

 

Приведенные выше результаты расчета показали, что в бетоне при нагружении возникают трещины, которые могут способствовать нарушению сцепления жесткой арматуры с бетоном. Поэтому далее рассмотрена модель, учитывающая и возможность появления трещин в бетоне, и контакт на границе «металл – бетон».

Решалась контактная задача типа “поверхность-поверхность” для проверки обеспечения совместной работы бетона и жесткой арматуры, на которой отсутствует рифление, в конструкции при заданном внешнем воздействии. Для моделирования контактного взаимодействия использовались элементы: CONTACT173 и TARGET170.

 

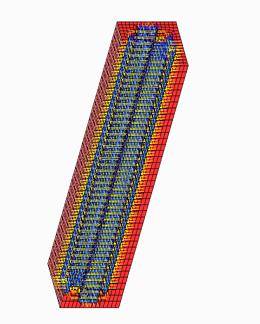
Рис. 10. Контактные элементы CONTACT173 и TARGET170

 

Контакт в программе ANSYS представлен последовательным положением точек на одной поверхности контакта – CONTACT относительно линий и областей поверхности внедрения - TARGET (рис.10). Поверхностью внедрения назначается более жесткая поверхность, т.е. поверхность жесткой арматуры, поверхностью контакта  - поверхность бетона. Задавался начальный контакт со склеиванием (опция KEYOPT (12)=6).

Программа использует элементы контакта для отслеживания относительных положений двух поверхностей [1, 9].

Расположение и перемещение контактных элементов относительно связанных с ними ответных поверхностей при действии нагрузки определяют статус контактных элементов.

Решение задачи показало, что все контактные элементы для данного загружения имеют статус 3 – контакт с прилипанием.

На рис. 11, 12 приведены результаты расчета контактного давления в направлении нормали на границе «металл – бетон» и величин зазора в зоне контакта, а на рис. 13, 14 показаны  изополя  напряжений  и картина трещин в бетоне.

 

    

Рис. 11. Нормальное контактное давление на границе «металл – бетон»

 

                

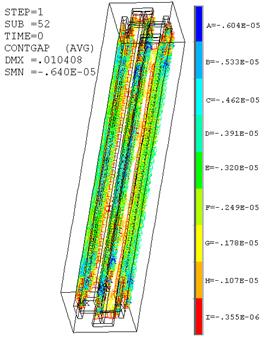
Рис. 12. Величины зазора в зоне контакта

 

      

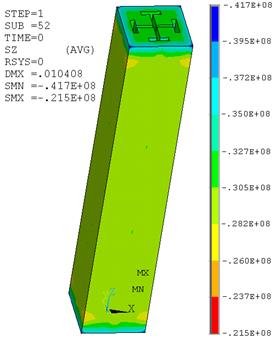
Рис. 13. Изополя напряжений в бетоне

 

            

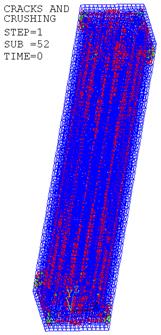
Рис. 14. Картина трещин в бетоне

 

5. Модель колонны с учетом дополнительной гибкой арматуры

 

Реальная конструкция колонны кроме жесткой арматуры обязательно включает гибкую арматуру [10] в виде вертикальных гибких стержней и хомутов (см. рис.1).

Гибкая арматура может быть смоделирована:

1) слоем железобетона с эффективными физико-механическими характеристиками, либо

2) непосредственным моделированием вертикальных стержней и хомутов в бетоне.

 

Рис.15. Конечно-элементная модель слоя железобетона и жесткой арматуры

 

На рис 15 показан первый вариант модели, возможность применения которого обеспечена в ПК ANSYS при использовании  конечного элемента SOLID65.

Эффективные характеристики тензора жесткости железобетона определяются, как смесь упругих характеристик компонент с учетом их направлений по формулам:

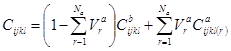,             (1)

где N_a – номер армирующего материала;  - относительная объемная доля материала арматуры r-го типа;  - симметричный тензор жесткости изотропного материала бетона, ненулевые компоненты которого равны:

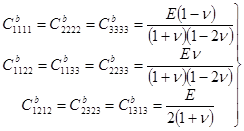;                      (2)

а с учетом структурного разрушения его компоненты зависят от направления и количества трещин [6, 7].

 - компоненты тензора жесткости арматуры r - го типа, известным образом [7] преобразованные из локальной системы координат , связанной с конкретным типом арматуры, к глобальной декартовой системе координат . В локальных координатах тензор  имеет одну ненулевую компоненту , равную модулю упругости материала арматуры r - го типа (ось  совпадает с направлением укладки арматуры).

Осреднение жесткостей в данном случае достаточно обосновано, так как предполагается полное прилипание всех компонент материала между собой [11, 12].

Результаты, полученные при решении этой нелинейной задачи, также показали наличие трещин в бетоне. Но эти трещины сосредоточены только в верхней и нижней зонах колонны (рис.16).

 

 

                             

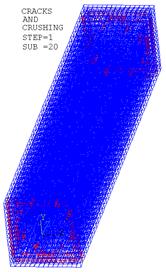
Рис. 16. Пошаговый процесс развития трещин в бетоне колонны

 

На рис. 17, 18  приведены изополя напряжений в бетоне, жесткой арматуре и в армированном слое.

 

             

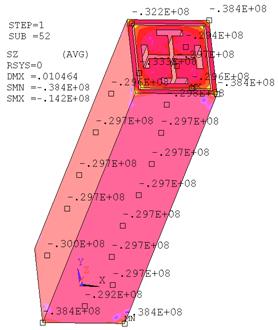
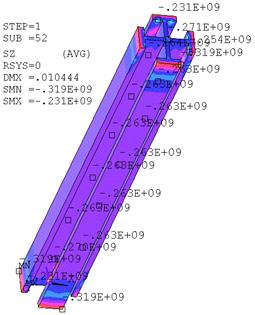
Рис.17. Напряжения в бетоне и жесткой арматуре

 

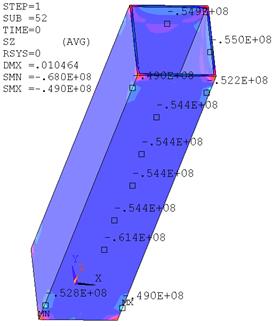
Рис.18. Напряжения в армированном слое

 

Результаты нелинейного расчета колонны с непосредственным моделированием вертикальных стержней и хомутов в бетоне (рис. 20) представлены на рис. 19, 21, 22.

 

 

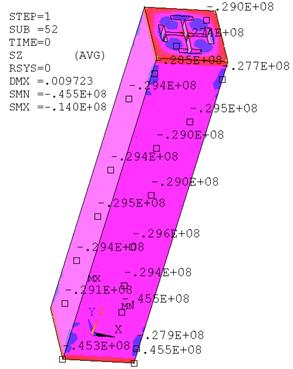
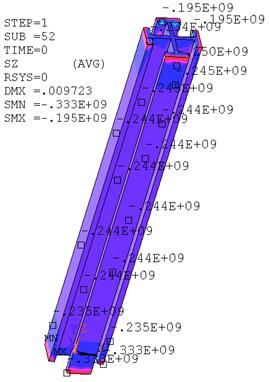
Рис.19. Напряжения в бетоне и жесткой арматуре

 

    

Рис. 20. Гибкая арматура

 

         

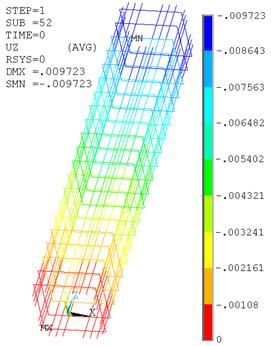
Рис. 21. Перемещения в гибкой арматуре

 

     

Рис. 22. Процесс развития  трещин в бетоне с включением гибкой арматуры

 

При учете гибкой арматуры напряжения в бетоне и арматуре для двух вариантов моделей, рассмотренного загружения и заданных классов бетона и арматуры, получились ниже расчетных значений, за исключением особых точек, что связано с математической сингулярностью. Разница результатов в этих моделях не превышает 3%. Обе эти модели можно использовать для расчета, хотя с точки зрения трудоемкости моделирования на этапе препроцессинга,  первый вариант предпочтительней.

В целом эти расчеты подтверждают требуемую прочность сечения колонны.

 

6. Выводы

 

1. Визуализация процесса деформирования и разрушения конструкции железобетонных колонн с жесткой арматурой позволила непосредственно увидеть распределение напряжений и деформаций на поверхности и внутри колонны, визуально представить зоны появления и распространения трещин при использовании разных расчетных моделей.
2. Линейный конечно-элементный анализ дал возможность определить наиболее опасные зоны в конструкции бетонной колонны с жесткой арматурой.
3. Моделирование с учетом нелинейных свойств бетона  по принятой диаграмме деформирования позволило получить картину трещинообразования. В дальнейшем  целесообразно  использовать диаграммы деформирования бетона при сжатии, учитывающие накопление повреждений и ниспадающую ветвь.
4. Учет контактного взаимодействия на границе жесткой арматуры и бетона дает возможность оценить совместную работу композита. При рассмотренном виде нагружения и учете трещинообразования наблюдается практический контакт с прилипанием, хотя появление трещин в бетоне в какой-то мере способствует нарушению сцепления с металлом.
5. Гибкая арматура, хотя и воспринимает относительно небольшую часть сжимающей нагрузки,  существенно влияет на восприятие изгибающих моментов в колонне. 
6. Моделирование гибкой арматуры в виде  в виде слоя железобетона с эффективными физико-механическими характеристиками и модель в виде вертикальных стержней и хомутов в бетоне дают достаточно близкие результаты по напряжениям (разница не более 3%), хотя картина трещинообразования  несколько отличается. Во втором случае она ближе к реальной картине разрушения. Но с точки зрения трудоемкости моделирования на этапе препроцессинга, первый вариант предпочтительней.

 

 

Список литературы

 

1. Басов К.А. ANSYS. Справочник пользователя. М.: изд-во ДМК Пресс, 2005 г.-640 с.

2. Попов Н.Н., Чарыев М. Железобетонные и каменные конструкции. М.: Высшая школа, 1996. 255 с.

3. Бенин А.В., Семенов А.С., Семенов С.Г., Мельников Б.Е. Математическое моделирование процесса разрушения сцепления арматуры с бетоном. Часть 1. Модели с учетом несплошности соединения. Инженерно-строительный журнал, №5, 2013. с. 88-144.

4. Перельмутер А.В., Сливкер В.И. Расчетные модели сооружений и возможность их анализа. – М.: ДМК Пресс, 2007. – 699с.

5. Блехман И.И., Мышкис А.Д., Пановко Я.Г. Механика и прикладная математика: Логика и особенности приложений математики. 2-е изд. – М.: Наука, 1990. – 360 с.

6. Willam K.J., Warnke E.D. Constitutive Model for the Triaxial Behavior of Concrete. Proceedings, International Association for Bridge and Structural Engineering. Vol.19. ISMES. Bergamo, Italy. Р.174 (1975).

7. Кашеварова Г.Г., Труфанов Н. А. Численное моделирование деформирования и разрушения системы «здание-фундамент-основание». Екатеринбург – Пермь: УрО РАН, 2005, 225с.

8. Вильдеман В.Э., Соколкин Ю.В., Ташкинов А.А. Механика неупругого деформирования и разрушения композиционных материалов. М.:Наука. Физматгиз, 1997. 288с.

9. Морозов Е.М., Муйземнек А.Ю., Шадский А.С. ANSYS в руках инженера. Механика разрушения. – М.: ЛЕНАНД, 2008. 456 с.

10.  Schnobrich, W. C., Suidan, M. Finite Element Analysis of Reinforced Concrete. ASCE Journal of the Structural Division, ST10. Р. 2109-2122 (October, 1973).

11.  Кравчук А.С., Майборода В.П., Уржумцев Ю.С. Механика полимерных и композиционных материалов. М.: Наука, 1985. 304с.

12.  Пинежанинов Ф. Осреднение свойств в конечном элементе. Научно-практический журнал "Exponenta Pro. Математика в приложениях". № 1, – 2004. http://pinega.da.ru/

---

USE OF IMAGING IN THE FORECASTS OF COMPOSITE COLUMNS DAMAGE WITH STIFF REINFORCEMENT

G.G. Kashevarova¹, A.S. Martirosyan², V.I. Travush³

 ¹ Perm National Research Polytechnic University (PNIPU), Perm, Russia

 ² Perm National Research Polytechnic University (PNIPU), Perm, Russia

 ³ Russian Academy of Architecture and Construction Sciences (RAASN), Moscow, Russia

¹ggkash@mail.ru, ²anka_31@mail.ru, ³travush@mai.ru

 

Abstract

This work is devoted to modeling and visualization of the deformation and fracture design process of reinforced concrete columns with a rigid fixture. Studies allow directly see the distribution of stresses and strains on the surface and inside the column, zone visualize the appearance and propagation of cracks using various calculation models. It is necessary for the verification of the results of calculations with field experiments.

Columns of the lower floors of multi-storey high-rise buildings perceive significant load of 10,000 tons or more. These loads are not only compression columns, but bending caused by accidental eccentricities. To reinforce columns it  is advisable to apply a rigid reinforcement along with a flexible fitting.

Traditionally joint work of reinforcement and concrete in construction is provided by the corrugations on the surface of the flexible fittings. On a rigid fixture there is no such corrugation, therefore a study of the joint work of the reinforcement and concrete is required.

In this paper a number of computational models is illustrated by the use of visualization tools to analyze the process of deformation and fracture of column design: 1 - column model, which takes into account only the rigid reinforcement and concrete with linear properties of both materials; 2 - the same model, but with the nonlinear properties of concrete (the possibility of cracking and crashing); 3 - the same model, but with the non-linear properties of the concrete and the contact interaction of "metal - concrete"; 4 - the nonlinear model of the column including the more flexible fitting except a tight one.

The effect on the bearing capacity of the structure of all components (rigid and flexible reinforcement), the nonlinear properties of materials, taking into account contact interaction of elements is shown. The discrepancy between the results of numerical simulation and the possibility of simplifying the calculation model is given.

 

 Keywords: numerical modeling, computational model, reinforced concrete column with a tight fitting, contact interaction.

 

References

1. Basov K.A.  ANSYS. Spravochnik polzovatelya.  [Manual]. M .: DMK Press, 2005. -  640 p.

2. Popov N.N., Charyev M. Zhelezobetonnie i kamennie konstrukcii.  [Reinforced concrete and stone structures]. M .: High School, 1996. 255 p. [In Russian]

3. Benin A.V., Semenov A.S., Semenov S.G., Melnikov B.E. Matematicheskoe modelirovanie  processa  razrusheniya  scepleniya armature s betonom. Chast 1. Modeli s uchetom nesploshnosti soedineniya. [Mathematical modeling of bond failure of reinforcement with concrete.  Part 1: Models with the discontinuity connection].  Inzhenerno-stroitelnii zhurnal.  [Civil Engineering magazine], №5, 2013. p. 88-144. [In Russian]

4. Perel'muter A.V.,  Slivker V.I.  Raschetnie modeli sooruzhenii I vozmozhnost  ih analiza. [Computational models of structures and the possibility of their analysis]. M .: DMK Press, 2007. 699p. [In Russian]

5. Blehman I.I., Mishkis A.D., Panovko I.G. Mehanika i prikladnaya mathematika: Logika i osobennosti prilozhenii mathematiki. 2-e izd. [Mechanics and Applied Mathematics: Logic and particularly applications of mathematics. 2nd edition ]. M.: Nauka, 1990. 360s. [In Russian]

6. Willam K.J., Warnke E.D. Constitutive Model for the Triaxial Behavior of Concrete. Proceedings, International Association for Bridge and Structural Engineering. Vol.19. ISMES. Bergamo, Italy. R.174 (1975).

7. Kashevarova G.G., Trufanov N.A. Chislennoe modelirovanie deformirovaniya  i  razrusheniya sistemi “zdanie – fundament – osnovanie. [Numerical simulation of deformation and failure of the "building- foundation –soil"]. Ekaterinburg - Perm, Ural Branch of Russian Academy of Sciences, 2005. -  225 p. [In Russian]

8. Vildeman V.E., Sokolkin U.V., Tashkinov A.A.  Mechanika neuprugogo leformirovaniya  i  razrusheniya kompozicionnih materialov. [The mechanics of inelastic deformation and fracture of composite materials]. Moscow: Nauka. Fizmatgiz, 1997. - 288p.  [In Russian]

9. Morozov E.M., Muyzemnek A.Y., Shadsky A.S.  ANSYS  v rukah inzhenerov. Mechanika razrusheniya. [ANSYS in the hands of the engineer. Fracture mechanics]. M .: LENAND, 2008. 456 p. [In Russian]

 10. Schnobrich, WC, Suidan, M. Finite Element Analysis of Reinforced Concrete. ASCE Journal of the Structural Division, ST10. R. 2109-2122 (October, 1973).

 11. Kravchuk  A.S., Mayboroda V.P., Urzhumtsev Y.S. Mechanika polimernih I kompozicionnih materialov [ Mechanics of polymer and composite materials]. M.: Nauka, 1985. 304c. [In Russian]

 12. Pinezhaninov F. Osrednenie svoistv v konechnom elemente. [Averaging properties in finite element]. Scientific journal "Exponenta Pro. Mathematics in Applications." Number 1, - 2004. http://pinega.da.ru/. [In Russian]