ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК ПОВЕРХНОСТНОГО ВОЛНЕНИЯ МЕТОДАМИ ЦИФРОВОЙ ВИЗУАЛИЗАЦИИ В РАМКАХ ЛАБОРАТОРНОГО МОДЕЛИРОВАНИЯ ВЗАИМОДЕЙСТВИЯ АТМОСФЕРЫ И ОКЕАНА.
Д.А. Сергеев1,2, А.А. Кандауров1,2, М.И. Вдовин1,2, Ю.И. Троицкая1,2
1Институт прикладной физики РАН, Россия
2ННГУ им. Н.И. Лобачевского
Содержание
2. Описание аппаратной части системы и особенностей получения видеоизображений поверхностных волн.
3. Описание алгоритмов обработки видеоизображений волн, поиска границы поверхности.
4. Схема экспериментов и Измерений. полученные результаты.
Аннотация
Предложена и реализована в лабораторном эксперименте новая методика определения формы взволнованной водной поверхности. Исследования проводились в рамках моделирования ветро-волнового взаимодействия в пограничных слоях атмосферы океана. Методика основана на применении лазерной подсветки совместно со скоростной видеосъемкой и специальными алгоритмами анализа изображений. Она позволяет находить форму поверхности на отдельных кадрах с высокой точностью и пространственным разрешением, в том числе для случая интенсивного обрушения волн с образованием пены и брызг. На основе накопленного ансамбля реализаций удалось найти средние спектры по волновым числам коротковолновой части соответствующей эффектам, связанным с обрушением волн. Эти данные дополняют спектры длинноволновой части волнения, полученным с помощью струнных волнографов.
Ключевые слова: ветер, обрушение волн, визуализация, лабораторное моделирование
1. Введение
Лабораторное моделирование является одним из основных инструментов при исследовании процессов взаимодействия воздушных потоков атмосферы с поверхностным волнением океана (см. [1-3]). Параметры шероховатости поверхностного волнения (формы волны) являются определяющими для аэродинамического сопротивления воздушному потоку и описания обмена импульсом в пограничном слое. Особую роль в этих процессах играет обрушение волн появляющееся при сильных ветрах (экстремальные гидрометусловия) (см. [4, 5]). Исследование взаимодействия волн с ураганными ветрами в лабораторных экспериментах является весьма важным, т.к. подобных данных, на которых построены имеющиеся теоретические модели, накоплено недостаточно и они характеризуются сильным разбросом (не являются достоверными).
Одной из главных задач при проведении экспериментов по исследованию ветро-волнового взаимодействия является измерение характеристик поверхностного волнения. Для исследования процессов обрушения ветровых волн необходимо иметь возможность измерять не только временные, но и пространственные характеристики взволнованной поверхности с высокой точностью. Методы можно условно разделить: 1) измерение возвышений водной поверхности в фиксированных точках 2) измерение формы поверхности волны путем анализа ее фото видеоизображений.
В качестве датчиков для измерений первого типа обычно используют хорошо зарекомендовавшие себя струнные волнографы (см. [3]), а также лазерные измерители уровня поверхности (см. [1]). С их помощью можно измерить временные характеристики колебаний, а затем получить частотные спектры поверхностного волнения. При использовании нескольких разнесенных в пространстве датчиков и специального метода обработки WDM (подробное описание см. в [6]) можно найти и пространственные характеристики поверхностного волнения, включая спектры по волновым числам. Однако, они позволяют находить возмущения с характерным масштабом не менее 3 - 4 10-2 м. Подобные и более мелкие возмущения образуются при обрушении гребней длинных волн. Как было показано в работе [7] учет этой коротковолновой части возмущений (шероховатости поверхности) принципиально необходим для правильного нахождения коэффициента сопротивления воздушному потоку.
Измерение формы поверхности по анализу изображений волн (чаще всего сбоку) проводится уже достаточно давно (см. [8]). В отличие от точечных методов измерений они сразу позволяют находить пространственные характеристики волнения. Однако их основной недостаток заключается в сложности анализа быстропротекающих мелкомасштабных процессов, образующихся при сильном обрушении волн. Сильная поперечная неонородность волн, паразитная засветка от бликов, наличие брызг и пены приводит к большим сложностям при съемке и анализе видеоизображений. Поэтому в основном ограничиваются исследованием режима слабого обрушения (gentle spilling breaking) [9, 10].
В настоящей работе предлагается методика измерения формы поверхности и получения усредненных по турбулентным флуктуациям характеристик поверхностного волнения в широком диапазоне скоростей воздушного потока. Она основана на использовании лазерной подсветки, скоростной видеосъемки и специальных алгоритмов анализа изображений. Основное внимание уделено возможности исследования коротковолновых возмущений, образующихся при обрушении волн. Для исследования длинноволновой части поверхностного возмущения используется комбинация с дополнительными измерениями струнными волнографами.
2. Описание аппаратной части системы и особенностей получения видеоизображений поверхностных волн.
Эксперименты по исследованию формы поверхностных волн генерируемых ветром проводились в лабораторных условиях на новой экспериментальной установке Высокоскоростном Ветро-волновом Термостратифицированном канале ИПФ РАН (ВВТК) (см. рис. 1). Параметры установки позволяют моделировать ветро-волновое взаимодействие в пограничных слоях атмосферы и океана при экстремальных гидрометусловиях. В том числе достигать ураганных скоростей ветра (до 40 м/с в пересчете для натурных условий) и реализовывать режим регулярного обрушения волн. Прямая часть канала над водной поверхностью имеет П-образное сечение (см. рис. 2) (крышка сверху) и общую длину 10 м. Рабочее сечение воздушного потока составляет 0.4×0.4 м, боковые стенки погружены в воду на 0.3 м (более подробное описание установки см. в [7]).
Рис. 1. Общий вид на ветро-волновой канал (вид с боку).
Общая схема измерений формы поверхности волн показана на рис. 2.
Для подсветки используется вертикальный лазерный нож, плоскость которого параллельна боковым стенкам канала. Лазерный нож формируется из параллельного пучка 532 нм твердотельного (Nd-YAG) лазера с диодной накачкой, мощность 4 Вт, с помощью системы цилиндрических линз. Профиль интенсивности ножа близок к гауссовому. Ширина области засветки менялась выбором радиуса цилиндрических линз и их взаимного расположения. При этом ширина области засветки выбиралась исходя из необходимости поддержания контраста границы раздела вода-воздух на определенном уровне.
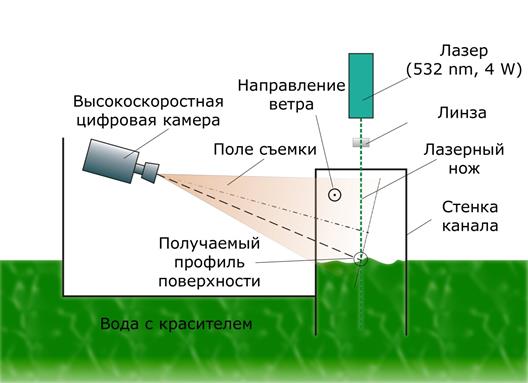
Рис. 2. Сечение ветро-волнового канала. Общая схема эксперимента.
Область пересечения лазерного ножа с взволнованной поверхностью снимается на скоростную CCD-камеру VideoScan, с базовым разрешением 1280 на 1000 пикселей, и скоростью 500 кадров/секунду и более (с пропорциональным уменьшением разрешения). Для установки камеры на расстоянии 8 м от начала канала перпендикулярно боковой стенки установлен прозрачный бокс (см. рис. 2). Таким образом, горизонт съемки может быть как ниже, так и выше уровня воды в канале.
Поверхностные волны в канале, не двумерны, поэтому, для того, чтобы большую часть времени линия пересечения лазерного ножа с водой была видна, съемка проводилась под углом к поверхности. При этом плоскость фокусировки пересекает плоскость лазерного ножа под некоторым углом (см. рис. 2), а значит при изменении уровня поверхности, линия пересечения лазерного ножа с водой будет неизбежно покидать плоскость фокусировки. Выбор угла, под которым производилась съемка поверхности, представляет собой компромисс между удовлетворительной глубиной фокусировки и минимизированием случаев перекрытия области съемки поперечными неоднородностями волны на ближнем фоне. Очевидно, оптимальный угол склонения зависит от уклона волн в поперечном направлении, и от амплитуды волн в целом. Для уменьшения эффекта дефокусировки при колебаниях поверхности, ось камеры направлялась выше, чем поверхность (см. рис. 2), так что образ невозмущенной поверхности располагался ближе к нижней части кадра. Такой подход позволил при том же угле съемки поверхности получить меньший угол между фокальной плоскостью камеры и плоскостью лазерного ножа, а значит и меньшую дефокусировку при отклонении поверхности от невозмущенного состояния.
Для больших амплитуд волн поверхность существенно выходит из области фокусировки. Исходя из того, что наиболее сложной для наблюдения и определения формы является область гребня волны, уровень фокусировки в таких случаях намеренно выбиралась ближе границы пересечения лазерного ножа с невозмущенной поверхностью. Скорость съемки выбиралась так, чтобы между кадрами форма поверхности изменялась незначительно; это условие существенно используется в обработке (см. ниже). Время экспозиции выбиралось максимальным (2 10-4 с), при данной скорости съемки (500 кадров/секунду) для обеспечения необходимого контраста границы раздела на получаемых изображениях.
При проведении тестовых экспериментов было обнаружено, что число бликов на изображениях достаточно велико. Причем, блик портит не только область изображения вблизи себя, но и в результате переотражений внутри приемной оптической системы (объектива) засвечивает значительную часть всего изображения. Частота возникновения бликов возрастала при увеличении скорости ветра настолько, что определить форму гребня волны не удавалось почти никогда. Для борьбы с бликами на объектив был установлен поляризационный фильтр. После его установки исчезла паразитная засветка крупных областей изображения, и остались только локальные засветки в области нахождения источников бликов (брызг, обрушающихся гребней). Применение фильтра уменьшило уровень экспозиции (изображения стали менее контрастными), но значительно возросла часть изображений, на которых может быть достоверно восстановлен профиль поверхности.
Для получения высокого контраста в воду бассейна было добавлено флуоресцирующее вещество – уранин (динатриевая соль флоуресцина). Полученный раствор обладает интенсивной флуоресценцией в зеленом свете.
3. Описание алгоритмов обработки видеоизображений волн, поиска границы поверхности.
Процесс сбора и обработки экспериментальных данных состоит из нескольких этапов. После выбора подходящего положения камеры и лазерного ножа, а также параметров записи, подсвеченная лазером поверхность снимается скоростной камерой. Камера имеет собственный буфер, в который может записываться до восьми секунд видео при частоте съемки 500 кадров в секунду. Запись перекодируется в последовательность .jpeg изображений.
На изображении, полученном с камеры (рис. 3 а), синими линиями показана область, в которой интенсивность лазерного ножа дает достаточный контраст на границе вода-воздух. Таким образом, определяются границы области поиска по горизонтали.
|
a) |
b) |
Рис. 3. a) изображение, полученное с камеры. Вертикальными синими линиями показаны границы области поиска. b) результат после вычитания фона.
Для того чтобы избавиться от статических шумов матрицы, периодически производится запись изображения при закрытом объективе, которая затем используется при вычитании подстилающего фона (см. рис. 3).
Для поиска границы (контура) взволнованной поверхности на изображении был выбран метод Канни (см. [11]). Суть алгоритма заключается в том, что для каждого пикселя изображения вычисляются величина градиента интенсивности и его направление. Затем пиксели, в которых достигается локальный максимум градиента интенсивности в направлении вектора градиента, формируют границу. Таким образом, одной границе ставится в соответствие линия толщиной в один пиксель. Затем, чтобы определить находится или нет граница в данной точке изображения, производится пороговая фильтрация.
Выбранный способ поиска границ считается одним из наиболее универсальных и удачных алгоритмов. Основное преимущество перед более простыми методами (например, метод Собеля) заключается в том, что в результате подавления «не максимумов» градиента, граница представляется однопиксельной линией, и нахождение положения границы не зависит способа дальнейшей бинаризации.
В ходе исследований, как альтернатива, рассматривалась возможность использования метода порога интенсивности для определения границы поверхности. При этом проводилась бинаризация изображения пороговой фильтрацией с фиксированным значением порога. Оказалось, что определяемое положение, при этом сильно зависит от выбора порога (на рис. 4 а две линии соответствуют разным порогам) и от конфигурации поверхности. При некоторых уклонах поверхности воды, на изображении имеются провалы интенсивности, которые не детектируются этими методами (такой провал виден в правой части изображения на рис. 4 а, где происходит разрыв линий). В аналогичных условиях метод Канни (рис. 4 б) показывает лучшие результаты, а при изменении пороговых значений не возникает систематических смещений. Кроме того, распределение интенсивности в лазерном ноже в действительности несколько отличается от гауссова профиля, и меняется со временем, что при поиске границы по интенсивности не позволяет выбрать единый порог для всей реализации, даже при использовании коррекции неоднородности засветки.
|
a) |
b) |
Рис. 4. а) Результат поиска поверхности по порогу интенсивности при разных значениях порога в сравнении с поиском методом Канни b) .
Перед применением метода Канни производится предварительная фильтрация изображения. Без этой фильтрации граница поверхности либо тонет в шуме флуктуаций интенсивности (рис. 5), либо определяется не на всей области выбранного поиска – подобрать оптимальные граничные значения не удается.
Рис. 5. Результат поиска границ интенсивности изображения по Канни без предварительной фильтрации.
Распределение интенсивности в лазерном ноже сильно
неоднородно, и для компенсации этой неоднородности вводится коррекция
изображения по следующему алгоритму. Искусственно синтезируется изображение
поля светового ножа для известного угла раствора (15 град) и гауссового
распределения интенсивности в нем 
. На рис. 6 а
показано модельное распределение интенсивности неоднородной засветки. Затем
интенсивность исходного изображения с вычтенным фоном нормируется на
интенсивность модели засветки: 
.
Скорректированное таким образом изображение показано на рис. 6 б.
Коррекция позволяет значительно увеличить горизонтальный размер области поиска
поверхности.
|
a) |
b) |
Рис. 6. Коррекция неоднородности засветки а) используемое модельное распределение интенсивности в лазерном ноже б) – результат коррекции.
После вычитания фона, на изображении все еще остается значительное количество шума (результат обработки методом Канни). Он складывается из естественных динамических шумов приемника (матрицы камеры), и из паразитной засветки поверхности вне области лазерного ножа дающей блики. Также источником паразитных бликов являются брызги, проходящие через область лазерного ножа. Основной задачей следующего этапа обработки является подавление шума над поверхностью, так как поиск границы осуществляется сверху вниз (см. ниже). Интенсивность шума приемника чаще всего меньше интенсивности границы поверхности, поэтому от него можно избавиться, проведя коррекцию уровней – интенсивность изображения линейным образом перенормируется. Для избавления от шума, интенсивность которого достаточно велика, но характерный размер мал, изображение сглаживается оконным средним (размер окна 10 пикселей). В результате шум размывается (см. рис. 7 а) и перестает детектироваться при поиске границ методом Канни (сравниваем рис. 7 б и рис.5) .
|
a) |
b) |
Рис. 7. a) результат применения коррекции уровней и размытия изображения (оконное среднее, размер окна 5 пикселей) b) примененный к отфильтрованному изображению метод поиск границ по Канни.
В результате проведенной предварительной фильтрации, изображение готово для поиска границ по Канни (рис. 7 б). Как видно, над границей поверхности в области поиска никаких особенностей не возникает.
Рис. 8 Поиск границы поверхности после применения метода Канни.
На рис. 8 показан заключительный этап определения границы
поверхности после обработки фильтрованного изображения методом Канни.
Горизонтальные границы области поиска устанавливаются вручную. Для определения
вертикальных границ используется профиль поверхности с предыдущего кадра (для
первого кадра он ориентировочно вводится вручную). Здесь используется
обстоятельство, что смещение поверхности на соседних кадрах мало. Для каждого
значения горизонтальной координаты область поиска по вертикали своя, и представляет
собой окрестность положения поверхности в этой точке, которая была определена
для предыдущего кадра: 
(см. рис. 8). Размеры
окрестности задаются в диапазоне ±100 пикс. В случае, если положение
поверхности на предыдущем кадре не было определено, область поиска для данной
точки расширяется до максимального и минимального значения вертикальных границ
определенных для предыдущего профиля. Поиск производится сверху внизу до
первого встретившегося ненулевого пикселя на изображении с выполненным поиском
границ по Канни (см. рис. 8). На рис. 9а показан результат такого поиска. Таким
образом, погрешность определения формы поверхности по полученным изображениям
на этапе применения метода Канни составляет 1 пиксель
|
a) |
b) |
Рис. 9. Найденная граница. Справа показан результат фильтрации, оставлены только связные области принадлежащие профилю.
При фильтрации получившегося профиля поверхности от неверно найденных участков, удаляются все точки, в заданной окрестности которых (3*3 пикс) присутствует недостаточное число найденных значений профиля поверхности (менее 7 точек). Результат фильтрации представлен на рис.9 б.
В сложных случаях, при большом количестве брызг и существенной недвумерности волны, неверно найденные участки имеют больший размер, и не отсекаются фильтрацией одиночных сегментов. Для того, чтобы определить их как ошибочные, вводится дополнительный критерий правильности – отсекаются все найденные точки, не находящиеся в окрестности границы, определенной по порогу интенсивности. При таком комбинированном методе поиска отсекаются ошибочные участки профиля, не принадлежащие поверхности, и не возникает систематических смещений определяемого уровня.
Участки, определенные как ошибочные (пропуски), восстанавливаются линейной интерполяцией. На таких участках, как показала статистическая обработка, среднеквадратичная ошибка при определении положения границы составляла 4 пикселя (0.5 мм в пересчете на масштаб съемки). Это значение можно использовать для оценки погрешности на конечном этапе обработки изображения. Полученные в результате профили поверхности сохраняются в файл таблицами. При таком описании полученный профиль представляет собой однозначную функцию y(x).
4. Схема экспериментов и Измерений. полученные результаты.
Была проведена серия тестовых экспериментов по исследованию пространственных характеристик ветровых волн в широком диапазоне скоростей воздушного потока в ВВТСК.
Для измерения характеристик ветрового потока использовались
трубки Пито, установленные на сканирующем устройстве. Они позволили найти
профили средней скорости в турбулентном пограничном слое и рассчитать
эквивалентную скорость ветра на десяти метровой высоте 
(9-25 м/с в наших экспериментах). Более
подробно методика измерения профилей скорости и вычисления представлена в [7].
В ходе экспериментов с увеличением скорости наблюдался переход от слабого обрушения волн к достаточно интенсивному обрушению волн с образованием брызг и пенных гребней.
На рис. 10 - 12 показаны снимки поверхности, полученные с помощью новой системы для четырех последовательно увеличивающихся скоростей ветра.
Рис. 10. Изображение формы поверхности в лазерном ноже при
=9 м/с (слабое
обрушение волн)
Рис. 11. Изображение формы поверхности в лазерном ноже при
=15 м/с
Рис. 12. Изображение формы поверхности в лазерном ноже при
=15 м/с
(сильное обрушение волн с образованием брызг).
Наряду с исследованием формы поверхности новой оптической системой в экспериментах проводились измерения возвышений поверхностного волнения с помощью 3-канального струнного волнографа, расположенного в 7 метрах от начала канала (на 1 метр ближе, чем оптическая система). Для получения статистического ансамбля реализаций возмущений, для каждого набора параметров экспериментов проводились 5 записей длиной по 1200 с каждая. По ним вычислялись усредненные спектры. В результате c их помощью были получены спектры по волновому числу в диапазоне 3 – 102 м-1 (длинноволновая часть поверхностного волнения).
Аналогично измерениям с помощью волнографов, для измерений формы поверхности с помощью новой оптической системы также требовалось накопление ансамбля данных для усреднения. В каждом эксперименте был накоплен ансамбль данных, состоящий из 5 фильмов по 4000 кадров в каждом. По этому ансамблю вычислялся усредненный пространственный спектр поверхностного волнения. Для этого сначала на каждом кадре из формы поверхности вычиталась низкочастотная составляющая волн путем полиномиальной аппроксимации, а затем от оставшейся высокочастотной части возмущений, обусловленной обрушениями, находился спектр. После этого вычислялся средний спектр по ансамблю. В результате были получены спектры поверхностного волнения по продольному волновому числу в диапазоне 2*102 – 2* 103 м-1 (коротковолновая часть, соответствующая обрушениям).
На рис. 13 приведены полученные спектры по волновому числу: и с помощью волнографов, и с помощью анализа формы поверхности. Несмотря на имеющийся небольшой провал в измерениях (102 - 2*102 м-1), значения на котором могут быть легко найдены интерполяцией, мы получили спектр в диапазоне от 3 до 2* 103 м-1. Фактически нам известны все параметры шероховатости взволнованной поверхности. Хорошо заметно увеличение амплитуды спектров, в том числе высокочастотной части, при увеличении скорости ветра. Они будут в дальнейшем использованы как входные данные о форме поверхности для квазилинейной модели взаимодействия турбулентного пограничного слоя с волнами.
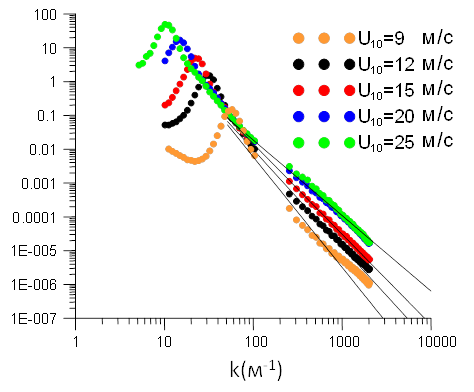
Рис. 13. Спектры по продольному волновому числу измеренные с помощью волнографа и по анализу формы поверхности для пяти значений скорости ветра.
5. Выводы.
В рамках работы создана лазерно-оптическая система получения видеоизображений волн, а также предложены новые алгоритмы их обработки. Особенность новой системы заключается в применении скоростной видеосъемки совместно с непрерывной лазерной подсветкой, которая позволила исследовать поверхность волн в режиме сильного обрушения, при моделировании ветро-волнового взаимодействия в ураганных условиях. С ее помощью были получены средние спектры коротковолновой части возмущений поверхности по волновым числам. Комбинирование этих данных, с результатами измерений системой струнных волнографов по методу WDM позволили найти спектры по волновым числам в широком диапазоне: от 0.1 до 20 см-1.
Благодарности
Авторы выражают благодарность за поддержку при выполнении работы: Сергеев Д.А., Вдовин, М.И., Кандаурров А.А. - грантам РФФИ № 14-05-31415 мол_а, № 15-35-20953 мол_а_вед, № 15-48-02382 р_поволжье , № 14-08-31740 мол_а и гранту президента № МК-3550.2014.5; Троицкаю Ю.И. - проекту РНФ № 14-17-00667.
Список литературы
1. Donelan M.A., Haus B.K, Reul N., Plant W.J., Stiassnie M., Graber H.C., Brown O.B., Saltzman E.S. On the limiting aerodynamic roughness of the ocean in very strong winds. Geophys. Res. Lett., 2004, vol. 31, L18306.
2. Veron F., Saxena G., Misra S. Measurements of the viscous tangential stress in the airflow above wind waves. Geophys. Res. Lett., 2007, vol. 34, L19603, doi: 10.1029/2007GL031242.
3. Troitskaya Yu.I., Sergeev D.A., Ermakova O.S., Balandina G.N. Statistical parameters of the air turbulent boundary layer over steep water waves measured by the PIV technique. J. Physical Oceanography, 41, 1421–1454.
4. Emanuel K.A. Sensitivity of tropical cyclones to surface exchange coefficients and a revised steady-state model incorporating eye dynamics. J. Atmos. Sci, 1995, vol. 52, p. 3969-3976.
5. Powell M.D., Vickery P.J., Reinhold T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature, 2003, vol. 422, pp. 279-283.
6. Donelan M.A., Drennan W.M., Magnusson A.K. Nonstationary Analysis of the Directional Properties of Propagating Waves. Journal of Physical Oceanography, 1996, vol. 26, pp. 1901-1914.
7. Troitskaya Yu., Sergeev D., Kandaurov A., Kazakov V. Air-sea interaction under hurricane wind conditions in "Recent Hurricane Research - Climate, Dynamics, and Societal Impacts" ISBN 978-953-307-238-8 Book edited by: Prof. Anthony Lupo, 2011, pp. 248-268.
8. Ван-Дайк, Альбом течений жидкости и газа M.: Мир. 1986. 183 с.
9. Duncan J.H., Qiao H., Philomin V., Wenz A. Gentle spilling breakers: crest profile evolution. J. Fluid Mech, 1999, vol. 379, pp. 191 – 222.
10. Rapp R.J., Melville W.K. Laboratory measurements of deep-water breaking waves, Phil. Trans. R. Soc. Lond, 1990, vol. A311, p. 735 – 800.
11. Canny J.A. Computational Approach To Edge Detection, IEEE Trans. Pattern Analysis and Machine Intelligence, 8(6): 679–698, 1986.
STUDYING OF THE SURFACE ROUGHNESS PROPERTIES BY VISUALIZATION METHODS WITHIN LABORATORY MODELING OF THE ATMOSPHERIC-OCEAN INTERACTION.
D.A. Sergeev1,2, A.A. Kandaurov1,2, M.I. Vdovin1,2, Y.I. Troitskaya1,2
1Institute of applied physics RAS, Russia
2Lobachevsky State University of Nizhni Novgorod, Russia
Abstract
Improved method of surface wave edge detection is developed in the present work. This studying is devoted to the problem of wind-wave interaction in the boundary layer atmospheric - ocean system. Method bases on laser sheet illumination, high rate video taking, and novel algorithms of image analysis. It allows obtaining surface profile on the frames with high accuracy and spatial resolution, also for the case of intensive wave breaking with spray of droplets generation and foam on the crests. The mean wave number spectra of the high-frequency (small scale) part of surface roughness were calculated from the ensemble of wave profiles. This part is determined by breaking events. These results add the spectra of low-frequency part of surface waves obtained by system of string wave gauges.
Keywords: wind, wave breaking, visualization, laboratory modeling
References
1. Donelan M.A., Haus B.K, Reul N., Plant W.J., Stiassnie M., Graber H.C., Brown O.B., Saltzman E.S. On the limiting aerodynamic roughness of the ocean in very strong winds. Geophys. Res. Lett., 2004, vol. 31, L18306.
2. Veron F., Saxena G., Misra S. Measurements of the viscous tangential stress in the airflow above wind waves. Geophys. Res. Lett., 2007, vol. 34, L19603, doi: 10.1029/2007GL031242.
3. Troitskaya Yu.I., Sergeev D.A., Ermakova O.S., Balandina G.N. Statistical parameters of the air turbulent boundary layer over steep water waves measured by the PIV technique. J. Physical Oceanography, 41, 1421–1454.
4. Emanuel K.A. Sensitivity of tropical cyclones to surface exchange coefficients and a revised steady-state model incorporating eye dynamics. J. Atmos. Sci, 1995, vol. 52, p. 3969-3976.
5. Powell M.D., Vickery P.J., Reinhold T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature, 2003, vol. 422, pp. 279-283.
6. Donelan M.A., Drennan W.M., Magnusson A.K. Nonstationary Analysis of the Directional Properties of Propagating Waves. Journal of Physical Oceanography, 1996, vol. 26, pp. 1901-1914.
7. Troitskaya Yu., Sergeev D., Kandaurov A., Kazakov V. Air-sea interaction under hurricane wind conditions in "Recent Hurricane Research - Climate, Dynamics, and Societal Impacts" ISBN 978-953-307-238-8 Book edited by: Prof. Anthony Lupo, 2011, pp. 248-268.
8. Van-Dajk, Al'bom techenij zhidkosti i gaza [Album of liquid and gas]. M.: World, 1986, 183 p.
9. Duncan J.H., Qiao H., Philomin V., Wenz A. Gentle spilling breakers: crest profile evolution. J. Fluid Mech, 1999, vol. 379, pp. 191 – 222.
10. Rapp R.J., Melville W.K. Laboratory measurements of deep-water breaking waves, Phil. Trans. R. Soc. Lond, 1990, vol. A311, p. 735 – 800.
11. Canny J.A. Computational Approach To Edge Detection, IEEE Trans. Pattern Analysis and Machine Intelligence, 8(6): 679–698, 1986.