ПОСТРОЕНИЕ МЕТОДОВ ВИЗУАЛЬНОГО АНАЛИЗА КЛАСТЕРНЫХ СТРУКТУР В МНОГОМЕРНЫХ ОБЪЕМАХ ДАННЫХ

А.Е. Бондарев, В.А. Галактионов

ИПМ им. М.В. Келдыша РАН

Содержание

1. Введение

2. Используемые методы

3. Построение технологической цепочки алгоритмов обработки многомерного объема данных

Аннотация

Работа посвящена вопросам построения алгоритмов для визуального анализа кластерных структур в многомерных объемах данных. Целью работы является построение комплекса алгоритмов визуализации и визуальной аналитики, позволяющего изучение кластерных структур в многомерных объемах данных без применения алгоритмов кластеризации, вносящих изменения в исходные данные. Для анализа кластерных структур в многомерном объеме данных предлагается использовать методы отображения точек исходного многомерного пространства на вложенные в это пространство многообразия меньшей размерности. Данный подход базируется на построении самоорганизующихся карт SOM, применении метода главных компонент PCA и построении упругих карт Elastic Maps с последующей реализацией процедуры отжига для этих карт. Для реализации полной и последовательной обработки многомерного массива данных вышеупомянутые методы и подходы выстраиваются в последовательность применяемых методов и алгоритмов, образуя единую технологическую цепочку обработки данных. Применение подобной цепочки позволяет получить информацию о кластерной структуре исследуемого объема многомерных данных на разных уровнях глубины анализа и детализации информации.

Ключевые слова: многомерные данные, кластерные структуры, визуальный анализ

1. Введение

Одной из основных современных задач практически во всех областях человеческой деятельности на сегодняшний день является анализ многомерных данных. Многомерные данные являются результатами численных исследований, технических показателей, обобщением экономической и финансовой информации и т.д. Необходимость обработки, анализа и адекватной трактовки этих данных породила такую интенсивно развивающуюся научную дисциплину, как анализ многомерных данных (Data Analysis). Одной из важнейших составляющих это направление дисциплин является кластерный анализ [1,2], рассматривающий различные способы группировки объектов внутри облака многомерных данных. Методов и алгоритмов кластерного анализа на современном этапе существует очень много, они постоянно развиваются и отличаются большим разнообразием. Это могут быть, например, алгоритмы, реализующие полный перебор сочетаний объектов или осуществляющие случайные разбиения множества объектов. Многообразие алгоритмов кластерного анализа обусловлено также множеством различных критериев, выражающих те или иные аспекты качества автоматического группирования. Надо заметить, что ряд источников [2,3] указывает на ряд специфических особенностей методов, алгоритмов и подходов кластерного анализа, которые исследователь должен учитывать в обязательном порядке:

А) Многие методы кластерного анализа — довольно простые процедуры, которые, как правило, не имеют достаточного статистического обоснования. Они — не более чем правдоподобные алгоритмы, используемые для создания кластеров объектов.

Б) Методы кластерного анализа разрабатывались для многих научных дисциплин, а потому несут на себе отпечатки специфики этих дисциплин. Это важно отметить, потому что каждая дисциплина предъявляет свои требования к отбору данных, к форме их представления, к предполагаемой структуре классификации. Так как кластерные методы порой не более чем правила для создания групп, то пользователь должен знать особенности области происхождения облака данных [2].

В) Разные кластерные методы могут порождать и порождают различные решения для одних и тех же данных. Это обычное явление в большинстве прикладных исследований. Одной из причин неодинаковых решений является то, что кластерные методы получены из разных источников, которые предопределяли использование различных правил формирования групп.

Г) Цель кластерного анализа заключается в поиске существующих структур. В то же время его действие состоит в привнесении структуры в анализируемые данные. Хотя цель кластеризации и заключается в нахождении структуры, на деле кластерный метод привносит структуру в данные и эта структура может не совпадать с искомой, «реальной». Кластерный метод всегда размещает объекты по группам, которые могут радикально различаться по составу, если применяются различные методы кластеризации. Ключом к использованию кластерного анализа является умение отличать «реальные» группировки от навязанных методом кластеризации данных.

Эти обстоятельства вызывают вполне естественное желание обойтись по возможности без вышеперечисленных сложностей. Возникает вопрос – нельзя ли получить представление о кластерной структуре рассматриваемого многомерного объема данных более простыми способами? При этом естественно хотелось бы оставить рассматриваемую исходную кластерную структуру в многомерном облаке данных без изменений, порождаемых применением алгоритмов кластеризации.

Положительный ответ на этот вопрос дают алгоритмы понижения размерности и визуального представления многомерных данных во вложенных в исходный объем многообразиях меньшей размерности.

К числу таких семейств алгоритмов можно отнести метод главных компонент и отображение исходного многомерного объема в главных компонентах (PCA) [2,5], построение самоорганизующихся карт (SOM) [4], построение упругих карт (Elastic Maps) [5,6] с разными свойствами упругости или эластичности и отображение исходного многомерного объема в этих картах.

Все эти методы позволяют тем или иным образом выделить из исходного многомерного объема данных содержащуюся в нем кластерную структуру, не внося практически изменений в исходные данные.

Общим свойством всех трех вышеперечисленных подходов является реализация визуального представления многомерного объема данных в виде проекции данных на вложенное многообразие меньшей размерности, обладающее следующими свойствами:

- размерность данного многообразия меньше либо равна трем, что дает возможность визуального представления на уровне человеческого восприятия;

- наличие устойчивых связей основных координатных направлений многообразия со всеми координатными направлениями в изучаемом многомерном объеме;

- возможность выделения наиболее информативных определяющих факторов в изучаемом объеме и отбрасывании малоценной информации.

Отметим, что общей идеей всех вышеперечисленных подходов является отображение многомерных данных в представимую человеком размерность, например, на плоскость так, чтобы точки данных, близкие на плоскости (на карте), были близки и в исходном пространстве. С помощью визуализации мы можем получать большое количество информации о данных сразу, без какой-либо обработки. Становятся видимыми области группировки данных и разреженные области. Упрощается решение задач классификации. Видно количество кластеров, их форма, взаимное расположение и т.д. Обратим внимание, что это естественная классификация данных, не требующая каких-либо специальных действий над исходными данными. Следует отметить, что подобная постановка задачи может оказаться весьма полезной при обработке, анализе и визуализации многомерных решений задач вычислительной газовой динамики, имеющих небольшую размерность [7-12].

2. Используемые методы

Данный раздел рассматривает общие основные подходы, применяемые для визуального выделения кластеров в многомерном объеме данных. К этим основным подходам относятся: построение самоорганизующихся карт (SOM), построение визуального представления многомерного облака данных в пространстве главных компонент (PCA), построение упругих карт (Elastic Maps).

Все три вышеперечисленных подхода обладают рядом общих свойств. Их применение не вносит изменений в исходную структуру данных, а значит, не создает искусственных кластерных структур и артефактов, подобно многим методам кластеризации. Все три основных подхода относятся к методам визуального представления, что позволяет провести оценку кластерной структуры облака данных максимально быстро и эффективно. Все подходы универсальны и позволяют параллельное применение к рассматриваемому облаку данных или последовательное в любых комбинациях. Также характерной чертой всех трех подходов является возможность для исследователя работать с данными в пространствах естественной для человеческого восприятия размерности – двумерных и трехмерных, а не с облаком данных абстрактной размерности. Приведем кратко основные черты и свойства алгоритмов и методов, составляющих три вышеперечисленных подхода.

Одним из первых и наиболее известных подходов подобного рода стал алгоритм построения самоорганизующихся карт SOM (Self-Organised Maps), предложенный Кохоненом [4]. В современном представлении карты SOM трактуются как двумерные сетки узлов, размещенные в изучаемом многомерном пространстве.

В упрощенном виде алгоритм построения карт SOM можно представить следующим образом. В пространство данных размещается двумерная решетка из элементов, которые способны сближаться или отдаляться друг от друга. Запускается итерационный алгоритм сближающий элементы решетки, соответствующие близким точкам в исходном многомерном пространстве данных, и отдаляющий элементы решетки, соответствующие далеким в исходном пространстве точкам. В результате получается картина, отражающая основные свойства изучаемого облака данных, в том числе и наличие кластерной структуры. Подчеркнем, применение карт SOM позволяет нам получить первичное представление о наличии кластеров в изучаемом объеме данных. Для получения более подробной информации о кластерной структуре изучаемого облака данных следует применять более совершенные подходы, такие, например, как метод главных компонент (PCA) и построение упругих карт.

Метод главных компонент (PCA) [2,5] позволяет уменьшить размерность исследуемого многомерного объема данных с наименьшей потерей информации. Главные компоненты представляют собой ортогональную систему координат, в которой дисперсии компонент характеризуют их статистические свойства.

Суть метода состоит в переходе к новому ортогональному базису в рассматриваемом многомерном пространстве, оси которого ориентированы по направлениям максимальной дисперсии набора входных данных, и ранжированию этого базиса в порядке убывания по признаку максимальной дисперсии вдоль осей базиса. Практическая реализация метода PCA сводится к выделению основных направлений (на практике двух или трех), понижению размерности многомерного облака данных до числа новых направлений, и проецированию всех данных на получившееся из новых направлений линейное многообразие. Это позволяет представить многомерный объем данных в проекции на плоскость или трехмерную область визуально. Визуальное представление, в свою очередь дает исследователю возможность понять структуру и суть многомерных данных, в том числе и кластерную структуру.

Другим важным подходом к нелинейному сокращению размерности данных является построение упругих карт (Elastic Map). Идеология и алгоритмы реализации этого подхода подробно представлены в работах [5,6]. По построению, она представляет собой систему упругих пружин, вложенную в многомерное пространство данных. Данный подход основывается на аналогии с механикой: главное многообразие, проходящее через «середину» данных, может быть представлено как упругая мембрана или пластинка. В отличие от карт SOM, метод упругих карт изначально формулируется как оптимизационная задача, предполагающая оптимизацию заданного функционала от взаимного расположения карты и данных. При создании критерия оптимальности авторы включили в него среднее расстояние от точки данных до ближайшего узла карты. Варьирование параметров упругости (процедура отжига) заключается в построении упругих карт с последовательным уменьшением коэффициентов упругости, в силу чего карта становится более мягкой и гибкой, наиболее оптимальным образом подстраиваясь к точкам исходного многомерного объема данных. После построения упругую карту можно развернуть в плоскость для наблюдения кластерной структуры в изучаемом объеме данных. Построение упругих карт на сегодняшний день является широко распространенным методом анализа данных. Применение упругих карт позволяет более точно и четко определять кластерную структуру изучаемых многомерных объемов данных.

3. Построение технологической цепочки алгоритмов обработки многомерного объема данных

Представленные в предыдущем разделе основные подходы визуального отображения многомерного пространства на вложенную двумерную карту обладают разным уровнем сложности при реализации, дают разный уровень глубины и детализации при анализе кластерной структуры многомерного облака данных, имеют различные возможности «подстройки» к рассматриваемому облаку. В свою очередь при анализе кластерной структуры многомерного объема данных у исследователя имеются различные по глубине и детализации задачи. С этой точки зрения было бы весьма разумным выработать некоторый универсальный подход, позволяющий проведение анализа кластерной структуры в многомерном объеме данных на различном уровне информационной детализации. Подобный подход должен быть выстроен в виде некоторой последовательности применяемых методов и алгоритмов, обеспечивающих по мере применения все более детализированный и глубокий уровень анализа. Такая технологическая цепочка представляет собой конвейер обработки данных, где уровень глубины анализа и информационной детализации увеличивается по мере продвижения по цепочке. Пример цепочки такого рода, реализуемый на основе применения всех трех подходов, перечисленных в предыдущем разделе, представлен на рисунке 1.

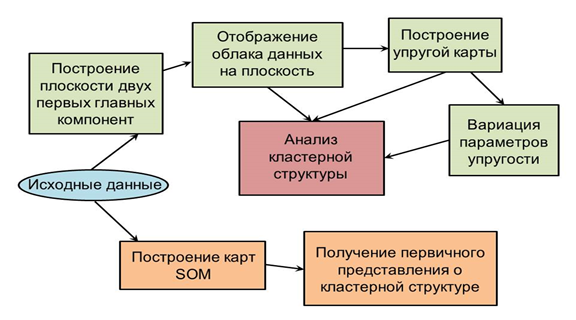
Рис. 1. Схема технологической цепочки обработки многомерного массива с целью исследования кластерной структуры.

Данная технологическая цепочка объединяет три подхода, обладающие общим и важнейшим для исследователя свойством – эти подходы не требуют применения алгоритмов кластеризации для анализа кластерной структуры в многомерном облаке данных и целиком основаны на визуальном представлении и анализе. На первом предварительном этапе используется самый грубый разведочный подход, состоящий в построении самоорганизующихся карт SOM. Он позволяет провести первичный, самый грубый анализ наличия кластерной структуры в облаке данных.

Для дальнейшего анализа часто бывает достаточно отобразить многомерное облако данных на плоскость двух первых главных компонент или в пространство первых трех главных компонент. Подобное визуальное представление обеспечивает следующий уровень анализа наличия и взаиморасположения кластеров.

Далее при необходимости обеспечить более глубокий уровень детализации и анализа, построенную плоскость двух первых главных компонент надо сделать гибкой, чтобы она могла наилучшим образом подстраиваться к исходному многомерному облаку данных. Для этого плоскость надо преобразовать в упругую карту. После построения упругой карты проводится ее развертка. Это обеспечивает более четкое (менее размытое) визуальное разделение кластеров. Далее следует вспомнить о том, что в отличие от предыдущих подходов, построение упругой карты является оптимизационной задачей, имеющей два внешних параметра – коэффициенты упругости карты λ и μ. Для того чтобы увеличить «резкость» изображения и обеспечить тем самым еще более четкое разделение кластеров, необходимо уменьшать коэффициенты упругости карты λ и μ. При этом карта становится более гибкой, лучше подстраивается к исходным многомерным данным, и при развертке обеспечивает максимально четкое разделение кластеров в рассматриваемой кластерной структуре.

Подытоживая вышесказанное, можно утверждать, что реализация подобной технологической цепочки в применении к практической задаче в подавляющем большинстве случаев позволит исследователю получить информацию о кластерной структуре многомерного облака данных на требующемся уровне. Причем, заметим, что все это происходит абсолютно без применения каких-либо простых или сложных алгоритмов кластеризации и без всякого искажения структуры исходных данных.

К применению всего огромного аппарата алгоритмов кластеризации можно всегда перейти в том случае, если с помощью описанной технологической цепочки обработки, анализа и визуализации многомерных данных не удалось получить нужную информацию или достичь требуемого уровня глубины анализа.

4. Пример реализации

Покажем, как работает технологическая цепочка на примере конкретной задачи. В качестве тестовой задачи возьмем широко известный тестовый объем многомерных данных IRIS [5]. Данный объем представляет собой набор данных, основанных на измерениях характеристик растений – цветков ириса. Набор данных описывает три сорта ирисов и состоит из 150 точек в четырехмерном пространстве признаков.

Согласно описанию технологической цепочки, приведенному в предыдущем разделе, на предварительном этапе строится самоорганизующаяся карта SOM для рассматриваемого исходного набора данных. Это должно позволить получить следующую информацию – есть ли кластерная структура, как таковая, и сколько классов она в себе содержит. На рисунке 2 представлены результаты построения самоорганизующейся карты SOM для рассматриваемого набора данных. Кластерная структура в объеме данных есть, и она содержит три класса.

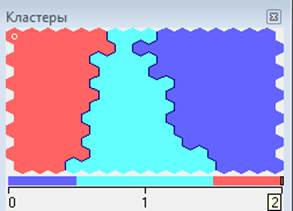
Рис. 2. Результат построения карт SOM.

Следуя технологической цепочке алгоритмов, далее необходимо применить метод главных компонент.

На рисунке 3 представлены результаты отображения исходного объема данных в исходных координатах для трехмерного случая. Различные классы выделены цветами – красным, синим и зеленым. На рисунке видно, что точки всех трех классов смешаны, хотя красные точки в своем большинстве лежат отдельно.

На рисунке 4 приведено представление рассматриваемого объема данных в объеме, образованном тремя первыми главными компонентами. Различные классы аналогично предыдущему рисунку выделены цветами – красным, синим и зеленым. Видно, что в данном представлении красные точки отделены от остальных достаточно четко, а синие и зеленые смешиваются. Применение метода главных компонент позволяет получить представление о взаиморасположении кластеров в многомерном пространстве.

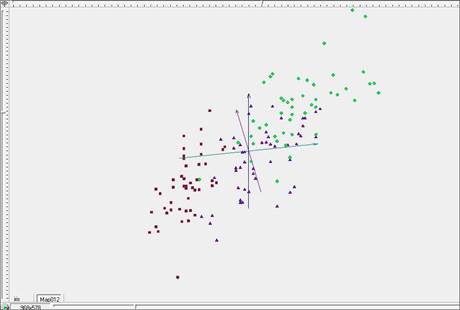
Рис. 3. Трехмерное представление исследуемого объема данных в исходных координатах.

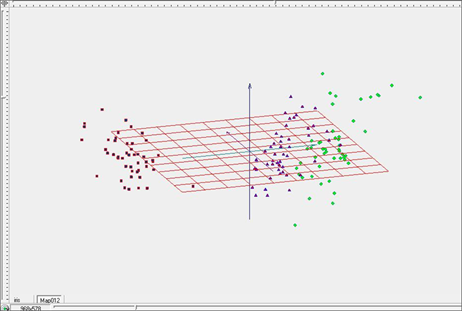
Рис. 4. Трехмерное представление исследуемого объема данных в пространстве главных компонент.

Продолжим продвижение по технологической цепочке обработки многомерных данных. На этот момент нам уже удалось установить, что кластерная структура в объеме есть, что она содержит три класса. Также в результате применения метода главных компонент нам удалось получить представление о взаиморасположении кластеров в многомерном пространстве.

Двигаясь по цепочке дальше, мы ставим целью получить более четкое визуальное представление о разделении данных внутри исследуемого объема на кластеры.

С этой целью начнем построение упругих карт и проецирование точек исследуемого объема на поверхности этих карт. (Для построения изображений упругих карт далее использована программа ViDaExpert [5].) На рисунке 5 представлена упругая карта в исходных координатах. Это так называемая «жесткая» упругая карта, построенная при значениях коэффициентов упругости λ=5, μ=5. На рисунке 6 представлена та же самая карта, но с раскраской по значению плотности данных.

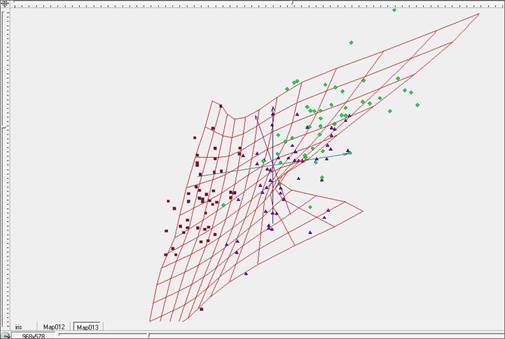
Рис. 5. Построение «жесткой» упругой карты при λ=5, μ=5 в исходных координатах.

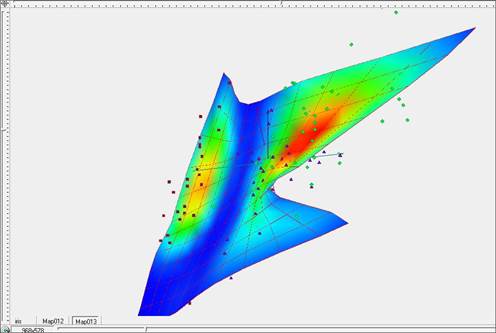
Рис. 6. Построение «жесткой» упругой карты при λ=5, μ=5 в исходных координатах с раскраской по плотности данных.

Однако для того, чтобы упругая карта наилучшим образом была ориентирована в многомерном пространстве, ее следует отображать в пространстве главных компонент, как рекомендуется в работах [5,6]. Переход в пространство главных компонент отражен на рисунках 7 – 9. Рисунок 7 представляет ту же самую «жесткую» упругую карту в пространстве главных компонент.

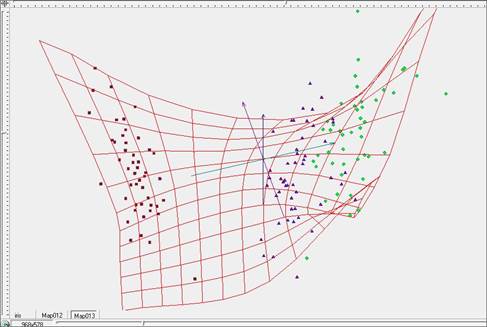
Рис. 7. Построение «жесткой» упругой карты при λ=5, μ=5 в пространстве главных компонент.

На рисунке 8 представлена упругая карта в пространстве главных компонент с раскраской по значению плотности данных. Видно, как плоскость главных компонент изгибается, стараясь наилучшим образом подстроиться к многомерному объему данных. На рисунке 9 представлена развертка упругой карты без раскраски. Разделение синих и зеленых точек улучшилось, впрочем, как и разделение на классы в целом. Картина разделения как бы «проявляется», становясь все более четкой.

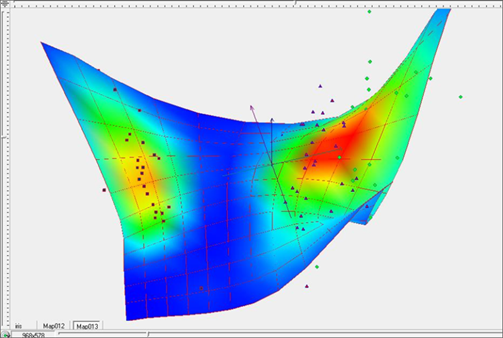
Рис. 8. Построение «жесткой» упругой карты при λ=5, μ=5 в пространстве главных компонент, с раскраской по плотности данных.

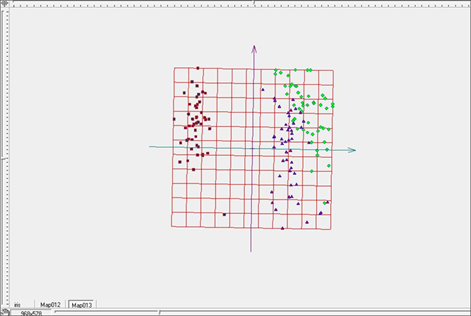
Рис. 9. Развертка «жесткой» упругой карты при λ=5, μ=5 в пространстве главных компонент.

Продолжая следовать технологической цепочке алгоритмов и методов, представленной в разделе 2, для дальнейшего улучшения четкости разделения на кластеры в исследуемом многомерном объеме данных применим так называемую процедуру отжига. Для этой цели будем уменьшать коэффициенты упругости λ и μ, делая карту более «мягкой». Это обеспечивает нам улучшенную адаптацию упругой карты к данным рассматриваемого многомерного объема.

На рисунках 10 – 12 представлены результаты построения упругой карты при значениях коэффициентов упругости λ=1, μ=1. Рисунок 10 представляет поверхность упругой карты для данных значений коэффициентов упругости. Рисунок 11 представляет ту же карту, раскрашенную в соответствии с плотностью данных. На рисунке 12 представлена развертка упругой карты в плоскость. Можно проследить некоторое улучшение разделения на классы.

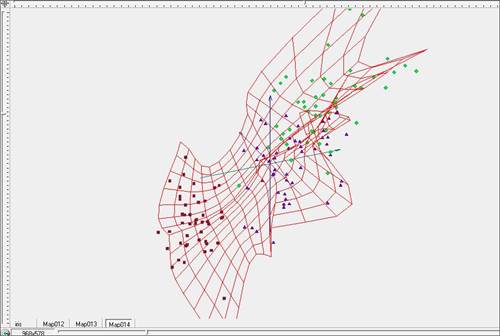
Рис. 10. Построение упругой карты при λ=1, μ=1 в пространстве главных компонент.

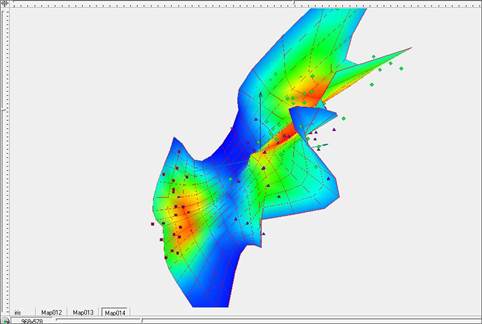
Рис. 11. Построение упругой карты при λ=1, μ=1 в пространстве главных компонент. с раскраской по плотности данных.

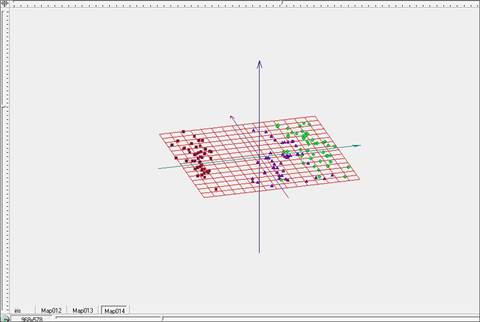
Рис. 12. Развертка упругой карты при λ=1, μ=1 в пространстве главных компонент.

Для дальнейшего улучшения качества разделения продолжим процесс отжига, то есть уменьшения коэффициентов упругости λ и μ. Зададим для дальнейшего построения их значения равными λ=0.01, μ=0.01. Визуальные представления упругой карты для этих параметров представлены на рисунках 13-15, представляющих поверхность упругой карты (Рис.13), поверхность упругой карты, раскрашенную в соответствии с плотностью данных (Рис.14), и развертку упругой карты в плоскость (Рис.15). Разделение на классы стало еще более четким и заметным (зеленые и синие точки на рисунке 15).

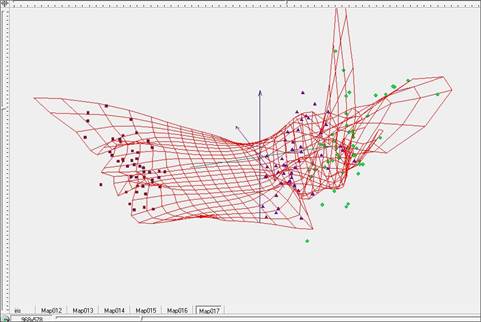
Рис. 13. Построение упругой карты при λ=0.01, μ=0.01 в пространстве главных компонент.

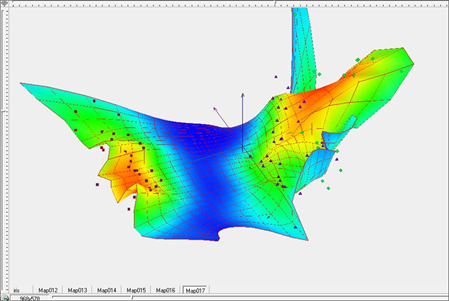
Рис. 14. Построение упругой карты при λ=0.01, μ=0.01 в пространстве главных компонент. с раскраской по плотности данных.

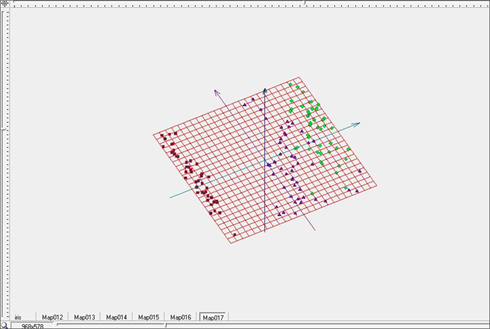
Рис. 15. Развертка упругой карты при λ=0.01, μ=0.01 в пространстве главных компонент.

Таким образом, на примере известного тестового объема многомерных данных проиллюстрирована вся технологическая цепочка, представленная в предыдущем разделе. Применение построения самоорганизующейся карты SOM позволило установить наличие кластерной структуры в исследуемом многомерном объеме данных и определить число классов в структуре. Отображение в пространство первых главных компонент позволило получить представление о форме и взаиморасположении кластеров в структуре. Применение построения упругих карт и реализация последующей процедуры отжига путем вариации коэффициентов упругости в сторону уменьшения позволили добиться четкого разделения данных на кластеры.

5. Обсуждение

Представленная концепция технологической цепочки визуального анализа кластерных структур в многомерном облаке данных является относительно простым, эффективным и наглядным средством получить представление о кластерной структуре облака, количестве кластеров, их взаиморасположении. Однако подобная информация должна иметь непосредственное практическое предназначение. Представленная концепция является частью гораздо большей последовательности алгоритмов, предназначенной для решения задач оптимизационного анализа и параметрического поиска в вычислительной газовой динамике и ее практических приложениях. Подробно данный подход в целом описан в цикле работ [7-12]. Подход в целом предполагает постановку и решение задач оптимизационного анализа и параметрического поиска с помощью параллельных вычислений, получение решений в виде многомерного облака данных [7-10], выделение кластерных структур в многомерном объеме решений. После выделения кластера предполагается уменьшение рассматриваемой области многомерного пространства и работа с отдельно взятым кластером. В кластере проводится поиск скрытых взаимозависимостей между ключевыми параметрами задачи оптимизационного анализа, визуализация и аппроксимация этих взаимозависимостей геометрическими примитивами с целью получения в итоге зависимостей в аналитической приближенной форме [11, 12]. Подход был применен в целом к задачам взаимодействия сверхзвукового потока со струйной преградой, поиску условий возникновения пульсационных режимов при взаимодействии струи с пластиной, анализу коэффициентов сопротивления удлиненных тел вращения.

6. Заключение

Для анализа кластерных структур в многомерном объеме данных предлагается использовать методы отображения точек исходного многомерного пространства на вложенные в это пространство многообразия меньшей размерности. Данный подход базируется на построении самоорганизующихся карт SOM, применении метода главных компонент PCA и построении упругих карт Elastic Maps с последующей реализацией последовательного уменьшения коэффициентов упругости, в силу чего карта становится более мягкой и гибкой, наиболее оптимальным образом подстраиваясь к точкам исходного многомерного объема данных. Для реализации полной и последовательной обработки многомерного массива данных эти методы и подходы выстраиваются в последовательность, образуя таким образом единую технологическую цепочку обработки данных. Применение подобной цепочки позволяет получить информацию о кластерной структуре исследуемого объема многомерных данных на разных уровнях глубины анализа и детализации информации. При этом не вносятся искажения в исходные данные.

Данная работа содержит описание построения подобной технологической цепочки и способов ее применения для анализа многомерных объемов информации.

Благодарности

Данная работа выполнена при частичной поддержке грантов РФФИ (проекты 13-0100367а и 14-01-00769а).

Литература

1. Мандель И.Д. Кластерный анализ. М.: Финансы и статистика, 1988. 176 с.

2. Ким Дж., Мюллер Ч. и др. Факторный, дискриминантный и кластерный анализ. М.: Финансы и статистика, 1989. 216 с.

3. Дюран Б., Оделл П. Кластерный анализ. М.: Статистика, 1977. 128 с.

4. Kohonen T. Self-Organizing Maps. Springer: Berlin – Heidelberg, 1997.

5. Зиновьев А. Ю., Визуализация многомерных данных, Красноярск, Изд. КГТУ, 2000. 180 с.

6. A. Gorban, B. Kegl, D. Wunsch, A. Zinovyev (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58, Springer, Berlin – Heidelberg – New York, 2007.

7. Bondarev A.E, Galaktionov V.A. Parametric Optimizing Analysis of Unsteady Structures and Visualization of Multidimensional Data. International Journal of Modeling, Simulation and Scientific Computing, 2013, V.04, N supp01, 13 p., DOI 10.1142/S1793962313410043. http://dx.doi.org/10.1142/S1793962313410043.

8. Bondarev A.E., Galaktionov V.A. State-of-the-Art in Data Visualization for CFD Problems. Scientific Visualization, 2013 vol.5, no. 4, pp. 18-30.

9. Bondarev A.E., Galaktionov V.A. Current Visualization Trends in CFD Problems. Applied Mathematical Sciences, 2014, vol. 8, no. 28, pp. 1357 - 1368,

http://dx.doi.org/10.12988/ams.2014.4155

10. Bondarev A.E. Multidimensional Data Analysis in CFD Problems. Scientific Visualization, 2014, vol. 6, no. 5, pp. 59-66.

11. Bondarev A.E., Galaktionov V.A. Analysis of Space-Time Structures Appearance for Non-Stationary CFD Problems. Proceedings of 15-th International Conference On Computational Science ICCS 2015 Rejkjavik, Iceland, June 01-03 2015, Procedia Computer Science, Volume 51, 2015, Pages 1801–1810.

12. Bondarev A.E., Galaktionov V.A. Multidimensional data analysis and visualization for time-dependent CFD problems. Programming and Computer Software, 2015, vol. 41, no. 5, pp. 247–252, DOI: 10.1134/S0361768815050023.

METHODS DESIGN FOR VISUAL ANALYSIS OF CLUSTERS IN MULTIDIMENSIONAL DATA VOLUMES

A.E. Bondarev, V.A. Galaktionov

Keldysh Institute of Applied Mathematics RAS

Abstract

The paper considers design of algorithms intended for visual analysis of cluster structures in multidimensional data volumes. The paper is aimed to design of a set of visualization and visual analytics methods for cluster structure studies without applying of clusterization methods influencing at original data. To analyze clusters in original data volume we propose to use the methods of original data points mapping to enclosed manifolds having less dimensionality. The proposed approach is based on self-organized maps (SOM) design, principal components analysis (PCA) and application of elastic maps with further varying of elasticity parameters for the last ones. To provide complete processing of original data volume all mentioned above methods and approaches should be organized in a form of pipeline. The applying of such pipeline allows one to get insight of cluster structures at the different levels of details for multidimensional data volume in question.

Keywords: multidimensional data, cluster structures, visual analysis

References

1. Mandel' I.D. Klasternyj analiz [Cluster analysis]. Finance and Statistics, 1988. 176 pp. [In Russian]

2. Kim j., Mjuller Ch. et al. Faktornyj, diskriminantnyj i klasternyj analiz [Factorial, discriminant and cluster analysis]. Finance and Statistics, 1989. 216 pp. [In Russian]