КОМПЬЮТЕРНАЯ ТОПОГРАФИЯ ГРАФИЧЕСКИХ ОБРАЗОВ В КОГНИТИВНЫХ ТЕХНОЛОГИЯХ НАУЧНОЙ ВИЗУАЛИЗАЦИИ
А.В.Мышев
Национальный исследовательский ядерный университет МИФИ – Обнинский институт атомной энергетики
Содержание
3. Проективный механизм компьютерной топографии
Аннотация
В работе рассматриваются методы компьютерной топографии графических образов (ГО) как новой парадигмы разработки средств научной визуализации на основе когнитивных технологий синтеза и анализа ГО. Такие образы являются, с одной стороны, базовыми сущностями научной визуализации в когнитивных технологиях синтеза, анализа и распознавания ГО на основе их информационных прототипов. А с другой – это модели–образы, посредством которых реализуется геометрия пространственной визуализации исследуемых информационных объектов (ИО). Логическая структура и организация ИО формализуется в виде параметрической зависимости целевой функции от его информативных признаков и характеристик. Формализм научной визуализации с целью выявления новых знаний (содержательных и смысловых) и скрытых закономерностей в информационном теле исследуемого объекта реализуется средствами технологий трехмерной когнитивной компьютерной графики. Они позволяют в наиболее концентрированной и содержательной форме дать логическое и математическое описание и представление исследуемого объекта, а также получить наибольший когнитивный эффект восприятия. Компьютерная топография ГО является интеллектуальной составляющей когнитивных технологий и позволяет выявить скрытые закономерности различного характера в информационных объектах.
Ключевые слова: графические образы, когнитивные технологии, научная визуализация, когнитивная компьютерная графика
1. Введение
Следует отметить, что в настоящее время во всех сферах научной и практической деятельности человека фактор воздействия информационного поля, порождаемого большими потоками данных, является определяющей доминантой при решении многих проблем и задач. В чем же это проявляется. С одной стороны, объекты информационного воздействия, каковыми являются исследователи, обычные клиенты информационных сетей и посетители “информационных библиотек” как различных “корпоративных” сетевых группировок информационной среды систем виртуальной реальности, так и глобальных информационных систем, погружаются и тонут в необозримом океане букв и цифр, картинок и видеоклипов и т.п. А с другой – эти гигантские потоки данных, генерируемых различными системами восприятия и детектирования, в каналах хранения и передачи сетевых информационных систем на физическом и логическом уровне имеют вербально–символьную природу, образуя горы информационной руды, из которой требуется добыть новые знания. Тогда в обозначенном контексте основная посылка доминанты взаимодействия человека с информационными полями больших потоков данных состоит в том, чтобы построить такой математический и логический аппарат, который позволяет “добывать” новые знания, сокрытые в этих потоках данных, т.е. выявлять новые закономерности. Как это сделать и реализовать? В рамках абсолютизации логических схем математических абстракций и формальной логики, определяющих остов методологии традиционных формально–логических способов добычи новых знаний, эта проблема неразрешима. Ибо здесь мы сталкиваемся с такими проявлениями процессов чистой дедукции и формальной логики, как модельная и логическая замкнутость, ограничения среды вычислений и интеллектуальных возможностей, обмен информацией и энергией с внешней средой, информационная неопределенность и диффузия информации и других факторов, в информационном поле взаимодействия исследователя с большими потоками данных вербально–логической природы. А это в свою очередь приводит, как правило, исследователя к тавтологии, проявляемой в неявной и скрытой формах, которые известны как методологические заблуждения, обозначенные Дж. Л. Сингом термином “синдром Пигмалиона”, при котором утрачивается четкое различие между D – миром (мир реальностей) и М – миром (мир моделей) [1,2,3].
Например, можно отметить, что в рамках методологии исследований в различных областях фундаментальной и экспериментальной физики проблема построения теоретического формализма на основе формально–логических способов добычи новых знаний, сокрытых в теоретических и экспериментальных данных, была обозначена еще Дж. Дж. Томсоном и Э. Резерфордом [2], а во второй половине прошлого столетия она получила более широкое и глубокое творческое развитие и практическое продолжение [4,5,6,7,8 и др.]. Ретроспектива и анализ основных посылок обозначенной парадигмы добычи новых знаний, или тоже самое, что и построение моделей декодирования информации, сокрытой в экспериментальных данных, на основе “специфического” теоретического формализма показывают, что его создание, по аналогии с [2,9], является ширмой буйного формализма, за которой скрыто ограниченность содержательно–смыслового контента потока данных и потеря когнитивного контакта исследователя с объектом исследования. И справедливости ради следует также отметить, что еще в первой половине прошлого столетия А. Эйнштейном [10] была обозначена и другая точка зрения. Основная посылка которой состоит в том, что добыча новых знаний, как главного конечного продукта фундаментальной и прикладной науки, не может быть сведено к чистой дедукции и формальной логики для построения логических схем восприятия и интерпретации экспериментальных и теоретических данных. Доминантную роль в когнитивных процессах добычи новых знаний играет интуиция [11]. В таком контексте интуицию, с одной стороны, можно обозначить как некие сингулярности в когнитивных процессах сетевых процессоров синтеза и анализа образов новых знаний. А с другой – ее можно представить как синергию когнитивных технологий алгебраического (или вербально–логического) и образного (зрительного) мышления, которая в явной или неявной форме (на уровне сознания и подсознания) определяет потенциал, функциональные возможности и механизмы когнитивных функций интеллекта человека. Потеря визуального контакта разрушает логические схемы когнитивного восприятия информации на уровне синтеза и анализа образов интуитивного мышления, т.е. разрушаются синергические связи и падает потенциал интеллекта. Проблема очевидна и обозначена. Как ее решать и какие методы использовать в различных ситуациях действительной реальности, используя аппаратно–программные возможности современных супер – и не супер – компьютеров?
С обозначенными выше метаморфозами построения математического и логического аппарата для разработки и реализации как технологий добычи новых знаний из информационной руды больших потоков модельных и экспериментальных данных, так и создания программных систем и продуктов для кодирования и декодирования информационных объектов различной природы, автору пришлось столкнуться при решении многих фундаментальных и прикладных задач.
Логические схемы базового тренда научного поиска способов построения решений различных задач в рамках обозначенных проблем строились на основе методологии научной визуализации больших потоков данных. А в качестве способов их реализации в виде когнитивных компьютерных технологий выбран механизм компьютерной топографии графических образов.
И здесь следует отметить, что большая заслуга в инициировании и развитии нетрадиционных подходов создания когнитивных компьютерных технологий научного поиска и “добычи” новых знаний, таких как научная визуализация и др., несомненно, принадлежит А.А. Зенкину [12], ибо его работы во многом определили тренд направлений исследований автора в области разработки методов и технологий научной визуализации.
Обзор и анализ многочисленных исследований в области разработки и реализации систем и технологий научной визуализации показывает, что их тренды направлены, с одной стороны, на поиск моделей визуализации и способов их формализации, в смысле построения логических и математических схем раскодирования содержательно–смысловой составляющей анализируемых информационных объектов (ИО). А с другой – поиск новых средств (технических и технологических) реализации моделей визуализации в среде образов зрительного восприятия информационных объектов [13,14,15,16,17,18 и др.]. В контексте обозначенной метафоры визуализации поиск нетрадиционных подходов и методов графического представления и отражения больших потоков данных для информационных и компьютерных технологий их интеллектуального анализа в виртуальной среде систем когнитивной и научной визуализации является актуальной и фундаментальной проблемой.
И прежде всего, следует определить содержательно–смысловую составляющую основной посылки методологии рассматриваемого в работе подхода “добычи” новых знаний в больших и супер–больших потоках данных на основе механизма компьютерной топографии графических образов. Принципиальным акцентом здесь является отказ от чистой дедукции и переход к индуктивному подходу, который на уровне визуализации позволяет трансформировать числа и символы в образы и увидеть невидимое, что открывает широкие и глубокие возможности “добычи” новых знаний и неизвестных открытий из информационной руды потоков данных. С другой стороны необходимо обозначить такие составляющие как, а именно. Во–первых, контент содержательно–смысловой составляющей отражает и представляет в виде структурированных данных (СД) некие параметризованные экспериментальные или модельные результаты. А такие результаты всегда являются носителями неопределенности, проявляемой в виде погрешностей, ограничений, замкнутости и других факторов [4,19,20]. Это хорошо поясняется иллюстрацией различия между определением измеряемая (или вычисляемая) величина и измеренная (или вычисленная) величина. В чем же состоит это различие? Ответ находится на “поверхности” : измеряемая величина – это детерминированная величина, а измеренная – это размытая (неопределенная) величина [21,22]. Во–вторых, исходя из выводов предыдущего пункта можно сказать, что размытые переменные, которые являются идентификаторами размытых данных, можно отражать и представлять в виде трехмерных графических образов (ГО). И тогда задача “добычи” новых знаний из информационной руды размытых данных сводится к задаче синтеза и анализа соответствующего трехмерного ГО, т.е. к похожим задачам теории образов [23,24].
В контексте схемы методологии обозначенного подхода логический и алгоритмический аппарат компьютерной топографии ГО можно представить, с одной стороны, как теоретическое развитие и практическое продолжение ранних опытов использования способов визуализации различных данных с целью “добычи” новых знаний во многих областях науки и практики: в географии и смежных с ней науках – это математическая картография [25], в физике – это статистическая топография [5,6], в математике – это методы изучения размытых функций на основе проекций [26,27], в медицине и технике – это компьютерная томография [28], рентгеновская томография и МР–томография [29,30] и др. А с другой – это разработка и реализация математических и логических моделей алгоритмов и процедур для интеллектуальных и когнитивных технологий Brainware нового поколения, ориентированных не на 3D изображения в плоскости 2D монитора, а на визуализацию 3D изображений в реальных 3D мониторах.
Практическая реализация компьютерной топографии ГО была мотивирована и обусловлена осуществлением новых форм компьютинга в среде вычислений компьютерных систем и сетей для решения различных задач [31]. При этом необходимо учитывать архитектурные особенности вычислительных систем, их схемотехнику и системотехнику при реализации соответствующих форм компьютинга [19,20]. Принципиальная и неустранимая сложность реальных задач, масштабность компьютерного моделирования приводит к генерации больших потоков данных, которые необходимо анализировать человеком как на физическом, так и на логическом уровне, т.е. необходимо присутствие аналитика (человека) в процессе его взаимодействия с моделируемой задачей. В среде вычислений это взаимодействие реализуется на основе компьютерных технологий научной визуализации соответствующих информационных объектов (ИО). В математическом аспекте информационные объекты представляют собой логические структуры данных, которые описывают и отражают состав и модель информации в них. И здесь следует еще раз отметить, что зрительное восприятие информации человеком является основным ее источником об объектах любой природы для сетевого процессора когнитивного синтеза изображения образа объекта, его аналитического созерцания и интеллектуального анализа. Двух и трехмерные образы объектов для зрительного восприятия являются естественными и другого человеку не дано. В таком контексте графические образы (ГО), обозначенных размерностей, являются, с одной стороны, базовыми сущностями когнитивных технологий научной визуализации, интеллектуального анализа и распознавания информационных объектов (ИО). А с другой – это модели–образы, которые позволяют описать ИО в виде зависимости целевой функции от его информативных признаков и характеристик средствами технологий трехмерной когнитивной компьютерной графики. Они являются наиболее концентрированной и содержательной формой описания и представления исследуемого объекта, которые позволяют получить наибольший когнитивный эффект как зрительного, так и аналитического восприятия. Компьютерная топография ГО является интеллектуальной технологией и позволяет выявить скрытые закономерности различного характера, сокрытых в размытой смысловой и содержательной структуре информационных объектов.
2. Компьютерная топография трехмерных графических образов размытых функций: базовые понятия и определения
Компьютерная топография ГО в системе базовых понятий и определений предметной и проблемной областях когнитивной графики является такой сущностью, посредством которой излагается аналитическое и логическое развитие методологии разработки и реализации новых методов исследования таких ИО, которые аналогичны таким объектам, как стохастические поля в физике или поверхности в картографии [5,6,25], с целью описания локальных неоднородностей и их «геометрическое» отражение средствами научной визуализации. В области практической реализации компьютерной топографии ГО в виде компьютерных технологий когнитивной графики основная посылка этой сущности состоит в том, что она в определенной мере, используя схемы и подходы компьютерной томографии [28,29,30], а также идеи исследования случайных функций по проекциям [26,27], отражает новую парадигму разработки средств научной визуализации на основе сетевых моделей когнитивных технологий синтеза и анализа ГО. Исходя из обозначенных посылок и предпосылок, обобщенное определение понятия компьютерная топография ГО можно сформулировать следующим образом.
Компьютерная топография ГО – это метод анализа трехмерных ГО размытых дискретных функций, геометрия значений которой представляет собой перспективную решетку в трехмерном пространстве, на основе проекций ее значений либо на координатные плоскости, либо на любую гиперплоскость трехмерного пространства. Эти проекции представляют собой в памяти среды когнитивных технологий научной визуализации ГО область структурированных данных (СД), которые являются информационными картами (ИК) картографических моделей (КМ) проекций ГО. На экране монитора ИК отражаются в виде разноцветной карты, которую можно интерпретировать как картографический образ (КО). Тогда множество подмножеств клеток КО одинакового цвета образует морфометрию “ландшафтной” структуры КО. КМ обладают рядом фундаментальных свойств, благодаря которым исследователь получает представление о конфигурации и пространственной структуре (внешней и внутренней) в пределах масштаба и шкалы. К этим свойствам можно отнести следующие, а именно: 1) содержательное соответствие, которое определяется уровнем полноты и достоверности исходной информации; 2) абстрактность – наличие математической модели; 3) избирательность – возможность декомпозиции КМ с целью ее анализа; 4) синтетичность КМ обеспечивает целостность изображения; 5) метричность КМ обеспечивается математическим законом проекции, точностью синтеза и воспроизведения карты; 6) однозначность определяется отношением изоморфизма и гомоморфизма; 7) непрерывность изображения; 8) наглядность, как фактор образного восприятия КМ; 9) обзорность, как фактор выявления скрытых закономерностей. Следует также отметить факторы зрительного восприятия КО, которое ведется на трех уровнях: 1) восприятие частей КО; 2) восприятие всего изображения КО; 3) анализ изображения КО.
Теоретические и прикладные исследования разработки методов компьютерной топографии для реализации когнитивных технологий научной визуализации проводились автором для решения двух проблем, а именно: во–первых, создание методов и технологий сетевых процессоров синтеза и анализа образов решений размытых задач, их отражения и интерпретации на основе результатов математического моделирования в условиях модельной и алгоритмической замкнутости, обмена, ограничений среды вычислений и многофакторной неопределенности [32,33,34,35]. Во–вторых, создание технологий виртуализации каналов передачи и хранения информации, распознавания и идентификации ИО [36,37]. При решении первой проблемы методы компьютерной топографии использовались для анализа временной эволюции фазовых координат моделируемой задачи на размытых подмножествах дискретных квантовых пространств (анализ дискретных размытых функций) с целью определения горизонта предсказуемости, выявления условий и определения механизма фазовых переходов, определения типов динамики и других характеристик поведения имитируемой динамической системы в условиях ограничений и неопределенности [32,33,34]. В этом случае решение моделируемой задачи определялось по каждой фазовой координате и представлялось в виде трехмерного ГО на размытых подмножествах, которые определены на осях системы координат PxOt. В этой системе координат трехмерного пространства ГО определен и представлен в виде перспективной сетки. Геометрическая иллюстрация обозначенной системы координат и ГО в виде перспективной сетки показаны на рисунке 1, где PO – ось изменения вероятностей, Ox – ось изменения фазовой координаты, Ot – ось изменения времени. Все оси квантованы с соответствующими шагами. Ось Ox также является информационной шкалой дискретного измерения или областью задания размытой функции x(t) (семейство шкал может быть любым). Ось Ot, с одной стороны, задает физическую шкалу параметрической переменной размытой функции x(t) как порядковую шкалу квантов времени. А с другой – эту ось также можно интерпретировать, как ось информационного времени, которое, в отличие от физического времени в привычном понимании, не является однонаправленным. Координатная решетка в плоскости xOt определяется как квантовое дискретное пространство, которое задается априори, как сцена для отражения результатов размытой функции x(t). Узел является геометрическим и информационным атрибутом кванта на решетке.
В качестве целевой функции выступает плотность вероятностей P(x,t), аргументами которой являются x и t. Геометрическая иллюстрация ее ГО представлена на рисунке 1. На координатных плоскостях xOt, PОt, POх определены два типа решеток - координатные и перспективные (см. рис.2). Первый тип - это базовая координатная решетка Z1 2 , которая является информационной системой привязки для размытых значений, определяемых по осям системы координат PxOt. В геометрическом смысле эти решетки квантованы по осям с соответствующими шагами: ∆P1, ∆x1, ∆t1 которые являются неизменными для заданной степени геометрической детализации ГО. В информационном смысле это означает, что цифровая шкала координатных осей разбита с фиксированным и постоянным шагом, т.е. количество значащих цифр для информационной идентификации узлов решетки Z1 2 и соответствующих им фиксировано и неизменно. С математической точки зрения на узлах семейства решеток Z1 2 определяется и отражается перспективная решетка трехмерного ГО целевой функции P(x,t). А посредством информационных атрибутов задается область определения отображения ГО в информационном пространстве активной памяти – их домен, – и область их значений – их диапазон. В таком аспекте данная работа является развитием и разработкой нового направления теории отображений для описания и представления трехмерных ГО посредством их информационных прототипов с переменными доменами-диапазонами.
Методология конструирования таких отображений основана в определенной мере на положениях комбинаторной логики [38] и на теории метода виртуальной перспективы [33,36,39]. На множестве узлов семейства решеток Z1 2 можно также строить клеточные структуры более крупного масштаба, базовым элементом которых является квант-“клетка”. Квант-“клетка”, с одной стороны, – это объединение соседних узлов решетки Z1 2, которые локально структурированы и упорядочены, а с другой – это узел другой координатной решетки более крупного масштаба.
В алгоритмических схемах компьютерных технологий синтеза ГО семейство решеток Z1 2 также является системой координат информационной привязки и поверки при построении перспективной решетки ГО целевой функции P(x,t) в трехмерном пространстве и анализе размытой функции x(t), которая отягощена различного рода ошибками и неопределенностью.
Второй тип – это перспективные решетки (семейство решеток Z2), на которых задаются и отражаются моделируемые или измеряемые размытые значения переменных x и t целевой функции P(x,t). Следует заметить, что переменная x целевой функции P(x,t) является размытой функцией, для которой P(x,t) определяется как функция принадлежности. Т.е. для общепринятого обозначения функции принадлежности через μ(x) это будет означать следующее, а именно: μ(x)= P(x,t) для любого фиксированного t. Эти решетки квантуются по осям с переменными шагами: ∆P, ∆x, ∆t , геометрический и информационный смысл которых аналогичен описанным выше. Смысловое и содержательное назначение этих решеток состоит в том, что множество их узлов образуют геометрическую и информационную среду формирования и синтеза перспективной сетки ГО.
Поясним некоторые свойства геометрических и топологических структур на множестве узлов решеток Z1 2 и Z2 применительно к алгоритмам компьютерных технологий синтеза трехмерного ГО целевой функции P(x,t) в виде перспективной сетки в пространстве PxOt. Каждый узел решетки Z1 2 является идентификатором и центром строго определенного подмножества узлов Z2 с заданным радиусом сферы информационного влияния, конечные топологии на которых являются частично упорядоченными. С каждой частичной упорядоченностью связана единственная диаграмма, которая представляет собой ориентированный граф, на котором могут как разрешены, так и запрещены определенные типы конфигураций. Тогда подмножества размытых узлов решеток Z2 в окрестностях узлов решеток Z1 2, с одной стороны, порождают дискретную информационную среду, в которой формируется изображение ГО размытой функции в виде перспективной сетки. А с другой – образуют алгоритмическую схему синтеза ГО размытой функции x(t) в размытой информационной среде, являющейся отражением трехмерного декартова пространства PxOt, координатные оси которого имеют квантовую природу. А это означает, что координаты ГО и значения целевой функции P(x,t) выражаются в виде целых чисел или символьных цепочек .
![]()
![]()
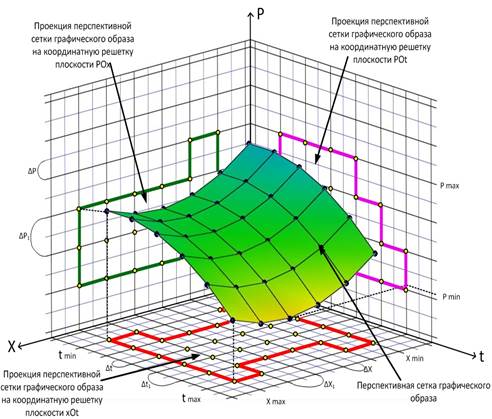
Рис.1. Геометрическая иллюстрация: а) трехмерного ГО дискретной размытой функции в виде пространственной перспективной сетки; б) механизма компьютерной топографии – проектирование перспективной сетки на координатные плоскости.
В контексте введенных и обозначенных выше базовых понятий и определений компьютерная топография ГО образа целевой функции P(x,t) состоит в том, что перспективная сетка ее ГО в пространстве PxOt проектируется на координатные плоскости xOt, PОt, POх. Геометрическая проекция ГО на плоскость образует клеточную топологию на множестве узлов решетки Z1 2, а информационная проекция в памяти представляется в виде вероятностной карты, которая аналогична КО в картографии [25]. На рисунке 2 показана геометрическая иллюстрация представления трехмерного ГО и его проекций в виде вероятностных карт. Числа на вероятностных картах в плоскостях xOt, PОt, POх означают значения функции плотности вероятностей P(x,t) в узлах перспективной сетки ее ГО, представленные в целочисленной квантовой шкале по оси OP. В памяти вычислительной системы такие карты представлены в виде эволюционной структуры данных (СД), которые могут быть реализованы в виде связанного списка или матрицы структурных чисел, которые можно интерпретировать как ИК для КМ [25]. Проекции такого типа в когнитивной компьютерной графике [12] называют пифограммами, которые аналогичны ИК соответствующих картографических образов на экране монитора. Логическая схема построения алгоритма интеллектуального анализа размытой функции x(t) (на рисунке 2 x(t) представлено как решение размытой задачи) состоит в том, что скрытые закономерности этой функции исследуются опосредованно через целевую функцию P(x,t). Т.е. с помощью пифограмм ГО целевой функции P(x,t) выявляются, определяются и анализируются скрытые закономерности размытой функции x(t) (локализация сингулярных фазовых переходов, определение масштабов информационной диффузии). Механизмы и способы реализации технологий компьютерной топографии могут быть различными. Это во многом определяется моделью ГО, интеллектуальными возможностями и инструментальными средствами исследователя.
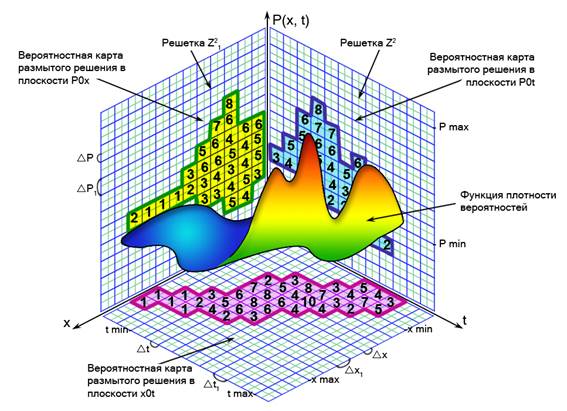
Рис. 2. Геометрическая иллюстрация представления проекций трехмерного ГО на координатные плоскости в виде вероятностных карт.
3. Проективный механизм компьютерной топографии
Важным этапом в построении моделей алгоритмов и процедур научной визуализации и интеллектуального анализа ГО является разработка технологии взаимодействия следующих объектов, а именно: модели целевой функции (ее ГО) и исследователя с виртуальной информационной средой компьютерного восприятия, то есть создания механизма реализации систем виртуальной и когнитивной реальности.
Такая система позволяет анализировать информационные прототипы ГО P(x,t) для размытых функций x(t) также в многомерном пространстве на основе пифограмм P(x,t) (x = (x1,x2,…,xm) – может быть вектором произвольной размерности m) в виртуальном окне, которое может быть реализовано на уровне инструментальной среды КДС (компьютерная динамическая система), например, плоскость или пространство монитора, информационные структуры памяти и др. Одно из важных свойств пифограмм P(x,t) состоит в том, что они позволяют визуализировать и сделать наглядной абстрактную связь между абстрактными свойствами многомерного образа P(x,t).
Суть рассматриваемого проективного механизма компьютерной топографии построения пифограмм P(x,t) состоит в следующем. Виртуальное окно представляет собой ограниченную область в проективной плоскости любой природы, в которой определена размытая функция x(t). В многомерном фазовом пространстве координат P(x,t) в качестве проективной плоскости выбирается любая координатная плоскость xiOt (i=1,…,m). Виртуальные окна в Х (в данном частном случае в качестве Х рассматриваются трехмерные ГО) также могут проектироваться в другие виртуальные окна вне Х любой другой природы.
Технологии и процедуры проектирования и механизм построения пифограмм реализуются на основе ИКГ(интерактивная когнитивная графика) – технологий в двух режимах: статическом и мультипликации. Первый тип механизма позволяет получить последовательность пифограмм P(x,t) в одну и ту же проективную плоскость для произвольных фрагментов (кадров) ГО, не связанных по параметрической переменной или последовательностью шагов алгоритма анализа ГО. Второй – формирует такую же последовательность пифограмм, когда математические и геометрические размеры ГО не согласуются с условиями степени его детализации и размерами виртуального окна. В этом случае ГО разбивается на кадры и анализируется в режиме мультипликации.
Информационная модель механизмов системы компьютерного восприятия, включая синтез, декомпозицию и анализ изображения ГО размытой функции, с позиции системного анализа строится на основе композиционного подхода.
Так как объект P(x,t) обладает рядом фундаментальных свойств таких как сложность, структурированность, упорядоченность, регулярность, алгоритмичность и т.д., то для выявления этих свойств в изображении ГО объекта используется механизм построения пифограмм в проективных плоскостях POxi и xiOt (i=1,…,m). Пифограммы позволяют не только произвести декомпозицию объекта, но также выявить и наглядно отразить свойства объекта для раскрытия неопределенности его изображения на основе композиционного анализа.
4. Компьютерная топография в когнитивных технологиях научной визуализации и интеллектуального анализа информационных объектов: основные понятия и определения
Математическая модель информационного объекта в технологиях виртуализации каналов хранения и передачи информации задается в виде кортежа < X, Nm> на бинарном множестве, где X – это множество цепочек символов алфавита Nm , а Nm – это множество бинарных цепочек длины m [35]. Моделью ИО в технологиях интеллектуального анализа являются ГО. В качестве интеллектуальных инструментов исследования и анализа ИО (файлов или других логических сущностей) используются методы компьютерной топографии как новой парадигмы разработки технологий научной визуализации ГО и интеллектуального анализа ИО. Научная визуализация – это класс интеллектуальных технологий исследования и изучения ИО на основе методов когнитивной компьютерной топографии. Базовыми сущностями технологий научной визуализации информационных объектов являются ГО. Эти образы–модели в технологиях интеллектуального анализа позволяют описать и отразить зависимость целевой функции от информативных признаков и характеристик информационных объектов средствами трехмерной когнитивной компьютерной графики. В проводимых исследованиях ИО в задачах кодирования информации в качестве целевой функцией был выбран коэффициент сжатия, а параметрических переменных – длина буквы и объем информационного объекта. Трехмерные ГО являются наиболее концентрированной и содержательной формой описания и представления исследуемого объекта, которые позволяют получить наибольший когнитивный эффект восприятия. В работе представлены трехмерные ГО информационных объектов различных форматов, которые описывают и отражают функциональную зависимость коэффициента сжатия от длины буквы и объема файла. Анализ трехмерных графических образов методами компьютерной топографии позволяет получить наибольший когнитивный эффект восприятия как при определении экстремальных и оптимальных характеристик и свойств целевой функции, так и выборе стратегии проведения каждого шага анализа, т.е. это система когнитивной реальности, когда объект анализа, среда восприятия и отражения образа и исследователь объединены в активной динамике когнитивного процесса и реального времени. Например, анализ коэффициента сжатия как целевой функции от объема V информационного объекта и длины буквы m алфавита Nm позволяет оперативно, более полно и содержательно определить область значений V и m, при которых коэффициент сжатия достигает максимального значения и др.
Бинарное информационное множество – это множество элементов базового алфавита, образующих логическую структуру в виде сегмента памяти в физической среде канала хранения или поток логически и функционально связанных данных в канале передачи. В каналах передачи и хранения любой информационный объект (файлы и другие логические структуры) рассматриваются как бинарные информационные множества, на которых определяются информационные пространства, задаваемые в виде кортежа <Х,Nm>, где Х – множество символьных цепочек алфавита Nm, который представляет собой множество бинарных цепочек длиной m битов.
Информационное пространство, которое задано в виде кортежа <Х,Nm>, является математической моделью информационного объекта, определенного как бинарное множество. Вероятностно-статистической характеристикой информационного объекта (IO) в <Х,Nm> для фиксированного алфавита Nm будет таблица информационной насыщенности IO (см. рисунок 3), которая представляет собой дискретное распределение вероятностей букв Nm в IO.
![]()
Рис. 3. Шаблон таблицы информационной насыщенности.
Информационные объекты, определенные как бинарные множества в каналах хранения и передачи компьютерных систем, могут описываться различными моделями. В качестве основных свойств и характеристик информационных объектов в моделях выбраны: информация (шенноновская), В– энтропия, коэффициент сжатия, фрактальная размерность ИО.
Шенноновская мера информации задается в виде выражения
In = ![]() ,(1)
,(1)
где pi – это вероятность появления i-ой буквы алфавита Nm в информационном объекте IO, |М| - мощность алфавита Nm .
В – энтропия определена на метрическом вероятностном пространстве и определяется следующим выражением:
![]() ,(2)
,(2)
0![]() ρij
ρij![]() 1 - рандомизированная мера на
метрическом вероятностном пространстве, которая определяется выражением (хотя
можно использовать множество и других)
1 - рандомизированная мера на
метрическом вероятностном пространстве, которая определяется выражением (хотя
можно использовать множество и других)
ρij = | pi – pj |(3)
Количественная характеристика информации на основе В – энтропии отражает степень насыщенности IO буквами Nm с учетом их близости по вероятности, т.е. она позволяет оценить «информационную геометрию» IO.
Коэффициент сжатия определен как отношение объема исходного информационного объекта до кодирования после кодирования.
Фрактальная размерность информационного объекта определяется следующим выражением:
![]() ,(4)
,(4)
где ![]() = d(Ci, Ci+1)
– кодовое расстояние между соседними словами Сi и Сi+1
, а
= d(Ci, Ci+1)
– кодовое расстояние между соседними словами Сi и Сi+1
, а ![]() –
минимальное расстояние между парами соседних кодовых слов в IO.
–
минимальное расстояние между парами соседних кодовых слов в IO.
5.Модель алгоритмов и процедур когнитивных компьютерных технологий научной визуализации трехмерных образов
Проиллюстрируем логическую схему модели алгоритмов и процедур когнитивных компьютерных технологий научной визуализации на примере отражения некоторых шагов при решении практических задач упаковки, защиты, восстановления и анализа больших потоков данных произвольного формата в каналах хранения и передачи информационных систем и сетей [35]. Одним из важных этапов при решении обозначенных задач является определение оптимальных значений независимых переменных некоторых целевых функций, вид которых заранее неизвестен и не имеется никакой априорной информации о них. Такие функции являются дискретными конечномерными функциями и задача определения их экстремальных точек непростая не только в ее практической реализации, но и также в теоретической постановке. В логических и алгоритмических схемах компьютерных технологий решения такой задачи целевая функция задается либо в виде многомерного массива данных, либо конкретной структуры данных (СД). В этом случае такую функцию можно рассматривать как информационный объект, а в качестве способов определения ее экстремальных точек выбираются методы научной визуализации ее графических образов. Тогда задачу определения экстремальных точек обозначенной функции в технологиях научной визуализации можно сформулировать как задачу анализа информационных объектов и выявления в них скрытых закономерностей, которые посредством виртуальных образов отражают его логическую организацию, свойства и характеристики [40]. Следует также отметить, что в математическом и логическом аспекте целевая функция в задачах “добычи” новых знаний и/или выявления скрытых закономерностей является формальной моделью алгоритмов построения решений таких задач, а технологии научной визуализации – это способ их реализации в различных формах компьютинга. Способы построения таких моделей для формализации различных задач уникальны и оригинальны – унифицировать их представляется весьма проблематичным. Моделью зрительного восприятия информационного объекта в технологиях научной визуализации выступают двухмерные и трехмерные графические образы. На рисунке 4 приведена иллюстрация трехмерного графического образа информационного объекта, посредством которого отражается функциональная зависимость коэффициента сжатия Ксж файла от его начального объема V и длины буквы L алфавита Nm , т.е. Ксж=f(V,L). Заметим, что независимые переменные этой функции (объем V и длина буквы L) принимают целочисленные значения, а Ксж – вещественные (функция целочисленных переменных). Оси системы координат на рис.4 обозначим следующим образом: через OZ обозначим ось изменения значений Ксж; через OY – ось изменения значений V , а через OX – ось изменения значений L. Трехмерные графические образы дают наибольший эффект зрительного восприятия информационного объекта “аналитиком” при его анализе и позволяют повысить когнитивный фактор поиска скрытых закономерностей различного характера. В отличие от двухмерных графических образов, трехмерные являются наиболее емкими для зрительного и когнитивного восприятия, а в пространстве зрительного восприятия 3D монитора эти свойства 3D ГО будут проявляться наиболее эффективно и полно (надо ожидать, что в недалеком будущем 3D мониторы станут бытовым атрибутом). Прокомментируем некоторые аспекты синтеза и анализа целевой функции Ксж=f(V,L), ГО которой приведен на рис.3, в виде кратких пояснений и иллюстраций. Алгоритмическая схема процедур построение графического образа обозначенной целевой функции Ксж от параметрических переменных V и L осуществлялось на основе префиксного кодирования по методу Шеннона–Фано. Логическая схема этапа формирования значений целевой функции в виде массива данных в компьютерных технологиях сжатия информации (файлы и другие логические структуры) может быть описана в виде следующего алгоритма:
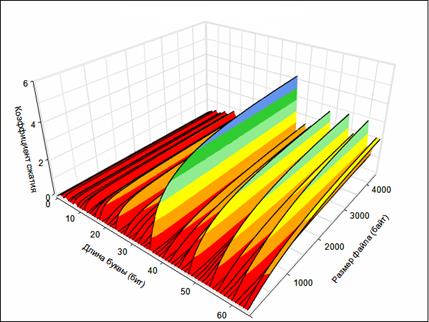
Рис. 4. Геометрическая иллюстрация целевой функции Ксж=f(V,L) в виде трехмерного ГО.
1. Задание границ интервалов изменения независимых переменных V и L целевой функции Ксж : начального объема файла и длины буквы входного алфавита Nm – [Vmin; Vmax] и [Lmin; Lmax], где Vmin и Vmax – минимальное и максимальное значения объем файлов, для которых вычислялись значения Ксж , Lmin и Lmax – минимальное и максимальное значения длины буквы входного алфавита Nm. Эти значения являются входными исходными данными.
2. Построчное формирование значений целевой функции Ксж (в виде двухмерного массива) на основе метода Шеннона–Фано: фиксируем значение переменной V из интервала [Vmin; Vmax] и вычисляем строку значений Ксж для всех LЄ [Lmin; Lmax].
2.1. Для фиксированных значений V и L вычисляем и формируем таблицу информационной насыщенности объекта сжатия.
2.2. Ранжируем таблицу информационной насыщенности по элементам второго столбца: по убыванию вероятностей.
2.3. Формирование префиксных кодов букв выходного алфавита по методу Шеннона–Фано.
2.4. Вычисление значения Ксж для фиксированных значений V и L .
2.5. Выборка следующего значения L из интервала [Lmin; Lmax].
3. Выборка следующего значения V из интервала [Vmin; Vmax] и вычисление новой строки значений Ксж .
После завершения процедуры формирования массива значений Ксж реализуется алгоритм определения значений V и L, при которых Ксж принимает максимальные значения. Эта задача реализуется в виде когнитивной технологии научной визуализации на основе механизма компьютерной топографии ГО целевой функции Ксж . Поясним содержательно–смысловое значение геометрии проекций перспективной решетки трехмерного ГО целевой функции Ксж на координатные плоскости.
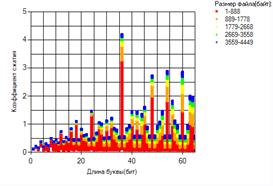
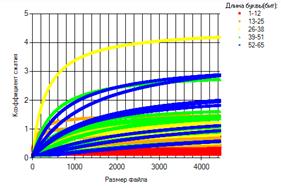
При проецировании перспективной решетки трехмерного ГО на координатную плоскость XОZ получаем двухмерный графический образ, отражающий зависимость целевой функции Ксж от одной из параметрических переменных L (длина бинарной цепочки элемента входного алфавита см. рисунок 5а); при проецировании на плоскость YОZ получаем двумерный графический образ, отражающий зависимость коэффициента сжатия Ксж от объема информационного объекта V (см. рисунок 5б).
|
а) |
б) |
Рис. 5. Иллюстрация картографических образов двумерных проекций трехмерного ГО целевой функции Ксж=f(V,L) на координатные плоскости: a) – на XОY; б) – на YОZ.
Проекции перспективной решетки трехмерного ГО целевой функции Ксж на координатные плоскости XОZ и YОZ являются ее картографическими образами в плоской перспективе. Морфометрия всех цветов проекции отражает “ландшафтную” структуру КО, на которой ясно и понятно для зрительного восприятия показаны решения исходной задачи. КО в плоскости XОZ (см. рис.4а) показывает при каких значениях L и для каких значений V функция Ксж достигает своих экстремальных точек (максимальных). Как видно из рисунка 4а Ксж → max, когда L=36,48…и значения V Є [3559÷4449](байт), т.е. при большем объеме кодируемого файла для обозначенных значений L достигаем наилучшего результата (на КО – это морфометрия точек синего цвета). И это в онлайновом режиме – все видно, ясно и доказательно (упакуйте файл с заданными значениями V и L и получите реальное практическое доказательство, а не абстрактное теоретическое). Теперь аналогично прокомментируем КО в плоскости YОZ (см. рис.5б). Как ясно и доказательно видно из рисунка 5б Ксж → max, когда L Є [26÷38] при больших значениях V (см. на рис.5б кривая желтого цвета). Цветные КО на рис.5 достаточно полно, ясно и доказательно отражают решение исходной задачи когнитивными технологиями научной визуализации на основе механизма компьютерной топографии ГО.
Здесь также следует отметить, что двухмерные графические образы, в отличие от трехмерных образов, обладают меньшим объемным когнитивным эффектом зрительного восприятия при анализе ГО большей размерности, но позволяют исследовать информационные объекты и анализировать зависимости разного рода в них с большей степенью детализации. Метод компьютерной топографии трехмерного образа в виде двумерных его проекций на координатные плоскости позволяет определить те значения одной функциональной переменной, при которых целевая функция достигает своего оптимального значения, а также оценить пределы, в которых лежит значение другой функциональной переменной. И по такой схеме выстраивать алгоритм анализа целевой функции на основе технологий научной визуализации, когда количество функциональных переменных более двух.
6. Заключение
Разработанный метод компьютерной топографии графических образов можно рассматривать как новую парадигму в технологиях научной визуализации и интеллектуального анализа информации на когнитивном уровне ее восприятия был реализован в процедурах сжатия информации для определения их оптимальных параметров. Метод является новым подходом разработки моделей алгоритмов и процедур сжатия данных на основе бинарных преобразований информационных объектов [41,42,43] и выбора оптимальных параметров. Он позволяет наиболее эффективно определить и локализовать области изменения значений оптимальных параметров процедур сжатия информационных объектов на основе методов компьютерной топографии в технологиях научной визуализации ГО качественно расширить возможности интеллектуального анализа ИО любой природы. Проведенные исследования информационных объектов различных форматов позволили выявить уникальные особенности метода следующего характера. Во–первых, методы компьютерной топографии в технологиях интеллектуального анализа и распознавания ИО можно использовать в режиме динамических аппликаций, посредством которых определяются трендовые составляющие поведения целевой функции ИО произвольного и неограниченного информационного объема. Во–вторых, методы компьютерной топографии являются уникальным и эффективным интеллектуальным инструментом в технологиях распознавания и идентификации ИО (например, определить тип формата, к которому относится ИО – DOC, TXT, JPEG или др.) в каналах передачи и хранения информационных систем, представляющего либо часть, либо целое неизвестного формата полученных данных [44]. В–третьих, разрабатываемый подход разработки и реализации технологий интеллектуального анализа и распознавания ИО на основе методов компьютерной топографии ГО имеет перспективу и продолжение в научном, практическом и прикладном аспекте для более глубокого и детального изучения и исследования различных логических сущностей ИО в каналах передачи и хранения информационных систем.
Список литературы
1. Синг Дж. Л. Беседы о теории относительности. М.: Мир, 1973, 168 с.
2. Лаврентьев М.М. История повторяется. Библиотека конференции; вып.2. V Сибирская междисциплинарная конференция “Математические проблемы физики пространства–времени сложных систем” (ФПВ–2004). Новосибирск, изд. СО РАН, филиал “Гео”, 2005, с. 238–248.
3. Уитроу Дж. Дж. Естественная философия времени. М.: Прогресс, 1964, – 432 с.
4. Касти Дж., Калаба Р. Методы погружения в прикладной математике. М.: Мир, 1976, 223 с.
5. Кляцкин В.И. Статистическая топография и ляпуновские экспоненты в динамических системах. УФН, 2008, т. 178, №4, с. 423–431.
6. Займан Дж. Модели безпорядка. М.: Мир, 1982, 592 с.
7. Козырев Н.А., Насонов В.В. Новый метод определения тригонометрических параллаксов на основе измерения разности между истинным и видимым положениями звезд. Астрометрия и небесная механика. М.–Л., 1978, с. 168–179.
8. Gryzinski M. Low energy scattering and the “free–fall” atomic model. Jour. Chem. Phys., 1975, 62, pp. 2629–2636.
9. Грызинский М. Об атоме точно: Семь лекций по атомной физике. Ред. М. М. Лаврентьев. Новосибирск, 2004; М.: Editorial URSS, 2005. – 94 с.
10. Эйнштейн А. Физика и реальность. М.: Наука, 1965, 359 с.
11. Гильберт Д. Основания геометрии. Л.–М.: ОГИЗ, 1948, 492 с.
12. Зенкин А.А. Когнитивная компьютерная графика. М.: Наука, 1992, 192 с.
13. Захарова А.А., Шкляр А.В. Метафоры визуализации. Научная визуализация. 2013. Т.5. №2. С. 16–24.
14. Пилюгин В., Маликова Е., Пасько А., Аджиев В. Научная визуализация как метод анализа научных данных. Научная визуализация. 2012. Т.4. №4. С. 56–70.
15. Горбань А.Н., Зиновьев А.Ю., Питенко А.А. Визуализация данных. Метод упругих карт. Нейрокомпьютеры. 2002. №4. С. 19–30.
16. Волобой А.Г., Галактионов В.А. Машинная графика в задачах автоматизирования проектирования. Информационные технологии в проектировании и производстве. 2006. №1. С. 64–73.
17. Bernhard Flury and Hans Riedwyl. Graphical Representation of Multivariate Data by Means of Asymmetrical Faces. Journal of the American Statistical Association. Vol. 76, No. 376 (Dec., 1981), pp. 757-765
18. Workshop at Visweek 2010: The Role of Theory in Information Visualization, October 25, 2010, Salt Lake City, Utah, USA http://eagereyes.org/infovis-theory-workshop
19. Мышев А. В. Архитектура виртуальной потоковой вычислительной системы на основе информационной модели нейpосети. // Информационные технологии, 2014, №5, с.65–73.
20. Мышев А.В. Виртуальная потоковая вычислительная система, основанная на информационной модели искусственной нейросети и нейрона. Патент на изобретение №2530270. Официальный бюллетень "Изобретения. Полезные модели", 2014,№28, 30с.
21. Голубев Э.А. Неопределенность измерений и ГОСТ Р ИСО 5725. ”Заводская лаборатория. Диагностика материалов”, 2007, т. 73, № 2, с. 63–68.
22. Кузнецов В.П. Сопоставительный анализ погрешности и неопределенности измерений. Измерительная техника, 2003, №8, с.21–27..
23. Гренандер У. Лекции по теории образов: синтез образов. М.: Мир, 1979, 384 с.
24. Гренандер У. Лекции по теории образов: анализ образов. М.: Мир, 1981, 448 с.
25. Берлянт А.М. Образ пространства: карта и информация. М.: Мысль, 1986, 240 с.
26. Ушаков В.Г., Ушаков Н.Г. Восстановление вероятностных характеристик многомерных случайных функций по проекциям. Вестник Московского университета. Серия 15. Вычислительная математика и кибернетика, 2001, №4, с. 32–39.
27. Шестаков О.В. Влияние погрешностей в проекционных данных на алгоритм восстановления распределения случайной функции из распределений ее проекций. Вестник Московского университета. Серия 15. Вычислительная математика и кибернетика, 2002, №2, с. 35–40.
28. Тихонов А.Н., Арсенин В.Я., Тимонов А.А. Математические задачи компьютерной томографии. М.: Наука, 1987, 158 с.
29. Хермен Г. Восстановление изображений по проекциям. Основы реконструктивной томографии. М: Мир, 1983, 352 с.
30. Наттерер Ф. Математические аспекты компьютерной томографии. М: Мир, 1990, 288 с.
31. Мышев А. В. Информационная модель нейpосети в технологиях вычислительного интеллекта и формах реализации компьютинга. Информационные технологии, 2012, №1, с.62–70.
32. Мышев А.В и др. Информационные технологии системного анализа динамики объектов задачи N-тел в условиях неопределенности. Труды регионального конкурса научных проектов в области естественных наук. Вып.5. - Калуга, “Эйдос”, 2003,С. 9-22.
33. Мышев А.В. Метод виртуальной перспективы в моделировании размытых задач. Информационные технологии и вычислительные системы, 2011, №3, с.62–73.
34. Мышев А.В. Виртуальные модели активной памяти для построения нейросетевых процессоров синтеза образов решений размытых задач в технологиях вычислительного интеллекта. // Третья международная конференция “Системный анализ и информационные технологии” САИТ–2009 (14–18 сентября 2009г., Звенигород, Россия): труды конференции М.: ИСА РАН, 2009, с.873–882.
35. Мышев А.В. Модели активной памяти в технологиях виртуализации каналов передачи и хранения информации. Программные продукты и системы, 2010. №1. с.54–58.
36. Мышев А.В. Метод виртуальной перспективы и нейросетевые алгоритмы в технологиях компьютерного моделирования. Нейрокомпьютеры: разработка и применение, 2007. №9. с.390–415.
37. Мышев А.В. Компьютерная топография графических образов в технологиях интеллектуального анализа и распознавания информационных объектов. “Системный анализ и информационные технологии”: труды четвертой международной конференции (17–23 августа 2011г., Абазково, Россия): в 2 т., т.2. Челябинск: изд. ЧГУ,2011, с.184–190.
38. Curry H.B. Functionaly in combinatory logic. Proc. National Academy of Science of the USA. 1934, v.20.
39. Мышев А.В. Компьютинг и моделирование размытой задачи Коши методом виртуальной перспективы. Программные продукты и системы, 2012. №3. с.215–222.
40. Myshev A.V., Chunyaev N.V., Shelyakov M.A. Cognitive computer technologies of graphic images analysis. Pattern recognitions and information processing (PRIP’2011): proceedings of the 11th international conference (18–20 may, Minsk, Republic of Belarus). Minsk: BSUIR, 2011. pp. 216–219.
41. Brailovsky I., Kravtsunov E., Plotkin D. A new low complexity entropy coding method. Proceedings of the 14th International conference of computer graphics and vision. Moscow, MSU, 2004
42. Burrows M., Wheeler D.J. A block-sorting lossless data compression algorithm. Digital System Research Center, Research report, 124, 1994
43. ISO/IEC 10918 – 1, 2, 3, JPEG (Digital compression and coding of continuoustone still images). IS, 1994, 1995, 1997.
44. Мышев А.В., Тельнов В.П. О практической реализации модели активной памяти. Программные продукты и системы, 2014. №2. с.69–74.
COMPUTER TOPOGRAPHY OF GRAPHIC PATTERNS IN COGNITIVE TECHNOLOGIES OF SCIENTIFIC VISUALIZATION
A.V. Myshev
Obninsk Institute for Nuclear Power Engineering of the National Research Nuclear University "MEPhI". 249040, Obninsk, Russia, Studgorodok 1, IATE, department of computer science;
Abstract.
The paper the methods of computer topography graphic patterns (GP) as a new paradigm for the development of scientific visualization tools based on cognitive technologies synthesis and analysis of GP is considered. Such patterns are, on the one hand, the basic nature of scientific visualization techniques cognitive synthesis, analysis and detection, based on their information prototypes. And on the other – model–patterns through which implemented geometry studied spatial visualization of information objects (IO). The logical structure and organization of information objects is formalized in the form of parametric dependence the objective function from its informative features and characteristics. The formalism of scientific visualization to identify new knowledge (content and semantic) and hidden laws in information structure of investigation object is realized by means of three–dimensional cognitive technologies of computer graphics. They allow a more concentrated form and content to give a logical and mathematical description and presentation of the object, as well as get the most cognitive effect of perception. Computer topography of GP is the intellectual component of cognitive technologies and allows to reveal hidden patterns in the different nature of information objects.
Keywords: graphic patterns, cognitive technologies, scientific visualization, cognitive computer graphics
References
1. Sing J.L. Besedy o teorii otnositel'nosti [Conversations about the theory of relativity]. Moscow: Mir, 1973, 168 p. [In Russian]
2. Lavrent'ev M.M. Istorija povtorjaetsja [History repeats itself]. Conference proceedings, part. 2. V Siberian Interdisciplinary Conference “Mathematical problems of space-time physics of complex systems” (FPV–2004). Novosibirsk, publishing house. Russian Academy of Sciences, a subsidiary of "Geo", 2005, pp. 238–248. [In Russian]
3. Uitrou J.J. Estestvennaja filosofija vremeni [The natural philosophy of the time]. Moscow: Progress, 1964, 432 p. [In Russian]
4. Kasti J., Kalaba R. Metody pogruzhenija v prikladnoj matematike [immersion method in applied mathematics]. M.: Mir, 1976, 223 p. [In Russian]
5. Kljackin V.I. Statisticheskaja topografija i ljapunovskie jeksponenty v dinamicheskih sistemah [Statistical topography and Lyapunov exponents in dynamical systems]. UFN, 2008, vol. 178, no. 4, pp. 423–431. [In Russian]
6. Zajman J. Modeli bezporjadka [Models disorder]. Moscow: Mir, 1982, 592 p. [In Russian]
7. Kozyrev N.A., Nasonov V.V. Novyj metod opredelenija trigonometricheskih parallaksov na osnove izmerenija raznosti mezhdu istinnym i vidimym polozhenijami zvezd [The new method of determining the trigonometric parallax based on the measurement of the difference between the true and the apparent position of the stars]. Astrometry and celestial mechanics, 1978, pp. 168–179. [In Russian]
8. Gryzinski M. Low energy scattering and the “free–fall” atomic model. Jour. Chem. Phys., 1975, 62, pp. 2629–2636.
9. Gryzinski M. Ob atome tochno: Sem' lekcij po atomnoj fizike [About atom precisely: seven lectures on nuclear physics]. Ed. Lavrent'ev. Novosibirsk, 2004; Moscow: Editorial URSS, 2005, 94 p. [In Russian]
10. Einstein A. Fizika i real'nost' [Physics and Reality]. M .: Nauka, 1965, 359 p. [In Russian]
11. Gil'bert D. Osnovanija geometrii [Foundations of Geometry]. L. M .: OGIZ, 1948, 492 p. [In Russian]
12. Zenkin A.A. Kognitivnaja komp'juternaja grafika [Cognitive computer graphics]. Moscow: Nauka, 1992, 192 p. [In Russian]
13. Zakharova A.A., Shklyar A.V. Metafory vizualizacii [Visualization metaphors]. Scientific Visualization, 2013, vol. 5, no. 2, pp. 16–24. [In Russian]
14. Pilyugin V., Malikova E., Pasko A., Adzhiev V. Nauchnaja vizualizacija kak metod analiza nauchnyh dannyh [Scientific Visualization as Method of Scientific Data Analysis]. Scientific Visualization, 2012, vol. 4, no. 4, pp. 56–70. [In Russian]
15. Gorban' A.N., Zinov'ev A.Ju., Pitenko A.A. Vizualizacija dannyh. Metod uprugih kart [Data Visualization. Method of elastic cards]. Neurocomputers, 2002, no. 4, pp. 19–30. [In Russian]
16. Voloboj A.G., Galaktionov V.A. Mashinnaja grafika v zadachah avtomatizirovanija proektirovanija [Computer graphics in the problems of design automation]. Information technology in the design and manufacture, 2006, no. 1, pp. 64–73. [In Russian]
17. Bernhard Flury and Hans Riedwyl. Graphical Representation of Multivariate Data by Means of Asymmetrical Faces. Journal of the American Statistical Association, vol. 76, no. 376 (Dec., 1981), pp. 757-765
18. Workshop at Visweek 2010: The Role of Theory in Information Visualization, October 25, 2010, Salt Lake City, Utah, USA http://eagereyes.org/infovis-theory-workshop
19. Myshev A.V. Arhitektura virtual'noj potokovoj vychislitel'noj sistemy na osnove informacionnoj modeli nejposeti [Architecture virtual stream computing system based on the information model neyposeti]. Information technology, 2014, no. 5, pp. 65–73. [In Russian]
20. Myshev A.V. Virtual'naja potokovaja vychislitel'naja sistema, osnovannaja na informacionnoj modeli iskusstvennoj nejroseti i nejrona [Virtual stream computing system based on artificial neural network information model and neuron]. The patent for the invention №2530270. Official Bulletin "Inventions. Utility models", 2014, no. 28, 30 p. [In Russian]
21. Golubev Je.A. Neopredelennost' izmerenij i GOST R ISO 5725 [Measurement uncertainty and GOST R ISO 5725]. "Factory laboratory. Diagnostics Materials ", 2007, vol. 73, no. 2, pp. 63–68. [In Russian]
22. Kuznecov V.P. Sopostavitel'nyj analiz pogreshnosti i neopredelennosti izmerenij [Comparative analysis of the error, and measurement uncertainty]. Measuring equipment, 2003, no. 8, pp. 21–27. [In Russian]
23. Grenander U. Lekcii po teorii obrazov: sintez obrazov [Lectures on the theory of images: a synthesis of images]. Moscow: Mir, 1979, 384 p. [In Russian]
24. Grenander U. Lekcii po teorii obrazov: analiz obrazov [Lectures on the theory of images: image analysis]. Moscow: Mir, 1981, 448 p. [In Russian]
25. Berljant A.M. Obraz prostranstva: karta i informacija [Image Space: Map and Information]. Moscow: Misl`, 1986, 240 p. [In Russian]
26. Ushakov V.G., Ushakov N.G. Vosstanovlenie verojatnostnyh harakteristik mnogomernyh sluchajnyh funkcij po proekcijam [Restoration of the probability characteristics of multidimensional random functions from projections]. Moscow University. Series 15. Computational Mathematics and Cybernetics, 2001, no. 4, pp. 32–39. [In Russian]
27. Shestakov O.V. Vlijanie pogreshnostej v proekcionnyh dannyh na algoritm vosstanovlenija raspredelenija sluchajnoj funkcii iz raspredelenij ee proekcij [Effect of errors in the projection data on the reconstruction algorithm of the random function of the distribution of its projections]. Moscow University. Series 15. Computational Mathematics and Cybernetics, 2002, no. 2, pp. 35–40. [In Russian]
28. Tihonov A.N., Arsenin V.Ja., Timonov A.A. Matematicheskie zadachi komp'juternoj tomografii [Math tasks of computer thomography]. Moscow: Nauka, 1987, 158 p. [In Russian]
29. Hermen G. Vosstanovlenie izobrazhenij po proekcijam. Osnovy rekonstruktivnoj tomografii [Restoring image from projections. Basics reconstructive tomography]. M: Mir, 1983, 352 p.[In Russian]
30. Natterer F. Matematicheskie aspekty komp'juternoj tomografii [mathematical aspects of computer tomography]. M: Mir, 1990, 288 p.[In Russian]
31. Myshev A. V. Informacionnaja model' nejposeti v tehnologijah vychislitel'nogo intellekta i formah realizacii komp'jutinga [Information model of a neural network in computational intelligence techniques and forms of realization of computing]. Information technology, 2012, no. 1, pp. 62–70.[In Russian]
32. Myshev A.V. et al. Informacionnye tehnologii sistemnogo analiza dinamiki obektov zadachi N-tel v uslovijah neopredelennosti [Information technology system analysis of the dynamics of objects N-body problem under uncertainty]. Proceedings of the regional competition of scientific projects in the field of natural sciences. Issue 5. - Kaluga, "Eidos", 2003, pp. 9-22.[In Russian]
33. Myshev A.V. Metod virtual'noj perspektivy v modelirovanii razmytyh zadach [Method of virtual perspectives in modeling fuzzy problems]. Information technology and computer systems, 2011, no. 3, pp. 62–73.[In Russian]
34. Myshev A.V. Virtual'nye modeli aktivnoj pamjati dlja postroenija nejrosetevyh processorov sinteza obrazov reshenij razmytyh zadach v tehnologijah vychislitel'nogo intellekta [Virtual models of the active memory to construct a neural network processor solutions blurry image synthesis tasks in computational intelligence technologies]. The Third International Conference "System analysis and information technologies" SAIT-2009 (14-18 September 2009., Zvenigorod, Russia): Proceedings. ISA RAS, 2009, pp. 873–882.[In Russian]
35. Myshev A.V. Modeli aktivnoj pamjati v tehnologijah virtualizacii kanalov peredachi i hranenija informacii [Models of active storage virtualization technologies in transmission channels and storage media]. Software and systems, 2010. no. 1. pp. 54–58.
36. Myshev A.V. Metod virtual'noj perspektivy i nejrosetevye algoritmy v tehnologijah komp'juternogo modelirovanija [Method of virtual perspectives and neural network algorithms in computer simulation technologies]. Neurocomputers: development and application, 2007, no. 9, pp. 390–415.[In Russian]
37. Myshev A.V. Komp'juternaja topografija graficheskih obrazov v tehnologijah intellektual'nogo analiza i raspoznavanija informacionnyh obektov [Computed tomography of graphic images in mining technology and identification of information objects]. "System Analysis and Information Technologies": Proceedings of the Fourth International Conference (August 17-23, 2011., Abazkovo, Russia): 2 m., V.2. Chelyabinsk ed. CSU, 2011, pp.184–190.[In Russian]
38. Curry H.B. Functionaly in combinatory logic. Proc. National Academy of Science of the USA. 1934, v.20.
39. Myshev A.V. Komp'juting i modelirovanie razmytoj zadachi Koshi metodom virtual'noj perspektivy [Computing and Simulation fuzzy Cauchy problem by the virtual perspective]. Software and systems, 2012. no. 3, pp. 215–222.[In Russian]
40. Myshev A.V., Chunyaev N.V., Shelyakov M.A. Cognitive computer technologies of graphic images analysis. Pattern recognitions and information processing (PRIP’2011): proceedings of the 11th international conference (18–20 may, Minsk, Republic of Belarus). Minsk: BSUIR, 2011. pp. 216–219.
41. Brailovsky I., Kravtsunov E., Plotkin D. A new low complexity entropy coding method. Proceedings of the 14th International conference of computer graphics and vision. Moscow, MSU, 2004
42. Burrows M., Wheeler D.J. A block-sorting lossless data compression algorithm. Digital System Research Center, Research report, 124, 1994
43. ISO/IEC 10918 – 1, 2, 3, JPEG (Digital compression and coding of continuoustone still images). IS, 1994, 1995, 1997.
44. Myshev A.V., Tel'nov V.P. O prakticheskoj realizacii modeli aktivnoj pamjati. Programmnye produkty i sistemy [The practical implementation of the model of the active memory]. Software and systems, 2014, no. 2, pp. 69–74.[In Russian]