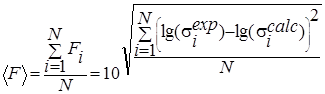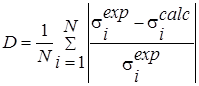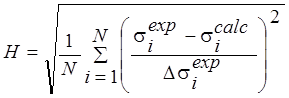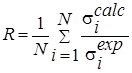ВИЗУАЛИЗАЦИЯ МЕТОДА СТАТИСТИЧЕСКОГО СРАВНЕНИЯ ДАННЫХ

А.В. Максимушкина*, В.В. Смирнова**

* НИЯУ МИФИ, Москва, Россия

** Институт физики высоких энергий, Протвино, Россия

AVMaksimushkina@mephi.ru, Vera.Smirnova@ihep.ru

 

Содержание

1. Введение

2. Метод и программа для статистического сравнения расчетных и экспериментальных данных

3. Выбор параметров модели

4. Заключение

Литература

 

Аннотация.

Для анализа расчетных данных, выбора расчетной модели или сравнения расчетных моделей в зависимости от поставленной задачи используются различные методы. Одним из новых методов, который может быть применён для таких задач является метод статистического сравнения данных [1]. Данный метод был использован для анализа сечений ядерных реакций, полученных с применением специализированных расчетных программ.

 

Ключевые слова: сечения ядерных реакций, анализ данных, визуализация, нейронная сеть, аппроксимация.

 

1. Введение

 

Подготовка данных по сечениям ядерных реакций является важной задачей для расчетных и практических задач в областях, где используются ядерные технологии. Получение этих данных экспериментальным путем является технически сложной задачей, требующей больших затрат. Поэтому часто используются специализированные расчетные коды и программы, в основе которых лежат физические модели, описывающие сложные процессы, происходящие при взаимодействии ядер с протонами или нейтронами. Таким образом, актуальными задачами являются: проверка, насколько эффективно модель описывает экспериментальные данные, выбор модели или выбор параметров модели. Существует достаточно много методов сравнения экспериментальных и/или расчетных данных [1], конкретное применение которых зависит от класса решаемых задач.

Пусть даны два набора данных одинакового объема, представляющие собой измеренные или вычисленные значения некоторой случайной переменной (или случайных переменных) в зависимости от другой (пусть неслучайной) переменной.  Для каждого значения неслучайной переменной значения реализации случайной переменной в каждом из наборов данных получены при обработке независимых выборок.  Требуется определить насколько совместимы эти два набора данных. Под совместимостью наборов данных предполагается то, что для каждого значения неслучайной переменной обе обработанные выборки взяты из одной генеральной совокупности.

Большинство методов сравнения данных основано на вычислении некоторой одномерной тест-статистики, позволяющей оценить насколько сравниваемые данные различаются между собой. Обычно предполагается известным возможное распределение данной тест-статистики (например, χ2 или статистики Колмогорова). Для решения подобных задач может быть использован метод статистического сравнения данных [2]. В данном методе используется двумерная тест-статистика. Возможные распределения тест-статистики (калибровочное и тестовое) строятся методом Монте Карло. Степень различия построенных распределений определяется проверкой двух гипотез, а именно, проверяется основная гипотеза H0: сравниваемые наборы данных совместимы (соответствующие выборки взяты из одной генеральной совокупности) против альтернативы H1: сравниваемые наборы данных несовместимы (соответствующие выборки взяты из разных генеральных совокупностей). Представление результата сравнения двух наборов данных в виде двух двумерных распределений (калибровочного и тестового) позволяет как визуально показать интегральное различие наборов данных, так и дать численную оценку этого различия.  

 

2. Метод и программа для статистического сравнения расчетных и экспериментальных данных

 

Метод статистического сравнения данных является развитием метода сравнения гистограмм [3-5]. В нем используются статистические моменты распределения («значимость различия») , где число точек в сравниваемых таблицах данных. Это распределение, состоящее из M значений, в случае если оба набора данных получены из одной и той же генеральной совокупности, близко к стандартному нормальному распределению, поскольку каждая реализация  случайной величины для каждой точки измерения i является реализацией стандартной нормальной величины. 

Таким образом, в качестве расстояния между наборами данных выступает двухмерная величина

 SRMS = (, RMS),

где 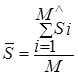 есть среднее значение распределения «значимостей различия», а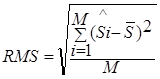– среднее квадратичное отклонение этого распределения.

 

Для сравнения двух наборов данных значимость различия в соответствующих точках измерения задается следующим образом:

 ,

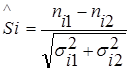где nik – наблюденное значение в точке измерения i-ого набора данных k, σik – соответствующее стандартное отклонение.

Для каждого из сравниваемых наборов данных создается определенное количество подобных наборов данных (клонов) в соответствии с рассматриваемой моделью. Значение в каждой точке измерения генерируется по закону нормального распределения. Это позволяет создать две имитационные модели генеральных совокупностей наборов данных для сравниваемых наборов данных. При построении калибровочного распределения возможных значений двумерной тест-статистики для первой имитационной модели генеральной совокупности проводятся сравнения наборов данных, полученных при построении наборов данных подобных первому исходному набору. При построении тестового распределения возможных значений двумерной тест-статистики проводятся сравнения наборов данных, полученных при клонировании первого исходного набора данных, с наборами данных, полученных при клонировании второго исходного набора данных.   В ходе каждого сравнения строится распределение значимостей различия в соответствующих точках измерения и определяется среднее и среднеквадратическое значения полученного распределения. Данные величины используются для проверки гипотезы о совместимости наборов данных.

Для различимости гипотез при сравнении наборов данных задается уровень значимости критерия, то есть вероятность совершить ошибку первого рода α. Для двумерного распределения (S,RMS)
после задания уровня значимости критерия для определения мощности
критерия подбирается критическая линия, относительно которой и
находится ошибка II рода.  Затем вычисляется мощность критерия 1-β, где β – вероятность ошибки второго рода. Вероятность правильного решения о том, что наборы данных различимы, определяется как [6]:

.

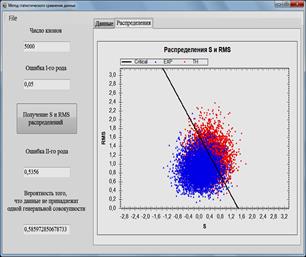
Метод статистического сравнения данных был реализован в программе [7], предназначенной для анализа данных или расчетных моделей. Программа написана на языке программирования C# [8] и имеет интуитивно понятный интерфейс. Пользователю необходимо задать число клонов (повторных генераций), ошибку первого рода и выбрать файл с данными, которые будут сравниваться. Результат выводится в виде графиков распределений и RMS (рис. 1-2.), так же производится расчет вероятности того, что сравниваемые данные не принадлежат одной генеральной совокупности.

 

Рис. 1. Программа для анализа данных и расчетных моделей. Сравнение расчетных и экспериментальных данных.

 

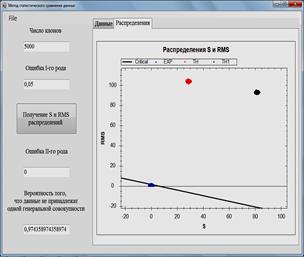
Рис. 2. Программа для анализа данных и расчетных моделей. Сравнение расчетных данных, полученных по двум моделям с экспериментальными данными.

 

Выбор нейронной сети для эффективной аппроксимации данных

Одним из способов получения оцененных данных является аппроксимация, имеющихся экспериментальных значений. Для аппроксимации экспериментальных значений могут быть использованы нейронные сети. Эффективность и качество такой аппроксимации показаны в статье [9], где рассмотрены  несколько структур нейронных сетей и оценено качество аппроксимации с помощью факторов согласия. В качестве альтернативы такой анализ был проведен с помощью метода статистического сравнения данных для определения структуры нейронной сети, которая дает наилучшее согласование с экспериментальными данными. Данными, для которых была проведена аппроксимация с помощью нейронных сетей, являются сечения реакций 209Bi (p,4n)206Po, которые были взяты из библиотеки экспериментальных данных EXFOR [10]. На рис. 3 представлены данные по сечениям в мбарн в зависимости от энергии в МэВ.

 

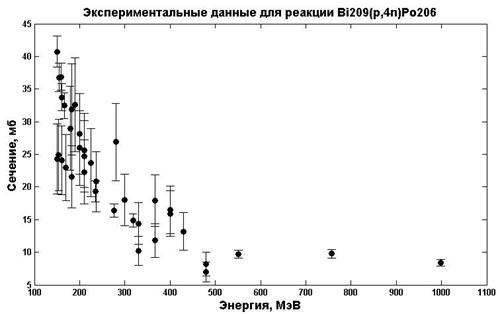
Bi209Po206.jpg

Рис. 3. Зависимость сечения реакции 209Bi (p,4n) 206Po от энергии.

 

Было выбрано четыре нейронные сети (Newfit, Newpr, RBF, GRNN) [11-14], которые являются встроенными в систему MatLab [13, 14]. Реализация производилась в системе MatLab, которая позволяет детально составить и описать нейронную сеть путем варьирования различных параметров сети и использования различных активационных функций.

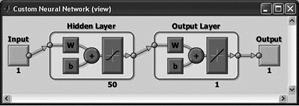
Схемы сетей, которые использовались для расчетов, представлены в табл. 1.

Для каждой конфигурации сети была проделана аппроксимация выбранных данных, с целью выявления сети, наилучшим образом описывающей поведение данных.

Далее было получено двумерное распределение значений  и RMS для исходного набора данных и для каждого набора расчетных значений, полученных с помощью четырех конфигураций нейронной сети (Newfit, Newpr, RBF, GRNN). Распределения представлены на рис. 4.

 

Таблица 1. Схемы нейронных сетей

Сеть

Описание сети

Newfit

niwfit.jpg

В качестве функций активации можно использовать любые дифференцируемые функции активации, например, гиперболический тангенс, сигмоидальная функция. В качестве обучающей функции можно использовать любые функции на основе алгоритма обратного распространения. Первый слой состоит из 50 нейронов с функцией активации гиперболический тангенс, второй слой – из одного нейрона с линейной функцией активации.

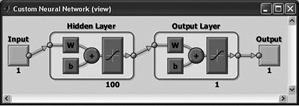
Newpr (pattern recognition network)

newpr.jpg

В качестве функций активации любые дифференцируемые функции активации ( гиперболический тангенс, сигмоидальная функция). В качестве обучающей функции можно использовать любые функции на основе алгоритма обратного распространения. Первый слой состоит из 100 нейронов с функцией активации гиперболический тангенс, второй слой – из одного нейрона с такой же функцией активации.

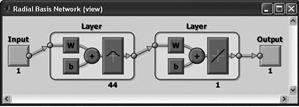
RBF (радиально-базисная)

newrb.jpg

Двухслойная сеть без обратных связей, содержит скрытый слой радиально симметричных скрытых нейронов. Функцией активации является функция Гаусса.

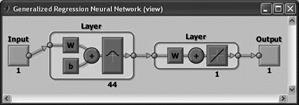
GRNN (обобщенно-регрессионная)

newgrnn.jpg

Первый промежуточный слой сети GRNN состоит из радиальных элементов. Второй промежуточный

слой (линейный) содержит элементы, которые служат для

оценки взвешенного среднего. Функцией активации является функция Гаусса.

 

Далее было получено двумерное распределение значений  и RMS для исходного набора данных и для каждого набора расчетных значений, полученных с помощью четырех конфигураций нейронной сети (Newfit, Newpr, RBF, GRNN). Распределения представлены на рис. 4.

 

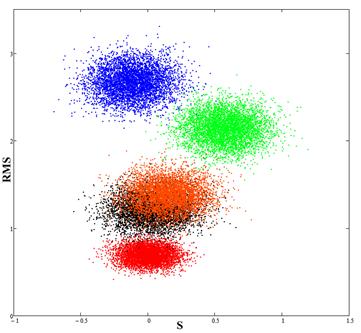
Рис4.jpg

Рис. 4. Красное пятно (калибровочное) соответствует экспериментальным данным, синее пятно-результат сравнения данных для Newfit и экспериментальных данных, зеленое пятно - результат сравнения Newpr с экспериментальными данными, черное и оранжевое пятна (почти полностью пересекающиеся) - результат сравнения RBF и GRNN с экспериментальными данными.

 

Таким образом, данные, полученные с помощью RBF (радиально-базисной) и GRNN (обобщенно-регрессионной) сетями, находятся ближе всего к экспериментальным данным.

Так же была проведена оценка качества аппроксимации расчетов с использованием факторов согласия [15] (табл. 2).

 

Таблица 2. Описание факторов согласия

F-фактор

 

Оценка интегральной близости к эксперименту, для сильно различающихся данных.

D-фактор

Отражает допустимую степень компенсации малых значений одних слагаемых большими значениями других. Чем больше значение, тем больше степень возможной компенсации.

H-фактор

R-фактор

Оценка интегральной относительной близости данных.

 

N – общее число экспериментальных точек, - экспериментальные значения сечений, - расчетные значения сечений, - погрешности экспериментальных значений сечений. 

Результаты расчета факторов согласия представлены в табл. 3.

 

Таблица 3. Результаты расчета факторов согласия

 

F

D

R

H

Newfit

1.854

0.226

1.02

2.484

Newpr

1.237

0.168

0.973

1.99

RBF

1.114

0.065

1.006  

0.72

GRNN

1.135

0.09

1.009

0.99

 

Как видно из табл. 3, аппроксимации, полученные с помощью RBF и GRNN, имеют наилучшее согласование с экспериментальными данными, что сочетается с результатами, полученными с помощью метода статистического сравнения данных.

Также был проведен анализ данных, полученных с помощью RBF сети для сечений реакции 209Bi (n, 3n) 207Bi. Данные сравнивались с экспериментальными значениями и данными, взятыми из библиотеки FENDL [16] (рис.5).

 

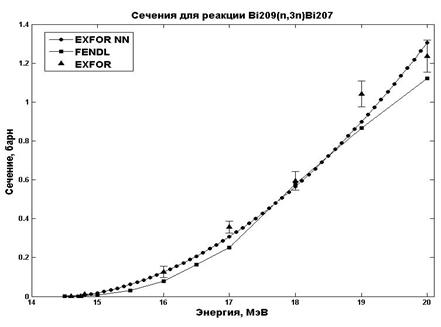
Bi209Bi207.jpg

Рис. 5. Данные по сечениям для реакции 209Bi (n, 3n)207Bi

 

Результаты построения распределения представлены на рис.6.

 

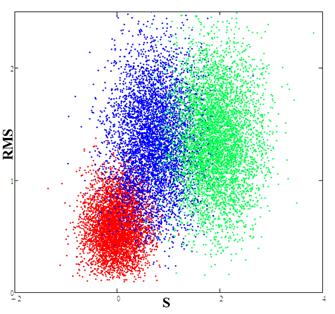
Рис6.jpg

Рис. 6. Красное пятно (калибровочное) соответствует экспериментальным данным, синее пятно-результат сравнения для RBF сети и экспериментальных данных, зеленое пятно - результат сравнения данных из библиотеки FENDL с экспериментальными данными.

 

Из рис.6  видно, что распределение, полученное для нейронной сети RBF, лежит ближе к калибровочному, а значит, модель, построенная с помощью нейронной сети, лучше описывает экспериментальные данные. Таким образом, для получения более точных дальнейших расчетов, в которых используются данные по сечениям, например, как в работах [17,18], предпочтительнее использовать данные, полученные с помощью RBF сети.

 

3. Выбор параметров модели

 

Были проведены расчеты сечений ядерных реакций в программе ALICE/ASH для различных значений параметров E0 (параметр, отвечающий за предравновесную эмиссию кластеров) и PLD (параметр плотности уровня) [19]. Проведен анализ с целью выбора значений параметров, при которых расчетные данные лучше согласуются с экспериментальными. На рис.7-8 Приведены результаты расчетов для реакции natFe(p,x)10Be.

 

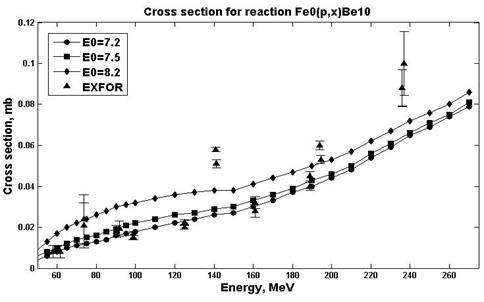
ALICE_DATA1

Рис. 7. Экспериментальные и расчетные сечения реакций natFe(p,x)10Be (PLD=12.7)

 

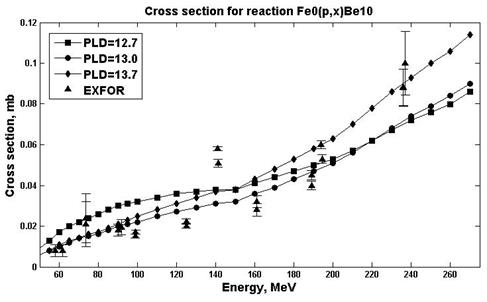
ALICE_DATA_PLD

Рис. 8. Экспериментальные и расчетные сечения реакций natFe(p,x)10Be (E0=7.5)

 

Для всех значений параметров был проделан расчет факторов согласия (табл.4).

 

Таблица 4. Результаты расчета факторов согласия

 

F

D

R

H

E0=7.2, PLD=12.7

1.27

0.13

0.89

1.10

E0=7.5, PLD=12.7

1.22

0.16

1.05

2.11

E0=8.2, PLD=12.7

1.60

0.54

1.54

6.64

E0=7.5, PLD=13.0

1.23

0.19

1.09

2.19

E0=7.5, PLD=13.7

1.33

0.31

1.23

4.33

 

Результат анализа с помощью факторов согласия показал, что при значениях E0=7.5, PLD=12.7 модель лучше описывает данные, чем при других значениях параметров, но этот результат не совсем очевиден.

Был так же проведен анализ с помощью метода статистического сравнения данных. Результаты представлены на рис.9.

 

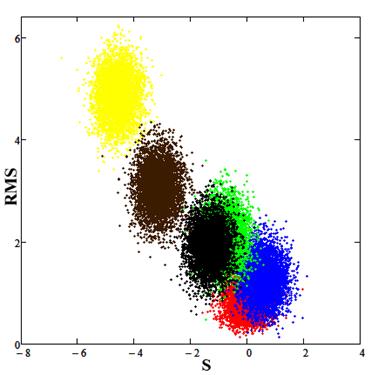
Fe0Be10

Рис. 9. Красное пятно (калибровочное) соответствует экспериментальным данным, cинее пятно - при E0=7.2, PLD=12.7, зеленое пятно при E0=7.5, PLD=12.7, черное пятно при E0=7.5, PLD=13.0, коричневое пятно при E0=7.5, PLD=13.7, желтое пятно при E0=8.2, PLD=12.7.

 

Был проведен расчет ошибки II-го рода β и вероятности того, что данные не совместимы 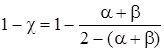, при α=0.005 (табл.5).

 

Таблица 5. Значения β и 1-χ

 

b

1-χ

E0=7.2, PLD=12.7

0.78

0.35

E0=7.5, PLD=12.7

0.44

0.71

E0=8.2, PLD=12.7

0

0.997

E0=7.5, PLD=13.0

0.054

0.969

E0=7.5, PLD=13.7

0

0.997

 

Анализ с помощью метода статистического сравнения данных показал, что расчетная модель с параметрами E0=7.2, PLD=12.7, наилучшим образом описывает экспериментальные значения.

 

4. Заключение

 

Программа, основанная на методе статистического сравнения данных, предназначена для визуализации получаемых распределений и расчета вероятности того, что данные не принадлежат одной генеральной совокупности. Метод позволяет провести анализ расчетных и экспериментальных данных, а также определить какая модель лучше описывает экспериментальные данные. Универсальность метода статистического сравнения позволяет проводить анализ данных в задачах, где требуется их сравнение, выбор расчетных моделей, определение доверительных интервалов параметров расчетной модели, в пределах которых модель хорошо согласуется с экспериментом.  Визуализация получаемых результатов позволяет значительно усилить эффективность анализа, придавая естественную наглядность результатам вычислительных процедур.

 

Литература

 

1.      O. Thas, Comparing Distributions, Springer Series in Statistics, 2010.

2.      Битюков С.И., Красников Н.В., Максимушкина А.В., Никитенко А.Н., Смирнова В.В. Метод статистического сравнения данных и его применение для анализа экспериментальных ядерно-физических данных. Известия Вузов. Ядерная энергетика, № 3, 2014.

3.      Bityukov S.I., Krasnikov N.V., Nikitenko A.N., Smirnova V.V. A method for statistical comparison of histograms arXiv:1302.2651 - 2013.

4.      Bityukov S., Krasnikov N., Nikitenko A., Smirnova V.//Eur.Phys.J.Plus- 2013.- №128:143.

5.      Bityukov S.I., Krasnikov N.V., Nikitenko A.N., Smirnova V.V. Vestnik RUDN. Seriya: matematika, informatika, fisika. 2014, no.2, p. 324.

6.      Bityukov S.I., Krasnikov N.V., Distinguishability of Hypotheses// Nucl.Inst.&Meth. – 2004 -A534. P.152.

7.      Программа для ЭВМ «Статистическое сравнение расчетных и экспериментальных данных», свидетельство №2015614094 от 06.04.2015 г.

8.      http://www.c_sharp.com.

9.      Коровин Ю.А., Максимушкина А.В. Использование нейронных сетей для аппроксимации ядерно-физических данных // Ядерная физика и инжиниринг, том 5, №3, 2014.-С. 237-246.

10.  https://www-nds.iaea.org/exfor/exfor.htm

11.  Осовский С. Нейронные сети для обработки информации / Пер. с польского И.Д. Рудинского. – М.: Финансы и статистика, 2002. – 344с.

12.  Дьяконов В., Круглов В. Математические пакеты расширения MatLAB. Специальный справочник. – СПб.: Питер, 2001. - 488 с.

13.  http://www.mathworks.com/products/neural-network/

14.  Mark Hudson Beale, Martin T. Hagan, Howard B. Demuth. Neural Network Toolbox TM User’s Guide R2013b

15.  https://www-nds.iaea.org/spallations/cal/ fom_definition.pdf

16.  Pashchenko A.B. et al., "FENDL/A-2.0 Neutron activation cross section data library for fusion applications", report IAEA(NDS)-173 (IAEA October 1998) https://www-nds.iaea.org/fendl/fen-activation.htm  

17.  Коровин Ю.А., Максимушкина А.В., Наталенко А.А. Интерактивная система по расчету изотопного состава и наведенной активности облученных материалов перспективных ЯЭУ. Вестник НИЯУ МИФИ, том 2, №1, 2013.-С. 79-84.

18.  Коровин Ю.А., Максимушкина А.В. Расчет изотопного состава и наведенной активности облученных материалов инновационных электроядерных установок. Известия Вузов. Ядерная энергетика, №2, 2014. – С.51-59 .

19.  A.V. Ignatyuk, K.K. Istekov, G.N. Smirenkin, Sov. J. Nucl. Phys. 29(4) (1979) 450.



METHOD FOR DATA STATISTICAL COMPARISON VISUALIZATION

A.V. Maksimushkina1, V.V. Smirnova2

1National Research Nuclear University MEPhI (Moscow Engineering Physics Institute)

2National research centre "Kurchatov Institute" Institute for high energy physics

AVMaksimushkina@mephi.ru, Vera.Smirnova@ihep.ru  

 

Abstract.

Different methods for the calculated data analysis, the choice or comparison of the calculation models are used  and their specific application depends on the tasks set. One of the new techniques that can be applied to such problems is the data statistical comparison method. This method is used for the nuclear reaction cross sections obtained using specialized calculation programs analysis.

 

Keywords: nuclear reaction cross-section, data analysis, visualization, neural network, approximation

 

References

 

1.      O. Thas, Comparing Distributions, Springer Series in Statistics, 2010.

2.      Bityukov S.I., Krasnikov N.V., Maksimushkina A.V., Nikitenko A.N., Smirnova V.V. Metod statisticheskogo sravnenija dannyh i ego primenenie dlja analiza jeksperimental'nyh jaderno-fizicheskih dannyh [A method for statistical comparison of data sets and its uses in analysis of nuclear physics data]. Proceedings of Universities. Nuclear Power, 2014, № 3, pp. 43-51. [In Russian]

3.      Bityukov S.I., Krasnikov N.V., Nikitenko A.N., Smirnova V.V. A method for statistical comparison of histograms arXiv:1302.2651 - 2013.

4.      Bityukov S., Krasnikov N., Nikitenko A., Smirnova V. Eur.Phys.J.Plus- 2013.- №128:143.

5.      Bityukov S.I., Krasnikov N.V., Nikitenko A.N., Smirnova V.V. Vestnik RUDN. Seriya: matematika, informatika, fisika. 2014, no.2, p. 324. [In Russian]

6.      Bityukov S.I., Krasnikov N.V., Distinguishability of Hypotheses. Nucl.Inst.&Meth. – 2004 -A534. P.152.

7.      The computer program "Statistical comparison of the calculated and experimental data," the certificate of №2015614094 from 06/04/2015.

8.      http://www.c_sharp.com.

9.      Korovin Yu. A., Maksimushkina A. V. Use of Neural Networks for Nuclear Data Approximation [Ispol'zovanie nejronnyh setej dlja approksimacii jaderno-fizicheskih dannyh]. Nuclear physics and engineering, vol. 5, no. 3, pp. 237-246, 2014. [In Russian]

10.  https://www-nds.iaea.org/exfor/exfor.htm

11.  Osovsky S. Neural networks for information processing [Nejronnye seti dlja obrabotki informacii]. Finance and Statistics, 344 pp., 2002. [In Russian]

12.  Diyakonov V. Kruglov V. Matematicheskie pakety rasshirenija MatLAB. Special'nyj spravochnik [Mathematical packages of extension of MatLAB. Special handbook]. Peter, 488 pp. 2001.  [In Russian]

13.  http://www.mathworks.com/products/neural-network/

14.  Mark Hudson Beale, Martin T. Hagan, Howard B. Demuth. Neural Network Toolbox TM User’s Guide R2013b

15.   https://www-nds.iaea.org/spallations/cal/ fom_definition.pdf

16.  Pashchenko A.B. et al., "FENDL/A-2.0 Neutron activation cross section data library for fusion applications", report IAEA(NDS)-173 (IAEA October 1998) https://www-nds.iaea.org/fendl/fen-activation.htm  

17.  Korovin Yu. A., Maksimushkina A. V., Natalenko A. A. Interaktivnaja sistema po raschetu izotopnogo sostava i navedennoj aktivnosti obluchennyh materialov perspektivnyh JaJeU [Interactive System for Calculating the Isotope Composition and Induced Radioactivity of  Irradiated Materials on Nuclear Power Facilities]. Bulletin MEPhI, vol. 2, №1, p. 79-84, 2013. [In Russian]

18.  Korovin Yu. A., Maksimushkina A. V. Raschet izotopnogo sostava i navedennoj aktivnosti obluchennyh materialov innovacionnyh jelektrojadernyh ustanovok [Calculation of isotopic composition and induced activity of irradiated materials in innovative accelerator-drive systems], Proceedings of Universities. Nuclear Power, no. 2, pp.51-59, 2014. [In Russian]

19.  A.V. Ignatyuk, K.K. Istekov, G.N. Smirenkin, Sov. J. Nucl. Phys. 29(4) (1979) 450.