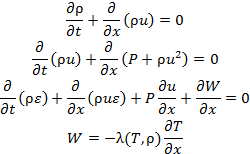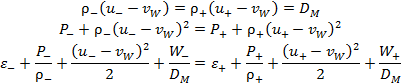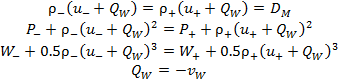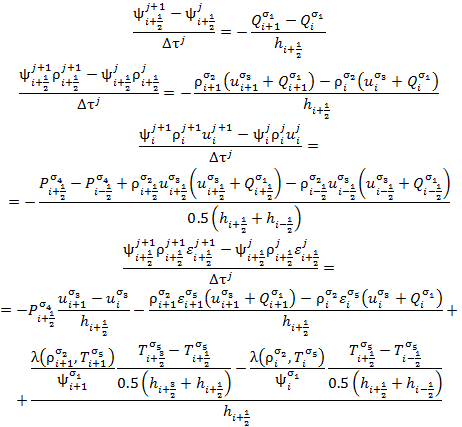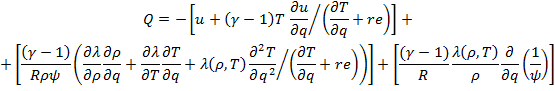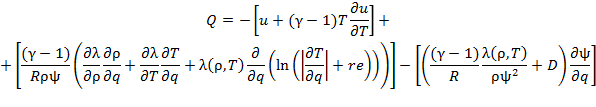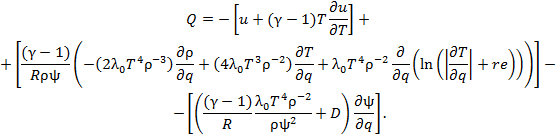МОДЕЛИРОВАНИЕ ЭВОЛЮЦИИ ПЛАЗМЕННЫХ ОБРАЗОВАНИЙ В ГАЗОВОЙ СРЕДЕ С ВИЗУАЛИЗАЦИЕЙ ДИНАМИКИ УЗЛОВ СЕТКИ, ВЗАИМОДЕЙСТВИЯ УДАРНЫХ И ТЕПЛОВЫХ ВОЛН

П.В.Бреславский¹, О.Н.Королева^1,2, А.В.Мажукин^1,2

¹ИПМ им.М.В.Келдыша РАН, Москва, Россия

e-mail: vim@modhef.ru

²Национальный исследовательский ядерный университет "МИФИ", Россия

Содержание

1. Введение

2. Математическая постановка задачи

3. Произвольная нестационарная система координат

4. Разностная аппроксимация

5. Выбор функции адаптации

6. Результаты моделирования

7. Заключение

Список литературы

Аннотация

Исследуется структура ударных и тепловых волн в воздухе при разлете плазмы. Моделирование показало, что характеристики плазменных образований, возникновение ударных и тепловых волн зависят от ряда параметров воздействия и свойств окружающей среды. Характер взаимодействия тепловых и гидродинамических потоков качественно изменяется с изменением величины теплопроводности среды. Высокая теплопроводность приводит к появлению температурных волн двух различных типов - сверхзвуковых и дозвуковых. Структура решения сверхзвукового режима представляется в виде двух следующих друг за другом волн - температурной и гидродинамической. В дозвуковом режиме структура решения представляется в виде трёх волн: изотермической ударной волны, расположенной между двумя (дозвуковой и сверхзвуковой) температурными волнами. Для решения нелинейных уравнений гидродинамики с теплопроводностью используется конечно-разностный подход, совмещенный с процедурой динамической адаптации расчетной сетки, что позволяет явным образом выделять сильные (ударные волны) и слабые (фронт тепловой волны) разрывы. Визуализация и анализ полученных результатов расчетов на сетке, содержащей 30 узлов, осуществляется в сравнении с найденными для подобной задачи автомодельными решениями. Работа выполнена при финансовой поддержке РНФ (код проекта 15-11-00032).

Ключевые слова: лазерно-плазменные процессы, гидродинамика , метод динамической адаптации разностных сеток, нелинейная теплопроводность, визуализация.

1. Введение

Значительный прогресс в компьютерной индустрии, касающийся и технической, и программной ее составляющих, не мог не затронуть такой сферы в научной деятельности, как удобство и наглядность отображения получаемых в процессе исследований результатов. Развитие интернет технологий и появление электронных публикаций позволяют ускорить не только анализ решений, но и, благодаря визуализации, вывести на новый уровень само восприятие представляемых результатов. Все вышесказанное касается не только многомерных задач, но даже в одномерных модельных исследованиях появляется возможность наглядно увидеть динамику рассматриваемых процессов.

Класс задач, описывающих реально происходящие физические процессы и, имеющих при этом точные или автомодельные решения, достаточно узок [1-5] и, зачастую, для их реализации требуется существенное упрощение исходной постановки. Однако, несмотря на это, они по-прежнему остаются актуальными [6]. Разработка новых вычислительных алгоритмов и достоверность численных решений сложных нелинейных систем, в первую очередь в таких областях, как газовая динамика и гидродинамика [7-10], лазерное воздействие [11-14] и физика плазмы [15-17], во многом опираются на автомодельные решения упрощенных модельных задач [6].

Многочисленные приложения импульсного лазерного воздействия (импульсная лазерная абляция(PLA)[18-20], импульсное лазерное осаждение (PLD)[21], производство наноматериалов [22-24]) делают его привлекательным направлением для фундаментальных исследований. Многие предыдущие экспериментальные и теоретические работы были направлены на исследования адиабатического расширения лазерной плазмы в вакууме, несмотря на то, что большинство приложений из PLA выполняются в присутствии окружающего газа [25, 26]. Присутствие внешней газовой среды резко меняет режим лазерного воздействия на мишень, изменяет условия возникновения лазерной плазмы и усложняет описание процесса лазерной абляции из-за изменения структуры плазменного факела, особенностей расширения плазмы и возникновения радиационных и ударных волн [27-29].

В задачах газовой динамики, описывающих разлет полностью ионизованной плазмы, основными механизмами переноса энергии, наряду с радиационным, являются конвективный и кондуктивный. Основу математических моделей в этом случае, вместе с уравнениями переноса излучения, составляют уравнения гидродинамики с нелинейной теплопроводностью. Влиянию нелинейной теплопроводности на особенности взаимодействия тепловых процессов с гидродинамическими ранее уделялось большое внимание [6,30]. Было установлено, что решения данного класса задач отличаются большим разнообразием, а в относительно узком диапазоне параметров возможно появление автомодельных решений. Характер взаимодействия тепловых и гидродинамических потоков качественно изменяется с изменением величины теплопроводности среды. При низкой теплопроводности превалирующими становятся гидродинамические явления, типа ударных волн. Высокая теплопроводность среды приводит к появлению сверхзвуковых и дозвуковых температурных волн, взаимодействующих с ударными волнами.

С вычислительной точки зрения решение уравнений гидродинамики с нелинейной теплопроводностью, относится к проблемам повышенной сложности. Типичное решение подобных задач имеет сложную структуру и включает в себя сильные (фронт ударной волны) и слабые (фронт температурной волны) разрывы, зоны больших градиентов температуры, давления, плотности и скорости. Наличие разрывных решений, зон больших градиентов и их быстрое распространение по пространству предъявляет жесткие требования к эффективности используемых вычислительных алгоритмов, в первую очередь, не столько к качеству разностных схем, сколько к принципам построения оптимальных расчетных сеток [31, 32].

Решение нелинейных уравнений гидродинамики с теплопроводностью осуществляется конечно-разностными схемами, совмещенными с динамической адаптацией. В основу используемых конечно-разностных схем положены принципы консервативности [33] и монотонности [34]. Принципы построения вычислительных алгоритмов с динамической адаптацией для широкого класса уравнений параболического и гиперболического типов с подвижными и неподвижными границами подробно изложены в работах [35–38]. Там же содержится цитируемая литература по методам адаптации.

Основной целью данной статьи является исследование динамики плазменных образований и взаимодействующих между собой ударных и тепловых волн в газовой среде. Еще одной из целей является разработка эффективного вычислительного алгоритма с управляемым распределением узлов сетки и возможностью явного выделения сильных и слабых разрывов в задачах гидро-газодинамики с нелинейной теплопроводностью. Как правило, применение динамической адаптации [35–38] приводит к уменьшению общего количества узлов на несколько порядков, по сравнению с сетками с фиксированными узлами. Визуализация и анализ результатов моделирования, полученных на сетке с динамическим распределением узлов, осуществляется в сравнении с найденными ранее автомодельными решениями [38, 39].

2. Математическая постановка задачи

Постановка задачи о разлете лазерной плазмы с нелинейной теплопроводностью в переменных Эйлера описывается полной системой уравнений газовой динамики с теплопроводностью:

(2.1)

с уравнениями состояния

Принятые обозначения: ρ - плотность, u – скорость, P – давление, ε, T – внутренняя энергия и температура, R – газовая постоянная, g - показатель адиабаты, W – тепловой поток, l – коэффициент теплопроводности. Предполагается, что коэффициент теплопроводности является степенной функцией температуры и плотности λ(T, ρ)= λₒ T^aρ^b.

Начальные условия. В начальный момент времени t = 0 предполагается нулевой фон скорости и постоянное по пространству значение плотности и температуры:

(2.2)

Граничные условия. Формулировка граничных условий производится с учетом того, что применение метода динамической адаптации позволяет явным образом выделять сильные и слабые разрывы. Левая плоскость при является источником движения и нагрева, поэтому на ней формулируются два граничных условия, определяющих скорость движения и величину теплового потока:

(2.3)

Конкретные значения показателей a, b, n будут согласованы с автомодельным решением и указаны позднее.

На правой границе сохраняются фоновые значения

(2.4)

Соотношения на фронте УВ. С учётом непрерывности температуры на фронте УВ выписываются три закона сохранения (условия Гюгонио):

(2.5)

Индексы (–) и (+) относятся к параметрам на разных сторонах ударной волны, ʋ_W – скорость ударной волны, а D_M – поток массы через нее.

3. Произвольная нестационарная система координат

В соответствии с методом динамической адаптации (см. [35]) осуществим переход к произвольной нестационарной системе координат. В новых переменных (q, τ) система (2.1) примет вид:

	(3.1)
	(3.2)
	(3.3)
	(3.4)

где ψ- якобиан обратного преобразования, Q - функция преобразования, подлежащая определению.

Учитывая, что все возмущения возникают на левой границе и распространяются в направлении правой, в целях экономии вычислительных ресурсов целесообразно исключить из рассмотрения область, неохваченную возмущением. С этой целью правая граница смещается к левой и располагается на некотором малом расстоянии от неё. В момент появления на правой границе возмущения она объявляется свободной границей, и распространяется со скоростью тепловых или газодинамических возмущений. Новая граница будет совпадать с фронтом температурной волны. Фронт температурной волны представляет собой слабый разрыв, и скорость его перемещения ʋ_T определяется соотношением, полученным из уравнения движения в подвижной системе координат. Остальные условия переносятся из (2.4) без изменений:

Таким образом, переход в произвольную нестационарную систему координат сопровождается трансформацией исходной дифференциальной модели (2.1) в расширенную модель (3.1) – (3.4), дополненную уравнением обратного преобразования (3.4). Соответственно в начальные (2.2) и граничные условия (2.3) – (2.4) вносятся необходимые дополнения:

		(3.5)
		(3.6)
		(3.7)

Разрывы в нестационарной системе координат выделяются явным образом и, после появления УВ решение системы (3.1) – (3.4) производится в двух подобластях, разделенных фронтом УВ. Решение на фронте сшивается при помощи условий Гюгонио:

(3.8)

4. Разностная аппроксимация

Для численной реализации системы (3.1) - (3.8) использовалась разностная сетка:

Аппроксимация дифференциальных уравнений осуществлялась при помощи метода конечных разностей на разнесенных сетках; выписывалось семейство разностных схем, в которых в полуцелых точках определяются плотность ρ_i_+1/2, температура T_i_+1/2, давление P_i_+1/2 и внутренняя энергия ε_i_+1/2, а в целых – скорость u_i и функция Q_i.

(4.1)

где , а σ_r= σ₁, σ₂, … - весовые множители, определяющие степень неявности разностной схемы. Если σ₁= σ₂ =…= 0, получаем полностью явную разностную схему с погрешностью аппроксимации O(Δτ + h²). В случае σ₁= σ₂ =…= 1 схема является полностью неявной с тем же порядком аппроксимации. Значению σ₁= σ₂ =…= 0.5 соответствует схема с порядком аппроксимации O(Δτ² + h²). Вычисления производились по полностью неявной разностной схеме с порядком аппроксимации O(Δτ + h²).

Функции {u, Q } = ƒ, заданные в целых узлах сетки w, в полуцелых узлах определялись по формуле: . Аналогично значения остальных функций {ψ, ρ, T, P, ε } = ƒ в целых узлах находились через известные значения этих функций в полуцелых: . Блок-схема алгоритма расчета показана на рис.1. Алгоритм расчета заключается в последовательном итерировании методом Ньютона двух блоков, первый из которых содержит разностный аналог уравнения энергии, а второй – аналоги уравнений неразрывности, движения и уравнения, отвечающего за перестройку сетки (первых трех уравнений системы (4.1)). Оба блока включались в глобальный итерационный цикл. В тех случаях, когда количество внешних итераций в глобальном цикле превышало 15, или внутренних итераций оказывалось больше 20, временной шаг уменьшался на 10%. Если количество глобальных итераций становилось меньше 4, следующий шаг по времени увеличивался на 1%. В качестве начального приближения для каждой из искомых сеточных функций выбиралось значение .

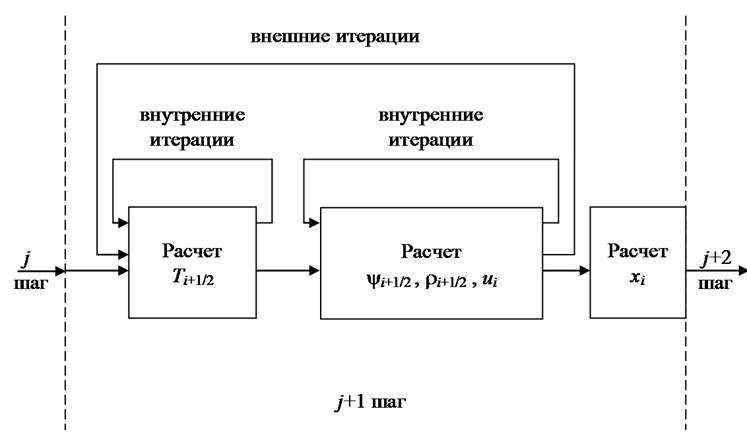
Рис. 1. Блок-схема алгоритма расчета.

На ударной волне требуется выполнение соотношений Гюгонио (3.8). Так как эти уравнения задают связь шести величин, то три из них определяются из решения системы (3.1) – (3.4) в граничных точках, а именно плотность ρ_– и скорость u_– перед фронтом ударной волны и скорость u₊ за фронтом. Остальные три - скорость движения разрыва ʋ_W, плотность ρ₊ за фронтом ударной волны и температура на ней T_–= T₊ находятся из соотношений (3.8).

5. Выбор функции адаптации

Управляемое распределение узлов сетки в методе динамической адаптации осуществляется посредством функции преобразования Q. Функция преобразования для адаптации под большие градиенты решения обычно определяется из принципа квазистационарности [35 - 38], согласно которому необходимо выбрать такую нестационарную систему координат, в которой все физические процессы протекали бы стационарно, а характеризующие их временные производные были бы достаточно малы. Приравнивая временные производные в уравнениях к нулю, получают необходимую функцию преобразования.

Общее решение полной системы уравнений гидродинамики (3.1) – (3.4) определяется суммой функций скорости, плотности и температуры. Эти функции имеют различные пространственно-временные распределения, зачастую противоположного направления. Управляемое распределение узлов сетки для системы уравнений должно учитывать особенности пространственно- временного распределения всех компонент решения.

В задачах гидродинамики в общем случае для определения необходимой функции преобразования можно использовать всю систему уравнений [36 - 38]. В данной работе для определения функции Q используется уравнение энергии (3.3), решение которого зависит от скорости, плотности и теплопроводности. В недивергентной форме уравнение энергии имеет вид:

Исходя из принципа квазистационарности, полагаем, что и получим уравнение:

(5.1)

Учитывая конкретный вид уравнений состояния, и дифференцируя выражение для теплового потока , функцию Q путем несложных преобразований определим из уравнения (5.1):

(5.2)

где re - регуляризующая константа, ограничивающая снизу значение производной при её стремлении к нулю.

В полученном выражении (5.2) слагаемое в первой квадратной скобке, после разностной аппроксимации, оказывает сжимающее воздействие на узлы сетки по переменным u и T. Слагаемое во второй квадратной скобке учитывает влияние нелинейной теплопроводности и оказывает сжимающее воздействие по переменным ρ и T. Последнее слагаемое является слагаемым диффузионного типа. В случае λ(ρ, T ) ≠ 0 оно обладает разглаживающим действием и, в частности, предотвращает пересечение траекторий движения узлов.

Особенности рассматриваемого класса задач определяются двумя факторами. Первый – степенная зависимость коэффициента теплопроводности от температуры. В области низких температур (вблизи нуля) из-за малости коэффициента теплопроводности расталкивающее воздействие диффузионного члена резко уменьшается и его может оказаться недостаточно для оптимального распределения узлов сетки. Второй связан с представлением исходной задачи в виде задачи со свободной границей. Исходная область может при этом увеличиваться на много порядков, соответственно на столько порядков возрастут значения функции y, что также будет вызывать сильное ослабление диффузионной составляющей. Для устранения указанных эффектов целесообразно полученную функцию преобразования Q дополнить функцией, получаемой из диффузионного приближения [37], учитывающей наличие подвижных границ:

где D - коэффициент диффузии, величина которого определяется через геометрические размеры одной ячейки (шаг h), скорости движения граничных точек (ʋ_l, ʋ_r) и минимальное для всей области значение функции (ψ_min):

Кроме того, отношение двух производных от температуры в уравнении (5.2), целесообразно представить в виде производной от медленно меняющейся логарифмической функции:

С учётом приведенных особенностей функция преобразования запишется в окончательном виде:

(5.3)

6. Результаты моделирования

Моделирование задачи о разлете лазерной плазмы в среде с нелинейной теплопроводностью, заключается в решении системы (3.1) – (3.4) с начальными (3.5) и граничными (3.6), (3.7) условиями, соотношениями Гюгонио (3.8) и функцией адаптации (5.3). Поскольку производится сравнение с автомодельными профилями, задача решается с константами соответствующими автомодельному решению [38]:

Функция преобразования (5.3) с учётом конкретной зависимости коэффициента теплопроводности от температуры и плотности λ(T, ρ)= λₒ T⁴ ρ^-2 приобретает вид:

(6.1)

Количество узлов N во всех вариантах расчетов составляет 30, положение которых на всех рисунках отмечено маркерами.

Константы λ₀ при коэффициенте теплопроводности соответствовали безразмерным коэффициентам теплопроводности в автомодельных решениях. Безразмерной константе λₒ = 1 соответствует значение 6.18·10^-24 м⁷/(кг·с³·К⁵) (далее приводятся значения безразмерной константы λₒ, для определенных автомодельных режимов).

Одной из целей данного исследования является сравнение характеристик развивающегося течения плазмы в зависимости от степени нелинейности происходящих в ней тепловых процессов. Моделирование показало, что характер взаимодействия тепловых и гидродинамических потоков качественно изменяется с изменением величины теплопроводности среды. Высокая теплопроводность среды приводит к появлению температурных волн, которые по виду вызываемого ими гидродинамического движения разделяют на два различных типа - сверхзвуковые и дозвуковые. В сверхзвуковых режимах тепло распространяется с конечной скоростью по начальному фону. За фронтом сверхзвуковой температурной волны возникает изотермическая ударная волна. Температурная волна, распространяющаяся с дозвуковой скоростью, располагается за идущей перед ней ударной волной, и характеризуются равенством нулю теплового потока W, максимумом плотности ρ и локальным минимумом температуры T. Смена режимов распространения тепла в рассматриваемом случае зависит от степени нелинейности теплопроводности и определяется значениями параметра λₒ. При значениях λ₀ меньше λ₀ < λ^* некоторого значения безразмерной константы λ^* (для рассматриваемых режимов λ^* ≈ 30) образуется дозвуковой режим распространения тепла, а при обратном соотношении λ₀ ≥ λ^* возникает сверхзвуковой. В данной работе рассматривались один вариант дозвуковой температурной волны с λ₀ = 10, рис. 2, и два с λ₀ = 50 и λ₀ = 200, рис. 3,4, соответствующих сверхзвуковому распространению тепла.

Моделирование дозвукового режима. Температурная волна с λₒ = 10 характеризует дозвуковой режим распространения тепла. После возникновения ударной волны 22 узла попадают в область между плазменным факелом и ударной волной, а в область между ударной волной и внешней границей - 8 узлов. На рис.2 показана динамика температуры, плотности, скорости и якобиана обратного преобразования от начала расчета t = 0 до его окончания t = 1 мс. Пунктир соответствует автомодельному решению, а сплошная линия с маркерами – численному (маркерами показывается положение узлов расчетной сетки). Якобиан обратного преобразования характеризует степень изменения пространственного шага по сравнению с его начальным значением. В момент возникновения ударной волны численное решение не имеет ничего общего с автомодельным. Однако после формирования ударной волны происходит существенное изменение параметров плазменного течения. Возникает дозвуковая температурная волна, изотермическая ударная волна приближается к внешней сверхзвуковой температурной волне. При этом появляются области с резким изменением решения, что приводит к перестройке расчетной сетки. Максимальное сгущение узлов возникает именно на фронтах температурных волн. Численное решение постепенно приближается к автомодельному. При t = 0.01 мс численное решение практически совпадает с автомодельным. На более позднем этапе t = 1 мс численное решение согласуется с автомодельным, и их пространственные профили полностью совпадают, рис.2.

Рис. 2. Результаты расчетов с λₒ= 10 (сплошная линия с маркерами - численное решение, пунктир - автомодельное).

Структура решения в дозвуковом режиме (рис.2) представляется в виде трёх волн, следующих друг за другом (справа налево):

· сверхзвуковой температурной волны, генерируемой ударной волной;

· ударной волны, представляющей собой изотермический скачок с непрерывной температурой и разрывными плотностью и скоростью;

· дозвуковой температурной волны, идущей после ударной.

На фронте сверхзвуковой температурной волны (слабый разрыв) производные от всех функций по x максимальны, но, как и в случае одного уравнения нелинейной теплопроводности без учёта влияния гидродинамики, все физические величины непрерывны. При этом за фронтом потоки тепла, скорость, плотность и температура резко возрастают.

Ударная волна (изотермический разрыв) характеризуется сильным изменением всех величин.

Ещё одной областью резкого изменения всех физических величин является фронт дозвуковой температурной волны. Он характеризуется максимумом плотности, нулевым потоком тепла и локальным минимумом температуры.

Размеры области и пространственных шагов сетки в физическом пространстве характеризуются функцией ψ(x, t), которая на каждый момент времени показывает, во сколько раз изменились размеры шага и области в целом. С учётом того, что рассматривалась область с подвижными границами, у которой скорость движения правой границы (фронт сверхзвуковой температурной волны) намного превосходила скорость движения левой (плазменный фронт), ʋ_T >> ʋ_p, геометрический размер физической области, охваченной возмущением, на указанном промежутке времени увеличился, согласно кривой ψ(x, t), более чем на 10 порядков. Локальные минимумы функции ψ(x, t) приходятся на области наибольших градиентов решения и совпадают с фронтами дозвуковой и сверхзвуковой температурных волн рис.2.

Сверхзвуковой режим. В случае сверхзвуковой температурной волны происходит слабое взаимодействие тепловых процессов с гидродинамическими. При сильной зависимости коэффициента теплопроводности от температуры и высоких скоростях распространения тепла сверхзвуковой режим может стать преобладающей формой теплопереноса.

Рис. 3. Результаты расчетов с λₒ= 50 (сплошная линия с маркерами - численное решение, пунктир - автомодельное).

На рис. 3, 4 показаны пространственные профили газодинамических функций, температуры и функции ψ для λₒ = 50, 200 соответственно. В расчетах использовалась сетка с общим количеством узлов N = 30, распределение которых отмечено маркерами.

Структура решения сверхзвукового режима много проще, чем у дозвукового и её можно представить в виде двух следующих друг за другом волн - температурной и гидродинамической. Скорости распространения их в этом режиме различны, и фронт температурной волны намного опережает фронт гидродинамической, рис.3,4. Положению фронта в каждой из них соответствует слабый и сильный разрыв, соответственно в окрестности которых происходит наибольшее сгущение узлов сетки.

В режиме с λₒ = 50, рис. 3, скорость температурной волны сравнима со скоростью ударной волны, и область сверхзвукового прогрева много меньше, чем для среды с высокой теплопроводностью (λₒ = 200), рис. 4, для которой скорость распространения температурной волны много выше. Пространственные профили газодинамических функций и температуры в режиме с λₒ = 50 при этом отличаются как от режима с дозвуковым распространением тепла с λₒ = 10, так и от режима с λₒ = 200, когда скорость температурной волны существенно превышает скорость ударной волны. Температура и плотность не имеют характерных для дозвукового распространения тепла экстремумов, однако из-за близости скоростей температурной и ударных волн в режиме с λₒ = 50 происходит взаимодействие тепловой и гидродинамической составляющих плазменного течения, что приводит к значительному спаду градиентов плотности и температуры при подходе к фронту ударной волны.

Во всех рассмотренных режимах рис. 2-4 проводилось сравнение полученных численных результатов (сплошная линия с маркерами) с найденными ранее автомодельными решениями для задачи о движении поршня по нулевому температурному фону (пунктирная линия)[38]. К моменту времени t = 0.01 мс численное решение приближается к автомодельному, что свидетельствует о достоверности и качестве получаемых результатов. Наибольшие значения температуры достигаются на левой границе к моменту окончания расчетов t = 1 мс и, как и следовало ожидать, максимальны при меньшей теплопроводности. Для λₒ = 10 – T_max ≈ 3 кэВ, в то время как для λₒ = 200 – T_max ≈ 1.9 кэВ.

Рис. 4. Результаты расчетов с λₒ= 200 (сплошная линия с маркерами - численное решение, пунктир - автомодельное).

Особенности динамической адаптации. С точки зрения построения расчетных сеток с динамической адаптацией краткий анализ дозвукового и сверхзвукового режимов, рис.2-4, позволяет выделить следующие особенности. Оба режима характеризуются тремя подвижными границами: левой подвижной границей с известным законом движения (2.3), фронтом ударной волны (сильный разрыв) и фронтом сверхзвуковой температурной волны (слабый разрыв), распространяющейся по температурному фону, законы, движения которых неизвестны и должны определяться по ходу решения. Все три подвижные границы выделяются явным образом.

Явное выделение левой границы и фронта сверхзвуковой температурной волны позволяет исключить из рассмотрения области тривиального решения. Это особенно актуально в нестационарных задачах, типа задач о распространении волн, в которых возмущение зарождается вблизи одной из границ и распространяется в направлении другой. При длительных временах рассмотрения возмущение охватывает область, размеры которой могут на несколько порядков отличаться от размеров первоначально заданной области. В подобных ситуациях исключение из рассмотрения областей, не охваченных возмущением, играет важную роль и позволяет строить экономичные вычислительные алгоритмы.

Явное выделение фронта УВ позволяет избегать проблем, связанных с разрывными решениями.

Кроме подвижных границ задачи о распространении температурных волн содержат по нескольку областей быстрого изменения всех функций решения: температуры, плотности и скорости. В сверхзвуковом режиме их две, в дозвуковом – три.

Таким образом, динамическая адаптация должна учитывать поведение всех функций: температуры, скорости и плотности, а также наличие подвижных границ. Всем этим требованиям удовлетворяет управляющая функция Q (6.1).

7. Заключение

Моделирование показало, что динамические характеристики плазмы существенным образом связаны со степенью нелинейности происходящих в ней тепловых процессов. К основным особенностям решения уравнений гидродинамики с нелинейной теплопроводностью относятся: наличие трёх подвижных границ и, в зависимости от исследуемого режима, две (сверхзвуковой режим) или три (дозвуковой режим) области быстрого изменения всех функций решения. Все подвижные границы выделяются явным образом. Для двух их них - фронта ударной волны и фронта сверхзвуковой температурной волны, закон движения заранее неизвестен и определяется по ходу решения.

На примере рассматриваемой задачи о разлете плазмы показана эффективность и применимость предлагаемого для решения метода динамической адаптации. Для исследуемой задачи используется функция адаптации, управляющая распределением узлов сетки в зависимости от особенностей решения. Управляющая функция имеет сложный вид и состоит из нескольких слагаемых. Одна часть их определяется из диффузионного приближения и учитывает изменение размеров области под влиянием движения фронта плазменного факела и распространения слабого и сильного разрывов. Другая часть слагаемых определяется из принципа квазистационарности и осуществляет сгущение узлов расчетной сетки в областях больших градиентов температуры, плотности и скорости.

Применение метода динамической адаптации позволяет получать численные решения на сетках с малым числом узлов. Во всех расчетах используются сетки с общим числом узлов N = 30, несмотря на увеличение расчетной области более чем на 10 порядков.

Применение средств визуализации позволяет наглядным образом отображать сложную динамику взаимосвязанных физических процессов и определяемое ими контролируемое распределение узлов расчетных сеток с динамической адаптацией.

Работа выполнена при финансовой поддержке РНФ (код проекта 15-11-00032).

Список литературы

1. Boudesocque-Dubois C., Lombard V., Gauthier S., Clarisse J. An adaptive multidomain Chebyshev method for nonlinear eigenvalue problems: Application to self-similar solutions of gas dynamics equations with nonlinear heat conduction. JCP, 2013, vol. 235, pp. 723-741.

2. Clark D., Tabak M. A self-similar isochoric implosion for fast ignition. Nucl. Fusion, 2007, vol.47, pp. 1147–1156.

3. Murakami M., Sakaiya T., Sanz J. Self-similar ablative flow of nonstationary accelerating foil due to nonlinear heat conduction. Phys. Plasmas, 2007, vol. 14, pp. 269-292.

4. Toque N. Self-similar implosion of a continuous stratified medium. Shock Waves, 2001, vol.11, pp. 157–165.

5. Полянин А.Д., Вязьмин А.В. Точные решения двумерных и трехмерных нелинейных уравнений тепло- и массопереноса. Доклады Академии наук, 2003, т. 390, № 2, с. 214-218.

6. Волосевич П.П., Леванов Е.И. Автомодельные решения задач газовой динамики и теплопереноса. M.: Изд – во МФТИ, 1997.

7. Полянин А.Д., Зайцев В.Ф., Журов А.И. Методы решения нелинейных уравнений математической физики и механики. М.: Физматлит, 2005, 256 c.

8. Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. Москва: Наука, 1992.

9. Андерсон Д., Таннехилл Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен: В 2-х томах. Т. 1: Пер. с англ. М.: Мир, 1990; 384 с.

10. Попов И.В., Фрязинов И.В. Метод адаптивной искусственной вязкости численного решения уравнений газовой динамики. Москва, КРАСАНД, 2014, 288 с.

11. Gladush G.G., Smurov I. Physics of Laser Materials Processing. Theory and Experiment. Springer, 2010, 390 p.

12. Mazhukin V.I. Kinetics and Dynamics of Phase Transformations, in: Metals Under Action of Ultra-Short High-Power Laser Pulses. Ch. 8, pp.219 -276. in: Laser Pulses – Theory, Technology, and Applications”, Ed. by I. Peshko. 2012, p. 544, InTech, Croatia.

13. Lasers in Materials Science. Editors: M. Castillejo, P. M. Ossi, L. Zhigilei. Springer Series in Materials Science, vol. 191, 387 p., Springer, 2014

14. Mazhukin V.I., Mazhukin A.V., Lobok M.G. Comparison of Nano- and Femtosecond Laser Ablation of Aluminium. Laser Physics, 2009, vol. 19, № 5, pp. 1169 - 1178.

15. Morel V., Bultel A., Cheron B.G. Modeling of thermal and chemical non-equilibrium in a laser-induced aluminum plasma by means of a Collisional-Radiative model. Spectrochimica Acta Part B, 2010, vol. 65, pp.830–841.

16. Sy-Bor Wen, Mao X., Liu C., Greif R., Russo R. Expansion and radiative cooling of the laser induced plasma. Journal of Physics: Conference Series 59, 2007, pp. 343–347.

17. Mazhukin V.I., Smurov I., Flamant G. Simulation of Laser Plasma Dynamics: Influence of Ambient Pressure and Intensity of Laser Radiation. J. Comp. Phys., 1994, vol.112, no. 20, pp. 78-90.

18. Synthesis and Photonics of Nanoscale Materials IX. Editors: F. Trager, J. J. Dubowski, D.B. Geohegan. Proceedings of SPIE, 0277-786X, vol. 8245, SPIE, Bellingham, WA, 2012.

19. Lee J.Y., Ko S.H., Farson D.F., Yoo Ch.D. Mechanism of keyhole formation and stability in stationary laser welding. J. Phys. D: Appl. Phys. 2002, vol. 35, pp.1570–1576.

20. Laser-Surface Interactions for New Materials Production. Editors: A.Miotello, P.M.Ossi. Springer Series in Material Science vol.130, 358 pp. Springer, 2010.

21. Chrisey D.B., Hubler G.K. Pulsed Laser Deposition of Thin Films. John Wiley & Sons, New York, 1994.

22. Al-Shboul K.F., Harilal S.S., Hassanein A. Spatio-temporal mapping of ablated species in ultrafast laser-produced graphite plasmas. Appl. Phys. Lett. 2012, vol. 100, 221106, pp. 1-4.

23. Menendez A.-Manjon, Barcikowski S., Shafeev G.A., Mazhukin V.I., Chichkov B.N. Influence of beam intensity profile on the aerodynamic particle size distributions generated by femtosecond laser ablation. Laser and Particle Beams, 2010, vol. 28, pp. 45–52.

24. Синтез наноразмерных материалов при воздействии мощных потоков энергии на вещество. Российская Академия наук. Сибирское отделение. Институт теплофизики им.С.С.Кутателадзе, Новосибирск, 2009, 461 с.

25. Panchatsharam S., Bo Tan, Venkatakrishnan K. Femtosecond laser-induced shockwave formation on ablated silicon surface. J. Appl. Phys., 2009, vol. 105, 093103.

26. Harilal S.S., Miloshevsky G.V., Diwakar P.K., LaHaye N.L., Hassanein A. Experimental and computational study of complex shockwave dynamics in laser ablation plumes in argon atmosphere. Physics of Plasmas, 2012, vol. 9, 083504, pp. 1-11.

27. Mazhukin V.I., Uglov A.A., Chetverushkin B.N. Low-temperature laser plasma near metal surfaces in the high-pressure gases. A Review. Kvantovaya elektronika, 1983, vol. 10, no. 4, 679-701.

28. Mazhukin V., Smurov I., Flamant G. Simulation of Laser Plasma Dynamics: Influence of Ambient Pressure and Intensity of Laser Radiation. J. Comp. Phys., 1994, vol. 112, no. 20, pp. 78-90.

29. Harilal S.S., Brumfield B.E., Phillips M.C. Lifecycle of laser-produced air sparks. Physics of Plasmas, vol.22, pp. 063301(1-13) (2015).

30. Marshak R . An influence of the radiation on the behavior of the shock waves. Phys. Fluids, 1958, no. 1, pp. 24 -29.

31. Liseikin V.D. Grid Generation Methods. Second Edition. Springer, 2010, pp.390.

32. Гильманов А.Н. Методы адаптивных сеток в задачах газовой динамики. Физматлит, 2000, 248 с.

33. Самарский А.А. Теория разностных схем. Москва: Наука. 1989, 616 с.

34. Samarskii A.A., Mazhukin V.I., Matus P.P., Mozolevskii I.E. Monotone Difference Scheme for Equations with Mixed Derivatives. Computers & Mathematics with Application, 2002, vol. 44, pp. 501 - 510.

35. Mazhukin V.I., Demin M.M., Shapranov A.V., Smurov I. The method of construction dynamically adapting grids for problems of unstable laminar combustion. Numerical Heat Transfer, Part B: Fundamentals, 2003, vol.44, N 4, pp. 387 – 415.

36. Бреславский П.В., Мажукин В.И. Динамически адаптирующиеся сетки для взаимодействующих разрывных решений. Журн. вычисл. матем. и матем. физ. 2007, т. 45, № 4, с.717 - 737.

37. Мажукин В. А., Мажукин В.И. Динамическая адаптация в параболических уравнениях. Журн. вычисл. матем. и матем. физ., 2007, т. 47, № 11, с. 1911 – 2034.

38. Бреславский П.В., Мажукин В.И. Метод динамической адаптации в задачах газовой динамики с нелинейной теплопроводностью. Журн. вычисл. матем. и матем. физ., 2008, т.48, № 11, с. 2067–2080.

39. Breslavskiy P.V., Koroleva O.N., Mazhukin A.V. Simulation of the dynamics of plasma expansion, the formation and interaction of shock and heat waves in the gas at the nanosecond laser irradiation. Mathematica Montisnigri, 2015, Vol XXXIII, pp. 5-24

THE EVOLUTION OF THE PLASMA FORMATION IN THE GAS MEDIUM, MODELING WITH VISUALIZATION OF THE GRID NODES DYNAMICS AND THE INTERACTION OF SHOCK AND THERMAL WAVES

P.V.Breslavskiy¹, O.N.Koroleva^1,2, A.V.Mazhukin^1,2

¹M.V. Keldysh Institute of Applied Mathematics, RAS, Moscow, Russia

²National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Moscow, Russia

e-mail: vim@modhef.ru

Abstract

The structure of the shock and thermal waves in the air in the expansion of the plasma is investigated. Simulations have shown that the characteristics of plasma formation, the occurrence of shock and heat waves are dependent on a number of influence parameters and environment properties. The nature of the interaction of thermal and hydrodynamic flow quality varies with the magnitude of the thermal conductivity of the medium. High thermal conductivity leads to thermal waves of two different types - subsonic and supersonic. The structure of the solutions of supersonic mode is represented as two consecutive waves - thermal and hydrodynamic. The subsonic structure of the solution presented in the form of three waves: the isothermal shock wave located between the two (subsonic and supersonic) thermal waves. To solve nonlinear equations of hydrodynamics with a thermal conductivity we use finite-difference approach, combined with the procedure of dynamic adaptation of the computational grid that allows us to explicitly locate the strong (shock waves) and weak (thermal wave front) discontinuities. Visualization and analysis of the results of calculations on a grid containing 30 nodes are carried out in comparison with self-similar solutions found for similar problems. The work was financially supported by the Russian science Foundation (project code 15-11-00032).

Keywords: laser plasma processes, fluid dynamics, dynamic grid adaptation method, nonlinear heat conduction, visualization.

REFERENCES

2. Clark D., Tabak M. A self-similar isochoric implosion for fast ignition. Nucl. Fusion, 2007, vol.47, pp. 1147–1156.

3. Murakami M., Sakaiya T., Sanz J. Self-similar ablative flow of nonstationary accelerating foil due to nonlinear heat conduction. Phys. Plasmas, 2007, vol. 14, pp. 269-292.

4. Toque N. Self-similar implosion of a continuous stratified medium. Shock Waves, 2001, vol.11, pp. 157–165.

5. Poljanin A.D., Vjaz'min A.V. Tochnye reshenija dvumernyh i trehmernyh nelinejnyh uravnenij teplo- i massoperenosa [Exact solutions of two-dimensional and three-dimensional nonlinear equations of heat and mass transfer]. Reports of the Academy of Sciences, 2003, vol. 390, № 2, pp. 214-218. [in Russian]

6. Volosevich P.P., Levanov E.I. Avtomodel'nye reshenija zadach gazovoj dinamiki i teploperenosa [Self-similar solutions of gas dynamics and heat transfer]. Publishing house MIPT, 1997. [in Russian]

7. Poljanin A.D., Zajcev V.F., Zhurov A.I. Metody reshenija nelinejnyh uravnenij matematicheskoj fiziki i mehaniki [Methods for solving nonlinear equations of mathematical physics and mechanics]. Fizmatlit, 2005, 256 p. [in Russian]

8. Samarskij A.A., Popov Ju.P. Raznostnye metody reshenija zadach gazovoj dinamiki [Difference methods for solving of gas dynamics]. Nauka, 1992. [in Russian]

9. Tannehill J.C., Anderson D.A., Pletcher R.H. Series in Computational and Physical Processes in Mechanics and Thermal Sciences, Taylor & Francis, 1997.

10. Popov I.V., Frjazinov I.V. Metod adaptivnoj iskusstvennoj vjazkosti chislennogo reshenija uravnenij gazovoj dinamiki [The method of adaptive artificial viscosity numerical solution of the equations of gas dynamics]. KRASAND, 2014, 288 p. [in Russian]