ВИЗУАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СОДЕРЖИМОГО ФАЙЛОВ ПРИ ПРОВЕДЕНИИ КОМПЬЮТЕРНЫХ ЭКСПЕРТИЗ С ЦЕЛЬЮ ВЫЯВЛЕНИЯ ДАННЫХ, БЛИЗКИХ К ПСЕВДОСЛУЧАЙНЫМ
В.С. Матвеева, A.В. Епишкина
Национальный исследовательский ядерный университет «МИФИ», Россия
vesta.matveeva@gmail.com, avepishkina@mephi.ru
Содержание
2. Предпосылки для разработки нового подхода
3. Оценка статистических свойств файла
4. Визуальное представление содержимого файлов
5. Программная реализация полученных результатов
Аннотация
При проведении компьютерной экспертизы важным этапом является поиск файлов с данными, близкими к псевдослучайным. Существующие подходы основаны на проверке статистических свойств данных в файле с использованием наборов тестов для оценки свойств последовательностей псевдослучайных чисел. Одни подходы не адаптированы под файловую систему и являются затратными по времени и ресурсам, другие дают значительную вероятность ошибок I или II рода. Поэтому авторами проведено исследование в этой области и предложен подход для оценки статистических свойств данных в файле на основе их визуального представления. С использованием этого подхода было разработано программное средство, тестирование которого показало, что вероятность ошибки I рода при обнаружении псевдослучайных данных сводится к нулю, а вероятность ошибки II рода для распространенных форматов файлов меньше 1 %.
Ключевые слова: Псевдослучайные данные, зашифрованные данные, плотность распределения, сжатые форматы файлов, вейвлет-анализ.
1. Введение
Поиск данных, близких к псевдослучайным, в файловой системе проводится в рамках компьютерной экспертизы при решении следующих задач:
- Обнаружение зашифрованных криптостойкими алгоритмами данных как признака сокрытия информации. При таком поиске также можно обнаружить зашифрованные модули вредоносных программ, которые скрываются в системе.
- Обнаружение файлов или областей, перезаписанных псевдослучайными данными, как признака удаления данных без возможности их восстановления.
- Обнаружение скрытых областей и файловых систем, содержимое которых зашифровано криптостойким алгоритмом, как признака работы вредоносных программ или сокрытия информации.
Если искомые файлы спрятаны в каталоги со служебными файлами операционной системы или намеренно переименованы, изменены, то выявить их путем обычного поиска невозможно. Автоматизированный поиск может осуществляться эффективно только на основании оценки статистических свойств содержимого файлов, для чего могут использоваться наборы тестов: NIST [1], DIEHARD [2], тесты Кнута [3], TestU01 [4], AIS31 Methodology [5], с помощью которых оцениваются свойства псевдослучайных последовательностей, поэтому они могут применяться для решения поставленных задач.
Подходы, отличные от применения наборов тестов, либо имеют значительные ошибки в обнаружении искомых данных, либо применяются для оценки отдельных свойств псевдослучайных данных.
Тесты безусловно не адаптированы под файловую систему, но для проверки отдельных файлов как массива бит или байт могут применяться. Для анализа всех файлов в файловой системе их применение является затратным по времени и ресурсам, так как целесообразно применение совокупности тестов, многие из которых основаны на сложной многократной проверке с разными параметрами, и, как следствие, число проверок для одного файла увеличивается. Кроме этого, на выходе получаются результаты по набору тестов, которые сложно однозначно интерпретировать. Также на выходе тестов оценка проводится на основе интегральной характеристики, которая не отражает наличие или отсутствие локальных отклонений в распределении содержимого файла.
Из существующих автоматизированных средств поиска зашифрованных файлов на практике используется программное обеспечение «Passware Forensic Kit» [6], модули которого внедрены в криминалистические комплексы: Belkasoft Evidence Center [7], EnCase Forensic [8], Oxygen Forensic Kit+Passware Edition [9]. Средства используют некоторые тесты оценки свойств псевдослучайных последовательностей и сигнатуры известных форматов файлов. В ходе тестирования модуля поиска зашифрованных файлов выявлено ограничение на минимальный размер для файлов без заголовка (> 273 КБ) и наличие значительных ошибок в обнаружении искомых файлов.
Поэтому авторами предложен способ визуализации содержимого файлов, который помогает оценить распределение байт в файле с целью поиска отклонений от распределения, характерного для псевдослучайной последовательности.
2. Предпосылки для разработки нового подхода
На основании статей [10, 11] основными «конкурентами» псевдослучайных и зашифрованных данных являются сжатые форматы файлов: pdf, docx, rar, zip, wmv, jpg, png, mpg и др.
По определению, данному в [1], последовательность псевдослучайных чисел обладает свойствами равномерности распределения элементов и их независимости между собой. Наборы тестов, приведенные во Введении, созданы для проверки именно этих свойств.
Алгоритмы шифрования, используемые современными средствами криптографической защиты (СКЗИ) и вредоносными программами, обладают следующими свойствами:
- хорошее перемешивание входных данных или, иначе говоря, зависимость каждой координатной функции отображения от возможно большего числа переменных. Полное перемешивание достигается в том случае, если существенной переменной является каждая переменная используемого отображения. Переводя это определение на алгоритмы шифрования получаем, что изменение одного символа входной последовательности открытого текста влияет на каждый выходной символ зашифрованного текста. Такая зависимость проверяется строгим лавинным критерием, которому удовлетворяют все используемые современными средствами алгоритмы шифрования;
- использование комбинаций шифров замены и шифров перестановки при реализации используемых алгоритмов шифрования;
- равномерность распределения элементов последовательности и их независимость между собой, так как свойства выходных последовательностей используемых алгоритмов шифрования близки к свойствам псевдослучайных последовательностей.
Таким образом, статистические свойства входных данных не влияют на статистические свойства данных после зашифрования этими алгоритмами.
Никаких требований к статистическим свойствам сжатых данных не выдвигается. Основной целью операции сжатия является уменьшение размера сжимаемых данных и возможность восстановить исходные данные по сжатым с потерями или без в зависимости от задачи: файлы-архивы используют сжатие без потерь, в то время как большинство форматов файлов-изображений, звуковых и видеофайлов – сжатие с потерями.
Алгоритмы сжатия не удовлетворяют строгому лавинному критерию, поэтому свойства сжимаемых данных влияют на свойства сжатых данных.
Сжатие без потерь, применяемое, например, для файлов-архивов, основывается на вероятностных алгоритмах сжатия данных, которые выравнивают частоты возникновения элементов сжимаемых данных: часто встречающиеся элементы заменяются короткими кодовыми словами, редко встречающиеся – более длинными. Таким образом, в сжатых данных выравнивается вероятность встречаемости символов, которая заведомо равна для значений символов в псевдослучайной последовательности. Например, обычные текстовые данные сжимаются по объему в разы, чего нельзя сказать о сжатии зашифрованных или псевдослучайных данных. Применение вероятностных алгоритмов сжатия приводит к тому, что сжатые данные имеют высокую энтропию и удовлетворяют некоторым тестам на равномерность распределения.
Сжатие с потерями, применяемое для аудио, видео файлов и файлов-изображений, имеет отличие от предыдущего метода сжатия только в части выделения значимых компонентов сжимаемых данных, к которым впоследствии применяется сжатие без потерь [2]. Таким образом, после применения алгоритмов сжатия с потерями выходные данные также имеют высокую энтропию и удовлетворяют некоторым тестам на равномерность распределения.
Остальные статистические свойства сжатых данных зависят исключительно от самих сжимаемых данных, наличия в них определенных значений символов и используемой комбинации алгоритмов.
Приведенные методы сжатия основываются на алгоритмах замены: RLE, LPC, DC, MTF, VQ, SEM, Subband Coding, Discrete Wavelet Transform, РРМ, кодирование Хаффмана и Шеннона-Фано, арифметическое и вероятностное кодирование и др. [11] Повторяющиеся последовательности элементов или заданные в словаре последовательности элементов заменяются на коды. Словарь кодов может строиться в процессе кодирования или задаваться при начале кодирования.
Хотя стоит отметить, что для улучшения качества сжатия применяются алгоритмы перестановки: BWT, MFT и др. Целью перестановки является такое преобразование сжимаемой последовательности, чтобы поместить элементы с одинаковыми значениями рядом с возможностью однозначного обратного преобразования после такой перестановки. Поэтому в ходе перестановки наоборот достигается бóльшая зависимость между элементами, которые впоследствии заменяются на коды.
Сжатые данные проходят многие статистические тесты. Удовлетворение свойству равномерности достигается за счет выравнивания частот встречаемости символов, однако оно справедливо с точки зрения распределения имеющихся в сжатых данных символов, но может не достигается с точки зрения распределения всех возможных значений символов.
Удовлетворение свойству независимости распределения элементов оцениваемой последовательности достигается за счет требования восстановления данных после сжатия и самой природой сжатия. Независимость символов внутри блоков сжатых данных и между блоками не гарантируется алгоритмом сжатия, поскольку целиком зависит от самих сжимаемых данных, а сами значения символов, которые стоят рядом, добавляются в сжатые данные без учета их взаимной зависимости. Таким образом, алгоритмами сжатия не обеспечивается отсутствие определенных зависимостей между блоками сжатых данных, однако они могут обеспечиваться сжимаемыми данными.
Таким образом, применяемые даже в совокупности алгоритмы замены и перестановки не обеспечивают хороших перемешивающих свойств сжимаемых данных и не удовлетворяет в полном объеме всем статистическим свойствам для проверки равномерности распределения элементов псевдослучайной последовательности и независимости элементов между собой. В связи с этим оценка их статистических свойств может быть использована для отделения сжатых форматов файлов от файлов, содержащих псевдослучайные данные.
Для этого предлагается использовать упрощенную модель оценки, которая приведена в разделе «Оценка статистических свойств файла».
3. Оценка статистических свойств файла
Существующие подходы, которые описаны выше, работают с
числовыми последовательностями, поэтому представим файл 
в виде конечной последовательности
байтов 
длины 
, где 
– мощность множества 
. Такая последовательность
обычно анализируется байт за байтом или по блоками слева направо для установки
равномерности распределения элементов и независимости их относительно друг
друга.
Для решения поставленных задач вводится статистическая
гипотеза 
:
«Свойства рассматриваемой последовательности близки к свойствам псевдослучайной
последовательности», и альтернативная ей 
: «Свойства рассматриваемой последовательности
отличны от свойств псевдослучайной последовательности».
Рассмотрим эту последовательность иначе. Нанесем
последовательность на плоскость, по оси абсцисс которой отложены значения от 0
до 
, а по оси
ординат – от 0 до 255. Заполним эту плоскость точками 
, такими что 
– номер байта в последовательности
байт файла, а 
–
значение этого байта.
Введем определение равномерности распределения точек на этой плоскости.
Определение
Точки на плоскости распределены равномерно, если вероятность
встретить точку на плоскости во фрагменте минимального размера 
одинакова для любого
фрагмента такого размера и равна 
Таким образом, на ней отсутствуют области
повышенной и пониженной концентрации точек.
Логично предположить, что для псевдослучайных данных и зашифрованных данных точки на этой плоскости будут нанесены равномерно. Это следует из того, что подпоследовательность псевдослучайной последовательности также псевдослучайна, а значит, имеет равномерное и независимое распределение по всем своим значениям. Т.к. элементы наносятся на плоскость в соответствии с их положением в последовательности и значением, то на этой плоскости они должны располагаться равномерно. Пример фрагмента такой плоскости (далее – плоскость распределения) приведен на риc. 1.
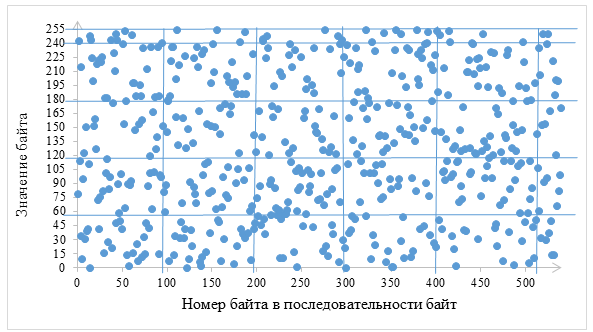
Рис. 1. Фрагмент плоскости, точки на которой задаются элементами последовательности байт файла
Разобьем эту плоскость на фрагменты размером 
, 
и 
задаются произвольно.
Для каждого фрагмента произведем подсчет плотности распределения точек в фрагменте относительно размера фрагмента, т.е.:
. (2)
Если распределение на плоскости равномерное, то и плотность
распределения элементов в каждом фрагменте близка к значению 
Осуществляя подсчет плотности каждого фрагмента, можно сформировать вектор плотностей, т. е. выполнить преобразование:
(3)
где 
– количество получившихся фрагментов в
результате прохождения по содержимому плоскости методом скользящего окна
размером .
Причем движение от фрагмента к фрагменту методом скользящего
окна целесообразно осуществлять слева направо, так как скопление значений байт
одного значения будут располагаться горизонтально. При вертикальном же движении
захватываются все значения, которые имеются в подпоследовательности длины , в связи с чем
существенный всплеск или падение значений плотности будет сглажен.
Также стоит отметить, что размер окна целесообразно выбирать, исходя из размера тестируемой последовательности (файла), так как целью является получить больший размер вектора плотностей, что при небольшом размере файла достигается путем уменьшения размера фрагмента.
Полученные для разных форматов файлов последовательности
плотностей будут существенно отличаться от последовательности плотностей для
файлов с псевдослучайными и зашифрованными данными в связи с наличием служебной
информации в файлах, которая задает распределение значений байт в файле, и
особенностей структуры и содержания файлов. Для псевдослучайных и зашифрованных
данных плотности для фрагмента любого размера должны быть близки к эталонному
значению 
В то
время как для остальных форматов файлов служебная информация, выраженная в
скоплении заданного диапазона значений байт на плоскости, будет приводить к
наличию всплесков и падений в значениях плотностей в последовательности. В
связи с этим имеется возможность производить идентификацию зашифрованных и
псевдослучайных данных путем проверки последовательности плотностей на наличие
выраженных отклонений от среднего значения плотностей в векторе плотностей. Примеры
таких распределений приведены в разделе «Визуальное представление содержимого
файлов».
4. Визуальное представление содержимого файлов
Получим визуальное представление зависимости значения
плотности от ее порядкового номера в последовательности плотностей для
различных форматов файлов с высокой энтропией. Возьмем файлы размером от 1МБ до
10МБ, размер окна: 
, и получим последовательность плотностей для
каждого из них.
Для эксперимента выбраны файлы сжатых форматов, представители которых описаны в таблице 1 вместе с соответствующими значениями некоторых математических статистик.
Таблица 1. Список представителей форматов файлов для тестирования
|
Имя файла |
Значение энтропии |
Значение величины «Критерия Хи-квадрат» |
Значение по методу Monte Carlo |
Арифметическое среднее |
|
test.jpg |
7.97 |
429711.58 |
3.23 |
124.59 |
|
test.ods |
7.99 |
1956.72 |
3.13 |
126.94 |
|
test.aes |
7.99 |
248.46 |
3.14 |
127.47 |
|
test.wmv |
7.97 |
99963.81 |
3.09 |
126.15 |
|
test.mp3 |
7.94 |
1542810.27 |
3.11 |
125.11 |
|
test.pdf |
7.90 |
218024.01 |
3.14 |
124.79 |
|
test.mpeg |
7.89 |
769440.90 |
3.28 |
116.38 |
|
test.7z |
7.99 |
231.99 |
3.14 |
127.49 |
|
test.zip |
7.99 |
933.50 |
3.16 |
127.48 |
|
test.m4a |
7.87 |
757648.04 |
3.17 |
118.03 |
|
test.mp4 |
7.98 |
244899.91 |
3.04 |
130.73 |
Как видно из таблицы, все выбранные файлы имеют высокую энтропию, характерную для зашифрованных файлов и файлов с псевдослучайными данными. Ниже на рис. 2 – 12 приводятся примеры фрагментов распределений плотностей, получаемые для файлов разных форматов.
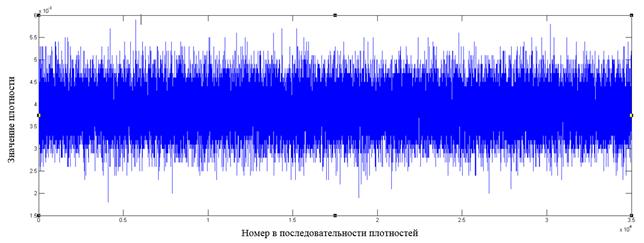
Рис. 2. Фрагмент распределения значений плотностей для файла, зашифрованного алгоритмом AES
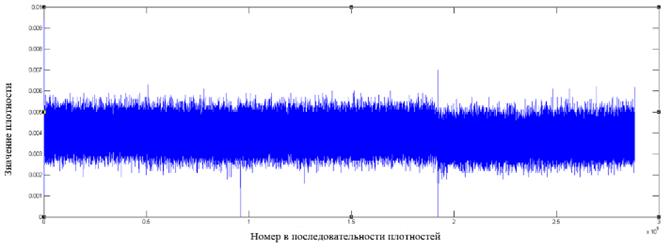
Рис. 3. Фрагмент распределения значений плотностей для файла формата jpg
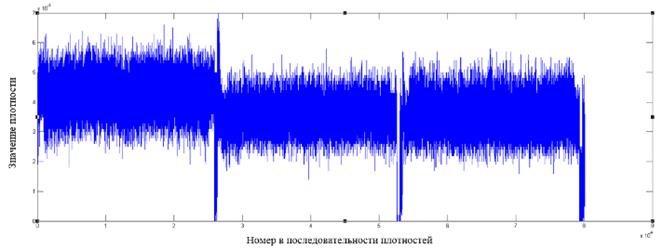
Рис. 4. Фрагмент распределения значений плотностей для файла формата m4a
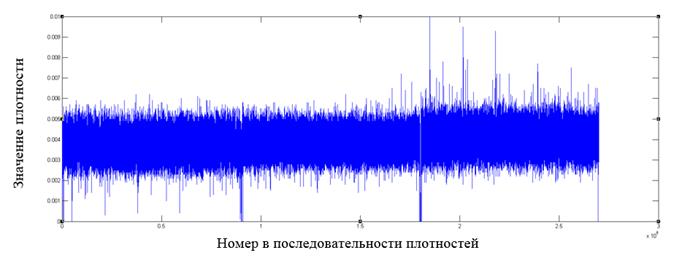
Рис. 5. Фрагмент распределения значений плотностей для файла формата mp4
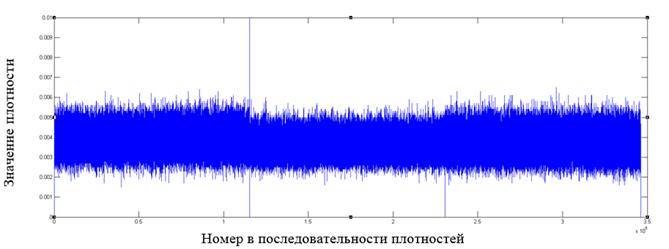
Рис. 6. Фрагмент распределения значений плотностей для файла формата mp3
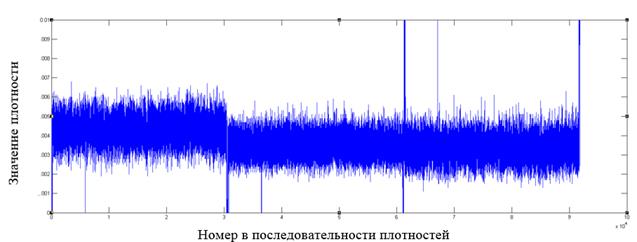
Рис. 7. Фрагмент распределения значений плотностей для файла формата mpeg
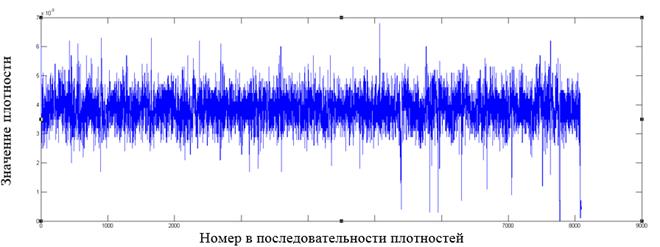
Рис. 8. Фрагмент распределения значений плотностей для файла формата ods
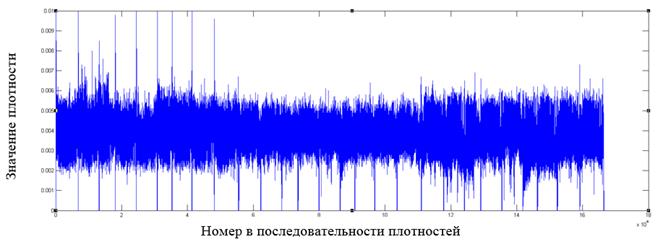
Рис. 9. Фрагмент распределения значений плотностей для файла формата odt
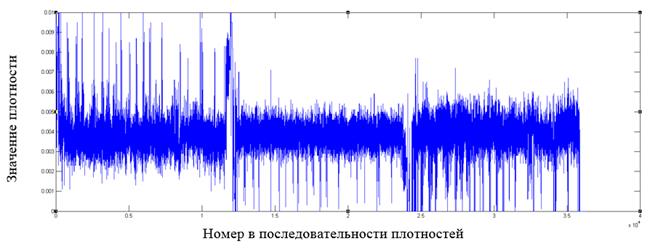
Рис. 10. Фрагмент распределения значений плотностей для файла формата pdf
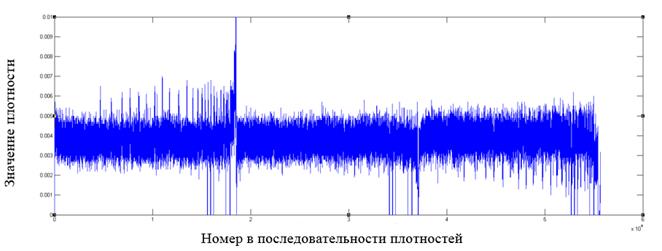
Рис. 11. Фрагмент распределения значений плотностей для файла формата wmv
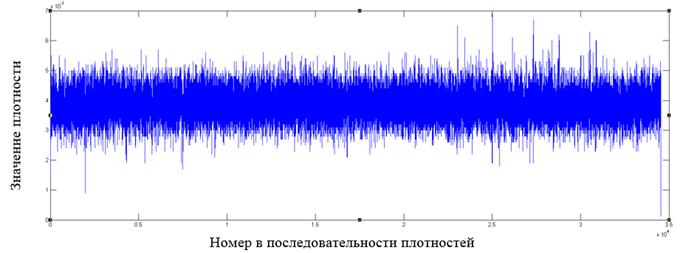
Рис. 12. Фрагмент распределения значений плотностей для файла формата zip
Как видно из графиков, у форматов файлов, отличных от зашифрованных алгоритмом AES, имеются в распределении плотностей видимые всплески относительно среднего значения, которые могут служить показателем неоднородности распределения байт в файле.
Причем экспериментально было установлено, что для сжатых
форматов и зашифрованных файлов среднее значение плотности колеблется около
значения 
.
Построение подобных графиков дает наглядное представление о распределении внутри файла и позволяет выявлять выраженные локальные отклонения от среднего значения как признака неоднородности в распределении байт.
5. Программная реализация полученных результатов
На основании приведенного метода визуализации содержимого файла было проведено исследование статистических характеристик содержимого файлов разных форматов и файлов, содержащих псевдослучайные данные. В результате исследования получены пороговые значения моментов первого и второго порядка, рассчитываемых по содержимому файла, а также вейвлет-коэффициентов с базисной функцией Хаара, рассчитываемых с разными параметрами. На основании полученных результатов разработано программное средство, архитектура которого приведена на рис. 13.
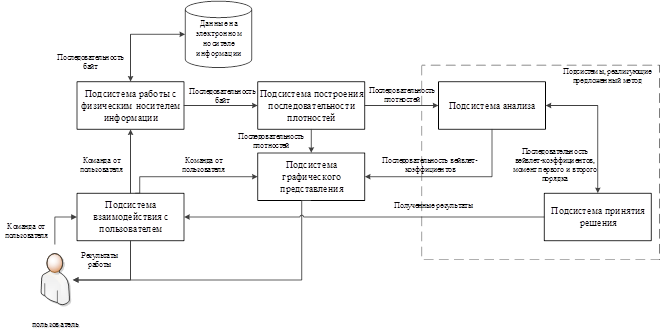
Рис. 13. Архитектура разработанного программного средства
Передаваемые данные отмечены на рис. 13 над стрелками между подсистемами.
Программное средство реализовано на языке программирования C# для операционных систем Microsoft Windows и файловой системы NTFS.
Результаты тестирования средства приведены в разделе «Тестирование».
6. Тестирование
Тестирование средства проведено на коллекции «filetypes1» [12], которая включает файлы различных форматов и файлы с псевдослучайными данными. Коллекция содержит 1 793 различных файла. В коллекции содержатся 445 файлов со случайными данными, которые в таблице 2 приведены отдельно.
При проведении тестирования использовался размеры окон: и 
.
Результаты тестирования приведены в таблицах 2, 3 и сравниваются с результатами тестирования критерия «Хи-квадрат» на равномерность (уровень значимости выбран 0.01) для той же коллекции.
Таблица 2. Вероятность ошибки I рода, полученная в результате тестирования
|
Оцениваемая величина Название коллекции |
Количество файлов |
Предлагаемый подход Вер.ошибки I рода (100x100) |
Предлагаемый подход Вер. ошибки I рода (50x20) |
Хи-квадрат Вер.ошибки I рода |
|
filetypes1(random) |
445 |
0% |
0% |
1,798% |
Таблица 3. Вероятность ошибки II рода, полученная в результате тестирования
|
Оцениваемая величина
Название коллекции |
Количе-ство файлов |
Предлага-емый подход Вер.ошибки II рода (100x100) |
Предлагаемый подход Вер.ошибки II рода (50x20) |
Пересечение результатов по двум размерам окон |
Хи-квадрат Вер.ошибки II рода |
|
filetypes1 |
1 348 |
9,718% |
8,754 |
7,806% |
7,715% |
Экспериментально проверено, что описанный подход дает нулевую вероятность ошибки I рода, а вероятность ошибки II рода обусловлена наличием в коллекции файлов-изображений формата jb2. Данные, сохраненные в этом формате, определяются всеми проверяемыми тестами как близкие к псевдослучайным. Кроме этого, указанный формат не являются распространенным графическим форматом. В отсутствие этого формата вероятность ошибки II рода у предложенного подхода меньше 1%. Для уменьшения значения вероятности ошибки I рода можно уменьшать уровень значимости для расчета порогового значения в критерии «Хи-квадрат» на равномерность, однако это приводит к увеличению вероятность ошибки II рода.
7. Заключение
При проведении компьютерной экспертизы стоит задача поиска данных, близких по свойствам к псевдослучайным. Существующие подходы основываются на статистических тестах оценки свойств псевдослучайных последовательностей, среди которых одни тесты не адаптированы под файловую систему и являются затратными по времени и ресурсам, другие имеют значительные вероятности ошибок I или II рода.
Авторами предложен способ визуализации содержимого файлов, основанный на построении новой последовательности из последовательности байт. В силу статистических свойств различных форматов файлов, в том числе сжатых, такое распределение будет иметь выраженные отклонения, которые могут быть выявлены при визуализации распределения.
В статье приведены примеры графиков для разных форматов файлов и показана разница между распределениями в файлах с псевдослучайными/зашифрованными данными и файлами сжатых форматов файлов. Показано, что путем визуализации содержимого файлов можно легко выявлять отклонения в распределении байт, в том числе локальные, что является признаком отсутствия псевдослучайных данных в нем.
На основании предложенного подхода визуализации было реализовано программное средство, которое в автоматическом режиме позволяет производить поиск файлов с содержимым, близким к псевдослучайным данным, на основе вейвлет-анализа. Результаты тестирования средства показывают, что вероятность ошибки I рода при поиске сводится к нулю, а вероятность ошибки II рода для файлов распространенных форматов файлов < 1%.
Список литературы
- NIST SP800-22. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications, NIST, 2010, p. 131.
- Marsaglia G. The Marsaglia random number CDROM including the diehard battery of tests. [Электронный ресурс], 1995, URL: http://stat.fsu.edu/pub/diehard/.
- Кнут Д. Э. Искусство программирования. Получисленные алгоритмы, М.: Издательский дом «Вильямс», 2003, 3-е изд, стр. 63 – 69.
- L’Ecuyer P., Simard R. TestU01: A C library for empirical testing of random number generators. ACM Transactions on Mathematical Software (TOMS), 2007, vol. 33, I. 4, no. 22.
- Killmann W., Schindler W. A proposal for: Functionality classes for random number generators. Tech. Rep. 2. Bundesamtf¨ur Sicherheit in der Informationstechnik (BSI), 2011, p. 133.
- Passware Kit Forensic 2015; http://www.lostpassword.com/kit-forensic.htm (last accessed 03/17/2015)
- Belkasoft Evidence Center 2015; http://ru.belkasoft.com/ru/ec (last accessed 03/17/2015)
- Using Passware Kit Forensic with EnCase; http://www.lostpassword.com/encase.htm (last accessed 03/17/2015)
- Oxygen Forensic Suite; www.oxygen-forensic.com/ (last accessed 03/17/2015)
- Jozwiak I., Kedziora M. and Melinska A. Theoretical and Practical Aspects of Encrypted Сontainers Detection. Digital Forensics Approach, Dependable Computer Systems, Springer Berlin Heidelberg, Berlin, Germany, 2011, pp. 75-85.
- Weston P., Wolthusen S. Forensic Entropy Analysis of Microsoft Windows Storage Volume. Information Security for South Africa, 2013, pp. 1 - 7.
- Digital corpora Filetypes1, 2014, URL: http://digitalcorpora.org/corp/nps/files/filetypes1/
VISUAL REPRESENTATION OF FILE CONTENT DURING FORENSIC ANALYSIS TO DETECT FILES WITH PSEUDORANDOM DATA
V.S. Matveeva, A.V. Epishkina
National Research Nuclear University «MEPhI»
vesta.matveeva@gmail.com, avepishkina@mephi.ru
Abstract
Searching for pseudorandom data is an important stage during forensic analysis. Existing approaches are based on verifying statistical properties of file contents by means of test suites for estimation of pseudorandom sequences. Some approaches are not adapted for work with file system and are time/resource consuming. The others have significant type I or II errors. That is why authors have conducted a research in this field and suggest an approach to estimate statistical properties of file contents by means of their visual representation. The approach was used for development of program for searching pseudorandom data. Its testing shows that type I error is reduced to zero and type II error for popular file formats is less than 1%.
Keywords: Pseudorandom data, encrypted data, density of distribution, compressed file formats, wavelet analysis.
References
- NIST SP800-22. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications, NIST, 2010, p. 131.
- Marsaglia G. The Marsaglia random number CDROM including the diehard battery of tests. 1995, URL: http://stat.fsu.edu/pub/diehard/.
- Knuth, D. E. The Art of Computer Programming, Volume 2: Seminumerical Algorithms, 3rd ed., Addison-Wesley Pearson Education, Canada, 1997.
- L’Ecuyer P., Simard R. TestU01: A C library for empirical testing of random number generators. ACM Transactions on Mathematical Software (TOMS), 2007, vol. 33, I. 4, no. 22.
- Killmann W., Schindler W. A proposal for: Functionality classes for random number generators. Tech. Rep. 2. Bundesamtf¨ur Sicherheit in der Informationstechnik (BSI), 2011, p. 133.
- Passware Kit Forensic 2015; http://www.lostpassword.com/kit-forensic.htm (last accessed 03/17/2015)
- Belkasoft Evidence Center 2015; http://ru.belkasoft.com/ru/ec (last accessed 03/17/2015)
- Using Passware Kit Forensic with EnCase; http://www.lostpassword.com/encase.htm (last accessed 03/17/2015)
- Oxygen Forensic Suite; www.oxygen-forensic.com/ (last accessed 03/17/2015)
- Jozwiak I., Kedziora M. and Melinska A. Theoretical and Practical Aspects of Encrypted Сontainers Detection. Digital Forensics Approach, Dependable Computer Systems, Springer Berlin Heidelberg, Berlin, Germany, 2011, pp. 75-85.
- Weston P., Wolthusen S. Forensic Entropy Analysis of Microsoft Windows Storage Volume. Information Security for South Africa, 2013, pp. 1 - 7.
- Digital corpora Filetypes1, 2014, URL: http://digitalcorpora.org/corp/nps/files/filetypes1/