VISUALIZATION AND ANALYSIS OF THE EXACT ALGORITHM FOR KNAPSACK PROBLEM BASED ON EXHAUSTIVE SEARCH

M.A. Kupriyashin, G.I. Borzunov

National Research Nuclear University “MEPhI”, Russia

kmickle@yandex.ru; parproc@gmail.com

Contents

1. Introduction

2. Visualization of computational complexity of the packing weighing operation.

3. Analysis of workload balancing by means of scientific visualization

4. Summary

References

Annotation

Knapsack packing vector testing procedures for the parallel exhaustive search algorithm have been analyzed. Graphs of computational complexity to test a single knapsack vector have been obtained via experiment for different values of knapsack element sizes. Diagrams of load balancing have been obtained and analyzed for the case when lexicographic sequence is split into equal-length segments.

Keywords: knapsack problem, exhaustive search, parallel computing

1. Introduction

Presently the interest in the knapsack cryptosystems resistant to the known attacks is increasing [1-3]. As a result, the exact algorithm for the knapsack problem based on exhaustive search attracts more attention, as it used to determine the practical strength of such cryptosystems. The applicability area of the algorithm should be broadened with the help of the latest advances in parallel computation [4]. It is necessary to take into account that the efficiency of massively parallel program depends essentially on even workload balancing [5]. In this paper we use scientific visualization to analyze the quality of workload balancing during massively parallel computation based on the exact knapsack problem algorithm based on exhaustive search.

The knapsack problem is a hard combinatorial optimization problem known in general case to be NP-complete and thus taking exponential time to be solved [6]. Let us define a vector , where are positive integers. Every  represents the weight of the i ^th object. Let us call such vector a knapsack vector. Among all the objects available, some may be inside the knapsack, while all the others are not. Let us define a vector  where  so that  the i ^th object is being put into the knapsack. Let us call these vectors “packing vectors’. The sum  equals to the overall weight corresponding to the  packing vector. Also, let us denote the total number of objects  as the task size. The problem goes as follows: find all packing vectors so that their weights are exactly equal to a pre-defined value, or either prove that no such packing exists.

The exhaustive search algorithm, being the simplest to implement and requiring the least amount of memory, is based on enumeration of all feasible packing vectors and finding among them those with the target weight. Packing vectors are generated in lexicographic order. As  possible packing vectors exist for a task of size , the time complexity of the algorithm is high enough to limit its applicability.

Development of parallel implementation for the exhaustive search algorithm and usage of massively parallel computation systems provides significant reduction of the algorithm run time. As long as we consider weighing a single packing to be the basic operation (for computational difficulty analysis), near-perfect distribution of workload between any number of computational nodes (m) is feasible.

Lexicographic order is natural for binary vectors enumeration. It provides  obvious conversions between the ordinal number of the vector and its representation, and vice versa. With that in mind, it is only necessary for the supervisor to send the ordinal numbers of the first and the last vector in their sub-task. In this case the expected time complexity class for the whole task is , and each worker processor has a thread with  complexity class. Thus the speedup value equals to , and the efficiency value for all the worker processors is . These estimates show that whenever the number of worker processors is very low in comparison with the number of packing vectors, the near-perfect workload balancing is achieved. However, the quality of these estimates was proved to depend on the selection of the basic operation [5], so additional research on the choice is in order. The rest of the paper describes the research on the problem by means of scientific visualization.

2. Visualization of computational complexity of the packing weighing operation.

There are reasons to believe that the amount of time required to weigh a packing depends on the properties of the packing vector. Thus, this amount of time is not constant. With that in mind, it is necessary to review the estimates on parallel algorithm efficiency given above. Let us study the packing weighing operation in detail. We have a binary representation of the packing vector as well as the knapsack vector as the input. In order to calculate the weight of the given packing it is possible to implement two different methods.

The first way to do that is to check each of the  consecutively and add  to the sum whenever  is non-zero. So, given the task of size  this implementation of this method requires  comparison operations and to  additions. Let us denote this method as IF-ADD for future reference.

The second way to do that is to compute   directly. This approach takes   additions and  multiplications. Let us denote this method as MUL_ADD.

The pseudo code implementation of both of the proposed methods is given below.

// TASK_SIZE — Task size (=n);

// *a[] — array of knapsack vector elements;

// p_list — concatenation of packing vectors to be analyzed;

// cursor — offset of the current pacing vector bit in the p_list array;

// *weight — buffer that accumulates the weight value;

// y — counter

*weight = 0;

for (int y = 0; y < TASK_SIZE; y++)

       if (p_list[cursor++]) *weight += (*a[y]);       // IF-ADD method

       // ИЛИ

       *weight += (p_list[cursor++])*(*a[y]);          // MUL-ADD method

if (*weight == *w) /* Solution processing<…> */;

A computational experiment was conducted to compare the efficiency of these two methods. Both of the algorithms were used to weigh a set of packing vectors, each having a set number of non-zero components, varying from 1 to 15. For each of these 15 groups 320000 vectors were used. The set of vectors was generated by filtering the lexicographic sequence based on the required number of non-zero coordinates and repeatedly reusing the filter output.

The dependence between the numbers of non-zero packing vector coordinates and the run time of the described methods is presented in Fig. 1.

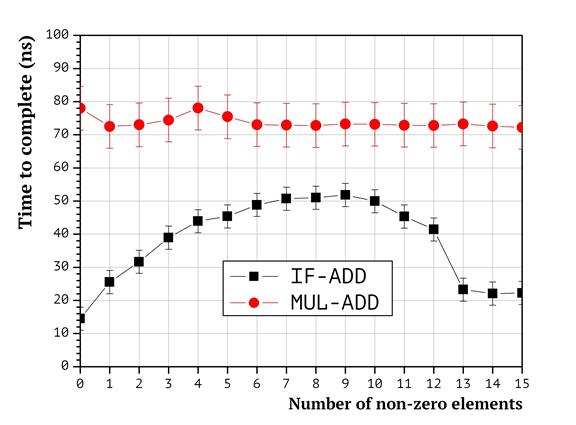
Fig. 1. MUL-ADD and IF-ADD efficiency comparison

Here on Fig. 1 and later on the graphs error bars indicate the maximal value of mean square deviation across the whole subset. The graph analysis shows that the run time of both the MUL-ADD and the IF-ADD implementations are distinctive, and the efficiency of the MUL-ADD implementation is faster under all the studied circumstances. Accordingly, in the rest of this paper only the IF-ADD method is taken into account.

This experiment, as well as all the other experiments described in this paper the following hardware and software platform configuration has been used: Intel Core 2 Quad Q9505 CPU with 4 cores; 8GB DDR3 RAM () with the Visual Studio 2013 Express IDE. Microsoft Visual C++ compiler version 12 was used to build the source codes. The operational system used is Microsoft Windows 7 Enterprise 64-bit with Service Pack 1 installed.

All the experiments described in this paper aimed to analyze chosen basic operations. Therefore, no hardware or software means of parallel computation were used. All data on efficiency and speedup values for parallel algorithms are  the estimates that do not take the latency of communication channels into account. Nevertheless, the quality of these estimates is deemed enough, as the task in question does not have significant data interconnection — the need for synchronization only exists during the initial load distribution.

The pseudo codes given above are only applicable if the length of the knapsack vector elements, as well as the maximal sum of thereof, does not exceed the size of processor registers. Otherwise, the implementation of addition takes much more effort, as it is necessary to split numbers into parts, and bit carry operations are to be taken into account as well. Later in the paper, the term “long arithmetic” is used to indicate that the processor registers capacity may be exceeded. In case of long arithmetic, the following implementations for addition and comparison are used.

// ELEMENT_SIZE — size of knapsack elements (number of memory blocks needed to store a single knapsack vector coordinate)

// __INT64_HI_DIGIT — bit mask corresponding to the highest bit in a 64-bit unsigned integer

// __INT64_LO_DIGIT — bit mask corresponding to the rest 63 bits of a 64-bit unsigned integer

// add_tmp — buffer that temporarily stores sums for pairs of memory block

#define __INT64_HI_DIGIT 0x8000000000000000

#define __INT64_LO_DIGIT 0x7FFFFFFFFFFFFFFF

// Addition (the result replaces the first operand)

_inline LargeAdd(unsigned __int64* a, unsigned __int64* b)

{

       unsigned __int64 add_tmp;

       for (int z = 0; z < ELEMENT_SIZE; z++)

       {

                   add_tmp = a[z] + b[z];

                   if (add_tmp&__INT64_HI_DIGIT)

                   {

                               a[z + 1]++;

                               a[z] = add_tmp&__INT64_LO_DIGIT;

                   }

                   else a[z] = add_tmp;

       }

}

// Comparison

_inline LargeCmp(unsigned __int64* a, unsigned __int64* b)

{

       for (int z = 0; z < ELEMENT_SIZE; z++)

                   if (a[z] != b[z]) return 0;

       return 1;

}

A computational experiment was conducted to evaluate the impact of long arithmetic on the time required to weigh knapsack packings. Knapsack vector elements taking 1, 2, 4 and 8 memory blocks were used (that corresponds to 64, 128, 256, 512 bits respectively). The results of the experiment are given in Fig. 2.

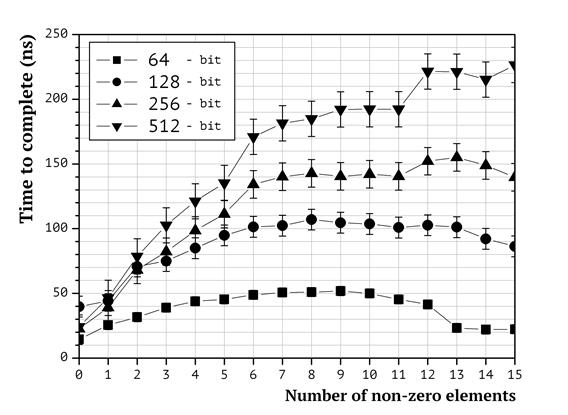
Fig. 2. Dependence between the size of knapsack vector elements and the complexity of weighing

On the graph in Fig. 2, the following dependence is clearly seen: the larger the size of knapsack vector elements, the faster the weighing time grows as the number of non-zero elements in packing vectors increases. The reason for this kind of behavior is the increased number of processor operations required to implement number additions as the size of operands grows. While for small numbers the impact is negligible, for 512-bit numbers “the hardest” packing takes 10 times longer to weigh than “the easiest” packing.

Let us note that large knapsack vector elements are common in cryptographic applications. In particular, superincreasing knapsack vectors always have large elements that take at least as many bits to store, as many elements there are in the knapsack vector.

3. Analysis of workload balancing by means of scientific visualization

Let us split the lexicographic sequence into consecutive subsequences of equal lengths. The data on these sequences obtained via experiment with task size  is presented in Fig. 3. The whole sequence has been split into 2, 4 and 8 subsequences of equal sizes and distributed between 2, 4 and 8 processors respectively  .

The distribution of packing vectors between processors in terms of the number of non-zero elements in them is presented as the diagrams in Fig. 3 (for two processors), Fig. 4 (four processors) and Fig. 5 (eight processors). The diagrams have been generated as follows: at first, the distribution of the packing vectors based on the number of non-zero elements was plotted (points in the left hand part of the diagram correspond to packing vectors with less non-zero items, in the right hand part – with the most non-zero elements. The height of the diagram corresponds to the number of packing vectors with exactly the given amount of non-zero elements. Then the surface of the diagram was split into non-intersecting shapes, so that the same processor would analyze only the vectors belonging to the same shape. The surface area of the shape equals to the number of packing vectors in it. The shapes are colored in accordance with the processor ordinal numbers (the less the processor number, the closer to the start the subsequence it analyzes). Red corresponds to the first processor, green to the second, etc. Dark blue corresponds to the 8^th processor. As shown above, the time required to weigh a packing vectors depends on the number of non-zero coordinates in it. In terms of the diagrams on Fig. 3-5, it means that the workload on each of the processors depends not only on the surface area of the shape, but also on the horizontal shift of the shape (representing the number of non-zero elements in packing vectors). That is, whenever the shape for a processor is shifted to the right, the corresponding task has more non-zero coordinates; thus, the workload value for the processor is higher.

It is obvious that the shapes in Fig. 3-5 are significantly shifted. Various shifts indicate that the workload distribution is not uniform.

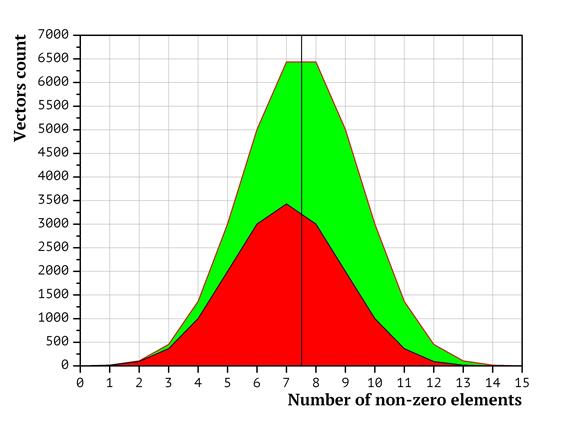
Fig 3. Distribution of packing vectors based on the total number of non-zero elements in them for two processors

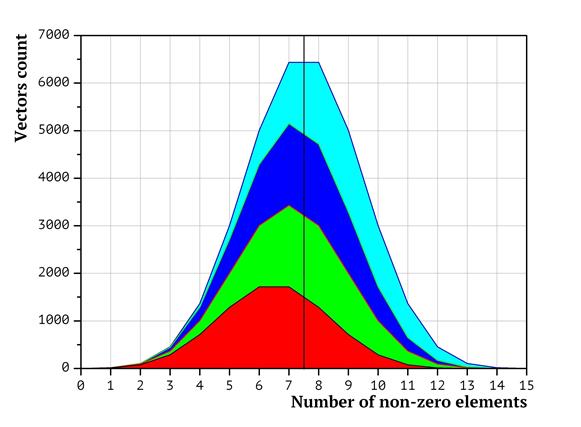
Fig 4. Distribution of packing vectors based on the total number of non-zero elements in them for four processors

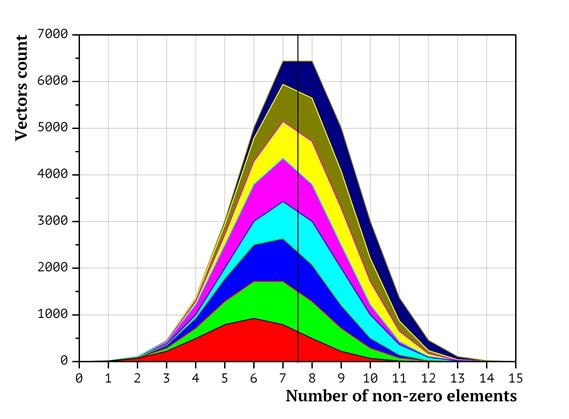
Fig 5. Distribution of packing vectors based on the total number of non-zero elements in them for eight processors

Additional diagrams in Fig 6-8 reflect the respective differences in the total counts of zero and non-zero coordinates for each of the processors. Bar numbers represent the ordinal numbers of the processors and the magnitude of the bars reflects the deviation of relative concentration of non-zero elements from the average value. For example, according to the diagram in Fig. 8, the first processor (its workload corresponds to the red shape in Fig. 5) gets a subsequence of knapsack vector having 60% zero and 40% non-zero coordinates in total for as long as the lexicographic sequence is split in the way described above (so the first bar has the value of “-10%”. On the contrary, the eights processor gets a subsequence with 60% non-zero and 40% zero elements. This emphasizes the workload imbalance.

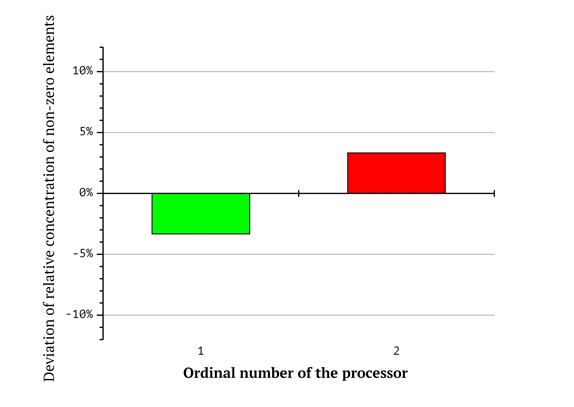
Fig 6. Deviation of relative concentration of non-zero elements from the average value for two processors

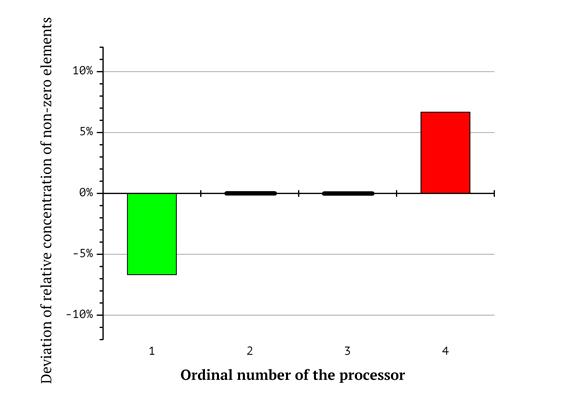
Fig. 7. Deviation of relative concentration of non-zero elements from the average value for four processors

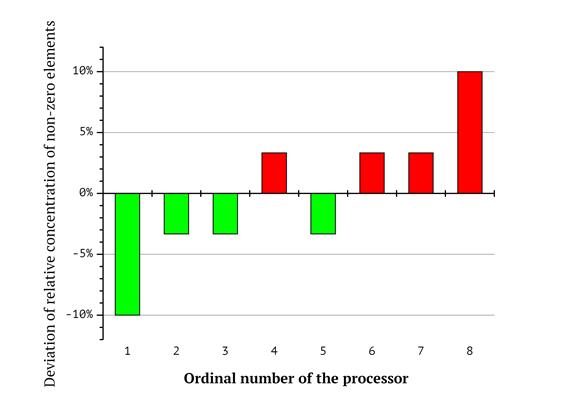
Fig. 8. Deviation of relative concentration of non-zero elements from the average value for eight processors

Therefore, visualization of the packing vector distribution formed by the split lexicographic sequences clearly shows that the processors with bigger ordinal numbers typically get more “hard” packing vectors, while the processors with lesser numbers get more “easy” packing vectors. The shapes in the Fig 3-5 being shifted either to the left (where the “easier” vectors are located or to the right (where the “harder” vectors are located reflect this.

The non-uniform distribution of the workload remains as the number of subsequences increases. Let us split each of the eight subsequences (for eight processors) into 16 more subtasks (blocks) and represent the result as a three-dimensional graph. The color of each block corresponds to each of the eight processors (as described above). Vertical axis represents the relative number of non-zero elements in each of the blocks. Horizontal axis indicates the ordinal number of the block — the less the number the closer its position to the start of the subsequence. The resulting diagram is given in Fig. 9.

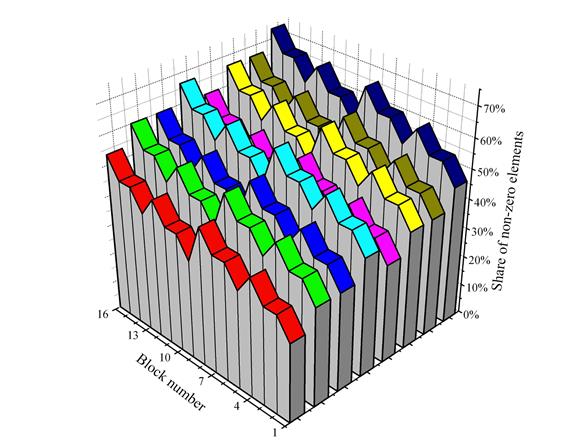
Fig. 9. Variations of block difficulties inside the subsequences.

The three-dimensional representation allows us to evaluate the difficulty variations inside each of the subsequences, as well as to compare the difficulty of each subsequence. The representation also highlights the regular internal structure of the subsequences (that is present due to the number of the subsequences being equal to ). It is obvious that the internal structures of all the subsequences are identical, but the relative share of non-zero elements in them is inconsistent. Moreover, the subsequence with larger ordinal number is not guaranteed to be harder; for example, the subsequence belonging to the fifth processor (purple) is “easier” than the sequence belonging to the fourth processor (cyan). This is also easy to see in Fig. 8.

As long as long arithmetic is concerned, the imbalance described above has a severe impact on workload balancing. The deviation of the workload represented as relative share of non-zero elements in the task may be evaluated with the help of diagrams like the ones on Fig. 6-8. For example, the task for the first processor in Fig. 8 only contains 40% non-zero elements (60% zero elements), while the eights processor has 60% non-zero elements and only 40% zero elements in its task.

Taking into account the research on long arithmetic impact, we can state that splitting the lexicographic sequence into subsequences of similar lengths leads to inadequate load balancing.

Taking both the packing speed experiment and the experiments on zero and non-zero element distribution given above into account, we can improve the estimate on the efficiency rate for the parallel implementation.

Let us choose processing of a single zero element as the basic operation. Also, let us consider the dependence between the weighing time and the number of non-zero elements in the packing vector to be linear. According to the graph in Fig. 2 the time needed to check a single non-zero element is determined as  relatively to the chosen basic operation. So, the average work needed to process a single element increases from  to  as the number of non-zero coordinates grows from (0) to (15). With these figures in mind, we can estimate the total workload for each of the processors.

The results obtained via the method described above are presented on the diagram in Fig. 10. The colors represent the sizes of knapsack vector elements. Note that in case the workload balancing is perfect, all the values given must be equal to (1) regardless of the processor count.

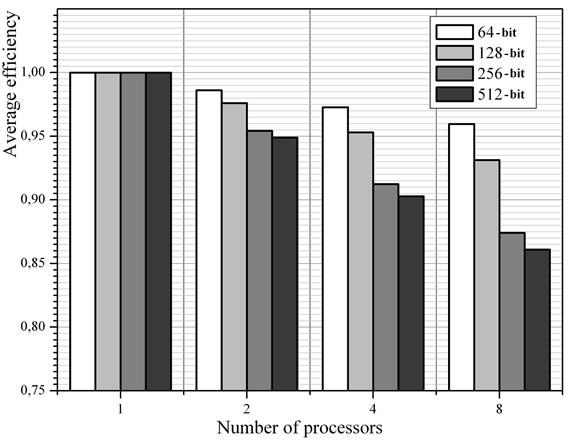
Fig. 10. Impact of the distribution of packing vectors between the processors

Fig.10 shows that the efficiency of parallel computation significantly deteriorates as either the processor count or the sizes of knapsack vector elements increase. For example, when eight processors are used to solve the knapsack problem with 512-bit knapsack elements, the average efficiency of the processors involved is as low as (0.86).

Let us emphasize the problem further by modeling the performance of the parallel algorithm for the knapsack problem. Firstly, let us take the experimental data from Fig. 2 to determine the time it takes to process a zero and a non-zero element. In accordance with the graph, let us set the processing time of zero elements to 25ns (the leftmost part of the graph) and the processing time for non-zero elements to 90ns (rightmost part). Second, we use the diagram in Fig. 9 to determine the performance of each processor in each of the blocks measured in vectors per second. Comparing this value integrated over time with the total size of the subsequence (the number of vectors in the task the processor is on) we get the percentage of the vectors processed by the moment. The method given was used to obtain a set of samples with a rate of . Using the samples, we can build a dynamic visualization of the task.

The modeling results are given in Fig. 11 as an animated GIF image.

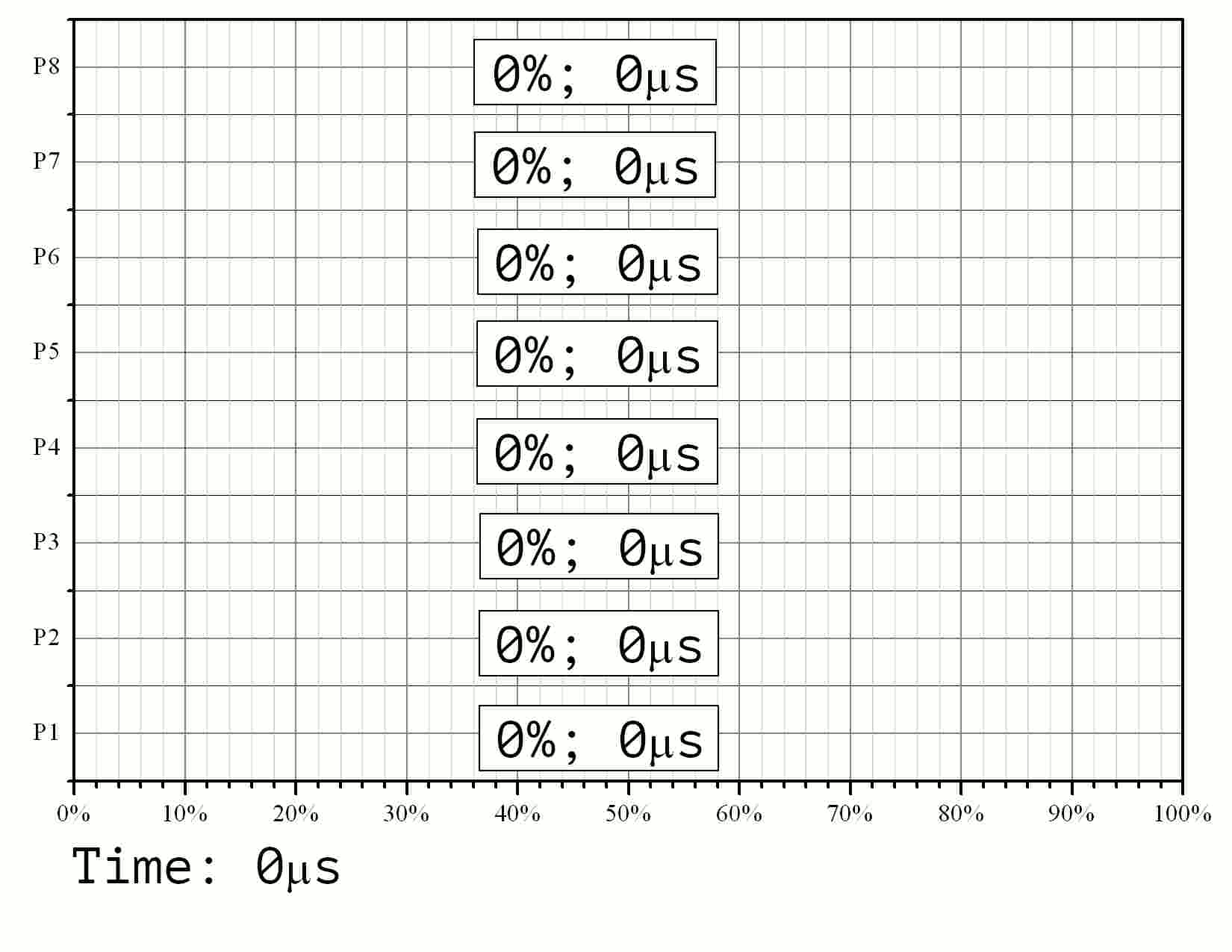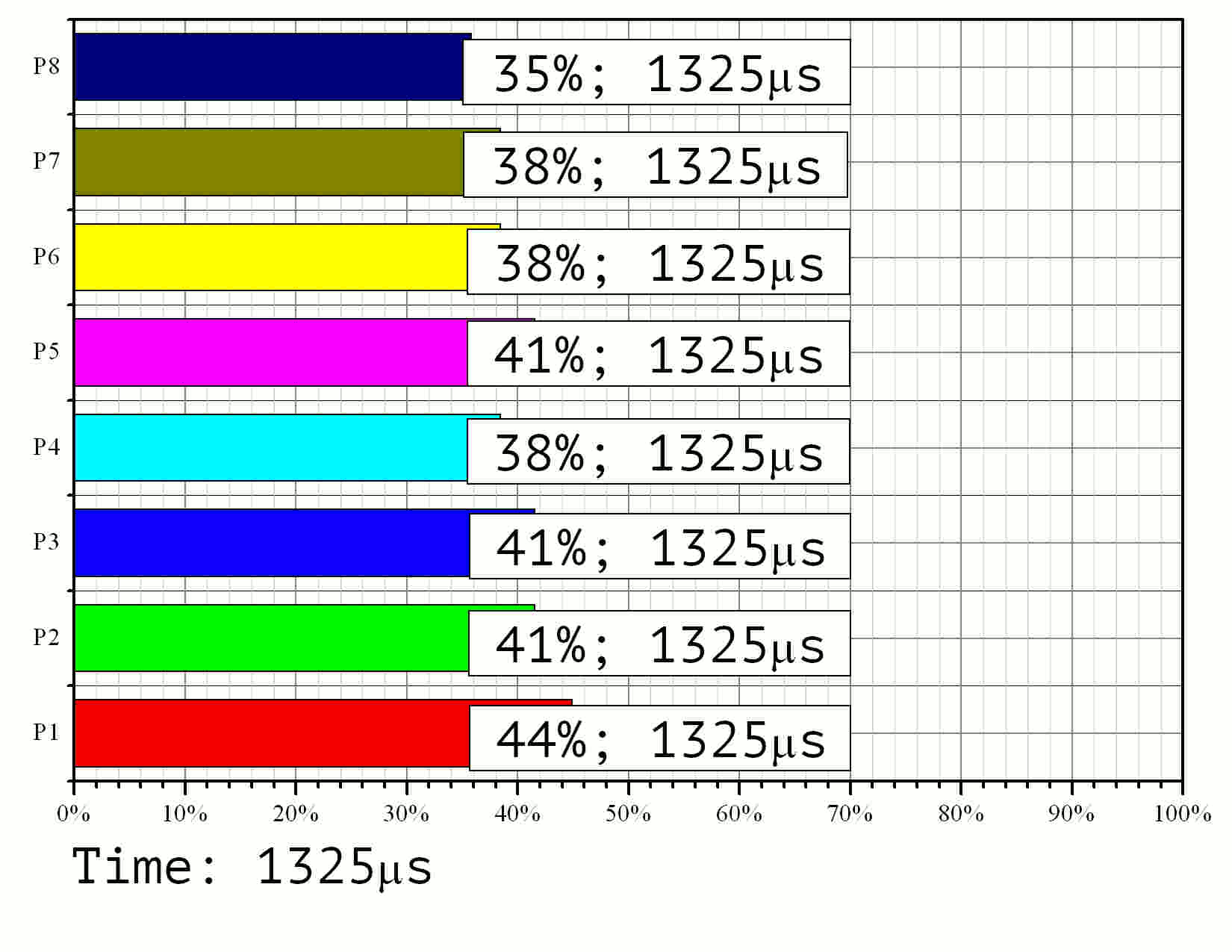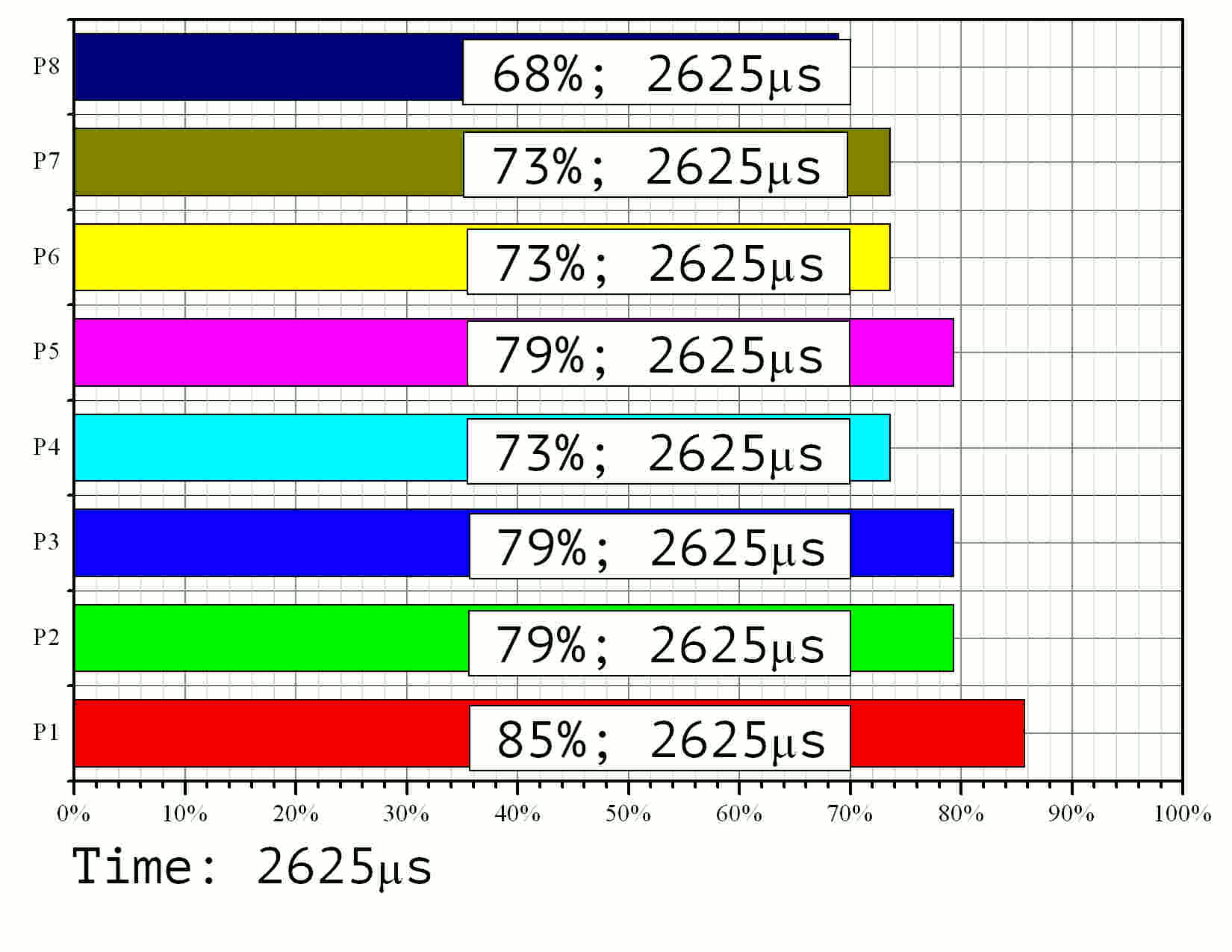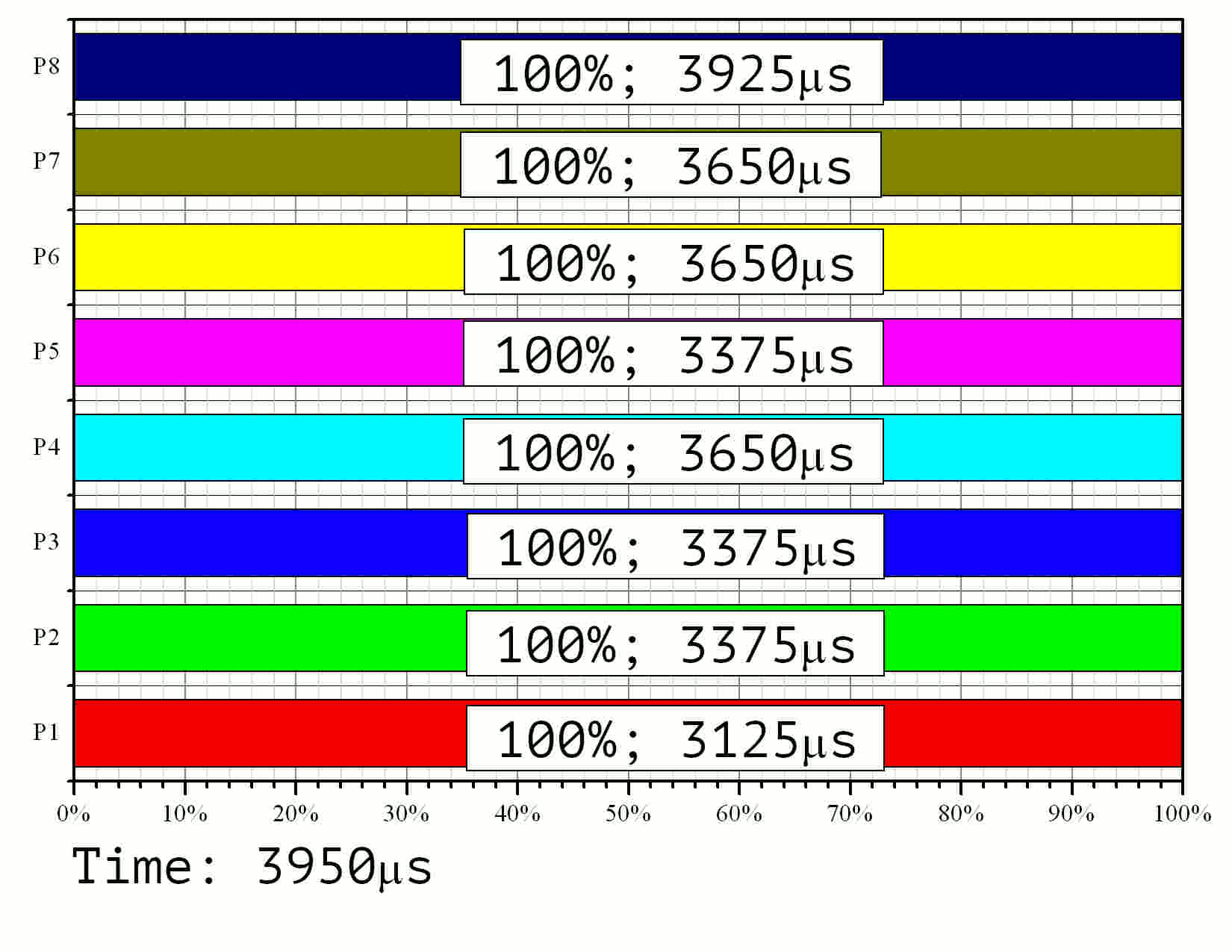
Fig 11. Modeling of the parallel implementation with 8 processors, task size ----- and 128-bit knapsack elements.

Observation of the run time shows that the processor with the least workload is only active 80% of the time. The corresponding efficiency value is (0.8). Among the rest 8 processors three were working with (0.86) efficiency, three more with (0.93). The speedup rate resulted to (7.17) instead of the theoretical limit of (8.0). The average efficiency rate equals to (0.9). This value should be (0.93) according to the diagram in Fig. 9 — the difference is due to different choices of element processing times given on the graph in Fig. 2.

4. Summary

Splitting the lexicographic sequence into continuous subsequences of equal lengths causes the workload to be significantly imbalanced. Thus, a more sophisticated method of load balancing that takes the described factors into account is required to implement the parallel algorithm for the knapsack problem based on exhaustive search efficiently.

References

1. Osipyan V.O. Razrabotka matematicheskih modelej sistem peredachi i zashhity informacii [Developing mathematical models of information security and transfer], 2007. [In Russian]
2. Kate A., Goldberg I. Generalizing cryptosystems based on the subset sum problem. International Journal of Information Security, 2011, vol. 10, no. 3, pp. 189–199.
3. Kupriyashin M.A., Borzunov G.I. Analiz sostojanija rabot, napravlennyh na povyshenie stojkosti shifrosistem na osnove zadachi o rjukzake [Analysis of papers on knapsack ciphersystems security enhancement]. Bezopasnost Informatsionnykh Tekhnology, 2013, no 1, pp. 111-112. [In Russian]
4. Gergel V.P. Teorija i praktika parallel'nyh vychislenij [Theory and practice of parallel computing]. INTUIT, Binom. Laboratoriya Znaniy, 2007. [In Russian]
5. Borzunov G.I., Petrova T.V., Suchkova E.A. Povyshenie jeffektivnosti masshtabirovanija nabora zadach pri poiske jekstremal'nyh razbienij [Task set scaling efficiency enchancement in extremal partitions search]. Bezopasnost Informatsionnykh Tekhnology, 2011, no. 3, pp. 116–120. [In Russian]
6. Karp R.M. Reducibility Among Combinatorial Problems The IBM Research Symposia Series. ed. R.E. Miller, J.W. Thatcher, J.D. Bohlinger. Springer US, 1972. pp. 85–103.