ВИЗУАЛИЗАЦИЯ ПРОСТРАНСТВА ПРИЗНАКОВ В МЕТОДЕ КОМПАКТНОГО ОПИСАНИЯ КОНТУРОВ

Д.А. Борисоглебский¹, Е.В. Чепин²

¹ ЗАО АИР, Россия

² Национальный исследовательский ядерный университет «МИФИ», Россия

denis.borisoglebsky@gmail.com, evchepin@gmail.com

Содержание

1. Введение

2. Обзор существующих методов представления форм силуэтов на цифровых изображениях

3. Описание основной идеи предлагаемого метода

4. Постановка задачи исследования пространства признаков

5. Выбор исходных данных

6. Схема эксперимента

7. Эксперимент

8. Заключение

9. Программное обеспечение

Список литературы

Аннотация

В статье рассмотрен один из подходов к решению задачи представления форм силуэтов на цифровых изображениях. Приведены результаты исследования разработанного контурного метода представления силуэтов в виде последовательности параметризованных примитивов с точки зрения покрытия пространства признаков. Полученные результаты были исследованы с помощью методов научной визуализации, что позволило быстро и наглядно сделать выводы о характере поведения анализируемых данных и применить соответствующие методы для решения поставленных в эксперименте задач. Разработанный метод будет полезен при решении практических задач представления формы силуэтов для различных областей обработки изображений.

Ключевые слова: представление формы силуэта, параметризованный примитив, регрессионный анализ, кластерный анализ, визуализация многомерных данных.

1. Введение

Метод научной визуализации (МНВ) широко используется во многих областях науки и техники. Следуя [25], можно определить общую задачу этого научного подхода следующим образом: «исходным анализируемым данным при помощи компьютера ставится в соответствие их некоторая статическая или динамическая графическая интерпретация, которая визуально анализируется, а результаты анализа этой графической интерпретации затем истолковываются по отношению к исходным данным» [25]. Области использования МНВ можно условно разделить на два больших сегмента:

1. визуализация данных, полученных с реальных физических или производственных установок/процессов;
2. визуализация данных, полученных как результат модельных/расчетных вычислительных экспериментов.

Важно, что в обоих случаях речь идет о том, что в результате применения МНВ мы получаем новую информацию об исследуемых процессах, которую невозможно или более сложно получить другими путями [25 - 26].

Примеров применения МНВ для наглядного представления результатов физического эксперимента достаточно много, например: визуализация наноструктур [25, 27, 31], моделирование процессов наноэлектроники [27], 3D-моделирование излучающей плазмы [28], визуализация в задачах вычислительной механики жидкости и газа [29], геометрические модели в биологии [32 - 33], визуализация задач геофизики [34], визуализация столкновений элементарных частиц [35, 38].

Рассматриваемая в данной статье проблема представления формы силуэта через описание контуров объектов на 2D-изображениях не является типичной задачей обработки изображений и МНВ. Цель такого подхода к обработке изображений состоит в том, чтобы получить компактное описание границ контуров объектов для задач, требующих, например, пересылки таких описаний по каналам передачи данных с малой пропускной способностью или для хранения большого количества описаний контуров в памяти. Важно отметить, что предложенный метод обладает свойством обратного преобразования, то есть обеспечивает восстановление контура по его описанию с приемлемой на практике точностью. Однако, вычислительная сложность предложенного подхода весьма высока, что приводит к необходимости использовать технологии параллельно программирования и методы обработки больших массивов данных (Big data).

Как правило, задача интерпретации больших массивов данных легко решается, если известно какую информацию и как извлекать. В контексте рассматриваемой задачи анализ многомерного пространства признаков (МПП) сводится к кластерному анализу. В этом случае ситуация меняется – с одной стороны задача кластеризации множества точек в МПП решается одним из большого количества существующих алгоритмов, с другой стороны – корректность результатов сильно зависит от информации о количестве искомых кластеров. Наиболее быстрый и простой способ узнать количество скоплений точек – визуализация МПП. При визуализации пространств, у которых больше трех измерений, также возникает необходимость понижения размерности данных в силу невозможности человеческого сознания воспринимать геометрические размерности больше трех [30]. Для понижения размерности данных используются методы регрессионного анализа.

Во многих задачах, связанных с обработкой изображений, разработчик сталкивается с необходимостью представления исходной видеоинформации в «сжатом» виде, в том смысле, что пиксельное изображение необходимо представить в виде какого-то структурированного описания, которое содержит всю важную информацию об особенностях конкретного изображения. Такая ситуация характерна, например, в задачах распознавания образов на изображениях, задачах компьютерной графики, системах технического зрения для робототехники, системах «понимания» изображений, системах для автоматизированных производств, ГИС-технологиях и многих других. Классическими подходами для решения подобных проблем являются теории, основанные на использовании систем признаков различного типа, с помощью которых, решение задачи «переводится» в пространство этих признаков [37]. Подобная идеология достаточно эффективно работает в ряде задач, однако она, безусловно, не обеспечивает полноты и достаточной универсальности в задачах обработки сложных по содержащейся информации 2D и, особенно, 3D изображений.

В данной статье рассматривается метод представления контуров цифрового изображения в виде последовательности параметризованных примитивов. Этот метод является модификацией метода семантического описания контуров [1-2], использующего идеи К.Фу [3] о структурном описании с подходом к решению задачи определения вида эмпирической модели [4]. Основная идея усовершенствованного метода описана в работах [5-10] и сводится к решению двух задач – декомпозиции контура и представлению каждого из фрагментов в виде параметризованного примитива.

Декомпозиция контура осуществляется на основе анализа функции кривизны. Подбор примитива и нахождение его параметров подразумевают применение нормирования к каждому фрагменту по преобразованиям параллельного переноса, масштабирования, поворота и зеркального отражения от осей. Для нормированного фрагмента вычисляется характеристика формы его кривой – вектор признаков (ВП). Эта характеристика позволяет перевести поиск параметризованного примитива для рассматриваемого фрагмента в МПП. Данный подход подразумевает предварительное обучение классификатора фрагментов контура, позволяющее получить множество ВП - точек в МПП, в которых определено соответствие признака формы кривой и параметризованного примитива.

Рассматриваемый метод был разработан в лаборатории «Робототехника» кафедры «Компьютерные системы и технологии» НИЯУ МИФИ в рамках проведения работ над мобильным робототехническим комплексом (МРК) [11-14].

2. Обзор существующих методов представления форм силуэтов на цифровых изображениях

Классическая теория представления формы силуэта (shape representation) делит все существующие подходы на две основные группы. В зависимости от исходной информации разделяют контурное (contour-based) и областное (region-based) представления [15 - 16].  В свою очередь, каждое из направлений делится на две подгруппы, в зависимости от локальности используемой информации различают структурные и глобальные. Рассматриваемый метод компактного описания контуров относится к структурному контурному подходу. Контурный подход позволяет представить форму рассматриваемого объекта наиболее компактно по сравнению с областным описанием. Структурный подход увеличивает гибкость описания.

Существует несколько основных групп методов, реализующих структурное описание контуров: кусочно-линейная аппроксимация [17 - 18], подбор параметров примитива [19-21], вычисление параметров примитивов с проверкой точности представления [1, 22 - 23], применение интерполяции сплайнами к параметрическому представлению контура [24], подбор примитивов и их параметров на основе меры близости в МПП [2, 5-10]. Кусочно-линейная аппроксимация является грубым приближением контура из-за невозможности представления гладких участков кривой и поэтому подходит не для всех задач. Методы, использующие подбор параметров примитивов, являются ресурсоемкими с точки зрения вычислений и ограничены небольшим количеством параметров. Интерполяция сплайнами подразумевает представление контура в параметрическом виде – в виде двух (для 2D контура) однозначных функций, что приводит к избыточному размеру описания кривой.

Методы, использующие МПП, быстрее методов с подбором параметров и позволяют получить более компактное описание по сравнению с методами, использующими интерполяцию сплайнами. В силу перечисленных выше причин была выбрана группа методов, использующих МПП, а рассматриваемый в этой статье метод компактного описания контуров является модификации основного метода этой группы – метода семантического описания контуров [2].

Метод компактного описания контуров основывается на МПП и результаты представления контуров изображения сильно зависят от того, как это пространство используется. Было установлено, что для получения приемлемого качества представления контуров необходима размерность пространства признаков от 8 до 12 [10].

3. Описание основной идеи предлагаемого метода

Основная идея метода [5-10] сводится к декомпозиции контура на фрагменты и представлению каждого из фрагментов в виде параметризованного примитива – аналитического представления кривой. С точки зрения исследования МПП наибольший интерес представляет вторая задача. Рассмотрим ее подробнее на примере трехмерного пространства признаков.

В методе компактного описания контуров изображения перед вычислением элементов ВП производится нормирование фрагмента контура по нескольким преобразованиям. В результате получается кривая, все точки которой удовлетворяют условию:

    (1)

где - общее количество точек фрагмента контура,  - крайняя левая точка,  - крайняя правая.

Элементы ВП вычисляются как координаты точек по оси , соответствующие равномерно распределенным значениям по оси  после нормирования:

        (2)

, где  - -й элемент ВП,  - размерность ВП, вычисляется следующим образом:

        (3)

Формирование ВП производится только для однозначных кривых. Процесс вычисления элементов ВП проиллюстрирован на рис.1: на нормированной кривой  выбираются точки , соответствующие для  следующим координатам по оси : . В качестве элементов ВП берутся координаты этих точек по оси .

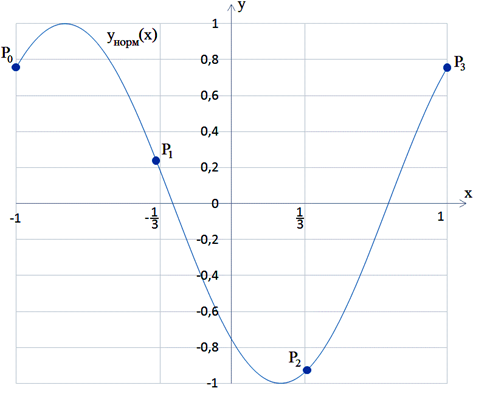
Рис.1. Формирование ВП в трехмерном пространстве признаков.

Сформированный ВП может быть представлен точкой в -мерном пространстве признаков, что позволяет производить визуализацию множеств ВП при  не более 3-х.

4. Постановка задачи исследования пространства признаков

Множество точек в МПП определяется ВП из БД классификатора фрагментов контура. В свою очередь, содержимое БД примитивов непосредственно зависит от обучающей выборки. Для конкретной обучающей выборки однозначно определено содержимое  БД примитивов. Для каждого ВП из БД примитивов в МПП определено соответствие формы кривой (ВП – дескриптор формы) и аналитического представления кривой. Указанное соответствие определяется в окрестностях точки ВП для некоторой заданной погрешности. А совокупность n-мерного объема пространства (площадь для 2-х измерений, объем – для 3-х и т.д.), в которых определено соответствие с заданной погрешностью, будем называть покрытием МПП. Отношение покрытия пространства признаков ко всему n-мерному объему пространства – степень покрытия. Если пространство признаков покрыто полностью, т.е. нет ни одной точки, в которой не определено соответствие ВП с аналитическим представлением кривой, то такое покрытие будем называть полным.

       Под промахом будем подразумевать ситуацию, когда для некоторого ВП не было найдено соответствие в МПП в пределах заданной погрешности. Таким образом, наличие промахов в процессе описания контура ухудшает компактность описания за счет увеличения количества фрагментов контура, поэтому возникает необходимость увеличения покрытия пространства признаков.

В идеале, пространство признаков должно иметь полное покрытие, с другой  стороны, такое покрытие будет обеспечено либо за счет больших погрешностей, либо за счет большого количества точек, что неприменимо на практике. Поэтому вместо полного покрытия целесообразнее обеспечить покрытие наиболее востребованных точек.

Под востребованными точками для некоторого набора входных данных (контуров) будем подразумевать множество ВП, для которых в процессе описания контура ищется соответствие с аналитическим представлением кривой. В данной работе интерес представляет величина, характеризующая покрытие некоторой доли  востребованных точек:

,   (4)

Где  – рассматриваемое количество востребованных точек;

– общее количество всех востребованных точек.

Таким образом, множество примитивов в БД в МПП должно покрывать некоторую заданную долю востребованных ВП в пределах заданной погрешности. Поскольку множество примитивов зависит непосредственно от обучающей выборки, то задача принимает следующий вид.

Для некоторого входного набора данных необходимо подобрать такую обучающую выборку, которая обеспечит покрытие заданной доли востребованных ВП в МПП. Для выполнения поставленной задачи необходимо решить несколько подзадач: выбрать входные данные, разработать схему эксперимента и провести эксперимент.

5. Выбор исходных данных

В качестве данных для эксперимента была использована база бинарных изображений, полученная из клипартов, находящихся в свободном доступе в интернете.

Рис. 2. Пример контуров, полученных из БД изображений.

Под клипартом подразумевается изображение с множеством силуэтов, как правило, одной тематики (Рис.2.). В общей сложности, созданная БД изображений состоит из 745 бинарных изображений, из которых можно извлечь ровно по одному контуру, поскольку исходные бинарные изображения содержат связные области без отверстий. Стоит отметить, что наличие только одного контура на изображении выбрано для удобства проведения эксперимента и не является ограничением метода.

6. Схема эксперимента

Для данного эксперимента было выбрано значение размерности ВП,  соответствующее размерности МПП, рекомендованное для работы с реальными изображениями [10] - . В качестве погрешности представления данных было взято отклонение опорных точек восстановленного контура от соответствующих точек исходного контура не более чем на 5 пикселей. В качестве критического значения доли покрытия востребованными ВП от общего числа точек в МПП, до которого проводился эксперимент, было взято следующее значение:

       (5)

Таким образом, эксперимент завершается при выполнении условия:

           (6)

В первую очередь, возникла необходимость определить общее число востребованных точек в МПП. Для этого на первом этапе эксперимента была произведена обработка всех контуров из базы изображений без обучения классификатора фрагментов контура. Поскольку обучающая выборка была пустой, то БД примитивов не содержала ни одной записи. Таким образом, все промахи в МПП в этом случае являлись востребованными ВП для данной базы изображений.

Второй и последующие этапы эксперимента подразумевали следующую последовательность шагов:

• Обучение классификатора фрагментов контура с помощью обучающей выборки.
• Определение множества промахов в МПП для данной обучающей выборки.
• Вывод о необходимости улучшения покрытия востребованных точек в МПП. Если улучшение покрытия востребованных точек необходимо, то:
• Определение количества предполагаемых кластеров.
• Кластеризация множества промахов с проверкой корректности разбиения при помощи визуализации.
• Получение опорных точек примитивов для  всех ВП. соответствующих центрам кластеров.
• Подбор параметризованного примитива для каждого множества опорных точек.
• Обновление обучающей выборки.

Таким образом, результатом эксперимента является обучающая выборка, обеспечивающая покрытие более 95% востребованных точек, что и требуется для решения поставленной задачи.

7. Эксперимент

Этап 1. Получение общего количества востребованных точек. Была произведена обработка контуров из базы изображений без предварительного обучения классификатора фрагментов контура. В результате были зафиксированы промахи:

    (7)

Стоит заметить, что найденные промахи соответствуют искомым востребованным точкам:      

       (8)

Данное значение позволяет на каждом этапе эксперимента определять долю востребованных точек в пространстве признаков от общего их числа с помощью формулы (4).

Этап 2. Исследование востребованных точек в МПП без обучения классификатора фрагментов контура.

На этапе 1 было получено множество востребованных точек, которое на данном этапе соответствует промахам в пространстве признаков, которые необходимо исследовать:

       (9)

Согласно схеме эксперимента исследование этого множества подразумевает его визуализацию. В результате возникает необходимость уменьшения размерности данных, для этих целей больше всего подходит один из методов регрессионного анализа – метод главных компонент (МГК) [36].

МГК позволяет выявить зависимости между переменными и представить данные в новом базисе меньшей размерности с возможностью контроля погрешности представления. Выходными данными метода являются матрицы счетов и нагрузок. Матрица счетов - это проекции исходных данных на подпространство главных компонент. Матрица нагрузок позволяет перейти из исходного пространства переменных в пространство главных компонент и наоборот. Декомпозиция исходных данных на компоненты в МГК является последовательным и итеративным процессом, который можно оборвать на любом шаге. Для оценки точности представления исходного множества точек с помощью некоторого числа компонент используют матрицу остатков – разницу между исходной матрицей и полученной из описания с помощью компонент. Оценка дисперсии  i-ой точки в N-мерном пространстве:

            (10)

Где -элемент матрицы остатков.

Общая оценка дисперсии для всех K точек принимает вид:

  (11)

Стандартные средства Statistica позволяют автоматически строить график зависимости точности представления множества точек от числа компонент (рис.3). Из этого графика видно, что наибольшая часть информации содержится в первых 3-4 компонентах.

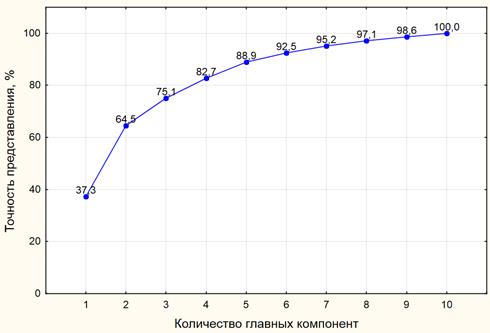
Рис. 3. График зависимости точности представления множества точек от числа компонент.

Для визуализации исходного множества точек в пространстве компонент удобнее всего использовать 3 компоненты, что соответствует моделированию 75.1% данных. Чтобы оценить визуально наличие кластеров в 3-мерном пространстве необходимо рассмотреть 3-мерное «облако» точек с различных ракурсов. Поэтому возникла необходимость вращения визуализированных данных. Для этих целей был использован пакет программ Statistica, с помощью которого была получена визуализация трехмерного пространства первых компонент (рис. 4). Из визуализации видно единственное ярко выраженное скопление точек, следовательно, кластерный анализ множества для дальнейшего анализа, в данном случае, не требуется. Такие же выводы можно сделать после визуализации 2 компонент (точность 64.5%) – см. рис. 5.

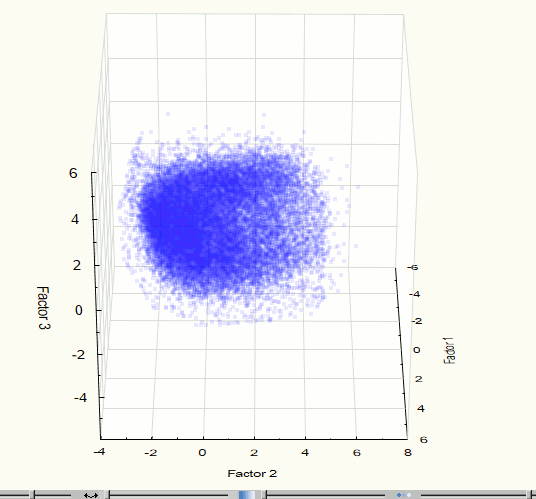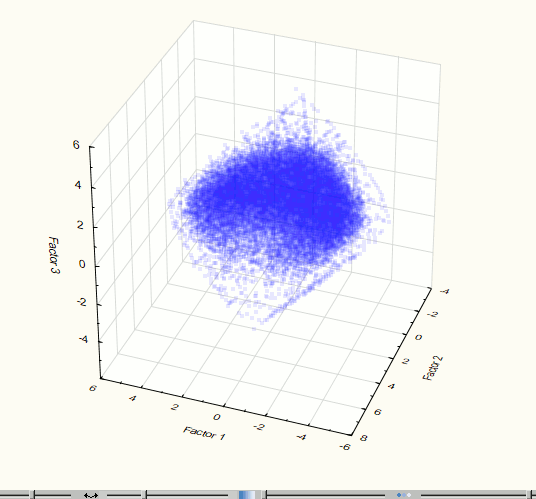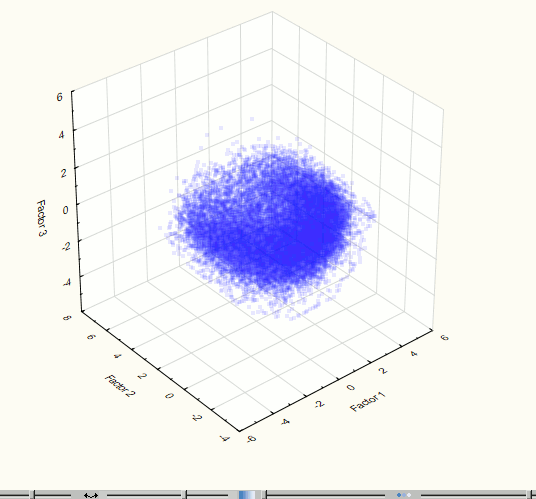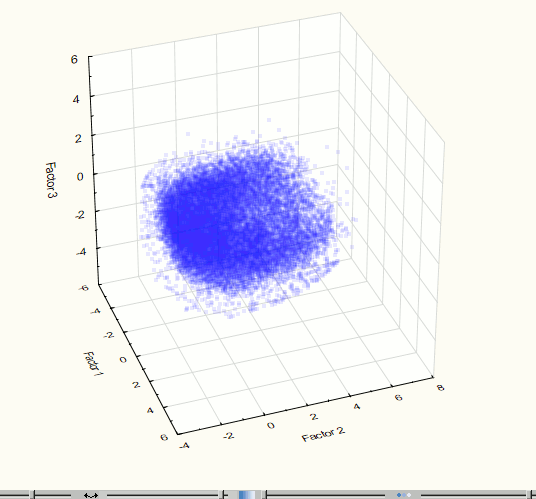
Рис. 4. Визуализация трехмерного пространства компонент на 2 этапе эксперимента.

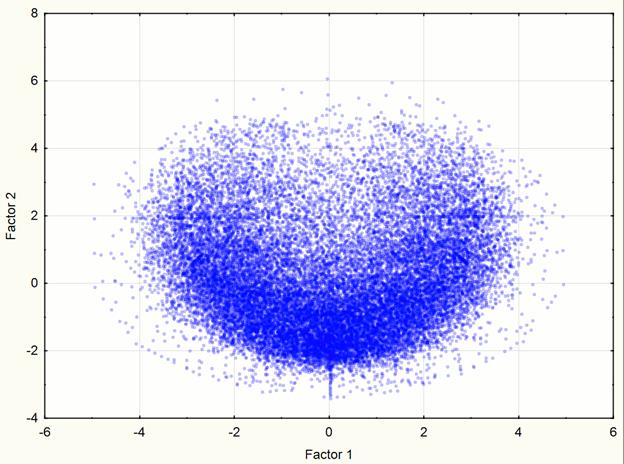
Рис. 5. Визуализация двухмерного пространства компонент на 2 этапе эксперимента

Наличие только одного скопления позволяет обойтись вычислением  его центра как средних значений координат всех точек исходного множества. Полученные результаты представлены в таблице 1.

Таблица 1. Координаты центра кластера исходного множества точек

i	0	1	2	3	4	5	6	7	8	9
v	0,70	0,26	-0,02	-0,21	-0,33	-0,36	-0,32	-0,21	-0,02	0,26

Координаты по оси  в таблице 2 получены по формуле (3) из геометрического смысла ВП – точки в МПП.

Таблица 2. Геометрическая интерпретация ВП, соответствующего центру кластера из Таблицы 1.

x	-1	-0,8	-0,6	-0,4	-0,2	0	0,2	0,4	0,6	0,8	1
y	0,70	0,26	-0,02	-0,21	-0,33	-0,36	-0,32	-0,21	-0,02	0,26	0,70

По данным из таблицы 2 был построен примитив фрагмента контура, соответствующий ВП из центра скопления точек в МПП (рис. 6).

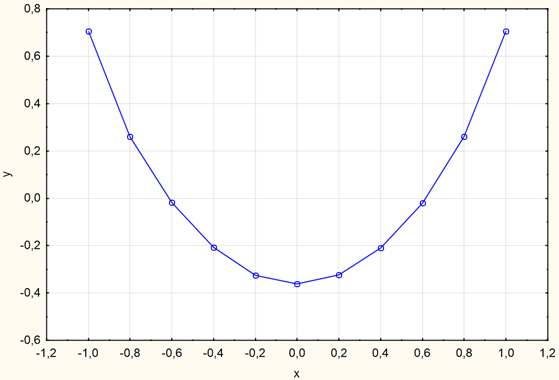
Рис. 6. Примитив фрагмента контура на 2-м этапе эксперимента по данным из таблицы 2.

По форме примитива на рис. 5 видно, что наиболее востребованным примитивом является дуга, поэтому в обучающую выборку добавляется именно этот примитив.

Этап 3. Исследование востребованных точек в МПП с обучением классификатора фрагментов контура одному классу примитивов.

На этом этапе также была произведена обработка контуров из базы изображений, но в этот раз классификатор фрагментов контура был обучен на семействе дуг. Поскольку значительная часть востребованных точек стала покрытой ВП, соответствующих семейству дуг, то количество промахов сократилось:

      (12)

Согласно формуле (4) доля покрытых востребованных точек примерно равна:

        (13)

Для этого значения условие завершения эксперимента (7) не выполняется, поэтому исследования пространства признаков были продолжены.

По аналогии с предыдущим этапом для визуализации полученных данных был применен один из методов регрессионного анализа – МГК. Визуализации трехмерного и двухмерного пространств компонент на этом этапе представлены на рис. 7-8.

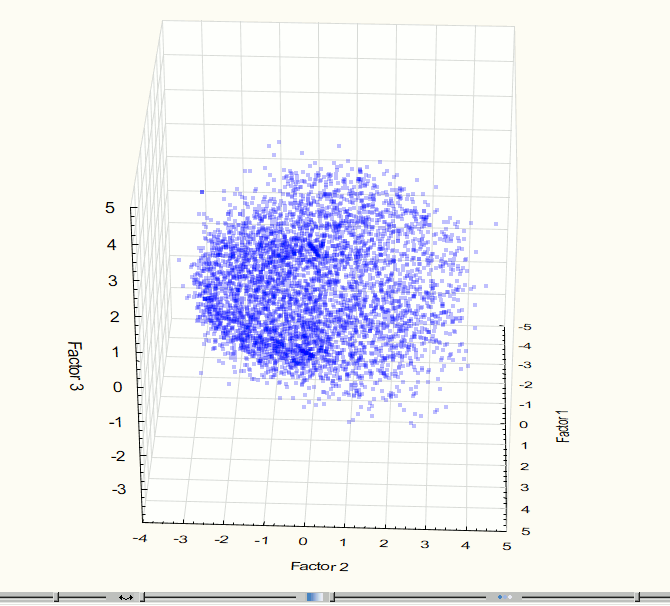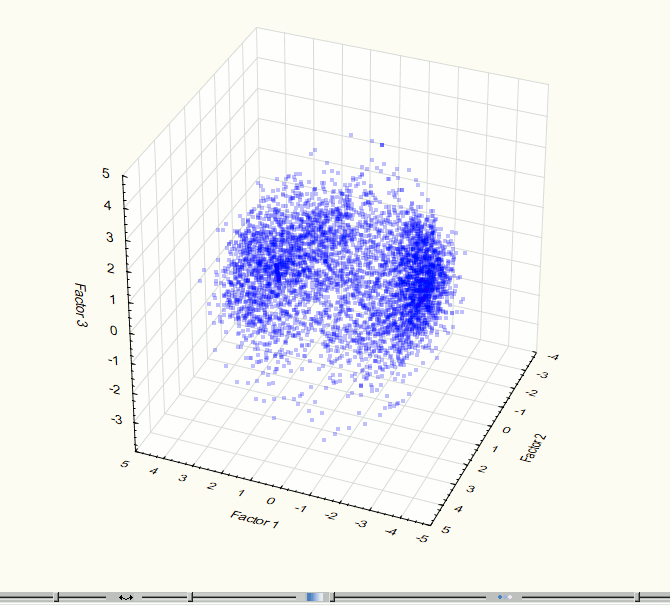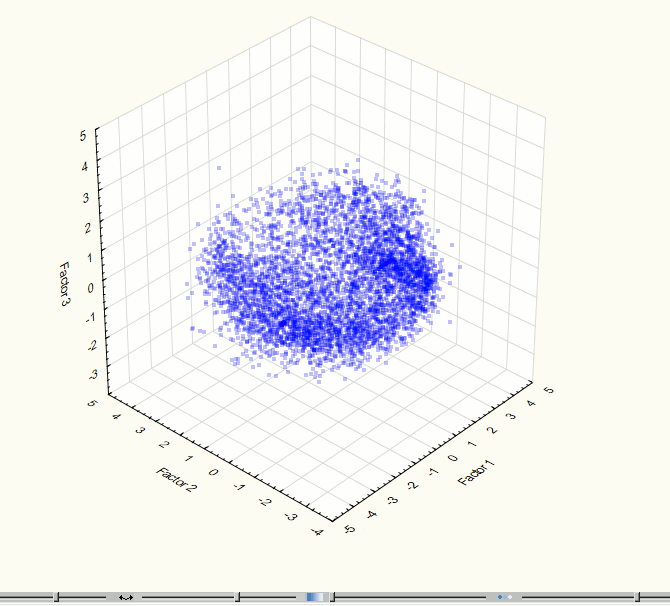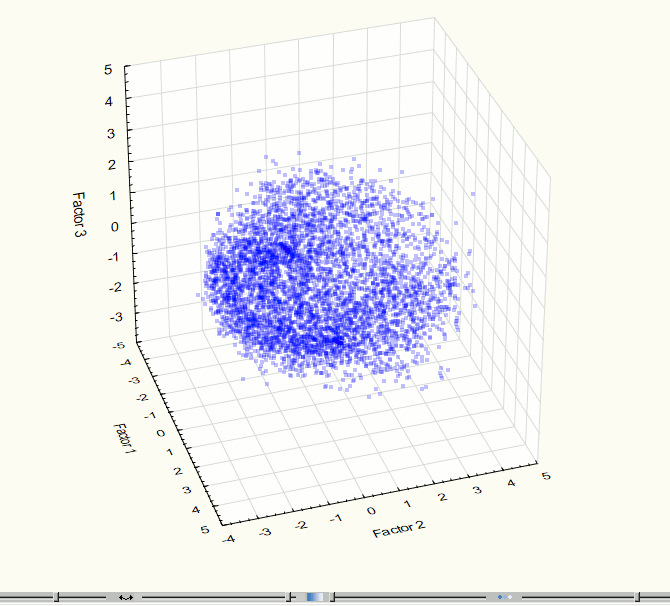
Рис. 7. Визуализация трехмерного пространства компонент на 3 этапе эксперимента.

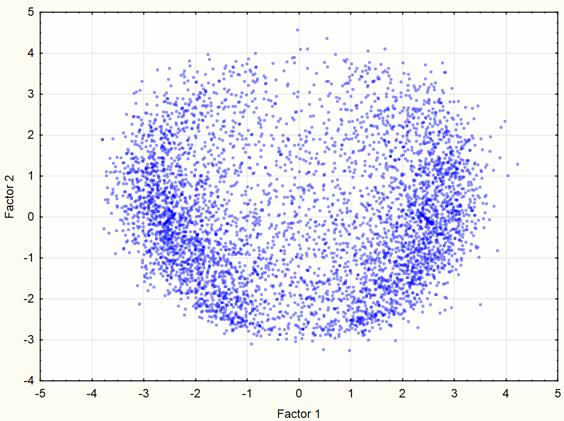
Рис. 8. Визуализация двухмерного пространства компонент на 3 этапе эксперимента.

Визуализация позволила выявить два явно выраженных скопления точек, поэтому возникла необходимость применения методов кластерного анализа. Для данной работы использовался метод кластеризации К-средних (K-means), который дает хорошие результаты, если известно количество искомых кластеров. Для проверки корректности разбиения исходного множества точек на группы была проведена визуализация данных после кластеризации (рис. 9 – 10). Полученные изображения подтверждают правильность разбиения.

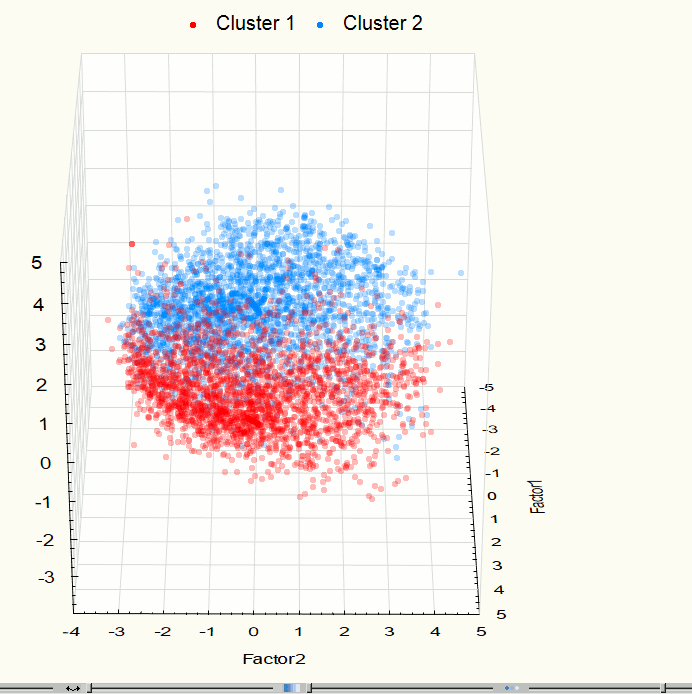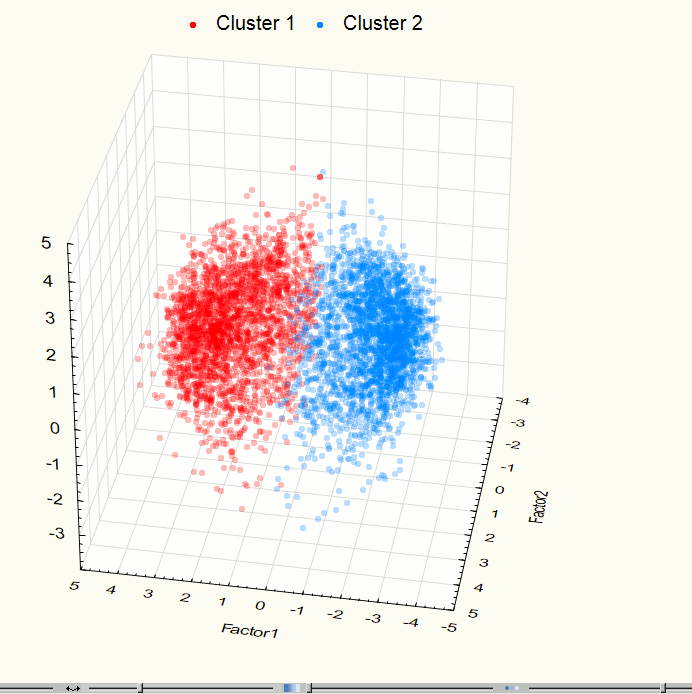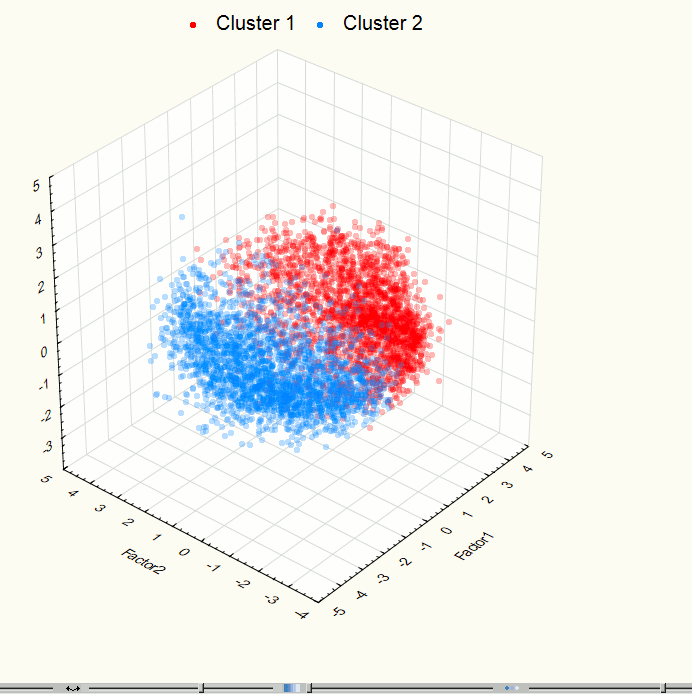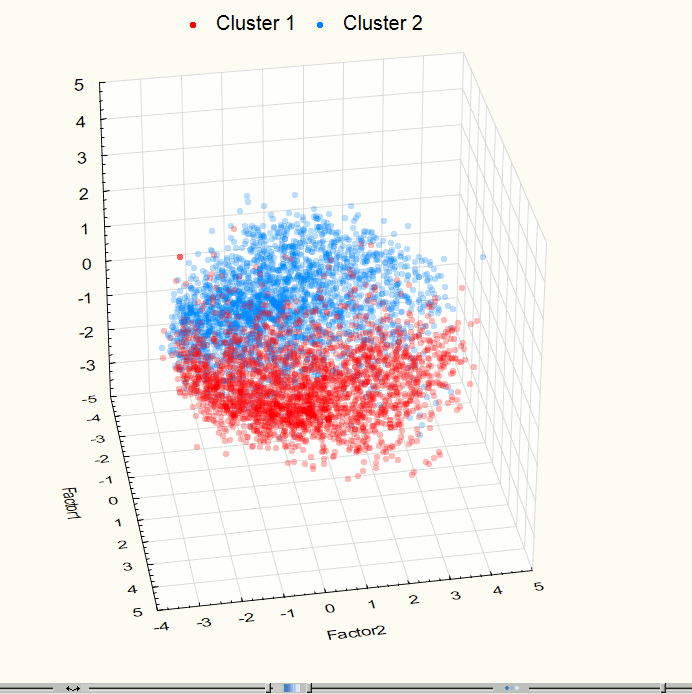
Рис. 9. Визуализация трехмерного пространства компонент на 3 этапе эксперимента после кластеризации.

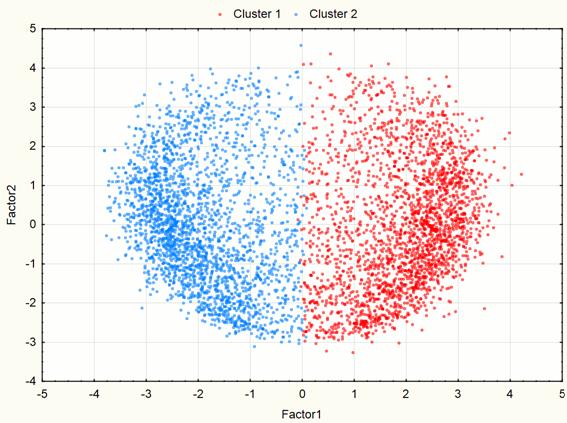
Рис. 10. Визуализация двухмерного пространства компонент на 3 этапе эксперимента после кластеризации.

После этого были определены координаты центров каждого из кластеров, для получения характерной формы востребованных примитивов. Координаты центров были посчитаны как средние значения координат точек каждого из кластеров, результаты вычислений приведены в таблице 3.

Таблица 3. Координаты центров кластеров множества точек, соответствующих промахам на 3-м этапе эксперимента.

i	0	1	2	3	4	5	6	7	8	9
Cluster 1	0,62	0,64	0,56	0,40	0,13	-0,15	-0,41	-0,55	-0,50	-0,16
Cluster 2	0,62	-0,13	-0,49	-0,54	-0,40	-0,15	0,16	0,41	0,56	0,62

Согласно геометрической интерпретации точек в МПП и формуле (3) были получены приближенные точки, через которые проходят наиболее востребованные на данном этапе эксперимента примитивы для каждого кластера (Таблица 4).

Таблица 4. Геометрическая интерпретация ВП, соответствующих центрам кластеров из Таблицы 3.

i	0	1	2	3	4	5	6	7	8	9	0
x	-1	-0,8	-0,6	-0,4	-0,2	0	0,2	0,4	0,6	0,8	1
y1	0,62	0,64	0,56	0,40	0,13	-0,15	-0,41	-0,55	-0,50	-0,16	0,62
y2	0,62	-0,13	-0,49	-0,54	-0,40	-0,15	0,16	0,41	0,56	0,62	0,62

Построенные примитивы фрагментов контура приведены на рис. 11. Визуализация результатов позволила увидеть симметричность примитивов относительно оси . С учетом того, что рассматриваемый метод представления контуров при кодировании фрагментов контура обеспечивает  инвариантность, в том числе и к преобразованиям зеркального отражения, был получен вывод о необходимости только одного примитива. Форма нормированной кривой с учетом  способа формирования позволила прийти к выводу об исходном аналитическом представлении примитива – синусоида, взятая на интервале . Было принято решение использовать для обучающей выборки семейство синусоид, что позволило увеличить степень покрытия востребованных ВП.

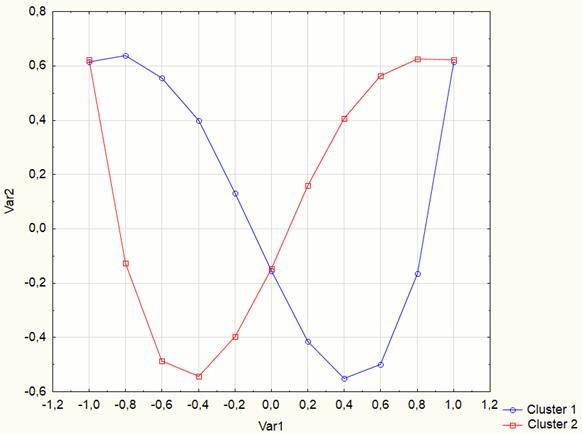
Рис. 11. Примитивы фрагментов контура на 3-м этапе эксперимента по данным из таблицы 4.

Этап 4. Исследование МПП с обучением классификатора фрагментов контура двум классам примитивов.

В этот раз, в состав обучающей выборки входили уже 2 класса кривых – дуги и синусоиды. Обработка контуров из базы изображений показала, что количество промахов после последнего изменения обучающей выборки сократилось:

       (14)

Согласно формуле (4) доля покрытых востребованных точек примерно равна:

        (15)

Таким образом, условие завершения эксперимента (6) выполняется, поэтому текущая обучающая выборка, состоящая из двух классов кривых, является искомой.

8. Заключение

Использование научной визуализации в данной задаче позволяет быстро и наглядно изучить характер поведения исследуемых данных и применить разрабатываемый подход к решению задачи описания контуров объектов на изображениях на практике. В данной работе было продемонстрировано применение методов научной визуализации для исследования МПП, используемых при распознавании нелинейных функций из базиса для описания контура объектов на изображении. Как было показано ранее, для получения грубых оценок о количестве кластеров можно быстро получить информацию, которую сложно получить аналитическими способами при практическом применении методики.

Следует отметить, что представленный подход с использованием МНВ применим для разных граничных условий. Условия , N=10 были выбраны с учётом особенностей метода, а не из-за ограничений МНВ. Также, наличие только двух кластеров (рис. 9-10) является частным случаем, предлагаемый подход прекрасно справится с любым небольшим числом скоплений в МПП, а большим это число не может быть в силу условий поставленной задачи.

Полученные результаты позволяют считать, что методы визуального анализа больших данных весьма эффективны при практическом использовании для такой нетрадиционной для данного научного метода задачи.

9. Программное обеспечение

Система кодирования/декодирования контуров была реализована на C++ при помощи библиотеки OpenCV. Для статистической обработки результатов рассматривалось следующее ПО: Matlab, OriginPro, Statistica. Исследование данных МПП подразумевало использование методов кластерного и регрессионного анализов, а также возможность визуализации обрабатываемых данных. Все эти возможности есть в каждом из перечисленных продуктов. Для написания этой статьи была использована Statistica.

Список литературы

1. Федоров Д.К., Чепин Е.В. Алгоритмы распознавания образов на основе атрибутных грамматик для цифровой обработки изображений. М.: Препринт МИФИ, 1988;
2. Lepeshenkov K.E., Tchepine E.V. Semantic Editor of 2-d Contour Images. Proceedings of Intern. Conf. “GraphiCon’99”, Moscow, 1999;
3. Фу К. Структурные методы в распознавании образов. М.: Мир, 1977;
4. Каташкин  В.И., Левахин  М.Г.,  Чепин  Е.В.  Об  одном  подходе  к решению  задачи  определения  вида  эмпирической модели. Инженерно-математические методы в кибернетике, 1979, №8;
5. Borisoglebskiy D.A. Improve parametric curves representations in the semantic description of contours. Proceedings of the 14th International Workshop on Computer Science and Information Technologies, vol. 1, Hamburg, 2012;
6. Борисоглебский Д.А., Чепин Е.В. Описание усовершенствованного метода представления контура в виде последовательности параметрических кривых. Труды VII международная научно-техническая конференция «Автоматизация и прогрессивные технологии в атомной отрасли», Новоуральск, 2012;
7. Борисоглебский Д.А. Рассмотрение одного из этапов усовершенствованного метода семантического описания контуров на примере мобильного робототехнического комплекса. Труды 55-й научной конференции МФТИ, Москва, 2012;
8. Борисоглебский Д.А. Система формирования компактного описания контуров изображения. Сборник трудов 16-й международная телекоммуникационной конференции молодых ученых и студентов «Молодежь и наука», Москва, 2013;
9. Борисоглебский Д. А., Чепин Е. В. Усовершенствованный подход к задаче векторизации контуров на изображениях. Прикладная информатика №44 (2), Москва, 2013;
10. Борисоглебский Д. А. Влияние модификации метода семантического описания контуров на характеристики подсистемы робототехнического комплекса. Прикладная информатика №48 (6), Москва, 2013;
11. Chepin E.V., Dyumin A.A., Shapovalov N.K., Sorokoumov P.S. Hardware and Software of Mobile Robots Group. Proceedings of the International Workshop on Computer Science and Information Technologies. Hamburg, 2012;
12. Данилов В.В., Дюмин А.А., Сорокоумов П.С., Чепин Е.В., Шаповалов Н.К. Программная система дистанционного управления роботом PATROLBOT. Сборник трудов "Наука и инновации НИЯУ МИФИ", Москва, 2010;
13. Dyumin A.A. Architecture of reconfigurable software for mobile robotic systems. Proceedings of the 12th International Workshop on Computer Science and Information Technologies, vol. 2, Crete, 2009;
14. Дюмин А.А., Сорокоумов П.С., Чепин Е.В. Архитектура системы управления командой мобильных роботов. Труды 54-й научной конференции МФТИ "Проблемы фундаментальных и прикладных естественных и технических наук в современном информационном обществе", Москва, 2011;
15. Dengsheng Zhang, Guojun Lu. Review of shape representation and description techniques. Pattern Recognition, №37, 2004;
16. Luciano Da Fontoura Costa, Roberto Marcondes Cesar Jr. Shape Analysis and Classification: Theory and Practice, 2000;
17. Kolesnikov A., Franti, P. Polygonal approximation of closed discrete curves. Pattern Recognition, no. 40, 2007, pp. 1282-1293;
18. Alexander Kolesnikov, Fränti Pasi, Bigün Josef (Bearb.), Gustavsson Tomas (Bearb.). Polygonal Approximation of Closed Contours. 2749. In: SCIA: Springer, 2003 (Lecture Notes in Computer Science). ISBN 3-540-40601-8, pp. 778-785;
19. Ширма А.А. Нейросетевая аппроксимация векторных объектов кривыми Безье. Нейроинформатика, 2011;
20. Белых С.В. Аппроксимация геометрии контура дугами при контроле точности изготовления деталей летательных аппаратов;
21. Левашов, Юрин. Система быстрого обнаружения параметрических кривых. Графикон, 2011;
22. Вишневский В.В., Калмыков В.Г. Структурный анализ цифровых контуров изображений как последовательностей отрезков прямых и дуг кривых. Искуственный интелект, №3, 2004;
23. Калмыков В.Г. Структурный метод распознавания отрезков цифровых прямых и контурных бинарных изображений.  Искуственный интелект, №2, 2002
24. Мязина Ю.С., Лисиенкова Л.Н. САПР Одежды, 2007
25. Стриханов М.Н., Дегтяренко Н.Н., Пилюгин В.В., Маликова Е.Е., Матвеева Н.А., Пасько А.А., Аджиев В.Д. Опыт компьютерной визуализации наноструктур в НИЯУ МИФИ. Научная визуализация, т. 1, № 1, 2009, C. 1–18.
26. Пасько А.А., Пилюгин В.В. Научная визуализация и ее применение в исследованиях наноструктур. Rusnanotech . Международный форум по нанотехнологиям. Сборник тезисов докладов научно-технических секций 2008. Москва. С . 189-190.
27. Поляков С.В., Якобовский М.В. Геометрическое моделирование и визуализация в задачах современной электроники, Научная визуализация, т. 1, №1, 2009, с 19-65.
28. Карташева Е.Л., Багдасаров Г.А., Болдарев А.С., и др. Визуализация данных вычислительных экспериментов в области 3D моделирования излучающей плазмы, выполняемых на многопроцессорных вычислительных системах с помощью пакета Marple, Научная визуализация, т. 2, №1, 2010, сс. 1-25.
29. Бондарев А.Е., Галактионов В.А., Чечеткин В.М. Научная визуализация в задачах вычислительной механики жидкости и газа, Научная визуализация, т.2 №4, с 1 – 26
30. Васев П.А., Перевалов Д.С. О создании методов многомерной визуализации. Тр. 12-й Междунар. конф. по компьютерной графике и машинному зрению “ГрафиКон’2002”, 16–21 сент. 2002 г. Нижегородский гос. ун-т. Нижний Новгород, 2002, c. 431–437.
31. А.А. Багатурьянц, К.Г. Владимирова, Н.Н. Дегтяренко и др. Визуализация и конструирование наносистем в рамках многомасштабного подхода: программа «Наномоделлер». Научная визуализация, т. 2, №4, 2010, с. 40-60.
32. Боженко В.К., Иванов А.О., Мищенко А.С. и др. Геометрические модели в биологии: как и что можно моделировать. Научная визуализация, т. 1, №1, 2009, сс. 66-99.
33. Константинов И.Н., Стефанов Ю.Э., Ковалевский А.А. и др. Трехмерная модель ВИЧ: графический обзор данных о строении вирусной частицы. Научная визуализация, т. 3, №1, 2011, сс. 53-54.
34. Ларичев В.А., Лесонен Д.Н., Максимов Г.А. и др. О подходе к трехмерному математическому моделированию сложной геологической среды с разрывами для визуализации и решения прямых и обратных задач геофизики. Научная визуализация, т. 2, №2, 2010, сс. 20-33.
35. Бородина Е.И. Контроль, мониторинг и визуализация данных эксперимента COSY-TOF в режиме реального времени, Автореферат канд. техн. наук., Москва, 2011, 20 с.
36. Метод главных компонент, электронный ресурс: http://rcs.chemometrics.ru/Tutorials/pca.htm Дата посещения: 2014-05-14.
37. Введение в методы статистического обучения http://www.recognition.mccme.ru/pub/RecognitionLab.html/sltb.pdf Дата посещения: 2014-06-14.
38. Герценбергер К.В., Мец С., Чепин Е.В. Визуализация событий эксперимента MPD коллайдера NICA для системы мониторинга. Научная визуализация, т. 6, № 1, 2014, с. 1–19.

---

FEATURE SPACE VISUALIZATION IN THE METHOD FOR COMPACT REPRESENTATION OF CONTOURS

D.A. Borisoglebskiy¹, E.V. Chepin²

¹ UAB AIA, Russia

² National Research Nuclear University MEPhI, Russia

denis.borisoglebsky@gmail.com, evchepin@gmail.com

Annotation

The article describes one of the approaches to solving the problem of silhouettes’ shape representation on digital images. The results of the research for developed contour-based method for representing silhouettes in the form of a sequence of parameterized primitives in terms of coverage of feature space. The results were studied by the methods of scientific visualization that made it possible to draw quick and visual conclusions about the behavior of the analyzed data and apply appropriate methods for solving the problems in the experiment. The developed method will be useful for solving practical problems of silhouettes’ shape representation in various areas of image processing.

Keywords: silhouettes’ shape representation, parameterized primitive, regression analysis, cluster analysis, visualization of multidimensional data.

Bibliography

1. D.K. Fedorov, E.V. Chepin. Algoritmy raspoznavanija obrazov na osnove atributnyh grammatik dlja cifrovoj obrabotki izobrazhenij [Pattern recognition algorithm based on attribute grammars for digital image processing]. Moscow, Preprint of MEPhI, 1988; [In Russian]
2. Lepeshenkov K.E., Tchepine E.V. Semantic Editor of 2-d Contour Images. Proceedings of Intern. Conf. “GraphiCon’99”, Moscow, 1999;
3. Fu K. Strukturnye metody v raspoznavanii obrazov [Syntactic Methods in Pattern Recognition]. Academic Press, 1974; [In Russian]
4. Katashkin V.I., Levahin M.G., Chepin E.V. Ob  odnom  podhode  k resheniju  zadachi  opredelenija  vida  jempiricheskoj modeli [An approach to solving the problem of determining the type of empirical model]. Engineering and mathematical methods in cybernetics, 1979, №8; [In Russian]
5. Borisoglebskiy D.A. Improve parametric curves representations in the semantic description of contours. Proceedings of the 14th International Workshop on Computer Science and Information Technologies, vol. 1, Hamburg, 2012;
6. Borisoglebskiy D.A., Chepin E.V. Opisanie usovershenstvovannogo metoda predstavlenija kontura v vide posledovatel'nosti parametricheskih krivyh [Description of an improved method of contour representation in the form of a sequence of parametric curves]. Proceedings of the VII International scientific-technical conference "Automation and advanced technologies in the nuclear industry", Novouralsk, 2012; [In Russian]
7. Borisoglebskiy D.A. Rassmotrenie odnogo iz jetapov usovershenstvovannogo metoda semanticheskogo opisanija konturov na primere mobil'nogo robototehnicheskogo kompleksa [Consideration of one of the stages of an improved method of semantic contour description on the example of a mobile robotic system]. Proceedings of the 55th scientific conference of MIPT, Moscow, 2012; [In Russian]
8. Borisoglebskiy D.A. Sistema formirovanija kompaktnogo opisanija konturov izobrazhenija [The system of formation of a compact description of image contours]. Proceedings of the 16th international telecommunication conference of young scientists and students "Youth and Science", Moscow, 2013; [In Russian]
9. Borisoglebskiy D.A., Chepin E.V. Usovershenstvovannyj podhod k zadache vektorizacii konturov na izobrazhenijah [An improved approach to the problem of vectorization of contours in images]. Applied Informatics no. 44 (2), Moscow, 2013; [In Russian]
10. Borisoglebskiy D.A. Vlijanie modifikacii metoda semanticheskogo opisanija konturov na harakteristiki podsistemy robototehnicheskogo kompleksa [Effect of modification in the method of semantic contour description on the characteristics of the subsystem robotic system]. Applied Informatics, no. 48 (6), Moscow, 2013; [In Russian]
11. Chepin E.V., Dyumin A.A., Shapovalov N.K., Sorokoumov P.S. Hardware and Software of Mobile Robots Group. Proceedings of the International Workshop on Computer Science and Information Technologies. Hamburg, 2012;
12. Danilov V.V., Dyumin A.A., Sorokoumov P.S., Chepin E.V., Shapovalov N.K. Programmnaja sistema distancionnogo upravlenija robotom PATROLBOT [Software system of remote control of PATROLBOT robot]. Proceedings of the "Science and Innovation MEPhI", Moscow, 2010; [In Russian]
13. Dyumin A.A. Architecture of reconfigurable software for mobile robotic systems. Proceedings of the 12th International Workshop on Computer Science and Information Technologies, vol. 2, Crete, 2009;
14. Dyumin A.A., Sorokoumov P.S. Arhitektura sistemy upravlenija komandoj mobil'nyh robotov [The architecture of system to control a team of mobile robots]. Proceedings of the 54th scientific conference of MIPT, Moscow, 2011; [In Russian]
15. Dengsheng Zhang, Guojun Lu. Review of shape representation and description techniques. Pattern Recognition, №37, 2004;
16. Luciano Da Fontoura Costa, Roberto Marcondes Cesar Jr. Shape Analysis and Classification: Theory and Practice, 2000;
17. Kolesnikov A., Franti, P. Polygonal approximation of closed discrete curves. Pattern Recognition, no. 40, 2007, pp. 1282-1293;
18. Alexander Kolesnikov, Fränti Pasi, Bigün Josef (Bearb.), Gustavsson Tomas (Bearb.). Polygonal Approximation of Closed Contours. 2749. In: SCIA: Springer, 2003 (Lecture Notes in Computer Science). ISBN 3-540-40601-8, pp. 778-785;
19. Shirma A.A. Nejrosetevaja approksimacija vektornyh ob#ektov krivymi Bez'e [Neural network approximation of vector objects using Bezier curves]. Neuroinformatics, 2011; [In Russian]
20. Belyh S.V. Approksimacija geometrii kontura dugami pri kontrole tochnosti izgotovlenija detalej letatel'nyh apparatov [Approximation of the geometry of the circuit using arcs in the control of precision manufacturing of aircraft details]; [In Russian]
21. Levashov, Yurin. Sistema bystrogo obnaruzhenija parametricheskih krivyh [System of quick detection of parametric curves]. Graphicon, 2011; [In Russian]
22. Vishnevskiy V.V., Kalmykov V.G. Strukturnyj analiz cifrovyh konturov izobrazhenij kak posledovatel'nostej otrezkov prjamyh i dug krivyh [Structural analysis of digital contours in the images as a sequence of line segments and arcs of curves]. Artificial Intelligence, №3, 2004; [In Russian]
23. Kalmykov V.G. Strukturnyj metod raspoznavanija otrezkov cifrovyh prjamyh i konturnyh binarnyh izobrazhenij [Structural method for recognizing segments of digital lines and binary contour images].  Artificial Intelligence, №2, 2002; [In Russian]
24. Myazina U.S., Lisienkova L.N. SAPR Odezhdy [CAD for clothing], 2007;
25. Strikhanov M.N., Degtyarenko N.N., Pilyugin V.V., Malikova E.E., Matveeva M.N., Adzhiev V.D., Pasko A.A. Opyt komp'juternoj vizualizacii nanostruktur v NIJaU MIFI [Computer visualization of nanostructures experience at NRNU "MEPhI"]. Scientific Visualization, vol. 1, no. 1, 2009, pp. 1–18; [In Russian]
26. Pasko A.A., Pilyugin V.V. Nauchnaja vizualizacija i ee primenenie v issledovanijah nanostruktur [Scientific visualization and its application in the research of nanostructures]. Rusnanotech, Nanotechnology International Forum, Abstracts of reports of scientific and technical sections. 2008, Moscow, pp. 189-190; [In Russian]
27. Polyakov S.V., Iakobovski M.V. Geometricheskoe modelirovanie i vizualizacija v zadachah sovremennoj jelektroniki [Geometrical simulation & vizualization in problems of modern electronics]. Scientific Visualization, vol. 1, no. 1, 2009, pp. 19-65; [In Russian]
28. Kartasheva E.L., Bagdasarov G.F., Boldarev A.S., Gasilova I.V., D S.V.'yachenko, Olkhovskaya O.G., Shmirov V.A., Boldyrev S.N., Gasilov V.A. Vizualizacija dannyh vychislitel'nyh jeksperimentov v oblasti 3D modelirovanija izluchajushhej plazmy, vypolnjaemyh na mnogoprocessornyh vychislitel'nyh sistemah s pomoshh'ju paketa Marple [Scientific visualization of data from parallel supercomputer 3D radiative plasma simulations implemented using code Marple]. Scientific Visualization, vol. 2, no. 1, 2010, pp. 1-25; [In Russian]
29. Bondarev A.E., Galaktionov V.A., Chechetkin V.M. Nauchnaja vizualizacija v zadachah vychislitel'noj mehaniki zhidkosti i gaza [Scientific visualization for computational fluid dynamics]. Scientific Visualization, vol. 2, no. 4, 2010 pp. 1 – 26; [In Russian]
30. Vasev P.A., Perevalov D.S. O sozdanii metodov mnogomernoj vizualizacii [About creation of methods for multidimensional visualization]. Graphicon 2002, pp. 431–437; [In Russian]
31. Bagaturyants A.A., Vladimirova K.G., Degtyarenko N.N., Malikova E.E., Minibaev R.F., Pilyugin V.V., Strikhanov M.N., Freidzon A.Y. Vizualizacija i konstruirovanie nanosistem v ramkah mnogomasshtabnogo podhoda: programma «Nanomodeller» [Visualization and design of nanostructures in multiscale approach: “Nanomodeller” program]. Scientific Visualization, vol. 2, no. 4, 2010, pp. 40-60; [In Russian]
32. Bojenko V.K., Ivanov A.O., Mishchenko A.S., Tuzhikin A.A., Schyschkin A.M. Geometricheskie modeli v biologii: kak i chto mozhno modelirovat' [Geometrical models in biology: what and how we can simulate]. Scientific Visualization, vol. 1, no. 1, 2009, pp. 66-99; [In Russian]
33. Konstantinov I.N., Stefanov Y.E., Kovalevsky A.A., Voronin Y.N. Trehmernaja model' VICh: graficheskij obzor dannyh o stroenii virusnoj chasticy [Three-dimensional Model of HIV: a Graphical Review of the Viral Particle Structure]. Scientific Visualization, vol. 3, no. 1, 2011, pp. 53-54; [In Russian]
34. Larichev V.A., Lesonen D.N., Maksimov G.A., Podyachev E.V., Derov A.V. O podhode k trehmernomu matematicheskomu modelirovaniju slozhnoj geologicheskoj sredy s razryvami dlja vizualizacii i reshenija prjamyh i obratnyh zadach geofiziki [About approach to 3D mathematical modeling of complex geological medium with a discontinuity for visualization and decision of direct and inverse problems of geophysics]. Scientific Visualization, Vol. 2, №2, 2010, pp. 20-33; [In Russian]
35. Borodina E.I. Kontrol', monitoring i vizualizacija dannyh jeksperimenta COSY-TOF v rezhime real'nogo vremeni [Control, monitoring and visualization of COSY-TOF experiment in real time], Abstract of the candidate of technical sciences, Moscow, 2011, 20 p; [In Russian]
36. Principal component analysis: http://rcs.chemometrics.ru/Tutorials/pca.htm
37. Introduction to statistical learning http://www.recognition.mccme.ru/pub/RecognitionLab.html/sltb.pdf
38. Gertsenberger K., Merz S., Chepin E. Vizualizacija sobytij jeksperimenta MPD kollajdera NICA dlja sistemy monitoringa [Event Visualization of the MPD Experiment at the Nica Collider for the Monitoring System]. Scientific Visualization, vol. 6, no. 1, 2014, pp. 1–19; [In Russian]