ПРОСТОЙ МЕТОД ПРЕОБРАЗОВАНИЯ ЦВЕТА RGB В СПЕКТР ДЛЯ ЗАДАЧ ФИЗИЧЕСКИ КОРРЕКТНОЙ ВИЗУАЛИЗАЦИИ
В.В. Афанасьев, А.В. Игнатенко, А.Г. Волобой
Институт прикладной математики им. М.В. Келдыша РАН
Лаборатория компьютерной графики и мультимедиа ВМК МГУ
vafanasjev@graphics.cs.msu.ru, ignatenko@graphics.cs.msu.ru, voloboy@gin.keldysh.ru
Содержание
Задачи физически корректной визуализации зачастую требуют моделирования таких эффектов волновой оптики как дисперсия, интерференция, дифракция. Однако даже при наличии модели определённого волнового явления возникает проблема получения исходных данных для визуализации: большинство доступных способов позволяет получить цвет и интенсивность излучения, но не его спектр, а приборы, позволяющие измерить спектр, сложны, дорогостоящи и труднодоступны. Данная статья описывает простой и гибкий итерационный метод получения спектра из цвета RGB, который позволяет строить результат с учётом заданных ограничений, соответствующих требованиям задачи визуализации.
Ключевые слова: спектр, RGB, физически корректная визуализация, синтез реалистичных изображений
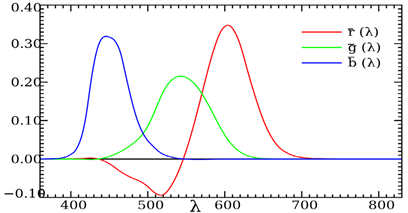
Одной из физических характеристик электромагнитного излучения является спектр – распределение мощности излучения по длинам волн. Цвет – это воспринимаемая человеком характеристика видимого света. Согласно экспериментам CIE, цвет может быть описан тремя числами, по количеству цветовых рецепторов в человеческом глазу. Также было показано, что видимые человеком цвета можно получить с помощью трёх излучателей с различным спектром. В зависимости от выбора типа излучателей, образуются различные линейные цветовые пространства, переход между которыми осуществляется с помощью домножения цвета из одного пространства на матрицу перехода. Здесь и далее будем работать с кривыми для условного линейного цветового пространства RGB, так как конкретное цветовое пространство не важно для описанного метода.
Рис. 1. Кривые CIE RGB
Спектральные кривые пространства CIE RGB для видимого диапазона с длинами волн от 380 до 780 нм приведены на рис. 1.
При визуализации некоторой сцены используются геометрические модели объектов, текстуры, модели источников освещения и модель камеры. Эти данные получают с помощью моделирования и съёмки реальных объектов. Последний способ даёт максимальное приближение к реальности, так можно получить, например, некоторые параметры источников освещения, текстуры, форму объектов.
Цифровые камеры, используемые для съёмки, имеют несколько
видов чувствительных элементов (обычно также три), каждый со своей кривой
отклика. Как правило, они соответствуют красному, зелёному и синему цветам: 
, 
, 
.
Отклик камеры на спектр 
,
пришедший на чувствительный элемент, выражается следующим преобразованием
свёртки:
В большей части задач синтеза изображений можно пренебречь спектральной природой света и проводить расчёты с цветом RGB. Однако для определённого класса задач, связанных с моделированием волновых свойств света, спектр важен. К таким задачам относится синтез изображений драгоценных камней, где дисперсия света в материале определяет итоговый цвет, который видит наблюдатель. В связи с тем, что обычные цифровые камеры позволяют получить цвет только в формате RGB, необходим алгоритм, позволяющий получить по имеющемуся цвету некоторый спектр, который можно затем использовать в расчётах.
Из прямого преобразования спектра в RGB следует, что существует бесконечное множество спектров, имеющих одинаковый цвет. Такие спектры называются метамерами. С математической точки зрения в качестве решения обратной задачи подходит любая функция, дающая после свёртки заданные числа RGB. Однако требование физической корректности накладывает на итоговый спектр ряд ограничений, например, бессмысленны спектры источника света с отрицательными значениями. При наличии априорной информации об исходном спектре на результат могут быть наложены дополнительные ограничения, например, непрерывность или гладкость.
Существующие решения основаны на представлении спектра в виде кусочно-постоянной функции, дискретизованной с постоянным шагом по длине волны.
В статье [1] спектр реконструируется как линейная комбинация трёх базисных функций, соответствующих излучающим фосфорам, с коэффициентами, вычисленными из исходного цвета RGB путём решения системы линейных уравнений.
В [2] предлагается взять такую же линейную комбинацию от заданных автором функций: константной, синусоидальной и косинусоидальной, с коэффициентами, полученными аналогичным способом.
Данные два подхода позволяют получить спектры, которые при свёртке с заданными кривыми отклика дают в точности исходный цвет RGB. Недостаток этих подходов состоит в том, что они не учитывают реальных физических свойств результирующего спектра, также результатом может быть функция, имеющая отрицательные значения.
Автор работы [3] ввёл дополнительные ограничения на гладкость спектра для того, чтобы результат лучше соответствовал спектрам отражения известных материалов. На основе этого ограничения был построен набор базисных функций, и итоговый спектр является некоторой их линейной комбинацией. Проблемой этого метода является невозможность построить спектр для некоторых цветов, соответствующих какому-то спектру в действительности.
В работе [4] спектрограмма строится как нормированная сумма допустимых частных решений, соответствующих множеству выбранных троек длин волн. Таким образом, авторы получают представительный спектр, где в целом всем длинам волн соответствуют ненулевые значения интенсивности. Также авторами представлены способы получения корректного спектра излучения и отражения. Однако такой метод работает достаточно долго.
Общей проблемой методов, позволяющих построить корректный итоговый спектр, является то, что ограничения корректности имеют частный вид и заложены в сам метод. Также эти методы достаточно сложны в реализации.
Отдельной проблемой методов преобразования цвета в спектр является устойчивость. В задачах визуализации данные алгоритмы применяются для построения спектрального изображения из обычного цветного изображения, а затем это спектральное изображение накладывается на объект в качестве текстуры, или используется как площадной источник освещения. Если близкие цвета соседних пикселей изображения будут преобразованы алгоритмом в сильно отличающиеся спектры, это приведёт к образованию шума на итоговом результате визуализации. Поэтому необходима устойчивость метода по цвету, которая неформально может быть выражена так: для любых двух близких цветов их спектры также должны быть близки. Устойчивость большинства методов не была исследована, некоторые методы ей не обладают. Например, итерационный метод [5] неустойчив из-за использования случайных начальных приближений.
В связи с описанными недостатками существующих методов появилась необходимость в создании нового метода, который обладал бы следующими свойствами:
В результате был предложен следующий итерационный метод восстановления спектра.
На вход алгоритма подаётся:
, ,
,
на основе которых из спектра можно получить цвет.
.
В качестве примера такой процедуры может быть функция, приравнивающая нулю
все отрицательные значения.
.Результатом применения алгоритма является спектр, цвет
которого приближает заданный с указанной точностью . Спектр и кривые
отклика могут быть заданы множеством дискретных способов или аналитически.
Начальным приближением 
является
нулевой спектр.
Далее последовательно циклически выбираются компоненты цвета R, G, B, R, … и производятся следующие действия (пример приведен для компоненты R):
на
функцию 
.
Коэффициент 
вычисляется таким образом, чтобы 
для
приведения спектра в соответствие с ограничениями.Процесс повторяется до тех пор, пока не будет достигнута
заданная точность по цвету: 
Базовые функции 
, 
, 
можно выбрать равными
соответствующим кривым отклика камеры, с использованием спектра источника
света, или другими, исходя из некоторой априорной информации о спектре.
В простейшем варианте без ограничений на спектр алгоритм сойдётся к некоторому решению из работы [1] с данными базовыми функциями, т.к. является покомпонентным спуском. В общем случае при наличии ограничений полученное решение не будет являться линейной комбинацией базовых функций. Также введение ограничений может повлиять на сходимость.
Сходимость и устойчивость алгоритма зависят от введённых ограничений на спектр и от базовых функций. Так как они задаются пользователем, в каждом конкретном случае нужно отдельно исследовать сходимость и устойчивость. В целом можно говорить только о расходимости для невозможных цветов заданного цветового пространства, для которых не существует спектра.
Сходимость и устойчивость алгоритма с ограничением неотрицательности спектра была исследована эмпирически для цветов единичного куба в пространстве sRGB, т.е. всех цветов, которые можно получить с использованием цифровой камеры. Эксперимент показал, что для каждого такого цвета алгоритм сходится к некоторому спектру, удовлетворяющему указанному ограничению. Результирующие спектры для близких цветов также близки друг к другу на всём пространстве, поэтому алгоритм удовлетворяет изначальным требованиям.
Устойчивость алгоритма позволяет предварительно рассчитать карту спектров для некоторого множества точек пространства sRGB, например, регулярную сетку, и затем интерполировать спектры в промежуточных точках.
Предложенный алгоритм был применён для перевода панорам из RGB в спектральное представление в задаче синтеза изображений бриллиантов, окруженных этой панорамой. Алгоритм применяется к изображению попиксельно и в силу устойчивости не вносит дополнительного шума.
Алгоритм реализован для кусочно-постоянных спектров в среде Matlab (реализация занимает 40 строк кода) и опробован на реальных данных. Использовано ограничение неотрицательности спектра. Время работы реализации алгоритма на Matlab на изображении размером 400×300 пикселей составило 4 секунды на процессоре Intel Core i7 3770K. Время работы для других изображениях прямо пропорционально числу пикселей.
Ниже приведён пример разложения тестового цветного изображения по длинам волн с шагом 5 нм. На рис. 2 показано исходное изображение и монохроматические составляющие для некоторых длин волн.
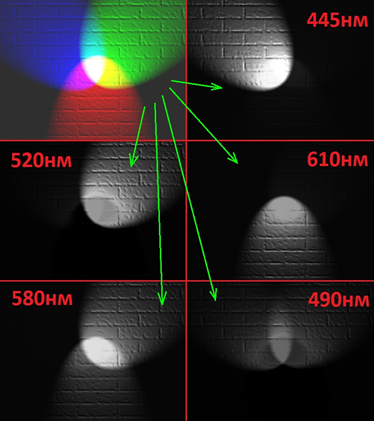
Рис. 2. Разложение цветного изображения по длинам волн
Метод описан и применялся для трихроматических данных, однако использование 3 цветов не является его принципиальным ограничением. Также возможна произвольная форма задания используемых функций при условии соответствующих изменений в процедурах суммирования, интегрирования и коррекции.
Универсальность метода обеспечена тем, что он описывает
общую процедуру итерационного процесса, а детали, относящиеся к конкретной
прикладной задаче, оставлены на усмотрение пользователя. Настройка вида спектра
осуществляется с помощью 2 параметров: это базовые функции и ограничения на
спектр. К примеру, если известно, что сцена освещалась источником D65, то
использование в качестве базовых функций произведения соответствующих кривых
отклика камеры на спектр источника может дать более близкий к действительности
результат. Для различных типов восстанавливаемого спектра пользователь может
задавать необходимые ограничения, например, для спектра отражения – ограничение
. При
этом для того, чтобы не терять общность метода и не работать с приведением спектра
к нужному виду, от пользователя потребуется эта процедура приведения. Также
ввиду произвольности настроек алгоритма исследование его сходимости для каждого
набора настроек остаётся открытым вопросом и ложится на пользователя.
Пример визуализации бриллианта в работе [6] с использованием спектральной панорамы окружения, полученной из RGB панорамы описанным методом, приведен на рис. 3.
Рис. 3. Результат визуализации в спектральной панораме
Разработан простой и универсальный метод восстановления спектра излучения по цвету, позволяющий итерационно строить итоговый спектр с учётом заданных ограничений. Он применяется в практических приложениях. Эмпирическим путём проверена сходимость и устойчивость метода с ограничением неотрицательности спектра на цветовом пространстве sRGB.
THE SIMPLE METHOD OF THE RGB TO SPECTRUM CONVERSION FOR TASKS OF PHYSICALLY BASED RENDERING
V. Afanasiev, A. Ignatenko, A. Voloboy
Keldysh Institute of Applied Mathematics RAS
Graphics & Media Lab, CS MSU
vafanasjev@graphics.cs.msu.ru, ignatenko@graphics.cs.msu.ru, voloboy@gin.keldysh.ru
Abstract.
Physically based rendering often requires simulation the effects of wave optics such as dispersion, interference, diffraction. However, even if a model of the wave phenomenon is known we have a problem getting the input data for rendering because the majority of the available methods allows to get the color and intensity of the radiation, but not its spectrum. And devices for spectrum measuring are complex, expensive and difficult to access. This article describes a simple and flexible iterative method for the spectrum construction from RGB color, which allows to build the result taking into account the specified limitations relevant to rendering task requirements.
Keywords: spectrum, RGB, physically based rendering, realistic rendering