THE SIMPLE METHOD OF THE RGB TO SPECTRUM CONVERSION FOR TASKS OF PHYSICALLY BASED RENDERING
V. Afanasiev, A. Ignatenko, A. Voloboy
Keldysh Institute of Applied Mathematics RAS
Graphics & Media Lab, CS MSU
vafanasjev@graphics.cs.msu.ru, ignatenko@graphics.cs.msu.ru, voloboy@gin.keldysh.ru
Content
Abstract.
Physically based rendering often requires simulation the effects of wave optics such as dispersion, interference, diffraction. However, even if a model of the wave phenomenon is known we have a problem getting the input data for rendering because the majority of the available methods allows to get the color and intensity of the radiation, but not its spectrum. And devices for spectrum measuring are complex, expensive and difficult to access. This article describes a simple and flexible iterative method for the spectrum construction from RGB color, which allows to build the result taking into account the specified limitations relevant to rendering task requirements.
Keywords: spectrum, RGB, physically based rendering, realistic rendering
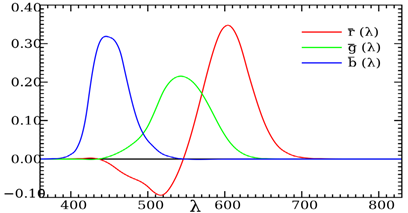
Spectrum is one of the physical characteristics of electromagnetic radiation. It is wavelength distribution of radiation power. Color is a human-sensible property of the visible light. According to CIE experiments color can be described by three numbers because there are three color receptors in a human eye. It was also shown that the visible color can be reproduced using three emitters with different spectrum. Various linear color spaces are formed depending on the choice of the emitters. The transition between them can be done by multiplication of color triplet by transformation matrix. Hereinafter we will work with the curves for some linear RGB color space since a specific color space is not important for the described method.
Fig. 1. CIE RGB curves
The spectral curves of CIE RGB color space for the visible range of wavelengths from 380 to 780 nm are shown in Fig. 1.
The geometric models of objects, textures, light sources and camera model are used during realistic image rendering. These data are obtained through simulation and real objects measurements or photography. The latter method allows the maximum approximation to reality: this way one can get, for example, parameters of light sources, texture, object shapes.
Digital cameras used for image capturing have several types
of sensitive elements (usually, there are three different elements also). Each
of them has its own response curve. They usually correspond to red, green and
blue colors: 
,
,
.
The response
of the camera on the spectrum 
which
came to the sensor element is expressed by the transformation of convolution:
In most cases we can neglect the spectral nature of light during image synthesis and perform calculations with the RGB color. However for a certain class of simulations associated with the modeling of light wave phenomena spectrum is important. This class includes the synthesis of gemstones images where light dispersion inside the material determines the final visible color. However the conventional digital cameras allow obtaining the color in RGB format. Therefore it was required to elaborate an algorithm which creates a spectrum from available color triplet.
There is an infinite number of spectra having the same RGB color as it is clear seen from direct spectrum-to-RGB conversion. Such spectra are called metameres. From a mathematical point of view any spectral distribution function that gives the specified RGB values is a solution to the inverse problem. However the requirement of the physical correctness provides a number of limitations, for example, spectra of the light source with negative values are meaningless. In the presence of a priori information about the source spectrum some additional restrictions can be imposed on the result, such as the continuity or smoothness.
It is known several solutions for our task. They are based on the representation of the spectrum in the form of a piecewise constant functions with a constant wavelength step.
In the article [1] the spectrum is reconstructed as a linear combination of three base functions corresponding to emitting phosphor. The coefficients are obtained from the original RGB color by solving a system of linear equations.
In [2] it is proposed to take the same linear combination of the functions specified by the author: constant, sine and cosine. The coefficients are obtained in a similar manner.
These two approaches allow obtaining spectra that give exactly the original RGB color after convolution with initial response curves. The disadvantage of these approaches is that they do not take into account the actual physical sense of the resulting spectrum. And the result may be a spectrum having a negative value.
The author of [3] introduced additional restrictions on the smoothness of the spectrum to get better matching of the resultant reflection spectra for the known materials. Using this restriction a set of base functions was built and the resulting spectrum is considered as a linear combination of them. The problem of this method is the inability to reconstruct a spectrum for some colors corresponding to really existing spectrum.
In [4] the spectrogram is constructed as a normalized sum of permissible partial solutions corresponding to a set of randomly selected wavelength triples. Thus the authors had obtained representative spectrum where all visible wavelengths correspond to non-zero intensity. The author also provides methods for getting the correct emission and reflection spectrum. However this method is very time consuming.
A common problem of the existent methods for the correct spectrum construction is that the correctness restrictions have some particular form and are incorporated inside the method itself. Also these methods are rather complex to implement.
Another problem of the RGB color to spectrum conversion methods is stability. In realistic rendering they are used to construct the spectral image from a conventional colored image. Then this spectral image is applied on the object as a texture or is used as an areal light source. If the similar colors of neighboring pixels on the image will be converted into very different spectra it will lead to the formation of noise on the final image. Therefore the color stability is one more method requirement. It can be expressed informally as follows: for any two similar colors their spectra must also be similar. Stability of most of the methods above has not been investigated and some of the techniques do not possess it. For example an iterative method [5] is unstable due to the use of random initial approximations.
Because of described disadvantages of existing methods there was a need for a new method which should satisfy to the following requirements:
As a result the following iterative method for spectrum construction was proposed.
The algorithm inputs are:
, ,
based
on which the RGB color can be calculated from spectrum.
.
An example of such procedure can be making all negative values equal to
zero.
.The result of applying the algorithm is a spectrum of original
color that approximates it with a specified precision . Spectrum and response
curves can be determined using one of the discrete ways or analytically.
The initial approximation 
is a
zero spectrum.
Then the color components R, G, B, R, ... are selected sequentially in cycle and the following actions are performed (example is shown for R component):
is
computed.
is
calculated.
by
function 
is
performed. The coefficient 
is calculated so that 
.
over
the spectrum to bring it into compliance with the restrictions is executed.The process is repeated until the predetermined color
accuracy is achieved: 
Base functions 
, 
, 
can be chosen as equal
to the corresponding camera response curves or using the spectrum of the light
source or in the other way basing on a priori information about the spectrum.
In the simplest version (without restrictions on the spectrum) the algorithm converges to a solution of [1] with selected base functions because it is a coordinate-wise descent. In general, the presence of constraints means that the solution is not a linear combination of base functions. Also restrictions may affect the convergence.
Convergence and stability of the algorithm depends on the applied restrictions and on the base functions. Since they are user-defined one need to examine the convergence and stability for each case separately. In general we can only claim the divergence for “impossible” colors of specified color space for which there is no spectrum.
Convergence and stability of the algorithm with the restriction of spectrum non- negativity has been studied empirically for the unit cube of sRGB color space, i.e. for all colors that can be produced using a digital camera. The experiment showed that for each of the colors the algorithm converges to a spectrum that satisfies the specified constraints. The resulting spectra of close colors are also close for the whole space. So the algorithm satisfies the initial requirements.
The stability of the algorithm makes it possible to calculate the preliminary map of the spectra for a set of points in sRGB space, for example, for a regular grid, and then to interpolate the spectrum from intermediate points.
The proposed algorithm was applied to convert HDRI panoramas from RGB to a spectral representation. Spectral HDRI panoramas were used for diamonds image synthesis. The algorithm is applied to the HDRI pixel by pixel and due to stability it does not introduce additional noise.
The algorithm is implemented for piecewise constant spectra in Matlab environment (the code consists of 40 lines only) and it was tested on real data. It uses a restriction of spectrum non-negativity. Execution time of the algorithm in Matlab on the image of 400 × 300 pixels was 4 seconds on the CPU Intel Core i7 3770K. Time for the other images is proportional to the number of pixels.
Below there is an example of the decomposition of the test color image into separate wavelengths with a step of 5 nm. Fig. 2 shows the original image and the monochromatic components for certain wavelengths.
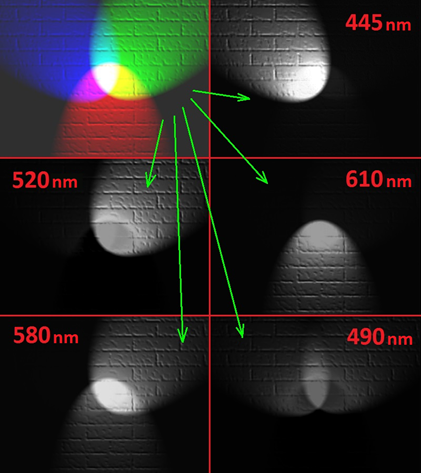
Fig. 2. Decomposition of the color image by wavelengths
In the article the method is described for and applied to RGB triplet. But the use of three color components is not its principal limitation. It is also possible to specify an arbitrary form of functions definition with the appropriate changes in summation, integration and correction procedures.
The versatility of the method is provided by the fact that
it describes the general procedure of iterative process, and details relating
to the particular application are left to the user. Tuning of the spectrum is
carried out by means of two parameters: the base functions and restrictions on
the spectrum. For example, if you know that the scene was illuminated with
light source D65 then using the base functions equal to the product of camera
response curves and D65 spectrum may give more realistic result. For different
types of recovered spectrum the user can set the necessary restrictions, such
as for reflectance spectrum - the restriction 
. At
the same time in order not to lose the versatility and not to work directly in
algorithm with transformation of spectrum to the desired form, the user will
need to provide a procedure to implement this restriction. Also, because of the
arbitrariness of the algorithm settings the examination of convergence for each
set of options should be investigated by the user.
Example of a diamond rendering [6] using the spectral environment panorama computed from RGB panorama by the described method is shown in Fig. 3.
Fig. 3. The diamond rendering result in spectral panorama
A simple and versatile method for spectrum construction from RGB (or other representation) color was developed. It allows building the final spectrum iteratively taking into account the specified restrictions. It is used in practical applications. Convergence and stability was empirically validated for restriction of spectrum non-negativity and the color space of sRGB.