МОДЕЛИРОВАНИЕ И ВИЗУАЛИЗАЦИЯ РАБОТЫ УЗЛА ЛОПАСТЕЙ СЛОЖНОЙ ФОРМЫ В ЭНЕРГЕТИЧЕСКОЙ УСТАНОВКЕ
С.В. Андреев1, А.Е. Бондарев1, А.В. Бондаренко2, Ю.В. Визильтер2, В.А. Галактионов1, А.В. Гудков2, С.Ю. Желтов2, В.Т. Жуков1, Е.Б. Иловайская2, В.А. Князь2, К.В. Мануковский1, Н.Д. Новикова1, М.В. Ососков2, Н.Ж. Силаев2, О.Б. Феодоритова1, Н.А. Бондарева1
1Институт прикладной математики им. М.В.Келдыша РАН, Москва, Россия
2ФГУП ГосНИИАС, Москва, Россия
e-mail: bond@keldysh.ru;
Содержание
2. Построение CAD модели и расчетных сеток
3.1. Математическая постановка
4. Визуализация. Построение стереомодели
Аннотация
Работа посвящена вопросам моделирования и визуального представления физических характеристик узла лопастей энергетической установки (ЭУ), который обладает сложной формой. Основной задачей работы является моделирование рабочего режима установки под нагрузкой. Рассматриваются вопросы построения математической модели и трехмерной расчетной сетки, как статической, так и динамической, а также вопросы организации визуального представления, позволяющего верификацию построенной модели и полученных результатов. Реализована полноценная технологическая цепочка алгоритмов, с помощью которой проводится моделирование ЭУ от построения исходной CAD модели до организации визуального представления результатов в стереорежиме. Итоги численного моделирования являются базовыми для последующего решения задачи глобальной оптимизации формы ЭУ с целью выработки оптимальных рабочих параметров.
Ключевые слова: визуализация многомерных данных, энергетическая установка, вычислительная газовая динамика, OpenFOAM
Основной задачей предлагаемой работы являлось создание полной технологической цепочки для аэродинамического моделирования работы объекта сложной формы (в нашем случае - узла лопастей энергетической установки), а также последующего анализа и оптимизации основных важнейших параметров, модификации формы объекта с целью улучшения его производственных характеристик.
Поставленная задача включает в себя несколько основных этапов, а именно, разработка приемлемой CAD модели, подбор адекватной математической модели, построение сетки на поверхности объекта и в окружающей его области, выбор вычислительной модели, проведение серии вычислительных экспериментов и их верификация, и наконец, визуализация и анализ полученных данных. Ниже мы остановимся на каждом из этих этапов подробнее.
Следует заметить, что описанный цикл может быть повторен многократно, что диктует необходимость использования мощных компьютеров. Все расчеты проведены в ИПМ им. М.В. Келдыша РАН на вычислительном кластере К-100 [1].
Аэродинамический расчет реального трехмерного объекта может быть успешным только при наличии геометрической сетки приемлемого качества, и подготовка такой сетки является одной из самых трудоемких частей вычислительного (равно как и всего технологического) процесса.
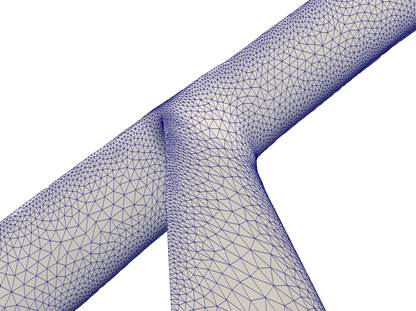
Сначала создается сетка на поверхности, ограничивающей рассматриваемое трехмерное тело. Как правило, поверхность импортируется из САD-пакета (полностью или частично) и в случае необходимости может быть отредактирована. При этом набор предлагаемых форматов описания геометрии достаточно широк. Таким образом, основой для построения объемной сетки вне тела является одна или несколько триангулированных поверхностей. Основные требования, предъявляемые к поверхностным сеткам: отсутствие самопересечений, замкнутость и некоторые другие. При работе с реальными промышленными объектами получаемые CAD-поверхности удовлетворяют названным критериям в редких случаях. Как правило, для получения объемной сетки нужного качества необходима дополнительная подготовка поверхности. Для достижения указанной цели используется ряд автоматических инструментов с широким набором средств контроля качества. Пример триангулированной сетки на поверхности приведен на рис.1.
Объемная сетка для моделирования течений жидкостей и газов, как правило, состоит из двух основных частей: призматической вблизи обтекаемых поверхностей и произвольной многогранной на удалении от поверхностей. Для создания пристеночного призматического слоя с заданным числом ячеек в направлении от стенки, с заданным законом роста размеров ячеек и полной толщиной слоя используются два возможных подхода. В первом строится поверхностная сетка, отстоящая от исходной на полную толщину слоя. Получившийся таким образом пристеночный объем разрезается на заданное число призматических слоев. Такой подход обычно не гарантирует создание призматического слоя с заданными параметрами и требуемой полной толщиной в областях со сложной геометрией. В таких случаях предпочтительней использовать метод последовательного создания призматических слоев, допускающий модификацию поверхностной сетки текущего слоя (коллапс ребер, разрезание ячеек, оптимизация положения вершин и т.д.), что позволяет создать слой призматических ячеек, проникающий значительно дальше от стенок вглубь расчетной области.

Рис.1. Пример построенной поверхностной сетки
Для заполнения внепристеночного объема также могут использоваться различные подходы: тетраэдры, усеченные ячейки (гексагональные во внутренней части и многогранные на границе расчетной области), а также многогранные ячейки во всей счетной области. Программный пакет OpenFOAM, который использовался при численном моделировании, позволяет проводить расчеты на сетках, состоящих из произвольных многогранных ячеек, ограниченных произвольным числом многоугольных граней. На рис.2 приведен общий вид объемной сетки для полной модели узла лопастей, рисунок представляет собой пример типичного построения сеточного разбиения расчетной области для данной задачи.

Рис. 2. Общий вид объемной сетки для полной модели узла лопастей.
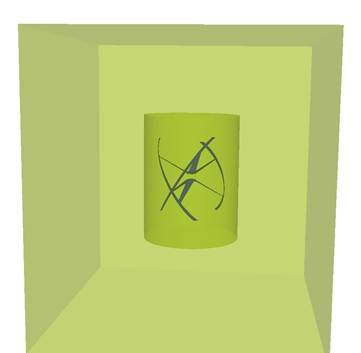
Рис.3. Пример двухобластной задачи.
Моделирование физических процессов при движении объекта требует построения как минимум двухобластной объемной сетки при условии их стыковки «узел в узел» на границе областей. Пример такой расчетной области, состоящей из двух подобластей, и примененной нами для расчета физических характеристик движущегося объекта, показан на рис. 3.
В настоящее время течения газовой сплошной среды рассчитываются на основе осредненных уравнений Навье-Стокса, в которые введены дополнительные члены, учитывающие эффекты турбулентности [2]. Система уравнений дополняется уравнением состояния: в простейшем случае - уравнением состояния идеального газа, который, однако, может служить хорошим первоначальным приближением. Вид турбулентных компонент не является универсальным и зависит от модели турбулентности, выбираемой с учетом свойства реальных физических течений в некотором диапазоне параметров. Вопрос выбора модели турбулентности вынесен за рамки данной работы. В работе реализованы расчеты как ламинарных, так и турбулентных течений.
Процесс математического моделирования предполагает выбор вычислительной модели, определение расчетных областей и подобластей, граничных и начальных условий, а также проведение цикла методических и параметрических расчетов. В современных расчетах необходимо также учитывать возможность хорошего распараллеливания алгоритма.
Для проведения расчетов мы воспользовались открытой интегрируемой платформой для численного моделирования задач механики сплошной среды OpenFOAM. Элементы OpenFOAM активно используются в промышленности, в академической сфере и экспертном сообществе, в частности для расчета энергетических характеристик ветроустановок [3]. Пакет представляет собой множество готовых моделей, но будучи открытым, позволяет вносить изменения и дополнения. В качестве базовой мы использовали модель rhoCentralFoam, которая реализует так называемую «центрально-противопотоковую» схему и, в полном соответствии с названием, представляет собой комбинацию центрально-разностной и противопотоковой схем [4]. Преимущество указанных схем состоит в том, что, применяя соответствующую технику уменьшения численной вязкости, можно добиться хорошей разрешимости и для разрывных решений (ударных волн в газовой динамике) и для решений, где основную роль играют вязкие явления. Суть центрально-противопотоковых схем состоит в специальном выборе контрольного объема. За прошедшее десятилетие этот метод интенсивно развивался и продемонстрировал свои достоинства при проведении предсказательных вычислений.
Для анализа движущейся установки использовалась модель pimpleDyMFоам, в основе которой лежит алгоритм PIMPLE. Внутренняя подобласть (в нашем случае это цилиндр) вращалась с заданной скоростью и на каждом шаге производилась корректировка потоков на интерфейсе.
Была проведена серия специальных методических расчетов, которая позволила сформировать топологию, форму и размеры расчетной области, наиболее соответствующие целям проводимого компьютерного моделирования и принятой постановке задачи. При этом первоначально рассчитывалась и анализировалась только часть ЭУ, а именно, одна неподвижная лопасть [5].
Среди аэродинамических характеристик прежде всего нас интересуют полная аэродинамическая сила и крутящий момент [6]. При рассмотрении одной неподвижной лопатки мы изучали влияние на эти характеристики скорости набегающего потока, его направления, температуры, гравитации. В методических целях проведены расчеты с измельчением расчетной сетки для ориентировочной оценки уровня измельчения сетки, необходимого для масштабных расчетов полной компоновки ЭУ. Полученные в расчетах силовые характеристики удовлетворительно согласуются с приближенной эмпирической оценкой. Предварительные выводы, которые можно сделать из проведенных серий расчетов обтекания ламинарным потоком лопасти ЭУ в неподвижном состоянии, следующие: рост скорости обтекания лопасти приводит к увеличению силы и момента, воздействующих на лопасть, что соответствует физической природе моделируемого процесса. Изменение температуры потока практически не оказывает влияния на силовые характеристики. Введение учета гравитации в расчетах приводит к небольшому изменению в силовых характеристиках.
При переходе к полномасштабным расчетам ЭУ в полной компоновке основной интерес представляет влияние на газодинамические характеристики изменение геометрии объекта: расположение лопастей относительно центральной оси установки, ширины и конструктивных особенностей самих лопастей и т.д.
Основным источником представления о физических процессах, происходящих при работе энергетической установки, является визуализация результатов решения задачи математического моделирования. Визуальное представление является незаменимым источником информации о деталях течения. Основные способы визуального представления численных данных в задачах вычислительной механики жидкости и газа представлены в работах [7,8].
Визуализация с функциональной точки зрения обеспечивает следующие возможности:
- получение информации о физическом процессе с разным уровнем детализации;
- своевременное выявление артефактов, облегчающее отладку численных методов и алгоритмов;
- верификация и оценка физичности результатов расчетов.
В силу функциональной необходимости к алгоритмам и методам визуального представления предъявляется ряд требований, апробированных на практике:
- адекватность визуального представления задаче исследования. Это означает, что визуальное представление должно соответствовать целям исследования;
- адекватность способам человеческого восприятия. Это означает, что, например, визуально представляя распределение температур на поверхности, мы используем для иллюстрации перехода от холодного к более горячему цветовую гамму от синего к красному. Аналогичная цветовая схема обычно используется для иллюстрации увеличения представляемой величины.
- визуальный образ не должен быть информационно перегружен.
- реализация (при наличии возможности) визуализации в режиме 3D (стерео), обеспечивающей объемность восприятия модели и учитывающей бинокулярность человеческого зрения.
Именно исходя из этих требований и выбирались в данной работе способы визуального представления результатов расчетов.
В данной работе использовались различные формы визуального представления: статическая форма для тщательного изучения распределения газодинамических функций по поверхности установки и в расчетной области, динамическая форма для изучения процессов перераспределения газодинамических функций в процессе движения и объемная динамическая форма в виде стереопредставления.
Для статического визуального представления использовалась концепция прозрачной счетной области и рендеринга распределения газодинамических функций (давление, температура) по поверхности неподвижного узла лопастей энергоустановки в потоке воздуха. Для одновременной оценки процессов распределения газодинамических функций на поверхности лопастей и в счетной области использовалась комбинация рендеринга по поверхности лопасти и в поперечном сечении, рассекающем лопасть.
Анимированное представление реализовывалось с помощью двух подходов. В первом подходе камера фиксировалась в определенном положении, и вращение узла лопастей происходило перед камерой. Это позволяло наблюдать процесс изменения газодинамических характеристик на всем узле в целом во время движения узла. Также этот подход использовался при решении задачи об обтекании потоком воздуха неподвижного узла лопастей. В этом случае подобный подход естественным образом трактуется как «облет» камеры вокруг неподвижного узла лопастей в потоке. Для неподвижного узла лопастей подобный подход дает возможность контролировать распределение газодинамических функций во всех точках объекта, вовремя выявлять появление расчетных артефактов и отлаживать численные методы и схемы организации расчета.
Второй подход заключался в фиксации камеры в определенном положении относительно узла лопастей и вращении камеры вместе с узлом. Этот подход обеспечивал возможность контроля изменения газодинамических характеристик на просматриваемой лопасти в процессе движения.
Для обозначения текущего положения узла на рисунках и кадрах анимированных визуальных представлений изображается ориентация координатных осей. При этом поток воздуха направлен по оси ОХ.
Рис.4. Анимация процесса обтекания неподвижного узла лопастей при «облете» камеры вокруг узла, показано распределение давления по поверхностям лопастей.
Рис.5. Анимация процесса обтекания неподвижного узла лопастей при «облете» камеры, показано распределение давления по поверхностям лопастей и в поперечном сечении.
На рисунке 4 представлена анимация процесса обтекания неподвижного узла лопастей при «облете» камеры вокруг узла с помощью рендеринга распределения давления по поверхностям лопастей узла. Поток направлен по оси ОХ. Аналогичным образом на рисунке 5 представлена анимация с помощью распределения давления по поверхностям узла и в поперечном сечении. Обе анимации позволяют получить достаточно ясное представление об образующемся на поверхности узла лопастей перепаде давления при обтекании.
Для визуализации движущегося узла лопастей под ветровой нагрузкой применялся второй подход анимации. Камера фиксировалась в одном положении относительно узла лопастей и вращается вместе с узлом. На рисунке 6 представлена анимация с помощью рендеринга распределения давления по поверхностям узла. Соответственно на рисунке 7 представлена аналогичная анимация, но с распределением давления в поперечном сечении.
Рис.6. Анимация процесса обтекания движущегося узла при фиксированной относительно узла камере, показано распределение давления по поверхностям лопастей.
Рис.7. Анимация процесса обтекания движущегося узла при фиксированной относительно узла камере, показано распределение давления по поверхностям лопастей и в поперечном сечении.
Для визуализации результатов расчетов в объемном виде (построение стереомодели) необходимо создание пары изображений, показывающие объект с различных ракурсов для правого и левого глаза соответственно, называемые стереопарой. То есть стереопара — это два плоских изображения одного и того же объекта (сюжета), имеющая различия между изображениями, призванные создать эффект объёма. В основном используются два метода создания стереопар: это смещение камеры параллельно на некоторое расстояние (линейная стереобаза), либо поворот камеры вокруг демонстрируемого объекта на определенный угол (угловая стереобаза). Нашей задачей являлось создание стереофильма, позволяющего продемонстрировать результаты расчетов (создание последовательности стереопар, каждая из которых является стереокадром фильма), поэтому для этих целей наиболее подходящим является метод «облета» камеры вокруг объекта, то есть угловая стереобаза.
Практически любая CAD-система позволяет визуализировать трехмерный объект с заданными координатами положения по отношению к пользователю. Поэтому задача сводилась к построению последовательности изображений CAD модели с зафиксированной осью Z, проходящей через ее геометрический центр, и смещением на определенный угол. После каждого такого смещения проводился рендеринг модели, позволяющей достичь фотореалистичности, и сохранение результата в виде графического файла в высоком разрешении. Для левого стереоканала устанавливалась начальная позиция, отличающаяся от правого стереоканала на угол, определяющий параллакс, и позволяющая добиться объемности объекта в результирующем стереофильме (Рис.8).
Данный метод привлекателен еще и тем, что для статической модели, то есть с неизменной геометрией и цветовым распределением, возможно использование уже рассчитанных кадров, например, если для левого стереоканала мы используем 1,2,3,4,… кадры, то для правого стереоканала достаточно начать последовательность со второго или с третьего кадра (2,3,4,5…), автоматически обеспечивая сдвиг объекта на необходимый угол стереобазы [9].
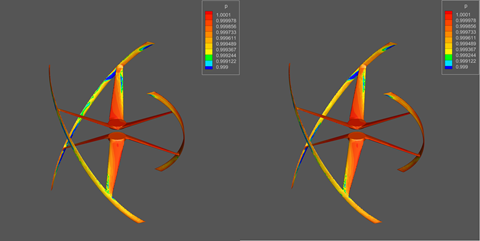
Рис. 8. Стереокадр с угловой стереобазой, демонстрирующий распределение давления по поверхности энергоустановки.
Таким образом, был создан ряд стереофильмов, визуализирующий вращение модели в объемном представлении при задании различных внешних условий.
Разработана численная модель, представляющая собой единую технологическую цепочку алгоритмов, включающую в себя построение CAD-модели для описания сложной геометрии, построение расчетной сетки на основе полученной геометрии, решение задачи моделирования обтекания на основе полной системы уравнений Навье-Стокса, визуализацию и анимацию результатов в моно- и стереорежимах. Разработанная технологическая цепочка позволяет проводить полноценное численное исследование и последующий анализ работы энергетической установки, начиная от создания CAD модели и заканчивая стереометрической визуализацией. Это дает возможность перейти к задачам оптимизации для уменьшения энергетических потерь и увеличения КПД установки.
Данная работа выполнена при частичной поддержке грантов РФФИ (проекты 13-0100367а и 16-01-00769а).
MODELLING AND VISUALISATION OF BLADE ASSEMBLY WITH COMPLICATED SHAPE FOR POWER TURBINE
S.V. Andreev1, A.E. Bondarev1, A.V. Bondarenko2, Yu.V. Vizilter2, V.A. Galaktionov1, A.V. Gudkov2, S.Yu. Zheltov2, V.T. Zhukov1, E.B. Ilovayskaya2, V.A. Knyaz2, K.V. Manukovsky1, N.D. Novikova1, M.V. Ososkov2, N.Zh. Silaev2, O.B. Feodoritova1, N.A. Bondareva1
1Keldysh Institute for Applied Mathematics RAS, Moscow, Russian Federation;
2GOSNIIAS, Moscow, Russian Federation
Abstract
The work is devoted to simulation and visualization of blade assembly for power plant (PP), which is the installation of vertical type and has a very complicated shape. The main goal is simulation of operating mode under load. Constructing of mathematical model and 3D calculation grid (both static and dynamic ones) as well as organization of the visual presentation to verify constructing model and obtained results are considered. Complete technological pipeline that allows simulating PP from constructing original CAD model up to visualization of results in stereo mode is implemented. The results of numerical simulation are the base to solve further the problem of global optimization of the PP shape in order to develop the optimal operating parameters.
Keywords: multidimensional data visualization, power plant, CFD problems, OpenFOAM