Классические методы вычислительной томографии, такие, как ART, широко используются для реконструкции объектов, снятых на рентгеновских установках, где в зависимости от мощности излучения можно сделать прозрачным практически любой объект и с некоторой точностью измерить его поглощение. Однако классическая модель не подходит для реконструкции объектов, поглощение которых настолько высоко, что задерживает полностью всё излучение: такие случаи возможны в рентгеновской томографии при недостаточной мощности источника излучения, а также часто встречаются в оптической томографии.

В статье описаны сложности, возникающие у классических алгоритмов ART для оптической томографии при наличии непрозрачных областей в сканируемом объекте. Предлагается модификация методов ART для этого случая.

Ключевые слова: томография, оптическая томография, ART.

1. Введение

С появлением методов синтеза реалистичных изображений, основанных на физически корректном моделировании распространения света, область применения компьютерной графики существенно расширилась. Созданные алгоритмы и программные средства стали представлять интерес для использования в архитектуре, градостроительстве, проектировании систем освещения, в автомобильной и авиационной промышленности и других областях. Предварительные расчеты освещения и реалистичная визуализация виртуальной модели существенно повышают эффективность производственного процесса.

Достаточно интересной задачей является применение реалистичных изображений в индустрии алмазообработки и огранки драгоценных камней. Здесь смоделированные изображения позволяют улучшить процесс изготовления технических и ювелирных изделий на разных стадиях обработки, от сканирования добытых камней до огранки. Особой сложностью этой задачи является высокая прозрачность материала. Визуализация проектируемых огранок требует как использования корректных алгоритмов моделирования распространения света, так и высокой точности задания геометрии исходного материала. Изначальная геометрия добытого камня воссоздается методами вычислительной томографии.

Вычислительная томография – класс задач восстановления внутренней структуры некоторого объёма по набору его проекций. Самой распространённой областью применения методов вычислительной томографии является рентгеновская томография. Более подробный обзор сделан в статье [1]. Рентгеновская томография как один из методов неразрушающего сканирования применяется в медицине для диагностики заболеваний у людей, для исследования животных [2][3], для поиска дефектов в различных деталях, в геологических исследованиях [4] и в других областях.

Установка для рентгеновской томографии состоит из излучателя, приёмника и места для исследуемого объекта между ними. Излучатель испускает рентгеновские лучи с фиксированной интенсивностью, внутри объекта происходит их поглощение, и приёмник регистрирует остаточную интенсивность лучей. При вращении объекта по некоторой траектории получается набор проекций, по которым затем восстанавливается внутренняя структура объекта.

Возможны различные конфигурации пучка лучей от разных источников: плоский/объёмный, параллельный/расходящийся пучок. В зависимости от этого, применяется плоская или объёмная томографическая реконструкция.

Поглощение излучения в материале подчиняется закону Бугера-Ламберта-Бера:

(1)

где – интенсивность излучения на приёмнике, – интенсивность излучения источника в данном направлении, – распределение показателя поглощения среды вдоль луча.

В показателе степени в формуле (1) находится собственный интеграл в пределах . Если перейти от него к несобственному интегралу на интервале , рассматривая всевозможные прямые, пересекающие исследуемый объём, приходим к понятию преобразования Радона.

Для наглядности будем рассматривать в иллюстрациях двумерные функции распределения показателя поглощения.

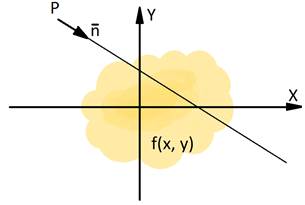
Рис. 1. Преобразование Радона для одной прямой

Преобразованием Радона от функции называется функция , определённая для каждой прямой в пространстве , каждое значение которой определяется несобственным интеграл от функции вдоль соответствующей прямой. На рис.1 это проиллюстрировано для двумерной функции . Аргумент функции представлен в векторном виде.

(2)

Предполагается, что несобственные интегралы от этой функции вдоль всех прямых сходятся, т.е. функция ограничена и достаточно близка к 0 на бесконечности. На практике рассматривают функции, заданные в некоторой области. Кроме того, функция должна быть ограничена, то есть не допускается бесконечное поглощение в какой-то части области рассмотрения.

Также можно рассматривать преобразование Радона как функцию от направления и смещения прямой от центра координат, как показано на рис.2. Получим двумерную функцию , где – смещение прямой относительно центра координат, – угол наклона прямой. Такая функция называется синограммой для параллельной проекции. На практике рассматривают функцию в конечной области и, соответственно, ограниченные по параметру синограммы.

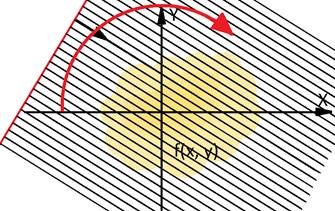
Рис. 2. Преобразование Радона

При определённых ограничениях на функцию и траекторию приёмника при съёмке существует обратное преобразование Радона. [5] Однако при наличии шумов и других погрешностей в исходных данных оно неустойчиво. Кроме того, вычисление обратного преобразования Радона затратно.

2. Существующие методы

Методы восстановления изображения по проекциям делятся на прямые и итерационные. [6] К прямым методам относятся методы свёртки и обратной проекции, методы Фурье-синтеза. Классическим итерационным методом является ART (algebraic reconstruction technique).

Идея группы методов ART состоит в том, чтобы путём минимизации отклонения наблюдаемого значения текущей проекции от истинного значения проекции на каждом отдельном ракурсе и последовательным учётом разных ракурсов добиться минимизации отклонения неизвестной изначально функции от её истинного значения, которое даёт наблюдаемые значения проекций. Существует множество реализаций этой идеи: аддитивный, мультипликативный и другие виды ART. [7]

Наиболее простым является аддитивный метод ART. На вход алгоритму подаётся синограмма (в двумерном случае – набор из проекций по значений в каждой) и геометрические характеристики каждой проекции (направление хода лучей и размер приёмника). На выходе должна получиться искомая функция , заданная на сетке фиксированного размера . Функция считается кусочно-постоянной, т.е. внутри одной ячейки сетки она имеет одно значение.

Изначально искомая функция инициализируется произвольными значениями (например, 0) на всей сетке. Затем итеративно производятся следующие действия либо заранее заданное число раз, либо до выполнения некоторого условия:

Выбор очередного значения проекции из некоторого пиксела ракурса . Как именно они выбираются, может быть определено специальным порядком обхода проекций и ракурсов, самый простой вариант – последовательная выборка.

Генерация прямой, соответствующей данному значению проекции. Параметры прямой вычисляются из геометрических параметров ракурса.

Расчёт интеграла от текущей функции вдоль прямой

Вычисление знаковой разности между известным наблюдаемым значением и текущим интегралом.

Проход по сетке и коррекция существующих значений функции вдоль прямой. Коррекция значения функции в одной ячейке сетки производится следующим образом:

(3)

Где – коэффициент регуляризации, – длина пересечения прямой с текущей ячейкой сетки, – общая длина пересечения прямой со всей сеткой.

Процесс схематично изображён на рис. 3:

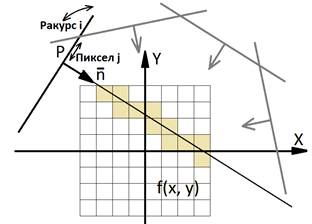
Рис. 3. Учёт ракурсов и пикселов

3. Данные и специфика оптической томографии

Для простоты здесь и далее будем рассматривать только такие преломляющие объекты, которые имеют плоские грани. При съёмке через изогнутую преломляющую поверхность появляются дополнительные искажения, связанные с оптической системой камер: области резкости и нерезкости. Компенсация этих эффектов не относится напрямую к алгоритмам томографии и не будет рассмотрена здесь.

Рис. 4. Схема установки для оптической томографии

Оптическая томография принципиально похожа на рентреновскую томографию, как видно из схемы на рис.4, но существуют следующие отличия:

· Источником освещения является некоторая светящаяся площадка с неравномерным распределением освещённости. Это распределение можно получить, сделав фотографию площадки без сканируемого объекта.

· Каждое значение проекции – не значение интеграла от функции, а остаточная яркость источника света с учётом затухания из-за поглощения среды и пропускания границы между средами по закону Френеля. Также вклад в яркость вносит переотражение света от всех поверхностей.

· На проекции возможно нулевое значение яркости, что соответствует бесконечному поглощению. Бесконечное поглощение согласованно выражается нулевыми значениями яркости на всех ракурсах в соответствующей области. В классической же модели берётся интеграл от показателя поглощения вдоль луча. Вследствие этого, любое значение проекции конечно. Поэтому в линейной модели не существует такого набора проекций, которые согласованно отображали бы бесконечное поглощение в какой-то области объёма. В рентгеновской томографии возможен аналогичный эффект от металлического предмета при малой мощности излучения.

· В общем случае на одном ракурсе лучи, которые в воздухе шли параллельно, преломляются на границе среды и проходят через целевой объём сразу с нескольких направлений.

· Шаг между лучами внутри преломляющей среды переменный и зависит от угла падения лучей на преломляющую поверхность.

Данные томографии изначально дискретны. Дискретизуются также остальные величины для записи в память и расчётов.

· Дискретизация по углу поворота объекта относительно приёмника. Имеется конечный набор ракурсов. Как правило, используется выборка ракурсов с равномерным шагом.

· Дискретизация смещения луча относительно центра координат. Приёмник излучения всегда имеет фиксированное число чувствительных элементов.

· Дискретизация значений остаточной интенсивности излучения.

· Дискретизация восстанавливаемой функции по аргументам. Функция задаётся на сетке с равномерным шагом.

· Дискретизация значений функции .

В отличие от рентгеновской томографии, в оптической томографии есть ситуации, в которых доступен лишь ограниченный набор ракурсов. Это происходит из-за преломления света. Например, в случае сканирования куба из материала с коэффициентом преломления алмаза (2.4) по круговой траектории внутренний объём виден только с половины всех ракурсов. На рис. 5 показаны ракурсы при взгляде через одну грань куба в воздухе и все ракурсы, с которых видна некоторая точка внутри преломляющего материала. Видно, что ракурсы внутри преломляющего материала образуют 4 группы направлений, между которыми есть разрывы.

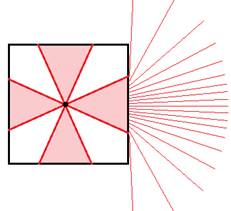
Рис. 5. Доступные ракурсы внутри преломляющего куба

4. Ограничения классической модели

При работе с данными оптической томографии, где содержатся непрозрачные области, обнаружились следующие недостатки линейной модели и классических методов:

4.1 Проблема полного затухания

Полностью поглощающие области невозможно корректно обработать в линейной модели вычислений, так как яркость пиксела на приёмнике, равная 0, соответствует бесконечному значению интеграла поглощения вдоль луча. Бесконечное значение в этом случае можно заменить некоторой достаточно большой константой . Однако это будет означать, что какой бы формы ни была на самом деле полностью поглощающая область, интеграл поглощения вдоль любого луча, проходящего через эту область, независимо от длины пересечения, равен . Возникает внутренняя несогласованность интегралов поглощения вдоль лучей, пересекающих область, идущих с разных направлений. Распределения поглощения внутри области, которое бы удовлетворяло таким измеренным интегралам поглощения, в общем случае не существует. Пример такой области показан на рис. 6: два луча с разных направлений имеют длину пересечения с ней и соответственно.

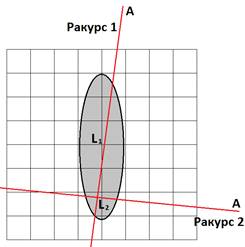
Рис. 6. Пересечение продолговатой поглощающей области

На каждой итерации алгоритма томографии применяется новый ракурс, на котором длина хода лучей внутри области может отличаться от предыдущего ракурса как в большую, так и в меньшую сторону. Соответственно, и коррекция поглощения также будет в обе стороны. Даже в случае отсутствия погрешностей во входных данных колебания показателя поглощения в этой области будут незатухающими. Группа ракурсов, с которых область пересекается лучами по меньшей длине, будет способствовать увеличению поглощения, и наоборот, ракурсы с большей длиной пересечения будут уменьшать поглощение в той же области.

Метод уменьшения артефактов от полного затухания в рентгеновской томографии, основанный на методе максимального правдоподобия, описан в статье [8]. В данной же статье предложен более простой подход к решению этой проблемы, который рассматривается на примере оптической томографии.

4.2 Проблема дискретности

Дискретная природа входных данных и расчётов вносит ещё одну проблему. Предположим, что абсолютно поглощающая область имеет чёткие границы. При этом они могут не совпадать с вокселями сетки. На разных ракурсах “растеризация” контура этой области на вокселях может быть разной, и от этого происходят колебания показателя поглощения вдоль всего луча от итерации к итерации. Такой эффект возможен при наличии погрешностей в положениях и направлениях ракурсов. Но также он наблюдается и в отсутствие погрешностей (на синтетических данных) из-за несовпадения частоты дискретизации приёмника и воксельной сетки, которое возникает неизбежно для разных направлений.

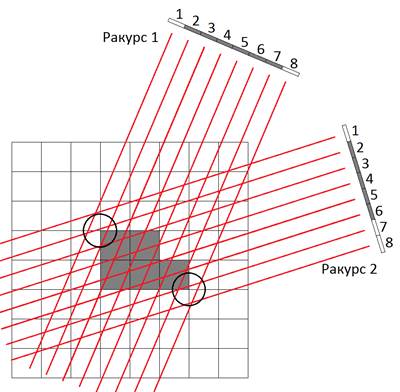
Рис. 7. Погрешности при пересечении лучами вокселей

На рис. 7 показаны образы непрозрачной области на двух ракурсах входных данных. Воксельная сетка находится в определённом состоянии, достигнутом после некоторого числа итераций. В тёмных вокселях показатель поглощения настолько велик, что даже при маленькой длине пересечения луча с таким вокселем результирующая яркость будет равна 0. На ракурсе 1 в исходных данных область занимает пикселы 2-7, на ракурсе 2 – пикселы 2-6. Кругами отмечены конфликтные области в воксельной сетке. Обратим внимание, что луч 2 с ракурса 1 проходит через поглощающий воксель, а с ракурса 2 – не проходит. Это означает, что на итерации, использующей ракурс 2, вдоль всего луча 2 поглощение должно возрасти так, чтобы компенсировать несоответствие наблюдаемой и расчётной яркости. Появляется ложная полоса тёмных вокселей. Аналогично, пиксел 7 с ракурса 2 проходит через тёмный воксель, однако на исходных данных ему соответствует пиксел с ненулевой яркостью, поэтому при использовании этого луча показатель поглощения в граничном вокселе должен будет уменьшиться до нуля.

Так на границах чётких непрозрачных зон хаотически появляется 2 типа артефактов: длинные ложные полосы высокого поглощения, которые затем частично срезаются с других ракурсов, и воксели с ложным низким поглощением. На рис. 8 видны такие полосы на результате томографии без преломления.

Рис. 8. Исходный поглощающий шар(слева) и визуализация результата томографии(справа)

Рис. 9. Срез воксельной карты, проходящий через поглощающий шар

Ограниченный набор ракурсов делает проблемы, описанные выше, ещё более ярко выраженными. На рис. 9 показан пример результата томографии с учётом преломления на непрозрачной области. Ложные следы от поглощающих областей ориентируются вдоль направлений доступных ракурсов, часто это крайние ракурсы. При переходе через разрыв между соседними группами направлений ложные линии с одного направления частично стираются, но появляются аналогичные линии для текущей группы направлений.

5. Предложенный метод

Для решения описанных проблем классических методов предлагается модификация алгоритма ART, связанная с уходом от линейной модели вычислений. Также используются модификации, необходимые для работы с данными в видимом диапазоне, такие как учёт преломления.

В качестве базового метода выбран ART из-за того, что в классическом варианте он даёт лучшие результаты на данных с непрозрачными областями, по сравнению с другими методами. Также метод ART легко конфигурируется из-за того, что основан на некоторой (произвольной) коррекции искомой функции вдоль прямых. ART менее чувствителен к малоракурсности [3], поэтому лучше других методов подходит для оптической томографии.

Входные данные:

· Набор фотографий объекта, снятый с разных ракурсов при повороте объекта на 360° вокруг вертикальной оси

· Геометрические характеристики кадров (положение и направление ракурсов, размеры плоскости проекции)

· Фотография источника света (фона) с той же камеры и того же ракурса

· Геометрические модели объектов сцены

· Показатели преломления прозрачных объектов

· Положение и размеры исследуемого объёма, заданного параллелепипедом

Результат:

· Функция распределения показателя поглощения среды в целевом объёме, заданная на сетке

Рис. 10. Пример исходной фотографии: алмаз в кубе из иммерсионного стекла

Исходные данные оптической томографии изначально непригодны для передачи их классическим алгоритмам реконструкции. Мы имеем данные об остаточной яркости источника света в каждом пикселе, которая зависит от исходной яркости источника света, поглощения в объёмной среде, разделения энергии света на отражённую и пропущенную на границах раздела преломляющих сред, света, пришедшего от других источников.
На рис.10 показана одна фотография исследуемого объекта из последовательности, снятой вокруг него. Через переднюю грань куб виден на просвет, на правой грани блик от источника света.

5.1 Выделение данных о поглощении

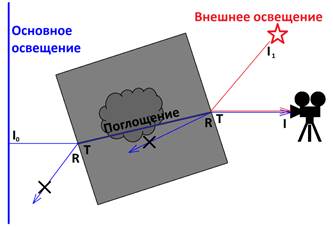
Рис. 11. Формирование итоговой наблюдаемой яркости

На рис. 11 показан ход лучей, вносящих основной вклад в яркость определённого пиксела изображения, для сцены с кубом. Измеренная интенсивность света в пикселе камеры равна:

(4)

Где
– интенсивность света, излучаемого источником в данной точке в данном направлении.
– коэффициенты Френеля для отражения и пропускания соответственно, вычисленные для данного угла падения и материала.
– интенсивность внешнего “паразитного” освещения, отражаемого материалом. Для простоты в данном примере будем считать, что только внешняя грань куба даёт такие отражения.
– настоящий коэффициент затухания вдоль луча.

Из этой формулы выражается , таким образом, можно посчитать значение интеграла Радона , стоящего в степени:

(5)

Если свет основного источника поглощается полностью, , то выражение под логарифмом может стать равным 0, или даже отрицательным в случае неточной оценки внешнего освещения. Решением может служить добавление достаточно маленькой константы к числителю, или органичение снизу значения этой дроби.

5.2 Предложенная модификация ART

Вместо того, чтобы вычислять значения интеграла по формуле (5), исходя из наблюдаемой и расчётной яркости, и затем использовать эти значения в методах реконструкции, предлагается использовать саму наблюдаемую и расчётную яркость для коррекции поглощения вдоль луча.

Обозначим разность между расчётной и наблюдаемой яркостью. Такая разность вычисляется для каждого пиксела приёмника.

(6)

где – это ожидаемая (расчётная) интенсивность света в пикселе приёмника с учётом упомянутых выше яркости источника света, коэффициентов Френеля, внешнего освещения и существующего распределения поглощения в воксельной сетке после обработки ракурсов.

Далее с использованием значения приближённо корректируется показатель поглощения в воксельной сетке вдоль луча. Основное правило любой коррекции: при показатель поглощения должен увеличиваться, при – уменьшаться, при – не меняться.

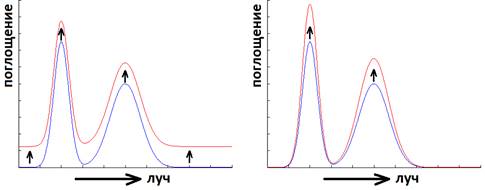
Рис. 12. Аддитивная и мультипликативная коррекция. Снизу исходная функция распределения поглощения вдоль луча, сверху – скорректированная.

(7)

(8)

Где – некоторый коэффициент, зависящий от длины хода луча в материале и определяющий скорость сходимости алгоритма.

Как и в классическом ART, существует несколько эмпирических способов коррекции показателя поглощения вдоль луча. Например, аддитивная коррекция (7) – фиксированное изменение показателя поглощения вдоль луча. Мультипликативная коррекция (8) – изменение показателя поглощения пропорционально значениям, полученным на предыдущей итерации. На рис. 12 показано, как изменяется показатель поглощения вдоль луча при таких коррекциях. Также использовалась аддитивно-мультипликативная коррекция и несколько других коррекций по более сложным законам.

Способы коррекции, предполагающие возрастающую зависимость значения коррекции от существующего показателя поглощения (например, мультипликативная), частично решают проблему дискретизации на краях поглощающих областей, т.к. в областях с изначально нулевым значением поглощения накопятся меньшие ложные ненулевые значения в случае описанных выше ошибок.

5.3 Реализация алгоритма

Изначально вся воксельная сетка инициализируется значением 0. Алгоритм заключается в последовательном учёте кадров. Одна итерация состоит из следующих этапов:

1) Фотореалистичная визуализация сцены с учётом текущего распределения показателя поглощения. Первый шаг трассировки лучей. Для каждого луча производится:

a) Пересечение луча с геометрией сцены

b) Расщепление на отражённый/преломлённый луч, вычисление коэффициентов Френеля для преломляющих поверхностей

c) Вычисление интеграла от функции на сетке вдоль луча

d) Пересечение с источником света, вычисление его яркости

e) Вычисление итоговой яркости, запись в пиксел на плоскости проекции

2) Вычисление на основе визуализированного кадра и фотографии карты коррекции – изображения размером с фотографию, содержащего значения необходимой коррекции для каждого пиксела

3) Коррекция значений показателя поглощения на основе имеющейся карты коррекции. Второй шаг трассировки лучей. Для каждого луча производятся те действия из первого шага трассировки, которые необходимы для коррекции искомой функции: пересечение с геометрией и проход сетки.

4) Применение глобальной коррекции к функции (сложение).

Согласно закону поглощения света (1), показатель поглощения входит в степень. После завершения некоторого числа итераций расчёта показатель поглощения в непрозрачной области станет достаточно большим, чтобы коэффициент пропускания стал близок к 0, а с учётом дискретизации, вычисленное значение яркости при таком коэффициенте пропускания будет в точности равно 0, то есть совпадать с входными данными. Входные данные о непрозрачных областях в этой модели вычислений оказываются согласованными.

Технически алгоритм реализован на основе алгоритма трассировки лучей. Процедуры, связанные с томографией, встраиваются в процесс трассировки одного луча, для этого подходит любая конфигурируемая система трассировки лучей. Использовалась система трассировки лучей Optix [9] на графических процессорах NVidia.

Для хранения показателя поглощения в вокселях сетки используется тип float32: одно число на воксель. Выбор числа бит и типа обусловлен удобством и скоростью работы с числами с плавающей точкой на видеокарте, а также из соображений точности коррекции набора вокселей, пересекаемых одним лучом, при условии того, что исходные данные (фотографии) имеют глубину 8 бит. Были проведены эксперименты, где каждый воксель был представлен другими типами данных, например, 8 бит с фиксированной точкой и 16 бит с фиксированной точкой. Они показали, что практически расчёты возможны при использовании чисел минимум в 16 бит, хотя проведённая теоретическая минимальная оценка оказалась выше.

Таким образом, воксельная сетка размером занимает 512 МБ памяти. Алгоритм требует хранения всей воксельной сетки в памяти видеокарты. На видеокарте NVidia GTX 980 вычисления занимают 3-5 минут для разных реальных примеров со следующими параметрами съёмки: 400 кадров вокруг объекта, каждый кадр имеет разрешение 1 мегапиксел, всего проводится 1600 итераций, или 4 полных оборота вокруг объекта.

6. Результаты

Предложенный алгоритм был опробован на реальных данных для построения моделей дефектов в драгоценных камнях. Важным достижением является то, что в процессе прохода итераций расчёта (использование разных ракурсов) не наблюдается колебаний показателя поглощения в поглощающих областях. На рис. 13 показан один горизонтальный срез из воксельной карты показателя поглощения, полученной при томографии реального куба из иммерсионного стекла с алмазом.

Рис. 13. Результат алгоритма оптической томографии в одном срезе на реальных данных (цветовая схема Jet)

Также проведено тестирование двумерного варианта предложенного алгоритма на синтетических данных без преломления и сравнение сходимости с классическим ART. В качестве эталона использовался показанный ниже срез, на котором чёрные области считаются непрозрачными.

Рис. 14. Эталон для синтетического тестирования

Для определённости выбрана стратегия обхода этой области по кругу, кадры выбираются последовательно. В целом, такая последовательность применения кадров приводит к самой быстрой сходимости у обоих алгоритмов (если в случае ART рассматривать реконструкцию полупрозрачной области)

Далее приведены несколько итераций сравниваемых алгоритмов на примере реконструкции эталона с рис.14. Расчёт начинается с горизонтального ракурса, что видно по первой итерации. Всего вокруг исследуемой области 400 ракурсов, распределённых равномерно. На рис. 15 и 16 показано немного более 10 полных обходов вокруг области.

0001

Рис. 15. Итерации алгоритма ART (1, 64, 128, 256, 512, 1024, 2048, 4096)

Рис. 16. Итерации предложенного алгоритма (те же, что у ART)

На первых итерациях оба алгоритма – предложенный и классический ART формируют образы исходных непрозрачных объектов на том месте, где они должны быть. Однако дальше они работают по-разному: классический ART входит в установившийся режим работы, при котором поглощение колеблется по всему объёму вытянутых эллипсов и в окружающих областях (рис. 15), а предложенный алгоритм продолжает сходиться к некоторому состоянию воксельной карты (рис. 16), которое может иметь следующие отличия от эталона:

Абсолютное значение показателя поглощения в вокселях. Это происходит из-за того, что истинное значение показателя поглощения нельзя определить по проекциям, оно достаточно велико, чтобы весь свет не проходил в обоих случаях.
Показатель поглощения в областях, закрытых с нескольких сторон непрозрачными областями, может быть реконструирован неверно из-за невидимости этих областей на проекциях.
Шумы, вызванные несовершенством алгоритма. Рядом с краями эллипсов видны “лучи” из шума, которые, однако, менее ярко выражены, чем в алгоритме ART.

Выявлены некоторые недостатки предложенного метода:

В случае полного поглощения света областью дефекта на восстановленной функции поглощение распределяется неравномерно в этой области: меньше по центру и больше по краям. Эта проблема присуща и классическим методам ART.
Низкая скорость сходимости в случае наличия тонких продолговатых дефектов.
Не найдено полного решения проблемы дискретизации сетки.

7. Заключение

Был предложен алгоритм оптической томографии, основанный на методе ART, для реконструкции карты поглощения внутри преломляющих объектов. Алгоритм позволяет корректно работать с преломлением, отражением и полным поглощением света. Он был интегрирован в программный продукт для огранки драгоценных камней и используется для построения моделей включений в неогранённых камнях.

Ссылки

Афанасьев В.В., Лебедев А.С., Игнатенко А.В. Оптическая томография преломляющих объектов. Материалы семнадцатого научно-практического семинара “Новые информационные технологии в автоматизированных системах”. – 2014. – С. 185-195.
Bartling, Soenke H., et al. Small animal computed tomography imaging. Current medical imaging reviews vol. 3, no. 1, 2007: 45-59 p.
Paulus, Michael J., et al. High resolution X-ray computed tomography: an emerging tool for small animal cancer research. Neoplasia vol. 2, no. 1, 2000: 62-70 p.
Mees, Florias, et al. Applications of X-ray computed tomography in the geosciences. Geological Society, London, Special Publications vol. 215, no. 1, 2003: 1-6 p.
Natterer, Frank. The mathematics of computerized tomography. Vol. 32. Siam, 1986.
Губарени Н. М. Вычислительные методы и алгоритмы малоракурсной компьютерной томографии. – 1979.
Gordon, Richard, Robert Bender, and Gabor T. Herman. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography. Journal of theoretical Biology vol. 29, no. 3, 1970: 471-481 p.
De Man, Bruno, et al. "Reduction of metal streak artifacts in x-ray computed tomography using a transmission maximum a posteriori algorithm." IEEE transactions on nuclear science vol. 47, no. 3 (2000): 977-981.
Parker, Steven G., et al. "Optix: a general purpose ray tracing engine." ACM Transactions on Graphics (TOG) vol. 29, no. 4 2010: 66 p.

OPTICAL TOMOGRAPHY OF REFRACTING OBJECTS WITH OPAQUE REGIONS

Afanasyev V.V., Ignatenko A.V., Voloboy A.G.

Keldysh Institute of Applied Math RAS

Graphics and Media Lab CMC MSU

vafanasjev@graphics.cs.msu.ru, ignatenko@graphics.cs.msu.ru, voloboy@gin.keldysh.ru

Abstract

Classic computed tomography techniques like ART are widely used for reconstruction of objects scanned in X-ray devices, where almost every object can be made transparent by increasing radiation power and its absorption can be measured with some accuracy. But the classic model cannot be applied to reconstruction of objects which absorption is so high that it does not transmit any radiation: such cases are possible in X-ray tomography with a low-power radiation source and also are frequent in optical tomography.

The article explains difficulties faced by classic ART algorithms in optical tomography in case of opaque regions presence in the scanned object. The ART method modification is proposed for this case.

Keywords: computed tomography, optical tomography, ART.

References

Afanasyev V.V., Lebedev A.S., Ignatenko A.V. Opticheskaja tomografija prelomljajushhih ob`ektov [Optical tomography of refracting objects]. Proceedings of 17-th seminar “New Information Technologies in Automated Systems” 2014: 185-195 p. [In Russian]
Bartling, Soenke H., et al. Small animal computed tomography imaging. Current medical imaging reviews vol. 3, no. 1, 2007: 45-59 p.
Paulus, Michael J., et al. High resolution X-ray computed tomography: an emerging tool for small animal cancer research. Neoplasia vol. 2, no. 1, 2000: 62-70 p.
Mees, Florias, et al. Applications of X-ray computed tomography in the geosciences. Geological Society, London, Special Publications vol. 215, no. 1, 2003: 1-6 p.
Natterer, Frank. The mathematics of computerized tomography. Vol. 32. Siam, 1986.
Gubareni, Nadiya. Vychislitel'nye metody i algoritmy malorakursnoj komp'juternoj tomografii [Algebraic Algorithms for Image Tomographic Reconstruction from Incomplete Projection Data]. INTECH Open Access Publisher, 2009. [In Russian]
Gordon, Richard, Robert Bender, and Gabor T. Herman. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography. Journal of theoretical Biology vol. 29, no. 3, 1970: 471-481 p.
De Man, Bruno, et al. "Reduction of metal streak artifacts in x-ray computed tomography using a transmission maximum a posteriori algorithm." IEEE transactions on nuclear science vol. 47, no. 3 (2000): 977-981.
Parker, Steven G., et al. "Optix: a general purpose ray tracing engine." ACM Transactions on Graphics (TOG) vol. 29, no. 4 2010: 66 p.