ВИЗУАЛИЗАЦИЯ КАК ИНСТРУМЕНТ ОЦЕНКИ ЗАЩИЩЕННОСТИ УРАНА

А.Н. Шмелев, Е.Г. Куликов, Н.И. Гераскин

Национальный исследовательский ядерный университет «МИФИ», Москва, Россия

shmelan@mail.ru, EGKulikov@mephi.ru, NIGeraskin@mephi.ru

Содержание

1. Принципиальная схема ГЯВУ ствольного типа

2. Расчетная модель для оценки “сверху” скорости соединения подкритических масс

3. Режим предетонации и “хлопка”

4. Изотоп ²³²U как мощный источник нейтронов

5. Рекомендации по обеспечению защищенности урана

6. Заключение

Список литературы

Аннотация

В настоящей работе разработана и визуализирована расчетно-теоретическая модель, направленная на количественную оценку защищенности урана с точки зрения возможности создания на его основе гипотетического ядерного взрывного устройства (ГЯВУ) ствольного типа. Для этого моделируются основные ядерно-физические, кинематические и тепловые процессы, которые протекают в ГЯВУ ствольного типа. Модель позволяет оценить энергетический выход ГЯВУ ствольного типа, собранного на основе урана заданного изотопного состава, а также выработать требования, выполнение которых способно снизить энергетический выход устройства до определенного уровня.

Принципиально новым аспектом является подход, который позволяет оценить достижимое время создания надкритического состояния в ГЯВУ ствольного типа, созданном на основе урана заданного изотопного состава. В разработке данного подхода используются элементы теории внутренней баллистики, теории сопротивления материалов, а также принимаются во внимание нейтронно-физические свойства урана заданного изотопного состава.

Стохастический характер цепного процесса деления учитывается в соответствии с методикой G.E. Hansen [1], определяющей вероятность возникновения непрекращающейся цепной реакции деления. Это позволяет увязать необходимое снижение энергетического выхода ГЯВУ ствольного типа с требуемым для этого источником нейтронов.

В настоящей работе в качестве делящегося материала в ГЯВУ ствольного типа рассматривается уран, а именно, смесь (²³⁵U + ²³⁸U) с различным обогащением по делящемуся изотопу. Защищенность высокообогащенного урана предполагается достичь путем введения в него небольшого количества ²³²U, поскольку [2, 3]:

1) ²³²U является мощным источником α-частиц, способных инициировать (α,n)-реакции на легких элементах, присутствующих в уране в виде примесей. Таким образом, введение в уран изотопа ²³²U приводит к созданию значительного источника нейтронов, а значит, к предетонации ГЯВУ;

2) продукты распада ²³²U – изотопы ²⁰⁸Tl и ²¹²Bi – являются источником жесткого γ-излучения, которое, помимо прочего, значительно улучшает возможность детектирования урана (уже при 1 ppb ²³²U).

Поскольку вопросы защищенности урана касаются не только инженеров-физиков, но и представителей некоторых гуманитарных специальностей, наглядная визуализация соответствующих вопросов имеет существенное значение. Кроме того, представленный в таком виде материал значительно проще усваивается студентами.

Ключевые слова: защищенность урана, гипотетическое ядерное взрывное устройство ствольного типа.

1. Принципиальная схема ГЯВУ ствольного типа

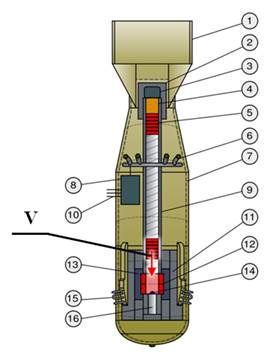
Действие ГЯВУ ствольного типа основано на эффекте быстрого соединения подкритических масс в надкритическую (рис. 1). Сближение подкритических масс осуществляется путем подрыва химической взрывчатки. Именно такой принцип действия имело ЯВУ “Little Boy”, сброшенное на г. Хиросима (Япония) 6 августа 1945 года [4].

1 – вертикальные стабилизаторы 2 – стальная казенная часть 3 – детонатор 4 – химическая взрывчатка (кордит) 5 – “снаряд” из ^235U: 6 колец (25,6 кг) 6 – барометрическое оборудование 7 – обшивка 8 – блок управления 9 – ствол (сталь, внутренний диаметр 10 см, длина 2 м, масса 450 кг) 10 – соединительные кабели 11 – темпер (сталь) 12 – “мишень” из ^235U: 2 кольца (38,5 кг) 13 – темпер (карбид вольфрама) 14 – нейтронный инициатор 15 – антенны радара 16 – гнездо для вытесняемого борного поглотителя

Рис. 1. Принципиальная схема ЯВУ “Little Boy”

Делящийся материал (90% ²³⁵U + 10% ²³⁸U) состоит из двух подкритических масс: “мишени” и “снаряда”. “Снаряд” имеет форму цилиндра диаметром 10 см и высотой 16 см. При подрыве химической взрывчатки “снаряд” разгоняется в направлении “мишени”. “Мишень” выполнена в виде полого цилиндра внешним диаметром 16 см и высотой также 16 см. В момент максимальной надкритичности, когда “снаряд” полностью располагается в “мишени”, образуются примерно три критические массы урана [4].

Настоящая статья опирается на основополагающую работу по данной тематике, выполненную в 1993 году Дж. Карсоном Марком [5], выдающимся ученым Лос-Аламосской национальной лаборатории и бывшим участником Манхэттенского проекта. Рассматривая устройство “Тринити” (первое в мире испытание технологии ядерного оружия, произошедшее 16 июля 1945 года в штате Нью-Мексико, США, в рамках Манхэттенского проекта), Дж. Карсон Марк показал, что энергетический выход цепной реакции деления пропорционален кубу достигнутой степени надкритичности:

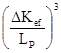~ ,                        (1)

где: – достигнутая степень надкритичности;

 – время жизни мгновенных нейтронов.

Вместе с тем, эта оценка носит лишь демонстративный характер этого эффекта, поскольку не учитывает свойств конкретного делящегося материала и собранного на его основе ГЯВУ ствольного типа. В настоящей работе разработан подход, который позволяет выработать количественные требования к обеспечению защищенности урана заданного изотопного состава.

В разработке данного подхода используются элементы теории внутренней баллистики, теории сопротивления материалов, а также принимаются во внимание нейтронно-физические свойства урана заданного изотопного состава (путем проведения нейтронно-физических расчетов методом Монте-Карло).

Итак, как следует из выражения (1), для достижения максимального энергетического выхода необходимо стремиться к созданию состояния с высокой надкритичностью. В свою очередь достигнутая степень надкритичности зависит от того, на какой стадии сближения подкритических масс развивающаяся цепная реакция деления приведет к началу разрушения целостности системы. Так, разрушение целостности системы на начальной стадии сближения подкритических масс приводит к тому, что достигнутая степень надкритичности будет небольшой (близкой к нулю). Достигнутая степень надкритичности окажется максимальной при условии, что разрушение целостности системы произойдет в момент, когда “снаряд” полностью располагается в “мишени”. Для этого требуется высокая скорость “снаряда”: действительно, в этом случае он успеет полностью войти в “мишень” прежде, чем произойдет разрушение целостности системы.

Увеличение скорости “снаряда” возможно за счет использования более мощной химической взрывчатки, разгоняющей его. Это в свою очередь неизбежно связано с повышением давления пороховых газов в стволе. Рассмотрим методику, позволяющую оценить достижимую скорость “снаряда”, при которой ствол выдерживает возникающее давление пороховых газов.

2. Расчетная модель для оценки “сверху” скорости соединения подкритических масс

Предположим, что “снаряд” движется под действием постоянного давления пороховых газов. В этом случае его движение является равноускоренным, и на основе второго закона Ньютона можно найти скорость “снаряда” на выходе из ствола (т.е. в момент соединения подкритических масс):

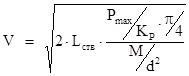,                        (2)

где: L_ств – длина ствола;

P_max – максимальное давление пороховых газов, выдерживаемое стволом;

K_P – коэффициент неравномерности давления пороховых газов;

M – масса “снаряда”;

d – диаметр “снаряда”.

Отметим, что в реальных орудиях коэффициент неравномерности давления пороховых газов K_P ≈ 2,15 [6]. В последующих рассмотрениях будем ориентироваться на эту величину.

Масса “снаряда” M и диаметр “снаряда” d определяются нейтронно-физическими свойствами урана. Для определения P_max воспользуемся условием А.В. Гадолина для случая, когда ствол выполнен в виде двухслойного цилиндра (прием, используемый в артиллерийской практике для упрочнения стволов) [7]:

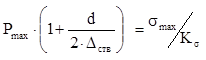,                    (3)

где: Δ_ств – толщина ствола;

σ_max – максимально-допустимое напряжение в материале ствола;

K_σ – коэффициент запаса прочности материала ствола.

Далее, подставляя величину P_max из выражения (3) в (2), можно оценить скорость “снаряда” на выходе из ствола (которая определяет то, насколько быстро создается надкритическое состояние, и, в конечном счете, энергетический выход ГЯВУ ствольного типа):

.

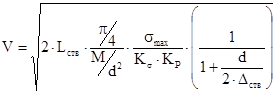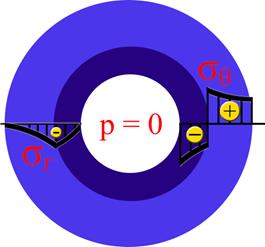
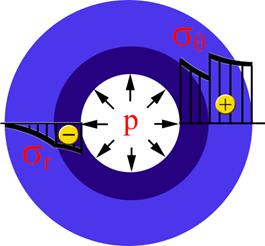
Отметим, что в настоящей работе рассматривается случай, когда ствол представляет собой двухслойный цилиндр. Визуальное представление нормального (s_r) и тангенциального (s_θ) напряжений в материале двухслойного толстостенного цилиндрического сосуда, нагруженного внутренним давлением, приведено на рис. 2. На практике также осуществляется изготовление стволов, состоящих более чем из двух соединенных с натягом цилиндров.

Рис. 2. Эпюры напряжений в стволе до и после нагрузки внутренним давлением (слева и справа соответственно)

Сформулируем основные положения расчетной модели для оценки “сверху” скорости “снаряда” на выходе из ствола:

1) движение “снаряда” является равноускоренным;

2) K_s = 1,0: выбран весь запас прочности для материала ствола;

3) σ_max = 8 000 кГ/см²: в предположении, что K_s = 1,0, максимально-допустимое напряжение в материале ствола (σ_max), на которое ориентируются при проектировании реальных орудий, составляет всего 5 000 ÷ 6 000 кГ/см²;

4) K_P = 2,15: данная величина характерна для реальных орудий [6];

5) ствол имеет длину L_ств = 10 метров и вес M_ств = 10 тонн: ствол с большими весогабаритными характеристиками сложен в обращении и транспортировке.

Отметим, что некоторые положения модели являются реальными (K_P = 2,15), в то время как некоторые – недостижимыми на практике (K_s = 1,0). В итоге данная модель приведет к оценке “сверху” скорости “снаряда” на выходе из ствольной части.

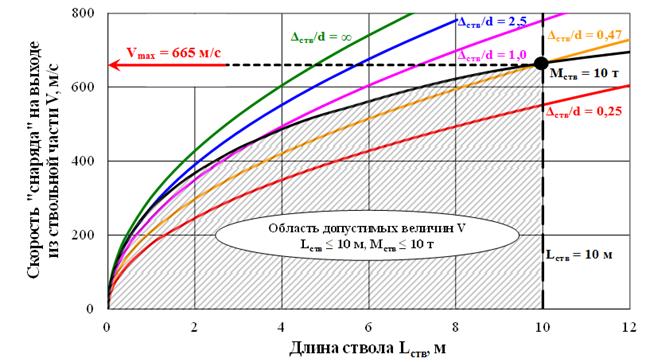
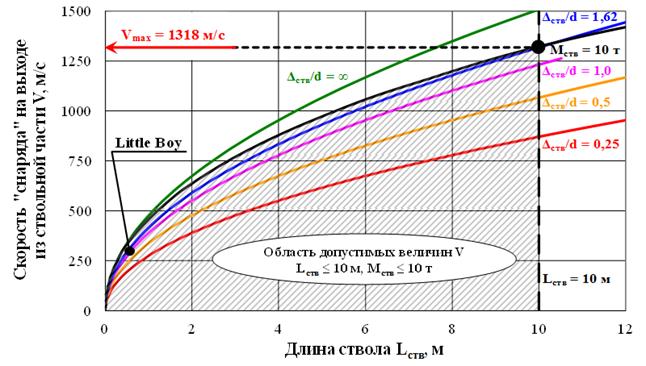
С помощью средств научной визуализации на основе сформулированной модели необходимо оценить максимально-достижимую скорость “снаряда” на выходе из ствола. В рамках данной задачи, которая при фиксированном обогащении урана зависит от двух параметров (длины и веса ствола), наиболее удобно использовать двумерные графики, поскольку область допустимых значений скорости “снаряда” будет ограничена двумя кривыми: одна кривая описывает ствол длиной 10 метров, а другая кривая описывает ствол весом 10 тонн. Заштриховав область допустимых значений скорости “снаряда”, следует выбрать максимальное значение, которое составляет 665 м/с в том случае, если делящимся материалом является (20% ²³⁵U + 80% ²³⁸U) и 1318 м/с в том случае, если делящимся материалом является (90% ²³⁵U + 10% ²³⁸U) (рис. 3).

а) делящийся материал: 20% ²³⁵U + 80% ²³⁸U

б) делящийся материал: 90% ²³⁵U + 10% ²³⁸U

Рис. 3. Определение максимально-достижимой скорости “снаряда” на выходе из ствольной части V_max

3. Режим предетонации и “хлопка”

Для оценки эволюции плотности нейтронов в делящемся материале ГЯВУ ствольного типа используется подход, в котором учитывается стохастический характер цепного процесса [8, 9].

Рассматривается линейный ввод реактивности в качестве режима перехода системой из подкритического состояния в надкритическое. В этом случае изменение эффективного коэффициента размножение нейтронов со временем может быть записано следующим образом:

где: – скорость изменения  от времени;

t₀ – время, за которое система переходит из критического состояния (K_ef = 1) в состояние максимальной надкритичности (K_ef = (K_ef)_max).

При этом предполагается, что t = 0 – момент перехода системой через критическое состояние, а начавшаяся в момент времени t₁ непрерывающаяся цепочка делений продолжается до некоторого момента времени t₂, когда происходит нарушение целостности системы и она переходит в стадию разрушения. Отметим, что стадия разрушения наступает, когда в системе произойдет e⁴⁵ делений [5].

При оценке относительного энергетического выхода ГЯВУ ствольного типа используется приближение “сильного” источника нейтронов, поскольку данная методика в своем основании не делает каких-либо предположений, а также учитывает возможность начала непрекращающейся цепочки делений до наступления критичности [8].

В приближении “сильного” источника нейтронов относительный энергетический выход ГЯВУ ствольного типа оценивается следующим образом:

             (4)

причем  определяется как:

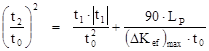,                   (5)

а t₁ является решением уравнения:

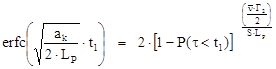,              (6)

где: L_P – время жизни мгновенных нейтронов;

 – максимальная величина надкритичности;

 – кумулятивная вероятность запуска непрекращающейся цепочки делений при τ < t₁ (вероятность предетонации);

– среднее число нейтронов на акт деления;

 – параметр Дайвена [10, 11].

Вероятность предетонации принимается равной 90%.

На основе оцененной максимально-достижимой скорости “снаряда” на выходе из ствольной части V_max (рис. 3) несложно определить время t₀, в течение которого наблюдается рост надкритичности системы.

На рис. 4. представлен процесс нарастания эффективного коэффициента размножения нейтронов K_ef в процессе соединения подкритических масс в ГЯВУ ствольного типа, собранного на основе делящегося материала (20% ²³⁵U + 80% ²³⁸U). При этом предполагается, что при сближении подкритических масс критичность (K_ef = 1) достигается в момент времени t = 0. Начиная с этого момента эффективный коэффициент размножения нейтронов K_ef превышает единицу и будет нарастать. Лишь в том случае, если процесс сближения подкритических масс продолжается до момента создания максимальной надкритичности (т.е. t₂ = t₀), будет достигаться максимальный энергетический выход (X_max = 100%), как это следует из выражения (4). Фактически, это штатный режим срабатывания ГЯВУ ствольного типа.

Для штатного режима срабатывания ГЯВУ (Х = 100%, т.е. t₂ = t₀) на основе выражения (5) несложно определить момент времени t₁ (момент начала непрекращающейся цепной реакции деления), который оказывается очень близким t₂ (момент нарушения целостности системы): различие составляет сотые доли t₀, т.е. в системе e⁴⁵ делений осуществляется очень быстро. Поэтому для обеспечения максимального энергетического выхода необходим запуск непрекращающейся цепной реакции деления лишь при t₁ » 0,98 ¸ 0,99 t₀.

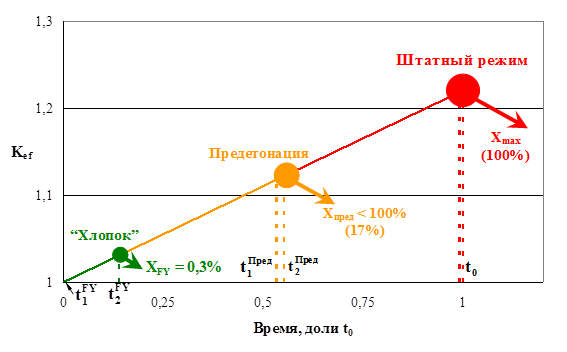
Рис. 4. Визуализация штатного режима срабатывания ГЯВУ ствольного типа, режима предетонации и “хлопка” (20% ²³⁵U + 80% ²³⁸U)

Преждевременный запуск цепной реакции деления (в момент времени ) определяется как режим предетонации: при этом стадия разрушения наступает в момент времени , что согласно выражению (4) приводит к пониженному энергетическому выходу X_пред < 100% (рис. 4). В частности, для представленного на рис. 4 случая предетонации (t₂ = 0,55∙t₀) относительный энергетический выход X_пред, который пропорционален (t₂)³, составляет 17%.

Среди режимов предетонации особо выделяется случай, когда непрекращающаяся цепная реакция деления запускается в момент создания критического состояния (K_ef = 1). Этот вариант срабатывания ГЯВУ ствольного типа называется “хлопок” (Fizzle Yield, FY). Он соответствует минимальному энергетическому выходу 0,3% (в приближении “слабого” источника нейтронов) [5].

Из рис. 4 можно сделать вывод, что для обеспечения защищенности урана (снижения энергетического выхода ГЯВУ на его основе) следует ввести в рассматриваемый уран источник нейтронов, достаточно мощный для того, чтобы непрекращающаяся цепная реакция деления запускалась в самый первый момент создания критического состояния. Именно в этом случае ГЯВУ будет обладать наименьшим энергетическим выходом.

Важным моментом является то, что рассматриваемый способ снижения энергетического выхода ГЯВУ ствольного типа за счет введения в делящийся материал источника нейтронов, имеет предел: путем введения источника нейтронов невозможно снизить энергетический выход до сколь угодно малых величин (применительно к практически достижимым источникам нейтронов).

Однако целесообразно ли ставить требование обеспечения “хлопка” или разумно остановиться на меньшем источнике нейтронов? Каков при этом будет энергетический выход? Для ответа на этот вопрос рассмотрим зависимость относительного энергетического выхода ГЯВУ ствольного типа X от мощности источника нейтронов S, введенного в уран (рис. 5). Рассмотрение проводится для урана двух изотопных составов: (20% ²³⁵U + 80% ²³⁸U) и (90% ²³⁵U + 10% ²³⁸U).

Относительный энергетический выход при “хлопке” составляет:

X_FY (20% ²³⁵U + 80% ²³⁸U) = 0,3%,

X_FY (90% ²³⁵U + 10% ²³⁸U) = 0,7%.

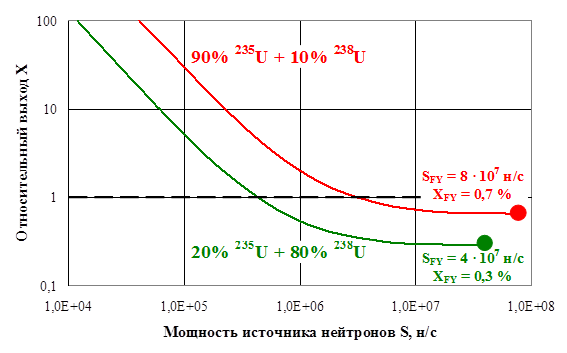
Рис. 5. Зависимость относительного энергетического выхода X от мощности источника нейтронов S (20% ²³⁵U + 80% ²³⁸U и 90% ²³⁵U + 10% ²³⁸U)

Можно видеть, что представленные зависимости относительного энергетического выхода X с ростом мощности источника нейтронов S становятся более пологими (рис. 5). Очевидно, что требование наличия источника нейтронов, необходимого для “хлопка”, является излишним и необоснованным. Действительно, если делящимся материалом является (20% ²³⁵U + 80% ²³⁸U), то при источнике нейтронов 10⁶ н/с (т.е. в 40 раз меньшем S_FY) относительный энергетический выход X » 2×X_FY (всего в 2 раза больше X_FY)_. Поэтому в качестве требования, предъявляемого к мощности источника нейтронов, по-видимому, разумно было бы взять S ~ 10⁶ н/с, так как дальнейшее увеличение не приводит к заметному снижению энерговыделения.

Поставим требование снижения относительного энергетического выхода X до 1% от номинального. Это достигается при наличии источника нейтронов:

0,4×10⁶ н/с для (20% ²³⁵U + 80% ²³⁸U);

3,1×10⁶ н/с для (90% ²³⁵U + 10% ²³⁸U).

4. Изотоп ²³²U как мощный источник нейтронов

Каким образом можно обеспечить значительный источник нейтронов, который был обозначен в предыдущем разделе (S ~ 10⁶ н/с, что способствует снижению относительного энергетического выхода до 1% от номинального)?

Предполагается в уран ввести изотоп ²³²U, который является мощным источником нейтронов спонтанного деления: 1300 н/с×кг [12]. Однако этой величины явно недостаточно для обеспечения источника нейтронов порядка 10⁶ н/с.

Важным является то обстоятельство, что в уране присутствует примесь легких элементов (таких как литий, бериллий и пр.). В результате a-распада тяжелых нуклидов (в основном ²³²U, у которого достаточно короткий период полураспада: 68,9 лет [13]) испускаемые a-частицы, сталкиваясь с ядрами легких элементов, приводят к генерации нейтронов в результате (a,n)-реакции. Выяснено, что скорость генерации нейтронов посредством (a,n)-реакции на ядрах легких элементов существенно превосходит скорость генерации нейтронов в результате реакции спонтанного деления ²³²U.

Отметим, что требуемое количество ²³²U для создания заданного источника нейтронов зависит от времени выдержки ²³²U. Действительно, с течением времени в результате a-распада ²³²U накапливаются продукты его распада, которые также являются радиоактивными изотопами, испускающими α-частицы: данные α-частицы в свою очередь будут инициировать дополнительные (a,n)-реакции на ядрах примесей легких элементов. При радиоактивном распаде ²³²U образуется ²²⁸Th, цепочка распадов которого включает в себя пять достаточно быстрых a-распадов, которые завершаются образованием стабильного изотопа ²⁰⁸Pb [13].

Поскольку в цепочке распадов ²³²U за a-распадом ²²⁸Th следуют еще несколько достаточно быстрых a-распадов и за счет того, что энергия a-частиц, испускаемых в результате этих распадов, достаточно высока, для создания источника нейтронов значительной мощности целесообразно предусматривать выдержку ²³²U с целью накопления ²²⁸Th.

В настоящем рассмотрении предполагается, что радиоактивные распады всех дочерних нуклидов ²²⁸Th (т.е. ²²⁴Ra и следующих за ним) происходят мгновенно вместе с распадом самого ²²⁸Th. На практике это выполняется с достаточно хорошей точностью: в то время как период полураспада ²²⁸Th составляет 1,91 год, периоды полураспада его дочерних нуклидов на несколько порядков меньше [13].

Уравнения изменения концентрации ²³²U и ²²⁸Th со временем имеют следующий вид:

               (7)

,                   (8)

где:             ,  – ядерные концентрации ²³²U и ²²⁸Th со временем;

,  – постоянные распада ²³²U и ²²⁸Th, определяемые как:

,                   (9)

где  – период полураспада:  лет,  год [13].

Тогда на основе известных концентраций ²³²U и ²²⁸Th, определяемых с помощью выражений (7) и (8), можно оценить мощность источника нейтронов S (создаваемого нейтронами спонтанного деления ²³²U, а также нейтронами, испускаемыми в результате (a,n)-реакции на ядрах легких элементов) в зависимости от времени выдержки ²³²U (рис. 6). При этом рассматривается удельная мощность источника нейтронов (на единицу массы ²³²U), а содержание примесей легких элементов соответствует характеристикам соединений урана, выпускаемых на Новосибирском заводе химконцентратов, который  является одним из крупнейших предприятий российского ядерного топливного цикла по выпуску ядерного топлива для энергетических и исследовательских реакторов [14].

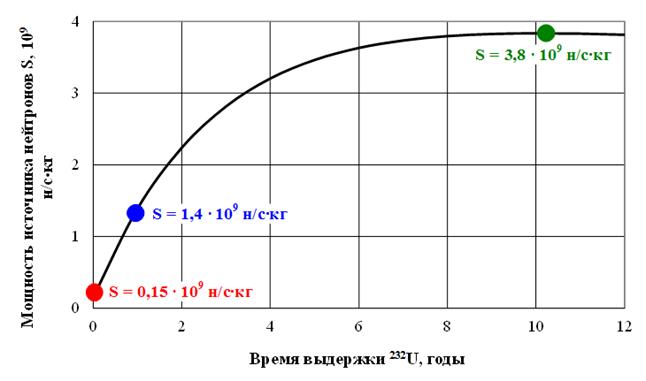
Рис. 6. Удельная мощность источника нейтронов, обусловленного наличием ²³²U и примесями легких элементов, в зависимости от времени выдержки ²³²U

Можно сделать вывод о целесообразности организации технологического процесса таким образом, чтобы предусматривалась возможность выдерживать некоторое время ²³²U перед тем, как вводить его в уран. Действительно, удельная мощность источника нейтронов, создаваемого ²³²U и примесями легких элементов, значительно возрастает с увеличением времени выдержки ²³²U, особенно на первых порах (рис. 6).

Из рис. 6 можно видеть, что выдержка ²³²U приводит к увеличению удельной мощности источника нейтронов с 0,15∙10⁹ н/с∙кг (выдержка отсутствует) до 3,8∙10⁹ н/с∙кг к моменту установления равновесной концентрации ²²⁸Th (скорость накопления ядер ²²⁸Th совпадает со скоростью их исчезновения). Это состояние отвечает времени выдержки ²³²U около 10 лет.

Будем предполагать, что для создания требуемого источника нейтронов, который обеспечил бы относительный энергетический выход X на уровне 1% от номинального, используется ²³²U годичной выдержки. Отметим, что в этом случае ²³²U является источником нейтронов мощностью 1,4∙10⁹ н/с∙кг (рис. 6). Случаи использования ²³²U без выдержки, а также со временем выдержки 10 лет будут представлены для сравнения как предельные случаи.

5. Рекомендации по обеспечению защищенности урана

Оценим количество ²³²U, введение которого в уран способно обеспечить обозначенные в разделе 3 источники нейтронов. Расчет проведем для трех времен выдержки ²³²U: выдержка отсутствует; время выдержки составляет 1 год; время выдержки составляет 10 лет (момент достижения равновесной концентрации ²²⁸Th). Визуализация полученных результатов в трехмерном виде представлена на рис. 7.

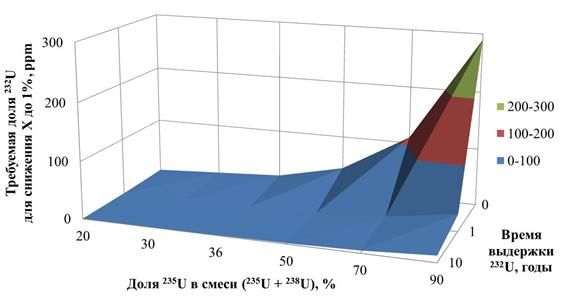
Рис. 7. Требуемое содержание ²³²U для снижения относительного энергетического выхода до 1% от номинального (при различном времени выдержки ²³²U)

Из рис. 7 следует, что время выдержки ²³²U является важным параметром: чем оно больше, тем меньше требуется ²³²U для защищенности урана. Ориентируясь в дальнейших оценках на время выдержки ²³²U, равное одному году, можно видеть, что требуемое количество ²³²U для снижения X до 1% от номинального составляет от 0,3 ppm (20% ²³⁵U + 80% ²³⁸U) до 30 ppm (90% ²³⁵U + 10% ²³⁸U) (рис. 8).

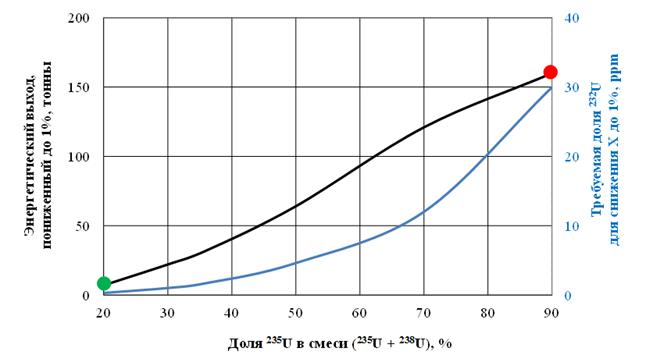
Рис. 8. Энергетический выход в режиме предетонации, а также требуемое для этого содержание ²³²U

На рис. 8 демонстрируется возможное снижение энергетического выхода за счет явления предетонации, а также требуемое для этого содержание ²³²U. Отметим, что для (20% ²³⁵U + 80% ²³⁸U) снижение X до 1% в абсолютном выражении соответствует величине 7 тонн. В то же время вес ГЯВУ, собранного на основе (20% ²³⁵U + 80% ²³⁸U), составляет, по крайней мере, 10 тонн (вес ствола). Таким образом, данное устройство не является привлекательным с точки зрения эффективности (обозначено зеленым цветом на рис. 8).

С другой стороны, применительно к (90% ²³⁵U + 10% ²³⁸U) снижение X до 1% в абсолютном выражении соответствует величине 160 тонн. Таким образом, следует признать эффективность данного устройства (обозначено красным цветом на рис. 8) и невозможность обеспечить защищенность (90% ²³⁵U + 10% ²³⁸U) путем введения в него источника нейтронов: даже чрезвычайно мощный источник нейтронов не смог бы понизить энергетический выход до приемлемых значений.

6. Заключение

На основе представленных в открытой литературе данных развита и визуализирована расчетно-теоретическая модель, позволяющая оценить энергетический выход ГЯВУ ствольного типа, собранного на основе урана заданного изотопного состава, а также выработать требования, выполнение которых способно снизить энергетический выход до определенного уровня.

Новизна модели ГЯВУ ствольного типа заключается в подходе, который позволяет оценить достижимое время создания надкритического состояния в ГЯВУ ствольного типа, собранном на основе урана заданного изотопного состава.

Установлено, что для снижения эффективности ГЯВУ ствольного типа целесообразно рассматривать введение в уран источника нейтронов, обеспечивающего уменьшение энергетического выхода ГЯВУ до ~ 1% от номинального с вероятностью 90%: дальнейшее увеличение мощности источника нейтронов не приводит к существенному снижению энергетического выхода.

Снижение энергетического выхода ГЯВУ ствольного типа до ~ 1% от номинального с вероятностью 90% требует введение от 0,3 ppm ²³²U (делящийся материал: 20% ²³⁵U + 80% ²³⁸U) до 30 ppm ²³²U (делящийся материал: 90% ²³⁵U + 10% ²³⁸U).

Наглядная визуализация вопросов защищенности урана имеет существенное значение, поскольку эта тематика касается не только инженеров-физиков, но и представителей некоторых гуманитарных специальностей. Кроме того, студенты более склонны к восприятию и усвоению представленного в таком виде материала.

Список литературы

1. Hansen G.E. Assembly of Fissionable Material in the Presence of a Weak Neutron Source // Nuclear Science and Engineering. – 1960. – Vol. 8. – P. 709–719.

2. Kang J. and F. N. von Hippel. U-232 and the Proliferation-Resistance of U-233 in Spent Fuel // Science and Global Security. – 2001. – Vol. 9. – P. 1-32.

3. Gilfoyle G. P. and Parmentola J. A. Using Nuclear Materials To Prevent Nuclear Proliferation // Science and Global Security. – 2001. – Vol. 9. – P. 81-92.

4. Little Boy – Wikipedia, the free encyclopedia [Электронный ресурс]. URL: http://en.wikipedia.org/wiki/Little_Boy (Доступен на 29.06.2015).

5. Mark J.C. Explosive Properties of Reactor-Grade Plutonium // Science and Global Security. – 1993. – Vol. 4. – P. 111-128.

6. Кофман В.Л. Японские линкоры Второй мировой. “Ямато” и “Мусаси”. – М.: Коллекция, Яуза, ЭКСМО, 2006.

7. Феодосьев В.И. Сопротивление материалов. – М.: Издательство МГТУ имени Н.Э. Баумана, 2001.

8. Hansen G.E. Assembly of Fissionable Material in the Presence of a Weak Neutron Source // Nuclear Science and Engineering. – 1960. – Vol. 8. – P. 709–719.

9. Шабалин Е.П. Импульсные реакторы на быстрых нейтронах. – М.: Атомиздат, 1976.

10. Уриг Р. Статистические методы в физике ядерных реакторов. Пер. с англ. – М.: Атомиздат, 1974.

11. Seifritz W. Nukleare Sprengkörper – Bedrohung oder Energieversorgung für die Menschheit? – München: Karl Thiemig AG, 1984.

12. Райли Д., Энслин Н., Смит Х. и Крайнер С. Пассивный неразрушающий анализ ядерных материалов. – М.: Бином, 2000.

13. Бабичев А.П., Бабушкина Н.А., Братковский А.М. и др. Под. ред. Григорьева И.С., Мейлихова Е.З. Физические величины: Справочник. – М.: Энергоатомиздат, 1991.

14. Соединения урана НЗХК [Электронный ресурс]. URL: http://www.nccp.ru/products/uranium_compounds/ (Доступен на 29.06.2015)

---

VISUALIZATION AS A TOOL FOR URANIUM PROLIFERATION PROTECTION ASSESSMENT

A.N. Shmelev, E.G. Kulikov, N.I. Geraskin

National Research Nuclear University MEPhI (Moscow Engineering Physics Institute)

shmelan@mail.ru, EGKulikov@mephi.ru, NIGeraskin@mephi.ru

Abstract

In the present paper calculation-theoretical model has been developed and visualized, which aims at quantitative assessment of uranium proliferation protection against creating gun-type hypothetical nuclear explosive device (HNED). The main nuclear, kinematic and thermal processes that occur in gun-type HNED are modeled. The model allows us to estimate the energy yield of gun-type HNED, assembled on the basis of uranium of a given isotopic composition, as well as to develop requirements that reduce energy yield down to a certain value.

Fundamentally new aspect is an approach that allows us to estimate the achievable time of subcritical masses assembling in gun-type HNED on the basis of uranium of a given isotopic composition. In this approach elements of interior ballistics and strength of materials theories are used, as well as neutron-physical properties of uranium of a given isotopic composition are taken into account.

The stochastic nature of the nuclear chain reaction is accounted for in accordance with the methodology of G.E. Hansen [1], which determines the probability of uninterrupted nuclear chain reaction. This allows us to link the necessary reduction of gun-type HNED energy yield with required neutron source.

In the present paper uranium is considered as fissionable material in gun-type HNED, namely, a mixture of (²³⁵U + ²³⁸U) with different enrichment on ²³⁵U. Proliferation protection of high-enriched uranium can be achieved by introducing a small amount of ²³²U, because [2, 3]:

1) ²³²U is a powerful source of α-particles capable of initiating (α,n)-reactions on light elements which are present in uranium as impurities. Thus, ²³²U creates large neutron source which leads to gun-type HNED pre-detonation

2) decay products of ²³²U (isotopes ²⁰⁸Tl and ²¹²Bi) are a source of hard γ-radiation, which, among others, significantly improves the possibility of uranium detection (even at the level of 1 ppb ²³²U).

As uranium proliferation protection issues concern not only engineers, but also representatives of some of the humanities, visualization of these issues is essential. Moreover, the material presented in such a form is much easier for students to understand.

Key words: uranium proliferation protection, gun-type hypothetical nuclear explosive device.

References

1. Hansen G.E. Assembly of Fissionable Material in the Presence of a Weak Neutron Source. Nuclear Science and Engineering, 1960, vol. 8. —709–719  p.

2. Kang J. and F. N. von Hippel. U-232 and the Proliferation-Resistance of U-233 in Spent Fuel. Science and Global Security, 2001, vol. 9. –1-32 p.

3. Gilfoyle G. P. and Parmentola J. A. Using Nuclear Materials To Prevent Nuclear Proliferation. Science and Global Security, 2001, vol. 9. –81-92 p.

4. Little Boy – Wikipedia, the free encyclopedia [Electronic resource]. URL: http://en.wikipedia.org/wiki/Little_Boy. (Available at 29.06.2015)

5. Mark J.C. Explosive Properties of Reactor-Grade Plutonium. Science and Global Security, 1993, Vol. 4. – 111-128 p.

6. Kofman V.L. Japonskie linkory Vtoroj mirovoj. “Jamato” i “Musasi” [Japanese battleships of the Second World War. “Yamato” and “Musasi”]. M.: Collection, Yauza, EKSMO, 2006.

7. Feodos’ev V.I. Soprotivlenie materialov [Strength of materials]. M.: Bauman Moscow State Technical University, 2001.

8. Hansen G.E. Assembly of Fissionable Material in the Presence of a Weak Neutron Source. Nuclear Science and Engineering, 1960, Vol. 8. –709–719 p.

9. Shabalin E.P. Impul'snye reaktory na bystryh nejtronah [Fast impulse reactors]. M.: Atomizdat, 1976.

10. Urig R. Statisticheskie metody v fizike jadernyh reaktorov [Statistical Methods in the Nuclear Reactor Physics]. M.: Atomizdat, 1974.

11. Seifritz W. Nukleare Sprengkörper – Bedrohung oder Energieversorgung für die Menschheit? – München: Karl Thiemig AG, 1984.

12. Reilly, Ensslin, Smith, and Kreiner. Passivnyj nerazrushajushhij analiz jadernyh materialov [Passive Nondestructive Assay of Nuclear Material]. M.: Binom, 2000.

13. Babichev A.P., Babushkina N.A., Bratkovsky A.M. et al. Fizicheskie velichiny: Spravochnik [Physical quantities: Reference book]. M.: Energoatomizdat, 1991.

14. Uranium compounds NCCP [Electronic resource]. URL: http://www.nccp.ru/en/products/uranium_compounds. (Available at 29.06.2015)