РАСЧЕТ, АНАЛИЗ И ВИЗУАЛИЗАЦИЯ ТЕЧЕНИЯ В МОДЕЛЬНОМ ТРАКТЕ ДВИГАТЕЛЯ ВЫСОКОСКОРОСТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА
В.Т. Жуков1, К.В. Мануковский2, Н.Д. Новикова1, Ю.Г. Рыков1, О.Б. Феодоритова1
1 Институт прикладной математики им. М.В.Келдыша РАН, Москва, Россия
2 Институт Теоретической и Экспериментальной Физики им. А.И. Алиханова, Москва, Россия
vic.zhukov@gmail.com, manu@itep.ru, nn@kiam.ru, yu-rykov@yandex.ru, feodor@kiam.ru
Содержание
1. Разработка вычислительной модели для расчета течений при высоких числах Маха и отсутствии горения
2. Технология построения расчетных сеток для моделирования трехмерных объектов сложной формы
3.1. Двумерный расчет модельного тракта двигателя
3.2. Двумерный расчет модельного тракта двигателя с расширенной счетной областью и поднятой лопастью
Аннотация
Развитие высокоскоростных летательных аппаратов активизировало интерес к изучению прямоточных воздушно-реактивных двигателей.
Сложность задачи математического моделирования нестационарных процессов в двигателе, необходимость изучения разномасштабных по времени и пространству физических процессов и их взаимодействия требуют привлечения методов и программных средств научной визуализации, как наиболее эффективного инструмента контроля и качественного анализа численных данных, объем которых огромен.
Для расчета высокоскоростных потоков в модельном тракте двигателя летательного аппарата используется математическая модель на основе системы уравнений Навье-Стокса, дополненная моделями турбулентных напряжений и тепловых потоков. Более конкретно, турбулентность описывается с помощью SST модели Ментера. Дискретизация проводится с помощью технологии центрально-противопотоковых схем и их модификаций средствами открытой вычислительной платформы OpenFOAM. Для проведения валидационных расчетов и калибровки выбранной математической модели использован экспериментальный материал из диссертационной работы Дж. Вагнера.
Исследуемая задача решалась на высокопроизводительном кластере К100, построенном в ИПМ им.М.В.Келдыша РАН
Ключевые слова: визуализация, высокоскоростной полет, уравнения Навье-Стокса, прямоточный двигатель, OpenFOAM, rhoCentralFoam
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 14-21-00025).
Введение
Успешное развитие высокоскоростных (в том числе гиперзвуковых) летательных аппаратов (ВЛА) непосредственно связано с прогрессом в разработке прямоточных воздушно-реактивных двигателей (ПВРД). Процессы, происходящие в ПВРД на гиперзвуковых скоростях полета, представляют собой сложную комбинацию газодинамических явлений, таких как развитие турбулентных пограничных слоев, их взаимодействие с ударными волнами и формирование псевдоскачка [1]. К ним также следует добавить комплекс физических явлений, связанных с горением топлива (как в дозвуковом, так и в сверхзвуковом потоке), которые ответственны за формирование и поддержание двигателем тяги, необходимой для устойчивого полета ВЛА. Вследствие высоких скоростей, сложной и зачастую сильно нестационарной структуры происходящих процессов и вытекающей отсюда сложности постановки и высокой стоимости натурных экспериментов (продувок) важную роль приобретает возможность проведения предсказательных численных расчетов, см., например, [2-3].
Задачи подобного уровня сложности требуют привлечения высокопроизводительных параллельных вычислительных систем и приводят к таким объемам данных, контроль и анализ которых практически невозможен без привлечения средств научной визуализации [4]. Исследователю-вычислителю необходимо изучить и проанализировать огромный числовой материал, отражающий происходящие сложные и разномасштабные физические явления, имеющие к тому же сильно нестационарный характер. В этой ситуации необходимо привлечение мощного аппарата визуализации, как стационарного (графики), так и динамического (анимация), для дополнительного анализа и контроля полей интересующих нас физических величин, верификации результатов численного моделирования, подбора параметров математической и вычислительной моделей.
ПВРД представляет собой тракт, как правило, нетривиальной геометрической формы, куда при полете проникает через воздухозаборник поток воздуха, в который затем в камере сгорания впрыскивается топливо, которое должно самовоспламениться и, выходя через сверхзвуковое сопло, создать необходимую тягу. Структура течения в тракте ПВРД является весьма сложной и достаточно подвижной, а поэтому и чувствительной к параметрам набегающего на воздухозаборник потока. Поэтому для повышения точности предсказательного моделирования течения в тракте ПВРД, вообще говоря, необходимо проводить расчет полной компоновки: ПВРД и самого ВЛА. Однако расчет внешнего обтекания ВЛА (как правило, тоже сложной геометрической формы) требует использования численных сеток существенно большего объема, что значительно увеличивает время расчета. В такой ситуации становится целесообразным проводить моделирование по частям. А именно, вначале определить из расчета внешнего обтекания ВЛА входной поток в воздухозаборник, который можно впоследствии использовать при моделировании течения внутри ПВРД в качестве граничного условия. Далее можно проводить расчеты в тракте ПВРД, варьируя различные параметры работы двигателя (расположение топливных форсунок, режим впрыска топлива, химический состав топливной смеси и т.д.).
Математическая модель расчета газодинамических параметров течения в тракте двигателя ВЛА должна учитывать все отмеченные выше особенности рассматриваемой задачи. При этом в потоке получаемой информации представляются важными именно детали, часто на первый взгляд незначительные. Визуализация расчетов в интересующей нас задаче является одним из важных способов изучения структуры возникающих течений, наряду, например, с проверкой на тестовых задачах, сравнением с экспериментом и изучением характера сходимости по сетке. Учитывая сильно нестационарный характер течения, даже просто «взглянуть» на полученные результаты в динамике представляется крайне полезным, поскольку анимация расчетов позволяет быстро проследить эволюцию течения, выделить временные диапазоны для дополнительного и более скрупулезного анализа, как аналитического, так и вычислительного. Разномасштабность изучаемых физических полей также требует выделения подобластей, сужения рассматриваемого диапазона изменения какой-либо из характеристик течения и использования специальных палитр для более тщательного анализа. Все эти средства могут быть предоставлены методами и алгоритмами визуализации.
1. Разработка вычислительной модели для расчета течений при высоких числах Маха и отсутствии горения
Течения газовой сплошной среды рассчитываются на основе уравнений Навье-Стокса, в которые вводятся дополнительные члены, учитывающие эффекты турбулентности. Указанная система уравнений имеет вид (см., например, [5]):
|
|
(1) |
Здесь ![]() есть вектор скорости с компонентами
есть вектор скорости с компонентами ![]() ;
; ![]() и
и ![]() – молекулярная и турбулентная
(полученная путем осреднения различных функционалов от мелкомасштабных
пульсаций) компоненты тензора вязких напряжений;
– молекулярная и турбулентная
(полученная путем осреднения различных функционалов от мелкомасштабных
пульсаций) компоненты тензора вязких напряжений; ![]() – удельная полная энергия газа,
– удельная полная энергия газа, ![]() – удельная внутренняя
энергия газа;
– удельная внутренняя
энергия газа; ![]() –
удельная полная энтальпия;
–
удельная полная энтальпия; ![]() и
и ![]() – молекулярная и турбулентная компоненты
векторов плотности теплового потока.
– молекулярная и турбулентная компоненты
векторов плотности теплового потока.
Система уравнений (1) дополняется еще уравнением состояния
газа. В простейшем случае идеального газа с ![]() степенями свободы (который может служить
хорошим первоначальным приближением для рассматриваемого случая)
степенями свободы (который может служить
хорошим первоначальным приближением для рассматриваемого случая) ![]() , где
, где ![]() – молекулярный вес,
– молекулярный вес, ![]() – универсальная
газовая постоянная (
– универсальная
газовая постоянная (![]() ),
), ![]() ,
, ![]() – удельная теплоемкость при постоянном объеме.
– удельная теплоемкость при постоянном объеме.
Молекулярный тензор вязких напряжений и молекулярный вектор теплового потока имеют следующий вид
|
|
(2) |
где ![]() – тензор скоростей деформации,
– тензор скоростей деформации, ![]() – коэффициент молекулярной
динамической вязкости,
– коэффициент молекулярной
динамической вязкости, ![]() – коэффициент теплопроводности.
– коэффициент теплопроводности.
Вид оставшихся турбулентных компонент уже не является универсальным и определяется выбором модели турбулентности. При этом предпочтение следует отдавать модели турбулентности, способной аккуратно воспроизводить свойства реальных физических течений в рассматриваемом диапазоне параметров.
Принимая во внимание высокую трудоёмкость рассматриваемых вычислительных задач, особое значение приобретает возможность проведения параллельных вычислений с хорошей масштабируемостью.
Используемая система уравнений (1), (2) обладает двумя основными особенностями – наличием ударных волн и довольно тонких вязких (турбулентных) эффектов. Ударная волна представляет собой скачок в значениях неизвестных функций, для расчета таких разрывных функций общепринятым подходом является построение той или иной противопотоковой (upwind) схемы (схемы типа Годунова), современное изложение см., например, в [6]. В соответствии с общими принципами метода конечных объемов (finite volumes) гиперболическая часть системы (1), (2) интегрируется по малому объему ячейки расчетной сетки. Неизвестные функции аппроксимируются константами, которые задаются в центрах ячеек. При подстановке аппроксимирующих значений в интегральную формулу получаются соотношения для средних значений неизвестных функций на следующем шаге по времени. При известных значениях функций в центрах ячеек с предыдущего шага по времени (или из начальных условий), задача сводится к определению потоков неизвестных функций через границы ячейки. Способ определения потоков зависит от характера распространения возмущений в начально-краевой задаче, а форма реализации определяется конкретным видом противопотоковой схемы.
В начале 2000-х годов возник новый подход к расчету гиперболических задач с вязкими потоками, к классу которых относятся уравнения Навье-Стокса с моделями турбулентности. Это так называемые «центрально-противопотоковые» (central-upwind) схемы, которые в соответствии с названием представляют собой комбинацию центрально-разностной и противопотоковой схем, [7, 8]. Суть центрально-противопотоковых схем состоит в специальном выборе контрольного объема, содержащего области двух типов: вокруг граничных точек – первый тип; вокруг центральной точки – второй тип. Границы контрольных объемов первого типа определяются при помощи локальных скоростей распространения возмущений. Таким образом, можно сказать, что вся разрывная часть решения находится в областях первого типа, а в области второго типа лежит гладкая часть решения. В соответствии с этим на верхнем слое по времени возникает не один набор усредненных значений неизвестных функций, которые затем необходимо спроецировать на изначальную сетку. Способ выполнения этого шага проекции будет определять разновидность центрально-противопотоковой схемы.
За прошедшее десятилетие этот метод интенсивно развивался и продемонстрировал свои преимущества при проведении именно предсказательных вычислений в практически важных задачах. Также решатель (solver) с использованием центрально-противопотоковой схемы реализован в открытой интегрируемой платформе для численного моделирования задач механики сплошных сред OpenFOAM (Open Source Field Operation And Manipulation CFD Toolbox) [9]. Расчеты, представленные в данной работе, выполнены на основе указанного пакета. Программный пакет OpenFOAM активно используются в промышленности, в академической сфере и экспертном сообществе, в частности, в Европейском космическом агентстве. Поэтому использование открытого кода OpenFOAM для решения поставленной задачи по созданию математической модели течения в тракте двигателя ВЛА представляется вполне обоснованным.
Важным моментом расчета высокоскоростных (гиперзвуковых)
потоков является выбор модели турбулентности. В обзоре [10] отмечалось
недостаточное количество экспериментального материала для более определенного
выбора наиболее подходящих моделей турбулентности при расчете гиперзвуковых
течений с использованием осредненных по Рейнольдсу уравнений Навье-Стокса (RANS).
Наиболее популярными для расчетов высокоскоростных потоков являются модели
турбулентности Спалларта-Алмараса, ![]() Уилкокса и SST Ментера. В то же время при
расчете течений с горением все более активно используется метод крупных вихрей LES.
Данный подход к описанию турбулентности позволяет точно рассчитывать достаточно
значимые вихри, которые играют важную роль в потоках с химически реагирующими
компонентами. Поэтому перспективным подходом является комбинирование LES и RANS
моделирования в соответствующих областях течения.
Уилкокса и SST Ментера. В то же время при
расчете течений с горением все более активно используется метод крупных вихрей LES.
Данный подход к описанию турбулентности позволяет точно рассчитывать достаточно
значимые вихри, которые играют важную роль в потоках с химически реагирующими
компонентами. Поэтому перспективным подходом является комбинирование LES и RANS
моделирования в соответствующих областях течения.
Таким образом, для расчетов высокоскоростных потоков в модельном тракте двигателя ВЛА используется следующая модель. Решается система уравнений Навье-Стокса, дополненная моделями турбулентных напряжений и тепловых потоков (RANS, общая структура уравнений выглядит одинаково, независимо от способа усреднения). Модель турбулентности – SST Ментера (наиболее гибкая модель). Дискретизация проводится с помощью технологии центрально-противопотоковых схем и их модификаций средствами открытой вычислительной платформы OpenFOAM.
2. Технология построения расчетных сеток для моделирования трехмерных объектов сложной формы
При расчетах реальных трехмерных объектов традиционно одним из наиболее трудоемких и затратных по времени этапов в процессе построения численной модели является подготовка расчетной сетки приемлемого качества. Для достижения указанной цели используется ряд автоматических инструментов с широким набором средств контроля качества и параметров получаемой объемной численной сетки, в том числе и визуальный анализ ряда сеточных объектов.
Как правило, начальным шагом для создания сетки является описание поверхности, ограничивающей заданное трехмерное тело. Эта поверхность обычно (полностью или частично) импортируются из CAD-пакетов. При этом поддерживается широкий выбор допустимых форматов. В случае необходимости импортированная CAD-модель может быть отредактирована. Таким образом, входные данные представляют собой поверхность (или несколько поверхностей в случае задачи с несколькими расчетными областями), которая служит основой для построения объемной сетки. Такая поверхность должна удовлетворять определенным требованиям: замкнутость, отсутствие самопересечений, триангуляция приемлемого качества и т.п.
Для этого применяются автоматические инструменты создания и редактирования поверхностных сеток, что позволяет значительно сократить затрачиваемое время и практически полностью исключить подготовку сетки «вручную». В первую очередь исправляются дефекты CAD-геометрии (отверстия, самопересечения и т. д.), что позволяет получить на выходе замкнутую поверхность с требуемой степенью детализации. Затем создается треугольная поверхностная сетка, обладающая необходимыми параметрами (степень гладкости в областях с высокой кривизной, уровень разрешения тонких мест, скорость роста характерного размера поверхностных ячеек при удалении от областей с высокой детализацией, сохранение топологических особенностей, локальное измельчение сетки и т. д.). Результирующая поверхностная сетка является основой для построения объемной сетки.
Объемная сетка для моделирования течений жидкостей и газов в окрестности твердых тел, как правило, состоит из двух основных частей: призматической и внутренней. Для создания пристеночного призматического слоя с заданным числом ячеек в направлении от стенки, законом роста и полной толщиной слоя используются два возможных подхода. В первом строится поверхностная сетка, отстоящая от исходной на полную толщину слоя. Получившийся таким образом пристеночный объем разрезается на заданное число призматических слоев. Такой подход обычно не гарантирует создание призматического слоя с заданными параметрами и требуемой полной толщиной в областях со сложной геометрией. В таких случаях предпочтительней использовать метод последовательного создания призматических слоев, допускающий модификацию поверхностной сетки текущего слоя (коллапс ребер, разрезание ячеек, оптимизация положения вершин и т. д.), что позволяет создать слой призматических ячеек, проникающий значительно дальше от стенок вглубь расчетной области.
Для заполнения внутреннего объема также могут использоваться различные подходы: тетраэдры, усеченные ячейки (гексагональные во внутренней части и многогранные на границе расчетной области), а также многогранные ячейки во всей счетной области). Программный комплекс OpenFOAM, который использовался при численном моделировании, в общем случае позволяет проводить расчеты на численных сетках, состоящих из произвольных многогранных ячеек, ограниченных произвольным числом многоугольных граней. Тем не менее, в представленных далее численных расчетах с использованием OpenFOAM применялись сетки с треугольными призматическими ячейками в пристеночных слоях и тетраэдрами во внутреннем объеме расчетной области.
3. Реализация вычислительной модели, двумерные и трехмерные расчеты течения в модельном тракте двигателя
3.1. Двумерный расчет модельного тракта двигателя
Для проведения верификационных тестовых расчетов и калибровки выбранной математической модели использован экспериментальный материал из диссертационной работы Дж. Вагнера [11]. В указанной работе исследовалось гиперзвуковое течение в модельном воздухозаборнике, схематическое изображение которого приведено см. рис. 1. Начальное сжатие осуществляется входной рампой с углом наклона 6о, а изолятор представляет собой протяженный (242.3 мм) прямоугольный тракт высотой 25.4 мм и шириной 50.8 мм. Для изучения явления «незапуска воздухозаборника» (unstart) в конце изолятора установлена специальная лопасть, при поднятии которой течение становилось существенно нестационарным с возможностью запирания потока.
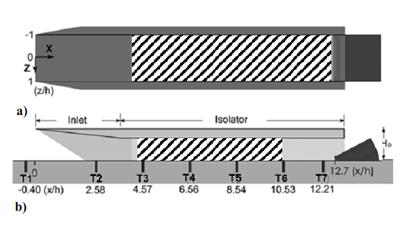
Рис. 1. Модель с углом на входе в 6о и длинным изолятором
При численном моделировании течения воздуха в рассматриваемом тракте использовался набор построенных расчетных сеток, имеющих сгущение в пристеночных областях, см. рис. 2. Сетки отличались степенью детализации (характерным размером ячеек внутри счетной области), что необходимо для проверки сходимости расчетов. В приведенных ниже результатах расчетов использовались расчетные сетки с полным числом ячеек: вариант А – 856000, вариант Б – 2720000, вариант В – 8406400.
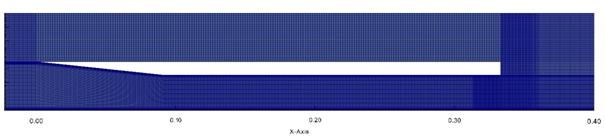
Рис. 2. Расчетная область и общий вид расчетной сетки
Для проведения расчетов на вычислительном комплексе с параллельной архитектурой используемые сетки распределялись по задействованным процессорам с помощью процедуры автоматического разбиения счетной области на необходимое число доменов, см. рис. 3.

Рис. 3. Пример распределения расчетной сетки по 64 процессорам с помощью программного пакета ParMetis.
Ниже приведена визуализация общей картины течения
(распределение числа Маха, продольной компоненты скорости и нормированного
давления) в модельном тракте воздухозаборника, рис. 4, полученная с
применением вычислительной платформы OpenFOAM на сетке из 2720000 ячеек
(вариант Б) с использованием решателя rhoCentralFoam и модели турбулентности ![]() SST. При этом
входной поток воздуха имеет профилированную скорость, а лопасть опущена.
SST. При этом
входной поток воздуха имеет профилированную скорость, а лопасть опущена.
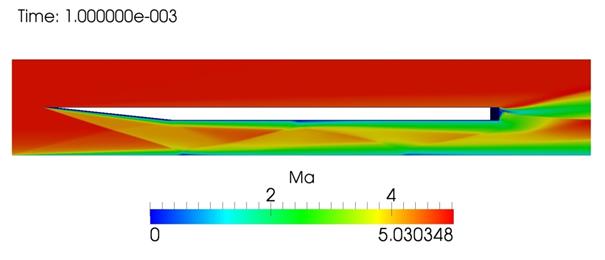
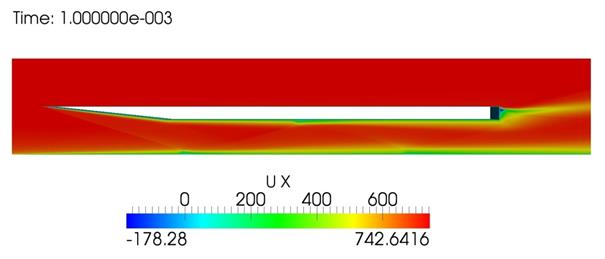
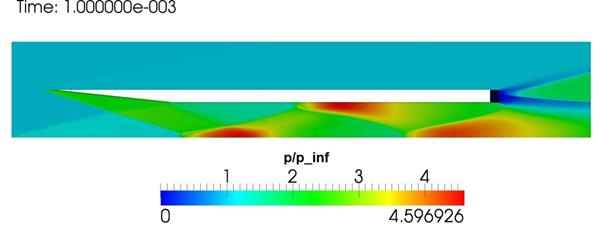
Рис. 4. Общая картина течения с опущенной лопастью. Число Маха, горизонтальная компонента скорости, нормированное давление (сверху вниз).
Визуальное представление полей основных физических полей позволяет увидеть конкретную ударно-волновую картину течения, обнаружить расположение и величину отрывных зон. Представленные распределения хорошо согласуются с теоретическими представлениями о свойствах подобных течений и результатами, полученными в [12-14]. Время установления течения в данном расчете на сетке из 2720000 ячеек (вариант Б) с задействованной моделью турбулентности занял на 64 процессорах около 8.5 часов.
Для более детальной проверки модели проведено сравнение профиля нормированного давления на нижней стенке тракта с доступными экспериментальными данными, приведенными в [11]. Ламинарные расчеты с использованием решателя OpenFOAM, опирающегося на центрально-противопотоковую схему, демонстрируют приемлемое совпадение расчетных и экспериментальных данных, см. рис. 5. Устранение различий в экспериментальной и численной визуализации газодинамического течения в процессе изучения асимптотической сходимости методом подбора сеточных параметров приводит к нахождению оптимальной для проведения расчетов сетки.
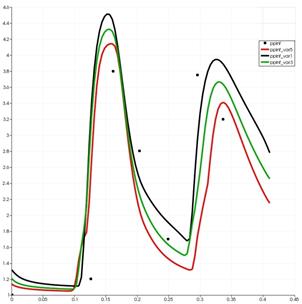
Рис. 5. Сравнение рассчитанного нормированного давления с
экспериментом. Ламинарный расчет. Эксперимент отмечен точками ![]() , расчетные кривые: вариант А
– черная, вариант Б – зеленая, вариант В – красная
, расчетные кривые: вариант А
– черная, вариант Б – зеленая, вариант В – красная
Учет турбулентности позволяет еще более повысить соответствие расчета и эксперимента, см. рис. 6.
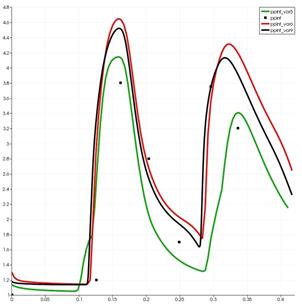
Рис. 6. Сравнение рассчитанного нормированного давления с
экспериментом. Расчет с турбулентностью. Эксперимент отмечен точками ![]() , расчетные кривые:
вариант А – черная, вариант Б – зеленая, вариант В – красная.
, расчетные кривые:
вариант А – черная, вариант Б – зеленая, вариант В – красная.
3.2. Двумерный расчет модельного тракта двигателя с расширенной счетной областью и поднятой лопастью
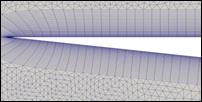
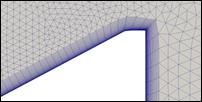
В конце изолятора присутствует специальная лопасть, при поднятии которой течение становится нестационарным, в результате чего может возникать запирание потока – явление «незапуска воздухозаборника». Данный двумерный и представленный далее трехмерный расчеты проводились при поднятой заслонке, что отражено на рисунках ниже. В процессе предварительного моделирования выяснилось, что для точного воспроизведения особенностей исследуемого течения расчетная область должна быть расширена. Общий вид расширенной счетной области и детали двумерной расчетной сетки представлены на рис. 7.
Таким образом, фактически выполнялся расчет, достаточно близко воспроизводящий условия работы реальной экспериментальной установки. Построенная сетка является неструктурированной со специальным выделением пограничного слоя (см. выше). В пристеночной области ячейки имеют четырехугольную форму и образуют призматические слои с заданными параметрами (полная толщина, скорость роста, толщина первого слоя) вдоль всей границы, что обеспечивает адекватное численное описание течения газа в пограничном турбулентном слое. Внутренняя часть счетной области заполняется треугольными ячейками (в двумерной постановке задачи), см. рис. 7.
|
|
||
|
|
|
|
|
Рис. 7. Общий вид расширенной счетной области (сверху) и фрагменты двумерной расчетной сетки (снизу): слева направо в порядке нумерации 1-3. |
||
Польза проведения двумерных расчетов с их непременной
детальной визуализацией состоит в возможности относительно быстро проверить
работоспособность выбранной вычислительной методологии, настроить и
откалибровать математическую и вычислительную модели, исследовать особенности
получаемого решения при различных допустимых значениях параметров задачи.
Особенно актуальным такой подход становится в случае особенно трудоемких
расчетов с возможным развитием сильной нестационарности течений, пример такого
расчета приводится далее. Для модельной геометрии, показанной на рис. 7,
проведен двумерный расчет при числе Маха набегающего потока равном 5 и поднятой
лопасти в конце тракта. Результаты этого расчета для трех моментов
безразмерного времени ![]() и
и ![]() показаны на рис. 8. Визуализация
установившейся в тракте воздухозаборника структуры псевдоскачка, содержащего
систему косых ударных волн, показывает процесс деформирования этой структуры
вследствие отражения потока от поднятой лопасти. На лопасти образуется область
повышенного давления, тем не менее, запирания потока не происходит.
показаны на рис. 8. Визуализация
установившейся в тракте воздухозаборника структуры псевдоскачка, содержащего
систему косых ударных волн, показывает процесс деформирования этой структуры
вследствие отражения потока от поднятой лопасти. На лопасти образуется область
повышенного давления, тем не менее, запирания потока не происходит.
При этом на входе в воздухозаборник можно наблюдать образование двух вихревых зон, которые ограничивают расход через воздухозаборник и снижают рабочие характеристики ПВРД, см. рис. 9.
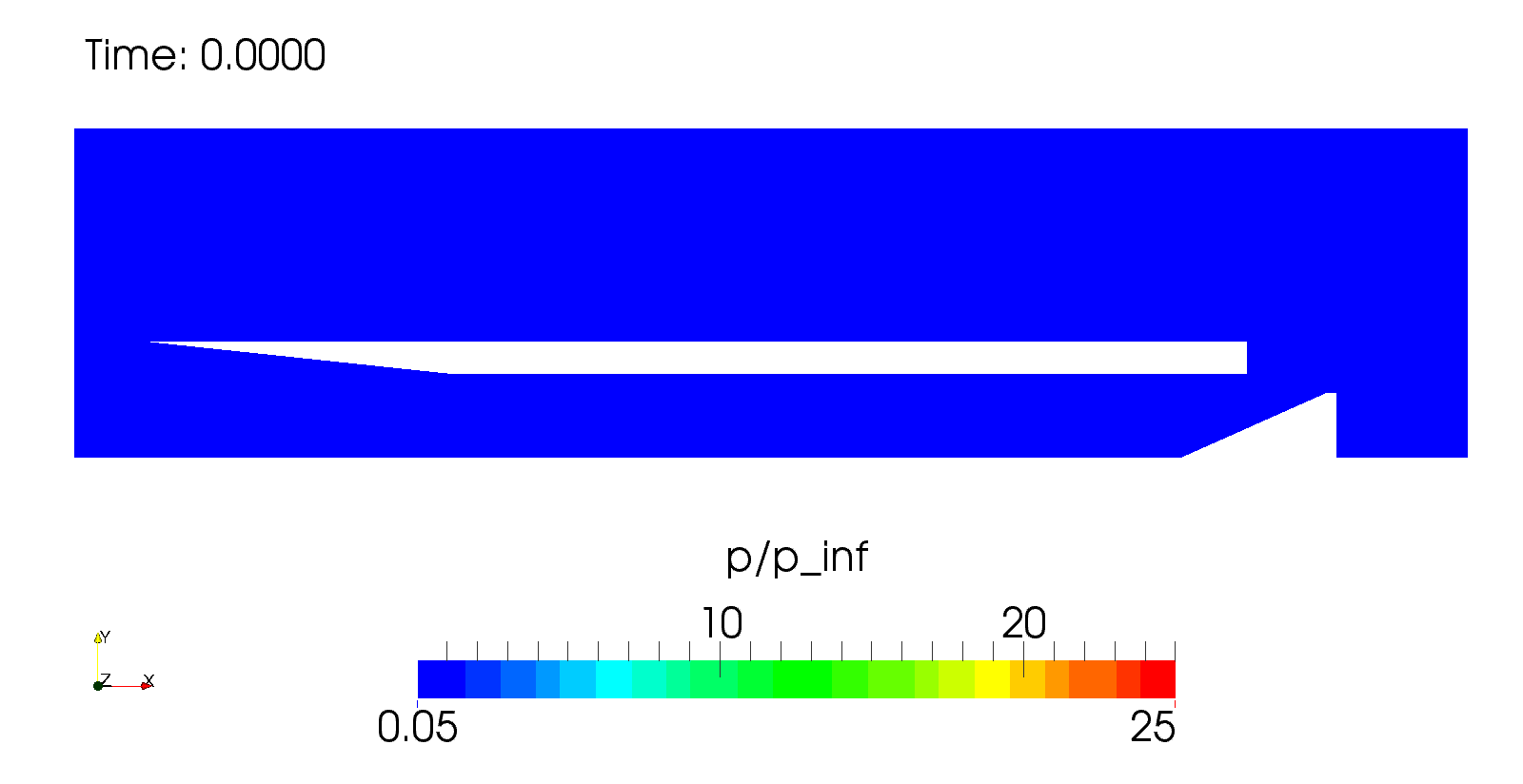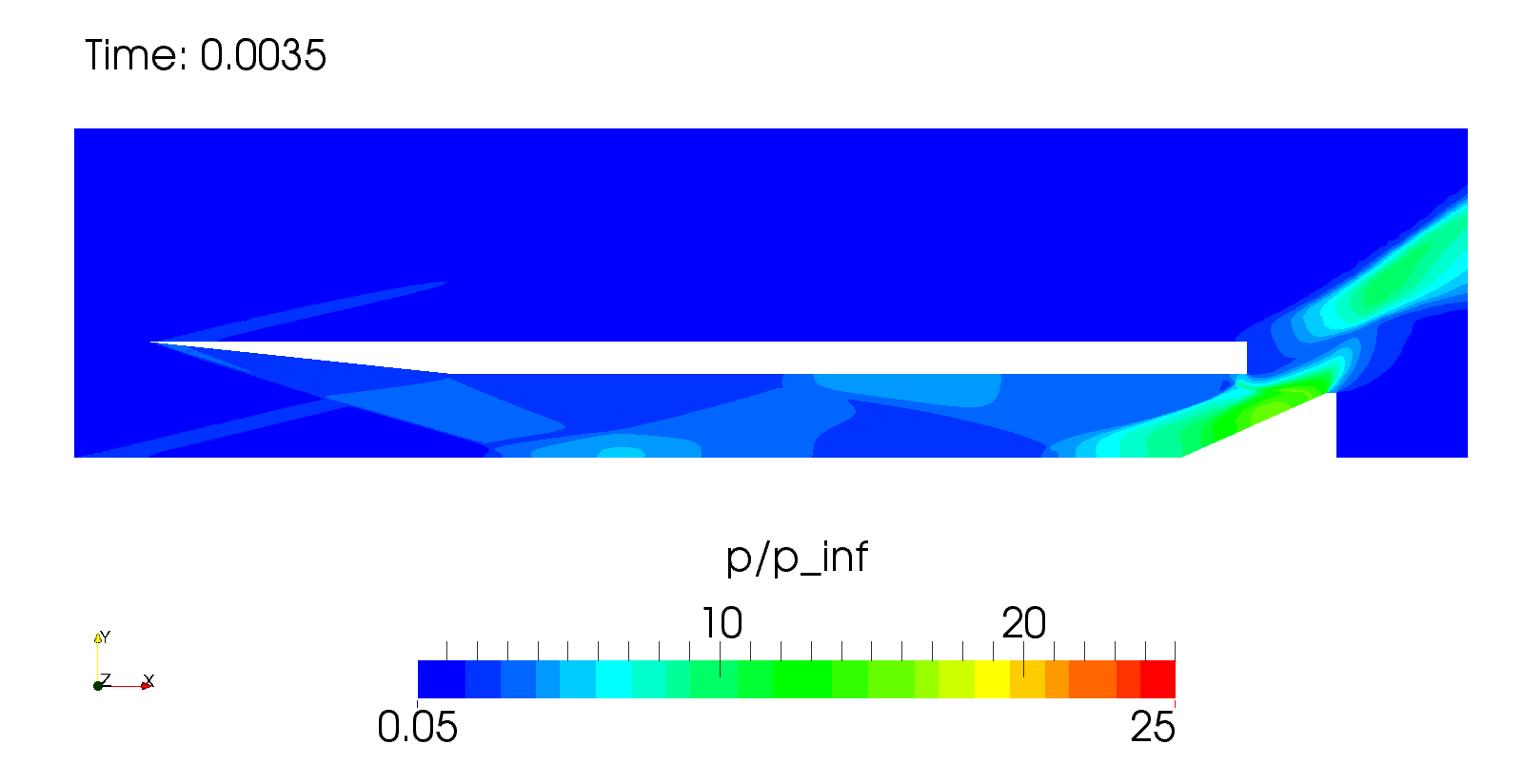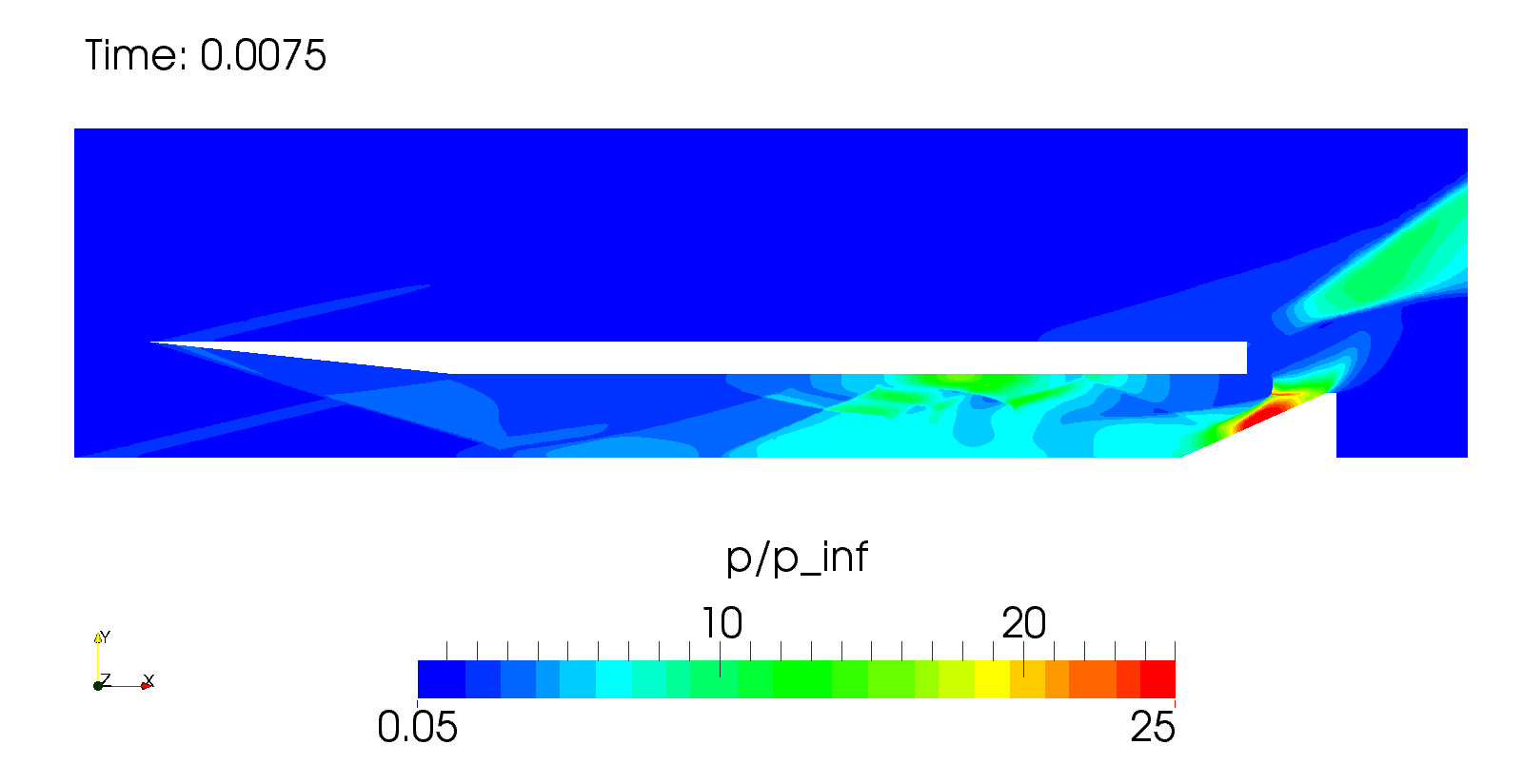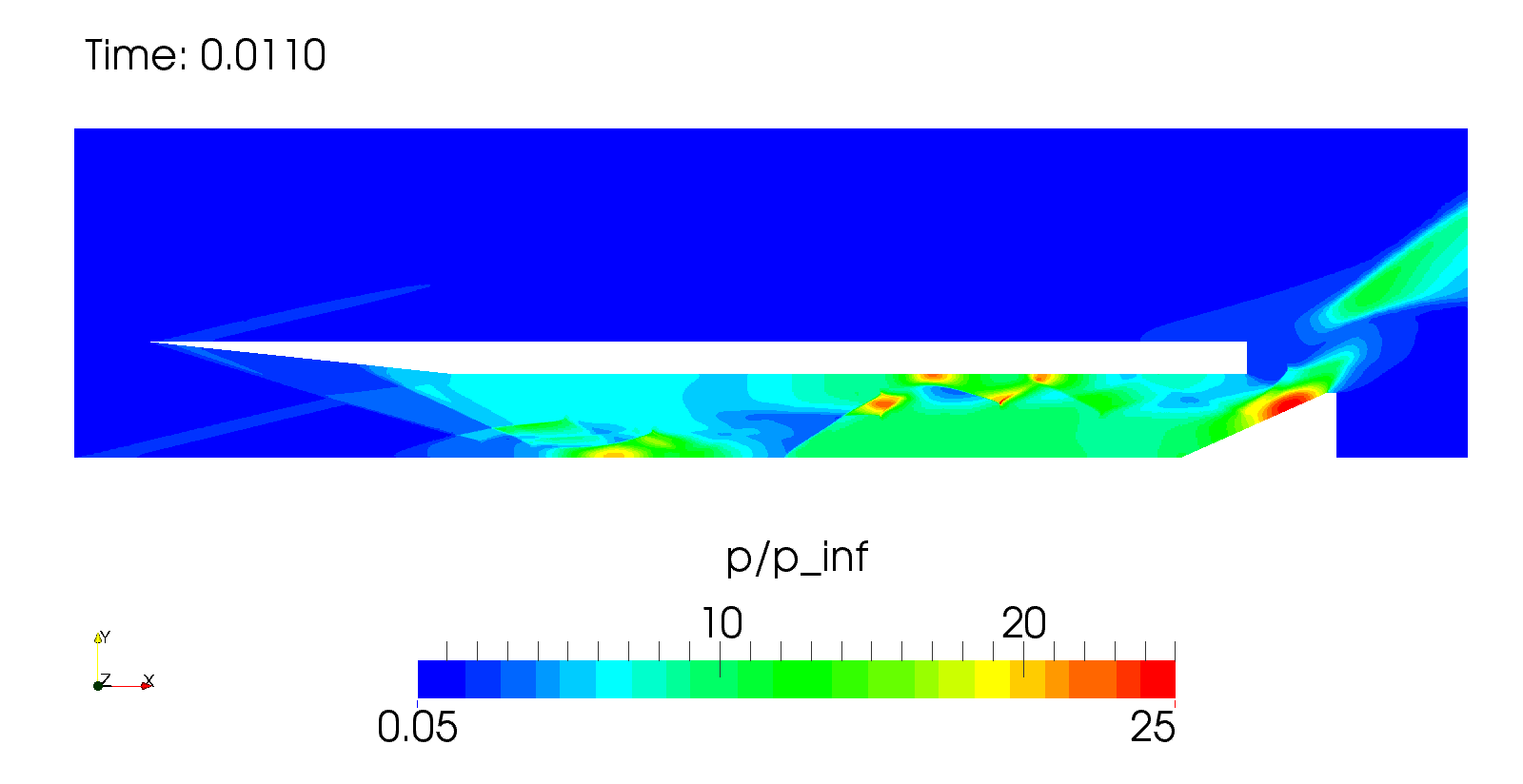
Рис. 8. Двумерное поле давлений для трех моментов безразмерного времени
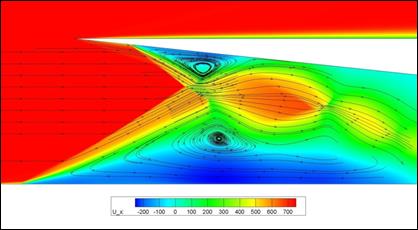
Рис. 9. Двумерное поле продольной скорости для момента
времени ![]() . Угол
поднятия лопасти 26о. Формирование двух вихревых зон.
. Угол
поднятия лопасти 26о. Формирование двух вихревых зон.
3.3. Трехмерный расчет модельного тракта двигателя с расширенной счетной областью и поднятой лопастью
В трехмерных расчетах использована сетка, общий вид и сечение которой показаны на рис. 10. Пристеночные слои состоят из ячеек, являющихся треугольными призмами, внутренний объем заполнен тетраэдрами. На рис. 11 показаны результаты трехмерного расчета для модельной геометрии воздухозаборника: показано трехмерное распределение нормированного давления по объему воздухозаборника, а также последовательность двумерных распределений, построенных в поперечных сечениях тракта.
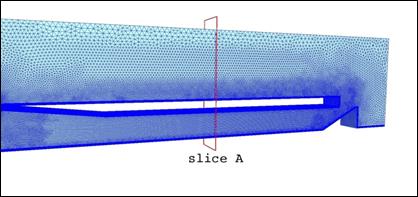
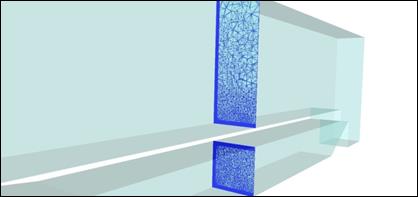
Рис. 10. Общий вид и сечение сетки для трехмерной компоновки
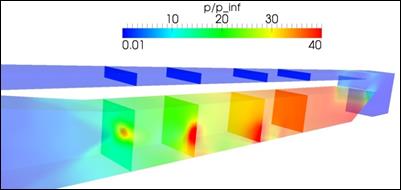
Рис. 11. Трехмерное поле нормированного давления. Двумерные распределения давления в поперечных сечениях тракта воздухозаборника
Из приведенного распределения давления хорошо видна потеря симметрии течением и формирование областей высокого давления внутри тракта. Визуализация линий тока внутри воздухозаборника прекрасно иллюстрирует образование интенсивного вихревого движения в начале тракта модельного ПВРД, рис. 12.

Рис. 12. Образование вихревых зон в течении на входе в
воздухозаборник на момент безразмерного времени ![]() .
.
Происходит запирание потока на входе с существенным ограничением расхода, что значительно замедляет течение и приводит к появлению локальных вариаций давления. Подробно структуру запирающего вихря можно наблюдать на распределении продольной компоненты скорости, рис. 13.
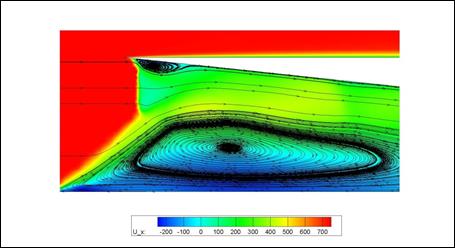
Рис. 13. Двумерное распределение скорости в плоскости
симметрии воздухозаборника на момент безразмерного времени ![]()
Из сравнения рис. 9 и 13 хорошо видно существенное отличие в структуре вихрей, полученных в двумерном и трехмерном случае, что указывает на важность проведения именно трехмерных расчетов для полного понимания характера течения в тракте реального ПВРД.
Для сравнения с экспериментальными данными использовались результаты, приведенные в [13]. Расположение датчиков в контрольных точках воздухозаборника показано на рис. 14. Зависимости давления в этих точках от безразмерного времени, полученные в трехмерном расчете, приведены на рис. 15.
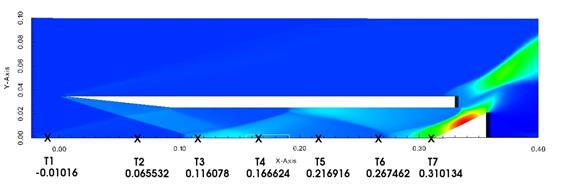
Рис. 14. Расположение контрольных точек на нижней стенке воздухозаборника
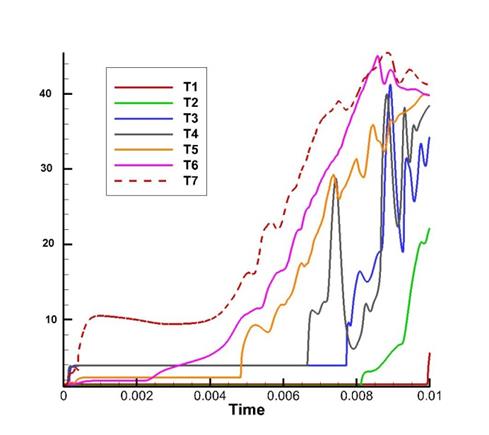
Рис. 15. Зависимость давления, выраженного в атмосферах, от безразмерного времени в контрольных точках Т1 - Т7
Видно, что наиболее нестабильное поведение демонстрирует давление, измеренное в контрольной точке Т4, где наблюдался локальный максимум давления на рис. 11. Сопоставление расчетных и экспериментальных данных для давления на нижней стенке воздухозаборника показано на рис. 16.
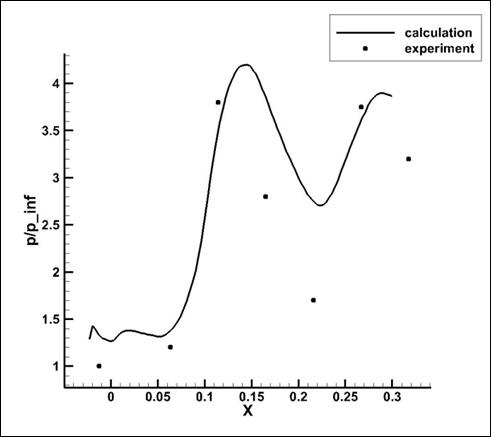
Рис. 16. Сравнение результатов расчета и эксперимента. Кривая - расчетные значения давления у нижней стенки воздухозаборника, точки - результаты экспериментальных измерений
Как можно видеть из сравнительного анализа графического представления численный расчет качественно воспроизводит характер течения в воздухозаборнике, при этом, однако, количественного совпадения получить не удается. Это можно объяснить сильной нестационарностью течения, возникающей при поднятии лопасти, что приводит к невозможности сопоставить результаты расчета и эксперимента на единой временной шкале, другими словами, выбрать идентичный момент времени для сравнения. Кроме того, недостаточно ясно соответствие неявных процессов усреднения данных в эксперименте и в расчете.
На рис. 17 показано сравнение расчетных и экспериментальных распределений нормированных компонент скорости (продольной и вертикальной) в поперечном направлении в различных сечениях вдоль тракта воздухозаборника. Отметим, что качество совпадения падает при движении вдоль тракта, что обусловлено причинами, указанными выше для давления.
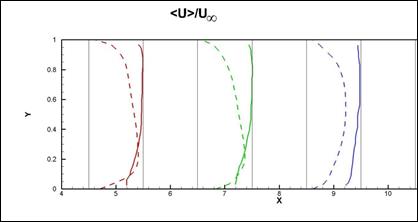
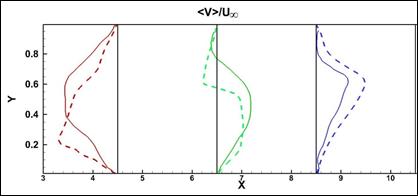
Рис. 17. Сравнение результатов расчета и эксперимента. Верхняя панель –поперечные профили продольной компоненты скорости. Нижняя панель – поперечные профили вертикальной компоненты скорости
4. Заключение
Используемая математическая модель течения в модельном тракте двигателя высокоскоростного летательного аппарата продемонстрировала необходимый уровень точности предсказательных вычислений. В ее основе лежит решение системы уравнений Навье-Стокса, усредненных по Рейнольдсу, получаемое с использованием центрально-противопотоковых схем. Для замыкания решаемой системы уравнений применяется модель турбулентности SST Ментера. Реализуется приведенная математическая модель при помощи модулей открытой интегрируемой платформы для численного моделирования задач механики сплошных сред OpenFOAM и автоматических программных средств построения двумерных и трехмерных расчетных сеток. Данная вычислительная методология позволяет описывать основные особенности трехмерных течений, возникающих в тракте ПВРД высокоскоростного (гиперзвукового) ЛА. Для достижения количественных совпадений необходимо проведение расчетов на сетках с достаточной степенью детализации.
Особо следует отметить роль современных способов визуализации, использованных в работе, для изучения, контроля и анализа результатов численных расчетов. Задачи подбора математической модели, адекватной поставленной физической задаче, настройки ее параметров с целью валидации и верификации численных результатов было бы невозможно решить без анализа двумерных и трехмерных графических представлений различных физических полей, а также анимации полученных в результате расчетов явлений.
Библиографический список
1. J. Anderson. Hypersonic and high-temperature gas dynamics, Second edition, AIAA, 2006.
2. D.E. Reubush, L.T.Nguyen & V.L. Rausch. Review of X-43A return to flight activities and current status, 12th AIAA International Space Planes and Hypersonic Systems and Technologies, Paper No. 2003-7085, 2003.
3. C. Peebles. Road to Mach 10: Lessons learned from the X-43A flight research program, AIAA, 2008.
4 . A.E. Bondarev, V.A. Galaktionov, V.M. Chechetkin. Scientific visualization in computational fluid dynamics. Scientific Visualization, vol. 2, no 4, 2010, pp. 1–26. Available at: http://sv-journal.org/2010-4/049ed2.html (valid on 16.02.2015)
5. А.В. Гарбарук, М.Х. Стрелец, М.Л. Шур. Моделирование турбулентности в расчетах сложных течений, Изд-во Политех. Ун-та, СПБ, 2012, 88 стр.
6. S. Pirozzoli. Numerical methods for high-speed flows, Annual review of fluid mechanics, Vol. 43, 2011, pp. 163–194.
7. A. Kurganov and E. Tadmor. New high resolution central schemes for nonlinear conservation laws and convection-diffusion equations, J. Comput. Phys., Vol. 160, 2000, pp. 241-282
8. A. Kurganov and E. Tadmor. Solution of two-dimensional Riemann problems for gas dynamics without Riemann problem solvers, Numer. Methods Partial Differential Equations, Vol. 18, 2002, pp. 584-608.
9. The OpenFOAM® Foundation, http://www.openfoam.org/index.php.
10. C.J. Roy, F.G. Blottner. Review and assessment of turbulence models for hypersonic flows, Progress in aerospace sciences, Vol. 42, 2006, pp. 469-530.
11. J.L. Wagner. Experimental studies of unstart dynamics in inlet/isolator configurations in a Mach 5 flow, PhD Thesis, The University of Texas at Austin, 2009.
12. H. Koo. Large-eddy simulations of scramjet engines, PhD thesis, The University of Texas at Austin, 2011.
13. H. Koo, V. Raman. Large-eddy simulation of a supersonic inlet-isolator, AIAA Journal, Vol. 50, No.7, pp. 1596-1613, 2012.
CALCULATION, ANALYSIS AND VISUALIZATION OF FLOW SIMULATION IN MODEL RAMJET ENGINE ON HIGH VELOCITY
V.T. Zhukov1, K.V. Manukovskii2, N.D. Novikova1, Yu.G. Rykov1, O.B. Feodoritova1
1 Keldysh Institute of Applied Mathematics RAS, Moscow, Russian Federation
2 Alikhanov Institute for Theoretical and Experimental Physics, Moscow, Russian Federation
vic.zhukov@gmail.com, manu@itep.ru, nn@kiam.ru, yu-rykov@yandex.ru, feodor@kiam.ru
Abstract
Investigation of ramjet engines is closely related with evaluation of high-velocity aerial vehicles. To calculate high-velocity flows inside a model engine we use Navier-Stokes equations added with turbulent tensions and heat flows. Turbulence is described by SST-Меnter model. Difference scheme is based on central-upwind methodology and its modifications implemented in open numerical platform OpenFOAM. Calculations for validation and calibration of the selected mathematical model are based on experimental data of J.Wagner work.
Key words: high-velocity flow, Navier-Stokes equations, ramjet engine, OpenFOAM, rhoCentralFoam
Bibliography
1. J. Anderson. Hypersonic and high-temperature gas dynamics, Second edition, AIAA, 2006.
2. D.E. Reubush, L.T.Nguyen & V.L. Rausch. Review of X-43A return to flight activities and current status, 12th AIAA International Space Planes and Hypersonic Systems and Technologies, Paper No. 2003-7085, 2003.
3. C. Peebles. Road to Mach 10: Lessons learned from the X-43A flight research program, AIAA, 2008.
4 . A.E. Bondarev, V.A. Galaktionov, V.M. Chechetkin. Scientific visualization in computational fluid dynamics. Scientific Visualization, vol. 2, no 4, 2010, pp. 1–26. Available at: http://sv-journal.org/2010-4/049ed2.html (valid on 16.02.2015) [In Russian]
5. A.V. Garbaruk, M.H.Strelets, M.L. Shur. Simulation of turbulence for complex flows [Modelirovanie turbulentnosty v raschetah slozhnyh techenii], Publishing House of Polytech. University, St. Petersburg, 2012, 88 p. [In Russian]
6. S. Pirozzoli. Numerical methods for high-speed flows, Annual review of fluid mechanics, Vol. 43, 2011, pp. 163–194.
7. A. Kurganov and E. Tadmor. New high resolution central schemes for nonlinear conservation laws and convection-diffusion equations, J. Comput. Phys., Vol. 160, 2000, pp. 241-282
8. A. Kurganov and E. Tadmor. Solution of two-dimensional Riemann problems for gas dynamics without Riemann problem solvers, Numer. Methods Partial Differential Equations, Vol. 18, 2002, pp. 584-608.
9. The OpenFOAM® Foundation, http://www.openfoam.org/index.php.
10. C.J. Roy, F.G. Blottner. Review and assessment of turbulence models for hypersonic flows, Progress in aerospace sciences, Vol. 42, 2006, pp. 469-530.
11. J.L. Wagner. Experimental studies of unstart dynamics in inlet/isolator configurations in a Mach 5 flow, PhD Thesis, The University of Texas at Austin, 2009.
12. H. Koo. Large-eddy simulations of scramjet engines, PhD thesis, The University of Texas at Austin, 2011.
13. H. Koo, V. Raman. Large-eddy simulation of a supersonic inlet-isolator, AIAA Journal, Vol. 50, No.7, pp. 1596-1613, 2012..
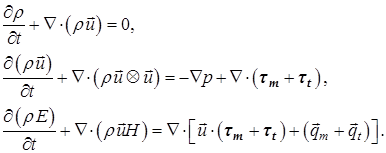
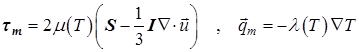 ,
,