МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И ВИЗУАЛИЗАЦИЯ ВНУТРИКАМЕРНЫХ ПРОЦЕССОВ В БАЛЛИСТИЧЕСКИХ УСТАНОВКАХ С ГИДРОДИНАМИЧЕСКИМ ЭФФЕКТОМ
Н.В. Быков(1, 2) , Е.А. Нестеренко(1, 3)
1Московский государственный технический университет имени Н.Э. Баумана, Россия
2Вычислительный центр им. А.А. Дородницына РАН, Россия
3Институт прикладной математики им. М.В. Келдыша РАН, Россия
bykovnv@bk.ru, nesterenko_ea@bk.ru
Содержание
2. Теоретическая модель процесса выстрела с гидродинамическим эффектом
3. Результаты численных расчетов и их визуализация
Аннотация
Рассмотрены вопросы математического моделирования и визуализации результатов численного расчета внутрикамерных процессов, происходящих в баллистических установках с гидродинамическим эффектом, который позволяет получать более высокую скорость метаемых тел благодаря ускорению передней части деформируемого поршня при прохождении его через сужающийся конический участок. Построена математическая модель выстрела, учитывающая двухфазность движения газопороховой смеси и вязкопластические свойства деформируемого поршня. Численное решение задачи проводится при помощи модифицированного метода конечных объемов годуновского типа на подвижной сетке. Поскольку рассматриваемая система уравнений, описывающая внутрикамерные процессы, имеет области потери гиперболичности, при определении потоков через границы ячеек используются две схемы: AUSM+ для расчета потоков газовой фазы и в области деформируемого поршня, и Русанова для расчета потоков в конденсированной фазе. В силу использования подвижной сетки особое внимание уделено особенностям визуализации результатов численного расчета, поскольку данные расположены на неструктурированной сетке. Рассмотрены два способа визуализации полученных данных: анимация скалярного поля и двумерное представление плотностей скалярных полей (density plot). Показано, что каждый из способов обладает своими достоинствами и недостатками.
Ключевые слова: баллистическая установка, гидродинамический эффект, метод Годунова, подвижные сетки, неструктурированные сетки.
1. Введение
Вопросы теоретического исследования и визуализации результатов численного моделирования внутрикамерных процессов в баллистических установках играют очень важную роль главным образом в силу того, что экспериментальная визуализация этих процессов чрезвычайно трудна или просто невозможна, в связи с экстремальными условиями, сопровождающими процесс выстрела.
В дальнейшем ограничимся рассмотрением класса лабораторных баллистических установок, которые используются в исследовательских целях для создания условий высокоскоростного соударения тел. Наряду с широко известным способом ускорения тел в легкогазовых установках, известному с середины прошлого века [1], в последние десятилетия рассматриваются альтернативные способы ускорения тел в метательных установках, одним из которых является использование баллистических установок с гидродинамическим эффектом, в которых ускорение тела обеспечивается повышением скорости деформируемого поршня при его прохождении через сужающееся коническое сопло в канале ствола [2].
В предыдущих работах авторов [3, 4] была построена приближенная математическая модель выстрела из баллистических установок рассматриваемого типа, которая учитывала только ключевые факторы процесса выстрела, определяющие выходные баллистические характеристики установки. При этом не учитывался ряд факторов, таких как реальные свойства газопороховой смеси или упругопластические свойства материала поршня. В то же время сейчас широкое распространение получили как двухфазные модели движения продуктов сгорания при выстреле из классических пороховых установок [5, 6], так и модели деформируемого поршня, учитывающие вязкопластические свойства материала при выстреле из легкогазовых установок [7]. Поэтому в настоящей работе для более адекватного рассмотрения влияния различных факторов на баллистические характеристики установок с гидродинамическим эффектом учтены как двухфазность газпороховой смеси, так и вязкопластические свойства деформируемого поршня. При решении такой комбинированной задачи возникла необходимость модификации численного метода, традиционно используемого для решения задач такого класса.
В работе рассматриваются сложные нестационарные двухфазные газодинамические процессы с учетом горения и тепломассообмена, сопровождающиеся образованием сложных структур, таких как ударные волны и волны разрежения.
Адекватная трактовка результатов в данном случае возможна с помощью визуализации полученных в результате численного решения данных: анимация внутрикамерных процессов во времени и построение скалярных полей величин в координатах x-t. При этом визуализация играет роль основного инструмента распознавания структур, верификации и адекватной трактовки результатов.
Особое внимание уделено визуализации результатов расчета на неструктурированных сетках, которые возникают при построении распределений скалярных полей величин в координатах x-t.
2. Теоретическая модель процесса выстрела с гидродинамическим эффектом
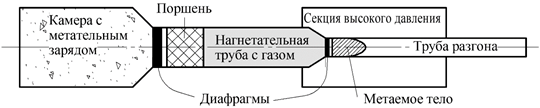
Схема и принцип действия баллистической установки с гидродинамическим эффектом пояснены на рис. 1.
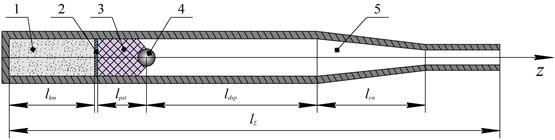
Рис. 1 Принципиальная схема устройства баллистической установки с гидродинамическим эффектом: 1 – пороховой заряд, 2 – инерционный поддон, 3 – пластический поршень, 4 – метаемое тело, 5 – конический канал (сопло)
В результате сгорания порохового заряда 1 происходит расширение образующихся газов, которые выталкивают сборку, образованную метаемым телом 4, деформируемым поршнем 3 и отделяющим его от пороховых газов инерционным поддоном 2. Сборка движется как единое целое по направляющей цилиндрической части ствола вплоть до достижения конического канала 5, в котором поршень 3 испытывает деформацию, в результате которой передняя его часть, а вместе с ней и метаемое тело 4, получает приращение скорости, а задняя часть, как правило, замедляется. В результате такого перераспределения скоростей метаемое тело приобретает дополнительное ускорение. В этом и заключается гидродинамический эффект.
Математическая модель процесса выстрела в рассматриваемом случае строится следующим образом. Область между дном канала и метаемым телом разбивается на две подобласти: в одной располагается газопороховая смесь, а в другой – деформируемый поршень. Эти две подобласти связаны друг с другом посредством уравнений движения перегородки 2 (см. рис. 1), которая их разделяет. В каждой из подобластей вводится своя подвижная сетка, концы которой жестко связаны с границами расчетных подобластей.
При описании поведения газопороховой смеси примем следующие допущения. Будем считать, что пороховые частицы представляют собой несжимаемую конденсированную фазу, что позволяет отказаться от уравнения энергии для её описания. Газ является несущей фазой, массовыми силами можно пренебречь, а конденсированные частицы друг с другом не взаимодействуют. В этом случае поведение двухфазной системы описывается следующими уравнениями:
![]() ;(1)
;(1)
![]() ;(2)
;(2)
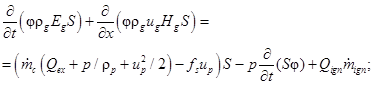 (3)
(3)
![]() ;(4)
;(4)
![]() ,(5)
,(5)
где x и t – пространственная координата и
время, соответственно; φ – объемная доля газовой фазы (пористость); ρg,
ug – плотность и скорость газовой фазы, соответственно; S
– площадь поперечного сечения канала ствола; ![]() – приток массы вследствие горения;
– приток массы вследствие горения; ![]() – приток массы от
воспламенителя; p – давление; β = 1 – φ –
объемная доля конденсированной фазы; ρp, up
– плотность и скорость конденсированной фазы, соответственно; fs
– сила межфазного взаимодействия, обусловленная разностью скоростей фаз; uign
– скорость потока, порождаемая воспламенителем;
– приток массы от
воспламенителя; p – давление; β = 1 – φ –
объемная доля конденсированной фазы; ρp, up
– плотность и скорость конденсированной фазы, соответственно; fs
– сила межфазного взаимодействия, обусловленная разностью скоростей фаз; uign
– скорость потока, порождаемая воспламенителем; ![]() - полная удельная энергия газовой
фазы;
- полная удельная энергия газовой
фазы; ![]() –
полная удельная энтальпия газовой фазы; eg – удельная
внутренняя энергия газовой фазы; Qex – экзотермическая
энергия, выделяемая в процессе горения конденсированной фазы; Qign
– энергия, выделяемая при горении воспламенителя; Rp –
межгранулярное давление.
–
полная удельная энтальпия газовой фазы; eg – удельная
внутренняя энергия газовой фазы; Qex – экзотермическая
энергия, выделяемая в процессе горения конденсированной фазы; Qign
– энергия, выделяемая при горении воспламенителя; Rp –
межгранулярное давление.
Система уравнений (1)–(5) замыкается перечисленным ниже набором определяющих соотношений, которые использованы в работе [8] при описании классической пороховой схемы метания.
Газ описывается уравнением состояния Дюпре
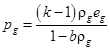 ,
,
где k – показатель адиабаты пороховых газов; b – коволюм.
Приток массы за счет сгорания твердых частиц пороха определяется соотношением
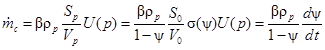 ,
,
где Sp, Vp – текущая
поверхность горения и объем частицы, соответственно; U(p) –
скорость горения частицы; S0, V0 –
начальная поверхность горения и объем частицы, соответственно; σ(ψ) –
относительная поверхность горения; ψ – функция газоприхода (относительный
объем сгоревшего пороха, ![]() ).
).
Обе фазы имеют общее давление p, но в конденсированной фазе вводится межгранулярное давление Rp, которое служит для препятствия слишком сильному уплотнению последней и включается при достижении критического значения плотной упаковки βc [5, 8]:
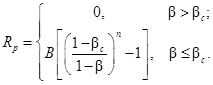
где B, n – эмпирические константы.
Сила межфазного взаимодействия fs определяется в приближении Эргана:
![]() ,
,
где fr – коэффициент сопротивления.
Функция ![]() зависит
от формы частиц. В данном случае используется следующий вариант:
зависит
от формы частиц. В данном случае используется следующий вариант:
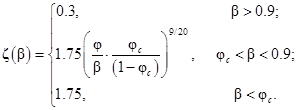
Критическое значение пористости φс обычно берется равным ее начальному значению.
Поскольку используется эйлерово описание, к уравнениям (1)–(5) необходимо добавить уравнение переноса скалярной величины z – относительной толщины сгоревшего пороха:
где e – толщина свода порохового элемента; U1 – единичная скорость горения пороха; ν – показатель в законе горения Вьеля:
![]() .
.
Прогрев пороховых элементов учитывается с помощью уравнения переноса удельной энтальпии частиц Hp:
![]() ,
,
где κp – температуропроводность конденсированной фазы; qt – тепловой поток с единичной межфазной поверхности:
![]() ,
,
Tps – температура поверхности конденсированной фазы, определяемая по квадратичному закону. Коэффициент теплоотдачи αt состоит из конвективной и радиационной составляющих. Пренебрегая последней, определим αt из соотношения
![]() ,
,
где kg – теплопроводность газа; Nu – число Нуссельта. Более подробное описание этого подхода дано в работе [8].
Деформируемый поршень описывается следующими уравнениями [9]:
![]() ;(7)
;(7)
![]() ;(8)
;(8)
![]() ,(9)
,(9)
где ρ, u, E – плотность, скорость и
полная удельная энергия материала поршня; ![]() – осевая составляющая напряжения; R –
радиус канала; индексом w отмечены величины, относящиеся к наружной
поверхности поршня:
– осевая составляющая напряжения; R –
радиус канала; индексом w отмечены величины, относящиеся к наружной
поверхности поршня: ![]() – касательное напряжение;
– касательное напряжение; ![]() – нормальное напряжение;
– нормальное напряжение; ![]() – тепловой поток.
– тепловой поток.
Эти уравнения замыкаются следующими эмпирическими зависимостями [10]. Касательное напряжение на стенке определяется как
![]() ,
,
где
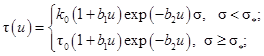
σ – давление осевого сжатия; для полиэтилена высокого
давления значения эмпирических констант следующие: ![]() МПа; k0 = 0.054;
b1 = 0.027 с/м; b2 = 0.00675
с/м;
МПа; k0 = 0.054;
b1 = 0.027 с/м; b2 = 0.00675
с/м; ![]() МПа
– трение при близкой к нулю скорости скольжения.
МПа
– трение при близкой к нулю скорости скольжения.
В силу недостаточности экспериментальных сведений о
реологическом поведении полиэтилена при высоких давлениях, деформируемый
поршень считается вязкопластической жидкостью [9]. В этом случае ![]() ;
; ![]() ;
;
![]() , где μ – динамическая вязкость; τs
– предел текучести при чистом сдвиге.
, где μ – динамическая вязкость; τs
– предел текучести при чистом сдвиге.
Скорости границ поршня находятся из следующих условий. Если
контактная левая поверхность имеет массу m и справа на нее воздействует
материал поршня с напряжением ![]() , а слева пороховые газы с давлением pg,
то уравнение движения границы имеет вид
, а слева пороховые газы с давлением pg,
то уравнение движения границы имеет вид
![]() .
.
В работе [7] использовалось следующее двучленное калорическое уравнение состояния материала поршня:
![]() ,
,
где для полиэтилена высокого давления значения постоянных, определенных на основании экспериментальных данных [11] имеют вид ρ0 = 919.03 кг/м3, c0 = 2380 м/c, k = 1.63098.
Для рассматриваемого уравнения состояния также следует оговорить случай ρ < ρ0. Формально при этом давление не становится отрицательным в отличие от простейших уравнений состояния типа Тэта, поскольку в уравнении состояния существует часть, заимствованная от идеального газа. В этом смысле можно считать до определенного предела, что материал испытывает растяжение до того момента, когда его давление не упадет до нулевого значения или некоторого условного предела, принятого за предел прочности на растяжение [12].
Для численного решения рассматриваемой задачи в силу наличия перемещающихся во времени контактных границ удобно пользоваться подвижной сеткой. В процессе решения использовалась двухшаговая конечно-объемная схема типа предиктор-корректор. При этом параметры на границах ячеек определяются из решения задачи о распаде разрыва с использованием процедуры AUSM+ [13, 14], которая аппроксимирует решение этой задачи с первым порядком точности. Принципиальная идея такой схемы для расчета внутренней баллистики была рассмотрена в работах [5, 9], однако в них используются гораздо более сложные процедуры определения параметров на границах ячеек, а в ряде случаев также и дополнительное расщепление по физическим процессам (так называемая модель «химии в закрытой коробке» [15]). Опыт проведения вычислений показал, что применение этой схемы с определением потоков только при помощи метода AUSM+ приводит к потере устойчивости. Это связано с существованием областей отсутствия гиперболичности системы уравнений (1)–(5), которое доказано в работе [8]. Для компенсации этого эффекта в указанной работе используется расчет потоков по значительно более робастной и диссипативной схеме Русанова первого порядка точности [16]. В то же время исследования показали, что нет необходимости использовать схему Русанова для определения всех потоков – для подавления неустойчивости достаточно использовать её только для нахождения потоков, касающихся конденсированной фазы. В случае интегрирования уравнений, описывающих деформируемый поршень, такой проблемы не возникает, поэтому там применяется только схема AUSM+.
Системы уравнений (1)–(5) и (7)–(9) могут быть представлены векторном виде
![]() .(10)
.(10)
Тогда на этапе предиктора и корректора происходит вычисления разностного решения по следующим формулам, соответственно:
![]() ;
;
![]() .
.
Здесь τn – шаг по времени; ![]() – шаг по
пространству;
– шаг по
пространству; ![]() –
объем ячейки, который вычисляется по формуле для объема усеченного конуса:
–
объем ячейки, который вычисляется по формуле для объема усеченного конуса:
![]() .
.
Потоки f на границах ячеек вычисляются из задачи о распаде разрыва с использованием процедуры AUSM+, а при вычислении потоков в уравнениях (4), (5) и (6) – с использованием схемы Русанова
![]() ,
,
где ![]() – максимальная скорость распространения
возмущений на границе между ячейками.
– максимальная скорость распространения
возмущений на границе между ячейками.
Этот вариант численной схемы на основе приведенной двухфазной модели был опробован на примере расчета классической баллистической установки и показал хорошие результаты при решении тестовой задачи AGARD и сравнении с экспериментальными данными [17].
3. Результаты численных расчетов и их визуализация
В качестве примера рассмотрим возможности разгона малых масс при помощи малокалиберных баллистических установок. Параметры задачи приведены в табл. 1.
Таблица 1. Параметры баллистической установки, используемые для расчета.
|
Параметр |
Значение |
|
Масса метаемого элемента, кг |
0.005; |
|
Масса инерционного поддона, кг |
0.1; |
|
Длина зарядной каморы, мм |
200; |
|
Начальная длина поршня, мм |
70; |
|
Длина пути снаряда в разгонной части ствола, мм |
879; |
|
Калибр разгонной части ствола, мм |
23; |
|
Калибр выходной части ствола, мм |
14; |
|
Длина конфузора, мм |
80; |
|
Марка пороха |
4/7; |
|
Плотность заряжания, кг/м3 |
840. |
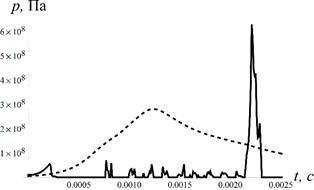
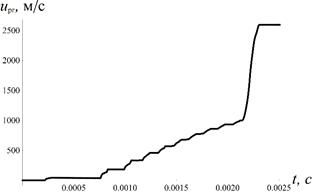
Расчетные зависимости давления пластического поршня на дно снаряда и давления газопороховой смеси на дно канала ствола, а также скорости метаемого тела приведены на рис. 2.
|
|
|
|
а |
б |
|
Рис. 2 Результат решения задачи: а - кривые давления на дно канала (пунктирная линия) и на дно снаряда (сплошная линия); б – скорость снаряда в канале ствола. |
|
Наиболее интересным здесь является процент прироста скорости за счет использования гидродинамического эффекта, который в данном случае составляет 136 % (скорость входа в конус 1100 м/с, дульная скорость 2600 м/с).
Распределение давлений показывает, что на дно канала приходится приблизительно стандартное для порохового выстрела распределение давления (рис. 2а, пунктирная линия) [18]. В то же время, несмотря на то, что давление на дно снаряда характеризуется сильным пиком в районе 2.1 мс, который как раз отражает прохождение снаряда с пластическим поршнем через конический участок ствола, величина этого пика порядка 600 МПа, что является вполне допустимым для современных материалов, используемых в баллистических установках.
Основная особенность класса внутрибаллистических задач состоит в наличии подвижных границ расчетных областей. Это приводит к тому, что любое скалярное поле в координатах x и t ложится на неструктурированую сетку, поскольку для каждого момента времени положение пространственных узлов сетки различно. Это несколько усложняет алгоритмы интерполяции и последующей визуализации результатов расчета. Наиболее информативной в этой ситуации является анимация некоторого скалярного поля во времени, которая демонстрируется на рис. 3 на примере давления.
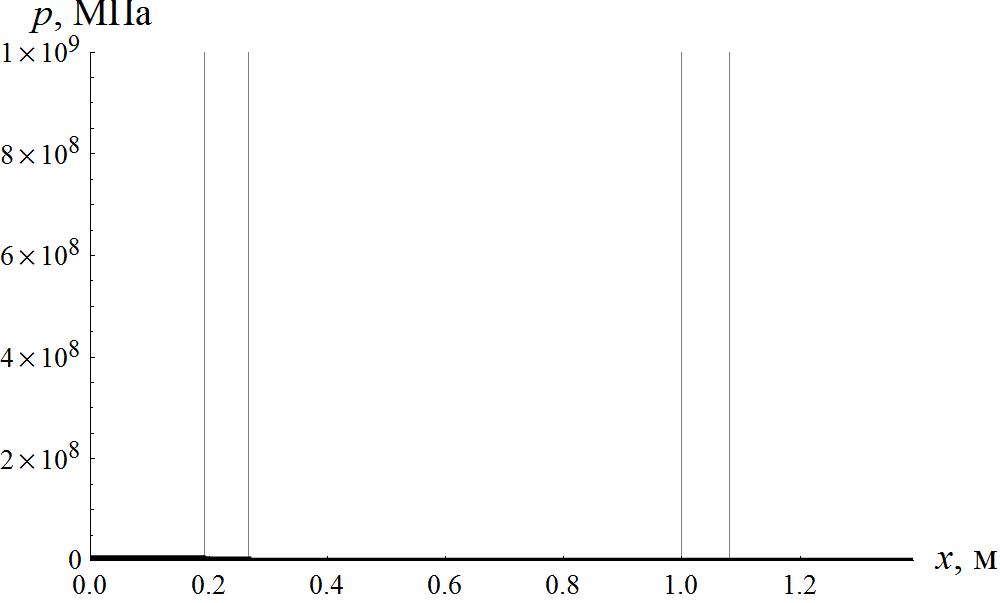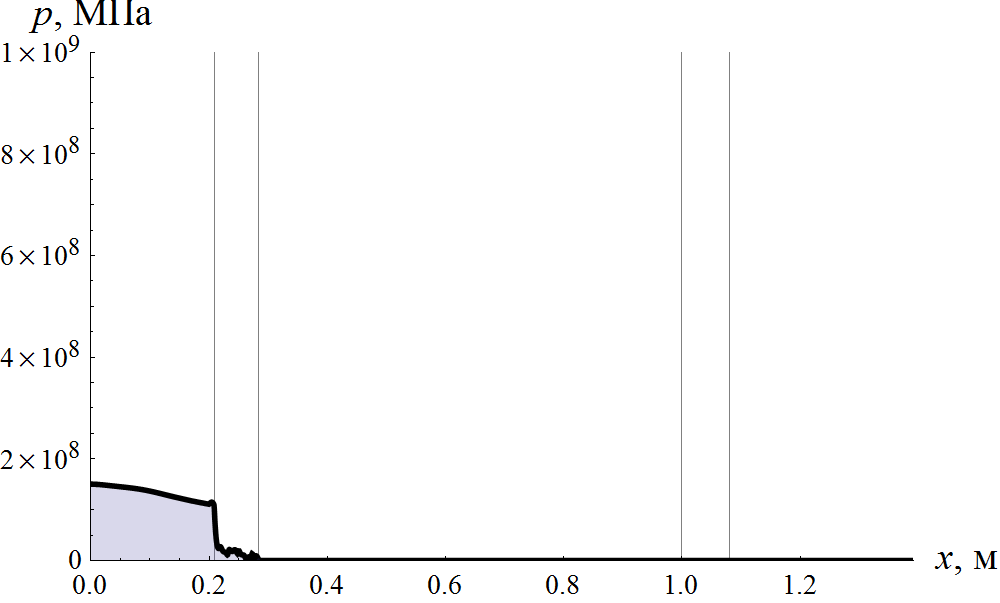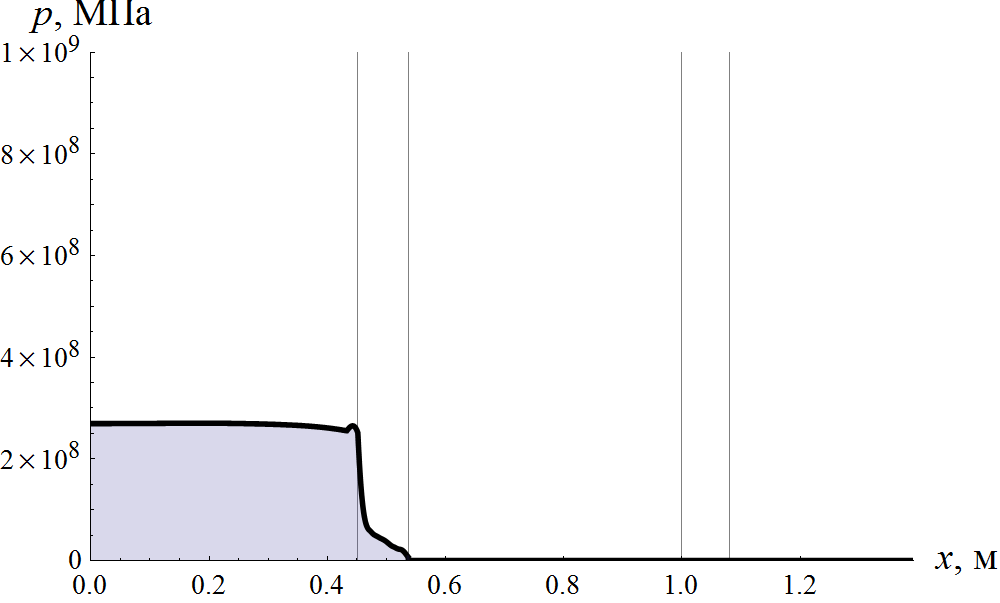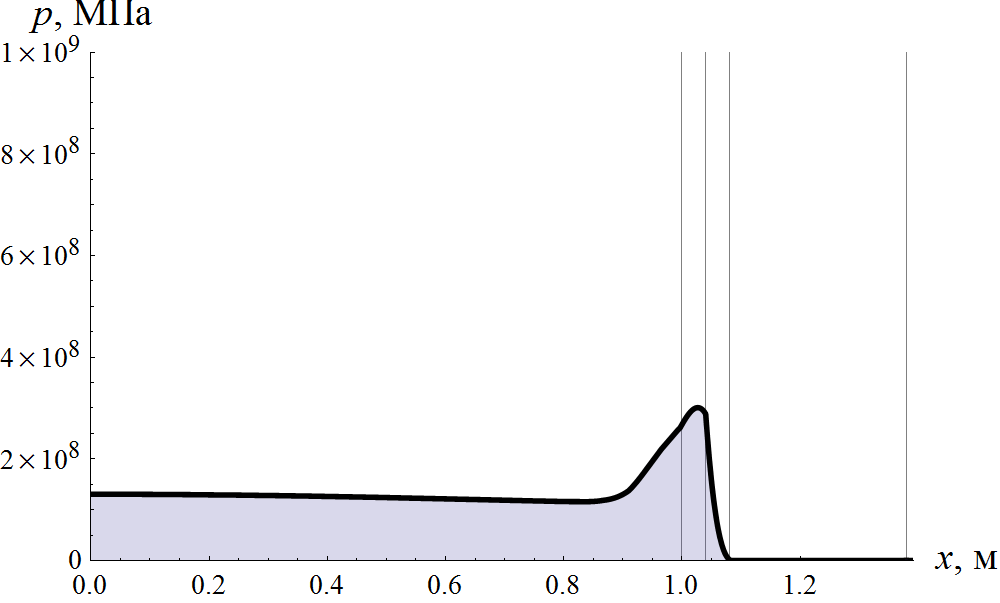
Рис. 3 Анимация поля давления в заснарядном объеме. Вертикальными линиями отмечены границы области деформируемого поршня и конфузора.
Визуализация при помощи анимации позволяет выявить временную эволюцию поля давления и отследить связь между геометрией канала и границами деформируемого поршня. При этом отчетливо виден ход волн между границами расчетных областей, а также резкий рост давления при входе деформируемого поршня в конус. Преимущество анимации перед другими способами визуализации заключается в том, что достаточно хорошо просматривается вся область изменения скалярного поля, в то время как в способе, который будет изложен ниже, видимость той или иной структуры существенно определяется контрастностью. Недостатком такого метода визуализации является необходимость воспроизведения анимации каждый раз для получения данных расчета.
В случае необходимости получения статических распределений наиболее информативны плоские графики распределения скалярных полей в координатах x-t, которые в английской литературе называются density plot. Визуализация результата на неструктурированной сетке требует использования пакетов визуализации, позволяющих работать с такими сетками. Одним из наиболее широко распространенных и простых в использовании пакетов является TecPlot, позволяющий строить неструктурированные данные из простых текстовых файлов после дополнительного проведения операции триангуляции области.
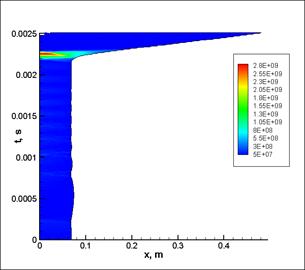
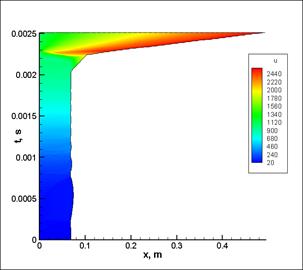
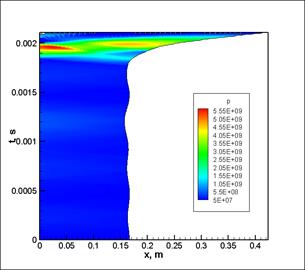
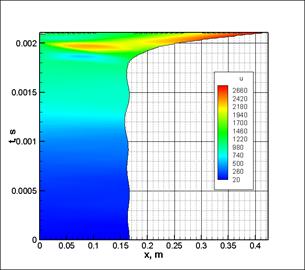
Перейдем к рассмотрению процессов, происходящих внутри деформируемого поршня. На рис. 4 показано распределение давлений и скоростей внутри деформируемого поршня в системе отсчета связанной с левой границей поршня (т.е. с инерционным поддоном).
Видно, что при прохождении конического сопла поршень испытывает значительные растяжения и увеличивает свою длину более чем в пять раз. Это приводит к резкому снижению давления внутри материала поршня после прохождения соответствующего конического участка, поэтому при дальнейшем движении метаемое тело уже не ускоряется поршнем. Из рис. 4а также видно, что максимальное давление достигается преимущественно в левой части поршня, а не на дне снаряда. Последний факт является следствием того, что инерционный поддон испытывает замедление при прохождении деформируемого поршня через конус, которое в результате приводит к локальному повышению давления. Распределение напряжений и скорости внутри поршня зависит от соотношения масс между инерционным поддоном и метаемым телом. В данном случае распределение давлений и скоростей отвечает случаю легкого метаемого элемента и достаточно массивного поддона.
|
|
|
|
а |
б |
|
Рис. 4 Распределение параметров внутри деформируемого поршня в системе отсчета, связанной с инерционным поддоном: а – распределение давления; б – распределение скоростей. |
|
На рис. 5 показаны аналогичные зависимости для случая другого распределения масс, отвечающего более тяжелому метаемому элементу и легкому инерционному поддону (масса метаемого тела 50 г, масса поддона 10 г) при длине поршня 170 мм. В этом случае давление распределено внутри поршня более сложным образом – имеется два участка с высоким давлением.
|
|
|
|
а |
б |
|
Рис. 5 Распределение параметров внутри деформируемого поршня в системе отсчета, связанной с инерционным поддоном: а – распределение давления; б – распределение скоростей. |
|
Визуальное представление позволяет в данном случае выявить распределение давления внутри деформируемого поршня в двух ситуациях. В обоих случаях отчетливо видны периодические изменения границ поршня, что говорит о наличии постоянно отражающихся от них волн сжатия. Наиболее отчетливо на рис. 4 и 5 видна картина изменения давления в поршне при прохождении конического участка. При входе в конус возникает ударная волна, которая отражаясь от метаемого тела, приходит на инерционный поддон. В случае более легкого инерционного поддона волна отражается и возвращается на метаемое тело, что позволяет в итоге получить большую скорость. Для более тяжелого поддона (рис. 4) влияние этой волны незначительно.
Интересно также рассмотреть внутреннюю баллистику легкогазовой установки с деформируемым поршнем, схема которой изображена на рис. 6.
|
|
|
Рис. 6. Схема двухступенчатой легкогазовой пушки |
Такая установка отличается от рассмотренной на рис. 1 наличием области с легким газом, располагающейся между деформируемым поршнем и коническим соплом.
При расчете использовались параметры, приведенные в табл. 2.
Таблица 2. Параметры легкогазовой баллистической установки, используемые в расчете.
|
Параметр |
Значение |
|
Калибр широкой части, мм |
23; |
|
Выходной калибр, мм |
14; |
|
Общая длина ствола, м |
6.5; |
|
Начальная плотность газа, кг/м3 |
250; |
|
Начальное давление газа, МПа |
200; |
|
Длина конического участка, мм |
80; |
|
Масса инерционного поддона между порохом и поршнем, кг |
0.01; |
|
Масса инерционного поддона между поршнем и легким газом, кг |
0.1; |
|
Масса метаемого тела, кг |
0.01; |
|
Длина каморы, м |
0.2; |
|
Длина поршня, м |
0.1; |
|
Длина области с легким газом, м |
0.7; |
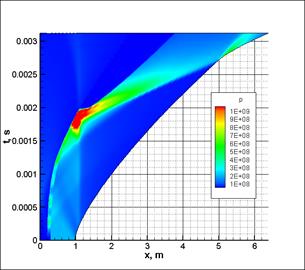
При этом давление форсирования между областью с порохом и поршнем отсутствует, а давление форсирования между областью с газом и снарядом равно 100 МПа. Технически это давление реализуется с помощью разрушающихся диафрагм. В расчете используется сетка {50, 90, 50}. Результаты расчетов показаны на рис. 7.
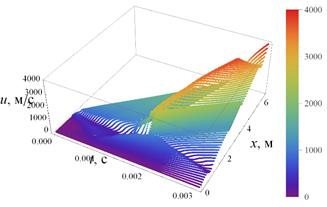
Как видно из полей давлений (рис. 7а) и скоростей (рис. 7б) основное ускоряющее действие, благодаря которому метаемое тело достигает скорости 4000 м/с заключается в действии ударной волны, создаваемой деформируемым поршнем при его прохождении через конический переходник и распространяющейся затем по легкому газу.
|
|
|
|
а |
б |
|
Рис. 7 Распределение параметров в заснарядном объеме легкогазовой баллистической установки: а – распределение давления; б – распределение скоростей. |
|
Отличие рассмотренного случая от традиционных легкогазовых установок состоит в следующем. Обычно в легкогазовых установках предполагается, что деформируемый поршень имеет специальную выемку на передней части, которая уменьшает давление при вхождении в конус, но одновременно снижает гидродинамический эффект. Техническое назначение поршня в легкогазовых пушках заключается в изоляции пороховой области от легкогазовой, что реализуется за счет торможения поршня в конусе. В процессе проведенного моделирования этот фактор не учитывался и после прохождения конуса поршень продолжал движение. Это, однако, не сказывается существенно на скорости метаемого элемента, определяемой исключительно первичной ударной волной, которую, как видно из рис. 7, поршень уже не догоняет.
Визуальное представление численного решения позволяет в данном случае увидеть волновую картину движения газа, места возникновения ударных волн и их влияния на скорость метаемого элемента.
4. Заключение
В результате проведенных исследований была построена математическая модель внутрикамерных процессов при выстреле из баллистической установки с гидродинамическим эффектом. Для решения уравнений модели использовался модифицированный метод конечных объемов с решением задачи о распаде разрыва методами AUSM+ для газовой фазы и деформируемого поршня и Русанова для конденсированной фазы. Анализ полученных результатов проводился путем визуализации на неструктурированной сетке с использованием программы TecPlot, что позволяет дать визуальную трактовку данных полученных с помощью численных расчетов.
Разработанная методика расчета может быть использована для численного исследования и оценки параметров баллистических установок широкого спектра.
Список литературы
1. Croizier W.D., Hume W. High‐Velocity, Light‐Gas Gun // J. Appl. Phys., 1957. Vol. 28, No. 8, P. 892-894.
2. Быков Н.В., Зеленцов В.В., Карнейчик А.С. Баллистическая бикалиберная установка с деформируемым поршнем // Инженерный журнал: наука и инновации. 2013. Вып. 9. URL: http://engjournal.ru/catalog/machin/rocket/945.html. Дата обращения: 20.12.2014.
3. Быков Н.В., Владимиров В.С., Зеленцов В.В. Численное моделирование внутренней баллистики цилиндроконических стволов с использованием пластических снарядов // Наука и образование: электронное научно-техническое издание. М.: МГТУ им. Н.Э. Баумана. 2012. № 3. ISSN 1994-0408. URL http://technomag.bmstu.ru/doc/310721.html. Дата обращения: 20.12.2014.
4. Быков Н.В., Владимиров В.С., Зеленцов В.В. Инженерная методика расчета внутренней баллистики систем высокоскоростного метания // Оборонная техника. 2011. № 8. С. 3‑9.
5. Семенов И.В., Уткин П.С., Ахмедьянов И.Ф., Меньшов И.С. Применение многопроцессорной вычислительной техники для решения задач внутренней баллистики // Вычислительные методы и программирование. 2011. Т. 12. С. 183-193.
6. Gollan R.J. et al. Development of Casbar: a Two-phase Flow Code for the Interior Ballistics Problem // 16th Australasian Fluid Mechanics Conference, Crown Plaza, Gold Coast, Australia, 2-7 December 2007, pp.295-302.
7. Касимов В.З., Ушакова О.В., Хоменко Ю.П. Численное моделирование внутрибаллистических процессов в легкогазовой пушке // ПМТФ. 2003. Т. 44. № 5. С. 13 - 22.
8. Nessbaum J., Helluy P., Herard J.-M., Carriere A. Numerical simulations of gas-particle flows with combustion // Flow, Turbulence and Combustion, 2006. Volume 76, Issue 4, pp 403‑417.
9. Хоменко Ю.П., Ищенко А.Н., Касимов В.З. Математическое моделирование внутрибаллистических процессов в ствольных системах. Новосибирск: Издательство СО РАН, 1999. 256 с.
10. Иоселевич В.А., Пилюгин Н.Н., Чернявский С.Ю. О влиянии трения на движение поршня под действием продуктов горения // ПМТФ, 1978. №5. С. 73-80.
11. Weir C.E. Temperature dependence of compression of linear high polymers of high pressures // J. Res. Nat. Bur. Stand. 1954. V. 53. N. 4. P. 245-252.
12. Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001. 608 с.
13. Liou M. S., Steffen C. J. A new flux splitting scheme // J. of Computational Physics. 1993. Vol. 107. P. 23–39.
14. Wada Y. A flux splitting scheme with high-resolution and robustness for discontinuities. NASA Techn. Memorandum 106452; AIAA-94-0083. 1994.
15. Bogdanoff D. W., Miller R. J. New higher-order Godunov code for modelling performance of two-stage light gas guns. S. l., 1995. (Rep. / NASA; N TM-110363).
16. Русанов В.В. Расчет взаимодействия нестационарных ударных волн с препятствиями // ЖВМиМФ. 1961. Т. 1. №2. С. 267-279.
17. Быков Н.В., Нестеренко Е.А. Анализ и сравнение вычислительных кодов для решения задачи внутренней баллистики на примере тестовой задачи AGARD // Оборонная техника. 2015. № 2. С. 21-36. (в печати)
18. Проектирование ракетных и ствольных систем / Под ред. Б.В. Орлова. М.: Машиностроение, 1974. 828 с.
MATHEMATICAL MODELING AND VISUALIZATION OF INTRACHAMBER PROCESSES IN A BALLISTIC SETUP WITH HYDRODYNAMIC EFFECT
N.V. Bykov(1, 2) , E.A. Nesterenko(1, 3)
1Bauman Moscow State Technical University, Russia
2Dorodnicyn Computing Centre of RAS, Russia
3Keldysh Institute of Applied Mathematics RAS, Russia
bykovnv@bk.ru, nesterenko_ea@bk.ru
Abstract
The questions of mathematical modeling and visualization of the results of intrachamber processes in ballistic systems with hydrodynamic effect numerical calculation were considered. Hydrodynamic effect allows one to receive a higher rate of muzzle velocity by accelerating the deformable piston front as it passes through a tapered conical section. A mathematical model of the shot process, taking into account the two-phase character of gas-powder mixture motion and viscoplastic properties of a deformable piston is constructed. Numerical solution of the problem is carried out using a modified method of Godunov type finite volume on a moving mesh. Since the considered system of equations, describing the intrachamber processes has areas in which it loses its hyperbolicity, in determining of the flow through the cell boundaries two different schemes were used: AUSM+ to calculate the flows of the gas phase and in the field of deformable piston, and Rusanov scheme to calculate the flows in the condensed phase. Due to the use of moving mesh particular attention is given to visualization the numerical calculation results, since the data is located on unstructured grids. Two methods of visualization of the data were considered: the animation of the scalar field and a two-dimensional representation of the density of scalar fields. It is shown that each of the methods has its own advantages and disadvantages.
Keywords: ballistic setup, hydrodynamic effect, Godunov method, moving mesh, unstructured grids.
References
1. Croizier W.D., Hume W. High-Velocity, Light-Gas Gun // J. Appl. Phys., 1957. Vol. 28, No. 8, P. 892-894.
2. Bykov N.V., Zelentsov V.V., Karneychik A.S. Bicaliber ballistic gun mount with the deformable piston // Engineering Journal: science and innovation. 2013. Issue 9. URL: http://engjournal.ru/eng/catalog/machin/rocket/945.html. Date handling: 20.12.2014. [in Russian]
3. Bykov N.V., Vladimirov V.S., Zelentsov V.V. Numerical simulation of cylindrical-conical barrels’ interior ballistics with plastic projectile body // Science and education: electronic science and technology publication. M.: BMSTU. 2012. No. 3. URL: http://technomag.bmstu.ru/en/doc/310721.html. Date handling: 20.12.2014. [in Russian]
4. Bykov N.V., Vladimirov V.S., Zelentsov V.V. Inzhenernaja metodika rascheta vnutrennej ballistiki sistem vysokoskorostnogo metanija [Engineering approach for calculating internal ballistics high-velocity system] // Oboronnaja tehnika. 2011. No. 8. Pp. 3-9. [in Russian]
5. Semenov I.V., Utkin P.S., Ahmed'janov I.F., Men'shov I.S. Primenenie mnogoprocessornoj vychislitel'noj tehniki dlja reshenija zadach vnutrennej ballistiki [Application of high performance computing to the solution of interior ballistics problems] // Numerical methods and programming. 2011. Vol. 12. Pp. 183-193. [in Russian]
6. Gollan R.J. et al. Development of Casbar: a Two-phase Flow Code for the Interior Ballistics Problem // 16th Australasian Fluid Mechanics Conference, Crown Plaza, Gold Coast, Australia, 2-7 December 2007, pp.295-302.
7. Kasimov V.Z., Ushakova O.V., Khomenko Yu.P. Chislennoe modelirovanie vnutriballisticheskih processov v legkogazovoj pushke [Numerical modeling of interior ballistics processes in light gas guns] // Journal of Applied Mechanics and Technical Physics, Vol. 44. No. 5. Pp. 612-619. [in Russian]
8. Nessbaum J., Helluy P., Herard J.-M., Carriere A. Numerical simulations of gas-particle flows with combustion // Flow, Turbulence and Combustion, 2006. Volume 76, Issue 4, pp 403 417.
9. Khomenko Yu. P., Ishchenko A. N., Kasimov V. Z. Matematicheskoe modelirovanie vnutriballisticheskih processov v stvol'nyh sistemah [Mathematical Modeling of Interior Ballistics Processes in Barrel Systems], Izd. Sib. Otd., Ross. Akad. Nauk, Novosibirsk (1999). [in Russian]
10. Ioselevich V.A., Piljugin N.N., Chernjavskij S.Ju. O vlijanii trenija na dvizhenie porshnja pod dejstviem produktov gorenija [On the effect of friction on the motion of the piston under the action of the combustion products] // Journal of Applied Mechanics and Technical Physics, 1978. No. 5. Pp. 73-80. [in Russian]
11. Weir C.E. Temperature dependence of compression of linear high polymers of high pressures // J. Res. Nat. Bur. Stand. 1954. V. 53. N. 4. P. 245-252.
12. Kulikovskij A.G., Pogorelov N.V., Semenov A.Ju. Matematicheskie voprosy chislennogo reshenija giperbolicheskih sistem uravnenij [Mathematical problems of the numerical solution of hyperbolic systems]. M.: Nauka, 2001. 608 p. [in Russian]
13. Liou M. S., Steffen C. J. A new flux splitting scheme // J. of Computational Physics. 1993. Vol. 107. P. 23–39.
14. Wada Y. A flux splitting scheme with high-resolution and robustness for discontinuities. NASA Techn. Memorandum 106452; AIAA-94-0083. 1994.
15. Bogdanoff D. W., Miller R. J. New higher-order Godunov code for modelling performance of two-stage light gas guns. S. l., 1995. (Rep. / NASA; N TM-110363).
16. Rusanov V.V. Raschet vzaimodejstvija nestacionarnyh udarnyh voln s prepjatstvijami [Calculation of interaction of non-steady shock waves with obstacles], J. Computational Mathematics and Mathematical Physics USSR, 1961, vol. 1, pp.267-279. [in Russian]
17. Bykov N.V., Nesterenko E.A. Analysis and comparison of computer codes for solving the problem of internal ballistics on the test problem AGARD // Oboronnaja tehnika. 2015. No. 2. P. 21-36. (in press) [in Russian]
18. Proektirovanie raketnyh i stvol'nyh sistem [Designing rocket and barrel systems] / Ed. by B.V. Orlov. M.: Mechanical Engineering, 1974. 828 p. [in Russian]