В данной статье рассмотрен анализ финансово-экономических показателей ряда кредитных организаций и осуществлено выделение отличающихся кредитных организаций с использованием интерактивного визуального интерфейса. Были взяты данные из открытых источников, рассмотрен этап обработки и улучшения этих данных, а так же их анализ. При проведении такого анализа была использована парадигма так называемой визуальной аналитики. Для анализа был предложен оригинальный алгоритм, по которому была разработана интерактивная программа. Проведен макроанализ и микроанализ исходных данных. Был сделан ряд суждений об отличающихся кредитных организациях.

Ключевые слова: визуальный анализ, анализ кредитных организаций, финансовый анализ, визуальная аналитика.

1. Введение

Исходные табличные данные о деятельности рассматриваемых кредитных организаций представляют собой многомерные данные, где число столбцов n и строк m составляют несколько десятков и несколько сотен соответственно. Каждая строка таблицы соответствует одной из этих организаций и в ней содержатся упорядоченные по столбцам значения соответствующих параметров, характеризующих деятельность этой организации. Эти данные были получены из открытых источников [6], и представляют собой статистические данные, являющиеся результатом мониторинга этих организаций в течение 13 месяцев. Анализ этих данных позволяет получать разнообразную и обильную информацию о деятельности как отдельных, так и групп кредитных организаций.

В данной статье рассматривается интересующая аналитиков информация о схожести (подобии) и различии отдельных строк (и соответствующих кредитных организаций), а также информация об отдельных параметрах рассматриваемых строк.

В рамках данной работы при проведении такого анализа мы использовали парадигму так называемой визуальной аналитики, которая предполагает решение задачи анализа тех или иных данных с использованием способствующего интерактивного визуального интерфейса [1]. Для этого была разработана оригинальная программа интерактивного визуального анализа многомерных данных. Данная программа, реализующая интерактивный геометрико-визуальный интерфейс аналитика с многомерными табличными данными, позволила осуществить эффективный и удобный для человека анализ этих данных, в процессе которого активно используется свойственное ему пространственно-образное мышление, обладающее огромными потенциальными возможностями [2, 3].

2. Характеристика анализируемых данных

Как было указано выше, исходные данные представляют собой многомерные табличные данные, полученные из финансовой отчетности 938 кредитных организаций (Газпромбанк, ВТБ, Дойче Банк и др.), с 47 параметрами (активы нетто, чистая прибыль, вклады физических лиц и др.), за 2013 и 2014 года.

Таблицы были сформированы следующим образом: по строкам располагались кредитные организации, по столбцам параметры организаций. Всего было рассмотрено 13 месяцев и каждому месяцу соответствовала отдельная таблица. Следует отметить, что часть данных отсутствовала, то есть имела место неполнота исходных анализируемых данных.

3. Первичная обработка данных

Первичная обработка данных осуществлялась в несколько этапов, причем это делалось для каждой из 13-ти таблиц. На первом этапе была осуществлена интерполяция недостающих значений по времени, там, где это было возможно. Была выбрана линейная интерполяция. Если для параметра банка и заданы, а не задано , то

Проведенная таким образом интерполяция позволила определить часть не заданных изначально данных. Фрагмент результирующих табличных данных, соответствующих июню месяцу 2014-го года, представлен на рис.1.

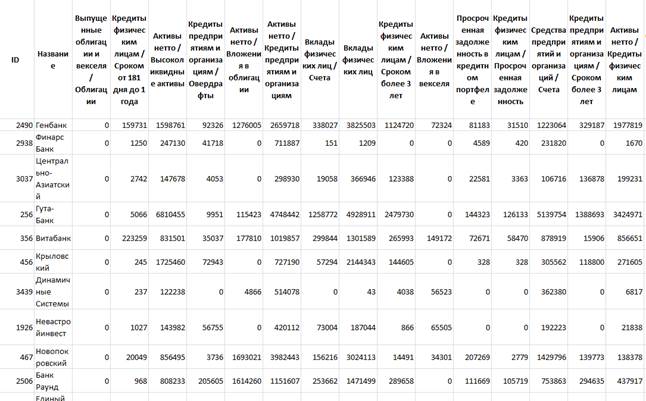
Рис. 1. Фрагмент интерполированных исходных табличных данных

Вторым этапом обработки и восполнения данных являлось окончательное избавление от неполноты исходных данных для всей совокупности 13-ти таблиц. Для этого вычислялся коэффициент полноты для каждой кредитной организации.

где N-количество параметров, T-количество временных срезов (таблиц), а показывает задан ли соответствующий параметр:

Если коэффициент полноты , то все параметры (столбцы таблиц), для которых выполняется , хотя бы для одного t убирались из рассмотрения. Если же параметр , то i-я кредитная организация убиралась из рассмотрения.

Третий этап заключался в уменьшении количества кредитных организаций для последующего анализа. Было принято решение убрать все кредитные организации, параметр «капитал» которых равен нулю. В результате получены таблицы, содержащие 40 столбцов и 81 строку.

Четвертый этап обработки и восполнения данных заключался в удалении (для каждой из 13-ти рассматриваемых таблиц) параметров, которые не являлись интегральными. Так, например, были удалены параметры «активы нетто основные средства и нематериальные активы», «активы нетто, выданные МБК», т.к. они включены в интегральный параметр «активы нетто».

Последней операцией обработки и восполнения данных была их нормализация и сведение к промежутку [0;100].

Фрагмент результирующих табличных данных, соответствующих июню месяцу 2014-го года, представлен на рис.2.

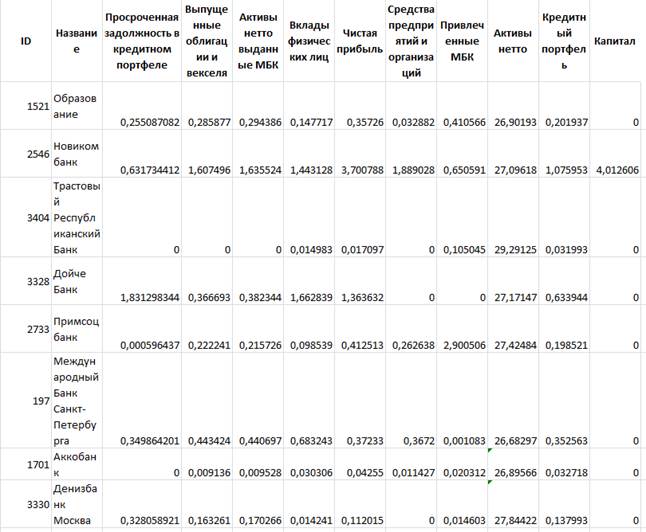
Рис. 2. Фрагмент данных, полученных на четвертом этапе обработки и восполнения данных

Таким образом, в результате выполнения первичной обработки были получены табличные данные, меньшей размерности по сравнению с исходными, включающие 81 строку и 9 столбцов в каждой из 13-ти таблиц. Эти табличные данные в дальнейшем подвергались процедуре анализа.

4. Постановка задачи анализа отфильтрованных данных

Как было отмечено выше, авторов в процессе анализа интересовала информация о схожести (подобии) отдельных строк (и соответствующих кредитных организаций), а также информация об отдельных параметрах схожих строк. При этом в качестве таких строк использовались строки 13-ти таблиц отфильтрованных данных. В качестве количественного критерия различия введем меру различия кредитных организаций:

где — кредитные организации — их параметры, а изменяется от 1 до 9

Для решения поставленной задачи проводится геометрическая интерпретация. Кредитным организациям (строкам таблицы) были поставлены в соответствие многомерные точки, а параметрам организаций — координаты этих многомерных точек. Мера различия кредитных организаций соответственно интерпретировалась как евклидово расстояние между точками многомерного пространства (чем больше расстояние, тем больше различаются организации). При такой интерпретации, задаче анализа схожести и различия кредитных организаций ставилась в соответствие задача анализа расстояния между точками n-мерного пространства.

Для анализа расстояния между точками n-мерного пространства использовалось визуальное отображение этих точек. В начале осуществлялось проецирование исходного множества точек на одно из трехмерных пространств. При этом:

Многомерная точка 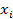проецировалась в сферу .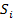
Если расстояние между точками n-мерного пространства 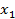и 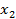меньше заданного d, то строился цилиндр, соединяющий сферы 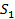и .
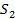Цвет цилиндра моделировал расстояние между точкам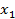и и 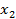от красного (малое расстояния) до синего (большое расстояние).

Затем выполнялось графическое проецирование сфер и цилиндров на картинную плоскость с последующим их визуальным анализом.

Результирующая совокупность сфер и цилиндров образовывала так называемую пространственную сцену с заданной геометрией и оптическими (цветовыми) характеристиками.

Таким образом, визуальный анализ пространственной сцены позволял судить о расстоянии между исходными многомерными точками. В процессе решения задачи анализа предлагалось задание в начале исходного большого значения d, а затем проводить его уменьшение и выделять подмножества многомерных точек в зависимости от получаемого изображения на картинной плоскости.

В зависимости от расстояния между точками и параметра d, изменяемого во время анализа, можно визуально выделять следующие подмножества многомерных точек:

Кластер — подмножество, при заданном множестве точек, попарное расстояние между которыми не превышает заданное d, а расстояние между точками кластера и остальными точками не меньше заданного d.

Удаленная (одиночная) точка — точка, удаленная от всех остальных точек исходного множества на расстояние, большее заданного d.

Сгусток — подмножество точек, большая часть расстояний между которыми не превышает заданное d.

Квазиудаленная (Квазиодиночная) точка — точка, не являющаяся удаленной, но и не входящая в сгусток или кластер при заданном разбиении.

Отметим, что выделение сгустков и квазиудаленных точек осуществляется человеком в процессе решения указанной выше задачи анализа.

5. Характеристика используемого программного средства

Для решения указанной выше задачи анализа расстояния между точками n-мерного пространства был предложен интерактивный алгоритм, блок-схема которого представлена на рис. 3.

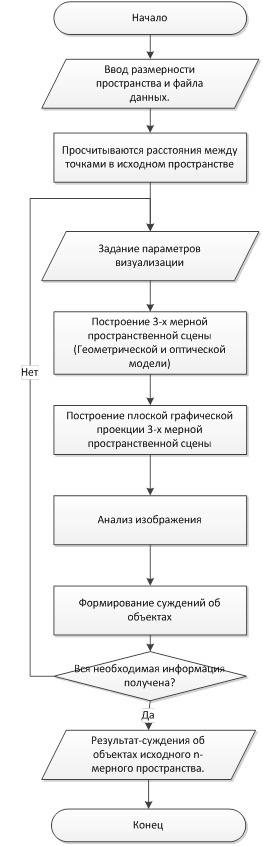
Рис.3. Блок-схема интерактивного алгоритма

Алгоритм предусматривает взаимодействие аналитика и компьютера. Предлагается следующее распределение функций между ними:

- компьютер в процессе решения задачи анализа расстояния между многомерными точками осуществляет функции расчета расстояний, построения проекций и графиков зависимости координат от времени;

- аналитик, осуществляет зрительное восприятие проекционного изображения на мониторе, анализирует взаимное расположение многомерных точек, выделяет подмножества и задает параметры визуализации.

Для реализации данного алгоритма была разработана соответствующая интерактивная программа. Данная программа была реализована на базе программного продукта Autodesk 3ds Max, с использованием внутреннего интерпретируемого языка maxscript. Так же использовалась библиотека, написанная на языке C# в Visual studio 2013 [4, 5].

Эта программа позволяет аналитику совершать следующие действия:

Ввод исходных данных.

Осуществляется один раз и в дальнейшем эти данные используются.

Визуализация исходных данных

Графическое проецирование выполняется в стандартном окне 3ds Max с помощью стандартного рендерера.

Получение информации о точках

Информацию о точках можно получать в виде таблицы, строки которой соответствуют каждой из отображаемых точек, а столбцы — их координатам. При этом, строки таблицы закрашены тем цветом, которым закрашены точки, т.е. в зависимости от цвета можно определять к какому подмножеству относится данная точка. Данные таблицы можно получать для каждого рассматриваемого момента времени.

Измерение расстояния (в исходном n-мерном пространстве) между двумя точками;
Задание параметров визуализации;

Параметрами визуализации является радиус сфер, поставленных в соответствие исходным точкам, их цвет, радиус цилиндров и трехмерное проекционное пространство. Данные параметры можно изменять, предполагается задание данных параметров при начале работы.

Использование стандартных средств 3ds Max для работы с пространственной сценой. Так, например, есть возможность использовать следующие средства:

а) Аффинные преобразования сцены;

б) Наложение разнообразных фильтров на изображение;

в) Преобразование оптических характеристик сцены;

Объединение точек в подмножество

Каждому подмножеству задается цвет, который в дальнейшем будет обозначать данное подмножество во время функционирования программы.

Построение плоских графических проекций многомерных точек

При микроанализе, а именно анализе удаленных точек, важным является то, какие именно координаты вносят больший вклад в расстояние — происходит ли это за счет всех координат или за счет большого отличия только нескольких координат. Для определения этого, предлагается строить графические проекции исходного множества на плоскости (x_i,x_i) и, меняя i, просмотривать все такие проекции.

Построение графиков зависимости координат точек от времени.

6. Проведение анализа.

6.1. Макроанализ

Под макроанализом в данной работе понимается разбиение исходного множества точек на подмножества с конечной целью выделения подмножества удаленных точек. Алгоритм работы с программным средством предполагает задание исходного значения d большим, а затем уменьшение параметра d и выделение удаленных точек.

Рассмотрим пример решения задачи макроанализа для случая заданной 81 многомерной точки в 9-мерном пространстве. В качестве трехмерного пространства, на которое осуществлялось проецирование многомерных точек, было выбрано пространство

Рис.4. Графическая проекция пространственной сцены при

На рис. 4 представлено графическое проекционное изображение пространственной сцены при . Видно, что все сферы соединены между собой и, значит, соответствующие им многомерные точки образовали кластер. Это значение d будет использоваться в качестве исходного и в дальнейшем его необходимо будет уменьшать.

Рис.5. Графическая проекция пространственной сцены при

На рис. 5 представлено графическое проекционное изображение пространственной сцены при d=120. Видно, что две сферы отсоединились от остальных и соответствующие им две многомерные точки образовали второй кластер. Судя по цвету цилиндра, близкому к ярко-синему, расстояние между этими точками близко к d. Отметим их синим цветом.

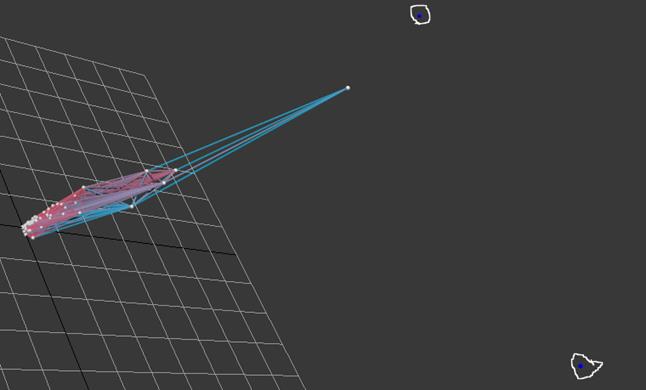
Рис. 6. Графическая проекция пространственной сцены при

На рис. 6 представлено графическое проекционное изображение пространственной сцены при . Две синие сферы обведены белым цветом. Цилиндрическая связь между ними пропала, а значит расстояние между соответствующими им точками больше 100. При этом d точки стали удаленными. Данные точки не будут влиять на дальнейший ход макроанализа. Исходя из цвета цилиндрических связей остального множества, можно сделать вывод, что одна из точек является квазиудаленной и, очевидно, при небольшом изменении d станет удаленной.

Рис.7. Графическая проекция пространственной сцены при

На рис. 7 показано графическое проекционное изображение пространственной сцены при . Получившуюся при этом d сферу, соответствующую удаленной точке, отметим голубым цветом (она обведена белым цветом). Данная точка не будет влиять на последующее разбиение множества точек на подмножества.

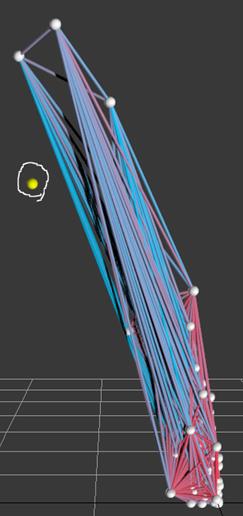
Рис.8. Графическая проекция пространственной сцены при

При уменьшении , отделяется ещё одна сфера, которая отмечена желтым цветом. На рис. 8 представлено проекционное изображение пространственной сцены при данном d, а сфера обведена белым цветом

При продолжении анализа аналогичным образом, можно выделить последующие отделяющиеся сферы, соответсвующие удаленным многомерным точкам.

Таблица 1. Зависимость d и цвета сфер для удаленных многомерных точек.

d при котором произошло изменение	Цвет отделяемых сфер удаленных многомерных точек
34.5	Зеленый
34	Розовый
26.3	Красный

В таблице 1 представлены некоторые последующие значения параметра d, при которых произошло образование удаленных многомерных точек.

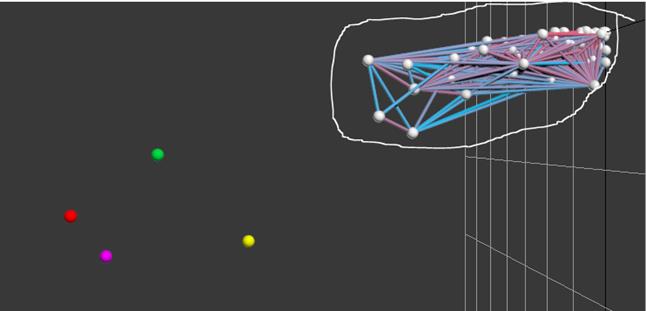
Рис.9. Графическая пространственная сцена при

На рис. 9 представлена пространственная сцена при .

В процессе макроанализа было выделено 7 удаленных многомерных точек при изменении d в диапазоне от 200 до 26.

При значении d=26, в рамках рассматриваемого примера, было решено прекратить последующий анализ. Однако можно было бы продолжить уменьшение d и выделение соответствующих удаленных точек.

В общем случае, конечное значение d выбирается аналитиком в соответствии с имеющейся у него информацией о конкретной решаемой им задаче анализа.

6.2. Микроанализ

Микроанализ заключался в покоординатном сравнении удаленных точек, выделенных в процессе решения задачи макроанализа.

6.2.1. Плоские графические проекции многомерных точек

При построении плоской графической проекции многомерной точки, можно оценить вклад координаты в расстояние между этой точкой и остальными многомерными точками, чтобы узнать — вызвано ли удаление точки от основного множества большим значением какой то одной или нескольких координат, или же оно вызвано большими значениями всех координат рассматриваемой многомерной точки.

Построению такой проекции совокупности рассматриваемых многомерных точек предшествовало проецирование этих многомерных точек на трехмерное пространство так, что многомерным точкам ставились в соответствие сферы, которым задавались цвета, ранее закрепленные нами за многомерным точкам в процессе решения задачи макроанализа.

Рис. 10. Графическая проекция , по которой можно судить о вкладе координаты (прощенная задолжность в кредитном портефеле) в расстояние между удаленными точками и точками сгустка

В рамках рассматриваемого примера анализа взаимного расположения 81-ой многомерных точек в 9-мерном пространстве, на рис. 10 представлена графическая проекция на плоскость всех многомерных точек, в том числе 7-и ранее найденных удаленных точек (выделены белым). На этой проекции видно, что соответствующие этим точкам 7 сфер отходят от основного сгустка, но одна из сфер (ID=1000) находится в удалении от всех остальных. Это значит, что данная координата вносит большой вклад в расстояние между этой многомерной точкой и всеми остальными.

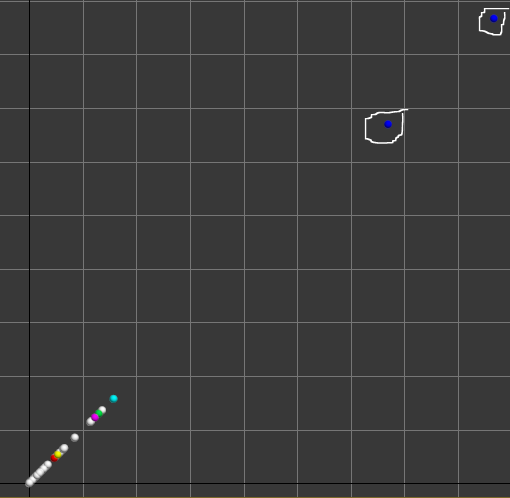
Рис. 11. Графическая проекция , по которой можно судить о вкладе координаты (чистая прибыль) в расстояние между удаленными точками и точками сгустка

На рис. 11 представлена графическая проекция всех многомерных точек на плоскость . На данной проекции видно, что координата не вносит большого вклада в расстояния для всех точек, кроме двух, которым соответствуют две синие сферы (отмечены белым на рисунке).

Рис. 12. Графическая проекция , по которой можно судить о вкладе координаты (активы нетто) в расстояние между удаленными точками и точками сгустка

На рис. 12 представлена графическая проекция всех многомерных точек на плоскость . На этой проекции все сферы, соответствующие удаленным точкам, находятся в тех же квадратах, что и сферы, соответствующие точкам основного сгустка, а значит, данная координата практически ничего не вносит в расстояние между точками.

6.2.2. Анализ зависимости координат многомерных точек от времени

Для анализа зависимости координат точек от времени используются традиционные графики зависимости координаты от времени. Единицей измерения времени на этих графиках выбран один месяц.

Первым шагом необходимо выбрать, какие точки отображать на графике (таблица слева), а затем выбрать координату, которую мы хотим проанализировать.

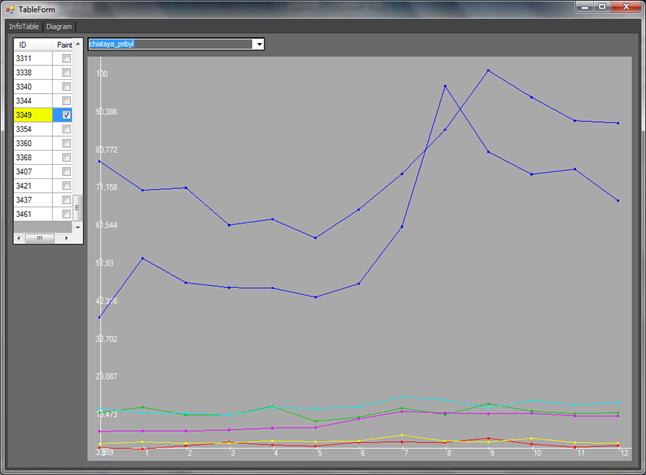
Рис. 12. График зависимости координаты (чистая прибыль) от времени для всех удаленных точек

На рис. 12 показан график зависимости координаты от времени для удаленных точек. По данному графику можно увидеть, что у обеих синих точек есть пик значения в моменты времени T=7 и T=8. Во время этих пиков, значения координат увеличивается приблизительно на 15-20 единиц (20-40%). После этого идет некоторое уменьшение значения.

Остальные точки на этом графике трудно анализировать, т.к. их значения координаты значительно меньше двух синих точек, поэтому был построен дополнительный укрупненный график зависимости координат от времени только этих точек.

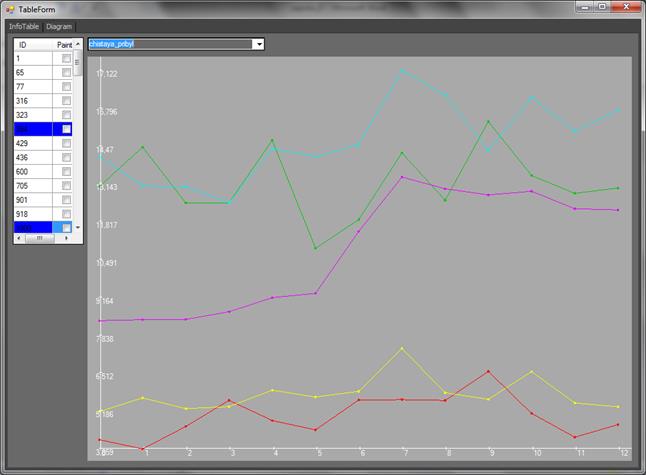
Рис. 13. График зависимости координаты (чистая прибыль) от времени для удаленных точек с небольшим значением этой координаты

На рис. 13 представлен график зависимости координаты от времени для удаленных точек с небольшим значением этой координаты. У всех точек (кроме красной) в момент времени T=7 происходит увеличение этой координаты, так же, как и у предыдущих, на 10-15%.

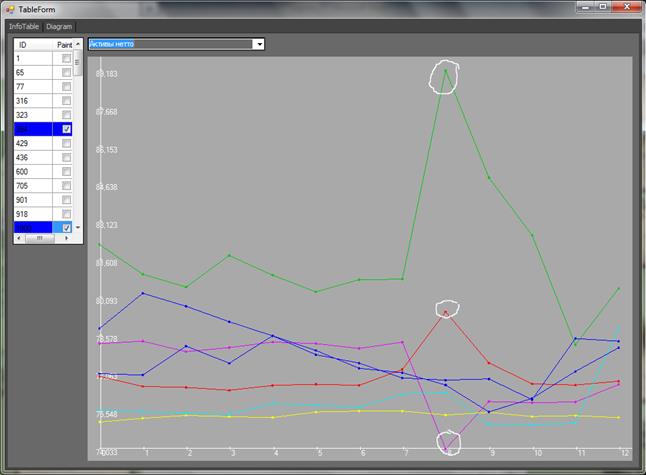
Рис. 14. График зависимости координаты (активы нетто) от времени для всех удаленных точек

На рис. 14 представлен график зависимости координаты от времени для всех удаленных точек. У красной и зеленой точек есть пик значения в момент времени T=, в тот же момент времени у фиолетовой точки происходит уменьшение значения данной координаты.

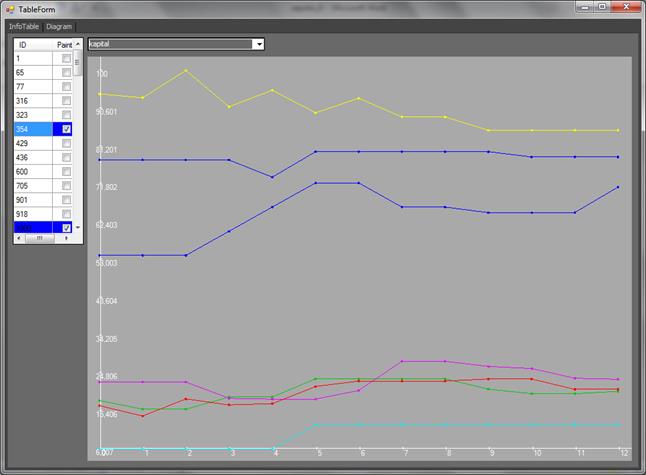
Рис. 15. График зависимости координаты (капитал) от времени для всех удаленных точек

На рис. 15 представлен график зависимости координаты от времени для всех удаленных точек. У синей точки с ID=354 значение координаты значительно изменяется на рассматриваемом промежутке времени в интервале от , а у желтой точки ID=3349 происходят колебания с одновременным уменьшением значения рассматриваемой координаты с 100 единиц (T=2) до 85 (T=12).

6.3. Результаты анализа

В рассматриваемом примере в процессе решения задачи анализа в целом (макроанализ и микроанализ):

Выделено 7 удаленных точек (отличающихся кредитных организаций)

Таблица 2. Соответствие кредитных организаций и удаленных точек.

Название	ID	Цвет
Газпромбанк	354	Синий
ВТБ	1000	Синий
Альфа-Банк	1326	Зеленый
ВТБ 24	1623	Розовый
ФК Открытие (бывш. НОМОС-Банк)	2209	Красный
Банк Москвы	2748	Голубой
Россельхозбанк	3349	Желтый

2. Проведен покоординатный сравнительный анализ удаленных точек (кредитных организаций, существенно отличающихся от остальных).

В результате этого сравнения можно сформулировать следующие суждения:

а) Кредитные организации, которые существенно отличаются от остальных, различаются по прощеным задолженностям в кредитном портфеле (рис. 10) и чистой прибыли (рис. 11), однако близки по активам нетто (рис. 12).

б) В моменты времени T=7, T=8 (соответствующие окончанию января и февраля 2014-го года) происходило возрастание чистой прибыли (рис. 12 и рис. 13)

в) У зеленой точки (ID=1326, Альфа-Банк) и красной точки (ID=2209, ФК Открытие) происходило сильное увеличение активов нетто, а у розовой точки (ID=1623, ВТБ 24), наоборот, снижение активов нетто к моменту времени T=8 (окончание февраля 2014-го года) (рис. 14).

г) В течение всего промежутка времени капитал у рассматриваемых точек (кредитных организаций) практически не изменялся (рис. 15)

Перечисленные выше суждения представляют собой предварительные результаты анализа кредитных организаций в рамках рассматриваемого примера. Дополнительные суждения аналитику можно было бы получить с использованием имеющейся у него дополнительной информации о конкретной решаемой им задаче анализа, учитывающей специфику деятельности кредитных организаций.

7. Заключение

Таким образом, в рамках данной работы был проведен анализ многомерных данных о деятельности ряда кредитных организаций. Решение задачи анализа было осуществлено с использованием современной парадигмы так называемой визуальной аналитики.

Соответственно была разработана оригинальная программа интерактивного визуального анализа многомерных данных. Данная программа, реализующая интерактивный геометрико-визуальный интерфейс аналитика с многомерными табличными данными, позволила осуществить эффективный и удобный для человека анализ этих данных.

Вначале исходные табличные данные подверглись обработке (фильтрации) с целью снижения их размерности.

Введены в рассмотрение задачи макроанализа и микроанализа отфильтрованных данных решение которых было проиллюстрировано в рамках конкретного примера.

В результате был сформулирован ряд предварительных суждений о деятельности рассматриваемых кредитных организаций. Было отмечено, что дополнительные суждения можно было бы получить с использованием имеющейся у аналитика дополнительной информации о конкретной решаемой задаче анализа, учитывающей специфику деятельности кредитных организаций.

Используемая литература

Thomas J., Cook K. Cook, Illuminating the Path: Research and Development Agenda for Visual Analytics. IEEE-Press, 2005. — p. 184
Масленников О.П., Мильман И.Е., Сафиуллин А.Э., Бондарев А.Е., Низаметдинов Ш.У., Пилюгин В.В. Интерактивный визуальный анализ многомерных данных // ГрафиКон’2014: 24-я Международная конференция по компьютерной графике и зрению: Ростов-на-Дону, Академия архитектуры и искусств ЮФУ Труды конференции. – с. 51 – 54.
Масленников О.П., Мильман И.Е., Сафиуллин А.Э., Бондарев А.Е., Низаметдинов Ш.У., Пилюгин В.В. Разработка системы интерактивного визуального анализа многомерных данных / Научная визуализация. Т.6, № 4, с.30-49, 2014, URL: http://sv-journal.org/2014-4/082139.html (Действительно на 07.02.2015)
MaxScript Help. Доступно по адресу (Действительно на 07.02.2015): http://docs.autodesk.com/3DSMAX/15/ENU/MAXScript-Help/index.html
Visual C#. Доступно по адресу (действительно на 07.02.2015): https://msdn.microsoft.com/ru-ru/library/kx37x362.aspx
http://Banki.ru (действительно на 07.02.2015)
Загоруйко Н.Г. Прикладные методы анализа данных и знаний.- Новосибирск: ИМ СО РАН, 1999, 270 с.

Data analysis of credit organizations by means of interactive visual analysis of multidimensional data.

I.E.Milman¹, A.P.Pakhomov¹, V.V.Pilyugin¹, E.E.Pisarchik¹, A.A.Stepanov², Yu.M.Beketnova², A.S.Denisenko¹, Ya.A. Fomin¹

igalush@gmail.com, sinrayasy@gmail.com, VVPilyugin@mephi.ru, episarchik@yahoo.com, beketnova@mail.ru

¹National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Moscow, Russia

²Federal Financial Monitoring Service (Rosfinmonitoring), Moscow, Russia

Abstract

In this article, analysis of financial and economic indexes of a number of credit organizations have been observed and picked out some different credit organizations using interactive visual interface. Data were collected from open sources, stage of processing and improvement data were considered as well as its analysis. In conducting this analysis, the so-called visual analytics paradigm has been used. For the analysis was proposed original algorithm, which was the base for developing an interactive program. Macroanalysis and microanalysis of the source data have been done. A number of judgments about the different credit organizations have been made.

Keywords: visual analysis, analysis of credit institutions, financial analysis, visual analytics.

References

1. Thomas J., Cook K. Cook, Illuminating the Path: Research and Development Agenda for Visual Analytics. IEEE-Press, 2005. — p. 184

2. Maslennikov O.P., Milman I.E., Safiullin A.E., Bondarev A.E., Nizametdinov Sh.U., Pilyugin V.V. Interaktivny vizualny analiz mnogomernykh dannykh [Interactive visual analysis of multidimensional data]// GraphiKon'2014: 24th International conference on computer graphics and vision: Rostov-on-Don, the SFU Academy of architecture and arts, Conference materials. - p. 51-54 (in Russian)

3. Maslennikov O.P., Milman I.E., Safiullin A.E., Bondarev A.E., Nizametdinov Sh.U., Pilyugin V.V. Razrabotka sistemy interaktivnogo vizualnogo analiza mnogomernykh dannykh [Development of a system for analyzing multidimensional data/ Scientific visualization. V.6, # 4, p. 30-49, 2014, URL: http://sv-journal.org/2014-4/089ed2.html (available as of February, 7, 2015)

4. MaxScript Help. See http://docs.autodesk.com/3DSMAX/15/ENU/MAXScript-Help/index.html (Available as of February, 7, 2015):

5. Visual C#. See https://msdn.microsoft.com/ru-ru/library/kx37x362.aspx(Available as of February, 7, 2015)

6. http://Banki.ru

7. Zagorujko N.G. Prikladnye metody analiza dannyh i znanij [Applied methods of data and knowledge analysis] – Novosibirsk, 1999. – 270 p