ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ И ВИЗУАЛИЗАЦИЯ ДАННЫХ МОДЕЛИРОВАНИЯ В КВАЗИКЛЕТОЧНЫХ СЕТЯХ

А.О.АРИСТОВ

Национальный исследовательский технологический университет «МИСиС», Россия

Оглавление

1. Введение

2. Общие сведения о квазиклеточных сетях

3. Визуализация состояния квазиклеточных сетей

4. Визуализация аддитивных параметров

5. Построение тепловых карт

6. Заключение

Список литературы

Аннотация

Рассмотрены вопросы применения нового типа дискретных структур – квазиклеточных сетей в задачах визуализации результатов моделирования. Квазиклеточные сети позволяют в рамках единой структуры моделировать на микро- и макроуровне системы, для которых характерно распространение потоков в ограниченном пространстве. Рассматривается визуализация состояния квазиклеточной сети, визуализации аддитивных параметров, построения тепловых карт.

Ключевые слова: квазиклеточная сеть, потоки, циркуляция, визуализация, состояние, система частиц, тепловая карта

1. Введение

Автором предложен новый тип динамических дискретных структур – квазиклеточные сети[1]. Квазиклеточные сети предназначены для моделирования систем, для которых характерно распространение потоков в ограниченном пространстве. Наряду с возможностями квазиклеточных сетей осуществлять микро- и макромоделирование системы в рамках единой структуры, они позволяют осуществлять визуализацию результатов моделирования на этих уровнях. В рамках данной работы рассмотрим три направления визуализации данных в квазиклеточных сетях – визуализацию состояния квазиклеточной сети, визуализацию макропараметров и построение тепловых карт.

2. Общие сведения о квазиклеточных сетях

Определение 1. Квазиклеточной сетью называется дискретная структура, включающая в себя множество круговых областей в двухмерном пространстве (или сферических в трёхмерном пространстве), имеющих радиус R (рис. 1), каждая из которых взвешена соответственно элементами из множеств , . Тогда для каждойнайдётся такая(, , ), что система уравнений:

(1)

имеет хотя бы одно решение[1].

Область, определяемую элементом множества называется элементом квазиклеточной сети, областью или клеткой.

Фактически, каждый элемент квазиклеточной сети — это вектор, задающий область пространства в виде. Радиус R является топологической характеристикой квазиклеточной сети, т. е.:

(2)

Расширим каждый элементом , характеризующим состояние каждой клетки :

(3)

где - фазовые переменные[1].

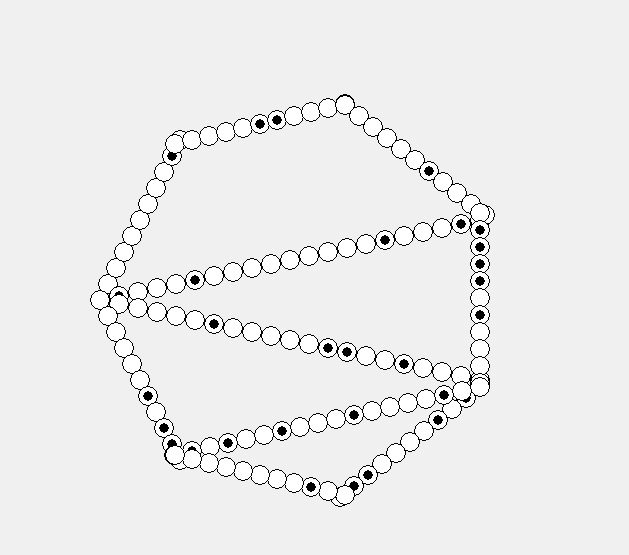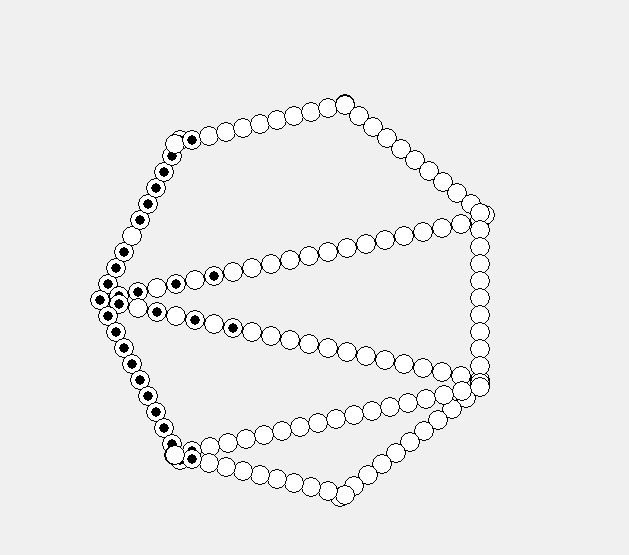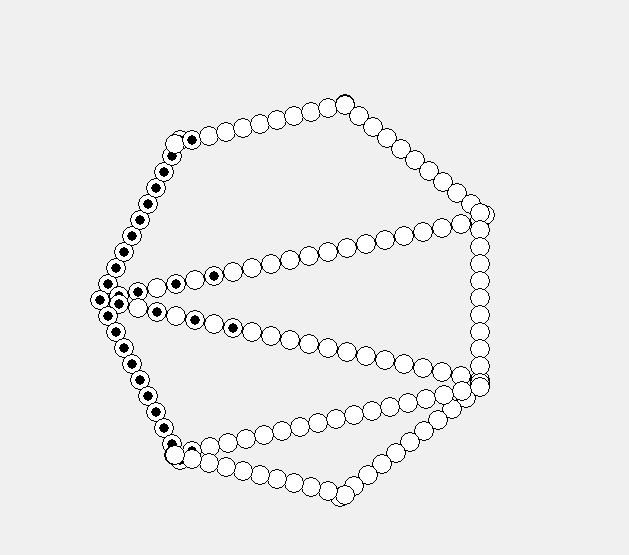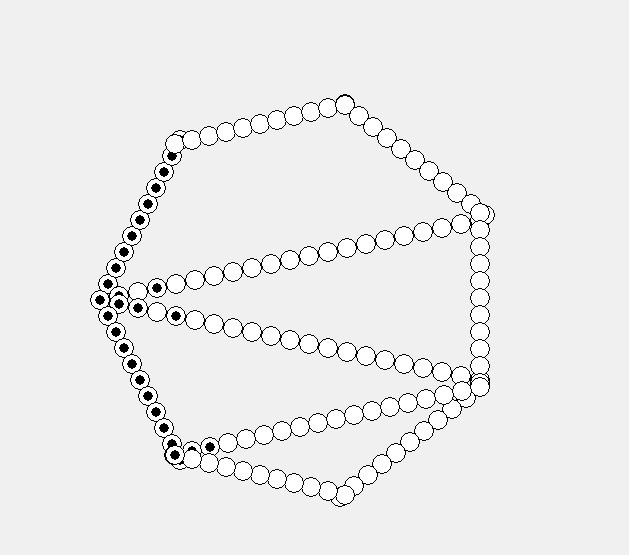
Функционирование квазиклеточных сетей тесно связано с понятием циркуляции[2], т.е. передачи состояния между соседними клетками (рис. 2). Пример циркуляции в квазиклеточной сети представлен на рис. 3.

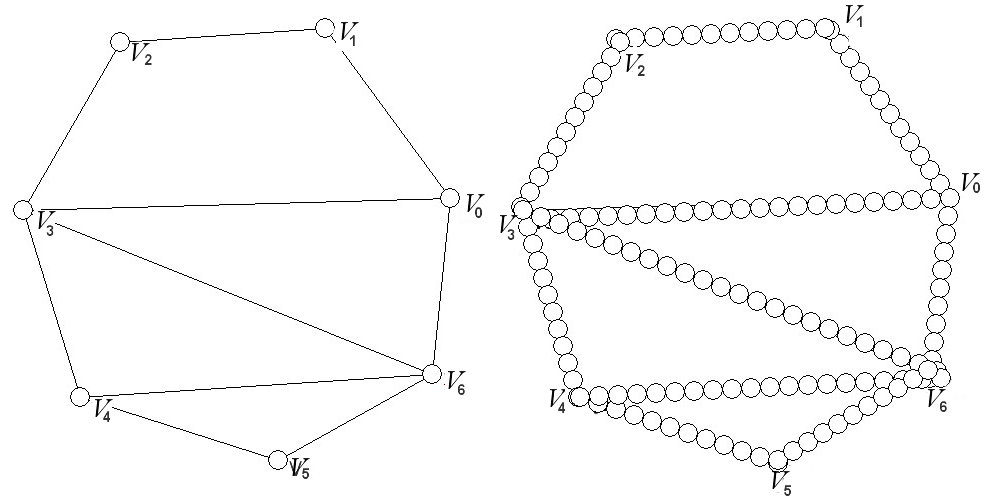
Рис. 1. Базовый граф и построенная на его основе квазиклеточная сеть

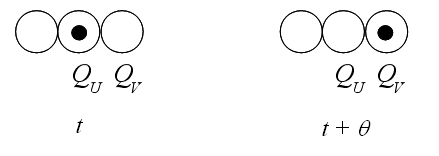
Рис. 2. Переход бинарного состояния между клетками

Определение 2. Циркуляцией в квазиклеточной сети называются изменения состояний клеток, вида

(4)

при , где для и справедливо

(5)


a	б

Рис. 3. Примеры циркуляции в квазиклеточной сети

а — случайная, б – направленная

Выше отмечено, что состояние клетки задаётся множеством фазовых переменных. Для интуитивно понятного представления о передаче состояния и циркуляции, автором рассматриваются[1,3] бинарные квазиклеточные сети, для которых, т.е. . Подобное состояние удобнее всего представить наличием фишки в клетке, по аналогии с сетями Петри. Следует однако отметить ряд отличий квазиклеточных сетей от сетей Петри. Фишки в сетях Петри, определяют состояние позиций. Каждая позиция моделирует состояние системы, а фишка показывает нахождение системы в этом состоянии. В квазиклеточной сети (в рассматриваемой постановке) – клетка – область пространства, фишка – микрообъект в области пространства. В сетях Петри предусмотрены запускаемые переходы, не предусмотрено модельное время (не считая расширенные сети Петри). В отличие от этого, в квазиклеточных сетях нет запускаемых переходов, а есть постоянная циркуляция. Следует также отметить, что сетей Петри и квазиклеточные сети предполагают принципиально разные подходы к моделированию. В сетях Петри предусмотрен дискретно-событийный, тогда как квазиклеточные сети предполагают имитационное моделирование (временной подход).

Отличительной особенностью квазиклеточных сетей является отсутствие явно заданной сигнатуры. Квазиклеточная сеть образована областями пространства (клетками). Расположение клеток в пространстве позволяют определить различные методы синтеза квазиклеточных сетей[2]. На этапе синтеза достаточно хорошо заметна связь квазиклеточных сетей с другими дискретными структурами. В случае синтеза квазиклеточных сетей методом базового графа[1], графовая макромодель фактически приобретает свойства динамической дискретной структуры (см. рис. 1). Синтез методом битого клеточного автомата предполагает использование в структуре квазиклеточной сети клеток из подмножества элементов клеточного автомата (рис. 4). Метод синтезирующей фишки основан на формировании элементов квазиклеточной сети, расположенных вдоль траектории движения некоторого микрообъекта [2]. Исходя из этого, видно, что квазиклеточные сети обладают некоторыми сходствами с теоретико-графовыми моделями, сетями Петри, моделями потоков в сетях, клеточными автоматами и др.

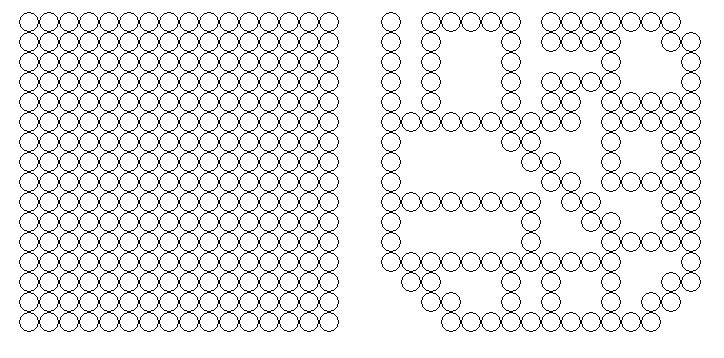
Рис. 4. Клеточный автомат и квазиклеточная сеть, синтезированная методом битого клеточного автомата

Основным назначением квазиклеточных сетей является моделирование систем, рассмотрение которых сводится к моделированию потоков в сетях[2,4,5]. Речь идёт о распространении каких-либо микрообъектов или частиц веществ в ограниченном пространстве.

Таким образом, квазиклеточные сети представляют собой фундаментальные дискретные структуры с возможностью приложения в различных предметных областях в задачах, сводящихся к моделированию систем, для которых характерно наличие потоков и их распространение в пространстве и времени.

В работах автора рассматриваются различные аспекты теории квазиклеточных сетей, а именно синтез[1,2,4], циркуляция[3], моделирование потоков[5], обучаемость структур[6], предметные интерпретации[7,8]. Отдельно следует остановиться на вопросах визуализации результатов моделирования квазиклеточными сетями.

3. Визуализация состояния квазиклеточных сетей

Наиболее очевидными приложениями квазиклеточных сетей в случае применения бинарного состояния следует рассматривать потоки, представляющие собой множество макрообъектов, например потоки транспорта и потоки людей на объектах массового массового пребывания людей. Применение квазиклеточных сетей при моделировании потоков людей, транспорта и др. позволяет получить распределённые во времени численные характеристики отдельных элементов таких систем. Однако следует отметить, что в настоящее время существует потребность не только в получении параметров отдельных объектов во времени, средних величин, но и в визуальном представлении результатов моделирования. Наряду с применением имитационного моделирования геометрические трёхмерные модели динамических систем применяются для оценки ряда трудноформализуемых и неформализуемых величин, в т.ч. в качестве инструментария систем поддержки принятия решений[9].

Следует отметить, что посетители объектов массового пребывания людей, транспортные потоки и т. п. с точки зрения геометрического моделирования и визуализации отвечают определению систем частиц[10]. Тогда согласно подходам, связанным с организацией геометрических динамических моделей и в частности моделей систем частиц (рис. 5), наблюдается течение дискретного модельного времени . При использовании подходов, описанных в ряде работ[9,10,11 и др.] c течением модельного времени предполагается изменение координат моделируемого динамического объекта, т. е.:

(6)

(7)

В соответствии со схемой, приведённой на рис. 5 координаты выступают в качестве изменяемых параметров. В отличие от представленного подхода, при использовании квазиклеточных сетей речь идёт не об изменении координат во времени, а о визуализации состояния сети в каждый момент времени. Тогда считая, что клетка

(8)

принимает некоторое состояние , схема визуализации состояния в квазиклеточной сети принимает вид, представленный на рис. 6.

Согласно приведённой схеме визуализации данных предполагается, что каждый такт модельного времени происходит визуализация состояния, что соответствует организации динамических геометрических моделей[10]. Следует также отметить, что визуализация состояния клетки осуществляется на основе значений , а также компонент вектора . Следует отметить, что в случае трёхмерного сеточного моделирования, применяемого при визуализации объектов в системах частиц, координаты фактически выступают в роли материальной точки или некоторого аналога центра трансформации трёхмерного объекта, относительно координат которого вычисляются координаты всех вершин сетки.

Таким образом, визуализация состояния квазиклеточной сети фактически соответствует принципам моделирования и визуализации систем частиц[10].

В качестве примера визуализации циркуляции в квазиклеточной сети целесообразно рассмотреть моделирование посетителей на объектах массового пребывания людей.

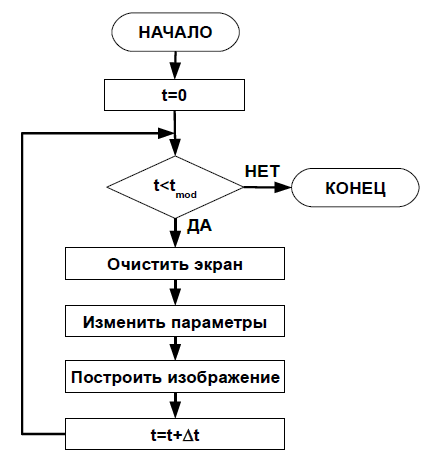
Рис. 5. Работа динамической геометрической модели

Выше были рассмотрены аспекты моделирования подобных систем. В простейшем случае применяется бинарное состояние клетки (фишка), обозначающее наличие в указанной области пространства (клетке) посетителя (), его координаты фактически тесно связаны с координатами клетки соотношением:

(9)

где random – случайная величина, равномерно распределённая в диапазоне [0,1].

Указанные координаты являются основой для визуализации объекта. Простейший пример визуализации приведён на рис. 7.

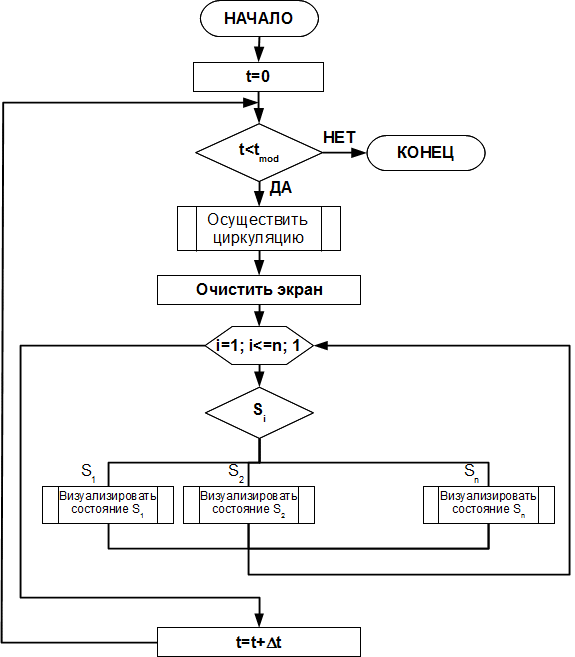
Рис. 6. Принципиальная схема визуализации работы квазиклеточной сети

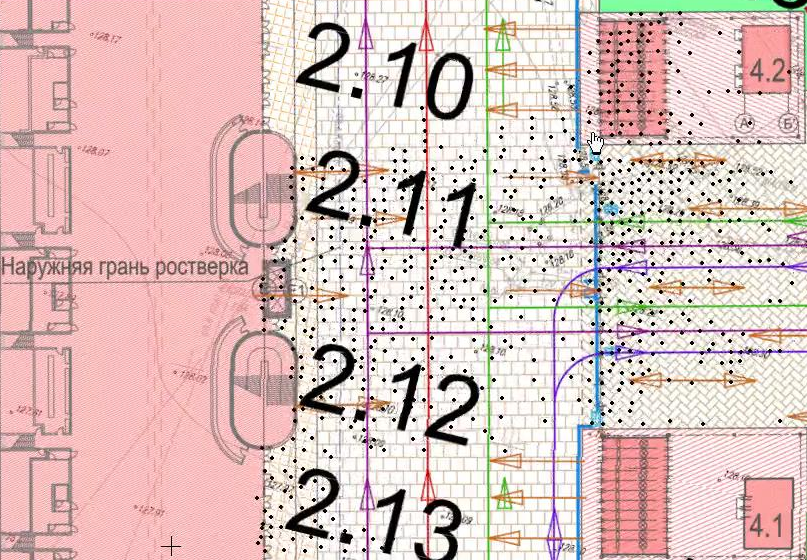
Рис. 7. Визуализация потока посетителей на стадионе «Спартак». Точками визуализированы посетители стадиона

Таким образом, одним из направлений визуализации данных в системах моделирования, построенных на основе квазиклеточных сетей является представление состояния клеток квазиклеточной сети в каждый момент времени с целью получения геометрической динамической модели системы частиц.

В отличие от микромоделирования координаты не являются параметрами самих частиц, а являются параметрами элемента квазиклеточной сети (области пространства, клетки).

4.Визуализация аддитивных параметров

Рассмотренное выше направление визуализации данных предполагало представление процесса циркуляции в виде динамической геометрической модели, однако немаловажным является и представление ряда величин, нахождение которых требуется согласно цели моделирования[11]. В частности речь идёт о средних величинах, а также о величинах, которые, как отмечалось ранее, представлены в виде численно заданных функций, значения которых формируются в процессе моделирования.

В работе [3] введено понятие измерительного участка квазиклеточной сети и счётчиков, являющихся параметрами клеток на измерительном участке. В частности рассматривая измерительный участок:

(10)

Структура клетки по сравнению с представленной в (8) усложняется до вида , в котором – переменные параметры клетки, значения которых изменяются в ходе циркуляции (англ. «changeable»).

Для измерительного участка находим аддитивные величины в моменты :

, ,	(11) (12)

а также средние значения указанных величин:

, .	(13) (14)

В процессе моделирования работы квазиклеточной сети фактически формируются значения указанных функций (11), (12), (13), (14), которые задаются численно и визуализируются в виде гистограмм и графиков их зависимостей от времени. С технической точки зрения визуализация данных в таком представлении не составляет сложности и сводится к построению графика функции по точкам (рис. 8)

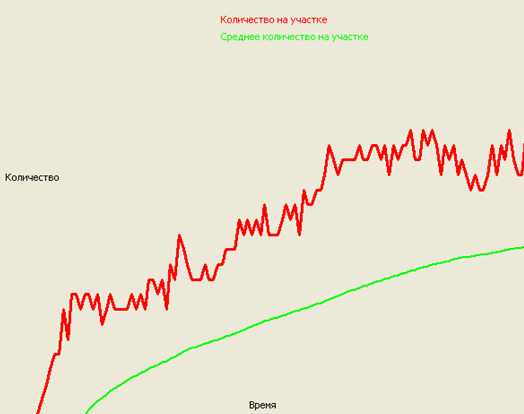
Рис. 8. Пример построения графика временной зависимости количества фишек и среднего количества фишек за время на измерительном участке квазиклеточной сети

5. Построение тепловых карт

Особое внимание в вопросах визуализации данных следует уделить возможностям применения квазиклеточных сетей для формирования тепловых карт. Тепловые карты достаточно широко используются для визуализации научных данных, распределённых в пространстве. Фактически при использовании квазиклеточных сетей речь идёт о представлении в цветовой шкале данных связанных с конкретной клеткой квазиклеточной сети согласно её структуре . Следует отметить, что величины, определяемые на тепловых картах чаще всего являются параметрами элементов пространства[12], поэтому при визуализации данных следует рассматривать изменяемые параметры , формируемые тем не менее под воздействием циркуляции, т. е. фактически зависящие от . Кроме того следует отметить, что при построении тепловых карт рассматривается случай квазиклеточной сети, где в качестве базовых параметров клетки выступают именно топологические координаты. Это связано с тем, что тепловая карта и соответствующая визуализация данных предполагает наличие точек пространства и значений определённых параметров в указанной точки. Примерами таких параметров в условиях объектов массового пребывания людей можно считать интенсивность потока людей (кол-во человек в единицу времени), а также количество человек, прошедших через клетку (единицу пространства) за время. В электротехнических системах в качестве такого параметра может выступать температура проводника, фактически зависящая от количества электронов, прошедших через участок провода. Указанные примеры с точки зрения квазиклеточных сетей показывают, целесообразность визуализации данных для тепловых карт при различных предметных интерпретациях через параметры .

Учитывая, что в процессе циркуляции в каждой клетке в содержатся счётчики, на основе которых вычисляются значения, которые необходимо визуализировать, то фактически имеем набор точек пространства, в каждой из которых задано значение . В настоящее время существует множество программных средств, обеспечивающих построение наборов точек в заданных координатах с заданным цветом, соответствующим значению параметра в указанной точке пространства. Тогда, фактически требуется привести значение к цветовой шкале, где цвет задаётся по системе.

Пусть имеем множество клеток, где . Тогда в ходе циркуляции получаем численно заданную функцию . Каждому элементу квазиклеточной сети соответствует значение , которое требуется привести в цветовой шкале, т. е. фактически построить точку в координатахцвета . Рассмотрим приведение значения к абсолютной и относительной цветовой шкале. Будем рассматривать цвет компоненты которого задаются в вещественном формате (каждая компонента от 0 до 1).

Простейший вариант цветовой шкалы – градация серого, для которой

(15)

При использовании абсолютной цветовой шкалы принимаются постоянные значения наименьшего и наибольшего значений по шкале. Тогда диапазону величиной соответствует цветовая шкала от 0 до 1. Тогда для приведения значения к цвету по шкале:

(16)

В случае относительной шкалы и примут значения:

, ,	(17) (18)

являющиеся наибольшим и наименьшим среди полученных при моделировании.

Для случая применения шкалы в цвете, а не в градации серого, целесообразно задавать цвет по системе HSL (Hue, Saturation, Lightness – тон, насыщенность, яркость), где тон измеряется в градусах на цветовом круге (от 0 до 360), а при условии использования только градации тона, насыщенность и яркость следует принять за 100% (,). Тогда для величина тона:

(19)

В ряде справочников [13,14] приведены соотношения для перевода цвета из системы HSL в систему RGB, что фактически соответствует вычислению цвета и визуализации данных по рассматриваемой шкале. Следует также отметить, что для формулы (19) также справедливо рассмотренное ранее представление об абсолютной и относительной шкале (17) и (18).

Предложенные подходы к визуализации данных позволяют построить тепловые карты по результатам моделирования. Примером визуализации данных является тепловая карта, построенная на основе модели пропускных пунктов стадиона, визуализация потоков людей на котором рассмотрена ранее (см. рис. 7). Тепловая карта (рис. 9) визуализирует количество посетителей объекта через области пространства.

Рис. 9. Пример визуализации данных на тепловой карте

6. Заключение

В рамках статьи рассмотрен один из аспектов теории квазиклеточных сетей, являющихся новым типом фундаментальных дискретных структур, применяемых в задачах моделирования систем, предполагающих наличие потоков и их распространения в ограниченном пространстве. Визуализация на основе квазиклеточных сетей позволяет наглядно представить состояние квазиклеточной сети в каждый момент времени, а также её измеряемые параметры. Таким образом, квазиклеточная сеть представляет собой не только дискретную модель, в рамках которой реализуется моделирование потоков на микро- и макроуровне в рамках единой структуры, но и структуру, на основе которой удобно организуется визуализация и геометрическое моделирование потоковых систем на различных уровнях.

Список литературы

Аристов А.О. Квазиклеточные сети. Синтез и циркуляция // Горный информационно-аналитический бюллетень №2'2013 — с.125-131
Аристов А.О. Циркуляция в квазиклеточных сетях и их классификация // Горный информационно-аналитический бюллетень №9'2013 — с.188-194
Аристов А.О. МЕТОДЫ СИНТЕЗА КВАЗИКЛЕТОЧНЫХ СЕТЕЙ // Научный вестник МГГУ. - 2013. - № 9 (42). - C. 16-21
Аристов А.О. Об элементах квазиклеточных сетей // Горный информационно-аналитический бюллетень №11'2013 — с.322-332
Аристов А.О. Потоки в квазиклеточных сетях // Устойчивое инновационное развитие: проектирование и управление. — Электрон. журн. — 2013. — №3(20)— с.36-41 — Режим доступа: http://www.rypravlenie.ru.
Аристов А. О. КВАЗИКЛЕТОЧНЫЕ СЕТИ КАК ОБУЧАЕМЫЕ СТРУКТУРЫ // Научный вестник МГГУ. - 2013. - № 10 (43). - C. 8-13
Аристов А.О. Теория квазиклеточных сетей и её приложения // Всероссийская выставка Научно-технического творчества молодёжи. II Международная научно-практическая конференция «Научно-техническое творчество молодёжи — путь к обществу, основанному на знаниях»:сборник научных докладов/ Мос. гос. строит. ун-т - М.:МГСУ,2013 — с.230-234
Аристов А.О. Квазиклеточные сети и их предметные интерпретации в задачах моделирования транспортной логистики открытых горных работ // Всероссийская выставка Научно-технического творчества молодёжи. II Международная научно-практическая конференция «Научно-техническое творчество молодёжи — путь к обществу, основанному на знаниях»:сборник научных докладов/ Мос. гос. строит. ун-т - М.:МГСУ,2013 — с.165-168
Компьютерные системы поддержки принятия решений : учебное пособие /А.О. Аристов, К.В. Моргачёв, Л.П. Рябов, А.В. Суворов, А.М. Фёдоров — М: МГГУ, 2012.— 172с.
Калитин Д.В., Аристов А.О. Геометрическое моделирование САПР : учебное пособие — М: МГГУ, 2011 — 145с.
Шеннон Р. Имитационное моделирование систем - искусство и наука - М.: Мир, 1978. - 420 с.
Шаропин К.А., Берестнева О.Г., Шкатова Г.И. ВИЗУАЛИЗАЦИЯ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ // Известия ТПУ . 2010. №5.
Шикин Е.В., Боресков А.В. Компьютерная графика. Полигональные модели — М.:Диалог-МИФИ,2001-464с.
Порев В.Н. Компьютерная графика - Спб.:БХВ-Петербург, 2002. - 432с.

Geometrical modeling and visualization of simulation results in quasi cellular nets

A.O. Aristov

National Institute of science and technology «MISIS», Russia

Batan-87@mail.ru

Abstract

It considered usings of the new type of discrete structures that named quasi cellular nets for visualization of simulation results. Quasi cellular nets may be used for simulation flow-based systems on micro and macro levels on single model structure. It considered visualizations of state of quasi cellular nets, additive parameters and creation heat maps.

Keywords: quasi cellular net, flows, circulation, visualization, state, particle system, heat map.

References

Aristov A.O. Quasi cellular nets. Synthesys and circulation. Mining Informational and Analytical Bulletin (scientific and technical journal) vol 2'2013 — pp.125-131 [In russian]
Aristov A.O. Circulation and classification in quasi cellular nets. Mining Informational and Analytical Bulletin (scientific and technical journal) vol 9'2013 — pp.188-194 [In russian]
Aristov A.O. Methods of quasi cellular nets synthesys. Scientific bulletin of MSMU vol 9(42) – pp.16-21 [In russian]
Aristov A.O. About the elements of quasi cellular nets. Mining Informational and Analytical Bulletin (scientific and technical journal) vol 11'2013 — pp.322-332 [In russian]
Aristov A.O. Flows in quasi cellular nets. SUSTAINABLE INNOVATIVE DEVELOPMENT: design and management vol. 3(20) – pp.36-41 [In russian]
Aristov A.O. Quasi cellular nets as educable structures. Scientific bulletin of MSMU vol 10(43) – pp.8-13 [In russian]
Aristov A.O. Theory of quasi cellular nets and their using. All-Russian Exhibition of Scientific and Technical Creativity of Youth. II International Scientific and Practical Conference "Scientific and technical creativity of youth - the path to a society based on knowledge": a collection of scientific papers / Mos. state. builds. Univ - M: MGRS, 2013 - pp.230-234 [In russian]
Aristov A.O. Quasi cellular nets and their using in transport logistics of open-cast mining. All-Russian Exhibition of Scientific and Technical Creativity of Youth. II International Scientific and Practical Conference "Scientific and technical creativity of youth - the path to a society based on knowledge": a collection of scientific papers / Mos. state. builds. Univ - M: MGRS, 2013 - pp.165-168 [In russian]
Aristov A.O., Morgachev K.V., Ryabov L.P., Suvorov A.V., Fedorov A.M. Computer-Aided Decision Support Systems. MSMU,Moscow, 2012.— 172 p. [In russian]
Kalitin D.V., Aristov A.O. Geometrical modeling in CAD-systems. MSMU,Moscow, 2011.— 145 p. [In russian]
Shennon R. Simulation modeling systems - the art and science - MIR,Moscow, 1978. - 420 p. [In russian]
Sharopin K.A., Berestneva O.G., Shkatova G.I., The visualization of resrarch results. Proceedings of the TPU vol 5'2010. [In russian]
Shikin E.V., Boreskov A.V. Computer graphics. Polygon models. Dialog-MEPhI,Moscow, 2001 – 464 p. [In russian]
Porev V.N. Computer graphics. BHV,St.Petersburg, 2002. – 432p. [In russian]
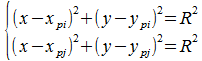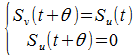
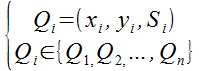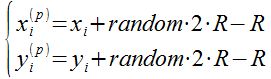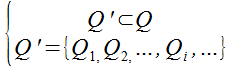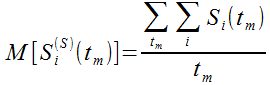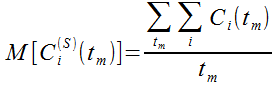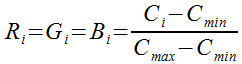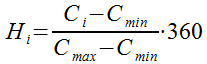