Анализ многомерных данных в задачах вычислительной газовой динамики
А.Е. Бондарев
Институт прикладной математики им. М.В.Келдыша РАН
Москва, Россия
Содержание
2. Анализ и визуализация многомерных данных
Аннотация
В работе рассматриваются вопросы анализа и визуализации многомерных объемов данных в задачах вычислительной газовой динамики. Многомерные данные появляются в вычислительной газовой динамике как результаты параметрических исследований и решения задач оптимизационного анализа. Основной целью исследования многомерного объема данных для таких задач является поиск скрытых взаимозависимостей между определяющими параметрами в изучаемом объеме. Это составляет основное отличие от общего подхода анализа данных, нацеленного в основном на задачи классификации и кластеризации. Предлагается приближенный подход, предполагающий отображение многомерного объема в пространстве главных компонент и аппроксимацию данных в объеме с помощью геометрических примитивов (в частном случае плоскостей). Приведен пример практического применения подхода.
Ключевые слова: визуализация многомерных данных, метод главных компонент, вычислительная газовая динамика
1. Введение
Задачи обработки, анализа и визуализации многомерных данных являются на сегодняшний день важным и актуальным направлением. Проблемы изучения многомерных объемов данных, задачи определения взаимного расположения точек в многомерном облаке данных, задачи выявления определяющих факторов и скрытых взаимосвязей между ними возникают практически во всех областях знания. Анализ многомерных данных (Data Analysis) интенсивно развивается как научная дисциплина, которая включает в себя: метод главных компонент (PCA-Principal Component Analysis) и его обобщения на нелинейные случаи, факторный анализ, кластерный анализ, дискриминантный анализ, построение самоорганизующихся карт (SOM – Self-Organized Maps) и упругих карт (Elastic Maps) [1,2]. Комбинированное применение методов, алгоритмов и подходов, разработанных в этих разделах, позволяет провести всестороннее исследование многомерного объема данных вне зависимости от их происхождения.
В задачах вычислительной газовой динамики проблемы анализа многомерных данных ранее практически не встречались. Для обработки и визуального представления результатов даже самых сложных расчетов вполне хватало наработанных методов и приемов научной визуализации [3]. Однако в настоящее время интенсивное развитие высокопроизводительных и параллельных вычислений позволяет решать задачи параметрического исследования и задачи оптимизационного анализа [4,5].
Параметрические численные исследования позволяют получать решение не для одной конкретной задачи математического моделирования, а для класса задач, заданного в многомерном пространстве определяющих параметров. Также применение параллельных алгоритмов на высокопроизводительной вычислительной технике позволяет численное исследование задач оптимизационного анализа, когда обратная задача решается в каждой точке сеточного разбиения многомерного пространства определяющих параметров. Основная особенность с точки зрения задач анализа и визуализации решений в подобных вычислениях заключается в том, что их результаты представляют собой многомерные массивы, размерность которых соответствует количеству определяющих параметров. Эти массивы нуждаются в обработке и визуальном представлении с целью их анализа и выявления внутренних взаимосвязей между определяющими параметрами. Подобные задачи начинают встречаться на практике все чаще, хотя следует отметить, что размерность подобных массивов на сегодняшний день ограничивается вычислительными мощностями и обычно составляет 4 – 5, в исключительных случаях – 6.
В этой ситуации естественно хотелось бы применить уже
наработанный аппарат методов и алгоритмов Data Analysis к подобным задачам.
Однако здесь возникают некоторые проблемы, обусловленные спецификой целей
исследования и происхождения самих данных. В задачах Data Analysis многомерные
данные рассматриваются как набор точек 
, и основной интерес для исследователя
представляет их взаиморасположение с целью выделения кластеров, решения задачи
классификации новых объектов. Когда мы рассматриваем многомерные данные в
задачах вычислительной газовой динамики (CFD), полученные как результаты
решения задач оптимизационного анализа или параметрических исследований, нас в
гораздо меньшей степени интересует взаиморасположение точек, так как разбиения
по определяющим параметрам 
задаются нами при организации расчета. То есть
эти координаты и их взаиморасположение нам хорошо известны. А параметр 
возникает как результат
массового решения некоторого класса задач математического моделирования. Для
получения этого параметра мы должны решить соответствующую задачу вычислительной
газовой динамики в каждой точке сеточного разбиения многомерного пространства
определяющих параметров .
Соответственно, в результате проведения серии массовых расчетов мы получаем
многомерный объем данных 
,
возникающий в результате объединения исходного сеточного разбиения определяющих
параметров с результатами расчетов. Полученный таким образом многомерный объем
данных можно рассматривать как дискретное обобщенное решение для класса задач,
задаваемого диапазонами изменения определяющих параметров.
Подобный многомерный объем данных нуждается в обработке, анализе и визуализации для обеспечения адекватной трактовки полученных результатов. Однако задачи кластеризации данных и их классификации для объемов данных, получаемых таким образом, имеют второстепенное значение.
Основная цель здесь - изучение зависимости 
, представленной по результатам
вычислений в виде многомерного объема данных, визуализация этой зависимости и
по возможности представление ее в квазианалитическом виде с помощью
приближений. Таким образом, задача адаптации методов Data Analysis для целей
исследования многомерных результатов расчетов газодинамических задач является
актуальной.
2. Анализ и визуализация многомерных данных
Наиболее эффективным путем анализа многомерных данных,
получаемых в результате решения задач вычислительной газовой динамики, является
визуальное представление зависимости и получение информации о характере этой
зависимости. Далее следует аппроксимация зависимости с помощью поверхностей
достаточно простого вида и получение, как следствие, искомого
квазианалитического выражения.
В работе [4] рассматривались современные попытки построения визуальной концепции для представления многомерных данных, а также отмечалось отсутствие на сегодняшний день адекватного и надежного способа подобного визуального представления для объемов, имеющих размерность, превышающую 3. Следовательно, для анализа информации, содержащейся в полученном многомерном массиве необходимо понизить размерность массива. Рассмотрим наиболее распространенные практические способы понижения размерности.
Рассматриваемые способы основаны на анализе дисперсий данных массива по координатным направлениям или нахождении в изучаемом многомерном пространстве вектора, по направлению которого дисперсия максимальна.
Первый способ представляет собой поиск координатного
направления с наименьшей дисперсией. Вычисляются дисперсии 
по всем координатным
направлениям, выбирается наименьшая из них, и в том случае, когда минимальная
дисперсия существенно (на порядки) меньше остальных, значения исследуемой
функции по координатному направлению с наименьшей дисперсией заменяются на
константу, равную среднему значению по направлению. Таким образом, размерность
исходного многомерного пространства понижается на единицу.
Более радикальный вариант данного способа выглядит следующим
образом. Вычисляются дисперсии по всем координатным направлениям и ранжируются
в порядке убывания. Выбираются три направления, соответствующих максимальным
дисперсиям 
. Далее
проверяется условие 
,
где 
- малая
величина, задаваемая пользователем. Если это условие выполнено, то полагаем
значения искомой функции по всем направлениям, кроме трех, соответствующих
максимальным дисперсиям, константами, равными соответствующим средним значениям
по направлениям. Таким образом, мы радикально понижаем размерность исходного
пространства и оказываемся в рамках стандартного трехмерного пространства.
Изложенный подход обладает рядом недостатков:
- он далеко не всегда осуществим, например, если данные в многомерном пространстве близки к гиперсфере;
- в выборе малой величины заложен произвол.
Однако, несмотря на эти недостатки, для пространств
небольшой размерности 
во
многих практических случаях данных подход работает успешно.
Второй распространенный способ понижения размерности
заключается в построении графических проекций на стандартное число измерений 
с фиксацией переменных, не
участвующих в построении проекции. В тех случаях, когда из набора дисперсий по
направлениям нельзя выделить существенно наименьшую, часто используется метод
разделения переменных.
Если из вида проекций в стандартных измерениях удается
сделать вывод о том, что для двух переменных при фиксированных остальных
переменных исследуемая функция может быть выражена с помощью аналитической
зависимости 
, а для
остальных переменных при фиксированных первых двух - с помощью зависимости 
, , то выдвигается гипотеза о
том, что итоговая аналитическая зависимость для искомой функции может быть
представлена в виде комбинации этих функций со сшивкой при фиксированных
значениях.
Оба вышеизложенных подхода не являются строго обоснованными. Скорее, это алгоритмы выдвижения гипотез, нуждающихся в проверках. Однако эти методы позволяют получать реальные практические результаты.
Не менее эффективным является применение метода главных компонент (PCA). Суть метода состоит в переходе от исходной системы координат к новому ортогональному базису в рассматриваемом многомерном пространстве, оси которого ориентированы по направлениям максимальной дисперсии массива данных. Реализации метода главных компонент и алгоритмам его применения в различных областях посвящено большое количество литературы. Различные варианты реализации метода главных компонент и его обобщений для нелинейных случаев подробно представлены в работах [1,2]. Геометрическая постановка задачи нахождения главных компонент формулируется согласно [1,2] следующим образом. В многомерном пространстве ищется вектор направления, задающий прямую, вдоль которой дисперсия максимальна (или сумма квадратов расстояний от точек данных до прямой минимальна). Таким образом определяется первая главная компонента. Далее рассчитывается множество векторов первых остатков, которое лежит в пространстве, ортогональном первой главной компоненте и имеющем размерность на единицу меньше исходной размерности. Для нового пространства, образованного этим множеством векторов, снова ищется направление с максимальной дисперсией. Так рассчитывается вторая главная компонента. Снова рассчитывается множество векторов вторых остатков и т.д.
Применение главных компонент дает нам возможность отобразить исследуемый многомерный массив на плоскость или в трехмерное пространство, образованное первыми тремя главными компонентами. Однако перед этим необходимо принять решение о применимости метода главных компонент и о том, сколько главных компонент необходимо для адекватного описания изучаемого многомерного облака данных. Для этих целей проводится вычисление собственных значений ковариационной матрицы, построенной по исходным многомерным данным. Вычисленные собственные значения ранжируются и визуализируются, что дает исследователю возможность наглядно представить вклад соответствующих главных компонент в общую дисперсию и принять необходимое решение. Естественно, что наиболее желательным вариантом является тот, где описание многомерного объема данных возможно с помощью не более чем трех первых главных компонент.
В этом случае схема обработки, анализа и визуализации исходного многомерного объема данных будет выглядеть следующим образом.
- Для исходного объема вычисляются 3 первые главные
компоненты 
, где каждая
главная компонента является линейной комбинацией исходных переменных 
.
- Далее координаты исходных точек исследуемого объема выражаются в координатах главных компонент
.
- Реализуется визуальное представление массива в двумерном
виде 
или в трехмерном 
.
- Далее изучается полученное визуальное представление
многомерного массива в главных компонентах и предпринимается попытка
аппроксимации данных массива с помощью примитивных функций, имеющих
аналитическое выражение. В простейшем случае применяется грубая линейная
аппроксимация с помощью плоскости вида 
. Так как плоскость при переходе от главных
компонент к исходным переменным сохраняет свои свойства, с помощью обратного
преобразования получаем 
,
которое уже можно рассматривать как искомую квазианалитическую зависимость .
В том случае, когда нельзя аппроксимировать одной плоскостью, можно
использовать кусочно-линейный подход, применив несколько плоскостей. Следует
также заметить, что применение квадратичных поверхностей может также оказаться
весьма полезным, однако этот вопрос заслуживает отдельного рассмотрения.
Следует затронуть вопрос о визуальном представлении и его
роли. Визуальное представление или своего рода составление «портрета»
многомерного облака данных в главных компонентах является ключевым моментом
предлагаемого подхода. В самом деле, наша цель –получение приближенной
зависимости в
аналитической форме. Принять решение о возможности реализации подобного
приближения, определить вид примитивов для этого приближения мы можем только с
помощью визуализации.
3. Практические результаты
Данный раздел содержит краткое описание практического применения вышеописанного подхода к задаче выявления скрытых взаимозависимостей в многомерном объеме данных, представляющем собой решение задачи оптимизационного анализа.
Данный приближенный подход был применен к многомерному объему данных, полученному, как результат решения задачи оптимизационного анализа нестационарного взаимодействия сверхзвукового потока вязкого сжимаемого теплопроводного газа со струйной преградой [5]. Преграда возникает благодаря недорасширенной спутной струе, истекающей из сопла, помещенного во внешний сверхзвуковой поток. При повышении скорости изменения степени нерасчетности струи возникает специфический режим течения, когда вещество струи распространяется вверх по потоку по внешней стенке сопла. Скорость изменения степени нерасчетности струи рассматривается как управляющий параметр задачи оптимизационного анализа. В качестве определяющих параметров задачи рассматривались характерные числа Маха, Рейнольдса, Прандтля и Струхаля. Эти четыре параметра варьировались в определенных диапазонах. Целью решения задачи было нахождение скорости изменения степени нерасчетности струи, при которой реализуется специфический режим течения во всех диапазонах изменения характерных чисел задачи.
В качестве результата решения задачи был получен 5-мерный
объем данных, где в качестве переменных были 4 характерных числа задачи 
и искомая скорость 
. Для полученного
многомерного объема были определены три первые главные компоненты. После
перехода к главным компонентам строилось визуальное представление точек массива
в главных компонентах (Рис.1). Полученное визуальное представление многомерного
массива в главных компонентах позволило предположить, что точки массива могут
быть грубо аппроксимированы параметрически заданной плоскостью.
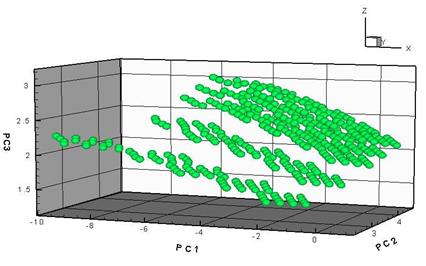
Рис.1. Представление многомерного объема в пространстве трех первых главных компонент.
После определения конкретного вида плоскости и ее
коэффициентов было проведено обратное преобразование к исходным переменным и
определение конкретного вида аппроксимирующей плоскости в исходных координатах.
Это дало возможность получить искомую зависимость 
в аналитическом виде. Полученные результаты
представляют собой решение для класса задач, заданного в многомерном объеме
определяющих параметров.
Следует отметить, что для рассматриваемого исходного многомерного объема данных было проведено построение упругой карты согласно основным подходам метода главных многообразий [1,2]. Упругая карта представляет собой гибкую поверхность, максимально подстраивающуюся к изучаемому облаку данных. Для этого плоскости двух первых главных компонент предоставляется возможность изгибаться. Для подстройки к облаку данных решается оптимизационная задача, в результате решения вычисляются коэффициенты изгиба поверхности. Основные принципы и способы построения упругих карт подробно описаны в работах [1,2]. Данный подход разработан для многомерных объемов данных, имеющих существенно нелинейный характер, и является весьма эффективным инструментом. На рисунке 2 представлена упругая карта, построенная для рассматриваемого многомерного объема в пространстве первых трех главных компонент. Видно, что для рассматриваемого объема, где взаимозависимости близки к линейным (Рис.1), применение подобного нелинейного подхода не позволяет получить представление о возможности построения приближенных зависимостей. Это обстоятельство никак не умаляет высокой эффективности упругих карт при решении задач кластеризации и классификации.
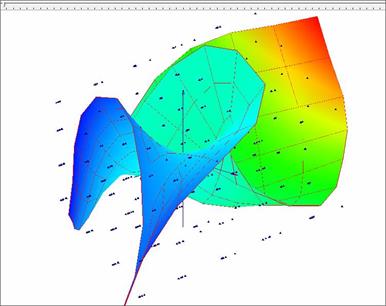
Рис.2. Построение упругой карты в пространстве трех первых главных компонент.
4. Заключение
Рассматриваемый приближенный подход, предполагающий отображение многомерного объема в пространстве главных компонент и аппроксимацию данных в объеме с помощью примитивов, в практическом примере - плоскостей, позволяет проводить оценку скрытых взаимозависимостей в многомерных объемах данных, получаемых в задачах вычислительной газовой динамики, как результаты решения задач параметрического поиска и оптимизационного анализа.
.
БЛАГОДАРНОСТИ
Данная работа выполнена при поддержке гранта Российского фонда фундаментальных исследований (проекты N 13-01-00367а и N 14-01-00769а).
Литература
[1] Gorban A., Kegl B., Wunsch D., Zinovyev A. (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58, Springer, Berlin – Heidelberg – New York, 2007.
[2] Зиновьев А. Ю. Визуализация многомерных данных, Красноярск, Изд. КГТУ, 2000. 180 с.
[3] Бондарев А.Е., Галактионов В.А., Чечеткин В.М. Анализ развития концепций и методов визуального представления данных в задачах вычислительной физики / Журнал вычислительной математики и математической физики, 2011, Т. 51, N 4, С. 669–683.
[4] Бондарев А.Е., Галактионов В.А. Анализ многомерных данных в задачах многопараметрической оптимизации с применением методов визуализации / Научная визуализация. Т.4, № 2, с.1-13, 2012.
[5] Bondarev A.E, Galaktionov V.A. Parametric Optimizing Analysis of Unsteady Structures and Visualization of Multidimensional Data // International Journal of Modeling, Simulation and Scientific Computing, Vol. 4, suppl. issue 1, 2013, DOI: 10.1142/S1793962313410043 http://www.worldscientific.com/doi/abs/10.1142/S1793962313410043
MULTIDIMENSIONAL DATA ANALYSIS IN CFD PROBLEMS
A.E. Bondarev
Keldysh Institute for Applied Mathematics RAS, Moscow, Russian Federation
Abstract
Theе paper is devoted to the questions of multidimensional data analysis and visualization for CFD problems. Multidimensional data are considered as results of parametrical search and optimizing analysis. For such types of multidimensional data volumes the main target of analyzing is to find some hidden dependencies of specific parameters. This is the main difference of proposed approach from general direction of data analysis targeted to solve the problems of classification and clusterization.
Rough approximate approach is proposed for data processing. The approach includes data visualization in principal components and data approximation by geometrical primitives (planes for particular case). An example of approach application to practical problem is considered.
Keywords: multidimensional data visualization, PCA, CFD problems
REFERENCES
[1] Gorban A., Kegl B., Wunsch D., Zinovyev A. (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58, Springer, Berlin – Heidelberg – New York, 2007.
[2] Zinovyev A. Yu. Vizualization of multidimensional data [Visualizaciya mnogomernyh dannyh], Krasnoyarsk, Krasnoyarsk Univ., 2000, 180 p. . [In russian]
[3] Bondarev A.E., Galaktionov V.A., Chechetkin V. M. Analysis of the Development Concepts and Methods of Visual Data Representation in Computational Physics. Computational Mathematics and Mathematical Physics, 2011, Vol. 51, No. 4, pp. 624–636. [In russian]
[4] Bondarev A.E, Galaktionov V.A. Multidimensional Data Analysis for Multiparametric Optimization Problems Using Visualization Methods [Analiz mnogomernyh dannyh v zadachah mnogoparametricheskoy optimizacii s primeneniem metodov vizualizacii]. Scientific Visualization. V.4, № 2, pp.1-13, 2012. [In russian]
[5] Bondarev A.E, Galaktionov V.A. Parametric Optimizing Analysis of Unsteady Structures and Visualization of Multidimensional Data. International Journal of Modeling, Simulation and Scientific Computing, Vol. 4, suppl. issue 1, 2013, DOI: 10.1142/S1793962313410043 http://www.worldscientific.com/doi/abs/10.1142/S1793962313410043