Использование технологий многомерного анализа для визуализации результатов анализа чувствительности в сложных процессах

Д.А. Жолобов

Национальный исследовательский ядерный университет «МИФИ»

 

Содержание

1. Введение  1

2. Обзор распространенных методов визуализации результатов анализа чувствительности  1

3. Системы многомерного анализа  2

4. Классификация исследуемых процессов  4

5. Алгоритм подготовки данных  5

6. Визуальный анализ чувствительности  5

7. Архитектура пакета  6

8. Визуализация результатов бизнес-планирования  6

9. Профилирование шахматного алгоритма  7

10. Заключение  8

Использованная литература  8

 

Аннотация

В статье представлен разработанный на кафедре Системного анализа МИФИ пакет для визуального многофакторного анализа чувствительности сложных процессов, описанных функционально либо с помощью имитационной модели. Пакет использует современные технологии многомерного анализа для визуализации. В качестве метрик используются интервальные значения целевых показателей. Показана возможность применения пакета для анализа чувствительности в бизнес-планировании. Также приведен пример внедрения пакета в проекте международной шахматной ассоциации FIDE.

 

Ключевые слова: анализ чувствительности, многомерный куб, бизнес-планирование, имитационная модель, целевой показатель

 

1. Введение

 

При прогнозировании результата какого-либо запланированного процесса, одной из больших проблем является вариативность определенного целевого показателя результата относительно множества случайных величин, влияющих на протекание этого процесса. Такими случайными величинами являются как входные параметры процесса, так и параметры среды, окружающей процесс. Подобная задача в математике носит название анализа чувствительности [1], существует большое количество методов исследования задач на чувствительность по отношению к одному или нескольким параметрам [2,3]. Ярким примером прикладной области, где человек сталкивается с подобной проблемой, является проблема оценки целесообразности экономического проекта, результаты которого значительно зависят как от макроэкономических показателей, так и от входных параметров: величина инвестиций, выбор сценария реализации и т.п [4]. Широта проблемы не ограничивается лишь этим примером, подобная проблема стоит в некоторых физических процессах (например, [5]), имитационном моделировании, теории игр и т.д.

Однако, увеличение числа случайных величин, не создавая значительных проблем для компьютера, создает проблемы для принимающего решения лица, поскольку ему становится непросто оценить приемлемые диапазоны, при которых реализация запланированного процесса имеет смысл. Основная цель данной статьи – представить возможности применения современных средств многомерного анализа для визуализации результатов проведенного анализа чувствительности в сложном процессе. На базе этих идей на кафедре Системного анализа НИЯЮ «МИФИ» разработано программное обеспечение, стандартизирующее такой подход.

 

2. Обзор распространенных методов визуализации результатов анализа чувствительности

 

Самым простым способом визуализации анализа чувствительности многофакторного процесса является раздельное представление зависимости целевого показателя относительно каждого фактора в виде одномерной зависимости, выраженной таблично. Все остальные факторы при этом фиксируются. Этот способ анализа чувствительности называется OFAT (акроним one factor at time). Типичным примером такого подхода обладает распространенный пакет Project Expert [7], предназначенный для бизнес-планирования. Визуализация может осуществляться как в табличном виде (рис.1), так и в виде графика (рис.2)

 

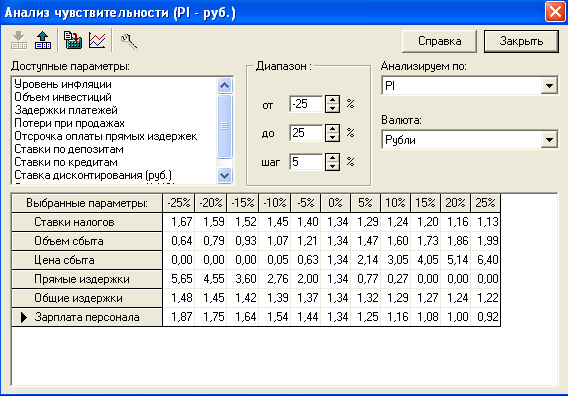
http://rudocs.exdat.com/data/34/34000/34000_html_m7db69ef1.png

Рис. 1. Табличное представление чувствительности параметров показателей к значению неизвестного фактора в пакете Project Expert

 

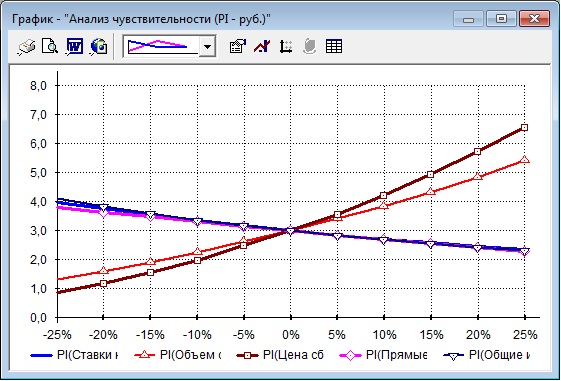
http://fa-kit.ru/users/gor/20.jpg

Рис. 2. Представление чувствительности параметров показателей к значению неизвестного фактора в пакете Project Expert в виде двумерного графика

 

 

Если связь фактора и показателей может быть представлена в виде суммы одномерных функций, например

            (1)

то подход OFAT работает хорошо, корректно отражая как прямую зависимость, так и скорость её изменения (первую производную). Как только возникает любая нелинейная композиция факторов, например, простейшая

            (2)

то разделение факторов по графикам делает невозможным принятие корректных решений.

Подобный подход может быть усовершенствован различными способами, например, в работе [8], применяется раскрашенная графическая карта для визуализации анализа чувствительности по двум факторам одновременно (рис.3)

 

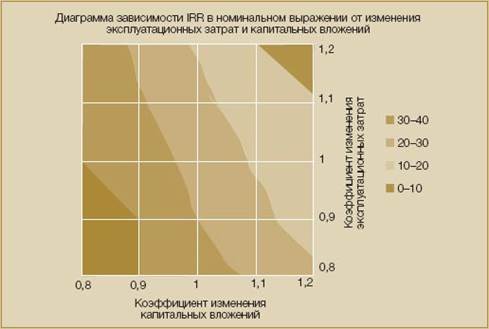
http://fd.ru/images/2008/07/diagramma2.jpg

Рис. 3. Визуализация двухфакторного анализа чувствительности в работе [8]

 

Другим подходом к понижению размерности многофакторного процесса с целью визуализации результатов анализа чувствительности в двумерном виде является сценарный анализ. В этом случае диапазоны значений нескольких факторов группируются в сценарии, и в каждом сценарии вычисляется диапазон изменения целевого показателя, который далее визуализируется тем же способом, что и описанные выше (рис. 1 и 2) однофакторные результаты анализа чувствительности.

Существует весьма интересный способ визуализации результатов анализа чувствительности, основанный на диаграммах рассеяния [9]:

 

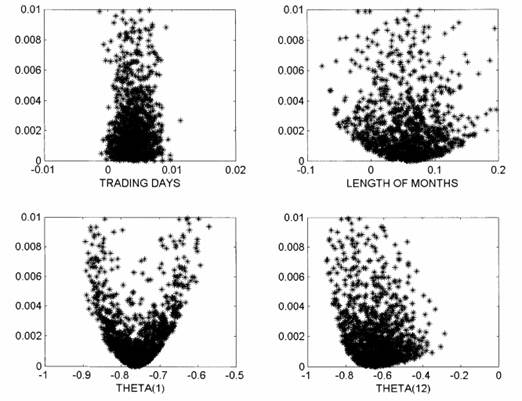
Рис. 4. Использование диаграмм рассеяния для визуализации многофакторного анализа чувствительности в работе [9]

 

В этом случае один и тот же набор данных располагают на нескольких последовательных диаграммах рассеяния. По оси ординат на всех диаграммах отображается целевой показатель, а по оси абсцисс – один из факторов. На каждый фактор приходится одна диаграмма. Значение целевого показателя при конкретной реализации совокупности факторов представляет собой точку, которая отображается на каждой диаграмме. Подобный способ визуализации позволяет не только отразить чувствительность показателя к каждому отдельному фактору, но и совокупное влияние этих факторов на показатель, что дает возможность корректной интерпретации процесса с функциональной связью вида (2).

 

3. Системы многомерного анализа

 

Как правило, системы многомерного анализа не рассматриваются в контексте задачи анализа чувствительности. Основным предназначением таких систем является организация хранения данных в виде многомерного куба, измерениями которого являются дискретные переменные, как количественные или качественные, для которых определены диапазоны их изменения (для количественных переменных), либо возможные значения (для качественных переменных). В ячейке куба хранится одно или несколько значений (метрики), адрес ячейки по каждой шкале измерения характеризует, к какому значению каждой переменной относится записанное в ней значение (рис.5).

 

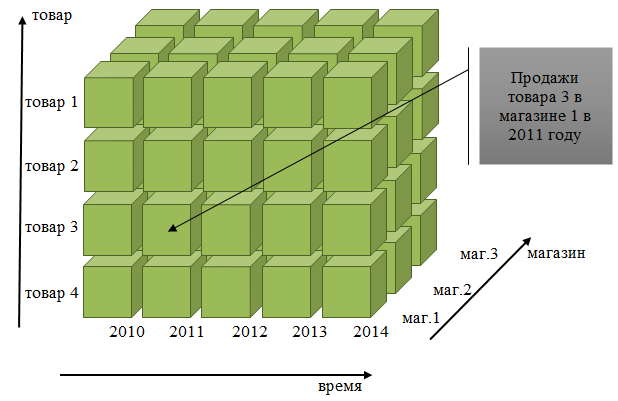
Рис. 5. Пример многомерного куба

 

Значения на шкале отдельного измерения (переменной) могут иметь иерархическую свертку, например, измерение времени может быть представлено в виде иерархии ГОД-МЕСЯЦ-ДЕНЬ. При этом переменная времени в каждой ячейке принимает значение конкретной даты, но в контексте запроса могут использоваться узлы группировки: месяцы и годы. Эта технология в основном создана для достижения двух независимых целей:

·         Ускорение работы алгоритмов выборки данных для пользователя, за счет внесения в хранилище массовой избыточности в виде предварительно посчитанных агрегатов (по годам, по всей продукции в целом, по всей компании и т.д.);

·         Унификация представления данных для анализа. Подобная модель существенно проще и понятнее для пользователя, чем реляционная модель сущность-связь.

Не вдаваясь в подробности отметим, что существуют разные способы разворачивания подобных хранилищ, позволяющие достигать как одну из целей, так и обе цели одновременно, в зависимости от поставленной задачи. В контексте настоящей работы первая цель не имеет особой важности, поэтому поговорим о распространенных инструментах визуализации многомерных моделей.

Одним из самых распространенных способов визуализации многомерных данных является сводная таблица и сводная диаграмма. Пользователь самостоятельно формирует нужный ему отчет путем перетаскивания в область сводной таблицы измерения и метрики, которые представляют для него интерес. Шкалы измерений доступны на любом уровне иерархической группировки. Также, учитывая двумерную форму представления данных, пользователь может использовать декартово произведение нескольких измерений в строках или столбцах для увеличения объема предоставляемой информации, либо зафиксировать какие-либо измерения конкретным значением на шкале, и в этом случае сводная таблица будет предполагать, что пользователь желает агрегировать данные при условии этого фиксированного значения. На рис.6 и 7 на базе многомерного куба детского книгоиздательства приведены примеры таких построенных отчетов.

 

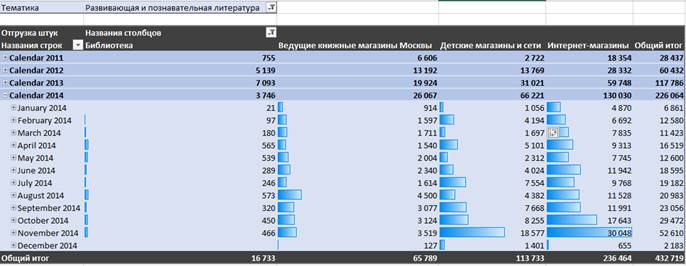
Рис. 6. Пример сводной таблицы из многомерного хранилища: динамика продаж книг в штуках развивающей литературы в разных каналах продаж

 

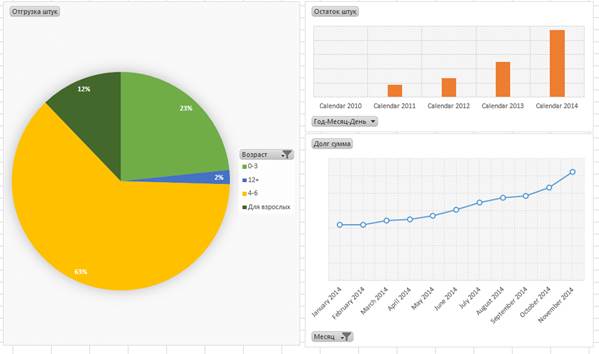
Рис. 7. Пример сводных диаграмм: распределение долей продаж по возрастным категориям читателя, динамика товарных запасов по годам, динамика дебиторской задолженности по месяцам

 

Главное преимущество такого способа извлечения данных, возникающее благодаря многомерной модели, заключается в том, что это своего рода самообслуживание, когда пользователь получает данные сам, используя простые инструменты, не обращаясь к программисту. Это обстоятельство стимулирует пользователя к активной генерации знаний, нежели к простому получению привычных данных: увидев какую-то аномалию в отдельной цифре пользователь может самостоятельно и мгновенно, не переключая внимания на другую задачу, детализировать эту цифру до любого уровня, таким образом исследовав непонятное ему явление и создав дополнительное знание, которым пользователь до этого не обладал.

Развитием технологии сводных таблиц являются т.н. панели мониторинга (перевод на русский язык не очень удачен – в английской литературе используется термин dashboards) и системы показателей (англ. – scorecards).

Панель мониторинга – это совокупность собранных в одной области, как правило, веб-странице, сводных таблиц и графиков, объединенных единым источником данных и единым набором инструментов, управляющих фильтрами по отдельным измерениям для всех таблиц и графиков в области. Типичный пример панели мониторинга приведен на рис.8

 

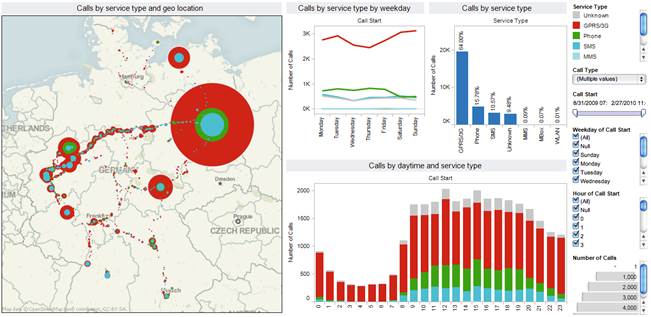
Рис. 8. Пример панели мониторинга, богато насыщенной средствами визуализации данных


Система показателей – это набор ключевых показателей, определенных принятой на предприятии методологией оценки его «здоровья», хранящийся в многомерной структуре в виде набора чисел <текущее значение, плановое значение, статус, тренд>, визуализация которых возможна в виде сводной таблицы либо в составе панели мониторинга. Как правило, открывая систему показателей, пользователь видит агрегированный набор показателей по предприятию в целом, но имеет возможность детализировать один или несколько показателей по подразделению, категории продукции и другим измерениям многомерного хранилиша. Типичный вид системы показателей приведен на рис.9.

 

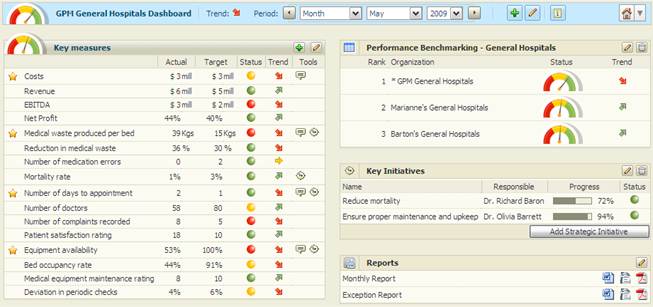
Рис.9. Типичная система показателей на примере сети больниц

 

В совокупности область технологий, связанная с описанными в данном параграфе технологиями и средствами визуализации, носит название Business Intelligence (BI). Согласно исследованиям компании Gartner, лидерами в этом области в 2014 году являются компании Microsoft, IBM, Tableau software, Qlik. Первые две компании делают акцент на технологиях хранения и обработки данных, обладая не самыми совершенными инструментами визуализации, две вторые производят первоклассные «витрины» в виде панелей мониторинга и систем показателей, отставая в области серверного ПО для хранения и обработки данных. Однако, в большинстве случаев это ПО совместимо, что позволяет комбинировать эти продукты, добиваясь оптимальной вычислительной и визуально составляющих одновременно .

Как следует из самого названия BI, основное применение эти технологии получили в анализе данных для нужд бизнеса. Однако, сама технология многомерного анализа не несет в себе какой-либо семантики и может успешно применяться в любых задачах, где данные могут быть представлены в многофакторном виде, и есть необходимость в обработке большого объема данных. Поскольку задача анализа чувствительности целевых показателей относительно неизвестных параметров в сложных процессах обладает всеми этими свойствами, адаптация технологий многомерного анализа для этой задачи представляется весьма актуальной и перспективной.

 

4. Классификация исследуемых процессов

 

В настоящей работе рассматриваются два способа описания связи между целевым показателем сложного процесса и случайными параметрами:

1.      Классическое представление зависимости в виде аналитической функции:

            (3)

где P – целевой показатель, xi – случайная величина, влияющая на целевой показатель. Будем считать, что каждый параметр является дискретным:

Тем самым мы избегаем необходимости исследования экстремумов функции , уходя в комбинаторную плоскость. Сложность функции  не имеет ограничений, принципиально лишь то, что эту функцию при работе с программой придется формализовать, что не всегда возможно из-за её сложности. Наиболее типичным примером прикладной задачи является исследование показателя эффективности бизнес-плана (представимого в виде суммы дисконтированных денежных потоков) относительно случайных величин (ставка по кредиту, валютный курс, уровень спроса, цены на сырье и т.п.).

2.      Зачастую представить аналитическую зависимость между показателем и входными параметрами невозможно. В таком случае будем использовать имитационную модель, как наиболее общий способ описания связи между ними. Сама имитационная модель при этом рассматривается как обычный «черный ящик»:

 

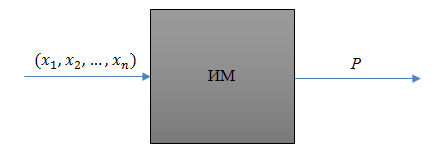
Рис. 10. Случай описания процесса с помощью имитационной модели

 

       Кроме того, по свойствам параметров можно выделить два случая:

1.      Параметры между собой не связаны. В этом случае множество всех возможных реализаций входных параметров являет собой декартово произведение множеств возможных значений каждого отдельного параметра. При таком подходе размерность множества растет в геометрической прогрессии с ростом числа параметров, что ограничивает максимальную сложность исследуемого процесса.

2.      Существует связь между возможными значениями параметров. Это означает, что множество возможных реализаций комплекса параметров меньше (как правило, существенно) декартова произведения возможных значений этих параметров. При таком свойстве процесса число параметров может быть очень большим, это зависит от степени обусловленности значений различных параметров.

 

5. Алгоритм подготовки данных

 

В общем, технология подготовки данных для визуального многомерного анализа чувствительности представлена на рис.11:

 

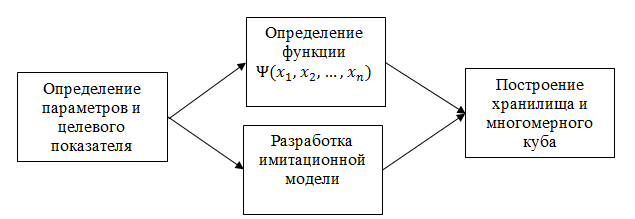
Рис. 11. Подготовка данных для визуального анализа

 

Определение параметров и целевого показателя производится в специальном приложении программного пакета. В случае, если параметры являются несвязанными (случай 1), тогда для них кроме описательных полей задаются возможные значения. Как правило, задается дискретная шкала этих параметров: минимальное и максимальное значения параметра, а также шаг значения параметра на шкале. Отметим, что параметр может быть не только количественным, но и качественным (описывать тот или иной сценарий), в этом случае необходимо перечислить все возможные значения, которые может принимать этот параметр.

Поскольку технология многомерного анализа допускает иерархическую свертку определенных значений параметров в родительские группы, возможно описание подобной иерархии на этапе ввода параметров. Например, макроэкономический параметр «инфляция» в бизнес-плане может быть представлен шкалой в интервале от 1 до 12%, с шагом 1%, что даёт 12 возможных значений, при этом значения 1-4% сворачиваются в групп «низкая инфляция», 5-8% - «средняя инфляция», 9-12% - «высокая инфляция». Это создаёт дополнительные возможности для визуального анализа, которые мы рассмотрим позже.

Определение функции (3) выполняется двумя способами: либо в специальном приложении пакета описывается аналитическая зависимость в виде формулы (чаще всего – временного суммируемого ряда), либо готовая зависимость экспортируется из внешнего ПО планирования.

В случае, когда генератором целевого показателя является имитационная модель, то она должна быть разработана по стандарту входов и выходов программного пакета и подключена к системе визуального анализа.

Если между различными параметрами существует определенная связь, т.е. не требуется проход по всем возможным комбинациям совокупности параметров, необходимо определить т.н. «нумератор», который будет генерировать совокупность параметров для теста. Этот нумератор подключается к системе визуального анализа и участвует в построении хранилища. Наличие поддержки такого нумератора открывает дополнительную гибкость в ситуации, когда параметры между собой не связаны, но их число не позволяет обеспечить полный проход всех возможных комбинаций. В этом случае подключается нумератор, работающий по методу Монте-Карло [3].

После того, как все метаданные исследуемого процессора введены и подключены к системе, выполняется автоматическая процедура построения хранилища. Схематически она изображена на рис.12:

 

Рис. 12. Автоматическая процедура построения хранилища и многомерного куба

 

Генерация совокупности параметров, расчет показателя и запись данных в БД выполняется в цикле, либо проходящем по всем возможным комбинациям совокупности параметров (случай 1), либо обращающемся к нумератору для получения очередной комбинации параметров.

После заполнения хранилища осуществляется построение многомерного куба, с которым непосредственно работает лицо, принимающее решение.

 

6. Визуальный анализ чувствительности

 

После окончания всех процедур, пользователь получает готовый многомерный куб, с помощью которого и производится собственно визуальный анализ чувствительности.

Здесь и далее в качестве клиентского приложения для иллюстрации работы метода будет использоваться распространенный пакет Microsoft Excel. Однако возможности визуализации не ограничиваются только этим продуктом. Любое приложение, способное запрашивать данные из модели UDM (семантика многомерных данных по версии Microsoft) будет совместимо в представленным пакетом. Среди таких приложений такие признанные лидеры, как Tableau software, MicroStrategy и др.

Поскольку визуализация сводных таблиц представляет собой двумерную визуализацию целевого показателя в виде матрицы на экране пользователя [6], при построении среза пользователь обладает тремя инструментами формирования удобного представления данных: установление для отдельных параметров фиксированных значений, вынесение на одну из двух осей декартова произведения измерений и группировка параметров с помощью иерархий. В любом случае для отображения среза будет осуществляться агрегация конкретных значений целевого показателя на различных реализациях параметров. Поскольку исследователя в данном случае будет интересовать диапазон изменения целевого показателя в данной ячейке сводной таблицы, пакет поддерживает агрегат в виде интервального числа: минимального и минимального значения целевого показателя для данной ячейки сводной таблицы. Наглядно этот процесс изображен на рисунке 13.

 

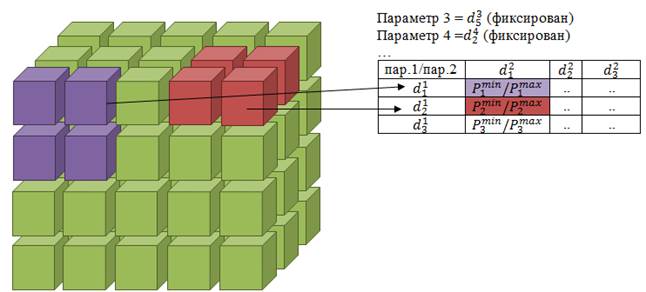
Рис. 13. Агрегация целевого показателя в виде интервального числа в сводной таблице

 

7. Архитектура пакета

 

Программный пакет состоит из следующих компонент (рис.14):

 

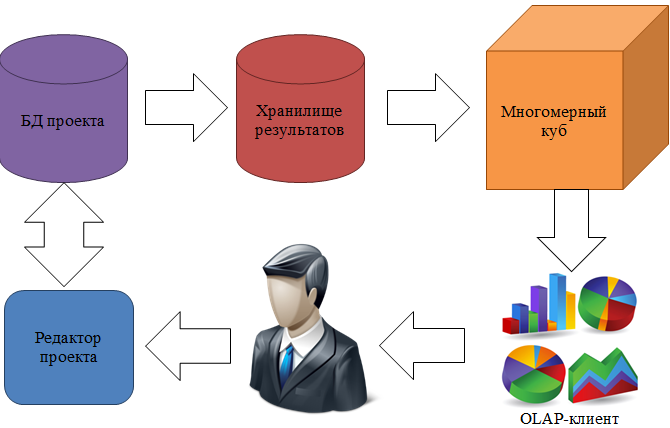
Рис. 14. Основные компоненты пакета и движение информации

 

Разработанная таким образом архитектура предоставляет максимальную гибкость приложения к различным сценариям использования, и, что самое главное, к его развитию в будущем, а наличие денормализованного хранилища в составе пакета обеспечивает высокую производительность расчетов и построения многомерного куба. В качестве средств визуализации могут использоваться решения, несовместимые с аналитической платформой компании Microsoft, поскольку этап генерации многомерного куба можно отключить, а данные черпать напрямую из реляционного хранилища с помощью SQL-запросов.

Как уже было сказано выше, технология агрегации многомерных кубов для визуализации результата очень удачно совпадает с интервальными свойствами целевого показателя сложного процесса, и это обстоятельство вкупе с поддержкой иерархических структур многомерными кубами обеспечивает широкий спектр применимости разработанной системы в различных прикладных задачах. Приведем примеры.

 

8. Визуализация результатов бизнес-планирования

 

Бизнес планирование проектов заключается в выделении экономических статей (продажи, сырье, заработная плата, аренда, покупка оборудования, кредиты, и т.п.) и вводе временного ряда денежных потоков по каждой статье. Определен ряд целевых показателей проекта, на основании которых инвестор принимает решение о его реализации, сравниваются альтернативные проекты. К таким показателям относятся чистый приведенный доход проекта, внутренняя норма рентабельности, период окупаемости и др. В то же время, существует широкий круг неопределенных факторов (ставка по кредиту, инфляция, спрос, валютные курсы и т.д.), сильно влияющих на эти показатели (т.е. конечный экономический результат). Актуальна задача анализа чувствительности целевых показателей к этим неопределенным факторам. Поскольку целевые показатели являются функцией от консолидированного по экономическим статьям временного ряда денежных потоков, разработан широкий круг методов этого анализа: статистический анализ, сценарный анализ и др. В качестве мощного дополнения, как средство визуализации предлагается использовать разработанный на кафедре Системного анализа НИЯУ МИФИ пакет.

Этот пакет позволяет импортировать денежные потоки бизнес-плана из специализированного приложения для бизнес-планирования Project Expert. После этого, в специальном интерфейсе, ориентированном на ввод временных рядов, пользователь определяет параметры и параметризует денежные потоки (заменяет введенные в Project Expert константы на аналитические функции от параметров):

 

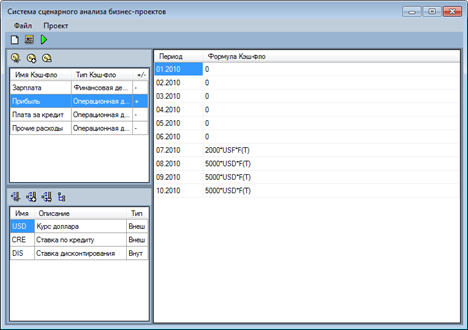
18-06-2011 3-41-55

Рис. 15. Интерфейс ввода денежных потоков

 

После этого пользователь запускает процедуру формирования хранилища, и через некоторое время получает возможность использовать сводные таблицы для визуального анализа своих целевых показателей относительно различных значений параметров реализации проекта:

 

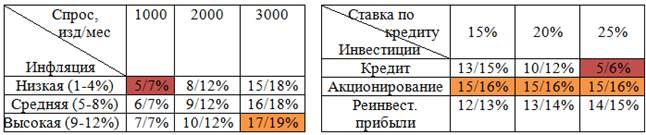
Рис. 16. Визуализация интервального значения показателя IRR при различных сценариях.

 

9. Профилирование шахматного алгоритма

 

В 2013 году в международной шахматной ассоциации FIDE возникла новая идея популяризации шахмат, основанная на создании международной букмекерской конторы, которая принимала бы у любых желающих (с учетом законодательства разных стран) ставки на исходы шахматных партий. Основная инновация, отличающая эту контору от других, заключалась в том, что ставки могли приниматься не только перед началом поединка, но и в его течение, при этом предлагаемые пари были рассчитаны именно для партий «блиц», которые можно было бы заключить быстро, и результат определялся бы также достаточно быстро (какой фигурой сходит игрок, на клетку какого цвета будет сделан ход, съест или не съест фигуру игрок  и т.п.).

Сложность создания такого рода пари заключается в том, что при большом числе одновременных партий невозможна экспертная оценка человеком вероятностей каждого отдельного события, и расчет на основе этой вероятности букмекерского коэффициента для пари. Поэтому в рамках проекта с FIDE был разработан математический алгоритм, опирающийся на мнение шахматной программы, профиль соперников и параметров поединка. Этот математический алгоритм требовал проведения испытаний перед запуском в коммерческую эксплуатацию.

Проведение испытаний предполагалось следующим образом: взять широкий исторический набор уже прошедших партий, и, зная состоявшиеся ходы, разработать имитационную модель антагонистической азартной игры, при которой игрок делает ставки на предложенные компьютером пари с автоматически рассчитанными коэффициентами. При этом модель, зная следующий ход, мгновенно рассчитывает результаты пари, и относит их на прибыль или убыток воображаемой букмекерской конторы. Обработав большой объем, предполагалось рассчитать норму прибыли конторы в зависимости от множества игровых параметров, таких как класс турнира, шахматные правила, персоны соперников, положение на доске (дебют, миттельшпиль, эндшпиль), поведение азартного игрока (азартный, умеренный, осторожный) и др. В качестве системы визуализации результатов описанного процесса был выбран освещаемый в настоящей статье программный продукт.

Следует отметить, что характер поставленной задачи определяет связанность возможных параметров. Поскольку ведется прогонка исторических партий, незачем проходить все комбинаторное множество параметров, ограничившись лишь теми комбинациями, которые отнесены к каждой отдельной партии. Например, если Г.Каспаров никогда не играл в исторической выборке в турнирах для новичков, бессмысленно рассматривать эту комбинацию параметров. Вследствие этого кроме имитационной модели также был разработан необходимый нумератор. Общая схема системы представлена на рис.17:

 

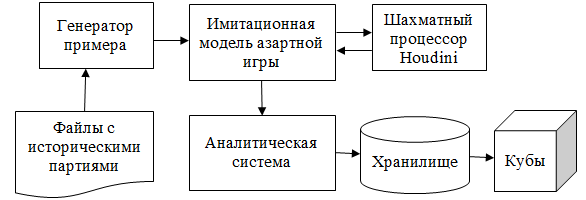
Рис. 17. Схема системы подготовки данных для анализа шахматного процессора

 

Представленная система визуального анализа была разработана, был осуществлен прогон 100’000 исторических позиций фигур на доске и сделанных по факту ходов, на основании этого прогона был сформирован многомерный куб, хранящий норму рентабельности воображаемой букмекерской конторы в зависимости от различных параметров поединка. На рисунке 18 приведен пример срезов, визуализация которых в сводных таблицах стала возможной благодаря разработанной системе:

 

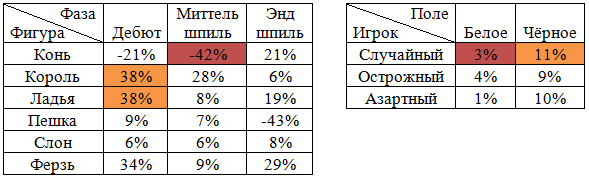
Рис. 18. Примеры визуализации нормы прибыли воображаемой шахматной букмекерской конторы в зависимости от типа пари, положения на доске, профиля игрока.

 

Аналитическая система показала принципиальную эффективность испытуемой шахматной программы, целесообразность начинания в целом. Также показатели прибыльности в различных срезах позволяют отлаживать алгоритм шахматной программы с целью минимизации возможных рисков при организации азартных игр. Демо-версия системы визуализации расположена в сети Интернет по адресу http://chess.skysense.ru/

 

10. Заключение

 

Представленный в статье программный пакет предназначен для визуализации результатов проведенного анализа чувствительности сложного процесса. С этой целью пакет использует техники многомерного анализа данных, в которых в качестве метрик используются интервальные значения исследуемых целевых показателей (в виде агрегатов MIN и MAX), а в качестве измерений – неопределенные параметры, влияющие на значение целевых показателей. Преимущества подобного подхода относительно классического однофакторного анализа заключаются в возможности развернуть массив значений целевых показателей в сложных срезах возможных значений параметров, используя мощные возможности визуализации многомерных данных, что позволяет исследователю раскрыть нелинейные связи между параметрами и показателями. Пакет позволяет исследовать процессы с функциональной связью между параметрами и показателями, а также процессы, формализованные с помощью имитационной модели. Пакет поддерживает как режим полного декартова произведения всех возможных значений параметров, так и режим определения допустимого множества возможных комбинаций, опираясь на понятие нумераторов.

С точки зрения программных компонент, пакет в целом использует возможности, предоставляемые современной BI-платформой компании Microsoft: семейство продуктов SQL Server на серверной стороне, и клиентские технологии визуализации, в первую очередь, Microsoft Excel.

Пакет был применен в порядке эксперимента для анализа чувствительности тестового бизнес-проекта, а также внедрен в организации FIDE в рамках проекта запуска международной букмекерской конторы, принимающей азартные ставки на исходы шахматных состязаний, направленного на популяризацию шахмат в широких кругах. Полученные с помощью пакета аналитические результаты показали его состоятельность в области решений для анализа чувствительности.

В будущем, по мнению автора, с точки зрения развития пакета представляют интерес в основном два направления:

1.      Разработка версии пакета для анализа чувствительности оптимизационных моделей к своим коэффициентам целевой функции, особенно для задач квадратичного программирования. Это могло бы придать свежее дыхание, например, модели Марковица в классической теории портфельного инвестирования. Сейчас эта модель представляет лишь академический интерес для изучающих дисциплину, однако, исследование чувствительности портфелей к возможным колебаниям дисперсий и корреляций отдельных активов и представление этой чувствительности в виде многомерного куба сделало бы интересным использование модели на практике.

2.      Разработка специализированной версии пакета для анализа непрерывно протекающих процессов реального времени. Например, в бесконечношаговых динамических алгоритмах принятие решения может быть основано на локальной оптимизации текущего состояния системы, в то время, как неопределенность состояния на следующих итерациях формирует интервал возможных значений результата, который связан с рядом параметров. Представляет интерес пакет, который позволял бы, исходя из текущего состояния системы, проводить непрерывный (от шага к шагу) анализ чувствительности и визуализировать лицу, принимающему решение, информацию о возможных интервалах отслеживаемых показателей в зависимости от возможных значений неопределенных параметров в будущем. Дополнительный импульс разработке такого пакета придает установившийся в последние годы на рынке BI-решений тренд на разработку сверхбыстрых решений, хранящих все данные в оперативной памяти сервера.

 

Использованная литература

  1. А.Дончев. Системы оптимального управления. Возмущения, приближения и анализ чувствительности.­– М:МИР, 1987
  2. Van der Heijden K. Scenarios, Strategies and the Strategy Process Nijenrode University Press, 1997.
  3. Соболь И.М. Метод Монте-Карло. – М.: Наука, 1972.
  4. Виленский П.Л., Лившиц В.Н., Смоляк С.А. Оценка эффективности инвестиционных проектов (теория и практика). – М.:Дело, 2001.
  5. Волкова Е.В. Методы анализа чувствительности для моделей фильтрации и массопереноса в подземной гидросфере : Диссертация на соискание ученой степени доктора технических наук.– М, 2009.
  6. Пилюгин В.В. – Компьютерная геометрия и визуализация. – М:МИФИ, 2005
  7. Алиев В. Практикум по бизнес-планированию с использованием программы Project Expert. .–М:Форум, 2010
  8. Тимофеев Т. – Анализ рисков инвестиционных проектов. Финансовый директор: 2008 №7
  9. Andrea Saltelli, Sensitivity Analysis for Importance Assessment, Risk Analysis, Vol.22, No.3, 2002

 

 

Using multidimensional analysis technologies for complex process sensitivity analysis visualization

D.A. Zholobov

National Research Nuclear University MEPhI

 

Abstract

This article presents visual multifactor sensitivity analysis software developed at MEPhI’s System analysis department. Process studied should be defined either functional or in imitation model form. The software uses modern multidimensional analysis technologies for visualization. Interval values of target indicators used as measures. Software capabilities demonstrated on example of business planning sensitivity analysis problem. In addition, article describes applying software in FIDE project.

 

Keywords: sensitivity analysis, multidimensional cube, business planning, imitation model, target indicator

 

Literature

  1. A.Donchev. Optimal Control Systems. Perturbations, estimations and sensitivity analysis.­– M:MIR, 1987 [In russian]
  2. Van der Heijden K. Scenarios, Strategies and the Strategy Process Nijenrode University Press, 1997.
  3. Sobol I.M. Monte-Carlo method. – M.: Nauka, 1972.
  4. Vilensky P.L., Livshitz V.N., Smolyak S.A. Estimation of effectiveness of investments projects (theory and practive). – M.:Delo, 2001. [In russian]
  5. Volkova E.V. Sensitivity analysis methods for models of filtration and mass transfer in underground hydrosphere: doctors dissertation.– M, 2009. [In russian]
  6. Pilyugin V.V. – Computers geometry and visualization. – М:MEPhi, 2005 [In russian]
  7. Aliev V. Business planning practicum with Project Expert.–М:Forum, 2010 [In russian]
  8. Timofeev T. – Analysis of investment projects risks. Finance Director: No.7, 2008 [In russian]
  9. Andrea Saltelli, Sensitivity Analysis for Importance Assessment, Risk Analysis, Vol.22, No.3, 2002