Оптимальная фильтрация упорядоченного набора точек визуализации дорожной сети на основе принципов дискретного динамического программирования

Ю.В. Бородакий1
, Н.А. Крицына2, А.К. Беляков3

1Национальный исследовательский ядерный университет (МИФИ), Москва, Россия (115409, г. Москва, Каширское ш., 31. E-mail kaf33@mephi.ru

2Национальный исследовательский ядерный университет (МИФИ), Москва, Россия (115409, г. Москва, Каширское ш., 31.), e-mail: nak332005@yandex.ru

3Национальный исследовательский ядерный университет (МИФИ), Москва, Россия (115409, г. Москва, Каширское ш., 31.), e-mail: belyakov.mephi@gmail.com

 

Содержание

Введение

1. Критерий выбора упорядоченных точек визуализации

2. Решение задачи минимизации критерия методом дискретного динамического программирования

3. Пример использования  принципов оптимальной фильтрации точек дорожной сети

Заключение

Список литературы

 

Аннотация

Рассматривается метод формирования оптимальной упорядоченной выборки М точек из общего набора интерполяционных точек кривой, обеспечивающие минимум интеграла квадрата ошибки интерполяции. Для решения задачи предлагается критерий, представленный в виде суммы частных интегральных критериев. Данный подход позволяет использовать для решения общей оптимизационной задачи принцип дискретного динамического программирования Беллмана. Предлагаемый метод разрабатывается для  использования в геоинформационных системах при формировании баз данных, содержащих интерполяционные точки линий (дорожная сеть, различные границы и прочие линейные объекты) для последующего их отображения на карте местности. А также для предварительной фильтрации данных, вызванной ограничениями оперативной памяти при использовании в специализированных навигационных устройствах.

 

Ключевые слова: динамическое программирование, геоинформационная система, интерполяция, линейный объект, критерий оптимизации, граф решения, узловые точки.

 

Введение

 

В настоящее время в различных областях народнохозяйственной деятельности нашли широкое применение геоинформационные системы различного назначения. Как правило, в геоинформационных системах границы областей и фронтов распространения различных физических процессов, линии уровня рельефа местности, траектории движения подвижных объектов, сеть автодорог и т.д. отображаются на карте  с помощью сплайн-интерполяции выбранного порядка по упорядоченному множеству большого числа точек визуализации. Например, сеть автомобильных дорог строится на основе обработки информации, получаемой от спутниковой навигационной системы ГЛОНАСС с интервалом в 1секунду. Эта информация [1] преобразуется в геоцентрические координаты текущей точки дорожной сети и сохраняется в базе данных дорожной сети. Очевидно, такое подробное представление существенно затягивает и усложняет процесс последующей обработки данных дорожной сети в целях дальнейшего использования. Причем, многое из этой информации является избыточным и может быть выведено из базы данных без существенной потери точности описания дорожной сети. Таким образом, возникает задача максимального сохранения степени кривизны исходного линейного объекта при заданном уровне фильтрации.

В этой связи актуальной становится задача выбора упорядоченного набора M точек визуализации из первоначального упорядоченного набора N точек визуализации, т.е., формирование упорядоченного множества точек  ().

 

1. Критерий выбора упорядоченных точек визуализации

 

В качестве критерия выбора точек рационально выбрать условие минимизации площади находящейся между линией, построенной по M упорядоченным точкам (линия ), и линии, построенной по N, упорядоченным точкам (линия ). Такой критерий эквивалентен интегралу квадрата отклонения точек линии  от соответствующих точек линии  (рис.1).

 

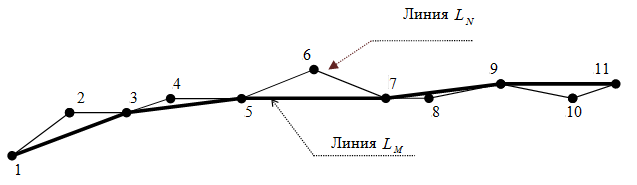
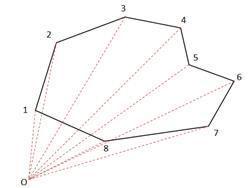
Рис. 1. Пример формирования линии . Для примера: N=11, M=6.

 

Пусть , – число точек множества  между точками множества , тогда справедливы следующие соотношения:

1.       -первые и последние точки множеств  и  совпадают;

2.       - узловые  точки линий  и  совпадают.

Так как узловые точки совпадают, то общая площадь между линиями может быть представлена в виде суммы площадей, заключенных между узловыми точками. При этом критерий оптимизации выбора точек из множества  запишем в виде суммы

                                            (1)

Где  площадь фигуры, находящейся между узловыми точками. .

Так как общее число точек множества  равно , то нетрудно заключить, что если первые  точек последовательностей совпадают, то интервал между последними точками  и  будет содержать   точек множества , и, наоборот, если последние  точек последовательностей совпадают, то интервал между первыми точками  и  будет содержать   точек множества . Кроме того, общее число точек – N. Таким образом, ограничения, накладываемые на аргумент оптимизации, будут иметь вид:

, - целое число.                      (2)

.                 (3)

 

2. Решение задачи минимизации критерия методом дискретного динамического программирования

 

Представление критерия (1) в виде суммы дает основание использовать принцип метода дискретного динамического программирования [2]. Решение данной оптимизационной задачи удобно представить в виде ограниченного графа на сетке решений (рис. 2) [3,4].

 

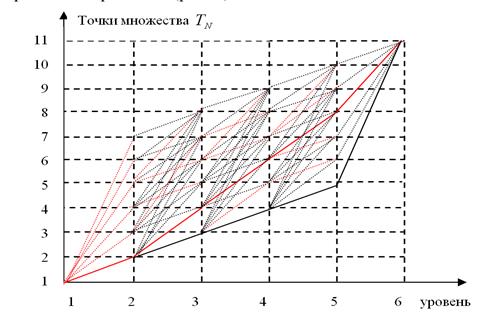
Рис. 2. Пример графа решения задачи методом дискретного динамического программирования.

 

Для примера: Красной пунктирной линией отмечены «условно» оптимальные пути, красной линией отмечен оптимальный путь.

 

По горизонтальной оси будем откладывать уровни решения задачи, причем число уровней соответствует числу точек множества . По вертикальной оси – точки множества , в которые можно попасть на i-том уровне. Очевидно, в силу ограничений (2) и (3), каждый уровень (кроме первого и последнего) содержит точек.

Так как на первом уровне имеется единственная точка , то в точку  второго уровня возможно попасть только единственным путем  (рис. 2). При этом каждой точке уровня 2 будет соответствовать площадь фигуры , опирающейся на хорду между точками  и  (рис. 1). Значения этих площадей запоминаем.

При формировании третьего уровня, в каждую точку  уровня 3 возможно попасть многими путями из точек 2-го уровня (рис. 2). При этом каждому пути  будет соответствовать свое значение суммы площадей

.                      (4)

               (5)

Очевидно, чем больше номер , тем больше путей могут привести в эту точку, и тем больше различных значений площадей будет соответствовать этой точке. Выберем путь в точку , который соответствует минимальной площади. С этой целью для каждой точки  найдем такое , которое обеспечивает минимум критерия (4),

,                 (6)

                      (7)

Полученные значения ,  запоминаем. На рисунке в качестве примера оптимальные пути для точек уровня 3 выделены красным цветом

Описанную выше процедуру формирования точек уровня 3 повторяем для уровней  В результате, для уровня  будем иметь следующие соотношения:

,               (9)

               (10)

Полученные значения ,  запоминаем.

Последний уровень M имеет только одну точку , попасть в которую можно из точек предыдущего уровня  (рис. 2). Причем, каждому пути  , будет соответствовать значение площади:

                        (11)

Найдем единственный путь, обеспечивающий минимум критерия (11):

,                        (12)

               (13)

Используя соотношения (12), (9) и (6), пройдем весь путь по оптимальным точкам в обратном направлении:

                   (14)

Перечисленная в (14) последовательность будет оптимальным набором точек множества , обеспечивающих минимум критерия (1).

Зная номера точек множества , входящих в множество , нетрудно найти оптимальное число точек между узлами , которые в дальнейшем не будут участвовать в процессе описания дорожной сети.

Для оценки эффективности предложенного алгоритма была проведены оптимизация набора точек визуализации

Зная номера точек множества , входящих в множество , нетрудно найти оптимальные число точек между узлами .

Особенностью приведенного выше метода является максимальное сохранение степени кривизны исходного линейного объекта при заданных коэффициентах фильтрации

 

3. Пример использования  принципов оптимальной фильтрации точек дорожной сети

 

Работоспособность предложенного алгоритма была исследована на базе упорядоченной последовательности точек, представленных в OSM [7] в формате WGS84 в виде широты/долготы (WGS84— трёхмерная система координат для позиционирования на Земле, в которой за основу взят эллипсоид с большим радиусом — 6 378 137 м (экваториальный) и меньшим — 6 356 752,3142 м (полярный)). Так как в качестве критерия выбора точек было поставлено условие минимизации площади между линией, построенной по M упорядоченным точкам, и линии, построенной по N упорядоченным точкам (N>M), то возникла необходимость подсчета площадей произвольных многоугольников, лежащих на эллипсоиде и задаваемых точками, геоцентрические координаты которых известны.

Для решения этой задачи координаты точек пути переводятся в координаты Меркатора  по формулам [6]:

 

,

где:

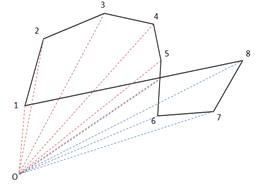
Как уже отмечалось выше, в качестве критерия выбора точек было поставлено условие минимизации площади между линией, построенной по M упорядоченным точкам визуализации, и линии, построенной по N упорядоченным точкам визуализации (N>M). Таким образом, задача нахождения критерия сводится к задаче нахождения площади произвольного многоугольника, заданного координатами вершин. Для подсчета площади берется произвольная точка О (например, начало координат). Тогда площадь многоугольника (рис.3) при обходе вершин в последовательности 1,2,…,N будет равна [4]:

 ,

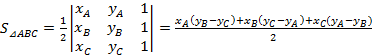, xi, yi – координаты Меркатора точки «i».

Видно, что  при обходе вершин против часовой стрелки, и  при обходе по часовой стрелке. Таким образом, с учетом знаков при сложении площадей треугольника,  получаем искомую площадь многоугольника.

 

http://cs521111.vk.me/u1559789/doc/25178f710860/ploschad_mnogoug.png

http://cs521111.vk.me/u1559789/doc/6f597471b93b/ploschad_mnogoug_samoper.png

Рис.3. К подсчету площади многоугольника (не самопересекающийся многоугольник).

Рис.4. К подсчету площади многоугольника
(самопересекающийся многоугольник).

 

Для случая самопересекающегося многоугольника для каждой пары отрезков решается задача о пересечении двух прямых. Если точка пересечения существует, то определяется, принадлежит ли она отрезкам, образующим многоугольник (рис.4). Далее самопересекающийся многоугольник делится в точке пересечения на не самопересекающиеся многоугольники, площадь которых находится изложенным выше методом.

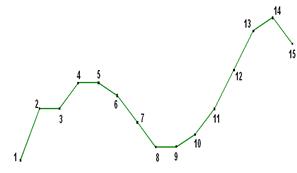
Рассмотрим работу алгоритма более подробно на примере N=15, M=7 (рис. 5).

 

Рис.5. Первоначальный набор из N=15 точек визуализации

Рис.6. Формирование точек  2-го уровня

 

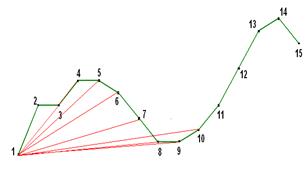
На первом уровне имеется единственная точка, из которой в точки второго уровня можно попасть N-M+1= 15-7+1=9 способом (рис.6). Каждой точке 2-го уровня соответствует площадь фигуры, опирающейся на хорду между 1-ой точкой и соответствующей точкой 2-го уровня. Эти площади подсчитываются и запоминаются.

При формировании третьего уровня, в каждую точку уровня 3 можно попасть из каждой точки 2-го уровня На рисунке 7 показаны возможные условно-оптимальные пути в точки уровня 3 из точки 2 уровня 2. Аналогичные рисунки могут быть представлены для точек 3, 4,…,11 уровня 2.

 

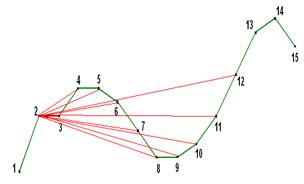
Рис.7. Формирование условно оптимальных путей 3-го уровня для точки 2 2-го уровня.

 

При этом, в соответствии с формулой (4), каждому пути  будет соответствовать свое значение суммы площадей перехода с уровня 1 на уровень 2, и с уровня 2 на уровень 3.

Для каждой точки 3-го уровня необходимо выбрать путь, который соответствует минимальной площади (см. соотношение (6, 7)). В результате получим набор условно-оптимальных путей для уровня 3.

Последний уровень имеет только одну точку, попасть в которую можно из точек предыдущего уровня. Необходимо найти единственный путь, обеспечивающий минимум критерия.

Проходя весь путь по оптимальным точкам в обратном направлении можно найти оптимальный набор точек, обеспечивающий минимум критерия. Представив решение данной задачи в виде ограниченного графа на сетке решений, можно найти набор оптимальных точек.

Для рассматриваемого примера это точки – 1, 2, 3, 4, 9, 14, 15 (рис. 8).

 

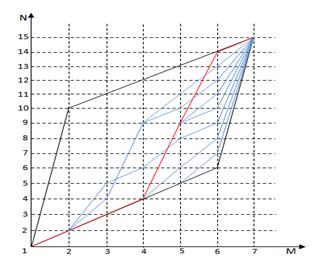
graph.png

Рис.8. Граф решения задачи. Красной линией отмечен оптимальный путь. Синими линиями отмечены условно-оптимальные пути.

 

Построенная по полученному оптимальному набору точек кривая представлена на рисунке 9. Ошибка фильтрации точек относительно первоначальной кривой при уровне фильтрации  составляет Sф=1,1у.е

 

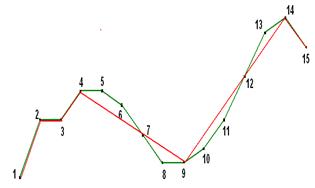
Рис.9. Желаемый набор из M=7 точек визуализации, , Sф = 1,1

 

Для оценки работоспособности разработанного математического и программного обеспечения был проведен тестовый расчет при N=54 (рис.10) при коэффициентах фильтрации 2, 3 и 5. Результаты моделирования приведены на рисунках 11, 12, 13.

 

Рис.10. Первоначальный набор из 54 упорядоченных точек визуализации

Рис.11., M=27, ошибка фильтрации точек визуализации Sф=1,937у.е.

Рис.12., M=18, ошибка фильтрации точек визуализации Sф=3,405 у.е.

Рис.13. , M=10, ошибка фильтрации точек визуализации Sф=6,598 у.е.

 

Видно, что кривизна исходного объекта сохраняется даже при уменьшении числа точек с 54 до 10.

 

Заключение

 

Как уже отмечалось, приведенный алгоритм может быть применен в информационных системах различного назначения для фильтрации большого объема данных при обработке линейных объектов, в частности, маршрутов (треков), полученных с помощью автоматизированных средств записи перемещения объектов (GPS/ГЛОНАСС-приёмники), для уменьшения времени изображений различных линейных объектов в ГИС.

Кроме того, многие специализированные навигационные устройства позволяют загружать в память пути (треки) с ограниченным количеством точек (например, максимальное количество точек пути, которые можно загрузить в популярные устройства серии FORERUNNER производства компании GARMIN составляет 500 точек) Приведенный метод позволяет осуществлять предварительную обработку данных для загрузки в такие устройства.

 

Список литературы

 

  1. Бабич О.А. Обработка информации в навигационных комплексах.-М.: Машиностроение, 1991, -512с.
  2. Крицына Н.А. Оптимизация параметров численного решения уравнений динамики. Сборник научных трудов «Алгоритмы цифрового оценивания, контроля и управления» под ред. Д.т.н,, профессора Иващенко Н.Н. – М: АТОИЗДАТ, 1990, – 180 с.
  3. Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. — М.: Наука, 1978.
  4. И. Х. Сигал, А. П. Иванова Введение в прикладное дискретное программирование: модели и вычислительные алгоритмы: Учеб. пособие. — Изд. 2-е, испр. — М.: ФИЗМАТЛИТ, 2003. — 240 с.
  5. Клейн.Ф. Элементарная математика с точки зрения высшей: В 2-х томах. Т.2.Геометрия: Пер. с нем. под ред. В.Г.Болтянского. – Изд. 2-е. – М.:Наука. Гл. ред. физ. мат. лит.,1987. – 416с.
  6. http://wiki.gis-lab.info/  Пересчет координат из Lat/Lon в проекцию Меркатора и обратно.
  7. http://habrahabr.ru/ Структура данных проекта OpenStreetMap.


Optimal filtering of an ordered set of visualization points of road network based on the principles of discrete dynamic programming

Y.V. Borodakiy1
, N.А. Kritsyna2, A.K. Belyakov3

1National Research Nuclear University (MEhPI), Moscow, Russia (115409, Moscow, Kashirskoe highway, 31). e-mail kaf33@mephi.ru

2National Research Nuclear University (MEhPI), Moscow, Russia (115409, Moscow, Kashirskoe highway, 31). e-mail: nak332005@yandex.ru

3National Research Nuclear University (MEhPI), Moscow, Russia (115409, Moscow, Kashirskoe highway, 31). e-mail: belyakov.mephi@gmail.com

 

Abstract

 

The paper focuses on the method of forming the optimal ordered selection of M points from the set of interpolation points of the curve, providing a minimum integral square error in-interpolation. A criterion presented as the sum of private in-integrally criteria is proposed to solve this problem. This approach allows to solve the general problem of optimization-term principle of the discrete Bellman dynamic programming. The proposed method is developed for use in geographic information systems in the formation of databases containing the interpolation points of lines (roads, borders and various other linear objects) for subsequent display on a map as well as the prefiltration of data caused by memory limitations when used in specialized navigation devices.

 

Keywords: dynamic programming, geographic information system, interpolation, linear object, optimization criterion, graphic representation of solution, solutions hotspots.

 

References

  1. Babich O.A. Information processing in the navigation komplexes. M .: Machine-building, 1991, 512 p.[In russian]
  2. Kritsyna N.A. Optimization of parameters of the numerical solution of the equations of dynamics. Collection of scientific papers «Algorithms for digital evaluation, monitoring, and managing» ed. By professor Ivashchenko N.N. PhD – M: ATOIZDAT, 1990 – 180 p.[In russian]
  3. Moiseev N.N., Ivanilov Y.P., Stolyarova E.M. Optimization techniques. - M .: Nauka, 1978.[In russian]
  4. Sigal I.Kh., Ivanov A.P. Introduction to applied discrete programming: models and computational algorithms: Textbook. - Ed. 2nd, rev. - M .: FIZMATLIT, 2003. - 240 p.[In russian]
  5. Kleyn F. Elementary mathematics from the point of view of the highest mathemathics: in 2 volumes. T.2.Geometry: Trans. From german. Ed. V.G.Boltyanskogo. - Ed. 2nd. - Moscow: Nauka. Ch. Ed. nat. mat. lit., 1987. – 416 p.[In russian]
  6. http://wiki.gis-lab.info/  Recalculation of coordinates Lat/Lon in Mercator projection and back.
  7. http://habrahabr.ru/ The data structure of the project OpenStreetMap.