МОЛЕКУЛЯРНО–ДИНАМИЧЕСКОЕ МОДЕЛИРОВАНИЕ И ВИЗУАЛИЗАЦИЯ ПЛАВЛЕНИЯ КРИСТАЛЛА АЛЮМИНИЯ В УДАРНОЙ ВОЛНЕ
Губин С. А. 1, Маклашова И.В.1, Селезенев А.А.1,2, Козлова С.А.1, Демиденко Т.С.1
1Национальный исследовательский ядерный университет «МИФИ», Москва
2ФГУП РФЯЦ ВНИИЭФ Саров
Содержание
Аннотация
Методом молекулярной динамики рассчитаны ударная адиабата алюминия и зависимость температуры кристалла алюминия от величины давления его ударного сжатия. Результаты молекулярно–динамического расчета с высокой точностью совпадают с результатами ударно-волновых экспериментов. Выделена область плавления кристалла алюминия при его ударно-волновом сжатии.
Ключевые слова: Молекулярно–динамическое моделирование, ударная волна, потенциал межмолекулярного взаимодействия, линия плавления
1. Введение
Смеси конденсированных взрывчатых веществ (ВВ) часто содержат в своем составе алюминий в виде дисперсных или нанодисперсных частиц. Массовая доля алюминиевых частиц в таком составе может достигать десятков процентов. В продуктах детонации (ПД) подобных ВВ образуются частицы твердого или жидкого алюминия, присутствие которых необходимо учитывать в выражениях для термодинамических потенциалов смеси продуктов при проведении термодинамических расчетов. Горение алюминия в продуктах детонации ВВ влияет на работоспособность устройств, использующих эффект детонации, изменяет скорость детонации и повышает энерговыделение. Поэтому важно знать область плавления алюминия в ударной волне и рассчитывать теплофизические свойства твердого и жидкого алюминия в области высоких давлений и температур.
В [1] был использован метод молекулярно-динамического (МД) моделирования для изучения плавления металлов, в том числе алюминия. Численно полученные зависимости температуры плавления при статическом сжатии сравнивали с диаграммами зависимости давления от массовой скорости (P-U) при ударном сжатии металлов. На основе такого сравнения были определены значения давления и температуры за ударной волной (УВ), при которых произошло плавление металла. Однако подход [1] не учитывает, что сжатие в ударной волне сопровождается ростом энтропии и принципиально отличается от статического сжатия вещества [2], а малые времена воздействия УВ на вещество 1–10 мкс не позволяют фазовым переходам, в том числе плавлению, реализовываться на линии термодинамического равновесия. Поэтому только прямое МД моделирование сжатия алюминия в ударных волнах может дать близкие к экспериментальным значения температуры плавления [2].
2. Методика расчета
В настоящей работе рассчитанные методом МД моделирования зависимость температуры плавления от давления в ударных волнах сравнивались с экспериментальными и вычисленными значениями для определения достоверных параметров плавления алюминия.
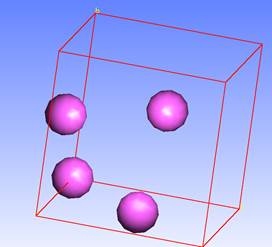
Молекулярно-динамическое (МД) моделирование процесса плавления алюминия при его ударном сжатии проводилось с использованием компьютерного кода SageMD [2]. Для расчета параметров алюминия расчетная ячейка представлялась в форме куба. В начальном состоянии структура решётки алюминия – кубическая гранецентрированная, период решётки 4.050 Å [3]. Элементарная ячейка кристалла алюминия содержит 4 атома. Расчетная суперячейка строилась из 10 элементарных ячеек в каждом направлении. Таким образом, расчетная суперячейка состояла из 4000 атомов алюминия, как показано на рис. 1. При проведении МД моделирования по всем трём пространственным направлениям использовались периодические граничные условия.
МД моделирование позволяет визуализировать структуру алюминия на атомистическом уровне и рассчитать свойства материала при нагреве в ударной волне. Кадры визуализации распределения атомов в микрообъеме за фронтом ударной волны при сохранении атомной структуры алюминия и при плавлении сильно различаются. Изменение расположения атомов алюминия внутри расчетной ячейки при плавлении наглядно указывает на потерю ближнего и дальнего порядка. Сопоставление функции распределения с расчетами визуализации распределения атомов позволяет точно интерпретировать плавление алюминия.
|
|
|
Рис. 1. Элементарная ячейка алюминия и расчетная суперячейка.
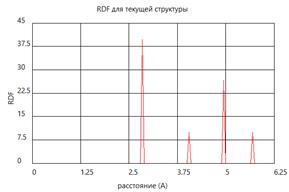
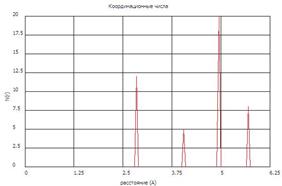
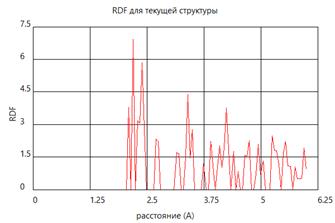
На рис. 2 показана расчетная функция радиального распределения атомов для исходного состояния кристалла алюминия. Сравнивая вид функции распределения атомов в состоянии за фронтом ударной волны с исходным, можно делать выводы о сохранении кристаллической структуры вещества или его плавлении.
|
|
|
Рис. 2. Координационные числа и функция радиального распределения атомов для исходного кристалла алюминия.
Взаимодействие между атомами алюминия для твёрдой и жидкой фазы описывалось потенциалом Морзе
![]() . (1)
. (1)
где r0— равновесное расстояние, U0— глубина потенциальной ямы.
Значения свойств алюминия, такие как межатомное расстояние а, атомарная масса m, длина волны де Бройля l, параметры потенциала взаимодействия (1), используемые для расчета приведены в таблице. Значения параметров потенциала (1) взяты из базы данных кода SageMD [2].
Таблица 1. Параметры потенциала Морзе для Al.
|
|
|
|
|
U0, эВ |
r0, Å |
a, 1/Å |
Радиус обрезания, Å |
|
Al |
2.863 |
26.981 |
6.72. 10-2 |
0.265915 |
3.203082 |
1.211824 |
8,7 |
Для описания ударного сжатия твердого тела плоской одномерной волной использовалось соотношение Рэнкина - Гюгонио для изменения внутренней энергии E в зависимости от давления Р и удельного объема V (физические величины с индексом "0" соответствуют параметрам среды перед ударной волной)
![]() ,
(2)
,
(2)
что позволяет рассчитать все термодинамические свойства вещества вдоль ударной адиабаты (УА).
При MД моделировании ударного сжатия кристалла алюминия использовался метод Гюгониастата [4], реализованный в коде SageMD [2]. После формирования расчетной ячейки, в ней задавались определенные значения давления P, а температура определялась из соотношения Рэнкина-Гюгонию (2). Для заданного давления Р и полученной температуры Т определялись теплофизические и термодинамические свойства алюминия за фронтом ударной волны. Плавление кристалла после его ударного сжатия идентифицировалось при анализе расчетной функции радиального распределения атомов и функции квадратичного смещения атомов кристалла.
3. Результаты
На рис. 3, 4 показана расчетная УА кристалла алюминия в сравнении с экспериментальными данными [5-14]. Из результатов, представленных на рис. 3,4 видно отличное согласие расчетных (линия) и экспериментальных данных (маркеры) как теплофизических (рис. 3), так и волновых характеристик (рис. 4) ударно-волнового сжатия алюминия во всем диапазоне изменения давления, как при небольших степенях сжатия, так и при экстремально высоких.
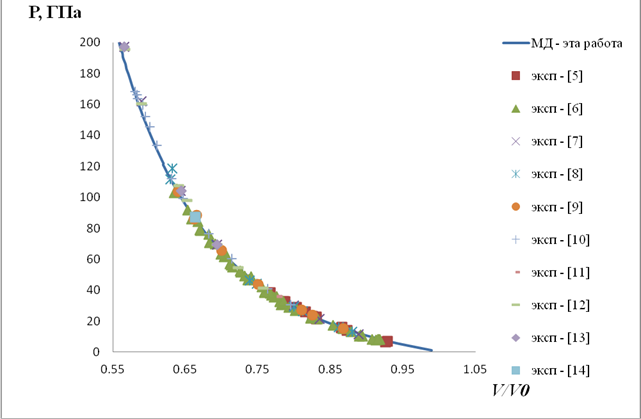
Рис. 3. Зависимость давления ударного сжатия алюминия от степени сжатия материала. Линия – эта работа, маркеры – экспериментальные данные [5 - 14].
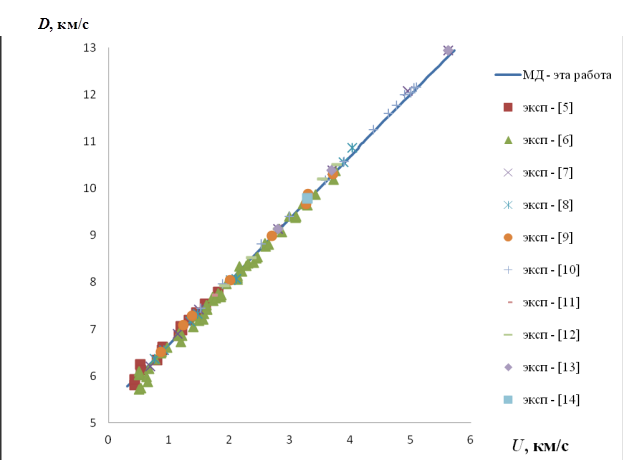
Рис. 4. Зависимость скорости ударной волны от массовой скорости за фронтом волны. Линия – эта работа, маркеры – экспериментальные данные [5 -14].
На рис. 5 приведена рассчитанная в данной работе зависимость температуры ударно сжатого кристалла алюминия от величины давления за фронтом УВ. На рис. 5 показаны экспериментальные значения давления плавления алюминия в УВ, полученные экспериментально в [15]. Величина температуры Al в [15] рассчитывалась.
Для сопоставления значений давления и температуры на УА с областями фазовой стабильности алюминия на рис. 5 показаны параметры плавления при статическом сжатии [16-22]. Из рис. 5 видно, что параметры УА при значениях давления до 100 ГПа лежат в области существования твердого алюминия. Экспериментальные данные [15], соответствующие плавлению алюминия в УВ, хорошо согласуются с изломом на расчетной зависимости давления за фронтом УВ. Это свидетельствует о том, что область плавления ударно-сжатого Al предсказана правильно. Параметры УА при высоких давлениях выше 120 ГПа наиболее вероятно лежат в области существования жидкого алюминия.
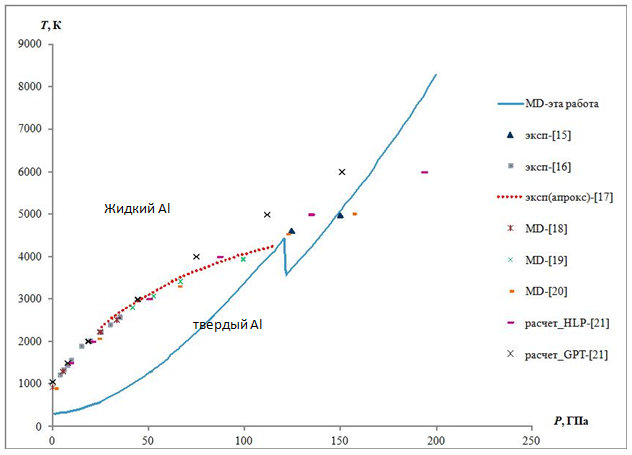
Рис. 5. Расчетные значения давления и температуры на УА алюминия. Линия – МД расчет данной работы давления и температуры ударного сжатия, маркеры [15] – экспериментальные значения давления плавления алюминия в УВ, маркеры [17] – [21] – значения температуры плавления алюминия при статическом сжатии.
|
|
|
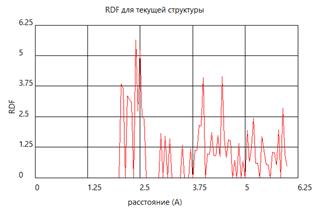
Рис. 6. Структура кристалла и функция радиального распределения атомов при ударно-волновом сжатии до 120 ГПа
На рис. 6 показана структура кристалла алюминия на УА при давлении 120 ГПа. Из рисунка видно, что в этих условиях пропадает упорядоченность структуры кристалла, расчет функции радиального распределения атомов также указывает на исчезновение дальнего порядка в кристаллической решетке, т.е. возможно, что при этих условиях начинается плавление кристалла алюминия. При давлении 120 ГПа наблюдается характерный излом на зависимости температуры от давления ударного сжатия, показанной на рис.5.
|
|
|
Рис. 7. Интерактивное графическое изображение структуры кристалла и функция радиального распределения атомов при сжатии в ударной волне 122 ГПа
На рис. 7 показаны интерактивное графическое изображение структуры кристалла и функция радиального распределения атомов при ударно-волновом давлении 122 ГПа. Ударно-волновой разогрев вещества показан изменением цвета атомов в расчетной ячейке. Из рисунка видно, что в расположении атомов не сохраняется ни ближний, ни дальний порядок, т.е. полученную конфигурацию атомов можно рассматривать как жидкую фазу.
Таким образом, результаты МД моделирования показывают, что плавление алюминия в УВ происходит при давлении около 122 ГПа и температуре 4200 K.
Использование современных инструментов визуализации для МД моделирования позволяет создавать анимационные интерактивные графические изображения для визуализации изменения структуры кристаллической решетки и фиксирования плавления в ударных волнах (рис. 7).
4. Заключение
Методом МД моделирования с использованием методики Гюгониостат рассчитаны свойства алюминия в твердой и жидкой фазах и зависимость температуры алюминия от давления в УВ. На полученной зависимости температуры кристалла от давления УВ наблюдается характерный излом при давлении 115-122 ГПа. Характер излома на полученной кривой может свидетельствовать о наличии фазового перехода в кристалле алюминия (плавление) в данной области температур и давлений. Визуализация структуры кристалла и расчет функции радиального распределения атомов показывают, что в расположении атомов при указанных температурах и давлениях отсутствует ближний и дальний порядок, что можно интерпретировать как плавление алюминия.
Сопоставление результатов, полученных в данной работе методом МД моделирования, с известными из литературы результатами моделирования зависимости температуры статического плавления алюминия [18 – 21], а также экспериментальных данных статического плавления [16 –17] и экспериментальных параметров плавления в УВ [15] от давления показывает их взаимную непротиворечивость.
Литература
- Ji-Wook Jeong, In-Ho Lee, K. J. Chang. Molecular-dynamics study of melting on the shock Hugoniot of Al // PHYSICAL REVIEW B, V.59, 1999, p.329-333.
- A.A. Selezenev, V.K. Golubev, A.Y. Aleinikov, O.I. Butnev, R.A. Barabanov, B.L. Voronin. Molecular Dynamics Simulation of Shock Wave Compression of Metals. // In proceedings of Int. Conference «Shock Compression of Condensed Matter» (SCCM), 2001, USA, Atlanta, p. 374-377.
- Химическая энциклопедия. В 5-ти т. / Редкол. Кнунянц И.Л. (гл. ред.). М.: Советская энциклопедия, 1988. — Т. 1.
- A.A.Selezenev, A.Yu. Aleynikov, N.S.Ganchuk, P.V.Ermakov, S.N.Ganchuk, J.B.Aidun, A.P. Thompson. Shock Compression Calculation of RDX and PETN Molecular Crystals Using Hugoniostat Method. // In proceedings of International Conference «Shock Compression of Condensed Matter» (SCCM), 2009, USA, Nashville.
- S. P. Marsh (Ed.), LASL Shock Hugoniot Data, (Univ. California Press, Berkeley, 1980).
- R. G. McQueen, S. P. Marsh, J. W. Taylor, J. N. Fritz, W. J. Carter, The equation of state of solids from shock wave studies. // High Velocity Impact Phenomena / Ed. R.Kinslow. - New-York: Academic Press, p.293-417; appendies on pp. 515-568 (1970).
- L. V. Al'tshuler, B. S. Chekin, Metrology of high pulsed pressures. // in: Proceed. of 1 All-Union Pulsed Pressures Simposium (VNIIFTRI, Moscow, 1974) V.1, 5-22 (in Russian).
- R. F. Trunin, L.F.Gudarenko, M. V. Zhernokletov, G. V. Simakov, Experimental data on shock compressibility and adiabatic expansion of condensed substances, RFNC, Sarov (2001) (in Russian).
- L. V. Al'tshuler, A. A. Bakanova, I. P. Dudoladov, E. A. Dynin, R. F. Trunin, B. S. Chekin, Shock adiabats for metals. New data, statistical analysis and general regularities. // Zh. Prikl. Mekh. Tekhn. Fiz. 2, 3-34 (1981) (in Russian) (J. Appl. Mech. Techn. Phys. 22, 145 (1981)).
- A. C. Mitchell, W. J. Nellis, Shock compression of aluminum, copper and tantalum. // J. Appl. Phys. v. 52, p. 3363-3374 (1981).
- L. V. Al'tshuler, A. P. Petrunin, Rentgenographic investigation of compressibility of light substances under obstacle impact of shock waves. // Zh. Tekhn. Fiz. 31(6), 717-725 (1961) (in Russian).
- L. V. Al'tshuler, S. B. Kormer, M. I. Brazhnik, L. A. Vladimirov, M. P. Speranskaya, A. I. Funtikov, The isentropic compressibility of aluminum, copper, lead at high pressures. // Zh. Eksp. Teor. Fiz. 38(4), 1061-1073 (1960) (in Russian) (Sov. Phys. - JETP 11(4), 766-775 (1960)).
- L. V. Al'tshuler, S. B. Kormer, A. A. Bakanova, R. F. Trunin, Equations of state for aluminum, copper and lead in the high pressure region. // Zh. Eksp. Teor. Fiz. 38, 790-798 (1960) (in Russian) (Sov. Phys. - JETP 11, 573-579 (1960)).
- M. A. Podurets, G. V. Simakov, R. F. Trunin, Transition of stishovite to a denser phase. // Izv. Akad. Nauk SSSR. Fiz. Zemli 4, 30-37 (1990) (in Russian).
- J.W. Shaner et al. // in "High Pressure Science and Technology", eds. C. Homan, R.K.MacCrone, E. Whalley (North Holland, Amsterdam, 1984), pp. 137-141.
- E. L. Baker and Ch. Capellos," Jaguar procedures for detonation properties of aluminized explosives", U.S. ARMY TACOM-ARDEC Picatinny Arsenal, New Jersey 07806.
- R. Boehler and M. Ross, Melting curve of aluminum in a diamond cell to 0.8 Mbar: implications for iron. // Earth Planet. Sci. Lett.153, 223, (1997).
- А. И. Ботячкова, С. А. Губин, И. Л. Соколова, Г. Г. Карпинский. Молекулярно-динамическое моделирование плавления алюминия в макросостоянии при повышенном давлении. // ЯДЕРНАЯ ФИЗИКА И ИНЖИНИРИНГ, том 4, № 5, с. 423–424, (2013 г).
- S. V. Starikov, V. V. Stegailov. Atomistic simulation of the premelting of iron and aluminum: Implications for high-pressure melting-curve measurements. // PHYSICAL REVIEW B 80, 2009, p. 220104-1 220104.4.
- J. Bouchet, F. Bottin, G. Jomard, G. Zérah. Melting curve of aluminum up to 300 GPa obtained through ab initio molecular dynamics simulations. // PHYSICAL REVIEW B 80, 2009, p. 094102-1 094102-5.
- J. A. Moriarty, D. A. Young, and M. Ross, "Theoretical study of the aluminum melting curve to very high pressure". // PHYSICAL REVIEW B, V. 30, 1984, рp. 578-588.
MOLECULAR DYNAMICS SIMULATION AND VISUALIZATION OF MELTING ALUMINUM CRYSTAL IN SHOCK WAVE
Gubin S.A. 1, Maklashova I.V.1, Selezenev A.A.1,2, Kozlova S.A.1, Demidenko T.S.1
1 National Research Nuclear University "Moscow Engineering Physics Institute", Moscow, Russia
2 Russian Federal Nuclear Center All-Russian Research Institute of Experimental Physics, Sarov, Russia
Abstract
The dependence of the melting temperature on the pressure under shock-wave compression of aluminum was calculated by molecular-dynamic modeling technique. The results of molecular-dynamic calculations with high accuracy are consistent with the experimental data on shock wave compressibility. The range of the aluminum melting under shock-wave compression was selected.
Keywords: Molecular-dynamic simulation, shock wave, the intermolecular interaction potential, melting line.
Bibliography
- Ji-Wook Jeong, In-Ho Lee, K. J. Chang. Molecular-dynamics study of melting on the shock Hugoniot of Al // PHYSICAL REVIEW B, V.59, 1999, p.329-333.
- A.A. Selezenev, V.K. Golubev, A.Y. Aleinikov, O.I. Butnev, R.A. Barabanov, B.L. Voronin. Molecular Dynamics Simulation of Shock Wave Compression of Metals. // In proceedings of Int. Conference «Shock Compression of Condensed Matter» (SCCM), 2001, USA, Atlanta, p. 374-377.
- Chimicheskaya entsiklopedia. In 5 t. / Redkol. Knunyants I.L. (gl.red). M.: Soviet encyclopedia, 1988 – T.1. (in Russian)
- A.A.Selezenev, A.Yu. Aleynikov, N.S.Ganchuk, P.V.Ermakov, S.N.Ganchuk, J.B.Aidun, A.P. Thompson. Shock Compression Calculation of RDX and PETN Molecular Crystals Using Hugoniostat Method. // In proceedings of International Conference «Shock Compression of Condensed Matter» (SCCM), 2009, USA, Nashville.
- S. P. Marsh (Ed.), LASL Shock Hugoniot Data, (Univ. California Press, Berkeley, 1980).
- R. G. McQueen, S. P. Marsh, J. W. Taylor, J. N. Fritz, W. J. Carter, The equation of state of solids from shock wave studies. // High Velocity Impact Phenomena / Ed. R.Kinslow. - New-York: Academic Press, p.293-417; appendies on pp. 515-568 (1970).
- L. V. Al'tshuler, B. S. Chekin, Metrology of high pulsed pressures. // in: Proceed. of 1 All-Union Pulsed Pressures Simposium (VNIIFTRI, Moscow, 1974) V.1, 5-22 (in Russian).
- R. F. Trunin, L.F.Gudarenko, M. V. Zhernokletov, G. V. Simakov, Experimental data on shock compressibility and adiabatic expansion of condensed substances, RFNC, Sarov (2001) (in Russian).
- L. V. Al'tshuler, A. A. Bakanova, I. P. Dudoladov, E. A. Dynin, R. F. Trunin, B. S. Chekin, Shock adiabats for metals. New data, statistical analysis and general regularities. // Zh. Prikl. Mekh. Tekhn. Fiz. 2, 3-34 (1981) (in Russian) (J. Appl. Mech. Techn. Phys. 22, 145 (1981)).
- A. C. Mitchell, W. J. Nellis, Shock compression of aluminum, copper and tantalum. // J. Appl. Phys. v. 52, p. 3363-3374 (1981).
- L. V. Al'tshuler, A. P. Petrunin, Rentgenographic investigation of compressibility of light substances under obstacle impact of shock waves. // Zh. Tekhn. Fiz. 31(6), 717-725 (1961) (in Russian).
- L. V. Al'tshuler, S. B. Kormer, M. I. Brazhnik, L. A. Vladimirov, M. P. Speranskaya, A. I. Funtikov, The isentropic compressibility of aluminum, copper, lead at high pressures. // Zh. Eksp. Teor. Fiz. 38(4), 1061-1073 (1960) (in Russian) (Sov. Phys. - JETP 11(4), 766-775 (1960)).
- L. V. Al'tshuler, S. B. Kormer, A. A. Bakanova, R. F. Trunin, Equations of state for aluminum, copper and lead in the high pressure region. // Zh. Eksp. Teor. Fiz. 38, 790-798 (1960) (in Russian) (Sov. Phys. - JETP 11, 573-579 (1960)).
- M. A. Podurets, G. V. Simakov, R. F. Trunin, Transition of stishovite to a denser phase. // Izv. Akad. Nauk SSSR. Fiz. Zemli 4, 30-37 (1990) (in Russian).
- J.W. Shaner et al. // in "High Pressure Science and Technology", eds. C. Homan, R.K.MacCrone, E. Whalley (North Holland, Amsterdam, 1984), pp. 137-141.
- E. L. Baker and Ch. Capellos," Jaguar procedures for detonation properties of aluminized explosives", U.S. ARMY TACOM-ARDEC Picatinny Arsenal, New Jersey 07806.
- R. Boehler and M. Ross, Melting curve of aluminum in a diamond cell to 0.8 Mbar: implications for iron. // Earth Planet. Sci. Lett.153, 223, (1997).
- A. I. Botyachkova, S. A. Gubin, I. L. Sokolova, G. G. Karpinskiy. Molecular dynamics simulation of melting aluminum in macrostate at high pressure.// Nuclear physics and engineering, 2013, tom 4,№ 5, c. 423-424. (in Russian)
- S. V. Starikov, V. V. Stegailov. Atomistic simulation of the premelting of iron and aluminum: Implications for high-pressure melting-curve measurements. // PHYSICAL REVIEW B 80, 2009, p. 220104-1 220104.4.
- J. Bouchet, F. Bottin, G. Jomard, G. Zérah. Melting curve of aluminum up to 300 GPa obtained through ab initio molecular dynamics simulations. // PHYSICAL REVIEW B 80, 2009, p. 094102-1 094102-5.
- J. A. Moriarty, D. A. Young, and M. Ross, "Theoretical study of the aluminum melting curve to very high pressure". // PHYSICAL REVIEW B, V. 30, 1984, рp. 578-588.