MOLECULAR DYNAMICS SIMULATION AND VISUALIZATION OF MELTING ALUMINUM CRYSTAL IN SHOCK WAVE
Gubin S.A. 1, Maklashova I.V.1, Selezenev A.A.1,2, Kozlova S.A.1, Demidenko T.S.1
1 National Research Nuclear University "Moscow Engineering Physics Institute", Moscow, Russia
2 Russian Federal Nuclear Center All-Russian Research Institute of Experimental Physics, Sarov, Russia
Contents
Abstract
The dependence of the melting temperature on the pressure under shock-wave compression of aluminum was calculated by molecular-dynamic modeling technique. The results of molecular-dynamic calculations with high accuracy are consistent with the experimental data on shock wave compressibility. The range of the aluminum melting under shock-wave compression was selected.
Keywords: Molecular-dynamic simulation, shock wave, the intermolecular interaction potential, melting line.
1. INTRODUCTION
Condensed high explosive mixture often contain the aluminum in its composition in the form of dispersed particles or nanoparticles. The mass fraction of aluminum particles in such high energy systems can reach tens percents in this composition. Aluminum is formed in the detonation products (DP) of similar systems as condensed or liquid particles. The presence of aluminum is necessary to consider in the expressions for the thermodynamic potentials of the product mixture in thermodynamic calculations. The burning aluminum in DP affects to the efficiency of devices using the effect of detonation, changes the detonation velocity and increases the energy release. It is therefore important to know the range of aluminum melting in the shock wave and calculate the thermal properties of solid and liquid aluminum at high pressures and temperatures.
Molecular dynamic method (MD) was used in [1] for studying the melting of aluminum. The melting temperature upon static compression was compared with the diagrams PU-diagram of shock compression of metals. The pressure and temperature behind the shock wave (SW), in which the metal was melting, were determined on the basis of this comparison. However, the approach [1] does not take into account features of shock wave compression of matter. The compression in the shock wave is accompanied by an entropy increasing and is different from the static compression of matter [2]. Small time of shock wave exposure to the substance 1-10 mks not allow phase transitions, including melting, to implement on the line of thermodynamic equilibrium. Therefore, only direct MD simulations of aluminum compression in shock waves can provide close to the experimental value of the melting point [2].
2. CALCULATION PROCEDURE
The numerically obtained MD dependencies of melting temperature vs shock wave pressure were compared to the experimental and theoretical data for determining reliable parameters of melting.
Molecular dynamics (MD) simulation of the melting of aluminum under shock compression was performed using the computer code SageMD [2]. The computational MD cell of aluminum presented in the form of a cube. In the initial state of the lattice structure of aluminum - face-centered cubic, lattice period 4.050 Å [3]. The unit cell of the crystal contains 4 aluminum atom. The computational MD supercell is constructed from 10 unit cells in each direction and consisted of 4000 atoms of aluminum as shown in Fig. 1. In carrying out MD simulations in all three spatial directions used periodic boundary conditions.
MD simulation allows to visualize the structure of aluminum on the atomistic level and to calculate the properties of the material by the shock wave heated.
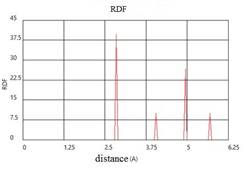
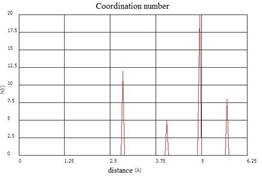
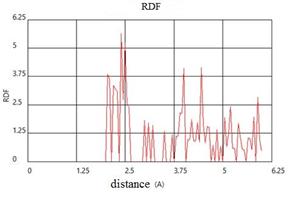
The visualization tools allow to fix the atomic structure, the distribution of atoms in a microvolume. The change of the atoms location in the computational cell during melting clearly indicates the loss of near and long-range order. The use of the radial distribution function in the MD modeling allows to analyze the destruction of condensed matter behind the shock wave front. The radial distribution function for the initial state of a crystal of aluminum and coordination numbers are shown in Fig. 2.
|
|
|
Fig. 1. The unit cell and the computational MD supercell.
Comparing the distribution function of the atoms in the state behind the shock front with the initial, it is possible to draw conclusions about the preservation of the crystal structure of the substance or its melting.
|
|
|
Fig. 2. The radial distribution function and coordination numbers for the initial state of the atoms of a crystal of aluminum
The Morse potential was used for the interatomic interaction for the solid and liquid phases of aluminum
![]() . (1)
. (1)
where r0— equilibrium distance, U0— depth of the potential well.
The values of the properties of aluminum, such as interatomic distance a, the atomic mass m, the de Broglie wavelength l, the parameters of the interaction potential (1) used for the calculation are given in the table. The values of the parameters of the potential (1) taken from the database code SageMD [2]. The cut-off radius was assumed to be 2.7r0. The parameters of the Morse potential are shown in table 1.
Table 1. The parameters of the Morse potential
|
|
|
|
|
U0, eV |
r0, Å |
a, 1/Å |
cut-off radius, Å |
|
Al |
2.863 |
26.981 |
6.72. 10-2 |
0.265915 |
3.203082 |
1.211824 |
8,7 |
To describe the shock compression of a solid by one-dimensional flat wave was used Rankine - Hugoniot relationship for change in the internal energy E as a function of the pressure P and the specific volume V (physical values with the subscript "0" correspond to the parameters of the medium in front of the shock wave)
![]() .
(2)
.
(2)
It enable to calculate all thermodynamic properties of matter along the shock adiabat.
Implemented in the SageMD code [2] the Hugoniotstat method [4] was used for MD simulation of shock compression of aluminum crystal. After the formation of the computational cell, it were set certain value of pressure P, and the temperature was determined from the Rankine - Hugoniot relationship (2). For set pressure P and obtained temperature T the thermophysical and thermodynamic properties of aluminum behind the front of the shock wave were determined. The melting of the crystal after shock compression was identified in the analysis of the calculated radial distribution functions of atoms and atomic displacement quadratic function of the crystal.
3. RESULTS
Fig. 3, 4 presents calculated SA of crystal of aluminum in comparison with experimental data [5-14]. It can be seen from Fig. 3, 4 that the calculated data (lines) are in excellent agreement with experimental data (markers) as thermophysical (Fig. 3) and so wave characteristics (Fig. 4) of shock wave compression of aluminum over the entire range of pressure, as with a small compression ratio, and so at extremely high.
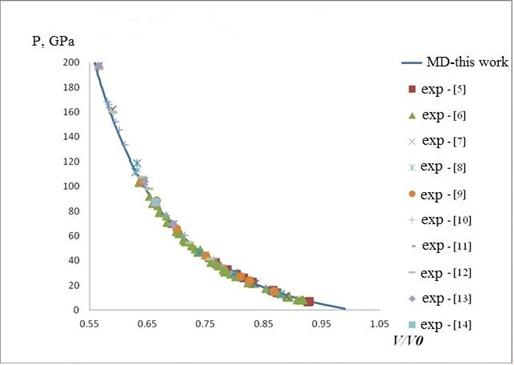
Fig. 3. The dependence of the pressure of aluminum shock compression on compression ratio of the material. Line is this work, markers is experimental data [5 - 14].
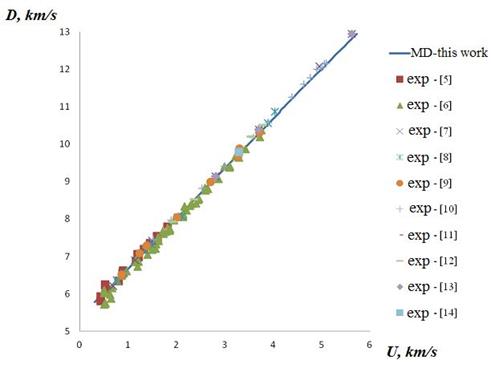
Fig. 4. The dependence of the shock wave velocity on the mass velocity behind the wave front. Line is this work, markers is experimental data [5 - 14].
Fig. 5 presents the calculated temperature dependence of the shock-compressed aluminum crystal on the pressure behind the shock wave front. Fig. 5 shows the experimental values of the pressure melting point of aluminum in the SW obtained experimentally in [15]. The magnitude of the temperature of Al in [15] was calculated.
To compare the values of pressure and temperature on the SW adiabate with the region of phase stability of aluminum the parameters of melting at static compression [16-22] were shown in Fig. 5. Fig. 5 shows that the SW parameters at pressures up to 100 GPa lie in the region of existence of solid aluminum. The experimental data [15], corresponding to the melting of aluminum in the SW, are in good agreement with a bend at the calculated dependence of pressure behind the shock wave front. This indicates that the melting region of shock-compressed Al predicted correctly. SA parameters at high pressures above 120 GPa, most likely lie in the existence of liquid aluminum.
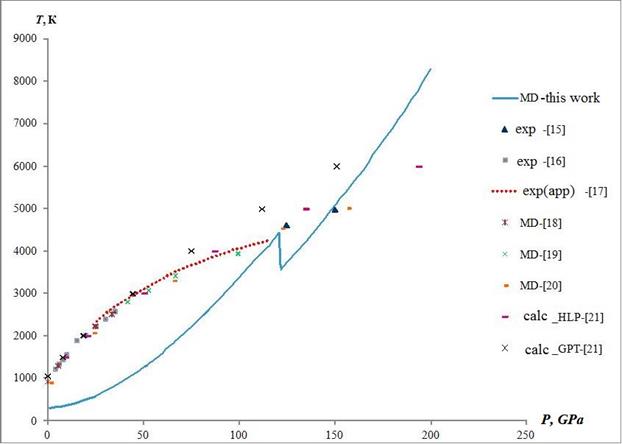
Fig. 5. The calculated values of pressure and temperature for SW adiabate of aluminum. Line are calculated values of pressure and temperature shock compression in this study, markers [15] are measured values of pressure aluminum melting in the SW, markers [17] - [21] are values of the melting point of aluminum with static compression.
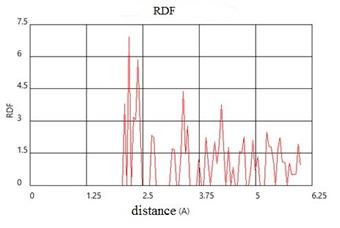
Fig. 6 shows the crystal structure of aluminum for SW adiabate at a pressure of 120 GPa. It can be seen that under these conditions order of crystal structure disappears, also the radial distribution function of the atoms indicates the disappearance of long-range order in the crystal lattice, ie, it is possible that under these conditions begins melting aluminum crystal. As shown in Fig. 5 there is a characteristic bend at the temperature-pressure dependence of shock compression at the pressure of 120 GPa.
|
|
|
Fig. 6. Crystal structure and function of radial distribution of atoms at shock-wave compression up to 120 GPa.
Fig. 7 shows an interactive graphic representation of the crystal structure and function of radial distribution of atoms under shock wave pressure of 122 GPa. Shock wave heating of the substance shows a change in color of the atoms in the computational cell. It can be seen that the arrangement of atoms is not saved any neighbor or long-range order, ie, atoms resulting configuration can be considered as the liquid phase.
|
|
|
Fig. 7. Interactive graphic representation of the crystal structure and function of radial distribution of atoms at compression in the shock wave P=122 GPa
Thus, the MD simulation results indicate the melting of aluminum in SW at a pressure of about 122 GPa and a temperature of 4200 K.
The use of advanced visualization tools for the MD simulation allows to create animated interactive graphics to visualize the changes in the structure of the crystal lattice and fix the melting in shock waves (Fig. 7).
4. CONCLUSIONS
By the MD simulation using Gyugoniostat techniques properties of aluminum in the solid and liquid phases and the temperature dependence of pressure in the shock wave were calculated.
The characteristic bend on the obtained crystal temperature dependence on the pressure of the SW is observed at pressure of 115-122 GPa. The nature of the bend on the curve may indicate the presence of a phase transition in the crystal structure of aluminum (melting) in this range of temperatures and pressures. Visualization of the crystal structure and the atomic radial distribution function indicate that the arrangement of atoms has not got order at these temperatures and pressures. This configuration can be interpreted as the aluminum melting.
The MD outcomes were compared to other experimental and theoretical data. Comparison of the results obtained in this work with published results of simulation of temperature static melting point of aluminum [18 - 21], as well as experimental data of static melting [16 -17] and experimental melting parameters in SW [15] on the pressure shows their mutual consistency.
Bibliography
- Ji-Wook Jeong, In-Ho Lee, K. J. Chang. Molecular-dynamics study of melting on the shock Hugoniot of Al // PHYSICAL REVIEW B, V.59, 1999, p.329-333.
- A.A. Selezenev, V.K. Golubev, A.Y. Aleinikov, O.I. Butnev, R.A. Barabanov, B.L. Voronin. Molecular Dynamics Simulation of Shock Wave Compression of Metals. // In proceedings of Int. Conference «Shock Compression of Condensed Matter» (SCCM), 2001, USA, Atlanta, p. 374-377.
- Chimicheskaya entsiklopedia. In 5 t. / Redkol. Knunyants I.L. (gl.red). M.: Soviet encyclopedia, 1988 – T.1. (in Russian)
- A.A.Selezenev, A.Yu. Aleynikov, N.S.Ganchuk, P.V.Ermakov, S.N.Ganchuk, J.B.Aidun, A.P. Thompson. Shock Compression Calculation of RDX and PETN Molecular Crystals Using Hugoniostat Method. // In proceedings of International Conference «Shock Compression of Condensed Matter» (SCCM), 2009, USA, Nashville.
- S. P. Marsh (Ed.), LASL Shock Hugoniot Data, (Univ. California Press, Berkeley, 1980).
- R. G. McQueen, S. P. Marsh, J. W. Taylor, J. N. Fritz, W. J. Carter, The equation of state of solids from shock wave studies. // High Velocity Impact Phenomena / Ed. R.Kinslow. - New-York: Academic Press, p.293-417; appendies on pp. 515-568 (1970).
- L. V. Al'tshuler, B. S. Chekin, Metrology of high pulsed pressures. // in: Proceed. of 1 All-Union Pulsed Pressures Simposium (VNIIFTRI, Moscow, 1974) V.1, 5-22 (in Russian).
- R. F. Trunin, L.F.Gudarenko, M. V. Zhernokletov, G. V. Simakov, Experimental data on shock compressibility and adiabatic expansion of condensed substances, RFNC, Sarov (2001) (in Russian).
- L. V. Al'tshuler, A. A. Bakanova, I. P. Dudoladov, E. A. Dynin, R. F. Trunin, B. S. Chekin, Shock adiabats for metals. New data, statistical analysis and general regularities. // Zh. Prikl. Mekh. Tekhn. Fiz. 2, 3-34 (1981) (in Russian) (J. Appl. Mech. Techn. Phys. 22, 145 (1981)).
- A. C. Mitchell, W. J. Nellis, Shock compression of aluminum, copper and tantalum. // J. Appl. Phys. v. 52, p. 3363-3374 (1981).
- L. V. Al'tshuler, A. P. Petrunin, Rentgenographic investigation of compressibility of light substances under obstacle impact of shock waves. // Zh. Tekhn. Fiz. 31(6), 717-725 (1961) (in Russian).
- L. V. Al'tshuler, S. B. Kormer, M. I. Brazhnik, L. A. Vladimirov, M. P. Speranskaya, A. I. Funtikov, The isentropic compressibility of aluminum, copper, lead at high pressures. // Zh. Eksp. Teor. Fiz. 38(4), 1061-1073 (1960) (in Russian) (Sov. Phys. - JETP 11(4), 766-775 (1960)).
- L. V. Al'tshuler, S. B. Kormer, A. A. Bakanova, R. F. Trunin, Equations of state for aluminum, copper and lead in the high pressure region. // Zh. Eksp. Teor. Fiz. 38, 790-798 (1960) (in Russian) (Sov. Phys. - JETP 11, 573-579 (1960)).
- M. A. Podurets, G. V. Simakov, R. F. Trunin, Transition of stishovite to a denser phase. // Izv. Akad. Nauk SSSR. Fiz. Zemli 4, 30-37 (1990) (in Russian).
- J.W. Shaner et al. // in "High Pressure Science and Technology", eds. C. Homan, R.K.MacCrone, E. Whalley (North Holland, Amsterdam, 1984), pp. 137-141.
- E. L. Baker and Ch. Capellos," Jaguar procedures for detonation properties of aluminized explosives", U.S. ARMY TACOM-ARDEC Picatinny Arsenal, New Jersey 07806.
- R. Boehler and M. Ross, Melting curve of aluminum in a diamond cell to 0.8 Mbar: implications for iron. // Earth Planet. Sci. Lett.153, 223, (1997).
- A. I. Botyachkova, S. A. Gubin, I. L. Sokolova, G. G. Karpinskiy. Molecular dynamics simulation of melting aluminum in macrostate at high pressure.// Nuclear physics and engineering, 2013, tom 4,¹ 5, c. 423-424. (in Russian)
- S. V. Starikov, V. V. Stegailov. Atomistic simulation of the premelting of iron and aluminum: Implications for high-pressure melting-curve measurements. // PHYSICAL REVIEW B 80, 2009, p. 220104-1 220104.4.
- J. Bouchet, F. Bottin, G. Jomard, G. Zérah. Melting curve of aluminum up to 300 GPa obtained through ab initio molecular dynamics simulations. // PHYSICAL REVIEW B 80, 2009, p. 094102-1 094102-5.
- J. A. Moriarty, D. A. Young, and M. Ross, "Theoretical study of the aluminum melting curve to very high pressure". // PHYSICAL REVIEW B, V. 30, 1984, ðp. 578-588.