ВИЗУАЛИЗАЦИЯ ЧУВСТВИТЕЛЬНОСТИ РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ СО СВОБОДНЫМИ ПАРАМЕТРАМИ НА ОСНОВЕ ДЕРЕВА РЕШЕНИЙ

 

С.В. Ктитров, А.А. Кокуев, Ю.П. Кулябичев, Н.А. Крицына, Г.А. Горелкин

SVKtitrov@mephi.ru, AAKokuyev@mephi.ru, YPKulyabichev@mephi.ru, NAKritsyna@mephi.ru, GorelkinG@yandex.ru

Национальный исследовательский ядерный университет «МИФИ», Москва

 

Оглавление

Введение  1

1. Дерево решений задачи линейного программирования  1

2. Построение дерева решений  1

3. Пример построения дерева решений  2

4. Диаграммы решений задачи линейного программирования  2

Заключение  6

Список литературы   6

 

Аннотация

Предлагается подход к анализу чувствительности решения задачи линейного программирования с использованием визуального представления зависимости решения задачи от ее параметров. Рассматривается алгоритм построения дерева решений, положенного в основу построения диаграмм решения задачи. Приводятся примеры диаграмм для задач различной размерности.

 

Ключевые слова: линейное программирование, симплекс-метод, дерево решений, анализ чувствительности, диаграмма решения

 

Введение

Многие оптимизационные задачи, возникающие, прежде всего, при планировании, а также параметрическом синтезе технических систем, часто могут быть сведены к задаче линейного программирования. Для решения таких задач широкое распространение получил симплекс-метод, позволяющий за конечное число шагов численно найти оптимальное решение. Однако, в случаях, когда параметры системы заданы со значительной погрешностью или если система, оптимальное решение которой ищется, является нестационарной, актуальной становится задача определения зависимости оптимального решения от одного или нескольких параметров системы, изменяющихся в заданном диапазоне. Разработанные методы решения таких задач, получивших название анализа чувствительности и устойчивости решения [1,2], решают поставленную задачу лишь для уже полученного оптимального решения и не являются наглядными. С другой стороны, при постановке задачи линейного программирования, в задачах параметрического синтеза систем было бы чрезвычайно полезно иметь инструмент, позволяющий получить зависимость оптимального решения от параметров исходной системы, проанализировать, какие ограничения являются определяющими, а какие несущественными при заданном изменении параметров системы. Подобно методу фазовой плоскости, применяемому для анализа решений систем дифференциальных уравнений, такой инструмент позволит облегчить анализ и повысить наглядность представления результатов анализа задач линейного программирования. Для решения поставленной задачи в статье предлагается использовать диаграммы решений, получаемые на основе дерева решений задач линейного программирования со свободными параметрами.

 

1. Дерево решений задачи линейного программирования

 

Задача линейного программирования обычно формулируется следующим образом: найти максимум функции

x)=(c,x)

при ограничениях

                (1)

где x – вектор оптимизируемых переменных. Матрица системы ограничений А, векторы параметров целевой функции c и ограничений b обычно рассматриваются как заданные константы. Размерность вектора x равна n, количество ограничений m.

Рассмотрим задачу линейного программирования со свободными параметрами.

Пусть какой-либо из коэффициентов системы (1) не определен и может меняться в заданном диапазоне , возможно неограниченном. Тогда оптимальное решение системы , где  – область оптимальных решений, может рассматриваться как результат отображения одномерной области P на .

Общая постановка задачи линейного программирования со свободными параметрами предполагает, что все параметры системы (1) неопределенны. Тогда общее число свободных параметров в системе составит k=n+n×m+m. При этом область изменения параметров  становится k-мерной.

Решение такой задачи может быть построено на основе симплекс-метода как наиболее разработанного и адаптированного для применения на ЭВМ. Симплекс-метод относится к классу переборных алгоритмов, реализующих последовательный обход вершин выпуклого многогранника, образуемого ограничениями, до достижения оптимального решения. Выполнение шагов симплекс-метода предполагает наличие информации о взаимном соотношении коэффициентов симплекс-таблицы, на основе чего принимается решение о введении той или иной компоненты вектора в базис. Предположим,  не находится в базисе. Если принято решение ввести в базис вместо , то данное решение будет верным при выполнении следующих условий

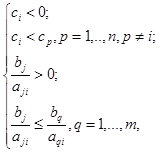                (2)

которые рассматриваются как гипотезы. В противном случае следует искать другого кандидата для введения в базис, что приведет к необходимости принятия гипотез, аналогичных (2). Таким образом, неопределенность одного или нескольких параметров приводит к ветвлению последовательности шагов симплекс-метода.

Совокупность всех шагов симплекс-метода, полученных при рассмотрении всех возможных гипотез о взаимном соотношении параметров задачи, позволяют построить ориентированный граф – дерево решений [3]. В узлах такого дерева – симплекс-таблицы, ребра графа взвешены принятыми при получении очередной симплекс-таблицы гипотезами. Количество ветвей дерева определяется числом свободных параметров задачи и заданными диапазонами их изменения. Следует также учитывать, что вследствие переборного характера симплекс-метода одно и тоже решение может быть получено вследствие разной последовательности шагов. На количество и расположение ветвей полученного дерева также влияет начальный базис, вследствие чего получаемое дерево не является однозначным, но содержит все оптимальные решения при заданной вариации параметров.

 

2. Построение дерева решений

 

Построение дерева решений, особенно в задачах с большим количеством свободных параметров, является трудоемкой задачей, требующей автоматизации. Для решения этой задачи авторами разработан прототип программного комплекса генерирования дерева решений для задач линейного программирования со свободными параметрами произвольной размерности.

Ядром программного комплекса является система поддержки истинности принимаемых гипотез, рассматриваемых при выполнении шагов симплекс-метода. Такая система поддержки истинности является ограниченной, поскольку не содержит механизма пересмотра истинности принятых предположений на основе новых, поскольку ложность ранее принятых предположений не может быть выявлена на основе новых. Предположения, противоречащие ранее принятым, не рассматриваются.

Основной задачей системы поддержки истинности является вычисление противоречий в переданном ей наборе предположений. Передаваемый набор предположений представляет собой конъюнктивную нормальную форму.

В основу алгоритмов системы поддержки истинности положено преобразование набора предположений из конъюнктивной нормальной формы в дизъюнктивную нормальную форму с последующей проверкой истинности каждого из конъюнктивных одночленов.

В программный комплекс включены следующие компоненты:

– программа построения дерева решений на основе системы поддержки истинности;

– программа построения графического представления дерева решений;

– программа, выдающая дерево решений в виде набора таблиц.

 

3. Пример построения дерева решений

 

Рассмотрим на примере формирование дерева решений для задачи линейного программирования с двумя свободными параметрами.

Пусть требуется найти максимум функции

при ограничениях

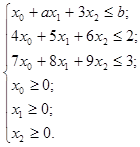                    (3)

В рассматриваемой задаче свободными выбраны параметры  и . Первые три ограничения приводят к необходимости введения ослабляющих переменных , и . Первый шаг метода приводит к гипотезам  или  при введении в базис . Дальнейшие шаги приводят к построению дерева решений. Для данного примера оно построено с использованием разработанного авторами программного комплекса. Итоговое дерево решений для рассматриваемой задачи приведено на рис. 1. Избыточная индексация свободных параметров определяется особенностями работы разработанного программного обеспечения.

Как следует из полученного дерева, возможны 4 варианта значений целевой функции – константа, независящая от параметров, и значения, зависящие от одного или двух параметров.

 

task

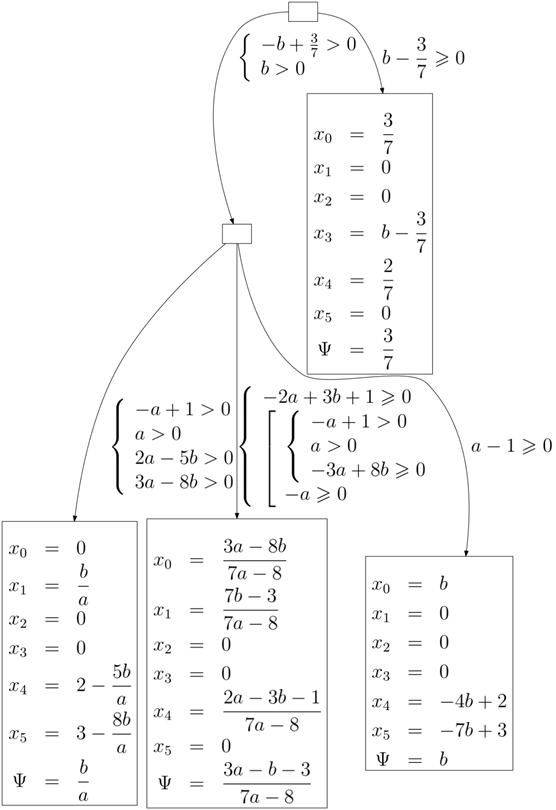
Рис. 1. Дерево решений для задачи размерности 3

 

4. Диаграммы решений задачи линейного программирования

 

1  

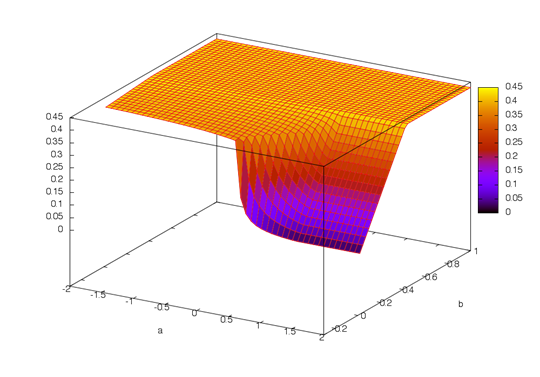
Рис. 2. График зависимости целевой функции от свободного параметра

 

Полученное дерево решений позволяет сформировать семейство диаграмм, позволяющих визуализировать взаимосвязь оптимального решения задачи и варьируемых параметров. Следует отметить, что полученные таким образом уравнения связи являются аналитическими. Наиболее простое, традиционное представление имеет зависимость оптимального значения целевой функции от варьируемых параметров (см. рис. 2)

График на рис. 2 не позволяет разграничить область соответствующие различным ветвям дерева решений, в которых решение имеет существенно разный характер. Для представления таких областей, можно построить проекцию графика на рис. 2 на плоскость, в которой границы можно выделить на основании аналитических условий, выявленных при построении дерева. Предложенную проекцию назовем диаграммой решения задачи линейного программирования (см. рис. 3). На рисунке 3 выделены 6 областей, причем область 6 соответствует отсутствию решения.

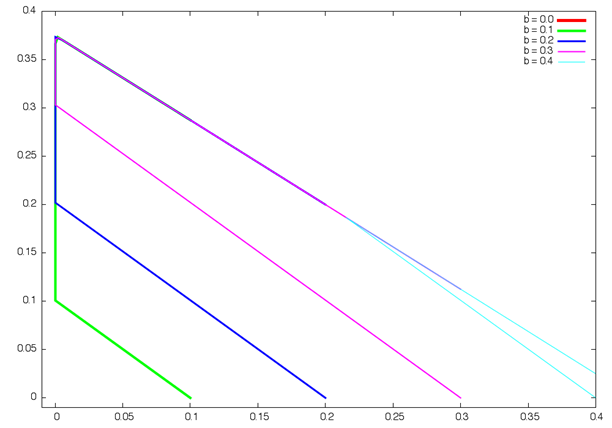
Одним из возможных типов диаграмм может быть параметрическая зависимость компонент оптимального вектора x от варьируемых параметров. В этом случае, один из параметров может задавать семейство траекторий в пространстве {x0, x1}, получаемых при изменении другого параметра. Вид такой зависимости изображен на рис. 4, где рис. 4а представляет собой семейство траекторий при фиксировании параметра  и изменении параметра , а рисунок 4б изображает траектории при фиксировании параметра , и изменении параметра .

Дерево решений на этапе параметрического синтеза системы позволяет решить задачу о влиянии того или иного ограничения на оптимальное решение.

Как следует из диаграммы, приведенной на рис. 3, при определенных значениях параметров (области 1 и 2), значение целевой функции не зависит от них. Это означает, что первое ограничение, в которое входят оба варьируемых параметра, не участвует в формировании решения. Изменение параметра ограничения может привести к ситуации, когда то или иное ограничение является несущественным хотя бы в ограниченном диапазоне изменения параметра. С использованием диаграммы несущественные ограничения могут быть выявлены по отсутствию влияния в них свободных параметров на значение целевой функции.

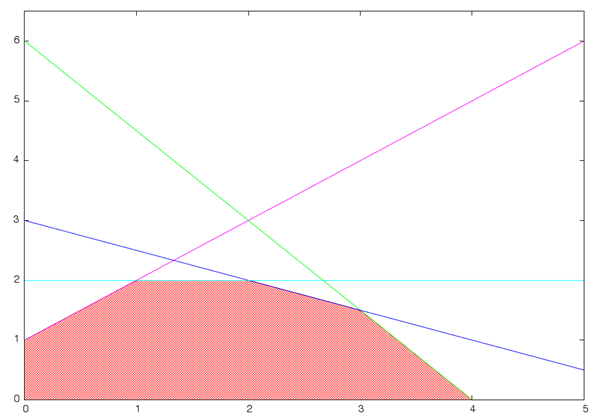
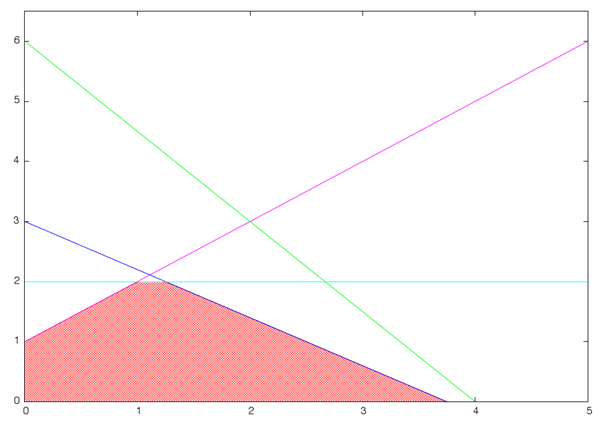
Множество ограничений, определяющих оптимальное решение, может меняться и при наличии свободных параметров в коэффициентах целевой функции, что иллюстрирует рис. 5. На рисунке приведено сечение симплекса, образованного ограничениями, совместно с линиями уровня целевой функции, наклон которых изменяется в зависимости от значения свободного параметра, соответствующее ему дерево решение изображено на рис. 6, а график зависимости критерия качества от параметров и диаграмма решений на рис. 7 и 8.

2_

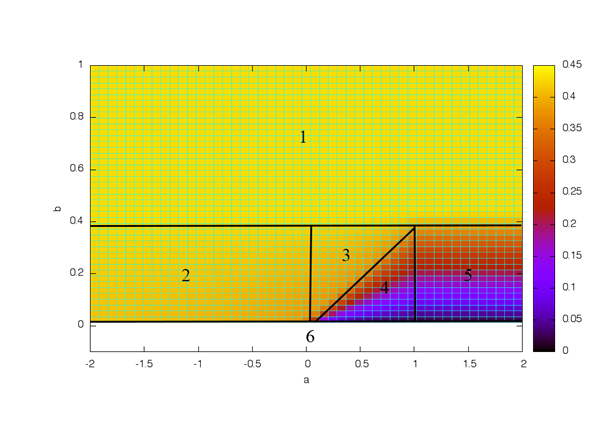
Рис. 3. Диаграмма решений задачи линейного программирования

4

а)

3

б)

Рис. 4. Фазовые портреты в задаче линейного программирования

 

5

6

Рис.5. Влияние ограничений на оптимальное решение при свободном параметре в ограничении

 

task

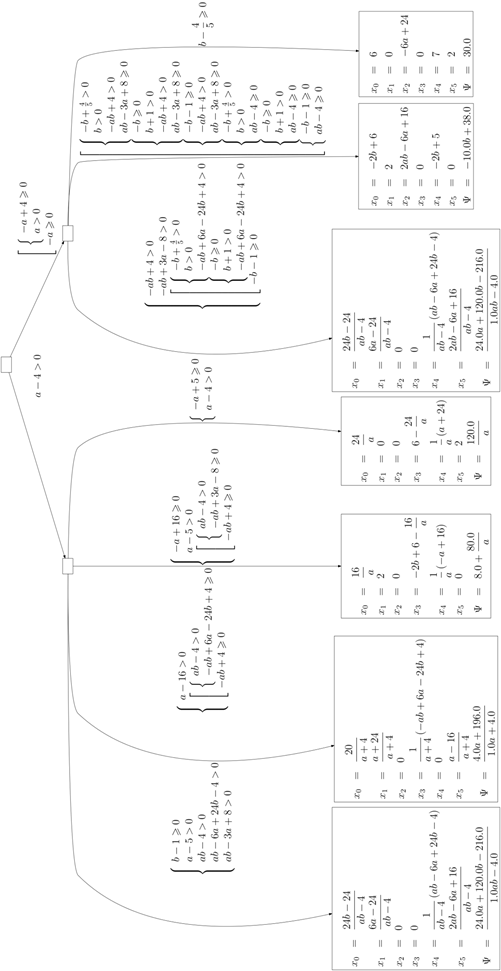
Рис. 6. Дерево решений для примера 2

7

Рис.7. График зависимости целевой функции от свободного параметра для примера 2

8

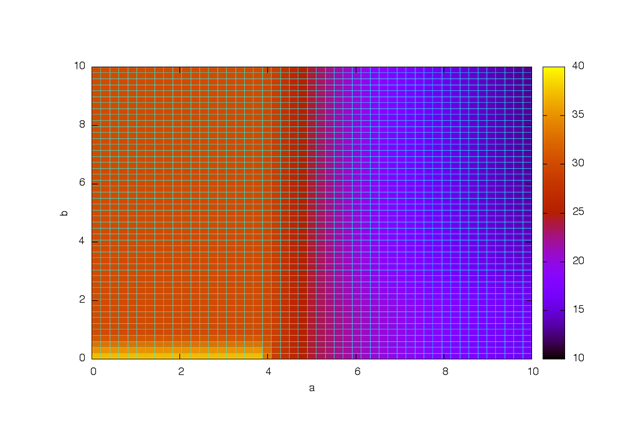
Рис.8. Диаграмма решений задачи линейного программирования для примера 2

 

Заключение

 

Построение дерева решений в задаче линейного программирования существенно облегчает анализ чувствительности решения к вариации параметров исходной системы. Предложенный метод визуализации влияния свободных параметров на оптимальное решение позволяет выявить требуемые диапазоны задания точности исходных данных и отсечь ограничения, несущественные в конкретной оптимизационной задаче.

Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта №13-07-00465А.

 

Список литературы

1. Таха Х. Введение в исследование операций. – 7 изд. – М.: Изд. дом «Вильямс», 2007. – 912 с.

2. Васильев Ф.П., Иваницкий А.Ю. Линейное программирование – Изд. 3-е испр. – М.:Факториал Пресс, 2008. – 328 с.

3. А.А.Кокуев, С.В.Ктитров. Построение дерева решений в задачах линейного программирования //Вестник Национального исследовательского ядерного университета «МИФИ», 2014, Т.3, №1, С.119-124.



VISUALIZATION OF SOLUNION SENCITIVITY FOR LINEAR PROGRAMMING PROBLEM WITH FREE PARAMETERS BASED ON DECISION TREE

S.V. Ktitrov, A.A.Kokuev, Y.P.Kulyabichev, N.A.Kritsyna, G.A.Gorelkin

SVKtitrov@mephi.ru, AAKokuyev@mephi.ru, YPKulyabichev@mephi.ru, NAKritsyna@mephi.ru, GorelkinG@yandex.ru

National Research Nuclear University “Moscow Engineering Physics Institute”, Russia

 

Abstact:

Developed in the article approach to solutions’s sensitivity analysis for linear programming problem is based on decision tree visualization in form of solution diagrams. Decision tree finding algorithm is point of view. Analysis based on proposed diagrams is illusrated by examples of different dimensions.

 

Keywords: linear programming, simplex method, decision tree, sensitivity analysis, solution diagram

 

References

 

1. Takha Kh. Introduction to operational research. - 7th ed. - M.: Publishing House. "Williams", 2007. - 912 p.

2. Vasiliev. F.P., Ivanitskiy A.Yu. Linear programing - 3rd rev. Ed. - M.: Factorial Press, 2008. - 328 p. [In russian]

3. A.A. Kokuyev, S.V. Ktitrov. Building a decision tree for linear programming problems. Bulletin of the National research nuclear University "MEPhI", 2014, T.3, No. 1, p. 119-124 [In russian]