Экспериментальная визуализация двумерного распределения критического тока в длинномерных высокотемпературных сверхпроводящих лентах
С.В. Покровский1,2, И.А. Руднев1,2, А.И. Подливаев1, В.С. Калитка3, А.В. Бледнов3, А.А. Адаменков3
1 Национальный исследовательский ядерный университет МИФИ, Москва, Россия
2 Международная лаборатория сильных магнитных полей и низких температур, Вроцлав, Польша
3 ЗАО «СуперОкс», Москва, Россия
Содержание
2.Алгоритмы магнитометрического определения токов и визуализации токовых путей
3. Техническая схема установки и программные средства визуализации
Аннотация
На основе визуализации протекания электрического тока предложена и реализована новая методика контроля качества сверхпроводящих лент. Представлено описание методики, а также результаты применения разработанной методики для визуализации двумерного (2D) распределения критического тока в длинномерных лентах на основе высокотемпературных сверхпроводников (ВТСП). Использованная методика базируется на измерении с помощью линейки преобразователей Холла (ПХ) захваченного магнитного потока сверхпроводящей лентой, и последующем численном решении обратной задачи Био-Савара-Лапласа для случая непрерывной перемотки ленты с катушки на катушку в режиме реального времени. Предложена модификация алгоритма расчета 2D распределения критического тока с целью улучшения устойчивости системы в случае выхода из строя одного и двух соседних датчиков магнитного поля, а также экспериментально выявлено влияние выхода из строя нескольких датчиков магнитного поля на результаты исследований однородного и неоднородного участков ленты. Продемонстрирована возможность применения методики для анализа распределения критического тока в ВТСП лентах длиной свыше 500 м.
Ключевые слова: визуализация тока, ВТСП лента, локальный критический ток, неоднородность критического тока.
1. Введение
Важным этапом производства длинномерных ВТСП лент второго поколения является контроль локальных токонесущих характеристик материала, при этом для определения и характеризации области с пониженным критическим током необходимо представлять данные в трехмерном графическом виде, а также проводить анализ получаемых распределений критического тока сверхпроводника. Развитие технологий производства высокотемпературных сверхпроводников сделало доступными для технического применения сверхпроводящие (СП) ленты, способные пропускать без диссипации энергии электрический ток с плотностью более 1 МA/см2 при температуре кипения жидкого азота, что абсолютно недостижимо при использовании традиционных электротехнических материалов. Длина единичных кусков СП лент может доходить до 1 км. Очевидно, что при сложнейших технологических циклах производства длинномерных СП лент чрезвычайно трудно выдержать все оптимальные технологические параметры, изменение которых неизбежно приводит к появлению локальных областей с пониженными токонесущими характеристиками [1] и, как следствие, ограничению возможности пропускания высоких плотностей тока по всей ленте. Особую важность это обстоятельство имеет при решении прикладных задач: производство кабелей, сверхпроводящих магнитов, токоограничителей. Таким образом, неразрушающая диагностика качества является необходимым элементом производственного процесса создания длинномерных СП лент. В настоящей статье представлена бесконтактная магнитометрическая методика визуализации дефектов токопереноса в СП лентах, основанной на измерении пространственного распределения магнитного поля тока, текущего в ленте и последующей программой обработке полученных экспериментальных данных.
2.Алгоритмы магнитометрического определения токов и визуализации токовых путей
Наиболее перспективной формой бесконтактного неразрушающего контроля качества СП ленты является магнитометрическое определение плотности критического тока, наведенного в пленке внешним однородным магнитным полем (смотри, например, обзор [2]). Существо метода заключается в следующем: СП пленка охлаждается ниже Тс, и помещается в магнитное поле (до 0.5 Тл), которое наводит в сверхпроводнике экранирующие токи. После снятия внешнего магнитного поля в сверхпроводнике остается захваченный магнитный поток, создаваемый незатухающими сверхпроводящими токами. Для локального распределения тока в сверхпроводнике необходимо измерить пространственное распределение захваченного магнитного потока. Далее, решая задачу инверсии уравнения Био — Савара — Лапласа (1) с привлечением модели критического состояния сверхпроводника [3] можно получить пространственное распределение локального критического тока, в том числе могут быть определены области с пониженной величиной критического тока:
, (1)
где 
–
магнитная проницаемость вакуума, 
– область локализации замкнутых, токов
пленочного образца. Для определения поверхностных токов при условии отсутствия
перетекания тока по в направлении оси Z вполне достаточно измерения в
плоскости над образцом единственной компоненты магнитного поля 
(предполагается, что в декартовых
координатах (X,Y,Z) СП пленка лежит в плоскости Z=0 , координата Y
направлена вдоль ленты, а координата X – поперек в соответствие с
рисунком 1.
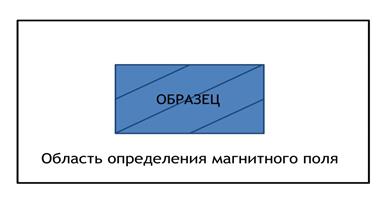
Наиболее эффективным методом решения задачи инверсии уравнения (1) является применение к этому уравнению двумерного преобразования Фурье. В импульсном пространстве уравнение (1) имеет диагональный вид (Фурье-образы магнитного поля и компонент тока связаны локально [2]). Однако, преобразование Фурье применимо только к периодическим функциям, в то время как измеряемое поле образца периодичностью не обладает. В стандартных подходах к решению задачи определения токов [2] для устранения влияния периодичности площадь измерения магнитного поля существенно превышает (5-9 раз) размер образца (смотри рисунок 1а).
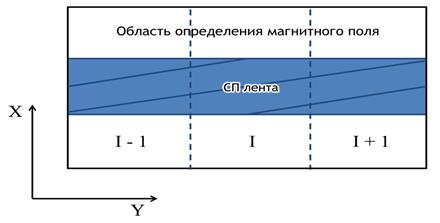
Такой стандартный подход для целей мониторинга неприменим по двум причинам: во-первых, качество СП ленты требуется контролировать по мере прохождения через измерительную систему в режиме реального времени. Во-вторых, экспериментальное определение магнитного поля далеко за пределами ленты заметно усложняют и удорожают техническую реализацию схемы измерения. При создании измерительной установки был разработан новый модифицированный алгоритм, который заключался в следующем. СП лента разбивалась на участки (I – порядковый номер участка). Инверсия проводилась по области, содержащей три смежных участка с номерами I-1, I, I+1 (смотри рисунок 2), но сохранялись результаты только I-го участка. Далее порядковый номер участка увеличивалась на 1 и процесс продолжался. Наш опыт работы с длинномерными образцами показал, что дальнодействие токов в ленте шириной a достигает величины, равной нескольким величинам a, но при удалении источника ошибки на расстояние 10a и более, влиянием столь удаленной границы можно пренебречь. Кроме того, было предложено и успешно реализовано решение задачи численного доопределения магнитного поля вне образца [4].Так как в этой области отсутствуют СП токи, магнитное поле подчиняется трехмерному уравнению Лапласа, граничными условиями для которого являются экспериментальные значения магнитного поля на краю СП ленты и нулевые значения на бесконечности (детали алгоритма восстановления даны в работе [4]).
|
|
|
|
а) |
б) |
Рис. 1. Расчетная область задачи инверсии уравнения Био — Савара — Лапласа. 1а – форма расчетной области при стандартном подходе для короткого образца. 1б – форма расчетной области, адаптированная к длинномерной ленте.
Практическое применение разработанного алгоритма в установке, использующей для измерения магнитного поля линейку датчиков Холла (ДХ), позволило существенно сократить число датчиков Холла в линейке и упростить систему сбора данных. Отметим, что число датчиков Холла в линейке является критическим параметром данного подхода, поскольку измерительная система должна позволить не только детально визуализировать структуру токового дефекта СП ленты, но и продолжать уверенно диагностировать дефекты при выходе из строя одного или даже нескольких датчиков в линейке.
3. Техническая схема установки и программные средства визуализации
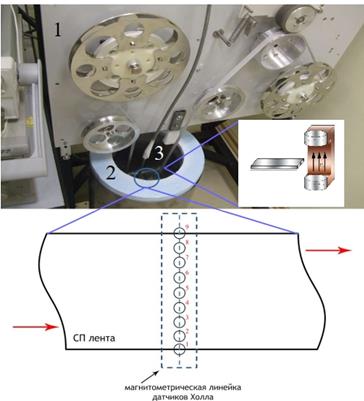
Для того, чтобы выполнять измерения длинномерных ВТСП лент была создана система протяжки ленты с катушки на катушку (рисунок 2а), при этом для точного измерения пространственного распределения тока, подача производится равномерно. Общий вид опытной установки представлен на рисунке 2. ВТСП лента поступает в азотную емкость, где охлаждается до Т=77 К. После охлаждения в сверхпроводнике создаются наведенные токи, для чего используется система намагничивания на основе постоянных NdFeB магнитов, расположенных в криостате вблизи ленты. После намагничивания лента проходит систему измерения, состоящую из линейки датчиков Холла (рисунок 2а) и измерительной аппаратуры, которая в непрерывном режиме выполняет запись результатов. После чего производится расчет локального распределения тока в образце, при этом результаты отображаются в непрерывном режиме (рисунок 2б). Управление процессом сканирования и визуализация токовых путей осуществляется пакетом программ, созданных авторами настоящей работы в среде LabView, а программа восстановления токовых путей по магнитометрическим данным – программами на языке FORTRAN. Стандартными средствами LabView выполняется общее управление системой, сбор данных, их организация и анализ, а также вывод на экран компьютера управления в режиме реального времени. Для получения общей статистики по длинномерной ленте строится линейное распределение тока вдоль ленты, позволяющее определять области с пониженными токонесущими характеристиками, одновременно производится визуализация двумерных поверхностей распределений компонент тока в образце, выявляющих локализацию найденного токового дефекта и позволяющих определить его геометрию и возможные причины возникновения.
|
|
|
|
а) |
б) |
Рис. 2. (Цветной рисунок в электронной версии). Экспериментальный стенд.
а) система измерения. 1 — система перемотки с СП лентой; 2 – система криостатирования; 3 – измерительная система и система намагничивания
б) система расчета и отображения результатов.
4. Результаты
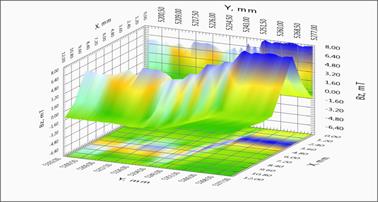
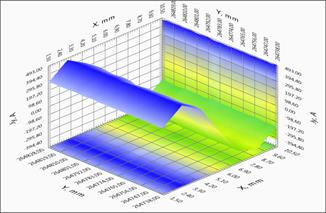
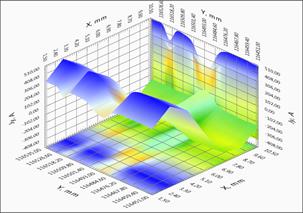
В данной статье для демонстрации результатов измерения захваченного магнитного потока ленты и восстановления распределения критического тока были выбраны образцы: длинномерная лента на основе YBCO (ширина 12 мм, длина 516,5 м) производства компании СуперОкс и Roebel кабель на основе данной ленты. На рисунке 3 представлены прямые данные магнитометрии и локальное распределения токов в кабеле. Геометрия кабеля, показанная на рисунке 3а, характерна для такого типа кабелей. Отдельные ленты укладываются таким образом, чтобы ток в каждой ленте протекал попеременно по правой и левой сторонам кабеля. На рисунках 3б, 3в, 3г показаны распределения захваченного магнитного потока куска кабеля и рассчитанные распределения компонент тока вдоль и поперек кабеля. Хорошо видны области перехода ленты с одного края на другой и возникновение поперечной компоненты тока, при этом в том же месте уменьшается компонента тока вдоль кабеля, сохраняя при этом величину полного тока в ленте. Приведенные результаты демонстрируют возможности метода для объектов со сложной геометрией.
|
|
|
|
а) |
б) |
|
|
|
|
в) |
г) |
Рис. 3. (Цветной рисунок в электронной версии). Геометрия Roebel кабеля, распределение магнитного поля и наведенных токов в СП ленте.
3а – Геометрия кабеля.
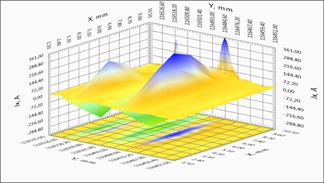
3б – зависимость компоненты поля BZ(X,Y) .
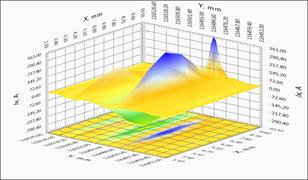
3в – зависимость компоненты тока JY(X,Y) вдоль ленты.
3г – зависимость компоненты тока JX(X,Y) поперек ленты.
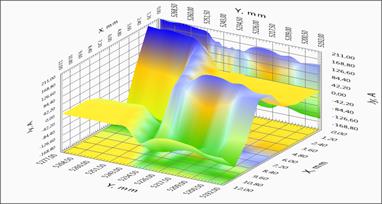
Для более детального исследования возможности исследования локальных неоднородностей токонесущих характеристик сверхпроводника были проведены исследования длинномерной прямой ленты. На рисунке 4 представлены прямые данные магнитометрии и локальное распределение токов на протяженном фрагменте СП ленты. На полученных распределениях тока хорошо видны геометрические особенности структуры, области перехода лент.
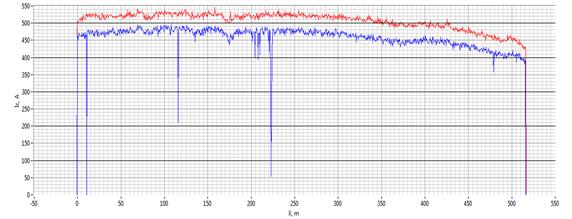
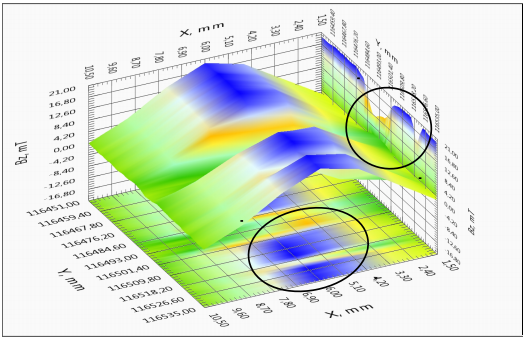
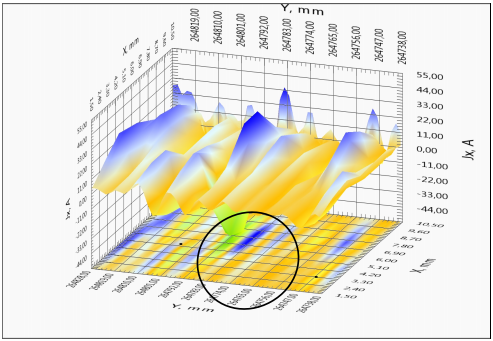
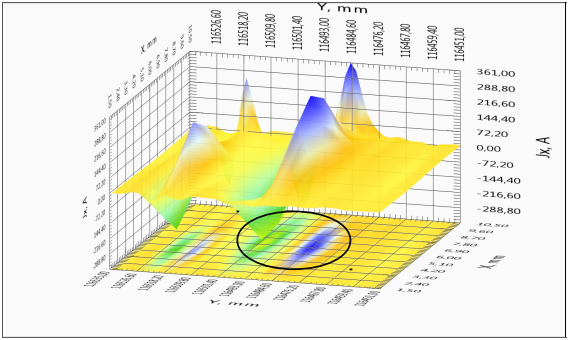
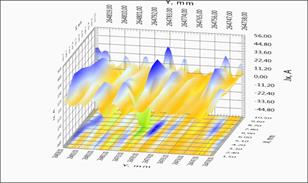
Для удобства анализа характеристик длинномерной ленты на рисунке 4а приведено полное линейного распределение критического тока вдоль образца. Можно выделить протяженные участки с высокой однородностью токонесущих характеристик, однако наблюдаются области со значительно более низкими значением критического тока. Такие участки с наличием дефектов или повреждений сверхпроводящего слоя и вносят значительное ограничение на величину критического тока всей ленты. Более подробно пространственные распределения магнитного поля и компонент тока двух участков с токовыми дефектами различной амплитуды представлены на рисунках 4б-4г. Для наглядности был выбран однородный участок с малым дефектом (x=264,7 м) и резко неоднородный участок (x=116,5 м) (см. рисунок 4а). Полученные результаты свидетельствуют о наличие перераспределения тока в образце. Более явно физическая картина наблюдается на линиях уровня распределения компонент тока участка ленты (рисунок 4в, 4г).
|
|
|
|
а) |
|
|
|
|
|
б) слева- однородный участок с малым дефектом; справа - неоднородный участок ленты. |
|
|
|
|
|
в) слева - однородный участок с малым дефектом; справа - неоднородный участок |
|
|
|
|
|
г) слева - однородный участок с малым дефектом; справа - неоднородный участок |
|
Рис. 4. (Цветной рисунок в электронной версии). Распределение магнитного поля и наведенных токов в СП ленте.
4а – Линейное распределение критического тока вдоль ленты, красная кривая – максимальное значение, синяя – минимальное значение тока на участке ленты
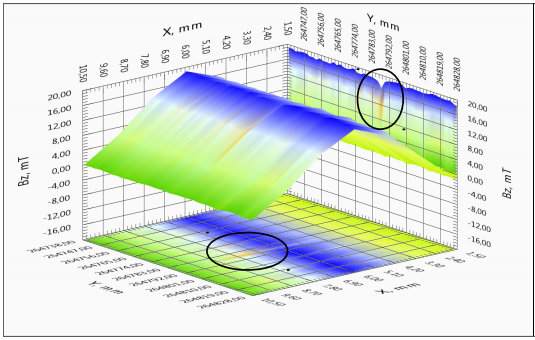
4б – зависимость компоненты поля BZ(X,Y) для однородного и неоднородного участков ленты. Выделены участки неоднородного протекания тока.
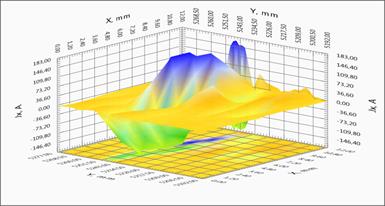
4в – зависимость компоненты тока JY(X,Y) вдоль ленты для однородного и неоднородного участков ленты
4г – зависимость компоненты тока JX(X,Y) поперек ленты для однородного и неоднородного участков ленты. Выделены участки неоднородного протекания тока.
Если бы образец был идеально однороден, линии наведенных токов в нем располагались бы строго параллельно продольной оси ленты, и, поскольку наведенные токи в образце замкнуты, компонента тока JX(X,Y) антисимметрична относительно центральной продольной линии ленты. В правой половине ленты ток течет в одну сторону, в левой – в противоположную. Параллельность линий тока наблюдается на рисунке 4в для однородного участка ленты. Для неоднородного участка с токовым дефектом более 50 % по амплитуде наблюдается антисимметрия 4в. Наиболее информативным индикатором неоднородности является компонента тока JY(X,Y), которая равна нулю на протяженном однородном участке СП ленты, и имеет экстремумы вблизи локальных неоднородностей (трещин, несверхпроводящих включений, областей сверхпроводника с пониженным значением критического тока и т.п.). На поперечной компоненте тока хорошо видно появление как малых по амплитуде перетеканий тока, так и наличие протяженных повреждений ленты со значительным подавлением величины критического тока ленты (рисунок 4г). Более подробно методика распознавания дефектов представлена в статье [5].
Нами был исследован вопрос устойчивости расчетной методики к выходу из строя одного или нескольких датчиков Холла в линейке. Так как при большом потоке образцов измерения необходимо проводить с минимальными задержками, а производить повторное сканирование длинномерной ленты в случае выхода из строя нескольких датчиков в процессе измерения требует значительных временных затрат. Возможность теоретически восполнить информацию от неисправного датчика без потери качества измерений значительно повышает надежность всей измерительной системы.
Суть метода заключается в выполнении
интерполяции/экстраполяции значений поврежденного датчика на основе показаний
ближайших работающих датчиков в рамках модели критического состояния
сверхпроводника. Следует ожидать различную чувствительность методики к
местоположению испорченного датчика. Действительно: на границе бесконечно
тонкой полосы с током вертикальная компонента магнитного поля обращается в
бесконечность (резкий максимум в реальном эксперименте), и замена этого
значения экстраполяцией данных соседних датчиков даст серьезное отклонение
данных экстраполяции от исходных. В то же время производная компоненты в поперечном направлении в
центре идеальной СП ленты равна нулю (dBZ(X,Y)/dY=0, Y=a/2) и
при интерполяции значение практически не будет отклоняться от точного. Влияние
отключения датчиков на линии токов исследовалось для того же образца, данные
по которому представлены на рисунке 4. Были сделаны две серии измерений – с одним
испорченным датчиком, расположенным в различных местах линейки датчиков, и с
двумя испорченными датчиками расположенными рядом друг с другом. В первой серии
последовательно отключались датчики с номерами 2 и 3 (нумерация датчиков
представлена на рисунке 2а). При этом наблюдалось незначительное изменение
результатов расчета по амплитуде тока (не более 5%), полностью совпали
координаты расположения токового дефекта и его размеры. Примеры распределения
поперечной компоненты тока для однородного и неоднородного участка ленты
представлены на рисунке 5.
|
|
|
|
а) Однородный участок без одного датчика (слева) |
б) Неоднородный участок без одного датчика (справа) |
Рис. 5. (Цветной рисунок в электронной версии). Распределения поперечной компоненты тока для однородного и неоднородного участка ленты при повреждении одного датчика в линейке.
Во второй серии отключались пары датчиков (2 и 3) (рисунок 2а). Примеры распределения поперечной компоненты тока для однородного и неоднородного участка ленты представлены на рисунке 6. Сравнение результатов, полученных с полной и частично поврежденной линейкой датчиков Холла показывают, что даже при выходе из строя двух соседних датчиков сохраняется корректность результатов, по-прежнему однозначно фиксируется как протяженный дефект, так и малая неоднородность ленты, также верно определяется амплитуда тока ленты. Наблюдается лишь искажение в геометрических размерах области перетекания тока (расширение поперек ленты) и незначительно в величине тока в области токового дефекта.
|
|
|
|
а ) Однородный участок без двух датчиков (слева) |
б) Неоднородный участок без двух датчиков (справа) |
Рисунок 6. (Цветной рисунок в электронной версии). Распределения поперечной компоненты тока для однородного и неоднородного участка ленты при повреждении двух датчиков в линейке.
5. Заключение
В настоящей работе представлены результаты разработки и применения научно обоснованного метода визуализации локального протекания тока в длинномерной сверхпроводящей ленте и кабеле Roebel со сложной геометрией. Показана возможность использования алгоритма решения задачи инверсии уравнения Био-Савара-Лапласа с привлечением модели критического состояния сверхпроводника для исследования локальных токонесущих характеристик сверхпроводников. Продемонстрированы результаты использования экспериментальной установки, позволяющей в непрерывном режиме тестировать длинномерные (свыше 100 м) отрезки ВТСП лент на основе измерения магнитного поля линейкой датчиков Холла и проводить визуализацию токовых дефектов. Исследован вопрос устойчивости математического алгоритма и программно-аппаратной реализации системы измерения и расчета к возникновению нештатной ситуации при выходе из строя одного и двух соседних преобразователей Холла.
Работа выполнена в НИЯУ МИФИ при финансовой поддержке Министерства образования и науки РФ в рамках Соглашения № 14.575.21.0050 (RFMEFI57514X0050).
ЛИТЕРАТУРА
1. Токонесущие ленты второго поколения на основе высокотемпературных сверхпроводников, Под. Редакцией А. Гояла, М.: Издательство ЛКИ, 2009.-432 с.
2. Ch. Jooss, J. Albrecht, H. Kuhn et al, Rep. Prog. Phys., 65, 651(2002).
3. C. P. Bean, Rev. Mod. Phys., 36 , 31 (1964).
4. S.V.Pokrovskiy, I.A. Rudnev, A.I. Podlivaev, Physics Procedia, 36, 1558 (2012).
5. I.A. Rudnev, S.V. Pokrovskiy, A.I. Podlivaev, IEEE Trans. on Appl. Supercon., 22, 9001304(2012).
Experimental visualization of two-dimensional distribution of critical current in long high temperature superconducting tapes
S.V. Pokrovskiy1,2, I.A. Rudnev1,2, A.I. Podlivaev1, V.S. Kalitka3, A.V. Blednov3, A.A. Adamenkov3
1 National Research Nuclear University “MEPHI”, 115409, Moscow, Russia
2 International Laboratory of High Magnetic Fields and Low Temperature, Wroclaw, Poland
3 SuperOx, Moscow, Russia
Abstract
Based on visualization of electrical current flow a novel method of superconductive tape quality control is proposed and realized. We present the description of method as well as the results of application of developed method of visualization of two-dimensional (2D) distribution of critical current in long high temperature superconducting (HTSC) tapes. The method is based on the measurement by array of Hall sensors of trapped magnetic flux and numerical solution of the inverse Biot-Savar problem for the case of reel-to-reel rewinding in the real time. The modification of algorithm of 2D calculation of critical current is proposed. The aim of modification of standard algorithm was to improve the stability of the system to failure of one or two neighboring Hall sensors. The possibility of application of the methodology for the HTS tape length of over 500 m is shown.
Key words: visualization of current flow, HTSC tape, local critical current, critical current inhomogeneous
Reference
1. Second-Generation HTC Conductors, by A. Goyal; ISBN 978-1-4020-8117-0.
2. Ch. Jooss, J. Albrecht, H. Kuhn et al, Rep. Prog. Phys., 65, 651(2002).
3. C. P. Bean, Rev. Mod. Phys., 36 , 31 (1964).
4. S.V.Pokrovskiy, I.A. Rudnev, A.I. Podlivaev, Physics Procedia, 36, 1558 (2012).
5. I.A. Rudnev, S.V. Pokrovskiy, A.I. Podlivaev, IEEE Trans. on Appl. Supercon., 22, 9001304(2012).