Abstract
In this paper, we propose two fast registration algorithms for histological images. Our first algorithm is based on matching the contour points of the observation and template, and performs in O(M log M) time, where M is the number of the contour points, with almost no loss in the quality of registration compared to the commonly used Hungarian algorithm, which has O(M3) time complexity. A high accuracy of the transform parameter estimation is achieved by an iterative exclusion of heavily mismatched contour points, followed by rectification of the parameters for the rest of the points. Our second algorithm takes advantage of a special structure of the histological images that contain elliptical gland slices, and finds corresponding ellipses on the observation and template. The resulting transform is obtained from the pair of ellipses with maximum overlap index. The first method suits well for all types of histological images, while the second one is intended to be used for high-precision content-based spatial alignment.
Keywords: image registration, contour-based registration, affine transformation, ellipse detection, histological images, microscopy analysis.
1. Introduction
Computer processing and analysis of digital medical images becomes now increasingly important in medical pathology. Nowadays, pathologists extensively use digital imaging, e.g. in the technology of virtual microscopy, modern morphometric studies, and automated evaluation of the results of immunohistochemical studies; all these methods are based on the use of digital images of histological preparations. Mathematical methods of image processing and analysis of histological samples can help to recognize different observable tissue features, assess their compliance with the standards, and identify certain abnormalities inherent to particular pathological processes, i.e. conduct morphological diagnosis.
One of the problems in the analysis of histological images is their standardization: all the images in the series should be uniformly oriented before the key morphological structures (glands, blood vessels, stromal elements, etc.) are recognized for the comparison. This problem can be solved using image registration methods. Registration implies spatial alignment of a pair of images of the scene, i.e. determining a transformation that maps points on the first image (observation) into points on the second image (template). Most of the existing methods finds the parameters of linear transformation [3, 8] (similarity, affine), although some applications also involve nonlinear transformations [18] (projective, polynomial, elasticity). In this paper, we focus on the isotropic affine transformations due to the specifics of the microscopic shooting of tissue slices.
Image registration methods can be divided into two major groups: methods based on the intensity analysis, and methods based on the keypoint analysis. Intensity-based methods either estimate the transformation parameters directly using the intensity in the regions of interest [11, 2], or solve computationally intensive nonlinear optimization problems for some image metrics [5]. However, it should be noted that these methods usually rely on the assumption of small transformation to achieve the global optima. Keypoint-based methods, on the other hand, extract keypoints that characterize the image [11, 4], e.g. closed contours, line intersections, corners, etc. The transformation parameters are recovered by solving a system of equations that establishes the correspondence between the keypoints by matching their descriptors. Commonly used descriptors include SIFT [10], SURF [1], and Gauss-Laguerre [12].
In this paper, we propose two registration methods for histological images. The first method is based on matching the contour points of the observation and template, and is described in sections 2 and 3. The second one takes into account the internal features of some types of tissues and is presented in section 4.
2. Contour-based registration
This method is a keypoint-based method and is a modification of the method described in [15].
The process of the proposed contour-based registration consists of the following four steps: calculating the contour point descriptors, establishing a correspondence between the contour points by matching their descriptors, calculating the parameters of the isotropic affine transformation, and the subsequent parameters rectification.
2.1 Contour point descriptor
In this subsection, we discuss the calculation of contour
point descriptors for a given contour. First, for each point ![]() of a contour
of a contour ![]() in the original
orthogonal coordinate system
in the original
orthogonal coordinate system ![]() , we
introduce a local positive-oriented orthogonal coordinate system
, we
introduce a local positive-oriented orthogonal coordinate system ![]() ,
where
,
where ![]() is the mass center of the contour,
is the mass center of the contour, ![]() is
the axis collinear to vector
is
the axis collinear to vector ![]() , and
, and ![]() is the
axis orthogonal to axis
is the
axis orthogonal to axis![]() , as
shown in Fig. 1. After introducing the local coordinate system
, as
shown in Fig. 1. After introducing the local coordinate system ![]() all
the contour points are projected onto axis
all
the contour points are projected onto axis ![]() .
Assuming
.
Assuming ![]() and
and ![]() are
the minimal and maximal projection values of the projected contour points, we
divide segment
are
the minimal and maximal projection values of the projected contour points, we
divide segment ![]() into
into ![]() subsegments as
follows:
subsegments as
follows:
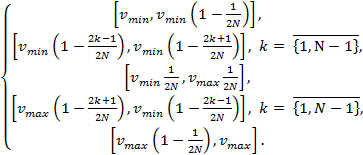 (1)
(1)
For each of these subsegments, we find two most distant
points of the contour ![]() and
and ![]() and
project them onto this subsegement. If such a pair of points is not unique, we
can choose any of them. Let us now form a list of points that characterizes
point
and
project them onto this subsegement. If such a pair of points is not unique, we
can choose any of them. Let us now form a list of points that characterizes
point ![]() :
:
![]() . (2)
. (2)
Since two different contour points can have the same lists
of points, we also add point ![]() at the end of the list. For each point
at the end of the list. For each point ![]() of the contour
of the contour ![]() the list of points
(2) is converted into a DOPM descriptor [16] as explained below.
the list of points
(2) is converted into a DOPM descriptor [16] as explained below.
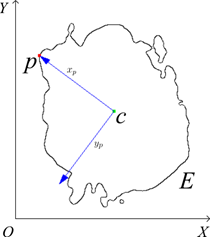
Fig. 1. Introducing a local coordinate system ![]() for a
point
for a
point ![]() of a
contour
of a
contour ![]() .
.
The list of points (2) can be written in matrix form as
![]() (3)
(3)
where each row ![]() holds
the coordinates of the i-th point of the list (2). One can rewrite it in the
homogeneous coordinates:
holds
the coordinates of the i-th point of the list (2). One can rewrite it in the
homogeneous coordinates:
![]() (4)
(4)
Now, any affine transformation can be defined by a matrix ![]() in
the homogeneous coordinates:
in
the homogeneous coordinates:
![]()
![]() (5)
(5)
where ![]() is
the translation vector, and
is
the translation vector, and ![]() is the
linear mapping. Let us consider another list of points
is the
linear mapping. Let us consider another list of points ![]() obtained from list
obtained from list ![]() by applying the
affine transformation and permuting the points:
by applying the
affine transformation and permuting the points:
![]() (6)
(6)
where ![]() is
the permutation matrix that establishes the correspondence between the points
of
is
the permutation matrix that establishes the correspondence between the points
of ![]() and
and ![]() . We
further assume that both
. We
further assume that both ![]() and
and ![]() have
full rank. It was shown [17] that if
have
full rank. It was shown [17] that if ![]() ,
, ![]()
![]() are
the orthogonal projection matrices on the range spaces of
are
the orthogonal projection matrices on the range spaces of ![]() and
and ![]() ,
respectively, then
,
respectively, then
![]() . (7)
. (7)
This equation shows that ![]() and
and ![]() are
permutation-similar matrices. It is known [6] that the diagonals of
permutation-similar matrices are related as follows:
are
permutation-similar matrices. It is known [6] that the diagonals of
permutation-similar matrices are related as follows:
![]() (8)
(8)
where ![]() ,
, ![]() are
the diagonals of
are
the diagonals of ![]() and
and ![]() ,
respectively. Thus, the diagonals contain the same elements but in different
order. Sorting them in, for instance, descending order yields an
affine-invariant descriptor.
,
respectively. Thus, the diagonals contain the same elements but in different
order. Sorting them in, for instance, descending order yields an
affine-invariant descriptor.
A detailed proof of the affine invariance of the DOPM descriptor is given in [15] and [16].
2.2 Contour matching
Consider a point ![]() on
the template contour and a point
on
the template contour and a point ![]() on
the observation contour. The cost of matching
on
the observation contour. The cost of matching ![]() of
two points is measured using
of
two points is measured using ![]() statistics
between the descriptors:
statistics
between the descriptors:
![]() (9)
(9)
where ![]() and
and ![]() are
the descriptors of the
are
the descriptors of the ![]() and
and ![]() points,
respectively. Given the set of costs
points,
respectively. Given the set of costs ![]() for
all point pairs
for
all point pairs ![]() of
two contours, we find the optimal correspondences by solving the following
minimization problem:
of
two contours, we find the optimal correspondences by solving the following
minimization problem:
![]() , (10)
, (10)
where minimization is performed over the set of all index
permutations ![]() . Problem (10) is a special case of
the assignment problem, which is commonly solved by the Hungarian algorithm,
which has
. Problem (10) is a special case of
the assignment problem, which is commonly solved by the Hungarian algorithm,
which has ![]() ) time
complexity, where
) time
complexity, where ![]() is the rank of the cost matrix.
is the rank of the cost matrix.
As we show in this work, in the case of isotropic affine
transformations the Hungarian algorithm can be seamlessly replaced with the
simpler greedy nearest neighbor search with time complexity ![]() [13] if
additional analysis of the matched contour points is applied. The proposed
accelerated approach is described in section 2.4.
[13] if
additional analysis of the matched contour points is applied. The proposed
accelerated approach is described in section 2.4.
2.3 Estimation of the isotropic affine transformation parameters
Now, let the coordinates of matched template and observation
contour points be written into the columns of matrices ![]() and
and ![]() ,
respectively. Since our goal is to determine an isotropic affine transformation
that maps
,
respectively. Since our goal is to determine an isotropic affine transformation
that maps ![]() to
to ![]() , we
restrict our considerations to transformations with linear maps
, we
restrict our considerations to transformations with linear maps ![]() of
the following form:
of
the following form:
![]() , (11)
, (11)
where ![]() is a scaling factor,
is a scaling factor, ![]() is an orthogonal
matrix that is responsible for rotating and flipping the tissue sample.
is an orthogonal
matrix that is responsible for rotating and flipping the tissue sample.
Since the scaling factor ![]() can
be obtained from the ratio of the areas of the given shapes, and the
translation vector
can
be obtained from the ratio of the areas of the given shapes, and the
translation vector ![]() of the transformation connects the mass
centers of the template and observation contours, these parameters can be
assumed to be known and fixed. Therefore, the only unknown is matrix
of the transformation connects the mass
centers of the template and observation contours, these parameters can be
assumed to be known and fixed. Therefore, the only unknown is matrix ![]() . We further assume
that
. We further assume
that ![]() and
and ![]() hold
already centered and scaled coordinates.
hold
already centered and scaled coordinates.
The problem of finding the optimal, in terms of the standard deviation, orthogonal matrix that maps one set of points to another is related to Wahba’s problem [14]:
![]() (12)
(12)
In our case, we omit the last constraint on the determinant
of ![]() since we are interested in capturing
reflections along with rotations. Problem (12) can be easily solved by the
Kabsch algorithm [7], which is based on the singular value decomposition of the
covariance matrix:
since we are interested in capturing
reflections along with rotations. Problem (12) can be easily solved by the
Kabsch algorithm [7], which is based on the singular value decomposition of the
covariance matrix:
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (13)
. (13)
The solution of our problem can be calculated in the form
![]() . (14)
. (14)
2.4 Rectification of the isotropic affine transformation parameters
Mismatched contour points can cause significant angular
errors during the estimation of the rotation. It leads to some solution ![]() , substantially
different from the exact solution. The key idea of the proposed rectification
approach is to exclude heavily mismatched contour points iteratively and
re-estimate the orthogonal matrix according to algorithm (11-14) for the
remaining points on each step. In our experiments, we exclude half of the point
pairs
, substantially
different from the exact solution. The key idea of the proposed rectification
approach is to exclude heavily mismatched contour points iteratively and
re-estimate the orthogonal matrix according to algorithm (11-14) for the
remaining points on each step. In our experiments, we exclude half of the point
pairs ![]() with largest matching error
with largest matching error ![]() . The
iterative process continues while the Jaccard index (see section 3) increases,
or until a single pair of points remains.
. The
iterative process continues while the Jaccard index (see section 3) increases,
or until a single pair of points remains.
The effectiveness of the proposed procedure can be
demonstrated with the following example. Consider N = 500 random points
uniformly distributed on the unit circle, the coordinates of which are written
into the columns of a matrix ![]() . We
rotate the points by a random angle ψ and randomly permute
. We
rotate the points by a random angle ψ and randomly permute ![]() of the points for
some
of the points for
some ![]() , obtaining
, obtaining
![]() , (15)
, (15)
where ![]() is
the permutation matrix, and
is
the permutation matrix, and ![]() is
the rotation matrix. Using algorithm (11-14) we can estimate the rotation angle
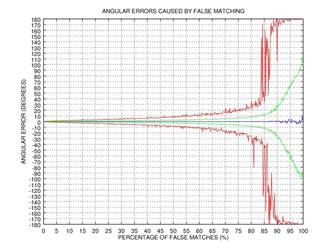
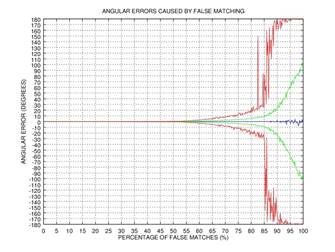
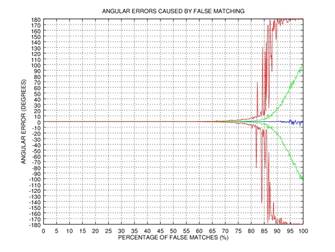
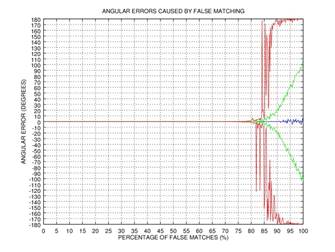
ψ after 0, 1, 2, or 3 rectification steps. Fig. 2 shows the angular error
of the estimation as a function of the percentage of incorrectly matched
(permuted) points on the results of 1000 tests: blue color represents the mean
of the error, green color represents the standard deviation of the error, and red
color represents the mode of the error. This simple example shows that even if
75% of the points are matched incorrectly, the angular error gets close to zero
after three iterations of our rectification procedure.
is
the rotation matrix. Using algorithm (11-14) we can estimate the rotation angle
ψ after 0, 1, 2, or 3 rectification steps. Fig. 2 shows the angular error
of the estimation as a function of the percentage of incorrectly matched
(permuted) points on the results of 1000 tests: blue color represents the mean
of the error, green color represents the standard deviation of the error, and red
color represents the mode of the error. This simple example shows that even if
75% of the points are matched incorrectly, the angular error gets close to zero
after three iterations of our rectification procedure.
3. Experimental results for contour-based registration
For accuracy evaluation of the contour-based registration method applied to segmented (binary) images two different metrics were used. First is the Jaccard index
![]() , (16)
, (16)
where ![]() is a template,
is a template, ![]() is an observation, and
is an observation, and
![]() is
the estimated transformation. The second metric is the peak signal-to-noise
ratio (PSNR):
is
the estimated transformation. The second metric is the peak signal-to-noise
ratio (PSNR):
PSNR = 20 log (![]() ), (17)
), (17)
where MSE is the sum of squared differences between the original images after alignment. The proposed method was applied to 62 histological images provided by Federal State Scientific Institution “B.V.Petrovsky National Research Center of Surgery”. Some of the histological images and the corresponding results of the contour-based
|
|
|
|
(a) |
(b) |
|
|
|
|
(c) |
(d) |
Fig. 2. Demonstration of the effectiveness of our rectification procedure: the angular error of the estimation as a function of the percentage of false matches; blue color represents the mean of the error, green color represents the standard deviation of the error, and red color represents the mode of the error: 0 iterations (a), 1 iteration (b), 2 iterations (c), 3 iterations (d).
registration method are shown in Fig. 3-6. Table 1 includes the results of the comparative analysis of the proposed and existing registration methods.
Table 1: Comparison of image registration methods.
|
Method |
Complexity |
Accuracy |
|
DOPM + Hungarian algorithm [15] |
|
0.9435 |
|
Moment-based method [2] |
|
0.8572 |
|
Proposed |
|
0.9429 |
|
|
|
|
|
a) Template |
b) Observation |
c) |
Fig. 3. Results of the contour-based registration
algorithm for tissue samples: red color represents the template ![]() , green color
represents the aligned observation
, green color
represents the aligned observation ![]() , and yellow
color shows their intersection.
, and yellow
color shows their intersection.
|
|
||
|
a) Template |
b) Observation |
c) |
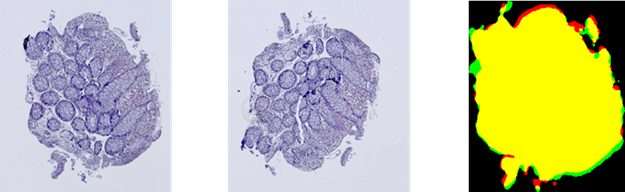
Fig. 4. Results of the
contour-based registration algorithm for tissue samples: red color represents
the template ![]() , green color represents the aligned observation
, green color represents the aligned observation ![]() , and yellow color shows their intersection.
, and yellow color shows their intersection.
|
|
|
|
(a) |
(b) |
|
|
|
|
(c) |
(d) |
|
|
|
|
(e) |
(f) |
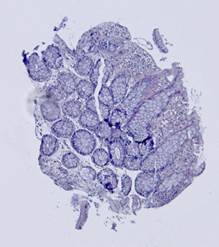
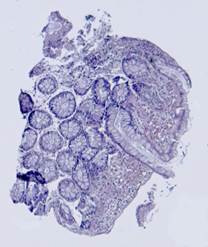
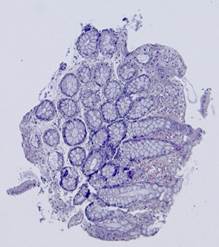
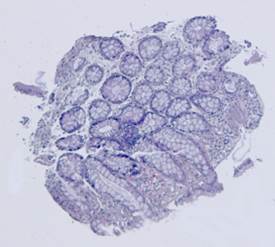
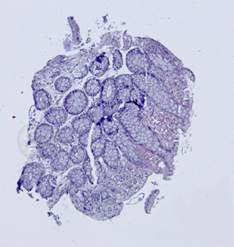
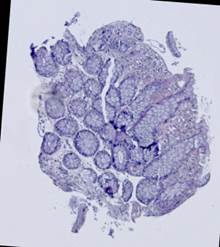
Fig. 5. Tissue slice samples before registration: template (a), observations (b)-(f).
|
|
|
|
(a) |
(b) |
|
|
|
|
(c) |
(d) |
|
|
|
|
(e) |
(f) |
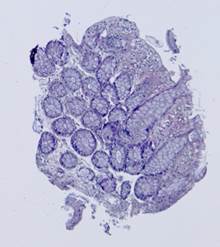
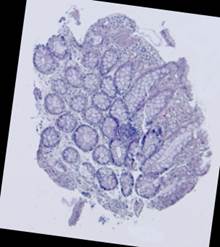
Fig. 6. Results of the contour-based registration algorithm applied to the images in Fig. 5: template (a), observations (b)-(f).
4. Ellipse-based registration
Some types of histological images, like the images of slices of the mucosa of a large intestine, have elliptical features which can be exploited for image registration.
The Hough transform [20] is one of the most widely used methods for ellipse detection. It analyzes the five-dimensional space of the ellipse parameters. However, it is not very efficient in practice due to an extremely high computational load for small quantization steps on the one hand, and very low accuracy for large quantization steps on the other. Some non-classical methods, such as [21], are able to detect ellipses much more efficiently by reducing the dimensionality of the parameter space, but they are unstable since they rely on certain ideal ellipse properties. We propose an alternative approach: search elliptical areas among the connected components of the inverted contour map.
Direct application of the Canny edge detector [22] to the original produces ragged contours. Thus, we preliminarily apply nonlinear anisotropic diffusion [23] to close the contours. This step implies solving the following partial differential equation
![]() , (18)
, (18)
where ![]() is the
image intensity at point
is the
image intensity at point ![]() and
time
and
time ![]() ,
, ![]() is a
diffusion tensor for
is a
diffusion tensor for ![]() at
point
at
point ![]() that
uses the Hessian of
that
uses the Hessian of ![]() to
direct the diffusion orthogonally to the gradient of
to
direct the diffusion orthogonally to the gradient of ![]() . The
result of the nonlinear anisotropic diffusion pre-processing is shown in Fig.
7(a). The Canny edge detector is then applied to the pre-processed image to
obtain the required contour map shown in Fig. 7(b).
. The
result of the nonlinear anisotropic diffusion pre-processing is shown in Fig.
7(a). The Canny edge detector is then applied to the pre-processed image to
obtain the required contour map shown in Fig. 7(b).
On the next step, the inverted contour map is divided into
connected components; the component with the largest area, which corresponds to
the background, is excluded from consideration (Fig. 7(c)). Furthermore, if the
ratio of the area of a component to the area of its convex hull is less than ![]() , the
component is considered to be non-elliptical and is also excluded. Remaining
connected components are approximated by ellipses (Fig. 7(d)).
, the
component is considered to be non-elliptical and is also excluded. Remaining
connected components are approximated by ellipses (Fig. 7(d)).
On the final step, the detected ellipses of the template and
observation are matched. The ellipses of the observation are preliminarily
scaled according to the ratio of the areas of the shapes obtained by
segmentation of the input images. Then, for each pair of the ellipses on the
template and observation, we transform the ellipses of the observation using
translation and linear orthogonal mapping so that the selected pair of ellipses
gets aligned (both valid rotations and both valid reflections are checked), and
calculate the corresponding overlap index ![]() :
:
![]() (19)
(19)
![]()
where ![]() and
and ![]() are
the centroids,
are
the centroids, ![]() and
and ![]() are
the minor axes,
are
the minor axes, ![]() and
and ![]() are
the major axes of the template and observation ellipses, respectively. The resulting
isotropic affine transformation is calculated using the pair of ellipses with maximum
overlap index. Fig. 7(e-f) demonstrates three pairs of ellipses with highest
overlap indices.
are
the major axes of the template and observation ellipses, respectively. The resulting
isotropic affine transformation is calculated using the pair of ellipses with maximum
overlap index. Fig. 7(e-f) demonstrates three pairs of ellipses with highest
overlap indices.
This approach, in contrast to contour-based registration, does not depend on the shapes of the slices. It is more robust to tissue lacerations, and it can also track changes in the internal structure of the samples. Experimental results with our ellipse-based registration method are shown in Fig. 8. Comparison with the contour-based registration method (Fig. 4) shows a slight decrease (by 0.01) of the Jaccard index and a significant improvement (by 0.9 dB) of the peak signal-to-noise ratio (PSNR), which indicates a more precise alignment of the internal structures.
|
|
|
|
(a) |
(b) |
|
|
|
|
(c) |
(d) |
|
|
|
|
(e) |
(f) |
Fig. 7. Steps of the ellipse-based registration algorithm: anisotropic diffusion (a), Canny edge detection (b), connected regions (c), detected ellipses (d), pairs of matched ellipses of the template (e) and observation (f).
|
|
|
|
|
à) Template |
b) Observation |
c) |
Fig. 8. Results of the ellipse-based registration
algorithm for tissue samples: red color represents the template ![]() , green color
represents the aligned observation
, green color
represents the aligned observation ![]() , and yellow
color shows their intersection.
, and yellow
color shows their intersection.
5. Conclusion
An efficient algorithm for registration of histological images
based on matching the contour points of the template and observation has been
proposed. Since the matching problem is reduced to the assignment problem, the classical
Hungarian algorithm is commonly used to perform matching in ![]() time,
where
time,
where ![]() is the number of the contour points. The
proposed method is able to perform effective matching in
is the number of the contour points. The
proposed method is able to perform effective matching in ![]() time
without affecting the quality of registration. The high accuracy of the
transform parameter estimation is achieved by an iterative exclusion of heavily
mismatched contour points, followed by a rectification of the parameters for
the rest of the points.
time
without affecting the quality of registration. The high accuracy of the
transform parameter estimation is achieved by an iterative exclusion of heavily
mismatched contour points, followed by a rectification of the parameters for
the rest of the points.
For some applications content-based registration is more important than shape-based alignment. Our second registration algorithm was designed specifically for tissues containing glands, which have elliptical shape. Experimental evaluation showed that the peak signal-to-noise ratio for our ellipse-based registration is higher than for the contour-based one, what indicates a more precise alignment of the internal structures.
Acknowledgements
This work was supported by Russian Scientific Foundation grant 14-11-00308.
References
[1] H. Bay, A. Ess, T. Tuytelaars, L. Gool, “SURF: Speeded up robust features”, Computer Vision and Image Understanding, vol.110, no.3, pp.346-359, 2008.
[2] C. Domokos, J. Nemeth, and Z. Kato, “Nonlinear shape registration without correspondences”, IEEE Transactions on pattern analysis and machine intelligence, vol.34, no.5, pp.943-958, 2012.
[3] J. Feldmar and N. Ayache, “Rigit, affine and locally affine registration of free form surfaces”, International Journal of Computer Vision, vol.18, no.2, pp.99-119, 1996.
[4] H. Guo, A. Rangarajan, S. Joshi, and L. Younes, “Non-rigid registration of shapes via diffeomorphic point matching”, Proceedings of the IEEE International Symposium on Biomedical Imaging: From Nano to Macro, pp.924-927, 2004.
[5] M. S. Hansen, M. F. Hansen, and R. Larsen, “Diffeomorphic statistical deformation models”, Proceedings of the IEEE International Conference on Computer Vision, pp.1-8, 2007.
[6] R. Horn, C. Johnson, “Matrix analysis”, Cambridge, U. K.: Cambridge University Press, 1985.
[7] W. Kabsch, “A solution for the best rotation to relate two sets of vectors”, Acta Crystallographica Section A, vol.32, no.5, pp.922-923, 1976.
[8] A. Kadyrov and M. Petrou, “Affine parameter estimation for the trace transform”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.28, no.10, pp.1631-1645, 2006.
[9] H. Kuhn, “The Hungarian Method for the assignment problem”, Naval Research Logistics Quarterly, vol.2, no.1-2, pp.83-97, 1955.
[10] D. G. Low, “Distinctive image features from scale-invariant keypoints”, International Journal of Computer Vision, vol.60, pp.91-110, 2004.
[11] S. Mann, R. W. Picard, “Video orbits of the projective group a simple approach to featureless estimation of parameters”, IEEE Transactions on Image Processing, vol.6, no.9, pp.1281-1295, 1997.
[12] D. Sorokin, A. Krylov, “Gauss-Laguerre-Hermite methods of keypoint extraction”, Pattern Recognition and Image Analysis, vol.21, no.2, pp.332-334, 2011.
[13] P. Vaidya, “An O(n log n) algorithm for the all-nearest-neighbors problem”, Discrete and Computational Geometry journal, vol.4, no.1, pp.101-115, 1989.
[14] G. Wahba, “A Least Squares Estimate of Satellite Attitude”, SIAM Review, vol.7, no.3, pp.409-411, 1965.
[15] W. Wang, Y. Jiang, B. Xiong, and others, “Contour matching using the~affine-invariant support point set”, IET Computer Vision, vol.8, no.1, pp.35-44, 2014.
[16] Z. Wang, M. Liang, “Locally affine invariant descriptors for shape matching and retrieval”, IEEE Signal Processing Letters, vol.17, no.9, pp. 803-806, 2010.
[17] Z. Wang, H. Xia, “Dimension-free affine shape matching through subspace invariance”, IEEE Conf. Computer Vision and Pattern Recognition, pp.357-364. 2009.
[18] L. Zagorchev and A. Goshtasby, “A comparative study of transformation functions for nonrigit image registration”, IEEE Transactions on Image Processing, vol.15, no.3, pp.529-538, 2006.
[19] B. Zitova and J. Flusser, “Image registration methods: a survey”, Image and Vision Computing, vol.21, pp.977-1000, 2003.
[20] S. Tsuji, M. Matsumoto, “Detection of ellipses by a modified Hough transform”, IEEE Trans. Comput, vol. 27, pp.777–781, 1978.
[21] X.Yonghong and J. Qiang, “A New Efficient Ellipse Detection Method”, International Conference on Pattern Recognition, pp. 957–960, 2002.
[22] J. Canny, “A Computational Approach to Edge Detection”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.PAMI-8, No. 6, 679-698, November 1986.
[23] Joachim Weickert, “Anisotropic Diffusion in Image Processing”, B.G. Teubner Stuttgart, 1998.