МЕТОДИКА ВИЗУАЛИЗАЦИИ ПОЛЕЙ ГАММА-ИЗЛУЧЕНИЯ В ПОМЕЩЕНИИ
А.Д. Модяев, Н.М. Леонова, А.С. Филатов, А.А. Шабынин
Национальный исследовательский ядерный университет «МИФИ», Россия
ADModyaev@mephi.ru, NMLeonova@mephi.ru, philatalexander@gmail.com, shabynin@gmail.com
Содержание
3. Визуализация пространственных полей гамма-излучения.
4. Проецирование полей гамма-излучения
Представлена методика визуализации, позволяющая по ряду пространственно распределенных измерений, проведенных из одной точки, сформировать полную панорамную картину радиационной обстановки в помещении. Методика открывает новый способ использования аппарата сферических сплайнов в задачах мониторинга окружающей среды.
Ключевые слова: гамма-видение, сферический сплайн, пространственные поля, интерполяция.
1. Введение
Появление многомодульных детектирующих устройств новой конструкции, состоящих из нескольких групп взаимно экранированных модулей, позволяет раздельно регистрировать гамма-кванты, приходящие с различных направлений. Поскольку такие детектирующие устройства обладают анизотропной чувствительностью и явно выраженными пеленгационными характеристиками, они способны осуществлять круговую регистрацию полей излучения. Использование нескольких таких пространственно разнесенных датчиков позволяет решить задачу нахождения местоположения источников излучения с последующим восстановлением поля излучения на плоскости [1-3].
Усовершенствование конструкции датчиков и применение подвижных коллиматоров делает возможным сканирование радиационных полей в заданном телесном угле [4]. В этом случае использование одного детектирующего устройства позволяет осуществлять регистрацию и последующую визуализацию трехмерных полей гамма-излучения. В результате открываются принципиально новые возможности регистрации и последующей визуализации полей гамма-излучения непосредственно в реальном времени. В этом случае отпадает необходимость в многократных измерениях уровней излучения обычными детекторами с изотропной чувствительностью на множестве точек пространства и в последующей длительной обработке данных для решения интерполяционной задачи восстановления полей излучения.
Разработка систем гамма-видения, оснащенных детектирующими устройствами с коллиматорами, предусматривает создание компьютерных средств управления ориентацией чувствительных элементов датчиков, средств обработки, хранения и визуализации данных на экране дисплея.
В представленной работе рассматривается и решается задача формирования алгоритмического обеспечения для регистрации и визуализации полей излучения с использованием метода сферических сплайнов. Развиваемая методика визуализации положена в основу разработки прикладного программного обеспечения для перспективной компьютерной системы гамма-видения нового поколения. Применение таких систем будет особенно эффективным при проведении оперативного радиоэкологического мониторинга жилых и нежилых помещений на предмет выявления внутри них и в элементах строительных конструкций источников радиационного загрязнения. Конечным результатом визуализации является документированная графическая информация о параметрах зарегистрированных радиационных полей внутри обследуемых помещений.
2. Регистрация полей гамма-излучения с использованием детектирующих устройств с коллиматором в режиме сканирования
Для исследования процессов регистрации и разработки алгоритмов восстановления трехмерных полей гамма-излучения вводится модель детектирующего устройства с подвижным коллиматором. За основу выберем конструкцию датчика, предложенную в работе [4]. Схема используемого в нем коллиматора представлена на рис. 1.

Рис. 1. Схема подвижного коллиматора многомодульного детектирующего устройства
Расчетная диаграмма направленности датчика с коллиматором представлена на рис.2.

Рис. 2. Диаграмма направленности анизотропного датчика
Методика проведения измерений интенсивности гамма-излучения по различным направлениям в трехмерном пространстве заключается в формировании четырех последовательных серий круговых наблюдений. В каждой из них регистрируется 15 измерений с шагом 24 градуса при фиксированной ориентации датчика. При переходе от предыдущей серии к последующей осуществляется поворот датчика по углу места. Таким образом может быть осуществлено сканирование всего трехмерного пространства. Данная методика применима для проведения измерений на малых расстояниях, например, для мониторинга помещений.
Проводимые измерения в общем случае можно представить в виде функции направления на обследуемую область помещения. Каждое измеренное значение является интегральным на области измерения. Функцию измерений можно описать частичной суммой вида
 ,
,
где w(Pi) - коэффициенты из диаграммы направленности на сетке, покрывающей конкретную область измерений, а Pi – точки этой сетки.
На основе проведенных измерений с учетом свойств помещения и его геометрических размеров можно спроецировать значения интенсивностей поля на стены, пол, потолок. Это позволяет применять методы приближения на нерегулярных массивах данных на каждой из плоскостей в отдельности. Такой подход сопряжен с необходимостью согласования отдельных плоскостей. Рассмотрим альтернативный подход, который заключается в использовании некоторого общего пространства или поверхности, в которой будут представлены все без исключения располагаемые данные измерений. В качестве такового может выступать как непосредственно трехмерное пространство, так и двумерная поверхность, отражающая все направления измерений.
Находясь в некоторой точке пространства внутри помещения, уместно рассматривать измерения в качестве значений, заданных на сфере с центром в данной точке. Это позволяет:
• получить связную картину, так как все измерения расположены на одной поверхности и участвуют в построении общего приближения;
• рассматривать показания независимо от формы помещения и интерпретировать их как свойство точки, в которой находится исследователь.
Применение датчика с анизотропной чувствительностью в режиме сканирования исключает необходимость его перемещения внутри рассматриваемого пространства. В этом заключается кардинальное отличие от традиционных детектирующих устройств, снимающих интегральное значение в точке поля без учета направления.
3. Визуализация пространственных полей гамма-излучения
В условиях, когда измерения распределены по поверхности сферы, для восстановления поля можно воспользоваться методами, схожими с методами сферической интерполяции, традиционно используемой в геодезии, метеорологии и других областях.[5]
Каждому измерению ставится в соответствие область на сфере, отвечающая направлению, в котором оно было произведено, что показано на рис. 3.
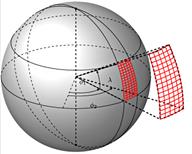
Рис. 3. Сетка на поверхности сферы, покрывающая область одного измерения.
Распределение интегрального значения, полученного в результате измерения, определяется угловым разрешением датчика.
Воспользуемся обобщенным описанием натуральных сплайнов[5]. Введём скалярное произведение, определяемое следующим образом
![]() ,
,
где Ω – сфера единичного радиуса.
При построении сплайна решается интерполяционная задача
![]() ,
,
где ki – линейно ограниченные операторы, отвечающие функционалу измерений A.
Указанный сплайн σ выбирается из условия минимума на линейно ограниченном операторе T – функционале гладкости, в качестве которого выбран оператор Бельтрами
 .
.
Этот сплайн представим в виде [5]
 ,
,
где G(x,P) – функция Грина, отвечающая энергетическому функционалу T; nj(P) – элементы ядра оператора T; λi, υj – некоторые действительные коэффициенты, определяющиеся из системы
![]() ,
,
 ,
,  ,
,
где gi(P)=(ki(x),G(x,P)).
Функционал измерений A определяется набором отдельных функционалов ki, которые численно описываются следующим образом:
 .
.
Интерполяционная задача для описанного сплайна выглядит так:
 ,
,
где wj – весовая функция j-го измерения (см. рис. 4), Pji – точки суммирования, покрывающие область j-го измерения, а σ – искомый сплайн.
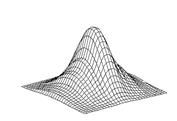
Рис. 4. Весовая функция для одного измерения.
Сужение области суммирования до одной точки ведет к вырождению интегрального функционала в точечный. Таким образом, введенная модель является расширением точечной модели. Это подтверждается в работе [6], где приводятся оценки ошибки при применении сплайна с интегральными интерполяционными условиями.
Приведенный сплайн позволяет рассматривать все измерения на одной поверхности и учитывать их взаимное влияние при построении общего приближения на сфере.
Исследование условий разрешимости показывает, что существования и единственности сплайна такого вида можно добиться, если каждая из областей, на которых заданы значения на поверхности сферы, обладает уникальной подобластью, не содержащейся ни в одной из оставшихся областей. Или, в случае численного интегрирования, необходимо, чтобы в частичных суммах, представляющих каждую из областей, была хотя бы одна уникальная точка. Это свойство нужно учитывать при непосредственном построении сплайна.
Следует иметь ввиду, что сами измерения заданы с некоторой ошибкой, а области, отвечающие этим измерениям, в силу неидеальности детектирующих устройств имеют свойство перекрываться. Чем сильнее перекрываются области измерений, тем хуже обусловлена задача построения сплайна. В результате на итоговом приближении проявляются характерные искажения, которые связаны с ошибками в измерениях. Сложностей, связанных с зашумленностью данных и плохой обусловленностью, можно избежать, заменив интерполяционный сплайн сглаживающим, как показано на рис. 5, 6.
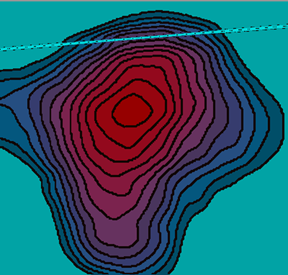
Рис. 5. Интерполяционный сплайн на зашумленных данных.
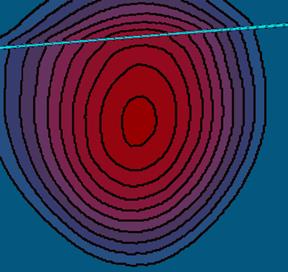
Рис. 6. Сплайн, построенный с применением сглаживания зашумленных данных.
Сглаживание происходит на этапе построения сплайна. Для этого при расчете коэффициентов сплайна вводится аддитивная поправка к матрице А на коэффициент сглаживания по главной диагонали:
![]() .
.
Существует ряд способов задания коэффициента сглаживания. В частности, его можно оценивать из входных данных с использованием метода перекрестной проверки, как показано в работе [7], или подбирать с помощью найденной ранее оценки ошибки.
4. Проецирование полей гамма-излучения
Введенная в рассмотрение сфера является промежуточной и служит для восстановления приближения, которое впоследствии должно быть спроецировано на помещение. Сплайн позволяет пересчитать значение в любой точке на поверхности сферы. Однако использование натурального сплайна для пересчета каждой точки, необходимой для построения проекций, связано со значительными вычислительными затратами. Поэтому пересчет осуществляется лишь для некоторых точек, значения между которыми при проецировании интерполируются. Для этого используется бикубические сплайны, широко применяемые в задачах интерполяции на регулярных сетках.
При этом могут возникнуть искажения, связанные с переходом со сферической поверхности на плоскую. Ограничимся несложным рассмотрением природы этих искажений (рис. 7)

Рис. 7. Иллюстрация к расчету коэффициента искажения в точке B между узлами регулярной сетки A и C для проецирования приближения на сфере с центром в точке O
Угловая координата точки B отрезка AC на сфере с центром в точке O равна γ/Δ. Координата точки B внутри отрезка характеризуется выражением:
![]() .
.
В предположении, что углы Δ и γ малы (не превышают нескольких градусов), это выражение можно упростить:
![]() .
.
В таком виде становится явным коэффициент k, характеризующий искажения. Хорошо заметно, что с уменьшением параметра t = Δ tan(α) ошибка затухает. Это можно наглядно представить, приняв во внимание тот факт, что значения угла γ колеблются в промежутке от 0 до Δ. При угле α менее 45 градусов и Δ менее 3 градусов коэффициент искажения при переходе с одной поверхности на другую не превышает 5%.
Большую ошибку при проецировании вносит растяжение, которое не связано с характером сетки на гранях помещения, а зависит только от ошибки построения сплайна на сфере и угла α между нормалью к грани помещения и направлением на ребро. При значении α = 45 градусов растяжение достигает 2-х раз. Если датчик расположен в центре помещения, то ошибка, получаемая при проецировании на удаленные участки, в два раза превышает ошибку, получаемую при проецировании на наиболее близкие участки.
Также при переходе со сферической поверхности на поверхности граней помещения требуется пересчет значений в соответствии с природой восстанавливаемой физической величины. Использование сферического сплайна дает возможность осуществить этот переход. В геодезии, где сферические сплайны активно применяются, используется механизм псевдодифференциальных операторов [8]. К их числу относится «оператор продолжения».
Использование псевдодифференциальных операторов основывается на свойствах преобразования Фурье. В данном случае имеется ввиду разложение по сферическим гармоникам. Найденный сплайн s считается приближением настоящего распределения T искомой величины по поверхности помещения, будучи модифицированным псевдодифференциальным оператором Λ:
![]() .
.
Это псевдодифференциальное уравнение решается в Фурье-пространстве, и производится обратный переход:
![]() .
.
Благодаря свойствам сферических сплайнов этот переход означает лишь поправку коэффициентов сплайна при подстановке значений [8]. Отличие предлагаемого способа пересчета заключается в использовании интегрального функционала измерений, что не вносит существенных изменений в силу линейности преобразования Фурье. Таким образом, поправка вносится еще на сфере и при проецировании производится ее подстановка в соответствующим образом модифицированный сплайн.
5. Заключение
В данной работе показана принципиальная возможность восстановления полей гамма-излучения в трехмерном пространстве по серии измерений, проводимых с использованием датчика с анизотропной чувствительностью. В работе описан алгоритм регистрации и визуализации полей излучения, позволяющий проводить сканирование трехмерного пространства из одной точки. Приведены формулы для расчета коэффициентов введенного сплайна, результаты исследования условий разрешимости данного типа сплайна, обозначены методы для достижения лучшей обусловленности задачи аппроксимации измерений с использованием данного типа сплайна, рассмотрены ошибки, сопровождающие процесс проецирования восстановленных значений интенсивности излучения на грани помещения.
Проведено теоретическое обоснование методов восстановления трехмерных полей из одной точки пространства, разработана модель сканирующего детектирующего устройства, алгоритмическое и прикладное программное обеспечение процессов визуализации, получены эмпирические оценки и изображения формируемых пространственных гамма-полей. Математическое моделирование подтвердило возможность использования предлагаемых подходов и методов для решения задачи восстановления трехмерных полей излучений.
Разработанные методы регистрации и визуализации пространственных полей предназначены для использования в перспективных компьютерных системах гамма-видения, осуществляющих радиационный мониторинг помещений в реальном времени.
Список литературы
[1] Исаков С.В. Применение многомодульных детектирующих устройств для измерения, восстановления пространственных характеристик и визуализации полей гамма-излучения [Текст] / С.В. Исаков, В.Т. Самосадный, В.В. Кадилин, А.Д. Модяев, Н.В. Коробков // Инженерная физика. - 1999. №2. - C.37-40.
[2] Исаков С.В. Методика проведения радиационного мониторинга с применением панорамного детектирующего устройства [Текст] / С.В. Исаков, В.В. Кадилин, А.Д. Модяев // Экологические системы и приборы. - 2000. №1. - С.9-10.
[3] Аль-хури В.С. Разработка аппаратуры направленного поиска локальных источников гамма-излучения [Текст] / В.С. Аль-хури, С.В. Исаков, В.В. Кадилин, В.Т. Самосадный // Научная сессия МИФИ-2002. Т.5 Медицинская физика и техника, биофизика. Математическое моделирование в геофизике. Охрана окружающей среды и рациональное природопользование. Теоретические проблемы физики - М.: МИФИ, 2002.
[4] Пат. 2160909 Российская Федерация, G 01 T 1/16, G 01 V 5/00. Устройство для поиска и обнаружения радиоактивных объектов [Текст] / Мухин В.И., Муслимов Р.Х., Самосадный В.Т. - № 99127111/28; заявл. 31.12.1999; опубл. 20.12.2000.
[5] Игнатов М.И., Певный А.Б. Натуральные сплайны многих переменных. - Л.: Наука, 1991.
[6] Филатов А.С. Оценка ошибки построения сплайна с интегральными интерполяционными условиями [Текст] / А. С. Филатов, А. А. Шабынин, Н. М. Леонова // Вестник национального исследовательского ядерного университета МИФИ – М.: МИФИ, 2013, том 2, № 2 - с. 208–211
[7] Grace Wahba Some new mathematical methods for variational objective analysis using splines and cross-validation [Текст] / Grace Wahba, James Wendelberger / Madison: Dept. of Statistics, University of Wisconsin - 1980.
[8] Willi Freeden A survey on spherical spline appriximation [Текст] / Willi Freeden, Michael Schreiner, Richard Franke // Surveys on mathematics for industry – 1995
METHODOLOGY OF GAMMA-RAYS VISUALIZATION IN INDOOR SPACE
A.D. Modyaev, N.M. Leonova, A.S. Filatov, A.A. Shabynin
National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Russia
ADModyaev@mephi.ru, NMLeonova@mephi.ru, philatalexander@gmail.com, shabynin@gmail.com
Abstract
Method of visualization presented here allows forming the whole panoramic radiation situation picture in indoor space using a range of space-distributed measurements, done from one point. This method gives a new approach of using spherical splines device in environmental task monitoring.
Key words: gamma-vision, spherical spline, space fields, interpolation.
Reference List
[1] Isakov S.V Multi-modul device application for measuring and reconstruction of space characteristics and gamma-emission fields visualization. [Text] Isakov S.V., V.T.. Samosadnyi V.V. Kadilin., A.D. Modajev, N.V. Korobkov // Engineering Physics . - 1999. №2. - p.37-40.
[2] Isakov S.V. Method of carrying out radiation monitoring with the help of panoramic detecting device. [Тext] / Isakov S.V., V.V. Kadilin, A.D. Modajev // Ecological systems and devices . - 2000. №1. – p.9-10.
[3] Al-huri V.S. Development of a guided search tools of a local sources of gamma-radiation. [Тext] / V.S. Al-huri, S.V. Isakov, V.V. Kadilin, V.T. Samosadnyi // Scientific Session NRNU MEPhI -2002. Т.5 Medical Physics and Technology, Biophysics. Mathematical modeling in geophysics. Environmental protection and conservancy. Theoretical problems of physics. - М.: NRNU MEPhI , 2002.
[4] Patent 2160909 Russian Federation G 01 T 1/16, G 01 V 5/00. Device for search and detection of radioactive objects. [Тext] / Muhin V.I., Muslimov R.H., Samosadnyi V.T., - № 99127111/28; applied 31.12.1999; published 20.12.2000.
[5] Ignatov M.I., Pevnyi A.B. Natural splines of several variables. - L.: Science, 1991.
[6] Filatov A.S. Estimated error of spline building with integral interpolated conditions [Тext] / A.S. Filatov, A.A. Shabynin, N.M. Leonova // Herald of NRNU MEPhI – М.: MEPhI, 2013, vol. 2, № 2 - p. 208–211
[7] Grace Wahba Some new mathematical methods for variational objective analysis using splines and cross-validation [Тext] / Grace Wahba, James Wendelberger / Madison: Dept. of Statistics, University of Wisconsin - 1980.
[8] Willi Freeden A survey on spherical spline appriximation [Текст] / Willi Freeden, Michael Schreiner, Richard Franke // Surveys on mathematics for industry - 1995