METHODOLOGY OF GAMMA-RAYS VISUALIZATION IN INDOOR SPACE
A.D. Modyaev, N.M. Leonova, A.S. Filatov, A.A. Shabynin
National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Russia
ADModyaev@mephi.ru, NMLeonova@mephi.ru, philatalexander@gmail.com, shabynin@gmail.com
Contents
3. Space fields gamma-radiation visualization
4. Projection gamma-radiation fields
Abstract
Method of visualization presented here allows forming the whole panoramic radiation situation picture in indoor space using a range of space-distributed measurements, done from one point. This method gives a new approach of using spherical splines device in environmental task monitoring.
Key words: gamma-vision, spherical spline, space fields, interpolation.
1. Introduction
New construction of multi-module detecting devices made of some groups of mutually screened modules allows registering gamma-quanta coming from different directions. As such detecting devices have anisotropic apprehensibility and evident direction-finding characteristics they are able to perform spherical registration of radiation field.
Using of such spaced-sensor detectors helps to solve the finding emission source problem with radiation fields following reconstruction on the plane [1-3].
Updating detecting devices construction and using mobile collimators makes scanning of radiation fields possible in a given solid angle [4].
Using of one detecting device in this case allows registration and following visualization of three-dimensional fields of gamma-radiation.
As a result, principally new registration possibilities and following visualization of gamma radiation fields exactly in real time are possible.
In this case there is no need in multiple levels radiation measurements using ordinary detectors with isotropic apprehensibility on the set of space points and following long data processing for solving interpolation problem of radiation field reconstruction.
Development of gamma-vision system, provided with detecting devices with collimators, foresees creating of computer environment controlling means of detecting device sensing element orientation, processing means, storing and data visualization on the screen.
In this article we consider and solve the problem of forming algorithmic ensuring of registration and visualization of radiation fields using spherical splines method. Developing method of visualization is a basic concept of applied software problem for perspective new generation gamma vision computer platform. Using of such systems will be especially effective while doing on-line radio-ecological monitoring of dwelling and nonresidential premise when we need to detect sources of radioactive pollution inside them and in the construction elements. Final result of visualization is stable graphic information about parameters of radioactive fields inside investigating places
2. Registration of gamma radiation fields by using detecting devices with collimator in scanning mode
For registration process investigation and developing the algorithm of 3D gamma radiation fields reconstruction, a model of detecting device with mobile collimator is introduced. Our basic unit will be controlling device construction suggested in paper [4]. Diagram of using collimator in it is presented on fig.1

Fig.1 Diagram of multimodule detecting device with mobile collimator.
Assumption diagram of sensor with collimator orientation is shown on fig. 2.

Fig.2. Directional characteristic of anisotropic sensor.
Method of taking gamma-radiation measurement in different directions in three-dimensional space consists in the forming of four successive series of spherical observations. Fifteen measurements are registered with the turn on 24 degrees with fixed sensor orientation. While transferring from the previous series to the following a turning of a sensor according to the elevation place occurs. Scanning of the whole three-dimensional space can be done using this approach. This technique can be used for measuring when distances are small, for example to monitor indoor spaces.
Being carried out measurements in general case can be introduced as a piloting actions directed to the inspecting area. Every measured value appears to be integral on the measuring area. Measurement facility partly can be described as a sum of aspects.
 ,
,
where w(Pi) – factors from directional characteristic on the net, covered the exact area of measurements, and Pi – a point in this net.
According to the measurements which have been done and taking into consideration properties of indoor space and its geometric sizes we can project the intension field value on the walls, floor and ceiling. It allows to apply approximation method on non-regular data arrays on each plane separately. This approach is matched with the necessity of correlation of separate plates. Let us consider alternative approach which consists in using some general space or surface where all data measurements without any exception will be presented. In the capacity of this as three- dimensional space can be performed as two –dimensional surface, showing all direction measurements.
Being in some point in indoor space it is appropriate to consider measurements as values set on the sphere in the center in a given point.
It allows:
• to get a coherent picture, as all measurements are situated on one plate and are taking part in general approach construction;
• data consideration doesn’t depend on shape of the space and interpret them as a point characteristics where the research is situated.
Using sensor with anisotropic sensitivity in the scanning regime, excluding the necessity of its moving inside considering space. It is here lies a great difference from traditional detecting devices measuring integral meaning in the field point not taking direction into consideration.
3. Space fields gamma-radiation visualization
In conditions when all measurements are spread on the sphere surface, for field reconstruction we can use approaches being similar to methods of spherical interpolation which are traditionally used in geodesy, meteorology and other fields [5].
Each measurement is assigned to a curtain area on the sphere, according to the direction in which it was produced. It is shown on fig. 3.
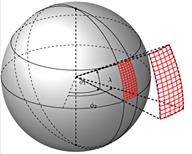
Fig. 3. Net on the sphere surface covering one area measurement.
Integral value distribution got as a result of measurement is defined as sensor angular resolution.
Let us use general description of natural splines [5]. Work in scalar product defining as following
![]() ,
,
where Ω – is a sphere of a single radius.
While constructing a spline, an interpolation problem is being solved.
![]() ,
,
where ki – linear bounded operators, corresponding to functional measurements A.
Specified spline σ is chosen according to the minimum conditions on the linear bounded operator T – functional smoothness, in this function we have chosen operator Beltrumi
 .
.
This spline will be present as follows [5]
 ,
,
where G(x,P) – Green function, corresponding to energy functional T; nj(P) – elements of operator kernel T; λi, υj – some real coefficients which are derived from the system
![]() ,
,
 ,
,  ,
,
Where gi(P)=(ki(x),G(x,P)).
Functional measurement A is defined as a set of separate functionals ki, which are numerically described as follows:
 .
.
Interpolation problem for spline description is presented as follows:
 ,
,
where wj – is weight function of j measurement (see fig.4), Pji – are summing points, covering j measurement area and σ is a required spline.
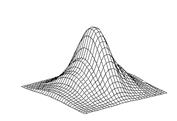
Fig. 4. Weight function for one measurement
Narrowing of region of summation to one point leads to degradation of functional to the point. It is proved in the paper [6] where the estimation of mistake while using spline with integral interpolation conditions is given.
Given spline allows to consider all measurement on the one plate and take into consideration their mutual influence to each other, while doing general approach on the sphere.
Investigation of solvability conditions shows that you can have the existence of a single spline if every area where the meaning of set-points on the surface has a unique sub-area, which doesn’t exist in any of the rest areas. Or, in case of numerical integration it is necessary that there should be at least one unique sub-area in the partial sum representing each area. This property should be taken into consideration while immediate spline construction
It should be taken into consideration that the measurements are given with some mistakes in the areas corresponding to these measurements and as detecting devices are not ideal these areas have the ability to overlap. The stronger effective ranges overlap effective changes the worse is ill-conditioned problem of spline construction. As a result, on the final approaching typical distortions show up, which are connected with the mistakes in the measurements. Difficulties connected with the noise level of data could be avoided changing interpolation spline to smoothing as it shown on fig. 5, 6.
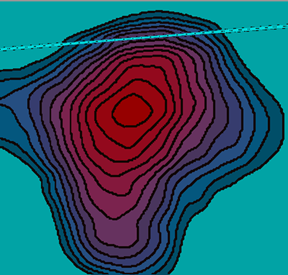
Fig.5. Interpolation spline on noise level data.
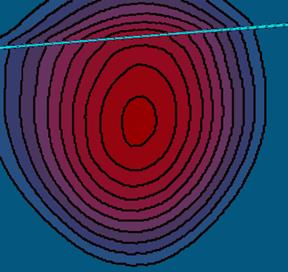
Fig.6. Spline built with using smoothing noise dada.
Smoothing occurs on the stage of building spline. Additive correction to matrix À to smoothing factor along main diagonal is introduced while calculating spline factors.
![]() .
.
There are some ways of smoothing coefficient unit. Particularly it can be estimated from input data by using the method of cross examination, as it is shown in paper [7], or the coefficient can be selected with the help of error estimation performed earlier.
4. Projection gamma-radiation fields
Sphere having been introduced into consideration is intermediated and works for restoration of approaching which later must be projected to the room. Spline allows to recount the meaning at any point of the sphere. But using of natural spline for recounting of every point needed for projection building connected with great calculation costs. That is why recount is done only for some points meaning between them while projecting interpolate. Bicubic splines widely used in solving interpolation problems on regular nets are used for this.
Distortions connected with the transfer from sphere surface to the flat can occur. Let us have elementary consideration about nature of distortions (fig.7).

Fig.7. Illustration for counting distortion factor at point B between the nods of a regular net A and C for projecting approach to the sphere with the center at point O.
Angular coordinate point B segment AC on sphere with the centre at point O is equal to γ/Δ. Coordinate point B inside the segment is characterized by the expression:
![]() .
.
Suggesting that the angles Δ and γ are small (not more than some degrees), this expression can be simplified:
![]() .
.
Coefficient k characterizing distortions becomes evident in this case. It is quite clear that with the decreasing of parameter t = Δ tan(α) a mistake is extinguished. It can be easily imagined taking into consideration the fact, that true angle γ oscillates in the range from 0 to Δ. When angle α is less than 45 degrees and Δ is less than 3 degrees distortion factor is not more than 5% while transferring from one surface to the other.
Extension which is not connected with the characteristic of a net on the sides of the room but depends only on the spline building on the sphere and angle α between normal to the side of the room and direction to the rib generates a very big mistake. When α = 45 degrees extension is twice more powerful. If the sensor is situated in the center of the room a mistake got while projecting to the remote areas of it is two times more than a mistake got while projecting to the closer areas.
So, while transferring from a spherical surface to the surface of room edges recount of meaning needs to be done according to the nature of restoring physical quantity. Using of spherical spline gives the opportunity to perform this transition. In geodesy where spherical splines are actively applied, method of pseudodifferential operators is used [8]. Operator of extension is from this list.
Using of pseudodifferential operators is based on characteristics of inverse Fourier transformation. Spherical harmonic expansion is meant in this case. Found spline s considers to be approaching of true distribution T sought quantity on room surface, being modified by pseudodifferential operator Λ:
![]() .
.
This pseudodifferential equation is solved in Fourier-space and back transformation is performed:
![]() .
.
Due to the spherical properties of splines this transition means only factor correction when meanings are substituted [8]. Difference of this method of recounting is in using of integral functional measurements, that doesn’t make any changes in the force of linearity inverse Fourier transformation. So correction is done on the sphere and while projecting its substitution is done to the aptly modified spline.
5. Conclusion
In this article we consider a principal possibility of gamma-radiation field restoration in 3D space with the help of series of measurements done by using a sensor with anisotropic sensitivity. In this paper algorithm of recording and visualization radiation fields is described, that allows scanning 3D space from one point. Formulae for accounting the factor worked in spline, research results of solvability conditions of a spline of a given type are given, methods for achieving better conditionality of a problem of measurements approximation with the use of a spline of a given type are denoted, mistakes following the process of projecting restored meaning of radiation intensity on the sides of the room are considered.
Theoretical justification of a method 3D radiation fields from a single point of a space, a model of a scanning detecting device has been built, algorithmic and application software of visualization of a process has been developed, empirical estimations and images of forming space gamma-fields have been got. Mathematical modeling proved the possibility of using suggested approaches and methods for solving 3D radiation fields.
Developed methods of registration and visualization of space fields are assigned to be used in perspective computer systems of gamma-vision, realizing on-line monitoring in in-door space.
Reference List
[1] Isakov S.V Multi-modul device application for measuring and reconstruction of space characteristics and gamma-emission fields visualization. [Text] Isakov S.V., V.T.. Samosadnyi V.V. Kadilin., A.D. Modajev, N.V. Korobkov // Engineering Physics . - 1999. ¹2. - p.37-40.
[2] Isakov S.V. Method of carrying out radiation monitoring with the help of panoramic detecting device. [Òext] / Isakov S.V., V.V. Kadilin, A.D. Modajev // Ecological systems and devices . - 2000. ¹1. – p.9-10.
[3] Al-huri V.S. Development of a guided search tools of a local sources of gamma-radiation. [Òext] / V.S. Al-huri, S.V. Isakov, V.V. Kadilin, V.T. Samosadnyi // Scientific Session NRNU MEPhI -2002. Ò.5 Medical Physics and Technology, Biophysics. Mathematical modeling in geophysics. Environmental protection and conservancy. Theoretical problems of physics. - Ì.: NRNU MEPhI , 2002.
[4] Patent 2160909 Russian Federation G 01 T 1/16, G 01 V 5/00. Device for search and detection of radioactive objects. [Òext] / Muhin V.I., Muslimov R.H., Samosadnyi V.T., - ¹ 99127111/28; applied 31.12.1999; published 20.12.2000.
[5] Ignatov M.I., Pevnyi A.B. Natural splines of several variables. - L.: Science, 1991.
[6] Filatov A.S. Estimated error of spline building with integral interpolated conditions [Òext] / A.S. Filatov, A.A. Shabynin, N.M. Leonova // Herald of NRNU MEPhI – Ì.: MEPhI, 2013, vol. 2, ¹ 2 - p. 208–211
[7] Grace Wahba Some new mathematical methods for variational objective analysis using splines and cross-validation [Òext] / Grace Wahba, James Wendelberger / Madison: Dept. of Statistics, University of Wisconsin - 1980.
[8] Willi Freeden A survey on spherical spline appriximation [Òåêñò] / Willi Freeden, Michael Schreiner, Richard Franke // Surveys on mathematics for industry - 1995