КОНТУРНЫЙ АНАЛИЗ В ЗАДАЧАХ РАСПОЗНАВАНИЯ И КЛАССИФИКАЦИИ ОБЪЕКТОВ
М.А. Макаров, С.Ю. Андреев
makarovf@sibmail.com, serga@td.tomica.ru
Институт кибернетики Национального исследовательского Томского политехнического университета
Оглавление
Аннотация:
В статье рассмотрен способ описания контура движущегося объекта с помощью дескрипторов. В качестве дескрипторов были выбраны амплитудные спектры Фурье-преобразования. Затем были найдены эталонные контуры для сравнения и классификации. Так же определены пороговые условия двух типов. Выделены два способа сравнения дескрипторов: сравнение с помощью коэффициента корреляции и сравнение с помощью лямбда-расстояний.
Ключевые слова: Контур, дескриптор, Фурье-преобразование, корреляция, классификация, инвариантность.
Введение
Системы видеонаблюдения получили широкое распространение с 90х годов XX века. Развитие средств кодирования, передачи, хранения и отображения видеоинформации привело к быстрому росту числа видеопотоков, поступающих от регистрирующих устройств в центры анализа данных.
Традиционно, вся работа по оценке ситуации на контролируемой территории, отводится оператору – наблюдателю, визуально оценивающему поступающую видеоинформацию. Это физически и психологически сложная работа, требующая постоянной сосредоточенности на однообразной информации, и как следствие приводящая к быстрой утомляемости и снижению качества анализа. Кроме этого, в силу физиологических свойств человека, существует ограничение на количество воспринимаемых одним оператором видеоизображений, также ограничено время концентрации на них. В исследованиях, проведенных отделением научных разработок полиции Великобритании, приводится информация, согласно которой один оператор может одновременно контролировать изображения, поступающие от шестнадцати камер видеонаблюдения, однако опрос операторов показал, что более половины из них считает, что число контролируемых камер не должно превышать четырех. При этом отмечается, что при увеличении числа мониторов, которые необходимо удерживать в поле зрения, эффективность слежения за целями уменьшается. Также указывается, что концентрация внимания оператора видеонаблюдения существенно уменьшается спустя тридцать – пятьдесят минут с момента начала работы [1].
На сегодняшний день ведутся работы, направленные на преодоление указанных трудностей. Существует два независимых направления, целью которых является снижение нагрузки на оператора:
· построение визуальных моделей данных [2], которые позволяют оптимизировать представление видеоинформации;
· внедрение видеоаналитических технологий, выполняющих часть функций оператора видеонаблюдения [3].
Сегодня наибольшие надежды связывают с технологиями видеоаналитики, которые ориентированы на поиск и классификацию движущихся объектов, а также детекцию и идентификацию лиц. Автоматическая классификация движущихся объектов на видео является одной из важных задач. [4] Приведем в пример пешеходный переход. Во избежание несчастных случаев на пешеходном переходе люди и автомобили должны не нарушать правила дорожного движения. Причем, для людей и автомобилей эти правила резко различаются. И для того, чтобы автоматически выявить нарушения, например, переход дороги в запрещенном месте или выезд на тротуар, необходимо знать, к какому классу относится объект, за которым идет наблюдение: пешеход или автомобиль.
Существуют алгоритмы поиска определенного класса изображения, основанные на обработке всего изображения видеокадра. Наибольшее распространение получил метод, основанный на вычислении гистограмм ориентированных градиентов (HOG). Входным параметром метода является двухмерное изображение, и для этого изображения вычисляются наборы гистограмм, которые оцениваются на предмет принадлежности одному из искомых классов. [5] Ниже на рисунке 1 представлен пример работы такого алгоритма.
Рис. 1. Пример работы алгоритма, основанного на гистограммах ориентированных градиентов
Существующие специализированные алгоритмы поиска движения и трекинга, в качестве промежуточной информации используют контур объекта, который локализует область движения. На рисунке 2 представлены примеры контуров, получаемых от данных алгоритмов.
Рис. 2. Пример работы алгоритма детекции движения и трекинга движущихся объектов
В отличие от исходного изображения, контуры являются высокоуровневыми данными, форма которых несет информацию о виде обнаруживаемых объектов. Исходя из этого, для решения данного класса задач целесообразно использовать именно контурный анализ, который обладает в этом случае рядом преимуществ:
§ малая вычислительная сложность, позволяющая обрабатывать видеоданные в режиме реального времени;
§ сокращение объема обрабатываемой информации за счет перехода от анализа функции двух переменных к функции одной переменной. [6]
В данной статье изложен способ представления контура в виде одномерного массива данных фиксированной длины, обладающего свойствами инвариантности к наклону, повороту и масштабированию. Также показаны способы их сопоставления на основе различных мер близости.
Контур объекта
Контур объекта – это граница вокруг объекта, которую можно представить в виде упорядоченной последовательности координатных пар:
;
,
где:
–
сам контур объекта;
–
точки (в случае работы с изображениями и видео – пиксели) контура;
–
общее число точек, составляющих контур;
–
координатная пара;
–
координаты точки на границе контура. [7]
Приведенное выше представление контура является двумерным, то есть каждый пиксель описывается парой значений. Чтобы сделать представление контура одномерным, необходимо использовать массив центромассных расстояний.
Массив центромассных расстояний – одномерная дискретная упорядоченная последовательность, каждый член которой равен расстоянию от центра масс контура до точки на его границе. Введем обозначение этой последовательности:
,
где:
–
массив центромассных расстояний;
–
расстояние от центра масс до точки на границе контура;
–
общее число точек, составляющих контур.
Расстояние от центра масс до точки на границе контура может быть вычислено с помощью выражения:
,
где:
–
расстояние от центра масс до точки на границе контура;
–
координаты центра масс;
–
координаты точки на границе контура.
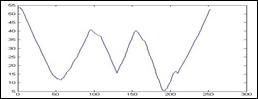
На рисунке 3 приведено изображение исходного контура и графическое представление соответствующей ему последовательности центромассных расстояний.
|
|
|
|
а) |
б) |
|
Рис. 3. а) Контур изображения; б) центромассные расстояния |
|
На оси абсцисс размещены порядковые номера последовательности точек контура, а на оси ординат соответствующие им расстояния до центра масс.
Дескрипторы
В теории распознавания образов активно используется понятие дескриптора, которое обозначает уникальную одномерную дискретную упорядоченную последовательность чисел, вычисляемую на основе каких либо свойств объекта. Одним из главных требований к дескриптору является его инвариантность к изменениям свойств объекта, не связанных с его узнаваемостью. Дескриптор контура должен быть инвариантен относительно:
1) поворота;
2) изменения масштаба;
3) параллельного переноса.
Последовательность центромассных расстояний не обладает инвариантностью ни к одному из приведенных выше изменений, кроме параллельного переноса, поэтому не может быть использована в качестве дескриптора. В связи с этим требуется осуществить вычисление дескриптора на основе выбранной формы представления контура.
Обозначим дескриптор как:
,
где:
–
дескриптор;
–
одно из чисел образующих дескриптор;
–
количество чисел в дескрипторе.
Для достижения инвариантности массива центромассных
расстояний к повороту и масштабированию необходимо провести
Фурье-преобразование данных центромассных расстояний . Количество Фурье-коэффициентов
. Будем
вычислять отдельно действительную и мнимую части Фурье-преобразования, затем
найдем амплитудный спектр, который будет:
1) инвариантен к повороту контура;
2) инвариантен к масштабированию контура.
Начинается вычисление Фурье-коэффициентов с коэффициентов нулевой гармоники:
;
,
где:
–
действительная и мнимая части Фурье-преобразования;
–
расстояние от центра масс до точки на границе контура;
–
общее число точек, составляющих контур;
Далее вычисляются остальные члены действительной части 
, кроме последнего. В
данном случае счетчик по коэффициентам 
. Члены действительной части вычисляются
по следующей формуле:
.
Затем вычисляется последний член действительной части 
:
.
После находятся оставшиеся члены мнимой части 
. В данном случае
счетчик по членам мнимой части 
. Мнимая часть вычисляется по формуле:
.
На основе коэффициентов и вычисляется амплитудный спектр 
. Счетчик по спектру 
. Коэффициенты
вычисляются по следующей формуле:
.
Затем амплитудный спектр нормируются по нулевой гармонике, и формируется дескриптор контура:
.
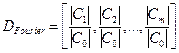Этот дескриптор инвариантен к повороту и масштабированию. Кроме того, в зависимости от необходимой точности можно анализировать только первые несколько коэффициентов [8].
Сравнение дескрипторов
Решение задачи классификации объектов лежит в плоскости сравнения дескрипторов наблюдаемых объектов с заранее подготовленными эталонами. Знание степени соответствия дескриптора классифицируемого объекта каждому из эталонов дает возможность принять решение о его принадлежности к тому или иному классу. Существует несколько способов сравнения дескрипторов, среди которых основанные на вычислении:
- коэффициентов корреляции;
- евклидовых расстояний;
- лямбда - расстояний.
Дескрипторы могут сравниваться с помощью коэффициента корреляции. Вычисляется коэффициент корреляции по следующей формуле:
,
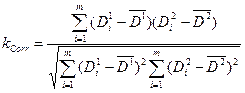где:
–
коэффициент корреляции;
–
члены двух сравниваемых дескрипторов;
–
средние значения среди членов двух сравниваемых дескрипторов;
–
общее количество членов в дескрипторе;
–
счетчик.
Величина коэффициента корреляции находится в интервале 
. Чем больше
коэффициент корреляции, тем выше сходство двух сравниваемых дескрипторных
массивов.
Коэффициент корреляции можно изменить следующим образом:
,
где:
–
модифицированный коэффициент корреляции.
Величина модифицированного коэффициента корреляции находится
на интервале 
.
Чем меньше модифицированный коэффициент корреляции, тем выше сходство двух
сравниваемых дескрипторов.
Евклидово расстояние между дескрипторами может быть вычислено на основе следующего выражения:
,
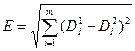где:
–
Евклидово расстояние;
–
члены двух сравниваемых дескрипторов;
–
общее количество членов в дескрипторе;
Величина Евклидова расстояния находится в промежутке 
. Чем меньше Евклидово
расстояние, тем выше сходство двух сравниваемых дескрипторных массивов.
Лямбда-расстояние учитывает нормированное расстояние между дескрипторами ( – Евклидово
расстояние, рассмотренное ранее) и характеристику локальной плотности - 
.
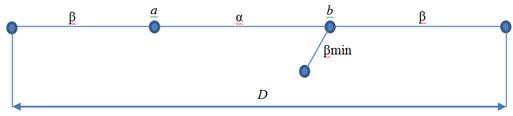
Рис. 4. Граф Евклидовых расстояний дескрипторных массивов
Если определить расстояния между всеми парами точек
множества (за
точку считаем дескрипторный массив, описывающий определенный контур объекта),
то можно построить полный граф, соединяющий все точки со всеми. В этом графе
существует самое длинное ребро – диаметр графа, которое обозначим за . Если выделить две любые
произвольные точки 
и 
, то может быть найдена длина
связывающего их ребра 
, а также ее нормированная величина:
.
Среди ребер, смежных ребру 
, может быть найдено самое короткое, длину
которого обозначим за 
. Отношение длин этих смежных отрезков
может быть вычислено на основе выражения:
.
Чтобы сделать эту величину нормированной в диапазоне от нуля
до единицы, найдем в полном графе наибольшее значение 
, тогда величина:
является нормированной характеристикой локальной
неоднородности плотности множества в окрестностях точек и . Величину:
называют лямбда-расстоянием между точками и . Параметр играет более важную роль по
сравнению с параметром , поэтому в качестве меры расстояния
используется величина:
.
По аналогии с Евклидовым расстоянием или модифицированным коэффициентом корреляции выбирается наименьшее лямбда-расстояние, так как оно соответствует более схожим дескрипторам [9].
Пороговые условия
Несмотря на то, что был определен ряд методов получения мер близости пар дескрипторов, требуется определить способ, который позволит перейти к бинарному (да, нет) показателю соответствия дескрипторов.
Для решения этой задачи введем пороговое условие, которое можно задать выражением:
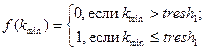(1)
где:
–
мера близости дескрипторов, в качестве которой выступает модифицированный
коэффициент корреляции или лямбда-расстояние;
‑
граница первого порогового условия, которая определяет строгость соответствия.
Выражение обращается в ноль, если фиксируется несоответствие пары дескрипторов, в то время как соответствие обращает его в единицу. Необходимость ввода пороговой границы обусловлена тем, что на практике не может быть получено строгое соответствие.
Очевидно, что допустима ситуация, когда среди всего множества эталонных дескрипторов, не найдется ни одного, обращающего выражение 1 в единицу. Это требует ввода нового класса объектов – «нераспознанный».
Необходимость ввода нового вида объекта также продиктована не нулевой вероятностью соответствия классифицируемого объекта эталонам двух разных классов объектов. Чтобы исключить ошибки подобного рода, введем второе пороговое условие:
,
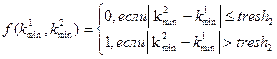где:
–
мера близости дескрипторов, в качестве которой выступает модифицированный
коэффициент корреляции или лямбда-расстояние одного класса;
–
мера близости дескрипторов, в качестве которой выступает модифицированный
коэффициент корреляции или лямбда-расстояние другого класса;
–
граница второго порогового условия.
Второе пороговое условие сравнивает два минимальных значения
модифицированных коэффициентов корреляции или лямбда-расстояний. Каждое
минимальное значение отвечает за сигнатуру эталонов, принадлежащую своему
классу. То есть, если – это минимум среди эталонов одного
класса, то –
минимум среди эталонов другого класса. Разность этих минимумов по модулю должна
быть выше определенного порога.
Принадлежность классифицируемого объекта двум классам обусловлена тем, что множества дескрипторов двух эталонных массивов пересекаются. Такое пересечение связанно с похожестью объектов разных классов в определенных ракурсах.
Введение пороговых условий позволяет сократить количество ошибок классификации. Если хотя бы одно из пороговых условий не будет выполняться, то контур следует считать неклассифицированным.
Испытания
Следует определить более предпочтительный метод вычисления меры близости для Фурье дескрипторов на основе сравнительного анализа эффективности классификации с использованием:
- модифицированного коэффициента корреляции;
- лямбда-расстояния.
Для этого были классифицированы 542 контура, с использованием каждой из исследуемых мер близости.
Контуры классифицируемых изображений были получены из Интернета, при этом каждый из них уже заранее был отнесен к одному из двух классов:
- 340 контуров людей;
- 202 контура автомобилей.
Результаты автоматической классификации были сопоставлены с данными априорной классификации, на основе чего были получены количественные характеристики эффективности использования каждого из метода сравнения.
Опытным путем были определены пороговые условия для способов сравнения. Пороговые условия представлены в таблице 1.
Таблица 1. Пороговые условия для способов сравнения дескрипторов
|
Способ сравнения |
|
|
|
Мод. коэффициент корреляции |
0.015 |
0.025 |
|
Лямбда-расстояние |
0.010 |
0.010 |
На диаграммах ниже показаны результаты классификации с помощью модифицированного коэффициента корреляции и лямбда-расстояния. До серой вертикальной черты на диаграммах оцениваются контуры людей, после серой черты – автомобилей. Самая первая диаграмма (рис. 5) показывает результат идеальной классификации – до серой черты все значения равны 1, после серой черты – 2.
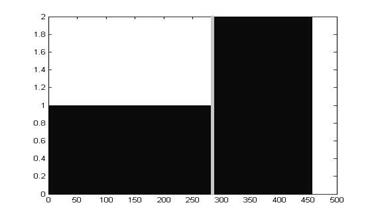
Рис. 5. Пример идеальной классификации
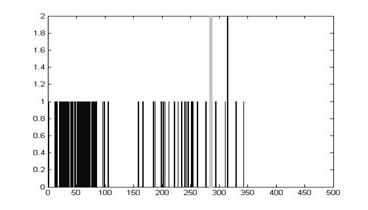
Рис. 6. Классификация с помощью модифицированного коэффициента корреляции
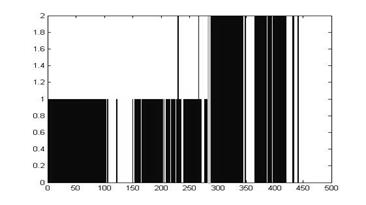
Рис. 7. Классификация с помощью лямбда-расстояния
Из диаграмм видно, что классификация с помощью лямбда-расстояний более похожа на идеальную классификацию. В таблице 2 приведены сравнительные результаты классификаций.
Таблица 2. Результаты классификации с помощью модифицированного коэффициента корреляции и лямбда расстояния
|
Методы сравнения |
Пешеходы |
Автомобили |
Все |
|
Модифицированный коэффициент корреляции |
правильно: 24.7 % ошибочно: 0 % нераспознано: 73.4 % |
правильно: 1.2 % ошибочно: 2.3 % нераспознано: 96.5 % |
правильно: 15.8 % ошибочно: 0.9 % нераспознано: 83.3 % |
|
Лямбда-расстояние |
правильно: 84.3 % ошибочно: 0.7 % нераспознано: 15.1% |
правильно: 78.1 % ошибочно: 0.0 % нераспознано: 21.9 % |
правильно: 81.2 % ошибочно: 0.4 % нераспознано: 18.5 % |
Из таблицы видно, что число всех правильно классифицированных контуров с помощью модифицированного коэффициента корреляции составляет 15.8 %, а с помощью лямбда расстояния 81.2 %. Метод сравнения с помощью лямбда-расстояния дал меньший в сравнении с модифицированный коэффициентом корреляции результат ошибочно классифицированных и нераспознанных контуров.
Выводы
Исходя из изложенного выше материала, можно сделать вывод, что контурный анализ является универсальным способом классификации объектов, основанным на анализе формы. Представленный метод вычисления контурных дескрипторов, обладающих свойствами инвариантности к повороту, масштабированию, а также параллельному переносу позволяет получить компактное представление формы объектов.
Предложенные методы вычисления меры близости дескрипторов с помощью модифицированного коэффициента корреляции и лямбда-расстояния, в совокупности с набором пороговых условий, позволяют производить классификацию объектов. Все это делает контурный анализ перспективным методом для решения задачи классификации движущихся объектов.
Тем не менее, необходимо отметить, что анализируемые контуры могут быть существенно искажены в результате воздействия внешних факторов. Наиболее сильное воздействие оказывает наличие тени от яркого солнечного света. По этой причине дальнейшие усилия будут направлены на развитие метода коррекции исходного контура с целью увеличения свойств инвариантности к внешним условиям регистрации видеоизображения.
Работа выполнена за счет средств субсидии в рамках реализации Программы повышения конкурентоспособности ТПУ.
Библиография:
2. А.А. Захарова, А.В. Шкляр Основные принципы построения визуальных моделей данных на примере интерактивных систем трехмерной визуализации // Научная визуализация, 2014. - №2.
3. Bui T.T.T., Phan N.H, Spitsyn V.G. Face Recognition Based on Combination of Wavelet Transforms and Principal Component Analysis // Proceedings of International Forum on Strategic Technology (IFOST - 2014)
4. A.A. Лукьяница, А.Г. Шишкин Цифровая обработка видеоизображений. - М: «Ай-Эс-Эс Пресс», 2009. - 518 с.
5. N. Dalal, B. Triggs Histograms of oriented gradients for human detection // IEEE Computer Vision and Pattern Recognition, 2005
6. Я.А. Фурман Введение в контурный анализ. - М.: ФИЗМАТЛИТ, 2003. - 561 с.
7. Р. Гонсалес, Р. Вудс Цифровая обработка изображений. - М.: Техносфера, 2005. - 1072 с.
8. Н.Н. Митропольский Агломеративная сегментация и поиск однородных объектов на растровых изображениях. - М.: МГТУ, 2010. - 137 с.
9. Н.Г. Загоруйко Прикладные методы анализа данных и знаний. - Новосибирск: ИМ СО РАН, 1999. - 270 с.
CONTOUR ANALYSIS IN PROBLEMS OF PATTERN RECOGNITION AND OBJECTS CLASSIFICATION
M.A. Makarov, S.Y. Andreev
Institute of Cybernetics. National Research Tomsk Polytechnic University, Tomsk, Russia
makarovf@sibmail.com, serga@td.tomica.ru
Abstract:
The article describes a method of describing the contour of the moving object using descriptors. Amplitude spectra of the Fourier transform was chosen as descriptors. Then etalon contours for comparison and classification were found and threshold conditions was defined of two types. Descriptor comparison was defined on two ways: compare with a correlation coefficient and compare with a lambda distances.
Keywords: Contour, descriptor, Fourier transform, correlation, classification, invariantion.
References
1. Wallace, E. CCTV control room ergonomics/ E. Wallace, C. Diffley // Published by Police Scientific Development Branch of the Home Office, Publication 1998. - №14.
2. A.A. Zaharova, A.V. Shklyar Basic principles of creating data visual models in example of interactive systems of 3D visualisation // Scientific visualization, 2014. - №2.
3. Bui T.T.T., Phan N.H, Spitsyn V.G. Face Recognition Based on Combination of Wavelet Transforms and Principal Component Analysis // Proceedings of International Forum on Strategic Technology (IFOST - 2014)
4. A.A. Lukyanica, A.G. Shishkin Digital processing of images. - Moscow: "Ai-Es-Es Press", 2009. - 518 p.
5. N. Dalal, B. Triggs Histograms of oriented gradients for human detection // IEEE Computer Vision and Pattern Recognition, 2005
6. Ya.A. Furman Introduction in contour analysis. - Moscow: FIZMATLIT, 2003. - 561 p.
7. R. Gonsales, R. Vuds Digital processing of images. - Moscow: Technosfera, 2005. - 1072 p.
8. N.N. Mitropolsky Agglomerative segmentation and search for similar objects on raster images. - Moscow: MGTU, 2010. - 137 p.
9. N.G. Zagoruiko Applied methods of data analysis and knowledge. - Novosibirsk: IM SO RAN, 1999. - 270 p.