РАСЧЕТНО-ЭКСПЕРИМЕНТАЛЬНАЯ ВИЗУАЛИЗАЦИЯ СВЕРХЗВУКОВОГО ОБТЕКАНИЯ УПРАВЛЯЮЩИХ ЩИТКОВ НА ТЕЛАХ ВРАЩЕНИЯ СЕГМЕНТНО-КОНИЧЕСКОЙ ФОРМЫ

С.И. Герасимов^1,2,3, И.И. Каныгин^1,2, В.А. Кикеев³, Р.В. Герасимова² , К.В. Тотышев¹, В.К. Голубев²

¹ Саровский физико-технический институт НИЯУ МИФИ, 607186 Саров, Россия

² Российский федеральный ядерный центр - Всероссийский научно-исследовательский институт экспериментальной физики, 607190 Саров, Россия

³ Нижегородский государственный технический университет им. Р.Е.Алексеева, 603950 Россия

E-mail: s.i.gerasimov@mail.ru, John013@yandex.ru, vkikeev@mail.ru, r.v.gerasimova@mail.ru

Оглавление

1. Введение

2. Описание эксперимента

3. Визуализация процесса обтекания модели на основе результатов численного моделирования

4. Заключение

Список литературы

Аннотация

Для управления, торможения и стабилизации сверхзвуковых и гиперзвуковых летательных аппаратов все более широкое применение находят щитковые органы управления. Использование подобных органов управления позволяет в достаточно широком диапазоне изменять аэродинамические коэффициенты летательных аппаратов. При сверхзвуковых скоростях полета возникает сложная картина обтекания летательных аппаратов, особенно в областях расположения щитков, где реализуются отрывные режимы обтекания. Получение достаточно реалистичных данных для отрывных режимов в различных условиях, особенно при больших углах атаки, возможно в настоящее время только с использованием экспериментальных методов. В то же время существующие расчетные методы позволяют достаточно корректно анализировать картину обтекания летательного аппарата в целом и получать вполне приемлемые результаты по определению аэродинамических коэффициентов в широком диапазоне изменения условий обтекания. Хорошее согласие этих результатов с данными отдельных экспериментальных измерений позволяет осуществлять прогнозирование для определения значений этих коэффициентов при любых произвольных условиях обтекания. Ниже представлены результаты исследования сверхзвукового обтекания потоком воздуха серии моделей гиперзвуковых летательных аппаратов. Исследуемые модели различались формой и размерами управляющих щитков.

Ключевые слова: сверхзвуковое обтекание, баллистическая установка, аэродинамический коэффициент, управляющий щиток, численное моделирование, визуализация.

1. Введение

Для управления, торможения и стабилизации сверхзвуковых и гиперзвуковых летательных аппаратов все более широкое применение находят щитковые органы управления. Использование подобных органов управления позволяет в достаточно широком диапазоне изменять аэродинамические коэффициенты летательных аппаратов. При сверхзвуковых скоростях полета возникает сложная картина обтекания летательных аппаратов, особенно в областях расположения щитков, где реализуются отрывные режимы обтекания. Получение достаточно реалистичных данных для отрывных режимов в различных условиях, особенно при больших углах атаки, возможно в настоящее время только с использованием экспериментальных методов. В то же время существующие расчетные методы позволяют достаточно корректно анализировать картину обтекания летательного аппарата в целом и получать вполне приемлемые результаты по определению аэродинамических коэффициентов в широком диапазоне изменения условий обтекания. Хорошее согласие этих результатов с данными отдельных экспериментальных измерений позволяет осуществлять прогнозирование для определения значений этих коэффициентов при любых произвольных условиях обтекания. Ниже представлены результаты исследования сверхзвукового обтекания потоком воздуха серии моделей гиперзвуковых летательных аппаратов. Исследуемые модели различались формой и размерами управляющих щитков. В частности, в работе приведены результаты, полученные для моделей без щитка, с плоским щитком площадью 0.080S₀, с двумя противоположно расположенными плоскими щитками, с уменьшенным плоским щитком площадью 0.040S₀ и с цилиндрическим щитком площадью 0.10S₀.

2. Описание эксперимента

Органы управления щиткового типа применяются на маневрирующих спускаемых аппаратах /1/. Структура обтекания носит достаточно сложный характер, сопровождающийся отрывом потока. Распределение давления по щитку носит неравномерный характер. Дополнительную сложность в изучение аэродинамических свойств подобных моделей вносит то обстоятельство, что теневые картины обтекания, полученные в обращенных экспериментах (модель крепится державкой) на аэродинамических трубах, могут заметно отличаться от реальных, полученных при отстрелах моделей в свободный полет (рис.1). Отсюда возрастает роль численного моделирования, которое при определенной точности расчета может существенно удешевить исследования и отменить необходимость опытной отработки на разных экспериментальных установках, находящихся в разных организациях.

а)	б)

Рис.1 Обтекание кормовой части модели с прямым щитком у донного среза потоком М=3 в эксперименте в аэродинамической трубе (а) и в свободном полете (б)

Экспериментальные испытания моделей в условиях свободного полета при скоростях до 2000 м/с проводились в аэробаллистическом тире ВНИИЭФ /2/. Тир имеет следующие базовые технические характеристики:

- диапазон реализуемых скоростей полета V и чисел Маха М: V = 130 - 3700 м/с, М = 0.4 - 11;

- калибр и длина испытываемых моделей: D = 0.016 – 0.140 м, L = 0.016 – 0.410 м;

- длина измерительного участка L_р = 123 м;

- среднее количество регистрируемых положений моделей в опыте:

при М = 0.4 - 6  n = 40-50 с шагом регистрации h_p = 1.5 - 3 м;

при М = 6 - 11  n = 20-25 с шагом регистрации h_p = 0.75 - 9 м.

Система управления и регистрации тира обеспечивает:

- включение блоков управления камерами в количестве 15 штук и открытие (закрытие) затворов аэрофотокамер в количестве 30 штук;

- управление средствами оптической регистрации в реальном масштабе времени от миллисекундного до секундного диапазона с микросекундной дискретностью;

- регистрацию времен срабатывания устройств с дискретностью 0.125 мкс;

- запуск баллистической установки  путем подачи управляющего сигнала, амплитудой ~ 250В и длительностью 20 мкс;

- питание системы осуществляется от трехфазной сети, напряжением 380 В и частотой 50 Гц;

- потребляемая мощность ~ 10 кВт.

Общий схематический вид тира, включающий расположение оборудования и схему проведения аэробаллистических экспериментов, показан на рис. 2.

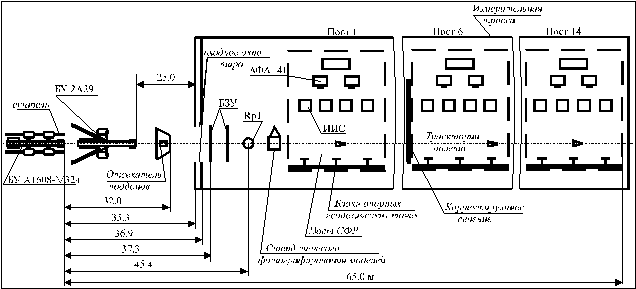
Рис.2. Схема проведения экспериментов в аэробаллистическом тире

При проведении испытаний модели отстреливаются из пороховой или легкогазовой баллистической установки с заданными программой испытаний начальными условиями по числу Маха М и углу атаки a. Синхронно с полетом модели, с помощью оптических средств системы внешнетраекторных измерений, осуществляется многократная регистрация в фиксированные моменты времени t_i линейного (координаты X_i, Y_i, Z_i) и углового (J_i, y_i, g_i) положения объекта испытания в пространстве. Порядок синхронизирующих команд на срабатывание импульсных источников света, обеспечивающих фоторегистрацию модели в полете, вырабатывается с помощью автоматической системы управления аппаратурой оптического измерительного комплекса /3/. Для получения изображений модели в полете при высокоскоростных режимах испытаний используются электровзрывные источники света ЭВИС. Для получения информации о состоянии модели, при разделении её с поддоном на участке от дульного среза баллистической установки до отсекателя поддонов, задействуются два фотопоста (на 6 и 9 м от дульного среза баллистической установки) системы ЭПОС, запускаемые с помощью радаров. Для получения теневых спектров обтекания моделей в полете используются два стенда теневого фотографирования моделей с применением точечных источников света ЭВИС.

       В работе представлены результаты, полученные для моделей четырех типов. Модель 1 была без управляющего щитка, модели 2 и 3 имели плоские управляющие щитки с относительной площадью 0.04 и 0.08S₀, модель 4 имела щиток цилиндрической формы с относительной площадью 0.10S₀. Все рассмотренные модели имели одинаковые номинальные обводы и одинаковый диаметр основания D₀.

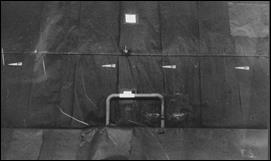
На рис. 3 для одного из опытов с моделью 2 показаны фотографии с двух стереопостов, по два и по четыре положения для каждого. Фотограмметрическая обработка подобных, сделанных на каждом из стереопостов, фотографий позволяет получать всю информацию о пространственном положении модели в процессе пролета измерительного участка тира.

Рис. 3. Регистрация полета модели 1 с двух стереопостов

На рис. 4, 5 приведены результаты обработки фотограмметрических данных для одного из опытов с моделью 2. Результаты, приведенные на рис. 4, характеризуют движение центра тяжести модели, а приведенные на рис. 5, описывают ее угловое положение в пространстве.

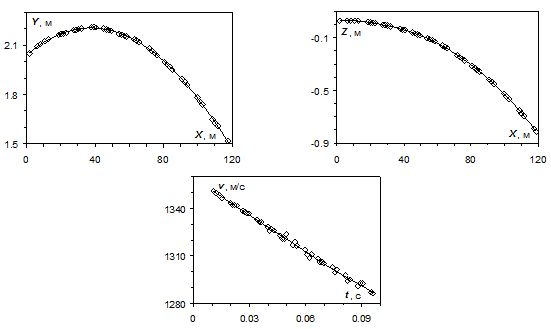Рис. 4. Пространственные координаты и скорость центра масс модели 2 при пролете измерительного участка тира

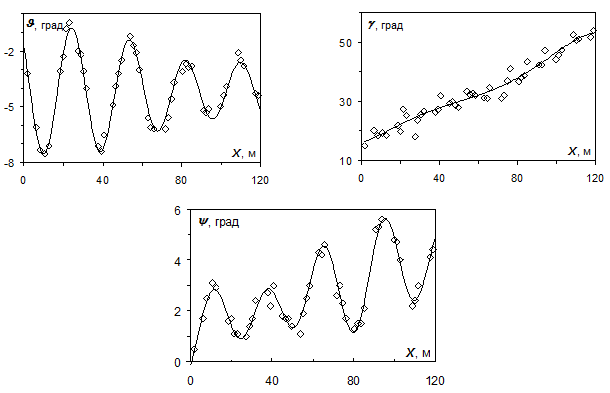Рис. 5. Угловые координаты модели 2 при пролете измерительного участка тира

Наличие используемых в моделях органов управления щиткового типа приводит к значительным радиальным отклонениям относительно основной линии прицеливания аэробаллистического тира (Y = 1.7 м, Z = 0 м). Эти отклонения по Y находятся в пределах от 2.3 м в начале измерительного участка до 0 м в конце измерительного участка, по Z в пределах от 0 м в начале измерительного участка до 2.5 м в конце измерительного участка. Модели со щитками характеризуются значительными балансировочными углами атаки. Так при скорости ~4М диапазон этих углов для рассмотренных моделей составляет 4.5 – 9.5°. При этом колебания по углу атаки носят затухающий характер. Вращение моделей относительно продольной оси (по γ), происходящее вследствие закрутки в стволе баллистической установки, осуществляется по часовой стрелке относительно направления движения и приводит к изменению угла γ на величину от 10 до 105° при движении на измерительном участке тира.

На рис. 6 показаны теневые спектры обтекания четырех моделей:

- модель 1 - (М = 3.25), (рис.6 а).

- модель 2 - (М = 4.13, a = 1.5°, γ = 15°), (рис.6 б).

- модель 3 - (М = 5.04, a = 2°, γ = 20°), (рис.6 в).

- модель 4 - (М = 4.00, a = 6°, g = 3°), (рис.6 г).

	а)
	б)
	в)
	г)

Рис. 6. Теневые спектры обтекания моделей 1 (М = 3.25), 2 (М = 4.13, a = 1.5°, γ = 15°), 3 (М = 5.04, a = 2°, γ = 20°) и 4 (М = 4.00, a = 6°, g = 3°).

Подобные результаты позволяют более детально подходить к решению вопросов обтекания. Действительно, наличие при больших углах атаки срывных нестационарных областей в зоне, прилегающей к щитку, может приводить к нелинейным эффектам в аэродинамических характеристиках. На характерных теневых спектрах обтекания регистрируются зоны отрывного течения перед щитком, косой скачок уплотнения (от точки отрыва течения) и более интенсивный прямой скачок уплотнения. В диапазоне скоростей (3 - 5)М для всех рассмотренных моделей определены расстояния от точки отрыва до щитка. Значения этих расстояний находятся в пределах от 15 до 41 мм и определенным образом зависят от типа щитка, скорости и угла атаки. В частности, переход к цилиндрической форме щитка приводит к ощутимому уменьшению этого расстояния. Для всех экспериментально исследованных моделей проведены расчеты их сверхзвукового обтекания потоком воздуха. Диапазон рассмотренных начальных скоростей обтекания находился в пределах от 2 до 6M. Диапазон углов атаки α изменялся в пределах от 0 до 10°.

На рис. 7-10 приведены результаты расчетного определения аэродинамических коэффициентов для рассмотренных моделей. Расчет процесса обтекания объектов проводился с использованием инженерного программного комплекса COSMOSFloWorks путем численного решения полных осредненных по Рейнольдсу уравнений Навье-Стокса /4/. Для учета турбулентности использовалась k-ε модель. Для воздуха применялось уравнение состояния совершенного газа. Расчет разбивался на несколько этапов, в конце каждого из которых проводился анализ полученного решения и основанное на этом анализе измельчение счетной сетки в высокоградиентных областях параметров течения. Полное число счетных ячеек в конкретном расчете, как правило, не превышало 2.5·10⁶.

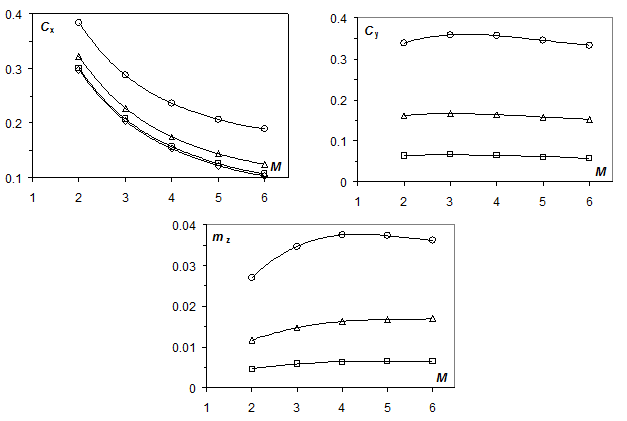Рис. 7. Расчетные аэродинамические характеристики модели 1

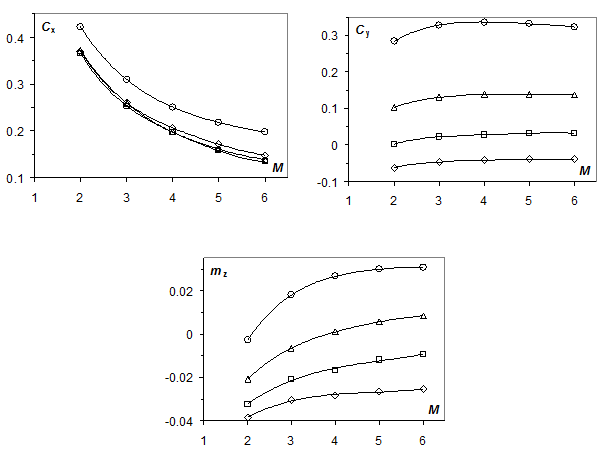Рис. 8. Расчетные аэродинамические характеристики модели 2

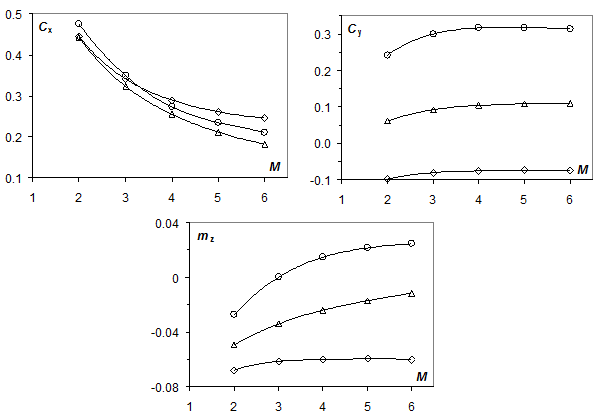Рис. 9. Расчетные аэродинамические характеристики модели 3

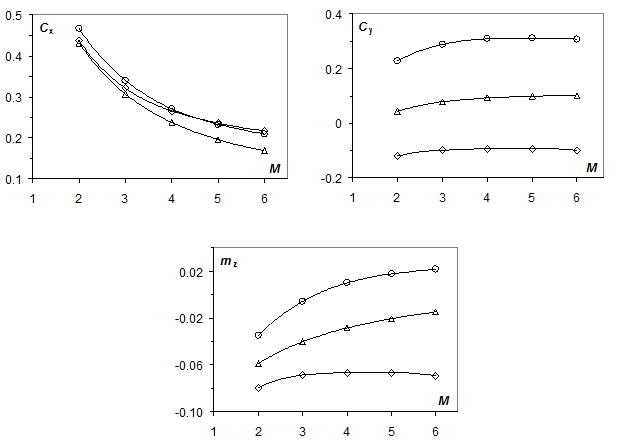Рис. 10. Расчетные аэродинамические характеристики модели 4

Точность полученных результатов оценивалась по характеру сходимости решения на каждом из рассматриваемых этапов расчета. Для уменьшения расчетных областей использовались условия симметрии. В процессе расчета определялись такие аэродинамические характеристики моделей, как коэффициенты сопротивления C_x, C_y и коэффициенты момента m_z(M), проводилась визуализация картин обтекания моделей.

На рис. 7-10 ромбы, квадраты, треугольники и кружки соответствуют углам атаки 0, 2, 5 и 10° соответственно. Эти результаты перекрывают более широкий, чем при проведении экспериментальных исследований диапазон параметров обтекания, что позволяет проводить более полный анализ явления. Определение экспериментальных значений аэродинамических коэффициентов осуществлялось с использованием полученных для всех моделей при различных скоростях полета результатов фотограмметрических измерений типа приведенных на рис. 4, 5. За основу был использован метод решения системы дифференциальных уравнений движения модели с использованием оптимизации по отношению к экспериментально зафиксированным ее пространственным и угловым положениям в процессе пролета измерительного участка тира /5/. Сделанные оценки погрешностей экспериментальных значений аэродинамических коэффициентов, как предельной систематической, так и случайной среднеквадратичной, не превышают 1%. Также было отмечено вполне приемлемое согласие расчетных и экспериментальных результатов по всем рассматриваемым аэродинамическим характеристикам, в частности, по аэродинамическим коэффициентам и по балансировочным углам атаки.

3. Визуализация процесса обтекания модели на основе результатов численного моделирования

Объем информации по расчетному определению характера обтекания моделей при всех рассмотренных условиях обтекания очень велик. Некоторые результаты по определения характера обтекания модели 4 показаны на рис. 11, 12. В первом случае ширина полос соответствует изменению плотности воздуха 0.045 г/м³. Во втором случае ширина полос соответствует изменению давления 5 кПа, а отсчет по x ведется от начала координат, находящегося в центре тяжести модели. Результаты подобного расчетного исследования позволяют выявить различные особенности в ближней и дальней зонах течения, определить полное поле давлений на поверхности модели сложной произвольной формы. Более того, они позволяют построить достаточно полную функциональную картину влияния скорости и углового направления обтекающего потока на все возможные аспекты обтекания. Подобная картина представляет большую ценность для прогнозирования и оптимизации при проектировании существующих и перспективных сверхзвуковых и гиперзвуковых летательных аппаратов.

Рис. 11. Характер обтекания (поле плотности) модели 4 (α = 0°, М = 5) в плоскостях z = 0, 10, 20, 30, 40 и 50 мм.

Рис. 12. Характер обтекания (поле давления) модели 4 (α = 5°, М = 5) в плоскостях x = 0, 100, 200, 300, 400 и 50 мм.

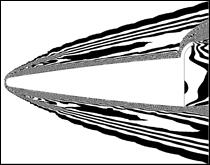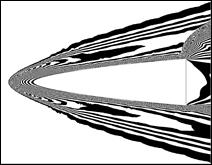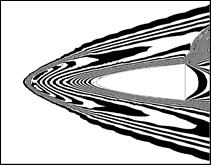На рис. 13 показано поверхностное распределение давления на наветренной стороне управляющих щитков и в их ближайшей окрестности для двух углов атаки при начальной скорости обтекания М = 3.

Рис. 13. Распределение давления на поверхности управляющего щитка и в его окрестности для углов атаки 0 и 5° при начальной скорости обтекания М = 3

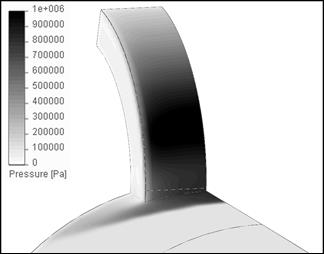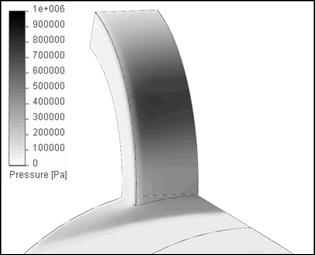4. Заключение

Полученные результаты показывают, что расчеты, проведенные с использованием инженерного программного комплекса COSMOSFloWorks и персонального компьютера с процессором Intel Pentium 4, достаточно достоверно передают основные особенности полей течения при сверхзвуковом обтекании рассмотренных моделей. Наблюдаемые тенденции влияния увеличения числа итераций и измельчения счетных ячеек на значения аэродинамических характеристик С_x, С_y и m_z позволяют вполне корректно прогнозировать реальные значения этих характеристик. Довольно четко выявляются тенденции влияния скорости обтекания и угла атаки на значения аэродинамических характеристик моделей. С практической точки зрения, это позволяет удешевить исследования, заменив численным моделированием дорогостоящие эксперименты в обращенной постановке.

_{Работа выполнена при поддержке Российского научного фонда, проект №14-19-01637.}

Список литературы

1. Калугин В.Т. Аэрогазодинамика органов управления полетом летательных аппаратов. М.: МГТУ им. Баумана, 2004. 688 с.

2. Герасимов С.И., Файков Ю.И., Холин С.А. Кумулятивные источники света. Саров: РФЯЦ-ВНИИЭФ, 2002.

3. Герасимов С.И., Костин В.И., Менде Н.П., Сперанский А.В. Алгоритмы определения внешнетраекторных параметров и аэродинамических характеристик движения тела вращения. Пособие для студентов вузов. СарФТИ НИЯУ МИФИ, 2013, 43с.

4. http://www.solidworks.ru/index.php?option=com_content&view=article&id=151&Itemid=66 (дата обращения 05.03.2013).

5. Герасимов С.И., Лысенков В.Е. Системы запуска и управления оптико-физической аппаратурой на аэробаллистических трассах. Пособие для студентов вузов. СарФТИ НИЯУ МИФИ, 2013, 65с.

---

NUMERICAL AND  EXPERIMENTAL VISUALIZATION OF SUPERSONIC FLOW AROUND CONTROL SHIELDS ON SEGMENT-CONICAL BODIES OF REVOLUTION

S.I.GERASIMOV^1,2,3, I.I. Kanygin^1,2, V.A.KIKEEV³, R.V.GERASIMOVA¹ , K.V. Totyshev², V.K. Golubev²

¹ Sarov Physics and Technical Institute of National Research Nuclear University «MEPHI», Nizhny Novgorod region, 607186 Russia

² Russian Federal Nuclear Center – All-Russia Research Institute of Experimental Physics, Sarov, Nizhny Novgorod region, 607188 Russia

³ Nizhny Novgorod State Technical University n.a. R.E. Alekseev, 603950 Russia

E-mail: s.i.gerasimov@mail.ru, John013@yandex.ru, vkikeev@mail.ru, r.v.gerasimova@mail.ru

Abstract
For control, braking and stabilization of supersonic and hypersonic aircraft with more and more applications are shield controls. The use of such controls, allow for a fairly wide range to change the aerodynamic coefficients of the aircraft. At supersonic flight velocities there is a complex pattern of the flow around aircraft, especially in the areas of location of the shields, where separated flow occurs. Obtaining realistic data for separated flows in various conditions, especially at high angles of attack is  possible now only with the use of experimental methods. At the same time, existing numerical methods enable one to correctly analyze the pattern about the aircraft as a whole and be able to get acceptable results on determination of aerodynamic coefficients in a wide range of flow conditions. Good agreement of these results with experimental data of a single measurement allows the prediction to determine the values of these coefficients at any arbitrary conditions of flow. Below are the results of the study of supersonic flow past the series models of hypersonic aircraft. The tested models were of different shape and size of control shields.

Keywords: supersonic flow, ballistic installation, aerodynamic coefficient, control shield, numerical modeling, visualization.

Literature

1. Kalugin V.T. Aerogasdynamics of the aircraft flight control system. М.: MGTU n.a. N.E.Bauman, 2004. 688 с.
2. Gerasimov S.I., Faikov Ju.I., Cholin S.A. Cumulative light sources. Sarov: RFNC-VNIIEF, 2002.
3. Gerasimov S.I., Kostin V.I., Mende N.P., Speransky A.V. Algorithms of determination of external trajectory parameters and aerodynamic characteristics of the rotation body. Textbook for University students. SarFTI NRNU “MEPhI”, 2013, 43с.
4. http://www.solidworks.ru/index.php?option=com_content&view=article&id=151&Itemid=66 (Date of access 05.03.2013).
5. Gerasimov S.I., Lysenkov V.E. Startup and control systems of optical and physical equipment for aeroballistic tracks. Textbook for University students. SarFTI NRNU “MEPhI”, 2013, 65с.