СИСТЕМА ВИЗУАЛЬНЫХ МОДЕЛЕЙ УПРАВЛЕНИЯ ПРОЕКТАМИ
КОЛЫЧЕВ В.Д., РУМЯНЦЕВ В.П.
VDKolychev@mephi.ru, VPRumyantsev@mephi.ru
Национальный исследовательский ядерный университет "МИФИ", Россия
Оглавление
2. Методика визуального решения управленческих задач проектного менеджмента
3. Структурные модели управления проектами и их визуальное представление
4. Графические модели структурных преобразований проектов
5. Визуальное моделирование числовых параметров проекта
6. Визуализация календарного ресурсного планирования прерываемых и непрерываемых операций
8. Инвестиционно-финансовое планирование проекта на основе визуальных моделей
9. Анализ рисков с применением методов визуальной аналитики
Аннотация
В данной статье раскрывается комплекс задач управления проектами и возникающие в связи с этим визуальные методы их решения. Предлагается применение системного подхода к управлению проектами и решению задач визуализации сложных объектов. В статье рассматриваются задачи бизнес-графики как современной области применения методов компьютерной геометрии и научной визуализации, направленной на формирование геометрической модели исходных данных проекта. Используются ставшие популярными в последнее время методы визуальной аналитики как базовые подходы к решению задач в сфере управления проектами, которым уделяется большое внимание практикующими специалистами. Предлагается применение визуального инструментального анализа с использованием оригинальных программных продуктов, разработанных авторами. Приведена технологическая последовательность визуального решения задач управления проектами для менеджеров, причем предлагается использование методов визуальной аналитики с целью определения необходимого вмешательства в проблемную ситуацию, возникающую в процессе управления проектами. Представлены инструментальные программные средства решения задач управления проектами, основанные на графическом анализе проблемной ситуации и выработке рекомендаций для лица принимающего решение. Рассматриваются визуальные модели структурного и риск-анализа, календарного, ресурсного и инвестиционно-финансового планирования. Работа представляет собой авторский обзор методов визуального анализа в сфере управления проектами.
Ключевые слова. Визуальная модель проекта, Управление проектами, Бизнес-графика, Графическое представление, Геометризация бизнес-данных, Бизнес-аналитика, Визуальный анализ, Проблемная ситуация, Расписание, Планирование проекта, Календарный план, Проект, Риск-анализ.
1. Введение
Специфика методов управления проектами заключается в обработке и анализе большого объема табличной и числовой информации, непосредственно относящейся к временным, стоимостным и ресурсным параметрам проектов.
Является общепризнанным, что визуальные подходы к решению управленческих задач являются наиболее эффективными, поскольку позволяют получить одновременно качественное и количественное решение поставленной задачи. Точность решения задач управления, получаемая при помощи методов визуальной аналитики, может существенным образом варьироваться в зависимости от предоставленных исходных данных и выбранной методики решения возникшей проблемной ситуации. Количество параметров, которое способна вобрать в себя визуальная модель, превышает в некоторых случаях разрешающую способность человеческих органов восприятия. В то же время, принимая решение на основе графического изображения пространственной сцены или плоского рисунка, лицо, ответственное за решение, не всегда способно выполнить прецизионное сопоставление возникающих геометрических образов. В связи с этим возможны некоторые погрешности в решении прикладных задач, однако, и в случаях с численными методами решения задач погрешности неизбежны.
В случае решения задач из сферы управления методы бизнес-графики являются предпочтительными, поскольку менеджеру оказывается более удобным использовать графическое изображение проблемной ситуации, чем оперировать числовыми объектами вместо геометрической модели.
В большинстве случаев числовые вычисления производят специализированные системы управления проектами, в то время как менеджеру предоставляется готовый геометрический образ или визуальная модель, на основе которой и принимается решение. Таким образом, в сфере управления проектами методы бизнес-графики, основанные на геометрическом представлении пространственных сцен или плоских рисунков, являются основными или базовыми, аналогов которым зачастую просто не существует.
В работе авторами представлен системный обзор существующих методов решения задач в сфере проектного менеджмента при помощи графических интерфейсов разработанных программных продуктов, реализующих функции визуального анализа и контроля информации, возникающей на различных этапах жизненного цикла проекта.
2. Методика визуального решения управленческих задач проектного менеджмента
Подход к визуальному решению задач из сферы управления, подразумевает реализацию определенных этапов, связанных с геометрическим моделированием и визуализацией проблемной ситуации. Технологическая схема процесса визуализации бизнес-данных [1], ориентированная на решение задач из области проектного менеджмента, представлена на рис. 1.
Визуальное бизнес-моделирование в сфере управления проектами опирается на системный подход к изучению проекта как объекту анализа.
Следовательно, необходимо перечислить комплекс графических моделей, используемых для визуального анализа бизнес-данных и проблемных ситуаций в проектном менеджменте, который можно назвать системой визуальных моделей.
Под бизнес-графикой [1] понимается формирование графических представлений табличных, числовых и символьно-числовых бизнес-данных с целью их анализа. Бизнес-графика является одной из современных областей применения компьютерной геометрии и визуализации.
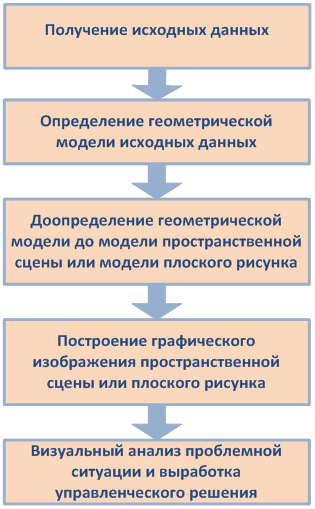
Рис. 1. Процесс визуального анализа проблемной ситуации.
Согласно [11] своду знаний по управлению проектами весь комплекс задач управления проектами представляется в виде набора проблемных областей, с которыми приходится иметь дело менеджеру проектов. К числу подобных областей или задач управления проектами относятся:
1. Управление интеграцией проекта;
2. Управление содержанием проекта;
3. Управление сроками проекта;
4. Управление стоимостью проекта;
5. Управление качеством проекта;
6. Управление человеческими ресурсами проекта;
7. Управление коммуникациями проекта;
8. Управление рисками проекта;
9. Управление поставками проекта.
На рис. 2. представлены используемые в управлении проектами графические изображения плоских рисунков или пространственных сцен (в зависимости от масштабов проекта и задач управления), применяемые в визуальном анализе задач проектного менеджмента [11].
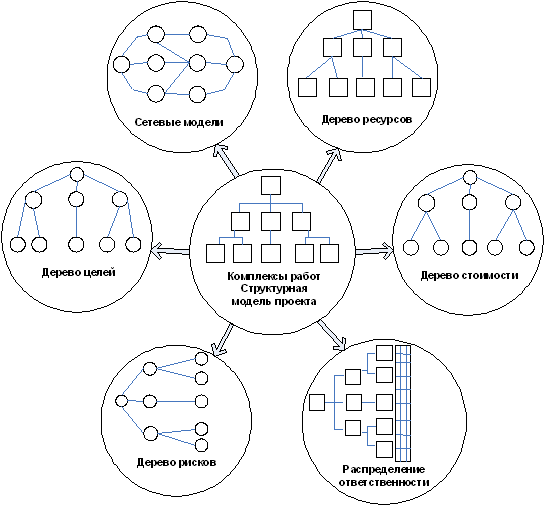
Рис. 2. Виды графических бизнес-моделей в задачах управления проектами.
Как видно из рис.2., в основном в качестве типовой геометрико-графической интерпретации, используемой в компьютерной визуализации бизнес-данных в рамках управления проектами, является модель теории графов [12]. Однако специфика задач бизнес-графики, связанная с управлением проектами, позволяет использовать инструментальные средства визуального контроля и анализа, ориентированные и на визуализацию многомерных данных, в том числе относящихся к финансово-экономическим показателям инвестиционных проектов.
Каждой перечисленной выше задаче соответствуют определенные исходные данные, получаемые как правило, на основе анализа содержания проекта, его этапов и управления интеграцией.
Исходные данные, как отмечалось ранее, в сфере управления проектами представляют собой в основном табличную числовую или преимущественно символьно-числовую формы представления.
Подбор исходных данных о проекте начинается на стадии предпроектного анализа, который начинается с определения предметной области проекта, а также на стадии предварительного планирования, рис. 3.
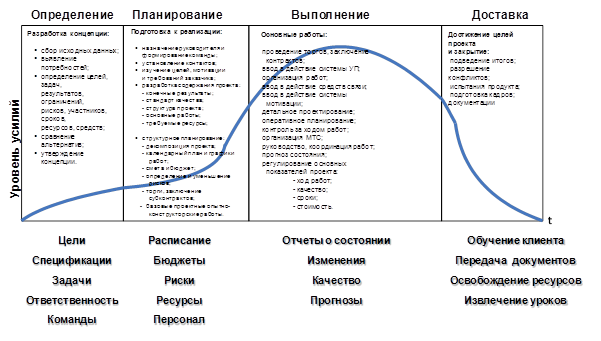
Рис. 3.Графическая структура жизненного цикла проекта с исходными данными для визуализации на каждом из его этапов.
На рис. 3 приведено графическое изображение жизненного цикла проекта [11] в виде плоского рисунка. На данном рисунке представлены типовые этапы жизненного цикла [8,9], а также перечень исходных данных, порождаемых на каждом из перечисленных этапов. Кроме этого на рис. 3 выполнена визуализация уровня усилий исполнителей проекта (кривая жизненного цикла помеченная синим цветом), приводящего к успешному завершению проекта в установленные сроки и с надлежащим качеством проектных работ. Как видим, количество и разнообразие исходных данных на всех этапах проекта достаточно велико.
На рис. 3 представлены фазы жизненного цикла, снабженные текстовыми комментариями, для каждой фазы (определение, планирование, выполнение, доставка) определены функции и подзадачи, которые выполняются в течение ее реализации (мелкий шрифт внутри каждой фазы). В нижней части рис.3 под соответствующей фазой изображены порождаемые на каждом этапе жизненного цикла исходные данные для визуализации. Например, для фазы планирования это расписание, бюджеты, риски, ресурсы и персонал.
Сложность решения задач управления проектами при помощи методов визуального анализа напрямую зависит от размерности исходных данных. Обратимся к рис. 4, на котором представлены уровни управления и размеры проектов, связанные с исходными данными о проектах, которые доступны для анализа специалистам соответствующего уровня. Размеры проектов приводят к увеличению размерности исходных анализируемых данных для визуализации. Таким образом, чем больше размер проекта, тем больше и размерность таблично-числовых и символьных параметров, принимаемых во внимание менеджером. Под размерностью исходных данных понимается количество операций, входящих в состав проекта. Каждая операция имеет временные, стоимостные и ресурсные параметры, которые также характеризуют размерность задачи управления проектами.
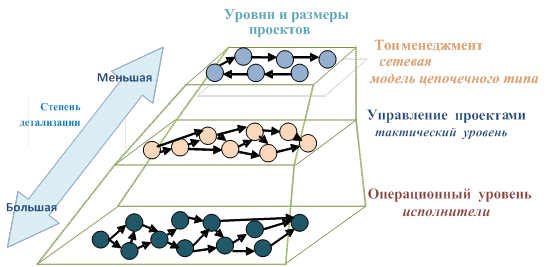
Рис. 4. Визуализация уровней управления и размеры проектов на каждом уровне.
В основном исходные данные о проекте могут быть получены следующими способами [1]:
1. Путем измерений (сроков, объемов работ, требуемых ресурсов, затрат и т.д. с учетом интервалов планирования работ).
2. Путем статистической обработки (построение статистических оценок и моделей операций).
3. Путем математического моделирования (построения математических моделей проекта и работ).
4. Привлечение экспертов для прогнозирования результатов или оценок сроков, объемов затрат, продаж и т.п.
5. Использование баз данных лучших практик о уже успешно выполненных проектах в компании.
По существу, две первые задачи проектного менеджмента позволяют собрать и обобщить исходные данные, используемые для решения последующего комплекса задач. Обобщенные исходные данные включают в себя следующий набор сведений:
Ø общую информацию о проекте;
Ø длительность проекта (сроки реализации, в т.ч. и директивные)
Ø участники (команда проекта);
Ø жизненный цикл проекта и его структура (рис. 3);
Ø окружение проекта;
Ø контракты;
Ø затраты на реализацию;
Ø финансирование;
Ø принципы контроля и управления;
Ø спецификация рисков.
Следует отметить также, что при решении задач, связанных с геометризацией исходных данных, ключевую роль играет визуальный анализ и сопоставление объектов.
Сопоставление геометрических объектов осуществляется при помощи понятия конгруэнтности фигур. По аналогии с этим можно ввести понятие конгруэнтности управленческих ситуаций при помощи геометрического образа (визуального представления) такой ситуации.
Будем считать, что каждой управленческой ситуации Di, (1=1..n) ставится в соответствие ее визуальное представление (визуальная ситуация) - Bi, т.е. имеет место отображение вида f:D→B. Каждой управленческой ситуации может быть поставлена в соответствие одна или несколько визуальных ситуаций, в зависимости от способа геометризации исходных данных модели управленческой ситуации. Таким образом, определено суръективное отображение D на B. Будем для определенности считать, что имеет место визуальная ситуация в формате плоского рисунка (замкнутой области или многогранника) или пространственной сцены (многогранного замкнутого объекта). Такой способ задания областей характерен для генерирования множества альтернатив в задачах поиска экстремума функции в задачах оптимизации, принятия решений, исследования операций.
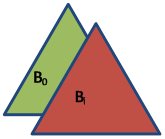
Требуется также ввести понятие эталонной (или плановой) управленческой ситуации D0, с которой осуществляется сопоставление (как графическое, так и содержательное). Графический образ (плоскую или пространственную сцену) эталонной ситуации обозначим через B0. Перейдем теперь от количественного описания бизнес-ситуации Di к ее визуальному анализу Bi . Кроме этого, каждая конкретная бизнес-ситуация, связанная с управлением проектом, может сопровождаться визуальным индикатором, в формате, например, лица Чернова, отображающим целесообразность принятия решения или выбора альтернативной стратегии поведения для менеджера проекта. Как известно, существует порядка 12 факторов, отражающих черты лиц Чернова, которые способны отображать характеристики управленческой ситуации. С точки зрения управления проектами, комбинирование факторов эффективности проекта и представление их в форме лица, оказывается весьма наглядным геометрическим представлением проектных характеристик. Рис. 5,6,7,8 сопровождаются подобными визуальными комментариями для менеджера.
Выделим возможные альтернативы в принятии управленческих решений в соответствии с введенным понятийным аппаратом:
1. Если Bi = B0, в управленческую ситуацию вмешиваться не нужно, ситуация развивается в соответствии с плановым сценарием развития событий, рис. 5.
|
|
|
Рис. 5. Случай совпадения областей B0 и Bi.
2.
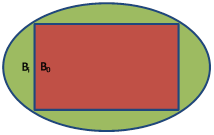
Если Bi![]() B0 , то фактическое развитие управленческой ситуации включает в себя
плановые результаты деятельности и вмешательства менеджера также не требуется,
однако, отличие плановой ситуации от фактической является фактором, который следует
принимать во внимание в любом случае, рис. 6.
B0 , то фактическое развитие управленческой ситуации включает в себя
плановые результаты деятельности и вмешательства менеджера также не требуется,
однако, отличие плановой ситуации от фактической является фактором, который следует
принимать во внимание в любом случае, рис. 6.
|
|
|
Рис. 6. B0 содержится в Bi.
3.
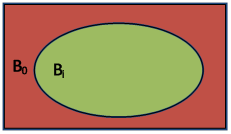
Если Bi![]() B0, то фактическое развитие управленческой ситуации может отличаться от
планового сценария поведения и требует вмешательства менеджера, рис. 7.
B0, то фактическое развитие управленческой ситуации может отличаться от
планового сценария поведения и требует вмешательства менеджера, рис. 7.
|
|
|
Рис. 7. Bi содержится в B0.
4.
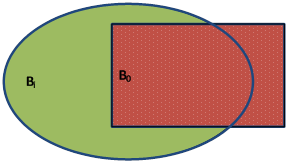
Если Bi![]() B0 и B0∩Bi≠
B0 и B0∩Bi≠![]() , то фактическое
развитие бизнес-ситуации отличается от планового и необходимо оперативное
вмешательство лица принимающего решение, рис. 8.
, то фактическое
развитие бизнес-ситуации отличается от планового и необходимо оперативное
вмешательство лица принимающего решение, рис. 8.
|
|
|
Рис. 8. Случай частичного совпадения Bi и B0.
Таким образом, оказывается возможным сформулировать путем визуального анализа проблемной ситуации: требуется ли вмешательство в ход ее реализации или в этом нет необходимости.
3. Структурные модели управления проектами и их визуальное представление
Первоначальной задачей геометрического изображения состава комплекса работ проекта является визуализация декомпозиции Иерархической структуры работ (ИСР). Исходными данными для построения ИСР является пооперационный перечень задач, подзадач, задаваемый в виде состава работ, соотносимый с различными уровнями управления. Кроме того, исходными данными могут являться исполнители операций, объемы и сроки работ, ресурсы, оборудование. Пример визуализации ИСР представлен на рис. 9.
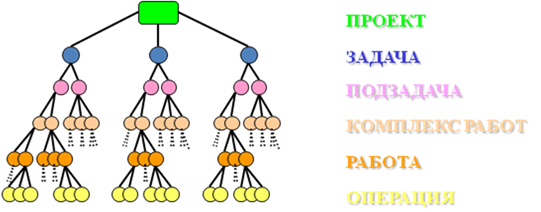
Рис. 9. Визуализация модели состава проекта.
Как видно из рис. 3 и рис. 9, графическое представление исходных данных проекта позволяет обоснованно подойти к задаче синтеза структуры проекта и определить в дальнейшем последовательность выполнения операций при помощи моделирования отношений между работами на соответствующих уровнях. ИСР является основой для визуализации деревьев:
Ø структуры,
Ø стоимости,
Ø распределения ответственности,
Ø целей,
Ø рисков.
Когнитивная визуализация ИСР предназначена для построения моделей проектов, соответствующих уровням управления, принятым в компании. Оказывается возможным проверить насыщенность уровней управления задачами, сбалансированность дерева по уровням, сделать вывод о размерах проекта, его обозримости, управляемости, необходимости подбора управленческой команды. ИСР используется в качестве исходных данных для построения сетевой модели комплекса работ, линейной модели и последующей их визуализации.
На рис. 10 представлена визуализация процесса создания организационной структуры проекта. Исходными данными для геометризации является матрица распределения ответственности в организации.
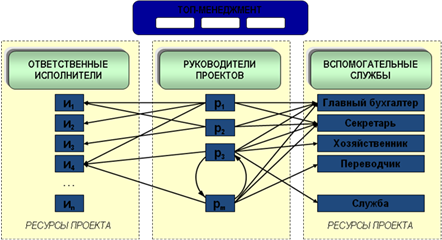
Рис. 10. Формирование организационной структуры проекта в компании.
Когнитивная функция данной визуальной модели состоит в определении принципов построения организационной структуры с учетом ресурсов, имеющихся в наличии, организационных штатных единиц с учетом схемы их взаимодействия.
С учетом доопределения геометрической модели формирования оргструктуры проекта до модели плоского рисунка, оказывается возможным визуализировать командную структуру исполнителей проекта и, таким образом, решить визуально задачу ее синтеза, рис. 11.
Визуализация организационной структуры проекта в формате командной структуры, основанной на геометрической модели теории графов, позволяет выполнить когнитивную функцию и демонстрирует действие закона Брукса, который утверждает, что привлечение дополнительной рабочей силы к запаздывающим проектам приводит к их еще большему запаздыванию. Данный эффект визуализируется при помощи усложнения оргструктуры проекта путем введения в нее дополнительных элементов (исполнителей). Это соответственно приводит к увеличению количества взаимодействий в команде, образуя, таким образом, геометрическую модель полного графа, число связей в котором зависит от количества вершин, и в общем случае равно n(n-1)/2. Где n - число вершин графа.

Рис. 11. Геометрическая модель структуры команды (участников) проекта.
В качестве исходных данных задачи визуализации топологической структуры проекта является модель теории графов. То есть математической моделью проекта является его сетевая модель - ориентированный граф G(X,U) без циклов и петель, где X-множество вершин, а U - множество ребер графа G, ориентированные слева направо [4]. В качестве весов ребер ориентированного графа выступают, как правило, продолжительности операций.
Основной формой задания ориентированного графа являются матрицы инцидентности и смежности, позволяющие определить его топологию. На рис. 12 представлена графическая интерпретация исходных данных проекта, заданных таблично, а также визуализация сетевой модели.
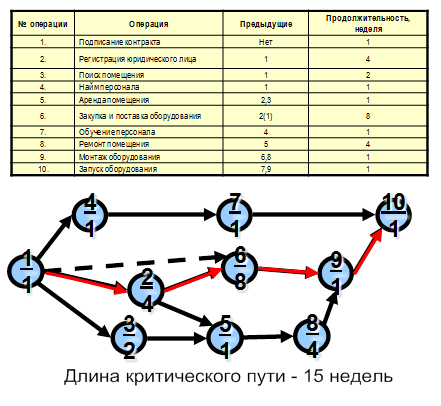
Рис. 12. Исходные данные в табличном виде и визуализация в виде сетевой модели комплекса работ проекта (критический путь обозначен красным цветом).
Доопределение геометрической модели проекта до модели плоского рисунка связано с возможностью отображения критического пути, в качестве пути, не имеющего временного резерва. Использование понятия критического пути и временных резервов операций играет важнейшую роль в процессе приятия управленческих решений [3].
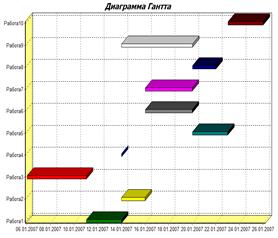
Визуализация сетевой модели комплекса работ проекта в виде плоского рисунка носит в основном когнитивный характер, поскольку позволяет наглядно отобразить отношения предшествования, следования между операциями проекта в графическом виде, а также выполнить синтез множества логически допустимых фронтов комплекса работ проекта. Сетевая модель оказывается удобной формой визуализации геометрических данных, поскольку обладает свойством обозримости и доступности внесения структурных изменений. Кроме этого, оказывается возможным выполнить визуализацию решения задачи отыскания топологии и продолжительности критического пути проекта. На рис. 13 представлена линейная модель проекта или Диаграмма Гантта. Исходными данными для визуализации является календарный план работ проекта в таблично-символьной форме с наименованиями операций. Доопределение модели до плоского графического рисунка позволяет визуально проанализировать временные резервы операций и длительности работ. Цветовое выделение операций графически отображает их критичность, помеченную на диаграмме красным цветом. Для сопоставления двух способов визуализации на рис. 13 совмещены сетевая и линейная диаграммы, которые позволяют проиллюстрировать альтернативные подходы к визуальному анализу бизнес-данных. Как можно заметить, визуально сетевая и линейная модели легко трансформируются одна в другую. Выделение на диаграмме красным цветом некоторых работ позволяет визуально идентифицировать критический путь проекта и временные параметры некритических операций.

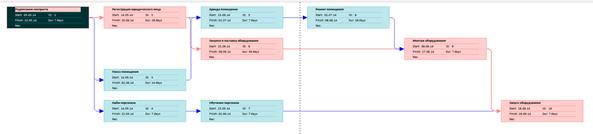
Рис. 13. Визуальные модели проекта: линейная и сетевая.
Относительно достоинств и недостатков каждого из методов визуальной аналитики бизнес-данных в форматах сетевой модели и диаграммы Гантта следует отметить:
Ø Исторически линейная модель была предложена ранее сетевого метода визуального анализа .
Ø Сетевая и линейная модели визуализации структуры проекта обе в достаточной степени отражают состав комплекса работ.
Ø Визуально сетевая модель отражает взаимозависимости между операциями более четко, чем линейная модель, с топологической точки зрения.
Ø Графическим когнитивным преимуществом сетевой модели перед линейной является то, что она более адаптирована для внесения изменений, постоянно возникающих в ходе реализации, планирования и управления проектами.
Ø При помощи сетевой модели может быть визуализирована технологическая последовательность тех операций, которые входят в критический путь, и определяют максимальные сроки реализации проектных работ.
Ø В то же время, визуально линейная модель проекта в формате плоского рисунка позволяет отслеживать сроки выполнения операций и визуально контролировать резервы некритических работ.
Выполнить ввод исходных данных в табличном виде, получить визуализацию сетевой модели проекта возможно при помощи программного средства, разработанного авторами [13]. Также доступны функции:
Ø календарного планирования с учетом ограничений на доступное количество ресурсов,
Ø выполнение визуализации линейной и ресурсной диаграмм для нескольких видов ресурсов.
4. Графические модели структурных преобразований проектов
Структурные преобразования сетевой модели комплекса работ, как формы геометризации исходных данных проекта, выполняются в основном визуально, в отличие, например, от процедур подсчета числовых характеристик событий и работ.
В основе структурных геометрических преобразований лежат процедуры объединения (параллельного и последовательного), разукрупнения и укрупнения сетевых моделей [4,5].
Исходными данными для визуализации процедуры объединения являются сетевые модели частных объединяемых сетевых фрагментов Gi(Xi,Ui),где i=1..n - общее количество подмоделей.
Визуализация процедур последовательного и параллельного объединения сетевых моделей приведена на рис. 14.
Визуальная модель исходных данных в форме модели теории графов позволяет решить задачу получения сводного сетевого фрагмента проекта структурно более сложного, чем частные сшиваемые сетевые графики.
Визуальный анализ сводной сетевой модели проекта позволяет оценить масштабность комплекса работ и в дальнейшем сопоставить структуру объединенного проекта со сложностью управленческой задачи.
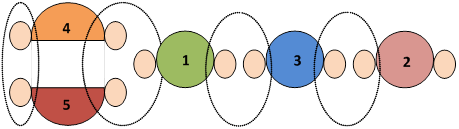
Рис. 14. Визуализация сводного сетевого графа как результат выполнения процедур последовательного и параллельного объединения частных сетевых моделей.
На рис. 14. схематично представлены сетевые фрагменты под номерами 4 и 5, которые объединяются параллельно. Фрагменты 1, 3 и 2 присоединяются последовательно к результату параллельного сшивания фрагментов 4 и 5. Визуальный анализ и сопоставление результата объедения дают возможность топологического соотнесения исходной модели данных и результата, принимая во внимание взаимное геометрическое расположение объектов анализа.
Следует также отметить, что процедура разукрупнения (декомпозиции) сетевой модели комплекса работ выполняется в основном, опираясь на геометрическое представление декомпозируемых частей графа, являющихся исходными данными для построения визуальной модели. На рис. 15 представлен пример визуального приведения сетевой модели к виду, позволяющему производить обработку и анализ проекта по частям, добиваясь, таким образом, снижения размерности решаемой задачи управления. Доопределение геометрической модели до модели плоского рисунка подразумевает отграничение подграфов меньшей размерности по сравнению с исходной сетевой моделью, путем выделения событий одинакового ранга [4].
Визуализация решения, в данном случае, имеет когнитивный характер, позволяя производить редукцию сетевой модели путем геометризации исходных данных, в виде модели теории графов.
Таким образом, визуально решена задача получения нескольких подграфов меньшей размерности и определен порядок дальнейшей обработки фрагментов 1-2-3 при визуальном или численном анализе сетевой модели.
Визуализация процедуры укрупнения сетевой модели жизненного цикла позволяет обоснованно подойти к формулировке и постановке задачи управления для менеджеров различного уровня. Специалисты пользуются на каждом уровне агрегированной или укрупненной информацией, уровень детализации которой убывает по мере продвижения вверх по организационной структуре управления (рис. 4).
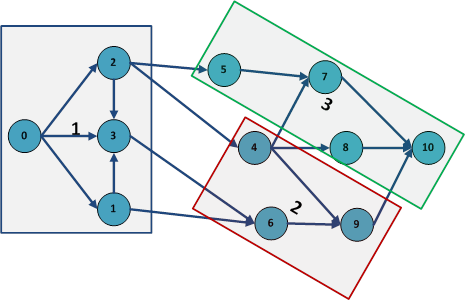
Рис. 15. Пример визуализации декомпозиции сетевой модели (выделены фрагменты 1, 2 и 3).
В результате процедуры укрупнения [18] образуется визуальная модель проекта, отображающая структуру более простую, содержащую меньшее количество элементов, вершин и дуг, чем исходная. В качестве исходных данных при визуализации процедуры укрупнения используется сетевая модель проекта, причем доопределение графической модели укрупненного проекта до плоского рисунка подразумевает и численное агрегирование, т.е. отображение кумулятивной информации, касающейся временных и стоимостных параметров проекта.
Известны некоторые случаи эквивалентного по времени и стоимости укрупнения комплекса работ [16, 18], позволяющие использовать визуальные модели геометризованных исходных данных в виде модели теории графов.
Рассмотрим ряд частных случаев укрупнения, эквивалентного по времени и стоимости, с использованием визуальных моделей агрегированных проектов цепочечного вида.
На рис. 16 представлена визуальная модель укрупнения, эквивалентного по стоимости и времени, имеющая место в задачах параллельного объединения частных сетевых фрагментов, содержащих сопряженные операции. Доопределение геометрической модели укрупнения до модели плоского рисунка связано с обозначениями работ в виде букв, а граничное событие укрупняемого частного сетевого подграфа (выделенного пунктирной линией) обозначено x1 и выделено бордовым цветом.
В качестве исходных данных для визуализации рассматриваются численные стоимостные и временные параметры работ и событий проекта (рис. 16), а также информация о внутренних событиях (выделены синим цветом) и граничных событиях (выделенны розовым) укрупняемого подграфа G сетевой модели. Исходными данными для визуализации результата процедуры укрупнения является сетевой граф G0 цепочечного вида, представленный на рис. 17. Доопределение до модели плоского рисунка связано с указанием сверху над дугами временных и стоимостных параметров укрупненных работ и цветовой индикацией оставшихся после укрупнения событий.
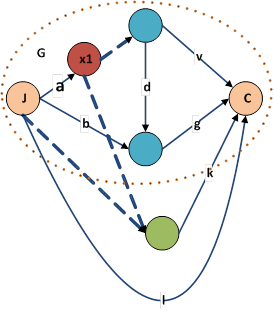
Рис. 16. Визуализация укрупняемого сетевого графа G, содержащего сопряженные операции.
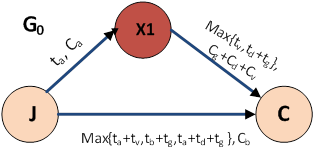
Рис. 17. Визуализация результата укрупнения G0, эквивалентного исходному G по времени и стоимости.
Когнитивная визуализация укрупненной модели позволяет определить геометрический образ объекта в виде графа специального цепочечного вида, характерного для модели жизненного цикла. Численные стоимостные параметры укрупненного сетевого графа могут быть получены в результате визуального решения задачи укрупнения:
|
|
(1) |
|
|
(2) |
|
|
(3) |
При помощи визуального анализа результата укрупнения, эквивалентного по времени и стоимости, могут быть определены стоимостные параметры работ в укрупненном графе G0 в общем виде:
|
|
(4) |
|
|
(5) |
|
|
(6) |
где ![]() ,
, ![]() ,
, ![]() - стоимость работ
соответственно предшествующих, следующих за и несравнимых с событием x1.
- стоимость работ
соответственно предшествующих, следующих за и несравнимых с событием x1.
На рис. 18. представлена визуализация структуры жизненного цикла изделия в виде сетевой модели, которая может быть получена в результате описанных выше процедур структурного геометрического преобразования проекта (рис. 14, рис. 17). Исходными данными для визуализации является последовательность этапов, представленная на рис. 3. Согласно [8,9] модель жизненного цикла на рис. 18 имеет наглядную визуальную интерпретацию в терминах основных и вспомогательных процессов, входящих в его состав. Дуги, соединяющие несмежные вершины ориентированного графа (0→2, 1→3, 2→4, 3→5 ) интерпретируются как вспомогательные и обеспечивающие процессы жизненного цикла, а соединяющие смежные вершины графа (0→1→2→3→4→5) как основные процессы.
Когнитивная геометрическая модель жизненного цикла продукта, как видно из рисунка, имеет специфическую цепочечную структуру, позволяющую сформулировать ряд важных и практически значимых свойств [2] на основе визуального анализа [16].

Рис. 18. Визуализация структуры полного жизненного цикла изделия в виде сетевой
модели комплекса работ.
Авторами разработана программная система [20], решающая задачи визуального анализа структуры проекта в виде сетевой модели комплекса работ. На рис. 19 представлен пример визуализации сводной сетевой модели комплекса работ проекта.
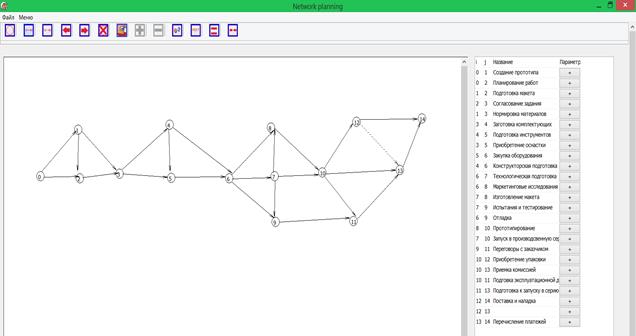
Рис. 19. Пример сетевой модели комплекса работ в виде модели плоского рисунка с табличным представлением исходных данных [22].
С использованием инструментального программного средства можно визуализировать произвольную топологию сетевой модели комплекса работ, в том числе и цепочечную структуру жизненного цикла проекта, используя средства когнитивного визуального анализа.
5. Визуальное моделирование числовых параметров проекта
При решении задачи управления проектами необходимо получить исходную информацию, касающуюся числовых характеристик операций, в том числе длительности и стоимости выполнения отдельной работы. Для построения математической модели операции необходимо воспользоваться вероятностным методом описания, основанным на визуальном представлении функции распределения случайной величины.
Для построения числовых оценок параметров работ выполним геометризацию исходных данных в виде вероятностного закона β-распределения [4]. Математическое ожидание M[t] продолжительности выполнения работы рассчитывается на основе трех числовых оценок - tmin - оптимистической оценки продолжительности выполнения работы, tmax - пессимистической оценки длительности выполнения операции и tн.в. - наиболее вероятной оценки ее продолжительности. Рассмотрим визуализацию исходных данных при помощи рис. 20, на котором изображена дифференциальная функция распределения плотности вероятностей β-распределения.
Доопределение геометрической модели исходных данных до плоского рисунка связано с введением коэффициентов α и γ - смещения (наклона) кривой в сторону пессимистического (в случае коэффициента γ) и оптимистического значения длительности (в случае коэффициента α).
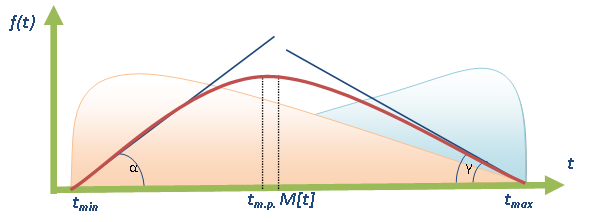
Рис. 20. Визуальная модель β-распределения дифференциальной функции распределения вероятностей длительности выполнения работы.
Визуальный анализ показывает, что смещение кривой β-распределения влево или вправо позволяет корректировать вероятностную оценку длительности или стоимости выполнения работы в сторону оптимистического или пессимистического сценария. Когнитивный визуальный анализ рис. 20 позволяет выявить, что значение моды распределения длительности выполнения работы не совпадает с математическим ожиданием, а также явно заметен характер унимодальности кривой.
Кроме того, оказывается возможным выполнить визуализацию функции распределения критической продолжительности выполнения проекта, причем критическая длительность проекта в силу центральной предельной теоремы будет распределена по нормальному закону.
Исходными данными визуализации функции распределения вероятностей продолжительности критического пути являются результаты статистических испытаний, которые, как правило, задаются таблично.
На рис. 21 представлена визуализация дифференциальной функции распределения продолжительности критического пути.
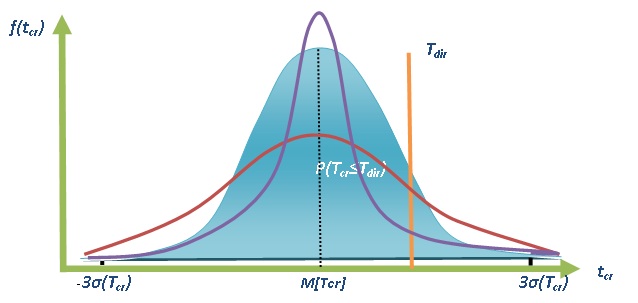
Рис. 21. Визуализация дифференциальной функции распределения вероятностей длительности критического пути для нормального закона распределения.
Визуальный анализ рис. 21 позволяет решить сразу несколько управленческих задач.
Ø Как видно на плоском рисунке доопределены формы и цвета различных кривых нормального распределения. Красному цвету кривой соответствует высокая степень неопределенности распределения длительности критического пути, синему - умеренная, а фиолетовому - низкая. То есть по форме кривой можно судить об уровне риска, присущему каждому из вариантов реализации проекта.
Ø Оказывается возможным визуально решить задачу нахождения вероятности завершения проекта за директивный срок, указанный на графике вертикальной линией (Tдир). Визуально вероятность завершения проекта за Tдир определяется при помощи площади фигуры, ограниченной функцией нормального распределения (любого цвета) и вертикальной линией Tдир.
Ø Также наглядно можно выполнить визуальный анализ правила трех сигм, известного в менеджменте.
Рассмотрим визуализацию числовых данных, используемых для моделирования проекта с использованием метода ПЕРТ-анализа [3,4].
В качестве исходных данных для визуализации модели планирования проекта на основе ПЕРТ - анализа выступают числовые оценки продолжительности и стоимости операций. Результат планирования проекта при помощи ПЕРТ-анализа, как правило, представлен в формате табличных данных, являющихся исходными данными для визуализации линейной диаграммы Гантта, отражающей структуру календарного плана комплекса работ. Средствами визуального анализа оказывается возможным соотнести друг с другом пространственное расположение операций на линейной диаграмме Гантта, представленной на рис. 22, в трехмерном формате.
Визуализация решения задач календарного планирования, используя ПЕРТ - метод, выполняется при помощи программного средства планирования проектов, разработанного авторами [13]. Наряду с линейной диаграммой проекта отображается вероятность завершения проекта за директивный срок, а также параметры полученного при планировании календарного плана, ранние и поздние сроки начала и окончания операций, временные резервы, среднеквадратические отклонения продолжительностей выполнения работ.
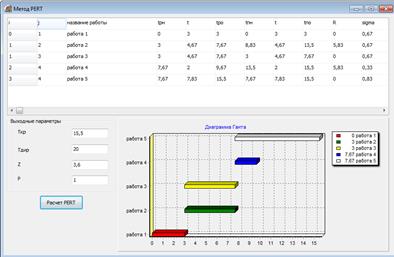
Рис. 22. Визуализация результата решения задачи календарного планирования [13] с использованием ПЕРТ-метода
6. Визуализация календарного ресурсного планирования прерываемых и непрерываемых операций
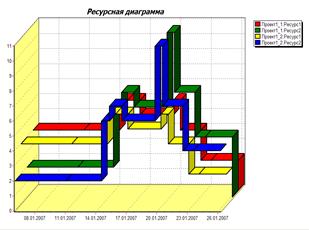
На рис. 23 приведена визуализация профиля потребности в ресурсах проекта без ограничений на доступное количество ресурсов. В качестве исходных данных для визуализации используются ресурсные числовые параметры операций. Доопределение геометрической модели до плоского рисунка подразумевает учет действующих ресурсных ограничений путем визуализации линии, помеченной на рисунке красным цветом, с целью индикации проблемной ситуации дефицита ограниченных ресурсов.
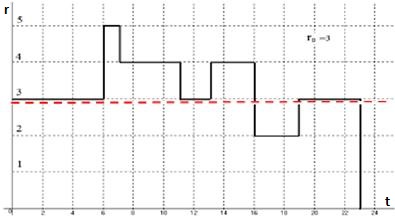
Рис. 23. Визуализация ресурсной диаграммы проекта с ограничением сверху на доступное количество ресурсов r0=3.
Визуальный анализ проблемной ситуации, складывающейся в связи с дефицитом доступных ресурсов, оказывается возможным выполнить с использованием рис. 24.
Как видно из рис. 24, наложение сверху ограничений на доступное количество ресурсов приводит к увеличению продолжительности критического пути до длительности равной 28, что является индикатором возникновения проблемной ситуации, в связи со сдвигами плановых сроков операций. В данном случае имеет место когнитивная визуальная модель проблемной ситуации, полученная из исходных табличных данных.
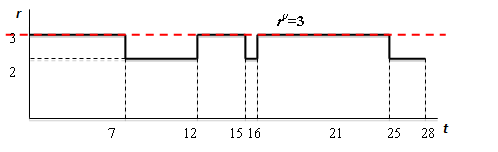
Рис. 24. Визуализация ресурсной диаграммы как результат решения задачи ресурсного планирования с учетом введенного ограничения на ресурсы (r).
Составление ресурсно-допустимого календарного плана комплекса работ проекта является важной задачей, которая решается регулярно менеджером проекта. Для решения задач календарного планирования с учетом ограничений на доступное количество ресурсов применяется ряд эвристических и точных методов, принимающих во внимание приоритеты, присваиваемые операциям. Авторами была разработана Web-ориентированная программная система решения задачи ресурсного календарного планирования комплекса работ проекта [19] при помощи параллельного и последовательного методов [4,5]. Визуализация структурной схемы разработанной системы приведена на рис. 25.
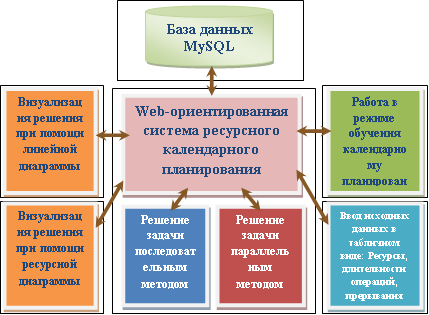
Рис. 25. Визуальная модель процесса календарного планирования проекта при помощи Web-ориентированной системы.
В качестве исходных данных, используемых для визуализации модели календарного плана, вводятся табличные данные, касающиеся длительностей выполнения операций, ресурсов (потребляемых работами) и наличия прерываний в операциях. Следует отметить, что последовательный метод ресурсного календарного планирования не учитывает прерываний в ходе выполнения работ, в то время как параллельный метод ресурсного планирования позволяет принять во внимание прерывания, возникающие при выполнении операций. На рис. 26 представлена визуализация сетевой модели комплекса работ проекта, для которого составляется ресурсно-допустимый календарный план.
Доопределение геометрической модели, в данном случае, состоит в отображении на дугах ориентированного графа временных параметров работ. Таким образом, визуализируется модель плоского рисунка, носящая иллюстративный характер.
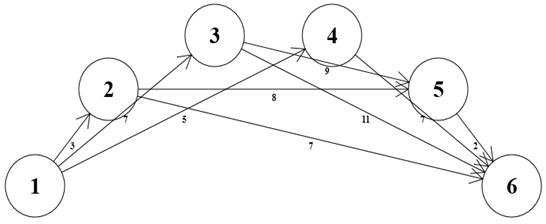
Рис. 26. Визуализация сетевой модели с использованием Web-ориентированной системы календарного планирования [19].
На рис. 27 представлена визуализация линейной диаграммы Гантта, создаваемой при помощи разработанного программного средства визуального решения задач календарного планирования проектов.
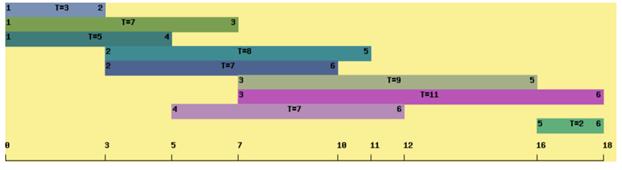
Рис. 27. Визуализация линейной диаграммы Гантта [19].
Визуальная модель, представленная на рис. 27, является доопределенной моделью плоского рисунка с указанием длительностей и индексов работ, которые являются исходными данными для визуализации.
Следует отметить, что процесс календарного ресурсного планирования комплекса работ выполняется итерационно (т.е. в "пошаговом" режиме).
На рис. 28 представлены исходные данные о проекте в формате календарного плана (таблицы) для решения задачи ресурсного планирования последовательным методом, а также результат визуализации в геометрическом формате сетевой модели. В состав исходных данных включена также информация о потребляемых операциями ресурсах.
В данном случае визуализация носит характер иллюстративный, позволяя уточнить топологическую структуру комплекса работ.
Следует отметить, что можно производить визуализацию решения задачи ресурсного календарного планирования для последовательного и параллельного методов на каждой итерации или шаге алгоритма. Однако, как правило, ограничиваются только итоговой визуальной моделью, получаемой на последнем итерационном шаге. Здесь в качестве визуальных моделей применяются линейная и ресурсная диаграммы проекта, обычно в формате плоских рисунков, позволяющих выполнять контрольный визуальный анализ полученного решения на соответствие ресурсным ограничениям и сглаженности профиля потребности в ресурсах. Сглаженный ресурсный профиль имеет как правило пирамидальный или треугольный профили [5].
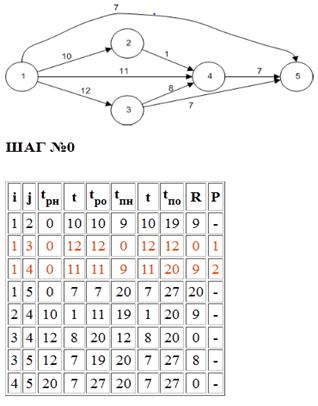
Рис. 28. Визуальное представление исходных данных для решения задачи календарного ресурсного планирования последовательным методом [19].
Результат, полученный при помощи последовательного метода планирования, приведен на рис. 29. Визуализация полученного решения выполнена в формате линейной и ресурсной диаграмм. Исходными данными для визуализации являются числовые параметры операций ресурсно-допустимого календарного плана, представленные в табличном виде на последнем шаге реализации последовательного метода.
Визуальный анализ позволяет определить, критическую продолжительность проекта в условиях ограничений на доступное количество ресурсов.
Представим теперь визуализацию решения задачи календарного ресурсного планирования с использованием параллельного метода, допускающего прерывания в ходе выполнения операций. На рис. 30 отображен формат представления исходных данных для решения задачи в табличном виде, в качестве исходных данных для визуализации сетевой модели используются временные и ресурсные параметры операций.
На рис. 31 представлен результат решения задачи ресурсного календарного планирования проекта с использованием параллельного метода, учитывающего прерывания. Как видно из рис. 31, когнитивная визуализация решения задачи позволяет определить параметры календарного плана проекта с учетом прерываний в ходе выполнения, а также ограничений на доступное количество ресурсов. Средствами визуальной аналитики может быть также подсчитано число прерываний, имевших место в ходе выполнения проекта.
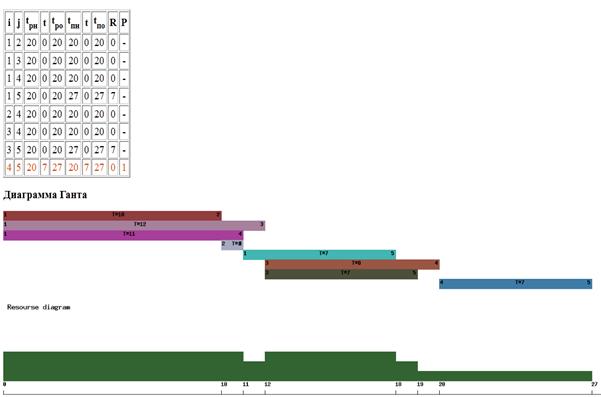
Рис. 29. Визуализация линейной и ресурсных диаграмм календарного плана проекта для последовательного метода [19].
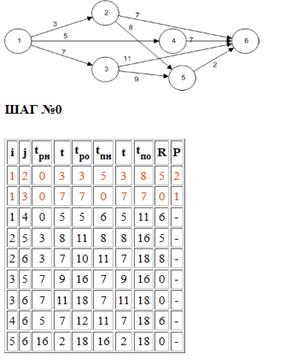
Рис. 30. Визуализация исходных данных проекта в форме сетевой модели для решения задачи параллельным методом [19].
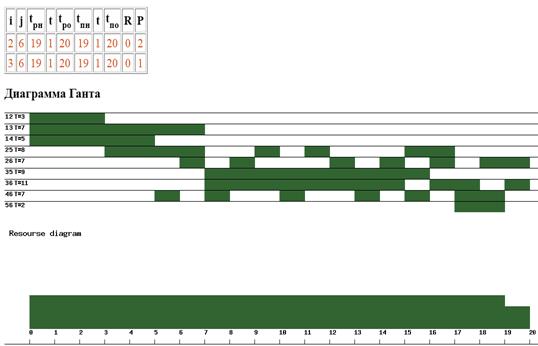
Рис. 31. Визуализация решения задачи календарного планирования параллельным методом в формате линейной и ресурсной диаграмм [19].
Визуальное обучение основам календарного ресурсного планирования проектов осуществляется в обучающем режиме программного тренажера, разработанного авторами [19]. Ознакомиться с визуальным тренажером можно, нажав на ссылку: Программа планирования. Программный продукт реализует функции:
Ø табличного ввода информации о проекте,
Ø визуализации сетевой и линейной моделей проекта,
Ø решения задачи ресурсного календарного планирования последовательным и параллельным методом,
Ø может быть использован в качестве программного тренажера.
Известны также и точные методы [5] аналитического решения задачи распределения ограниченных ресурсов между работами, входящими в состав комплекса операций сетевой модели проекта. В точном методе ресурсного планирования также допускается применение методов бизнес-графики и визуализации исходных бизнес-данных. Точные методы обладают некоторыми недостатками, такими, как например, размерность проектных исходных данных. Однако, несмотря на размерность, исходные данные допускают геометризацию и последующую визуализацию, позволяющую применить средства визуальной аналитики даже для задач большого масштаба.
Визуализация исходных бизнес-данных для решения задачи точным методом календарного планирования выполняется при помощи линейной диаграммы Гантта, рис. 32, а также при помощи визуализации ресурсного профиля потребности в ресурсах проекта для нескольких различных видов ресурсов (информация о потреблении которых является исходными данными для визуализации).
|
|
|
|
Рис. 32. Визуализация линейной диаграммы Гантта и ресурсной диаграммы в формате 3D модели [13].
|
|
Решение задачи ресурсного планирования комплекса работ проекта точным методом подразумевает [5] построение множества логически и ресурсно-допустимых фронтов комплекса работ. Возможно синтезировать множество фронтов, используя визуальную модель в формате диаграммы Гантта, получая фронт работ при помощи прямой, перпендикулярной оси времени (абсцисс).
Множество логически допустимых фронтов имеет графическую интерпретацию в формате графа отношения несравнимости. В свою очередь, исходными данными для визуализация графа отношения несравнимости является множество несравнимых операций, задаваемых в таблично-числовом или символьном форматах. На рис. 33 визуализирована сетевая модель проекта, для которой при помощи методов визуальной аналитики построен граф отношения несравнимости операций, рис. 34. Модели плоских рисунков являются когнитивными визуальными моделями, поскольку позволяют решить задачу синтеза множества фронтов, опираясь на геометрические свойства объекта анализа.
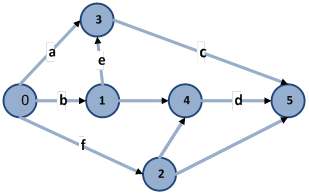
Рис. 33. Визуализация сетевой модели проекта для решения задачи ресурсного планирования точным методом.
При решении задачи ресурсного планирования точным методом применяется также граф расстояний, используемый для визуального анализа возможности перехода между фронтами комплекса работ при минимальном количестве прерываний между операциями, входящими в состав проекта, рис. 35.
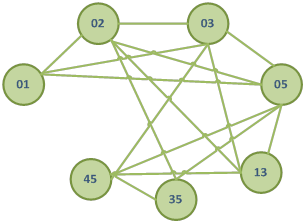
Рис. 34. Визуализация графа отношения несравнимости, получаемого при помощи графического анализа исходной сетевой модели проекта.
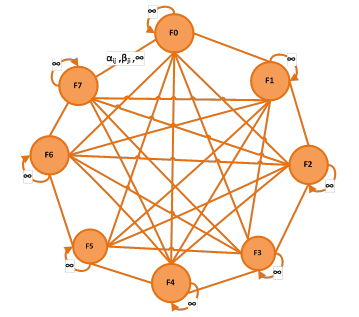
Рис. 35. Визуализация возможности перехода от одного фронта работ Fα к другому Fβ при помощи геометрической модели плоского рисунка.
Исходными данными для построения визуальной модели графа переходов является матрица расстояний, содержащая расстояние между фронтами комплекса работ. Доопределение геометрической модели исходных данных до плоского рис. 35 связано с заданием весов дуг - переходов между фронтами, которые отображаются в виде взвешенных ребер ориентированного графа расстояний, являющегося когнитивной визуальной моделью. На рис. 35 над дугами изображены расстояния между фронтами, равные количеству различных операций, входящих в оба фронта. Расстояние при переходе от фронта Fi к Fj обозначено при помощи αij, расстояние при переходе от Fj к Fi - обозначается через βji, при невозможности перехода между фронтами комплекса работ в качества параметра перехода над дугой графа используется символ ∞.
Кроме этого, при решении задач календарного планирования проектов возможно произвести визуализацию процесса изменения затрат, рис. 36 в ходе выполнения проекта при помощи пакета прикладных программ, разработанного авторами [13]. Исходными данными для построения визуальной модели является информация о затратах комплекса работ проекта, задаваемая численно.
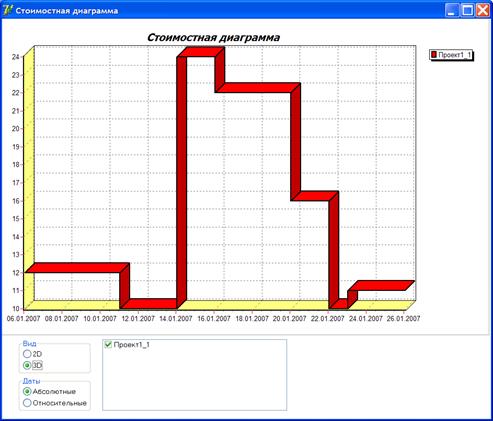
Рис. 36. Визуализация стоимостной диаграммы проекта, 3D-представление [13].
Визуальная модель, представленная на рис. 36, является когнитивной визуальной моделью пространственной сцены, которая может быть использована для решения задач определения необходимости распределения затрат (инвестиций) на реализацию комплекса работ проекта, а также визуальной оценки пиков затрат ресурсов в определенные моменты времени.
Ознакомиться с интерактивным макетом программного средства, решающим задачи ресурсного календарного планирования, можно пройдя по следующей ссылке. Программный продукт реализует функции календарного планирования комплекса работ проекта на основе оптимизационной модели перераспределения ограниченных ресурсов с учетом стоимостных параметров, влияющих на качество получаемого расписания. Программное средство реализует также функции визуализации исходных данных (представленных в табличном виде), сетевой и линейной моделей оптимального расписания проекта.
7. Оперативное планирование и управление комплексом работ проекта с использованием визуального анализа
Является широко признанным, что метод освоенного объема [11, 24], реализованный в ряде современных систем управления проектами, позволяет эффективно решать задачи оперативного планирования и управления ходом реализации проекта при помощи набора визуальных моделей.
Исходными данными для построения визуальных моделей метода освоенного объема являются плановые, фактические и освоенные затраты, представляющие собой числовые характеристики проекта. На рис. 37 представлена визуализация показателей освоенного объема. Визуальная модель доопределена до модели плоского рисунка путем нанесения на кривые графиков функции числовых и символьных характеристик.
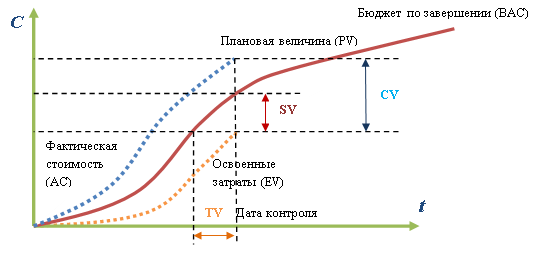
Рис. 37. Визуализация показателей освоенного объема.
Данная визуальная модель плоского рисунка является когнитивной визуальной моделью, поскольку позволяет контролировать плановые и фактические сроки завершения работ проекта, отслеживая также отклонения по стоимости операций или сопоставляя плановые и фактические значения освоенных затрат.
В методе освоенного объема используются следующие показатели, графически отображены на рис. 37:
Отклонение по стоимости:
|
CV = EV-AC |
(7) |
Отклонение по расписанию:
|
SV=EV-PV |
(8) |
Отклонение по времени TV, которое легко может быть вычислено геометрически на основе визуальной модели.
Измерение эффективности реализации проекта и прогнозирование будущего хода его исполнения выполняется при помощи следующих числовых индикаторов, являющихся исходными данными для построения визуальной модели контроля и оперативного управления проектом на стадии его реализации.
Индикаторы эффективности реализации проекта:
|
CPI = EV/AC |
(9) |
|
- индикатор эффективности затрат; |
|
|
SPI = EV/PV |
(10) |
|
- индикатор эффективности расписания; |
|
|
CR = CPI x SPI |
(11) |
|
- индикатор критичности выполнения проекта. |
|
Визуальная модель принятия решений на основе введенных выше индикаторов подразумевает когнитивную визуализацию плоского рисунка, отображающего прогресс в ходе реализации проекта, рис. 38.
Когнитивная визуализация позволяет определить тренды в изменении эффективности проекта, используя индикаторы с применением геометрических образов управленческих ситуаций, в том числе лиц Чернова. Значения индикаторов между определенными уровнями показателей позволяют наметить эффективные меры по вмешательству в проблемную ситуацию проекта, особенно если речь идет о красной зоне.
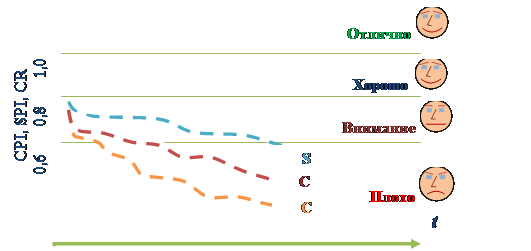
Рис. 38. Визуализация индикаторов освоенного объема, используемых при принятии решений менеджерами в сфере управления проектами.
С целью прогнозирования будущего хода выполнения работ проекта используется показатель - индикатор стоимости по завершению:
|
EAC = BAC/CPI |
(12) |
Визуализация геометрической модели исходных данных, доопределенная до модели плоского рисунка, представлена на рис. 39.
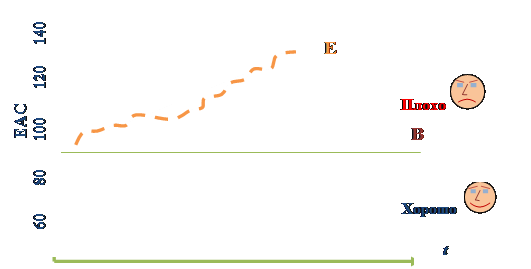
Рис. 39. Визуализация прогноза будущего хода выполнения проекта.
Прогнозирование будущих затрат по проекту осуществляется на основе визуальной модели, доопределенной до плоского рисунка, путем указания зон, в которые попадает индикатор стоимости по завершению. Как видно из рисунка, в случае попадания в красную зону необходимо вносить изменения в тренды развития проекта, вмешиваясь в проблемную ситуацию, производя корректирующие действия, которые будут заключаться в соблюдении сроков выполнения работ, поскольку удлинение сроков приводит к повышению затрат на реализацию проекта, что отражается при помощи индикатора EAC - стоимости по завершению.
Таким образом, при помощи стоимостных и временных параметров проектов, используемых в качестве исходных данных, можно выполнять визуальное аналитическое решение задач, основываясь на средствах бизнес-графики.
8. Инвестиционно-финансовое планирование проекта на основе визуальных моделей
Рассмотрим особенности использования визуальных моделей при решении задач инвестиционно-финансового планирования проектов с применением современных инструментальных систем бизнес-аналитики. Средства визуальной аналитики получили широкое распространение в сфере геометризации результатов бизнес-проектов.
На рис. 40 представлена схема визуализации исходных данных о проекте.
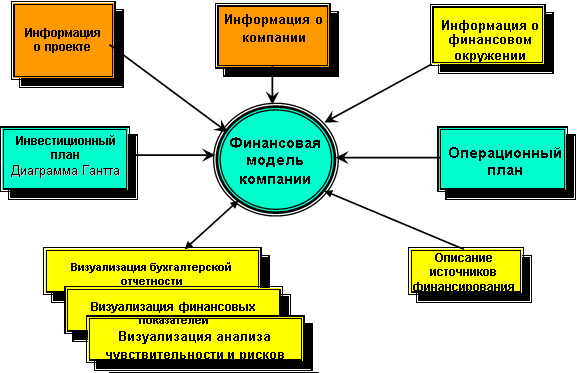
Рис. 40. Исходные данные для построения визуальной модели финансовой информации о проекте.
Исходные данные для построения визуальных моделей финансово-инвестиционного планирования достаточно разнообразны, хотя в основном они носят числовой характер и задаются, как правило, в табличном виде [17].
Важной задачей бизнес-аналитики в финансово-инвестиционном планировании проектов является построение визуальных моделей интегральных финансовых критериев. Основными критериями оценки эффективности финансовых результатов, согласно технологии UNIDO [10], являются следующие интегральные финансовые показатели: NPV, IRR, PI, DPB, MIRR.
Визуальными моделями интегральных финансовых показателей эффективности проектной деятельности являются доопределенные исходными бизнес-данными плоские рисунки или пространственные сцены, применяемые для принятия инвестиционно-финансовых решений, касающихся вопросов окупаемости вложенных средств в реализацию проекта.
На рис. 41 представлена визуальная модель плоского рисунка в формате линейной диаграммы Гантта, отображающая календарный план выполнения работ по проекту. Визуализация выполнена при помощи аналитической системы Project Expert, применяемой для решения задач финансового и инвестиционного планирования.
Методом визуализации анализируются затраты на выполнение этапов работ проекта и общая продолжительность его реализации, взаимное расположение этапов.
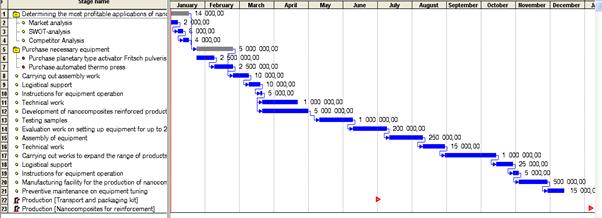
Рис. 41. Визуализация диаграммы Гантта при помощи инструментального средства Project Expert.
На рис. 42 представлена визуализация процесса окупаемости в виде модели пространственной сцены. Исходными данными для построения пространственной сцены являются потоки денежных средств, представляющие собой данные бухгалтерской отчетности во временном разрезе и табличном формате. Методом визуализации анализируется процесс окупаемости первоначальных инвестиций, скорость поступления дохода во временном контексте. Также визуальное доопределение геометрической модели исходных данных может состоять в установлении порогового уровня NPV, приемлемого для инвестора, а также соответствующего принятию решения об инвестировании в проект с пороговым уровнем дохода. На рис. 42 пороговый уровень интегрального дохода визуализирован горизонтальной пунктирной линией, по оси ординат отложено время по оси абсцисс интегральный эффект проекта в рублях.
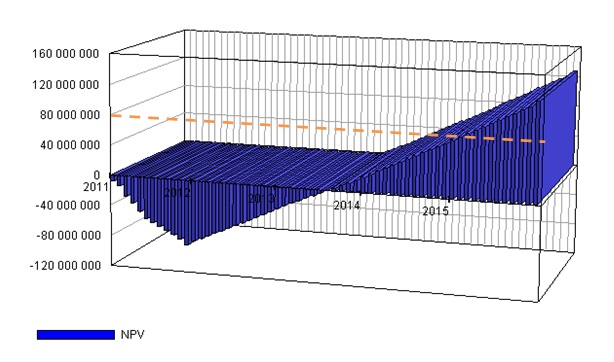
Рис. 42. Визуализация показателя NPV в виде пространственной сцены.
На рис. 43 представлена визуальная модель анализа чувствительности интегрального показателя эффективности проекта в зависимости от неопределенных факторов, таких как: объем сбыта, цена сбыта, ставки налогов, первоначальные затраты. Исходными данными для построения визуальной модели анализа чувствительности являются бизнес-данные отражающие: объемы продаж продукции, цены сбыта, ставки налогов, которые имеют числовой формат. Доопределение геометрической модели до модели плоского рисунка связано с заданием диапазонов отклонений неопределенных факторов и построением столбчатой диаграммы, выполняющей когнитивную функцию визуализации отклонения NPV.
Стоит отметить, что зависимости данного вида применяются для количественного и качественного анализа рисков результатов проекта, связанных с отклонениями случайных факторов в установленных диапазонах.
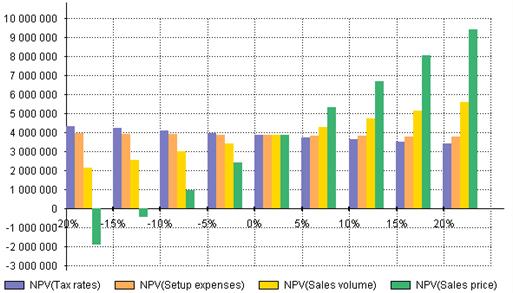
Рис. 43.Визуальная модель анализа чувствительности NPV в виде плоского рисунка.
На рис.44 визуальная модель анализа чувствительности чистого приведенного дохода представлена в виде пространственной сцены, позволяющей визуально количественно проанализировать риски и возможные перспективы выполнения проекта в случае альтернативных сценариев его реализации.
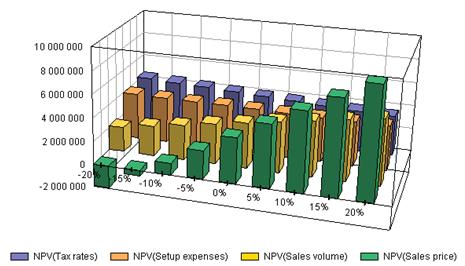
Рис. 44. Визуальная модель анализа чувствительности NPV в формате пространственной сцены.
Методом визуализации оказывается возможным проанализировать, например, что 20 % увеличение цен на продукцию приводит к возрастанию NPV c 0 до 10 000 000 рублей , или наоборот, 20% снижение цен приводит к появлению отрицательного эффекта от реализации проекта и падению приведенного дохода до неприемлемого уровня.
На рис. 45 приведена визуальная модель анализа чувствительности дисконтированного периода окупаемости в зависимости от изменения неопределенных данных. По осям абсцисс графиков, представленных на рис. 44 и 45, отложены диапазоны вариации неопределенных параметров, а по осям ординат диапазон изменения NPV в абсолютных единицах, например, в рублях.
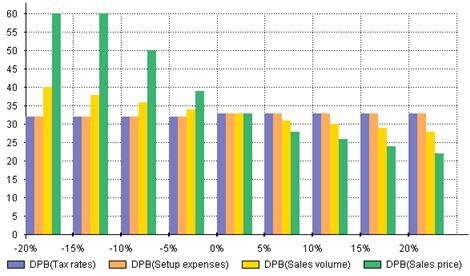
Рис. 45. Визуальная модель анализа чувствительности дисконтированного периода окупаемости в зависимости от цены и объема сбыта, ставок налогов и первоначальных затрат.
На рис. 46 приведена визуализация пространственной сцены, используемой в качестве когнитивной модели оценки рисков проекта на основе показателя дисконтированного периода окупаемости. Исходными данными для построения визуальной модели являются: значения объемов продаж, цен продаж, ставок налогов. Доопределение геометрической модели исходных данных до модели пространственной сцены связано с нанесением на оси диапазонов изменения анализируемых параметров.
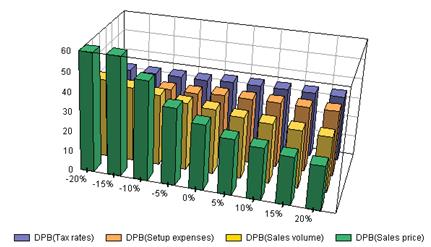
Рис. 46.Визуализация анализа чувствительности DPB в формате пространственной сцены.
Рассмотрим также пример визуализации пространственной сцены результатов моделирования рисков проекта при помощи метода Монте-Карло. Исходными данными для визуализации является разброс значений неопределенных факторов, являющихся источниками риска при реализации проекта, такими как объем инвестиций, затраты на материалы и комплектующие, объем и цена продаж продукции. На рис. 47 представлена визуальная модель метода Монте-Карло в виде пространственной сцены. Доопределение геометрической модели до модели пространственной сцены связано с заданием левой и правой границ разброса чистого приведенного дохода (по оси абсцисс рис. 47), а также статистических частот их получения, отложенных по оси ординат.
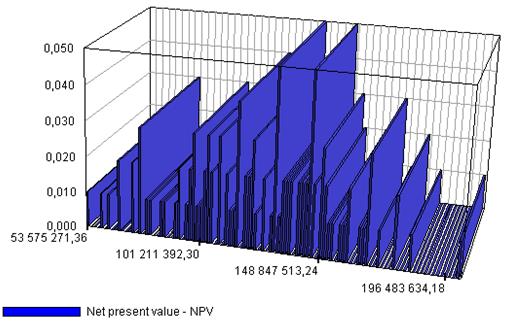
Рис. 47. Визуализация пространственной сцены на основе метода Монте-Карло.
Когнитивная визуализация результатов моделирования рисков с использованием метода статистических испытаний позволяет проводить наглядный визуальный анализ бизнес-ситуации, связанной с рисками, поскольку унимодальность кривой позволяет судить о невысоком уровне риска.
Авторами был разработан макет системы оценки и анализа бизнес-проектов [23] на основе Web-ориентированного подхода. Ознакомиться с интерактивной версией автоматизированной Web-ориентированной системы оценки бизнес-проектов можно, нажав на ссылку. Программная система выполняет функции ввода информации о бизнес-проектах в формате опросника или анкеты заявителя, также реализованы функции выполнения экспертной оценки проектов, опираясь на модели принятия решений, в том числе, и на основе методов визуального анализа показателей эффективности проектной деятельности.
9. Анализ рисков с применением методов визуальной аналитики
Методы визуальной бизнес-аналитики интенсивно применяются также в задачах анализа и оценки рисков реализации проектов. Как правило, высокими рисками обладают проекты из сферы НИОКР или R&D, обладающие неопределенностями результатов выполняемых работ и структуры проекта. В некоторых случаях операции могут быть не выполнены ни одного раза и при этом результат будет получен, а также некоторые работы могут быть реализованы более одного раза (многократно за счет переделок, корректировок и т.п.). Таким образом, в визуальную модель графической структуры проекта необходимо вносить изменения, расширяющие ее операционность в плане учета рисков и неопределенности. Известны сетевые модели проекта, называемые моделями GERT (Graphical Evaluation and Review Technique) [3,7], позволяющие учитывать неопределенность в параметрах работ и событий, в также в структуре комплекса операций [6].
Стохастическая сеть – сетевая модель, которая может быть выполнена только при реализации некоторого подмножества дуг [3,7]. Узлы сети можно интерпретировать как состояния системы, дуги - как переходы из одного состояния в другое [4,6]. Каждый внутренний узел стохастической сети выполняет две логических функции. Одна из которых реализует логическую функцию входа в узел, а другая – логическую функцию выхода.
Входная функция – определяет условие, при котором узел может быть выполнен.
Выходная функция – определяет совокупность условий, связанных с результатом выполнения узла. Т.е. выходная функция определяет: должны ли выполняться все операции, которым данным узел предшествует, или только одна из них [6,7] .
Типы входных функций:
· «И». Узел выполняется, если выполнены все дуги, входящие в него.
· «ИЛИ». Узел выполняется, если выполнена любая дуга, входящая в него.
· «Исключающее ИЛИ». Узел выполняется, если выполнена ровно одна из входящих в него дуг.
Типы выходных функций:
· «И». Все дуги, выходящие из данного события, выполняются. Это детерминированный выход.
· «ИЛИ». Как минимум одна дуга, выходящая из вершины, выполняется.
· «Исключающее ИЛИ». Если узел выполняется, то будет выполнена ровно одна исходящая дуга.
На рис. 48 представлена визуальная модель GERT-сети, в вершинах которой расположены события с функцией входа "XOR" - обозначение "|<", и функцией выхода "OR" - обозначение ">", представляющая собой широкий класс сетевых моделей, имеющих прикладное значение в анализе рисков и неопределенности.
Исходными данными для построения являются типы вершин сетевой модели, определяемые в символьно-числовом формате. Доопределение геометрической модели до модели плоского рисунка связано с заданием вероятностей выполнения операций или свершения событий сетевой модели.
Визуальный анализ проекта, представленного сетевой моделью типа GERT, можно выполнять при помощи специального дерева вариантов, позволяющего выделить успешные и неуспешные исходы, за счет удачной геометризации исходных данных.
На рис. 49 представлена визуальная модель проекта с неопределенной структурой. Доопределение геометрической модели проекта до модели плоского рисунка связано с заданием вероятностей выполнения работ, т.е. над дугам указаны веса в виде вероятностей (например, P01 - условная вероятность выполнения работы 01 при условии успешного завершения предшествующего события).
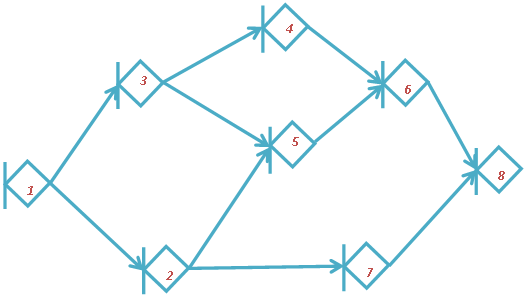
Рис. 48. Визуализация проекта с неопределенной структурой (плоский рисунок).
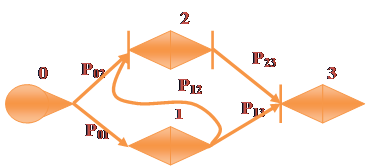
Рис. 49. Визуализация модели проекта в виде плоского рисунка.
Количество возможных комбинаций реализации проекта оценивается как 25=32, однако, не все из них логически реализуемы. Дерево вариантов, представленное на рис. 50, является когнитивной визуальной моделью и отображает множество успешных и неуспешных исходов проекта, используя в качестве исходных данных для визуализации модель на рис. 49. Когнитивная визуальная модель проекта в форме дерева вариантов позволяет существенно сократить перебор и решить визуально задачу идентификации рисков.
На рис. 50 геометрическая модель исходных данных доопределена до плоского рисунка путем отображения в вершинах дерева работ: в случае успешного выполнения без подчеркивания, в противном случае с подчеркиванием. Листья дерева помечены буквами N - в случае негативного варианта, S - в случае положительного исхода.
Методом визуализации дерева вариантов оказывается возможным построить функцию распределения вероятностей исходов проекта, вычислить математическое ожидание длительности критического пути и критической стоимости.
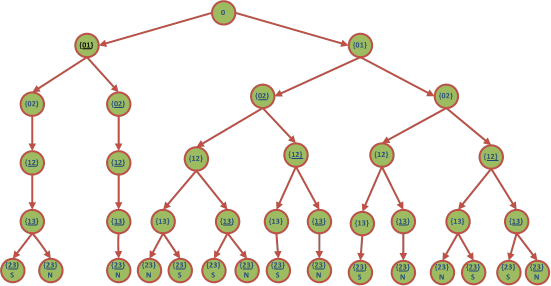
Рис. 50. Визуальная модель плоского рисунка в виде дерева вариантов проекта.
Рассмотрим визуальные модели в формате сетевой модели вида GERT рис. 51, которые возможно построить с применением инструментального средства анализа проектов с неопределенной структурой. Визуальные модели доопределены в виде плоских рисунков в формате отображения сетевых моделей типа GERT с указанием вероятностных числовых параметров операций, параметров математического ожидания продолжительности и дисперсии продолжительности работы [14,21].
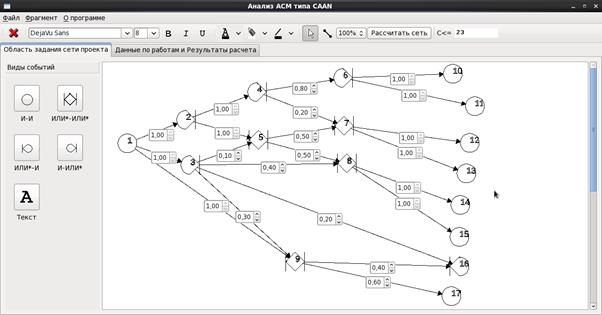
Рис. 51. Интерфейс программного средства [14] создания визуальной модели плоского рисунка в форме сетевой модели с неопределенной структурой.
При помощи визуального анализа проекта в формате плоского рисунка за счет геометризации исходных данных [6] удается выделить наиболее вероятные частичные варианты реализации [7], выделенные на рис. 52 синим цветом.
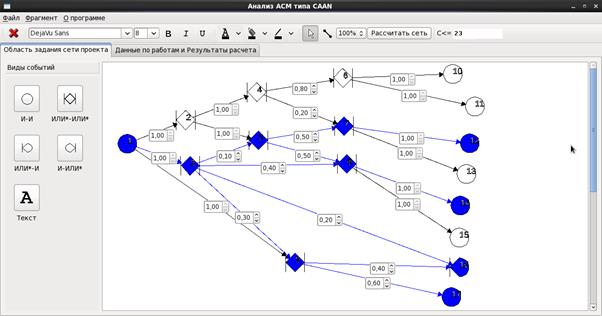
Рис. 52. Визуальная сетевая модель [14], доопределенная до плоского рисунка.
Ознакомиться с инструментальным программным средством построения визуальных моделей проектов с неопределенной структурой типа GERT можно проследовав по следующей ссылке. Программный продукт выполняет функции визуального графического анализа сетевой модели типа GERT на основе числовых исходных данных и позволяет получить возможные варианты реализации проекта с учетом наиболее вероятных исходов.
Разработанные авторами пакеты прикладных программ [14, 21] реализуют алгоритмы графического анализа вариантов, принимая во внимание вероятностные параметры комплекса работ, стоимостные и ресурсные характеристики операций. Следует отметить, что программные средства, направленные на визуальное решение задач подобного класса, позволяют оценить риски проектов, что особенно актуально для наукоемких проектов НИОКР (R&D - projects) с недетерминированными вариантами исходов.
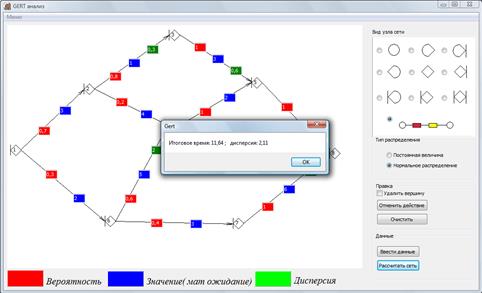
Рис. 53. Визуальная модель, создаваемая при помощи пакета прикладных программ [21] GERT-анализа.
Ознакомиться с интерактивным макетом программного средства можно проследовав по следующей ссылке. Программный продукт реализует функции ввода и визуализации сетевой модели комплекса работ проекта как для детерминированного, так и для стохастического вариантов, выполняя оценку продолжительности выполнения проекта при помощи метода PERT или GERT.
10. Заключение
В статье рассмотрены вопросы применения визуальных моделей проектного менеджмента для решения задач принятия решений с использованием набора инструментальных программных средств [13,14, 19, 20, 21, 22, 23], разработанных авторами.
Оказывается сложным дать единое определение графической модели проекта в связи с разнообразием графических методов, используемых для визуализации проектной информации [15]. Однако авторы поставили себе целью очертить возможный набор визуальных моделей, используемых для решения управленческих задач из сферы проектного менеджмента.
Представлены задачи проектного менеджмента, признанные в качестве международного стандарта, в статье рассмотрены визуальные модели проектных структур, а именно сетевые и линейные модели. Приведен подход к решению задач управления проектами при помощи методов визуализации и геометризации исходных данных.
Рассмотрены визуальные модели таких структурных преобразований комплекса работ проекта, как объединение, укрупнение, разукрупнение, на основе методов теории графов.
Методы визуальной аналитики были использованы при графическом моделировании числовых параметров операций и всего комплекса работ в целом, особенно при визуализации функций распределения случайных величин.
Средства бизнес-графики были применены при визуализации задач календарного ресурсного планирования, с использованием графических способов учета ресурсных ограничений. В качестве визуальных моделей применялись линейная и ресурсная диаграммы комплекса работ.
Визуализация бизнес-данных и методы визуальной аналитики были использованы для решения задач оперативного планирования и управления комплексом работ проекта на основе метода освоенного объема. На основе визуальных моделей показателей затрат и времени выполнения операций оказалось возможным использование когнитивных графических моделей принятия решений.
Отмечены также мощные возможности научной геометрической визуализации исходных данных при решении задач инвестиционно-финансового планирования проекта. Комплекс графических методов подразумевает применение визуальных моделей в формате пространственных сцен, особенно при моделировании рисков и статистическом анализе проектов.
Методы визуальной аналитики и бизнес-графики были использованы при решении задач риск-анализа проектов, используя сетевые модели комплексов работ специальной структуры, дополненные неопределенностью и вероятностными параметрами операций.
Наряду с существующими аналитическими и геометрическими моделями и методами предлагается применение инструментальных средств и моделей визуализации бизнес-данных, основанных на собственных разработках авторов.
Отмечая высокий потенциал применения инструментальных средств бизнес-графики в такой предметной области как управление проектами, авторы предполагают и дальнейшее интенсивное развитие бизнес-визуализации при решении проблем бизнеса и промышленности в корпоративных масштабах, опираясь на мощные вычислительные графические процессоры. Данная задача становится весьма актуальной в связи с все возрастающими размерами проектов и размерностью исходных данных для построения визуальных моделей проблемных ситуаций.
В тоже время, существующие системы управления проектами не в полной мере решают задачи визуализации проектной информации, особенно это касается структурных моделей проектов и операций над ними, визуальных моделей задач ресурсного планирования проектов, сетевых моделей с неопределенной структурой и вероятностными параметрами.
Список литературы
1. Пилюгин В.В. Компьютерная геометрия и визуализация. М.:МИФИ, 2005.- с.120
2. Колычев В.Д., Румянцев В.П. Об особенностях математических моделей полно-го жизненного цикла инновационных изделий. Интеграл. 2012. № 1. С. 50-51.
3. Математические основы управления проектами: Учебн. пособие / С.А. Баркалов, В.И. Воропаев, Г.И. Секлетова и др. Под. ред. В.Н. Буркова. М.: Высшая школа, 2005
4. Румянцев В.П., Низаметдинов Ш.У. Проектирование сетевых моделей плани-рования и управления. М.: МИФИ, 1987, 137 c..
5. Румянцев В.П., Низаметдинов Ш.У. Автоматизация календарного планирова-ния комплексов работ. - М., МИФИ 1989, 125 c.
6. Phillips D.T., Garsia-Diaz A. Fundamentals of network analysis. 1981. Prentice-Hall, Inc. Englewood Cliffs. New Jersy, pp:456.
7. Колычев В.Д. Планирование и анализ инновационных проектов с использованием сетевых моделей с альтернативной структурой. Естественные и технические науки. Том.1., 2012. стр: 278-284
8. 12207-2008 - ISO/IEC/IEEE Standard for Systems and Software Engineering - Software Life Cycle Processes. Date views 02.04.2014 //ieeexplore.ieee.org/servlet/opac?punumber=4475822.
9. 15288-2008 - Systems and software engineering System life cycle processes. Date views 02.04.2014 //ieeexplore.ieee.org/servlet/opac?punumber=6093921.
10. Behrens W., Hawranek P.M.1991. Manual for the preparation of industrial feasibility studies. Newly revised and expanded edition. United Nations Industrial Development organization. Vienna. 1991. pp: 386.
11. A Guide to the Project Management Body of Knowledge (PMBOK Guide) — Fourth Edition USA, Project Management Institute, 2008.
12. Касьянов В., Касьянова Е. Визуализация информации на основе графовых моделей. Научная визуализация. 2014. Том 6. Выпуск. 1. стр. 21-40
13. Колычев В.Д. " Пакет анализа и оптимизации проектов по временным, стоимостным и ресурсным параметрам (Project Optimization Software Tool )". Свидетельство о регистрации программы для ЭВМ №2011613606, 10.05.2011.
14. Колычев В.Д. "Программная система анализа и планирования проектов с альтернативной структурой". Свидетельство о регистрации программы для ЭВМ №2012613420, 11.04.2012.
15. Колычев В.Д. Программная реализация визуальных моделей управления проектами. Современные проблемы науки и образования. 2014. № 3. http://www.science-education.ru/117-13219.
16. Колычев В.Д., Румянцев В.П. Задача укрупнения сетевой модели жизненного цикла проекта. Сборник научных статей по итогам международной заочной научно-практической конференции «Инновационные преобразования, приоритетные направления и тенденции развития в экономике, проектном менеджменте». НОУ ДПО «Санкт-Петербургский институт проектного менеджмента» СПБ. 29-30 апреля 2014., стр. 80-81.
17. Project Expert User Guide. Pro Invest Consulting. 2008, Moscow, pp:456.
18. Kolychev V.D., Rumyantsev V.P. Procedure of equivalent enlargement and aggregation of product's life-cycle network model. American Journal of Applied Sciences. 2014
19. Колычев В.Д. "Программная система календарного ресурсного планирования инновационных проектов (TSR Planner)". Свидетельство о государственной регистрации программы для ЭВМ № 2014611524, 19.05.2014.
20. Колычев В.Д. "Программная система анализа жизненного цикла инновационной продукции". Свидетельство о государственной регистрации программы для ЭВМ № 2014613572, 28.03.2014.
21. Колычев В.Д. "Программная система анализа рисков инновационных проектов «ProRisk Analysis». Свидетельство о государственной регистрации программы для ЭВМ №2011615795, 25.07.2011 г.
22. Колычев В.Д. «Программная система решения задач сетевой оптимизации (NetOptim)». Свидетельство о государственной регистрации программы для ЭВМ №2011613776, 16.05.2011 г.
23. Колычев В.Д. «Web-ориентированная система экспертизы инновационных проектов (ASOE Project)» Свидетельство о государственной регистрации программы для ЭВМ №2011613607, 10.05.2011 г.
24. Frank T. Anbari. The earned value analysis method: extensions and simplifications. 17-th global congress on project management. Moscow. 4-6 June 2003.
Visual models’ system of project management
Kolychev V.D., Rumyantsev V.P.
VDKolychev@mephi.ru, VPRumyantsev@mephi.ru
National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Russia
Abstract
This article describes the project management problems complex and according visual methods applied in order to solve them. A systematic approach to project management and complex objects visualization problem solving is proposed. The article considers the problem of business graphics as modern techniques of computational geometry and scientific visualization, that aims the formation of a geometric model of the project initial data. Methods of visual analytics became popular in recent years and are used as a basic approaches to solve problems in the project management area, to those practitioners pay a lot of attention. Application of visual and instrumental analysis, using original software developed by the authors is proposed. The technological sequence in order to obtain the project management problem visual solution for managers is given; moreover, recommendations for the use of visual analytics methods to determine the necessary intervention in the problem situation arising in the process of project management are given. Decision making software tools for the project management tasks based on graphical analysis of the problem situation and on formulating recommendations for the decision making person are presented in the paper. Visual models of structural and risk analysis, calendar, resources, investments and financial planning are presented.This work is the author's review of methods of visual analysis in the sphere of project management.
Keywords: Visual model of the project, Project management, Business graphics, Graphical representation, Geometrization of business data, Business intelligence, Visual analysis, Problem situation, Schedule, Project planning, Project schedule, Project Risk analysis
References
1. Pilyugin V.V. 2005. Computer geometry and visualization. Moscow, MEPhI, pp.120
2. Kolychev, V.D., Rumyantsev, V.P., 2012. About peculiarities of mathematical models of complete life cycle of innovation products. Integral, 1, pp: 50-51.
3. Barkalov, S.A., Voropajev, V.I. , Sekletova, G.I., 2005. Mathematical bases of project management. Study book. High school, Moscow. ISBN: 5060041336, pp: 356.
4. Rumyantsev, V.P., Nizametdinov, Sh.U., 1987. Net-work models design for planning and management. MEPHI, Moscow, pp: 152.
5. Rumyantsev, V.P., Nizametdinov, Sh.U., 1989. Automation of calendar scheduling of work packages. MEPHI, Moscow, pp: 137.
6. Phillips D.T., Garsia-Diaz A. Fundamentals of network analysis. 1981. Prentice-Hall, Inc. Englewood Cliffs. New Jersy, pp:456.
7. Kolychev, V.D., 2012. Planning and innovation pro-jects analysis using networks with alternative structure. Journal of natural and technical sciences, 1, pp: 278-284.
8. 12207-2008 - ISO/IEC/IEEE Standard for Systems and Software Engineering - Software Life Cycle Processes. Date views 02.04.2014 //ieeexplore.ieee.org/servlet/opac?punumber=4475822.
9. 15288-2008 - Systems and software engineering System life cycle processes. Date views 02.04.2014 //ieeexplore.ieee.org/servlet/opac?punumber=6093921.
10. Behrens W., Hawranek P.M.1991. Manual for the preparation of industrial feasibility studies. Newly revised and expanded edition. United Nations Industrial Development organization. Vienna. 1991. pp: 386.
11. A Guide to the Project Management Body of Knowledge (PMBOK Guide) — Fourth Edition USA, Project Management Institute, 2008.
12. V. Kasyanov, E. Kasyanova Information Visualization on the Base of Graph Models. Scientific visualization. Electronic journal. 2014. Volume 6. Edition. 1. pp. 21-40
13. Kolychev V.D. 2011. "Package analysis and optimization projects on time, cost and resource parameters (Project Optimization Software Tool)". The certificate on the state registration of the computer program. Federal institute of industrial property. # 2011613606, 10.05.2011.
14. Kolychev V.D. 2014. " Software system analysis and planning projects with an alternative structure". The certificate on the state registration of the computer program. Federal institute of industrial property. # 2012613420, 11.04.2012.
15. Kolychev V.D. 2014. Program realization of project management visual models. Journal of modern issues of science and education. # 3. Date views 14.06.2014. http: //www.science-education.ru/117-13219.
16. Kolychev V.D., Rumyantsev V.P. 2014. "The task of enlargement of the network model of the project life cycle". Collection of scientific articles on the results of international correspondence scientific-practical conference "Innovative transformation, priorities and development trends in the economy, project management". NOU DPO Saint Petersburg Institute of project management" SPB. 29-30 April 2014., pp. 80-81.
17. Project Expert User Guide. Pro Invest Consulting. 2008, Moscow, pp:456.
18. Kolychev V.D., Rumyantsev V.P. Procedure of equivalent enlargement and aggregation of product's life-cycle network model. Research Journal of Applied Sciences. in 2014(10) issue, October, 2014.
19. Kolychev V.D. 2014. "Program system for innovation projects time-resource scheduling (TSR Planner)". The certificate on the state registration of the computer program. Federal institute of industrial property. Moscow. # 2014611524, 19.05.2014.
20. Kolychev V.D. 2014. "Program system for life-cycle innovation product analysis". The certificate on the state registration of the computer program. Federal institute of industrial property. Moscow. # 2014613572, 28.03.2014.
21. Kolychev V.D. 2011. "Program system for innovation project risks analysis «ProRisk Analysis». The certificate on the state registration of the computer program. Federal institute of industrial property. Moscow. # 2011615795, 25.07.2011.
22. Kolychev V.D. 2011. «The software system to solving problems network optimization (NetOptim)». The certificate on the state registration of the computer program. Federal institute of industrial property. Moscow. # 2011613776, 16.05.2011.
23. Kolychev V.D. 2011. «Web-oriented system of innovative project exper-tise (ASOE Project)». The certificate on the state registration of the com-puter program. Federal institute of industrial property. Moscow. # 2011613607, 10.05.2011.
24. Frank T. Anbari. The earned value analysis method: extensions and simplifications. 17-th global congress on project management. Moscow. 4-6 June 2003.
25. Kolychev V.D., Prokhorov I.V. Application of road mapping for hi-tech projects commercialization in corporate innovative entrepreneurship. Ecology, Environment and Conservation. in 2014(4) issue, December, 2014.