Визуализация
звездного неба
на имитационном стенде
Ю. Кулябичев, С. Пивторацкая
Национальный исследовательский ядерный университет «МИФИ», Москва, Россия
ypkulyabichev@mephi.ru, moeimechko@yandex.ru
Оглавление
2. Программный комплекс выделения и классификации звезд
4. Испытания программного комплекса выделения и классификации звезд на имитационном стенде
4.1. Перерасчет центра кадра участка звездного неба
4.2. Оценка погрешностей имитационного стенда
4.3. Результаты испытаний программного комплекса
Аннотация
Приведено описание программного комплекса выделения и классификации звезд, методов и алгоритмов распознавания образов, использующихся в нем. Изложены детали применения программного комплекса для определения высокоточной ориентации малого космического аппарата по участку звездного неба.
Рассмотрен способ визуализации звездного неба с помощью имитационного стенда «Системы высокоточной ориентации малого космического аппарата» для тестирования программного комплекса. Описаны технические характеристики имитационного стенда, а также входящих в него программных и технических средств научной визуализации звездного неба.
Приведены результаты тестирования программного комплекса посредством визуализации звездного неба на созданном имитационном стенде.
Ключевые слова: высокоточная ориентация, распознавание образов, научная визуализация, имитационный стенд, программный комплекс, звездное небо, классификация звезд, "опорная" звезда, "соседи".
В мире ежегодно запускается более ста спутников телекоммуникационного, метеорологического, навигационного, исследовательского и иного назначения [1], на каждый из которых устанавливается система определения ориентации в космическом пространстве. В настоящее время в мире наблюдается возрастающий интерес к созданию малых космических аппаратов с меньшей массой и состоящих из более дешевых компонент. Уменьшение массы достигается за счет меньшего энергопотребления и использования новых легких и прочных материалов. Однако, несмотря на необходимость уменьшения массы спутника, требуется обеспечивать достаточное качество ориентации малого космического аппарата (МКА).
Для создания конкурентоспособного товара на мировом рынке звездных датчиков требуется разработка и алгоритмов распознавания участков звездного неба, поскольку звездные датчики обычно функционируют во внешней среде, содержащей множество неблагоприятных факторов. Информация, содержащаяся в источниках со свободным доступом, часто является поверхностной, а также существует отличия в изготовляемых разными фирмами приборах, поэтому часто не представляется возможным спроецировать известные результаты тестирования на алгоритмы разрабатываемого звездного датчика. Следовательно, наилучшим путем оказывается проведение предварительных испытаний создаваемых алгоритмов.
Для испытаний был создан имитационный стенд «Системы высокоточной ориентации малого космического аппарата» позволяющий визуализировать звездное небо на мониторе по изображениям с камеры, содержащим участки звездного неба. На нем были отработаны и предложенная методика и алгоритмы распознавания образов. В качестве образа использован упорядоченный список звезд на текущем участке звездного неба.
На стенде проводилась визуализация звездного неба с возможностью имитации вращения звездной сферы относительно оптической оси, шумов, вносимых условиями открытого космоса, возможностью указания количества видимых звезд.
2. Программный комплекс выделения и классификации звезд
Программный комплекс выделения и классификации звезд (ПКВиКЗ) разработан в качестве эффективного средства высокоточной ориентации малого космического аппарата (МКА) по участкам звездного неба [2, 3]. ПКВиКЗ осуществляет алгоритмическую обработку зарегистрированных видеокамерой кадров, на которых присутствуют звезды.
Движение МКА во многом определяется той миссией, для которой он предназначен. В зависимости от назначения космические аппараты могут двигаться по существенно отличающимся друг от друга траекториям. По этому признаку выделяют две основные группы МКА: в первую входят искусственные спутники Земли, вторая группа включает МКА, предназначенные для полета и проведения исследований в дальнем космосе.
Основные характеристики любого небесного тела, такие как векторы положения и скорости, а вычисляются косвенно по сферическим координатам объекта, скоростям изменения этих координат и другим параметрам. Поэтому большое значение для определения ориентации МКА имеет определение сферических координат участка звездного неба в независимой от МКА системе координат с помощью закрепленного на нем звездного датчика.
ПКВиКЗ определяет ориентацию МКА по участкам звездного неба путем нахождения сферических координат центра заданного участка неба на основе цифровых изображений, полученных цифровой камерой.
Способ определения координат центра участка неба состоит в следующем. Пусть имеется цифровое полутоновое изображение участка звездного неба, на котором находится образ – упорядоченный список звёзд на данном участке неба. Предполагается, что все звезды в данном области нам известны, т.е. содержатся в звездной базе SAO [4], взятой за основу для расчетов. По разработанной методике распознавания образов разнотипных объектов находится максимально соответствующий списку набор звезд из звездной базы ссылок. После этого каждой звезде из списка сопоставляются ее сферические координаты (прямое восхождение a и склонение d). Далее на основе найденных координат определяются сферические координаты центра изображения по методу подобных треугольников, где двумя вершинами треугольника выбираются две распознанные звезды с известными координатами, а третьей вершиной – центр изображения.
Исходя из изложенного следует, что с помощью ПКВиКЗ оказывается возможным определять инерциальную ориентацию МКА как в околоземном космическом пространстве, так и за его пределами.
2.1. Методы и алгоритмы распознавания образов на основе структурного подхода с ипользованием унифицированных локальных признаков
Распознавание участка звездного неба осуществляется разработанными авторами методами и алгоритмами распознавания образов объектов на цифровых изображениях, которые основаны на структурном подходе с использованием унифицированных локальных признаков (УЛП) объектов [5, 6].
Авторами предлагается объединить два способа выделения признаков образа – экспертом и автоматически, использующихся на разных этапах формирования образа объекта. Участие эксперта желательно для максимально точной идентификации образов разнообразных объектов, таких как участки звездного неба, изображения лиц и других.
Структурный подход состоит в описании образов в терминах их
частей и отношений между ними. Образ объекта представляется в виде совокупности
выделяемых экспертом более простых образов (подобразов) ![]() , xi
– i-ый подобраз (см. рис. 1). Далее каждый из подобразов повторно
разделяется на другие подобразы:
, xi
– i-ый подобраз (см. рис. 1). Далее каждый из подобразов повторно
разделяется на другие подобразы: ![]() . Такое разделение выполняется до тех пор, пока не
останутся подобразы, которые нельзя разделить. Из них выделяются локальные
элементарные признаки, соответствующие исходному образу.
. Такое разделение выполняется до тех пор, пока не
останутся подобразы, которые нельзя разделить. Из них выделяются локальные
элементарные признаки, соответствующие исходному образу.
Для автоматического распознавания используется набор из
всех относящихся к образу x элементарных признаков ![]() , где fj
– j-ый локальный элементарный признак.
, где fj
– j-ый локальный элементарный признак.
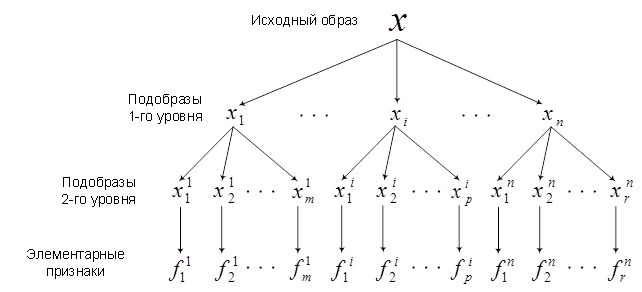
Рис. 1. Иерархическая структура подобразов для исходного образа
Последовательное нахождение всех элементарных признаков из соответствующего искомому образу набора, выполненное автоматически, позволяет сделать заключение о присутствии этого образа на анализируемом изображении. Для структурного подхода характерны следующие особенности.
Во-первых, при таком подходе эксперту во время выделения из образа значимых по его мнению подобразов не требуется учитывать, как будет происходить их автоматизированное обнаружение на изображении. Это обеспечивает методика распознавания, которая с помощью локальных элементарных признаков формирует удобное для автоматизированного анализа представление, соответствующее каждому подобразу, выделенному экспертом.
Во-вторых, представление образа как структуры подобразов повышает эффективность процесса обнаружения соответствующего ему объекта на цифровом изображении.
В-третьих, большому количеству образов соответствует небольшое число повторяющихся элементарных признаков.
Элементарный признак – это часть изображения, которая может быть отделена от соседних частей с ней каким-либо способом. Он обладает свойством локальности и, как правило, описывает изменения одного или нескольких свойств изображения в некоторой окрестности. К свойствам изображения причисляют интенсивность, текстуру и цвет. В случае анализа монохромных изображений цвет исключается из рассмотрения. В качестве элементарных признаков fj могут выступать: области интереса или кластеры; границы; точки интереса или углы.
Каждому элементарному признаку соответствует свой метод обнаружения (детектор). Для распознавания образа к предположительно содержащему его изображению последовательно применяется метод обнаружения каждого из сопоставленных с образом элементарных признаков. Если большинство этих признаков найдено на изображении, образ считается распознанным.
Выбор наиболее эффективных детекторов признаков произведен с использованием таких оценок, как оценка повторяемости и информационное содержание.
Для областей, определяемых как элементарные признаки, проводится измерение их параметров, свойств, на основе которых формируются описания (дескрипторы) простых признаков.
Для осуществления сравнения разных типов локальных признаков автором предложено их унифицировать и поместить в обобщенную базу признаков. Проблематика задачи заключается в том, что найденные локальные признаки одного типа обычно описаны с помощью соответствующего этому типу дескриптора, и дескрипторы отличаются не только способом определения, но и размерностью. Для эффективного поиска схожих признаков в обобщенной базе локальных элементарных признаков, их сжимают в компактные битовые вектора единообразного формата.
В данном исследовании дескрипторы трех вышеперечисленных типов признаков объединены в предложенный бинарный дескриптор. На хранение признака каждого типа выделено по 64 бита. Таким образом, бинарное представление дескриптора занимает 192 бита.
Сравнение анализируемого образа с образами идентифицируемых объектов на изображениях авторами предлагается осуществлять посредством решающего правила, применяемого к сгруппированным определенным образом данным из базы унифицированных локальных признаков (базы УЛП) разнотипных объектов. Качество распознавания напрямую зависит от объема выборки образов идентифицируемых объектов в базе УЛП. Поэтому особое значение приобретает компактное хранение данных в составленной базе признаков и выполнение быстрого нахождения в ней признаков объектов.
Быстрый поиск признаков по базе УЛП осуществляется в два этапа:
1. Хэширование базы УЛП и «грубый» поиск схожих признаков в базе УЛП, включающий в себя сравнение признаков объекта с унифицированными локальными признаками, являющимися центрами кластеров признаков в базе данных, и сопоставление с каждым признаком одного из кластеров.
2. Точный поиск схожих признаков в базе УЛП, реализующий сравнение признаков объекта с признаками из сопоставленных с ними кластеров.
Для проведения быстрого поиска признаков, принадлежащих распознаваемым образам объектов, по большой базе УЛП авторами используется хэширование, а именно представление элементов базы в кодированном бинарном виде. Такое представление позволяет применять для быстрого сравнения признаков между собой расстояние Хэмминга, расчет которого отличается скоростью вычисления по сравнению с другими способами сравнения.
Для осуществления хэширования данных в базе УЛП из-за неоднородности распределения унифицированных локальных признаков объектов в пространстве локальных признаков Rn размерности n введена предварительная кластеризация базы. При кластеризации похожие локальные признаки оказываются сгруппированными в один кластер, центром которого является отдельный усредненный признак – унифицированный локальный признак.
В данном исследовании для кластеризации базы УЛП применен метод k‑средних.
Количество кластеров для разделения k задаётся предварительно. В предлагаемой методике распознавания образов с использованием УЛП количество кластеров рассчитано как
![]() , (1)
, (1)
где ![]() – число кластеров
исследуемых образов,
– число кластеров
исследуемых образов, ![]() –
кластер не-образов,
–
кластер не-образов, ![]() .
.
Для первоначального выбора центров кластеров используется наиболее эффективный в настоящее время алгоритм k-means++ предложенный Артуром Д. и Вассильвицким С. [7], с некоторыми модификациями.
Поиск центров кластеров выполнен путем минимизации суммарного расстояния от каждого элемента кластера до ближайшего выбранного центра. Так, для центра классификации выполняется выражение:
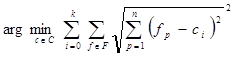 , (2)
, (2)
где f –
локальный признак, с – центр кластера, ![]() – p-ая и i-ая компоненты локального признака и кластера
соответственно, F – множество локальных признаков, C –
множество центров кластеров, n – общее число компонент локального признака.
– p-ая и i-ая компоненты локального признака и кластера
соответственно, F – множество локальных признаков, C –
множество центров кластеров, n – общее число компонент локального признака.
Количество бит Nb, выделяемых на хеш центра кластера, зависит от количества кластеров k как
Nb = 2s ³ k, (3)
где s – вычисляемое целое значение.
Хеширование осуществлено таким образом, чтобы выполнялось условие: для центров кластеров, между которыми евклидово расстояние максимально, было также минимально и расстояние Хэмминга, вычисленное для хеш-значений.
В предлагаемой методике распознавания образов объектов с использованием УЛП для точного сравнения локальных признаков использовано эвристически найденное соотношение kближ.соседей, являющееся отношением расстояния до ближайшего соседа d1 к расстоянию до второго ближайшего соседа d2:
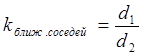 .
(4)
.
(4)
2.2. Применение методов и алгоритмов распознавания образов для определения высокоточной ориентации малого космического аппарата по участку звездного неба
Входным данным для определения ориентации является цифровое изображение участка звездного неба (рис. 2а). На этом изображении с помощью структурного подхода ищутся соответствующие звездам элементарные признаки для того, чтобы найти координаты выделенных звезд на изображении. Примеры находимых звезд приведены на рис. 2б.
Рис 2. a) Изображение
участка звездного неба; b) изображения выделенных на нем звезд. Функция, описывающая двумерное распределение освещенности
на изображении светящейся точки, называется функцией рассеяния точки
(ФРТ) [8]. Если распределение освещённости в изображении звезды
описывается круговой гауссовой поверхностью, то функция рассеяния точки: где x,
y – координаты звезды на изображении, x0, y0 – координаты
центра изображения звезды, а – характеристика интенсивности изображения,
s – характеристика размытости изображения. Тогда
освещенность заданной точки на плоскости изображения – это билинейная свертка,
ядро которой представляет собой распределение Гаусса: где I(x0,y0) – функция
исходной яркости звезды, h(x,y) – ФРТ, см. (5). Для определения ФРТ необходимо
найти параметры x0, y0, a, s. Освещенность изображения для одного пикселя будет иметь
вид: где i – номер
пикселя, xi, yi – координаты одного из углов пикселя, Dx, Dy – размеры пикселя по
осям x и y. Решив методом наименьших квадратов систему из уравнений
(7), построенных для всех пикселей звезды, можно получить неизвестные параметры
функции рассеяния точки. Несмотря на то, что в большинстве случаев для
широкополосного излучения фокусируемая объективом точка может быть
аппроксимирована функцией Гаусса (рис. 3а), ФРТ иногда искажается в результате
оптических аберраций, присущих конкретному объективу (рис. 3б). Рис. 3. а) Функция
рассеяния точки для объективов В таком случае для предварительного нахождения зашумленных
малых светлых областей, близких по форме кругу, на основе K
наблюдений светящейся точки строится фильтр требуемого размера, подобный ФРТ.
Применение этого фильтра в качестве ядра билинейной свертки (6) к каждому
пикселю найденных областей на цифровом изображении гарантирует устранение шума
и максимальное качество предварительного обнаружения малых круговых областей. В разработанном авторами ПКВиКЗ вид функции рассеяния точки
определялся по изображениям нескольким достаточно интенсивных объектов – звезд
2–4 звездной величины. Данный интервал был выбран, поскольку в случае
использования звезд с величиной, большей 4, заметен эффект «растекания» заряда
на соседние пиксели в точках, близких к центру звезды, из-за которого вид ФРТ
будет искажен. Для звезд с величиной слабее 2 ФРТ будет иметь слишком мало
пересечений с границами засвечиваемых пикселей области и, как следствие, недостаточно
точек для ее точной аппроксимации. После выбора наиболее «правильных» звезд производится
усреднение полученных значений интенсивности (значения ФРТ) с целью
формирования фильтра с наилучшей ФРТ. Трехмерная визуализация результирующей
ФРТ представлена на рис. 4. Рис. 4. Визуализация
результирующей функции рассеяния точки а) общий вид; б) вид сверху. В качестве каталога звезд, на основе которого строится база
УЛП для распознавания звезд на заданном участке звездного неба – звездная
база ссылок (ЗБС), используемая при высокоточной ориентации малого
космического аппарата, была выбрана звездная база SAO [4]. Из нее была
извлечена и преобразована соответствующая звездам информация, такая как номер
звезды в базе, прямое восхождение, склонение и видимая звездная величина. Из
базы выбирались звезды с 0 по 7 звездную величину включительно. При этом общее
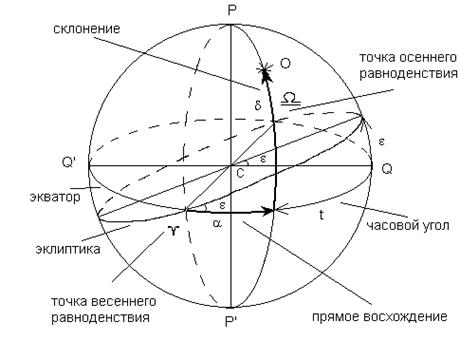
количество звезд составило 15 914 звезд. При распознавании звездного неба использовалась вторая
экваториальная система координат [9] (рис. 5). Основной плоскостью в ней
является плоскость небесного экватора, а началом отсчета - точка весеннего
равноденствия. Первой координатой является склонение d (declination) - это угловое расстояние от небесного экватора до центра
наблюдаемого участка неба, отсчитываемое по кругу склонения. Склонение
изменяется в пределах от -90° до 90°, причем участок неба с d>0
находится к северу от экватора, а с d<0 – к югу от него. Второй координатой, прямым восхождением a (right ascension), является дуга небесного экватора от точки весеннего
равноденствия ¡ до круга склонения центра наблюдаемого участка неба,
отсчитываемая против часовой стрелки. Она изменяется в пределах от 0° до 360° в
градусной мере или от 0h до 24h в часовой мере (360° соответствует 24h, 1h – 15°,
1m – 15', 1s –15"). Рис. 5. Вторая
экваториальная система координат. При составлении ЗБС из звездной базы SAO сначала
извлекаются выборки звезд, сформированные по принципу «“опорная” звезда – “соседи”»,
при этом количество соседних звезд ограничено 32 звездами при угле обзора 8°. Для каждой «соседней» звезды вычисляются расстояние от
«опорной» звезды (в радианах) drad : и угол
наклона этого расстояния, отсчитываемый против часовой стрелки α (рис. 5): В каждой ячейке ЗБС записываются следующие характеристики
опорной звезды: - звездная величина звезды; - прямое восхождение звезды; - склонение звезды; - максимальное число соседей; - искомое число соседей; - указатели на номера ячеек, соответствующим соседям; - список расстояний до соседей; - список углов наклона радиус-векторов от опорной
звезды до соседей; - номер в звездной базе SAO. Такой принцип позволяет сформировать выборки для всех звезд
на звездной сфере при выбранной предельной звездной величине. Выбор оптимальной звездной величины Оптимальная звездная величина была выбрана на основе
анализа статистики по количества «пустых» зон, возникающих при использовании
различного задаваемого количества звезд при заданной камерой области обзора –
8°. Для этого звездная сфера была разделена на перекрывающиеся зоны размером 4°×4°
с шагом 2° так, что общее количество зон составило 10588. Статистика перекрытия
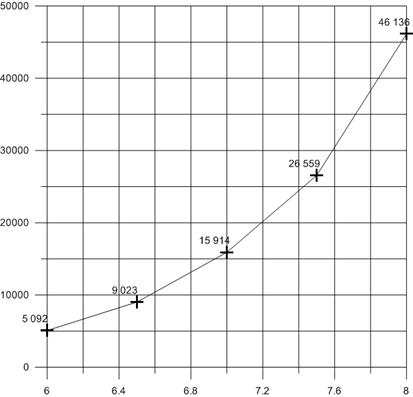
зон представлена в таблице 1. По ней были составлены графики (рис. 6, 7),
показывающие, что наилучшее соотношение количества звезд и процента «пустых»
зон – при предельной звездной величине 7,0. Таблица 1. Статистика перекрытия зон Макс. звездная величина Общее количество звезд Процент «пустых» зон, % Макс. количество «соседей» 6,0 5 092 10,72 29 6,5 9 023 0,85 47 7,0 15 914 0,028 76 7,5 26 559 0 123 8,0 46 136 0 206 Рис. 6. График
изменения общего числа звезд в Рис. 7. График
изменения числа «пустых» зон в Если обучающая выборка содержат шумовые выбросы, они будут
отрицательно влиять на качество построения разделяющей гиперплоскости. Этот
недостаток исключается при помощи коррекции входных данных привлеченными
экспертами. Определение сферических координат объектов В результате предыдущих вычислений имеются положения
объектов в прямоугольной системе координат, связанной с ПЗС-матрицей. Для того
чтобы сопоставить эти координаты со сферическими координатами на небесной
сфере, необходимо найти сферические координаты звёзд в ЗБС, изображения которых
имеются в кадре. Процесс определения сферических координат звезд в кадре, с
использованием одной опорной звезды и определением расстояния и угла наклона
относительно опорной звезды для остальных звезд в кадре состоит в следующем. В качестве входных данных выступает систематизированный
список – набор координат звезд на кадре (набор центров светлых областей) с
приближенной оценкой их звездной величины по размеру области, а также ЗБС,
содержащая связки «опорная звезда – соседи» на всей области звездной сферы с
учетом заданного поля зрения камеры. Таким образом, для большинства звезд, изображения которых
есть в кадре, известны прямое восхождение asc, склонение dec,
звёздная величина, координаты x и y в декартовой системе координат, связанной с плоскостью
матрицы. Эти данные позволяют определить координаты ascc, decc центра изображения,2 координаты x, y
которого известны (рис. 8). Рис. 8. Определение
центра кадра при использовании найденных звезд В основе вычислений лежит формула расчета расстояния на
сфере. Тогда сферические координаты центра кадра можно рассчитать как где dist_koeff – коэффициент перевода пикселей в радианы, dist_P – расстояние от первой звезды до центра кадра, dist_P2 – расстояние от
второй звезды до центра кадра, dist_P3 – расстояние от
третьей звезды до центра кадра, rasc, dec– сферические координаты первой звезды (прямое восхождение,
склонение), rasc2, dec2 – сферические
координаты второй звезды, rasc3, dec3 – сферические
координаты третьей звезды, dec_f, rasc_f – сферические координаты центра кадра. 3. Визуализация звездного неба на
имитационном стенде «Системы высокоточной ориентации малого космического
аппарата» Имитационный стенд, необходимый для проведения
исследований, состоит из следующих компонентов: камера, монитор, компьютер,
непросвечивающий кожух, программы «Распознавание участка звездного неба» (РУЗН)
и «Имитатор звездного неба» (ИЗН) (рис. 9). Рис. 9. Конструкция
стенда «Системы высокоточной ориентации малого космического В качестве датчика видеонаблюдения стенда была выбрана
цифровая видеокамера «Видеоскан-205-USB» с объективом Navitar TV LENS c фокусным расстоянием
50 мм. Камера имеет отличающийся высокой чувствительностью фотоприемник
ПЗС (прибор с зарядовой связью) и АЦП (аналого-цифровой преобразователь),
имеющий на выходе максимально 12 бит/пиксель. На таком фотоприемнике
располагается множество светочувствительных элементов – пикселей, расположенных
в виде матрицы. В выбранной камере используется ПЗС‑матрица размером
1380*1040 пикселей. Используемый объектив имеет широкий угол обзора –
4° 37′. Для работы ПКВиКЗ необходимо задать входные данные, а
именно сферические координаты и предельную звездную величину в области зрения,
при этом проверяется наличие в каталоге программы звездной базы ссылок
(ЗБС). На экран цифрового монитора, с помощью программы ИЗН,
проецируется участок небесной сферы (см. рис. 10), соответствующий заданным в
программе координатам звездного неба, при этом
плоскость экрана монитора находится в
фокальной плоскости видеокамеры. Рис. 10. Проекция
сектора звездной сферы на плоскость изображения. При
задании параметров движения спутника происходит моделирование движения звезд
так, чтобы обеспечивалась необходимая скорость перемещения звездного неба,
соответствующая движению МКА по заданной
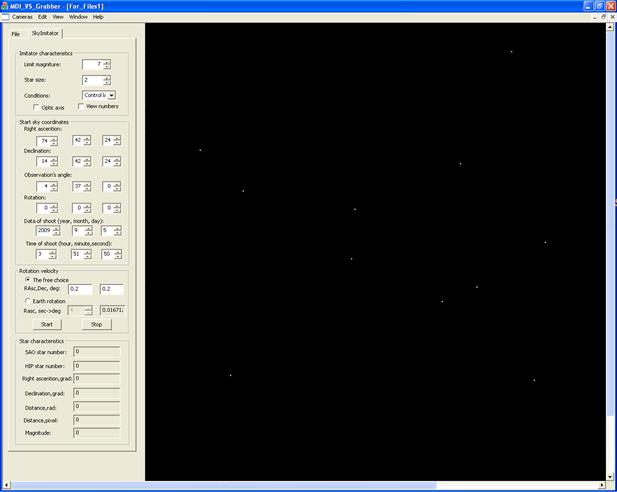
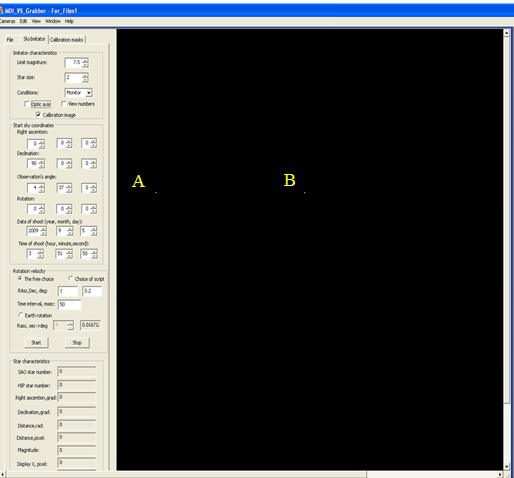
орбите. Интерфейс программы ИЗН, отображаемый на
мониторе оператора стенда, приведен на рис.11. Звезды представлены точками или
кругами серого цвета разной интенсивности. При проецировании на плоскость
монитора заданного участка небесной сферы звезды отображаются соответственно
угловым расстояниям между собой. Камера и монитор объединены в единый измерительный комплекс
ПКВиКЗ, управляемый компьютером. Это позволяет автоматизировать процесс сбора
наблюдений и их оценку. Рис. 11. Интерфейс
программы «Имитатор звездного неба». Для считывания изображения с монитора запускается программа
РУЗН, получающая и обрабатывающая изображение с камеры. В ней задается время
экспозиции, интервал между считыванием изображения, а также указывается имя
записываемого файла с изображениями. Кадр считанного участка звездного неба будет отображаться
на мониторе наблюдателя, как только он будет считан. На кадре выводятся 2
перпендикулярные линии с пересечением в центре кадра – расположение
рассчитываемой точки. По окончании наблюдений можно иметь доступ к записанному
набору изображений для участков звездного неба, также формируется файл с
информацией о распознанных звездах и определенных для каждого кадра
координатах наблюдавшегося участка звездного неба. Использование стенда в процессе
отработки звездного датчика позволяет корректировать ошибки в его программном
обеспечении, совершенствовать существующие алгоритмы и предлагать новые
решения. Точность отображения изображений
звезд на цифровом мониторе влияет на ошибки определения ориентации РУЗН на
стенде. На положение звезды на мониторе оказывают влияние его физические
свойства: отображение информации на мониторе в виде матрицы пикселей и ограничение
размеров этих пикселей. По данным причинам звезда отображается на мониторе в
виде пикселя или группы пикселей, максимально близких к заданному угловому
направлению на звезду. РУЗН определяет ориентацию путем сравнения угловых
расстояний между центрами звезд на наблюдаемом участке звездного неба и
координат в ЗБС, поэтому точность определения ориентации на стенде зависит от
угловых размеров пикселя цифрового монитора. Так, ошибки определения ориентации
в инерциальной системе координат на стенде составляют 20 угл.с. РУЗН устойчиво определяет
ориентацию, если ошибка рассогласования между априорной информацией, переданной
с ИЗН на звездный датчик, о положении системы координат МКА в инерциальной
системе координат и реальной ориентацией МКА в соответствии с положением
участка небесной сферы, представленного на экране цифрового монитора стенда, не
превышает 1°. Исследуя цифровое изображение, полученное с камеры, кроме
искомых объектов можно заметить также хаотично расположенные светлые и
темные пиксели, а также локальные изменения яркости фона. Рассмотрим основные составляющие шумов, создаваемых ПЗС, и
возможности их устранения [10]. Фотонный или
дробовый шум – шум, вызываемый эмиссией фотонов. Как дискретный процесс, он
описывается распределением Пуассона со значением среднеквадратического
отклонения Темновой ток – шум,
основной составляющей которого является термоэлектронная эмиссия, поэтому даже
неосвещенная матрица будет генерировать случайный сигнал. Поскольку
термоэлектронная эмиссия – дискретный процесс, темновой ток также подчиняется
закону Пуассона, и его среднеквадратическое отклонение равно Также значительно уменьшить влияние темнового тока можно
путем использования темнового изображения. Оно вычитается из каждого
изображения перед его анализом. Для формирования темнового изображения
попиксельно усредняются M кадров, сделанных с закрытым затвором объектива, с
экспозицией, идентичной экспозиции при будущей фотосъемке. Количество кадров M
подбирается для каждого конкретного ПЗС. Шум переноса или ток
смещения возникает при переносе сгенерированного зарядового пакета по
элементам ПЗС. Причина его возникновения кроется в том, что часть передаваемых
электронов теряется при взаимодействии со случайным образом расположенными в
кремнии дефектами и примесями. Предположив, что каждый зарядовый пакет
переносится независимо от других, получим следующую зависимость для шума переноса:
Шум считывания – шум,
возникающий, когда зарядовый пакет считывается с ПЗС-матрицы, преобразуется в
напряжение и проходит через усилитель. Шум считывания можно смоделировать
действительным числом R, подчиняющимся распределению Гаусса. Следовательно, на
изображении всегда будет присутствовать этот базовый уровень шума, даже если
установлен нулевой уровень экспозиции, когда матрица находится при полной
темноте и шум темнового сигнала будет равен нулю. Другими источниками неопределенности светового сигнала
можно пренебречь. Таким образом, функция яркости изображения где I0(x,y)
– исходная яркость звезды, Все составляющие шумов ПЗС порождены различными физическими
процессами, в силу чего некоррелированы и независимы. Для устранения большей части шумов ПЗС предлагается
использовать следующий способ. Для части кадра строится гистограмма интенсивности
пикселей. Далее отсекается левая часть гистограммы – некоторый процент от
общего количества пикселей, и значение пикселя, лежащего на границе отсечения,
считается порогом. Все пиксели, лежащие ниже порога, отсекаются как шумовые. Ввиду малой «скученности» звезд при использовании объектива
видеокамеры с углом обзора 8° (засвеченная площадь кадра составляет порядка 3%
от всей площади кадра), данный способ является результативным. 4. Испытания программного комплекса выделения и
классификации звезд на имитационном стенде 4.1.
Перерасчет центра кадра участка звездного неба Для определения точного направления оси визирования
положение центра участка звездного неба, видимого камерой, корректируется
относительно центра отображаемого на мониторе участка звездного неба. Для этого
перед измерениями направления оси визирования на экран монитора с помощью ИЗН
выводятся 2 белые точки А и В (см. рис. 12) с координатами A = Рис. 12. Калибровочные
точки для определения центра 4.2. Оценка погрешностей
имитационного стенда Для оценки погрешностей на созданном стенде для
тестирования ПКВиКЗ используются несколько сеток точек с заранее известным
координатами. Сетки отображаются на экране монитора с помощью ИЗН и считываются
РУЗН. Далее РУЗН получает координаты точек сетки и выполняет сравнения
полученных координат с действительными. Для этого вычисляются расстояния между соседними
вертикальными и горизонтальными точками сеток, которые сравниваются между
собой. Теоретически расстояния равны, но на практике присутствует погрешность.
Погрешность будет вычисляться как среднеквадратическое отклонение от среднего
значения расстояния. Виды сеток Сетки пронумерованы согласно последовательности их
использования. Виды погрешностей, выделяемые при использовании сеток с меньшими
номерами, включены в погрешности, выделяемые при использовании сеток с большими
номерами. Таким образом, при вычитании последовательно всех сеток с меньшими
номерами из большей получаем сравнительно «чистую» погрешность. Один пиксель монитора составляет 21,6’’. В таблице 3 приведены сетки для расчета погрешностей.
Опишем их более точно: 1.
Для определения погрешности определения центров звезд в центре и
на краю экрана a) Сетка
11*11 точек, шаг 10 пикселей в центре экрана. b) Сетка
11*11 точек, шаг 10 пикселей в углу экрана. 2.
Для определения погрешности отображения звезд на мониторе. Сетка 11*11 точек, шаг 10,1 пикселей в центре экрана. 3.
Для определения оптических искажений изображения (дисторсии,
астигматизма, наклона монитора в вертикальной плоскости). Сетка 15*15 точек, шаг 50 пикселей. 4.
Для определения искажения проекции положения звезд на звездной
сфере на плоскость монитора. Теоретически погрешность проекции составляет 14’’. Сетка 15*15 точек, шаг 0,25°. Таблица 2.
Сетки и соответствующие им типы погрешностей. Вид
Сетка погрешности 1a 1b 2 3 4 Пиксели монитора - - X* - X Центры звезд X X X X X Дисторсия - - - X X Астигматизм (на краях) - X - X X Наклон монитора по вертикали - - - X X Проекция - - - - X *X-погрешность искажает сетку 4.3. Результаты
испытаний программного комплекса выделения и классификации звезд Таблица 3. Параметры ПКВиКЗ. Показатели эффективности ориентации по участкам звездного
неба Достигнутые значения показателей эффективности Требуемые значения показателей эффективности Вероятность правильной
идентификации звезд, % 98 >95 Точность определения ориентации,
угл. секунды не менее 20 <20 Допустимая угловая скорость
вращения, град./сек. 0,05 >0,05 Частота обновления информации об
ориентации, Гц. 3-10 >1 Угол обзора камеры, град. 8 - Размер анализируемого
изображения, пиксель 1380*1040 - Максимальная звездная величина 7,0 6,0 Размер звездной базы, ед. 15 914 <20 000 Средняя ошибка первого рода, % 12 <15 Средняя ошибка второго рода, % 26 <20 По результатам испытаний ПКВиКЗ можно сделать заключение,
что разработанный авторами комплекс подходит для высокоточного определения
ориентации малого космического аппарата. В данной статье предлагается научная визуализация звездного
неба с помощью разработанного программного обеспечения для имитационного стенда
«Системы высокоточной ориентации малого космического аппарата». Такой способ тестирования позволил авторам в полной мере
провести исследование разработанных методов и алгоритмов распознавания образов
разнотипных объектов на основе структурного подхода с использованием
унифицированных локальных признаков для решения конкретной задачи, связанной с
распознавания участков звездного неба и осуществлением высокоточной ориентации
малого космического аппарата по участкам звездного неба. 1.Лисов И. Запуски: итоги 2010 года.//Новости
космонавтики №3(338), 2011. – С. 38-39. 2.Pivtoratskaya S.V.
High-precision navigating system for satellite’s
orientation in space //6-th International Conference “Earth from Space – the
Most Effective Solutions”.–M.–2011.– P.364-365.– (есть пер. на рус. яз.:
Высокоточная система ориентации спутника в космическом пространстве. //5-ая
международная конференция «Земля из космоса – наиболее эффективные решения». –
М.: Инженерно-технологический Центр «СканЭкс», НП «Прозрачный мир»,
Издательство Бином, 2011. – С. 164-166). 3.Пивторацкая С.В. Исследовательский стенд «Системы высокоточной
ориентации малого космического аппарата» // Актуальные проблемы российской
космонавтики: Труды XXXVI Академических чтений по космонавтике. Москва, январь
2012 г. 4.SAO Star Catalog. URL: http://tdc-www.harvard.edu/software/catalogs/sao.html 5.Пивторацкая С.В., Кулябичев Ю.П.
Структурный подход к выбору признаков в системах распознавания образов. //
Естественные и технические науки №4 (54), 2011. М.: OOO «Издательство
«Спутник+», 547 с. С. 420-423. 6.Пивторацкая С.В., Кулябичев
Ю.П. Об особенностях структурного подхода к распознаванию образов на цифровых
изображениях. // ВЕСТНИК НАЦИОНАЛЬНОГО ИССЛЕДОВАТЕЛЬСКОГО ЯДЕРНОГО УНИВЕРСИТЕТА
«МИФИ», Т.1, №1. – М.: ФГБОУ ВПО «НИЯУ «МИФИ», 2012. – С. 125-128. 7.Arthur D., Vassilvitskii S.
k-means++: the advantages of careful seeding // Proceedings of the eighteenth
annual ACM-SIAM symposium on Discrete algorithms. 2007. P. 1027–1035. 8.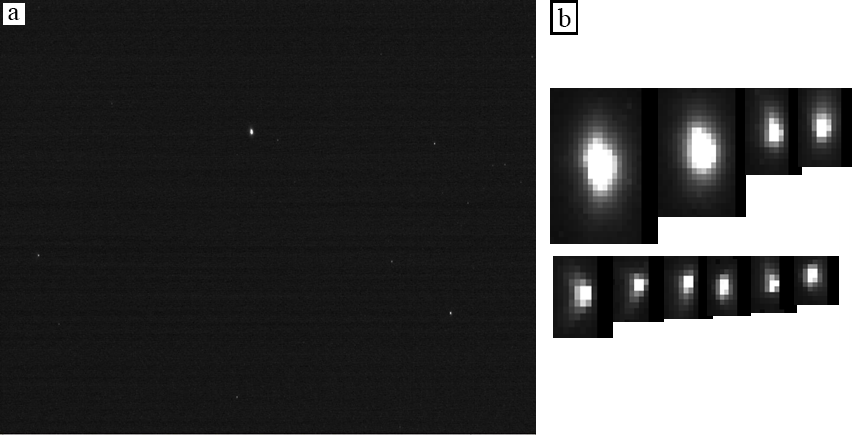
Определение
параметров изображений компактных объектов
![]() , (5)
, (5)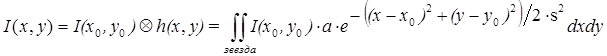 , (6)
, (6)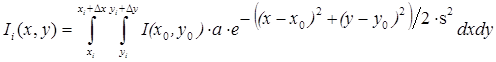 , (7)
, (7)
Pentax C2514-M; б) Fujinon HF25HA-1B.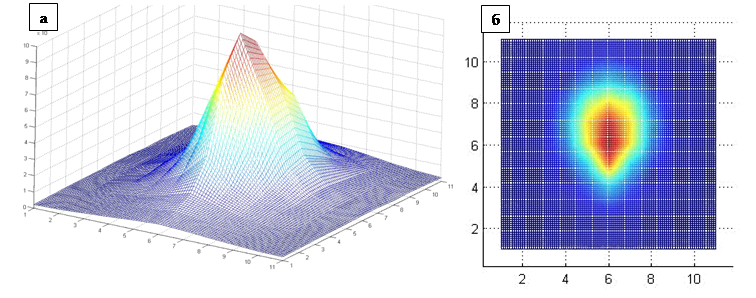
![]() , (8)
, (8)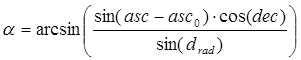 . (9)
. (9)
зависимости от максимальной звездной величины.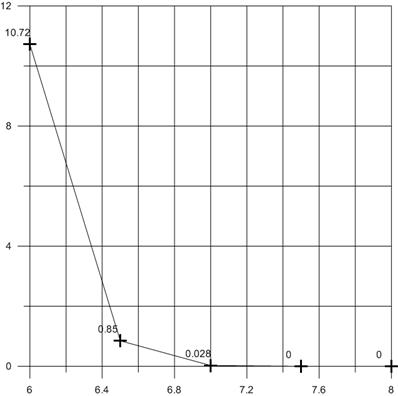
зависимости от максимальной звездной величины.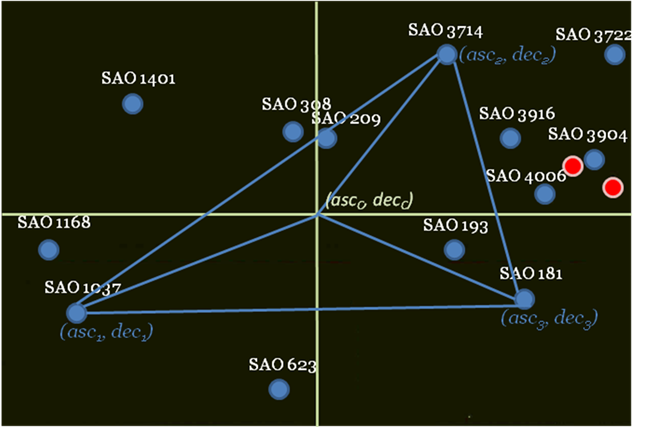
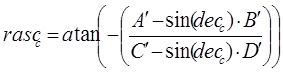 , (10)
, (10)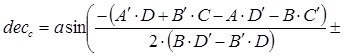
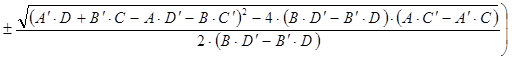 , (11)
, (11)![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,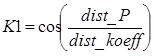 ,
, 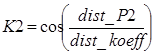 ,
, 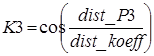 ,
,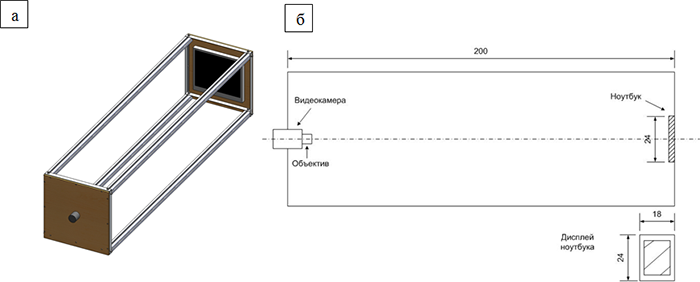
аппарата»: а) общий вид; б) отдельные компоненты стенда.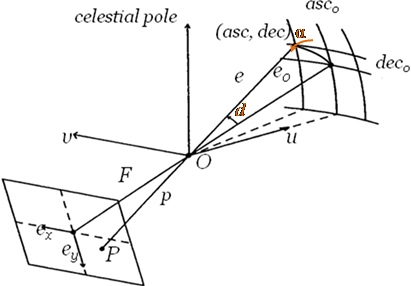
Шумы на
ПЗС-матрице
![]() , где
, где ![]() – фотонный шум, S – количество фотонов, падающее на один пиксель за единицу
времени. Несмотря на то, что данная составляющая шумов является принципиальным
свойством светового потока, она традиционно рассматривается в совокупности с
шумами, возникающими в ПЗС [11].
– фотонный шум, S – количество фотонов, падающее на один пиксель за единицу
времени. Несмотря на то, что данная составляющая шумов является принципиальным
свойством светового потока, она традиционно рассматривается в совокупности с
шумами, возникающими в ПЗС [11].![]() , где
, где ![]() – темновой ток,
– темновой ток, ![]() – число термически
сгенерированных электронов в общем сигнале. Для устранения этого вида шума
применяется активное охлаждение ПЗС-матрицы.
– число термически
сгенерированных электронов в общем сигнале. Для устранения этого вида шума
применяется активное охлаждение ПЗС-матрицы. ![]() , где e –
неэффективность отдельного акта переноса, n – число
переносов, N – количество переносимых зарядов.
, где e –
неэффективность отдельного акта переноса, n – число
переносов, N – количество переносимых зарядов.![]() , полученного с
ПЗС-матрицы, может быть смоделирована, как
, полученного с
ПЗС-матрицы, может быть смоделирована, как![]() ,
(12)
,
(12)![]() –
фотонный шум,
–
фотонный шум, ![]() – темновой
ток,
– темновой
ток, ![]() – шум
переноса, R(x,y) – шум считывания.
– шум
переноса, R(x,y) – шум считывания.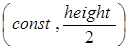 и B =
и B = 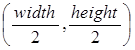 , где width – ширина
кадра, height – высота кадра, const – координата на кадре, удовлетворяющая условию
, где width – ширина
кадра, height – высота кадра, const – координата на кадре, удовлетворяющая условию ![]() . Координаты
центра участка звездного неба соответствуют найденным координатам для точки В(xB,yB). Угол поворота кадра относительно центра вычисляется как
. Координаты
центра участка звездного неба соответствуют найденным координатам для точки В(xB,yB). Угол поворота кадра относительно центра вычисляется как 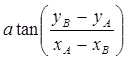 .
.
кадра и угла поворота кадра в плоскости экрана
5. Заключение
9.Машонкина Л.И., Сулейманов В.Ф. Задачи и Упражнения по Общей Астрономии: Методическое пособие к практикуму по Общей Астрономии. – Казань: Казанский университет, 2003. – 100 с.
10.Прэтт У. Цифровая обработка изображений. В 2 т. – М: Мир, 1982.
11.Быков Р.Е., Фраер Р., Иванов К.В. и др. Цифровое преобразование изображений: Учеб. пособие для вузов. – М.: Горячая линия-Телеком, 2003. – 228 с.
Starry sky visualiZation
by means of simulation stand
Yu. Kulyabichev, S. Pivtoratskaya
National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Moscow, Russia
ypkulyabichev@mephi.ru, moeimechko@yandex.ru
Abstract
This paper is devoted to a software complex of stars detection and classification, as well as its methods and algorithms of image recognition. The use of the software complex for high-precision orientation of small-size spacecraft based on the image of a starry sky's part is described in detail.
The authors consider the method of starry sky visualization by means of a simulation stand “High-Precision Navigating Systems of Small-Size Spacecraft” for testing the software complex. The simulation stand's construction is described, along with the software and hardware for scientific visualization of the starry sky.
The results of testing the software complex by visualizing the starry sky on the simulation stand are given.
Keywords: high-precision navigation, pattern recognition, scientific visualization, simulation stand, software complex, starry sky, stars classification, reference star, neighbors.
References
1.I. Lisov, Launches: Zapuski: itogi 2010 goda [Summary of 2010]. Novosti Kosmonavtiki [Cosmonautics News], vol. 338, no 3, 2011, pp. 38-39.
2.S.V. Pivtoratskaya, High-precision navigating system for satellite’s orientation in space. 6-th International Conference “Earth from Space – the Most Effective Solutions”, 2011, pp. 364–365.
3.S. Pivtoratskaya, Issledovatelskiy stend «Sistemy vysokotochnoy orientatsii malogo kosmicheskogo apparata» [Experimental stand “High-Precision Navigating Systems of Small-Size Spacecraft”]. Aktualnye problemy rossiyskoy kosmonavtiki: Trudy XXXVI Akademicheskikh chteniy po kosmonavtike [Current Issues of the Russian Cosmonautics: Proceedings of the XXXVI Academic Readings on Cosmonautics]. Moscow, January 2012.
4.SAO Star Catalog Available at: http://tdc-www.harvard.edu/software/catalogs/sao.html
5.S.V. Pivtoratskaya, Yu.P. Kulyabichev. Strukturnyy podkhod k vyboru priznakov v sistemakh raspoznavaniya obrazov [The structural approach to the feature choice for the image recognition systems]. Yestestvennye i Tehnicheskie Nauki (Natural Sciences and Engineering), vol. 54, no 4, 2011, pp. 420–423, 2011.
6.S.V. Pivtoratskaya, Yu.P. Kulyabichev. Ob osobennostyakh strukturnogo podkhoda k raspoznavaniyu obrazov na tsifrovykh izobrazheniyakh. [About characteristics of the structural approach to the image recognition on the digital image]. Vestnik Natsional'nogo Issledovatel'skogo Yadernogo Universiteta “MIFI” (Journal of National Research Nuclear University “MEPhI”), vol. 1, no 1, 2012, pp. 125–128.
7.D. Arthur, S. Vassilvitskii, k-means++: the advantages of careful seeding. Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, 2007, pp. 1027–1035.
8.V.K. Kirillovskij, Opticheskie izmereniya. Chast 4. Otsenka kachestva opticheskogo izobrazheniya i izmerenie ego kharakteristik [Optical measurements. Part 4. Quality evaluation of the optical image and measurement of its characteristics]. Tutorial, SPb, SPbSU ITMO, 2005, p. 67.
9.L.I. Mashonkina, B.F. Sulejmanov. Zadachi i Uprazhneniya po Obschey Astronomii [Tasks and exercises on General Astronomy]. Metodicheskoe posobie k praktikumu po Obschey Astronomii [Study guide to practicum on General Astronomy]. – Kazan, Kazan University, 2003, p. 100.
10.W. Pratt, Tsifrovaya obrabotka izobrazheniy [Digital image processing]. Vol. 2, Мoscow, Mir, 1982.
11.R.E. Bykov, R. Fraer, K.V. Ivanov et al., Tsifrovoe preobrazovanie izobrazheniy [Digital image’s conversion]. Tutorial for universities. Мoscow, Gorjachaja linija-Telekom, 2003, p. 228 p.