МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И ВИЗУАЛИЗАЦИЯ
ТЕЧЕНИЙ ВЕЩЕСТВА В АККРЕЦИОННЫХ ЗВЕЗДНЫХ ДИСКАХ
А. Луговский1,2, М. Абакумов3, В. Чечеткин1,2,4
1 Институт прикладной математики им. М.В. Келдыша РАН, Москва, Россия
2 Национальный исследовательский центр "Курчатовский институт", Москва, Россия
3 Московский государственный университет им. М.В. Ломоносова, Москва, Россия
4 Национальный исследовательский ядерный университет "МИФИ", Москва, Россия
alex_lugovsky@mail.ru, vmabk@yandex.ru, chechetv@gmail.com
Оглавление
2. Постановка задачи и методы решения
3. Результаты численного моделирования и их визуализация
3.1 Малые возмущения в диске с околокеплеровским распределением скорости
3.2 Локальное возмущение во внешней области диска с околокеплеровским распределением скорости
3.3 Возмущения в Кеплеровском аккреционном диске
Аннотация
В последние годы получен большой объем наблюдательных данных по аккреционным звездным дискам. Методы численного моделирования являются практически единственным способом всестороннего исследования таких астрофизических объектов. В результате расчетов образуются огромные объемы информации, поэтому их визуализация становится не только способом наглядного представления, но и исследования. В статье приведены результаты моделирования и изучения с помощью визуального представления структуры газодинамических течений в таких дисках с учетом гравитации, а также предложен новый механизм, определяющий и характеризующий аккрецию (падение) вещества на центральное тело. В работе рассмотрена проблема возникновения и развития крупномасштабного вихревого движения в сдвиговом течении вещества аккреционного диска. Исследован механизм переноса углового момента возникающими в результате развития начальных малых возмущений крупными вихревыми структурами. Рассматриваемые задачи подразумевают огромный объем вычислительной работы, поэтому их моделирование проведено на многопроцессорных вычислительных системах. Визуализация расчетов в рассматриваемых задачах является методом исследования и изучения структуры течений. Анимация расчетов позволяет проследить эволюцию течений. Сопоставление картин течения для разных его характеристик в виде линий уровня дает наглядное представление о вихревой структуре течения. Выделение исследуемых подобластей, использование специальных палитр, а также сужение рассматриваемого диапазона изменения какой-либо из характеристик течения дают возможность исследования достаточно мелкомасштабных особенностей течения.
Ключевые слова: визуализация в астрофизике, аккреционные звездные диски, угловой момент, ClcView.
Аккреционным диском называется газовый диск вокруг массивного (по сравнению с диском) компактного объекта (звезды-аккретора). Теоретические исследования аккреционных звездных дисков вблизи гравитирующих тел проводятся уже много лет. Аккреционные диски проявляют себя излучением, поскольку определяющей чертой аккреционного диска является переход гравитационной энергии аккрецирующего (падающего) на компактный объект вещества в тепловую энергию с последующим излучением. Наблюдения аккреционных дисков свидетельствуют о значительном потоке вещества, определяемом по излучению, на аккретор (центральное тело). Падение вещества возможно лишь при условии передачи наружным частям диска большей доли момента вращения аккрецирующего газа. Таким образом, одной из ключевых проблем физики аккреционных дисков является вопрос о механизмах отвода углового момента к внешним частям диска, обеспечивающих падение вещества на гравитирующий центр. В качестве механизма отвода углового момента предлагались различные физические процессы, однако, анализ различных способов передачи момента показывает, что все рассматриваемые механизмы встречаются с определенными трудностями при объяснении свойств аккреционных дисков.
В данной работе рассматривается проблема возникновения и развития крупномасштабного вихревого движения в сдвиговом течении вещества аккреционного диска. Исследуется новый механизм переноса углового момента возникающими в результате развития начальных малых возмущений крупными вихревыми структурами. Возможности аналитических оценок эволюции разномасштабных вихревых течений, возникающих в рассматриваемых астрофизических задачах, в общем многомерном случае весьма ограничены, поэтому основным методом изучения свойств таких течений является вычислительный эксперимент. Физические размеры моделируемых астрофизических объектов на несколько порядков превышают размеры характерных изучаемых структур вихревого течения, поэтому используемая сетка должна быть достаточно подробной. Шаг по времени, выбор которого обусловлен монотонностью схемы, пропорционален шагу по пространству и, соответственно, тоже мал. Расчеты проводятся на больших промежутках физического времени, при этом используемый шаг по времени на четыре-пять порядков меньше характерного времени одного оборота диска (количество шагов по времени в различных расчетах составляет от 30000 до 300000). Таким образом, рассматриваемые задачи подразумевают огромный объем вычислительной работы, поэтому их полномасштабное моделирование на персональном компьютере практически невозможно. В данном случае методы численного моделирования на многопроцессорных вычислительных комплексах являются едва ли не единственным способом полноценного исследования таких астрофизических объектов.
Огромные объемы получаемых результатов расчетов требуют особых подходов к их изучению, ведь в таком потоке информации важной может оказаться любая незначительная деталь. Визуализация расчетов в рассматриваемых задачах является не только способом «взглянуть» на полученные результаты, но и методом исследования и изучения структуры течений. Анимация расчетов позволяет быстро проследить эволюцию течений. Сопоставление картин течения для разных его характеристик в виде линий уровня дает наглядное представление о вихревой структуре течения. Выделение исследуемых подобластей, использование специальных палитр, а также сужение рассматриваемого диапазона изменения какой-либо из характеристик течения дают возможность исследования достаточно мелкомасштабных особенностей течения. Все эти способы и методы представления полученной в результате расчетов информации делают визуализацию неотъемлемой частью научного исследования рассматриваемых астрофизических задач изучения аккреционных дисков. В качестве инструмента визуализации выбрана программа ClcView [1], позволяющая использовать все указанные подходы к визуализации.
2. Постановка задачи и методы решения
В рамках гидродинамического приближения рассматривается аккреционный диск, находящийся в поле центрального гравитирующего тела массы M. Предполагая, что толщина диска много меньше его радиуса, будем рассматривать задачу в двумерной геометрии. Самогравитация вещества диска не учитывается.
Газ является сжимаемым, идеальным и его поведение описывается системой двумерных уравнений газовой динамики в переменных Эйлера в цилиндрических координатах:
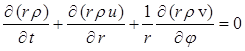 ,
,
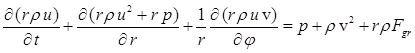 ,
,
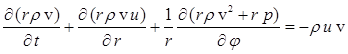 ,
,
![]() ,
,
![]() ,
, ![]() .
.
Уравнение состояния идеального газа используется в виде
![]() .
.
Здесь r
- радиус, j - полярный угол, t
- время, r -
плотность газа, p - давление, e
- удельная внутренняя энергия, e - полная удельная энергия, g - показатель адиабаты, h –
удельная энтальпия, ![]() - скорость газа, u
- ее радиальная компонента, v - азимутальная,
- скорость газа, u
- ее радиальная компонента, v - азимутальная, ![]() – радиальная компонента
удельной силы гравитации, G – гравитационная
постоянная, M – масса гравитирующего тела.
– радиальная компонента
удельной силы гравитации, G – гравитационная
постоянная, M – масса гравитирующего тела.
Для удобства перейдем к безразмерным переменным. В качестве масштабных множителей выберем величины R, M, G, где R – характерный пространственный размер задачи, и введем безразмерные переменные, помеченные далее штрихом, в соответствии с формулами:
![]()
Числа ![]() выражаются следующим образом:
выражаются следующим образом:
![]() .
.
В дальнейшем штрих в записи переменных будем опускать. Система уравнений в безразмерных переменных остается прежней. Выражение для удельной силы гравитации в безразмерных переменных примет следующий вид:
![]()
Рассмотрим течение газа в расчетной области ![]() .
.
На границах
расчетной области задаются “свободные” граничные условия вида 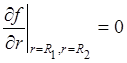 , где
, где ![]() .
.
Для
аппроксимации дифференциальной задачи используется явная схема
Роу-Эйнфельдта-Ошера третьего порядка аппроксимации по h и первого по τ [2].
Схема порядка ![]() используется для уменьшения
схемной вязкости. Ввиду большого объема вычислительной работы алгоритм был
распараллелен, и расчеты проводились на многопроцессорных вычислительных
системах. Используемая схема Роу-Эйнфельдта-Ошера в связи с ее явностью удобна
при реализации на многопроцессорных вычислительных комплексах.
используется для уменьшения
схемной вязкости. Ввиду большого объема вычислительной работы алгоритм был
распараллелен, и расчеты проводились на многопроцессорных вычислительных
системах. Используемая схема Роу-Эйнфельдта-Ошера в связи с ее явностью удобна
при реализации на многопроцессорных вычислительных комплексах.
3. Результаты численного моделирования и их визуализация
3.1 Малые возмущения в диске с околокеплеровским распределением скорости
Расчетная
область и конфигурация диска приведены на Рис. 1. В качестве начального
состояния аккреционного диска выбирается аналитическое решение ![]() , широко используемое при
моделировании аккреционных дисков (см., например, [3]) и являющееся равновесным
состоянием, полученным в [4], в случае двумерной модели. Здесь мы выберем
равновесное состояние в форме тора, распределение азимутальной скорости при
этом близко к кеплеровскому.
, широко используемое при
моделировании аккреционных дисков (см., например, [3]) и являющееся равновесным
состоянием, полученным в [4], в случае двумерной модели. Здесь мы выберем
равновесное состояние в форме тора, распределение азимутальной скорости при
этом близко к кеплеровскому.
Отметим, что расчетная область выбирается таким образом, что по радиусу ее размер приблизительно в два раза превышает характерный размер диска, т.е. область сосредоточения основной массы диска (Рис. 1). Отметим также, что плотность у внешнего края расчетной области мала и имеет значения на 5 порядков меньше, чем в области максимальной плотности. Все это делает влияние граничных условий несущественным, и расчеты это подтверждают, поэтому граничные условия в данной постановке могут быть любыми.
Под оборотом диска подразумевается время, за которое вещество диска из области максимальной плотности (r = 0.8) совершает один оборот вокруг центрального гравитирующего тела. В качестве примера укажем, что для аккреционного диска с характерным пространственным радиусом R = 7×1011 см, находящегося в поле центрального гравитирующего тела с массой M = 2×1033 г, физическое время одного оборота t = 2×105 с.
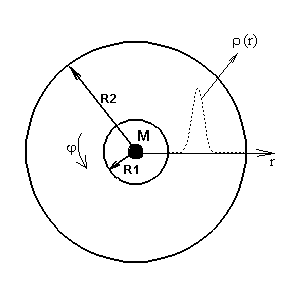
Рис. 1. Расчетная область и конфигурация диска.
С целью исследования устойчивости диска внесем в равновесное состояние диска малые возмущения. Отметим, что без внесения малых возмущений диск сохраняет свое состояние достаточно продолжительное время.
Расчеты
проводятся на равномерной по r и j сетке ![]() :
:
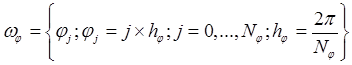 ,
,
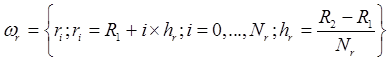 .
.
Расчетная
область и число точек по r (![]() )
постоянны для всех вариантов рассматриваемой задачи:
)
постоянны для всех вариантов рассматриваемой задачи: ![]() .
.
На фоне
исходного равновесного состояния диска зададим малые синусоидальные возмущения
азимутальной составляющей скорости: ![]() ,
, ![]() - азимутальная
скорость в начальном равновесном состоянии, А - амплитуда возмущений, n - количество периодов в интервале 0 ≤ j < 2p.
Ширина полосы возмущения по r, внесенного в начальный момент времени в
равновесное состояние, составляет две ячейки в области максимальных значений
плотности диска. Возмущение с А = 0.2, n = 10 задается
при 0≤j<2p. Расчеты проводятся на сетке w, где
- азимутальная
скорость в начальном равновесном состоянии, А - амплитуда возмущений, n - количество периодов в интервале 0 ≤ j < 2p.
Ширина полосы возмущения по r, внесенного в начальный момент времени в
равновесное состояние, составляет две ячейки в области максимальных значений
плотности диска. Возмущение с А = 0.2, n = 10 задается
при 0≤j<2p. Расчеты проводятся на сетке w, где ![]() . Сетка
подбирается таким образом, чтобы в возмущенной области форма разностных ячеек
была близка к квадратной. Это делается для того, чтобы разрешающая способность
сетки была одинакова по обеим переменным.
. Сетка
подбирается таким образом, чтобы в возмущенной области форма разностных ячеек
была близка к квадратной. Это делается для того, чтобы разрешающая способность
сетки была одинакова по обеим переменным.
Для визуализации первых полученных результатов с помощью ClcView [1] были построены картины течений в виде линий уровня плотности (Рис. 2) и линий уровня завихренности ½rotV½ (Рис. 3).

Рис. 2. Картины
течения в виде линий уровня плотности в области, соответствующей
области сосредоточения основной массы диска, до момента времени,
соответствующего половине оборота диска (слева направо).

Рис. 3. Картины
течения в виде линий уровня завихренности во всей расчетной области
до момента времени, соответствующего половине оборота диска (слева направо).
Полученные результаты показали, что малые возмущения, внесенные в равновесное состояние в малой области, развиваются и превращаются в крупномасштабные структуры, охватывающие значительную часть диска. Большое количество расчетных данных требовало ускорения визуализации для анализа результатов, для чего была использована анимация с использованием цветовой заливки (Рис. 4).
Рис. 4. Анимация с
цветовой заливкой плотности (слева) и завихренности (справа)
до момента времени, соответствующего двум оборотам диска.
Ожидаемое затухание бурно развивавшегося на начальном этапе вихревого движения, а также огромный диапазон изменения параметров показывают, что визуализации в виде линий уровня или анимации с цветовой заливкой во всем диапазоне параметра недостаточно для исследования и понимания структуры развивающегося течения. Рассмотрим более подробно поведение завихренности. На Рис. 5 представлены анимации завихренности в части области в более узких диапазонах ее изменения с отступом от максимума и минимума. Видно, что образуются крупные структуры, которые смещаются к внешнему краю области, но поскольку плотность у внешнего края мала (здесь плотность имеет значения на 5 порядков меньше, чем в области максимальной плотности), оттока вещества практически не происходит. Также видно формирование дорожек вихрей, возникающих в результате обтекания веществом диска образовавшихся вихревых структур. Кроме этого, во внутренней части области видны образовавшиеся структуры. Заметим, что на картинах с изображением плотности различить какие-либо структуры во внутренней и внешней частях расчетной области достаточно сложно ввиду малой плотности.
Рис. 5. Анимация с
цветовой заливкой завихренности в части области в диапазоне ее изменения от 0.1
до 100 (слева) и от 0.1 до 1000 (справа) до момента времени, соответствующего
двум оборотам диска.
Рассмотрим также анимацию удельной завихренности (½rotV½/r) в части области в узком диапазоне ее изменения (Рис. 6), на которой видно начало развития неустойчивости, зарождение дорожек вихрей и их развитие, а также образование спиральных структур, хорошо различимых на Рис. 2, 3, 4.
Рис. 6. Анимация с
цветовой заливкой удельной завихренности в части области в узком
диапазоне ее изменения до момента времени, соответствующего двум оборотам диска.
При задании в
качестве начальных двух локальных симметричных возмущений с А = 0.2, n = 10 при ![]() расчеты на сетке w, где
расчеты на сетке w, где ![]() показывают (Рис.
7), что образовавшиеся в течении вещества диска структуры качественно схожи со
структурами, отмеченными выше.
показывают (Рис.
7), что образовавшиеся в течении вещества диска структуры качественно схожи со
структурами, отмеченными выше.
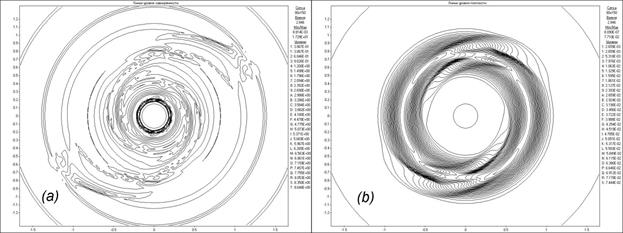
Рис. 7. Картины
течения в виде линий уровня завихренности (a) и линий уровня плотности (b) при задании двух
локальных симметричных начальных возмущений на момент времени, соответствующий 2/3
оборота диска.
В работах [5-6] указано, что независимо от выбора возмущаемого параметра, количества возмущений в начальных данных, задания амплитуды А в диапазоне от 0.01 до 0.2, задания возмущений в полосе шириной в одну или в две ячейки, задания числа локальных возмущений (от 1 до 10 при n = 10 и от 1 до 20 при n = 20), выбора сетки (от 40×130 до 320×1040) результаты расчетов показывают, что течения, порожденные этими возмущениями, качественно сходны между собой. Малые возмущения, внесенные в начальное равновесное состояние, приводят к образованию крупных вихревых структур, которые существуют достаточно долго, при этом перестройке подвергается течение практически во всей области, хотя начальное возмущение задано лишь в малой ее части. Кроме того, в [6] показано, что кинетическая энергия турбулентного движения (подразумевается кинетическая энергия радиального движения вещества в диске, отсутствовавшего в равновесном состоянии) независимо от начальной амплитуды А со временем выходит на квазистационарный режим, при котором она слабо изменяется со временем, колеблясь вблизи почти постоянного значения. Таким образом, можно утверждать, что кинетическая энергия турбулентности в квазистационарном режиме определяется начальной кинетической энергией и не зависит от энергии первичного возмущения. Это показывает физическую достоверность утверждения о развитии крупномасштабного турбулентного движения в сдвиговом течении аккреционных дисков и подтверждает то, что после прохождения пика развития возмущений, вихревые структуры не исчезают, течение остается вихревым, и как видно на Рис. 5, 6, крупные структуры переносят угловой момент к внешним частям диска.
Проанализируем изменение и перераспределение углового момента в течении. На Рис. 8 представлено распределение углового момента вдоль радиуса в начальный момент времени и на момент времени, соответствующий двум оборотам. Для построения графиков используется программа Advanced Grapher (http://www.alentum.com/agrapher/). Видно, что происходит перераспределение момента, максимум углового момента по сравнению с начальным уменьшается, а область, где в основном сосредоточен угловой момент, расширяется.
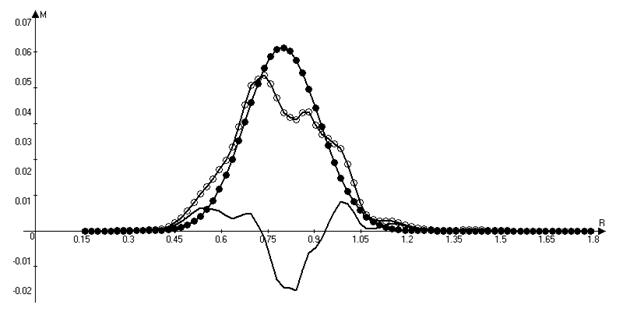
Рис. 8. Графики
распределения углового момента вдоль радиуса (j
= 0°) на моменты времени
t1 = 0 (●●●) и t2 =
2 оборота (○○○) и график разности угловых моментов M(t2) - M(t1) (▬▬).
В течение всего расчета происходят “выбросы” углового момента из зоны, где сосредоточена основная масса вещества, по радиусу в обе стороны. Вещество до внутренней границы этой области на начальный момент времени и, особенно, за внешней границей приобретает значительный угловой момент. Для наглядной иллюстрации описанных процессов используем анимацию графика распределения углового момента вдоль радиуса и отношения текущего момента к начальному со временем (Рис. 9).
Рис. 9. Распределение
углового момента вдоль радиуса (ρvr) и отношение текущего момента к
начальному (справа) в течение двух оборотов диска (синий цвет - j = 0°,
красный цвет - j = 90°)
В работе [6] показано, что энтропия в системе постоянна, а общий угловой момент и масса вещества диска в системе остаются практически неизменными, а это означает, что перераспределение углового момента происходит образовавшимися крупными вихревыми структурами (а не за счет потока вещества через границы) без заметного нагрева вещества диска, что согласуется с наблюдениями.
3.2 Локальное возмущение во внешней области диска с околокеплеровским распределением скорости
Помимо
изучения развития малых возмущений различных параметров в области
сосредоточения основной массы диска, большой интерес представляет собой процесс
эволюции малого возмущения, внесенного локально вблизи внешней границы
аккреционного диска, где плотность вещества мала (на несколько порядков меньше
средней плотности вещества диска). Возмущение скорости и плотности на краю
диска может быть связано с различными физическими процессами, например,
аккрецией вещества с другим угловым моментом на внешний край аккреционного
диска, приливным взаимодействием в двойных системах, пролетом тяжелого тела
через аккреционный диск. В данном варианте рассматривается задача в постановке,
аналогичной приведенной выше, но во внешней части аккреционного звездного диска
задается имитирующая возмущение область с плотностью ![]() и
скоростью
и
скоростью ![]() , занимающая объем
, занимающая объем ![]() . Возмущение во внешней
области диска задается в виде:
. Возмущение во внешней
области диска задается в виде:

Параметры
возмущения для представленного расчета выбираются следующими: ![]() Область возмущения содержит
две ячейки по r и пять ячеек по φ.
Область возмущения содержит
две ячейки по r и пять ячеек по φ.
На Рис. 10 приведены результаты расчетов в виде анимированного изображения изменения картины течения в виде линий уровня плотности и завихренности. Малое возмущение во внешней области диска, внесенное в равновесное состояние в малой области, развивается, и со временем происходит образование нескольких крупных структур, существующих на протяжении всего расчета. Заметим, что в связи с малой плотностью вне диска, на анимации, где изображена плотность, видна лишь часть структур, находящихся в области диска. Самая крупная структура находится вне области диска и видна только на картине завихренности. На ней на начальном этапе развития возмущения можно видеть сдвоенную дорожку вихрей за этой крупной структурой, напоминающую вихревую дорожку Кармана, образовавшуюся в результате обтекания вращающимся веществом диска возникшей в нем крупной структуры.
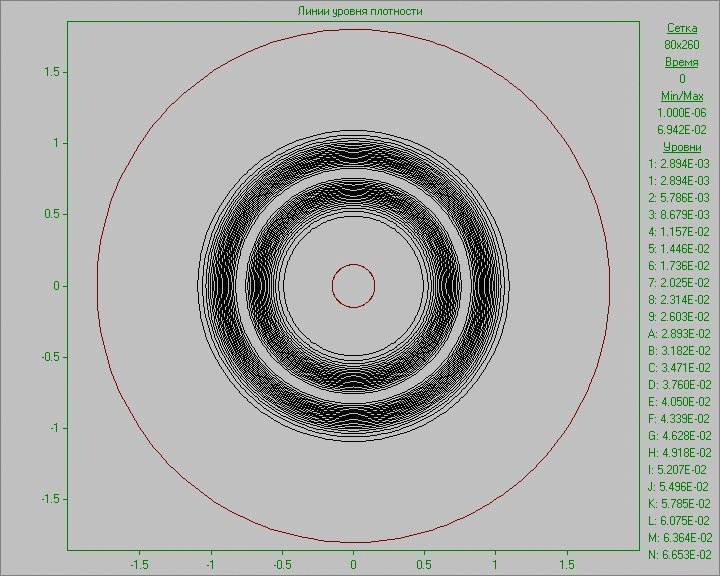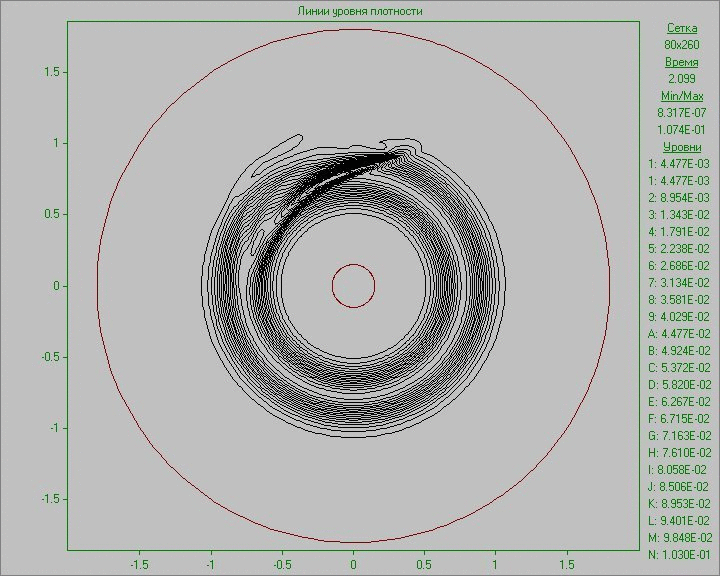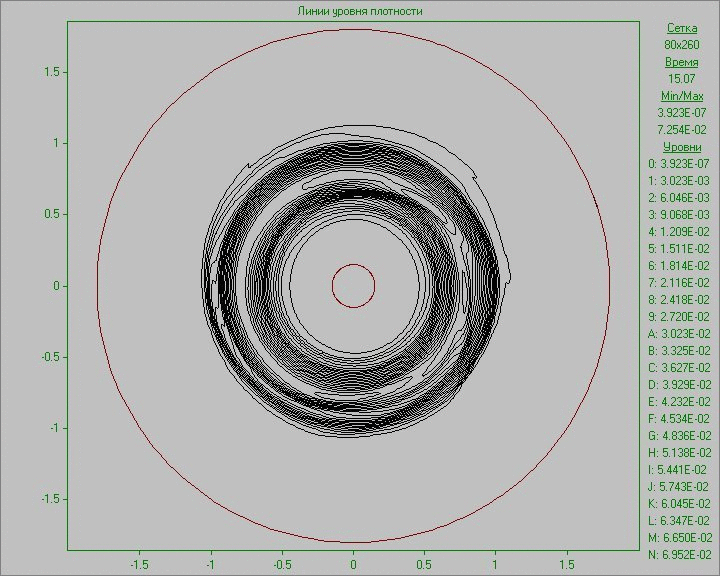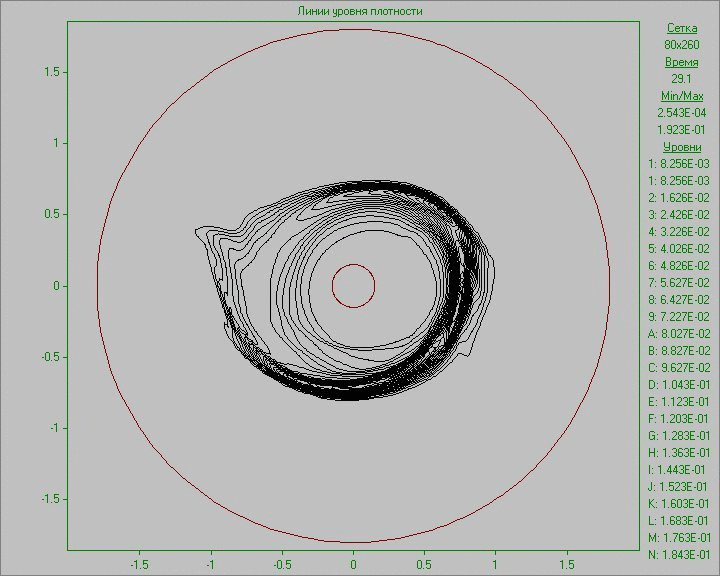
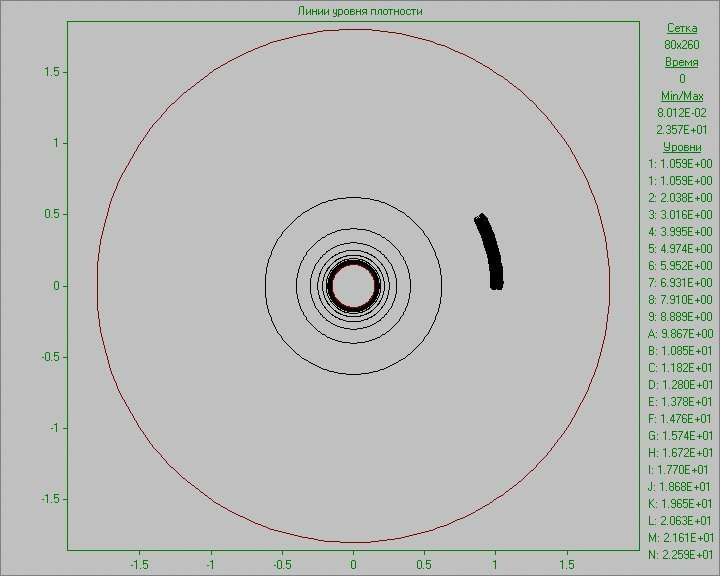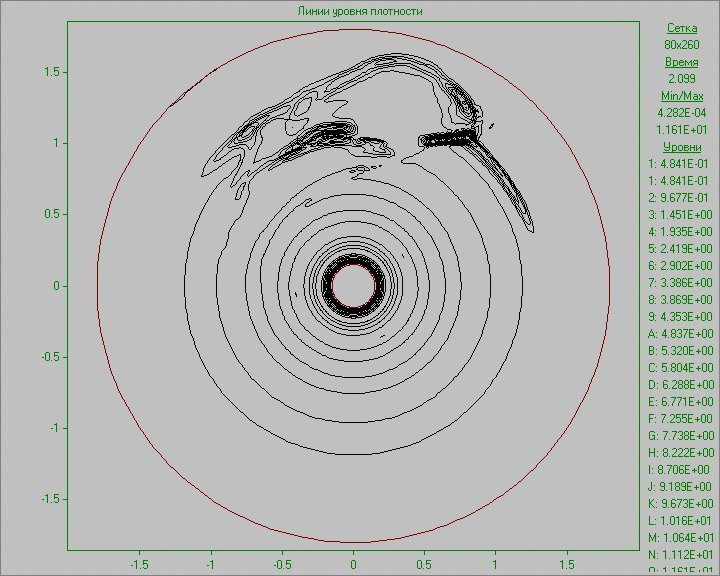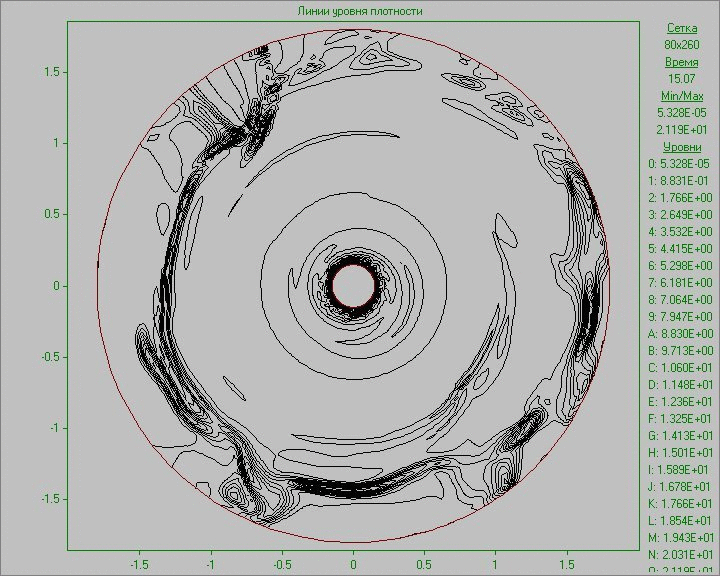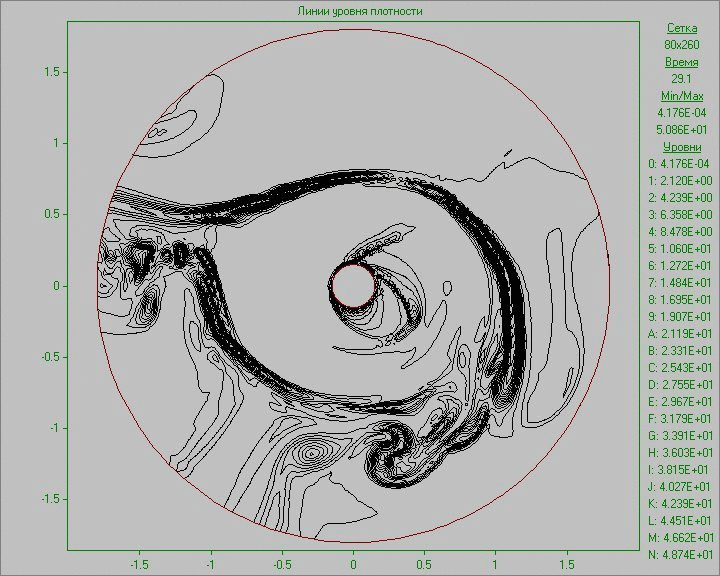
Рис. 10. Картины
течения в виде линий уровня плотности (слева) и линий уровня завихренности (справа)
при задании возмущения во внешней области диска до момента времени, соответствующего семи оборотам.
Возмущение, внесенное на краю диска, переходит в область больших плотностей и со временем захватывает значительную часть диска. Образование структур в центре расчетной области говорит об увеличившейся внутренней аккреции вещества. Течение в диске подверглось существенной перестройке, оставаясь при этом вихревым, в нем образовались крупные спиральные вихревые структуры, и произошло существенное перераспределение плотности.
Распределение углового момента вдоль радиуса в начальный момент времени и на момент времени, соответствующий пяти оборотам, представленное на Рис. 11 иллюстрирует существенное перераспределение углового момента в диске. Видно, что отвод углового момента в определенном угловом направлении несимметричен, что связано с интенсивной потерей углового момента веществом в области крупных структур во внешней части диска, приводящей к поджиманию с внешней стороны и увеличению максимума профиля углового момента.
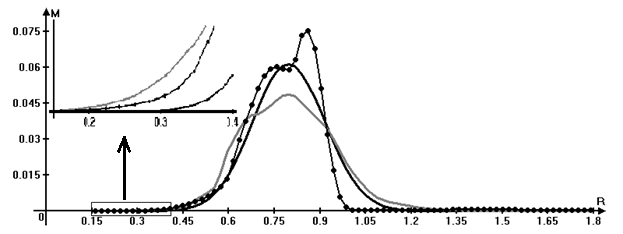
Рис. 11. Графики
распределения углового момента вдоль радиуса на моменты времени
t1 = 0 (▬▬)
и t2 = 5 оборотов (▬▬ - j=0°,
●●● - j=180°).
3.3 Возмущения в Кеплеровском аккреционном диске
Здесь мы изменим начальное состояние, выбрав закон распределения
азимутальной скорости, близкий к наблюдаемому, т.е. в качестве равновесного
состояния возьмем равновесное состояние с кеплеровским распределением скорости,
для которого в [4] также построено аналитическое решение. В
безразмерных переменных кеплеровский закон распределения азимутальной
скорости задается формулой ![]() . Данное
аналитическое решение описывает внутреннюю часть диска (приблизительно
половину), т.к. для диска с кеплеровским распределением скорости нет
равновесных состояний в форме тора. Следовательно, «свободные» граничные
условия на внешней границе рассматриваемой части аккреционного диска будут
оказывать существенное влияние на эволюцию течения, т.к. на внешней границе
будет существовать поток массы и углового момента вещества. На Рис. 12
представлены расчетная область и профиль начальной равновесной плотности.
. Данное
аналитическое решение описывает внутреннюю часть диска (приблизительно
половину), т.к. для диска с кеплеровским распределением скорости нет
равновесных состояний в форме тора. Следовательно, «свободные» граничные
условия на внешней границе рассматриваемой части аккреционного диска будут
оказывать существенное влияние на эволюцию течения, т.к. на внешней границе
будет существовать поток массы и углового момента вещества. На Рис. 12
представлены расчетная область и профиль начальной равновесной плотности.
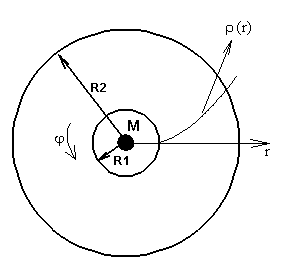
Рис. 12. Расчетная область и конфигурация диска с кеплеровским распределением скорости.
Здесь на фоне
исходного равновесного состояния диска аналогично параграфу 3.1 задаются малые
синусоидальные возмущения азимутальной составляющей скорости. Задача решается в
области ![]() , где
, где ![]() Расчеты проводятся на сетке w, где
Расчеты проводятся на сетке w, где ![]() . Возмущения задаются в полосе
шириной в одну ячейку по r при
. Возмущения задаются в полосе
шириной в одну ячейку по r при ![]() ,
0≤j<2p, т.е. вблизи внешней границы
рассматриваемой части диска, что примерно соответствует центральной части
полного диска. Рассмотрим поведение системы со временем. Под оборотом диска
будем подразумевать безразмерное время t ≈ 30, за которое вещество вблизи
внешней границы расчетной области совершит оборот вокруг центрального
гравитирующего тела.
,
0≤j<2p, т.е. вблизи внешней границы
рассматриваемой части диска, что примерно соответствует центральной части
полного диска. Рассмотрим поведение системы со временем. Под оборотом диска
будем подразумевать безразмерное время t ≈ 30, за которое вещество вблизи
внешней границы расчетной области совершит оборот вокруг центрального
гравитирующего тела.
Рассмотрим поведение системы со временем. На Рис. 13 представлена анимация плотности с цветовой заливкой до момента времени, соответствующего восьми оборотам диска.
Рис. 13. Анимация плотности с цветовой
заливкой для диска с кеплеровским распределением
скорости до момента времени, соответствующего восьми оборотам диска.
Происходит образование спиральных вихревых структур во всей области диска, т.е. малые возмущения, заданные в узкой полосе, превращаются в крупномасштабные структуры, охватывающие весь диск и существующие продолжительное время. Данные результаты качественно повторяют результаты для диска с околокеплеровским распределением скорости в параграфе 3.1.
В работе [8] показано, что на начальном этапе в момент образования вихрей происходит сброс массы и момента вещества через внешнюю границу, в результате которого система переходит в новое состояние, близкое к стационарному, при этом течение в диске остается вихревым. Течение вещества диска стремится к некоторому равновесному стационарному состоянию, но наличие крупных вихревых структур мешает этому, поэтому система продолжительное время находится в квазистационарном состоянии, характеризуемом периодическими пульсациями рассматриваемых параметров течения, вызванными периодическими оттоком и притоком массы и углового момента вещества через внешнюю границу. На Рис. 14 приведены картины течения в виде линий уровня плотности с векторами скорости, соответствующие началу и концу одного периода такого квазистационарного пульсационного состояния. На Рис. 14а видно, что основной отток вещества наружу идет между крупными структурами, т.к. структуры тормозят поток вещества, но сами при этом смещаются в сторону внешней границы, подталкиваемые общим потоком (отвод углового момента). На Рис. 14b основной приток вещества внутрь идет в области крупных структур, т.к. сами структуры смещаются ближе к центру, а вещество между структурами тормозится возникшим потоком внутрь диска сквозь внешнюю границу (аккреция).
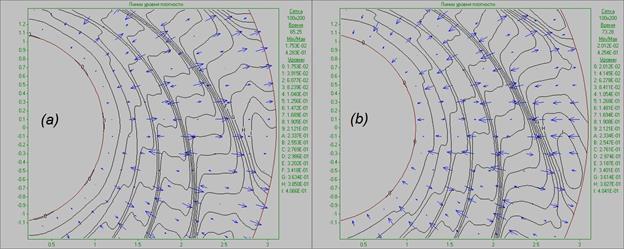
Рис. 14. Картины
течения в виде линий уровня плотности для кеплеровского диска
на моменты времени t = 2 оборота диска (а) и t
= 2.5 оборота диска (b).
В работе [8] показано, что со временем происходит существенное перераспределение углового момента по сравнению с начальным распределением, что согласуется с полученными ранее результатами для околокеплеровского диска (параграф 3.1).
Проведенные исследования показывают, что крупные вихревые структуры, образующиеся в диске, приводят к перераспределению углового момента в диске, а также к отводу вещества и углового момента через внешнюю границу, но возникающая в результате потери углового момента аккреция приводит к обратному притоку вещества и, соответственно, увеличению углового момента.
Дальнейшее исследование эволюции системы показывает, что со временем течение начинает терять симметрию (Рис. 15а), что приводит к качественному изменению картины течения, происходит объединение и укрупнение вихрей (Рис. 15b). На Рис. 15 изображены картины течения в виде линий уровня плотности на момент времени t = 550 (~18 оборотов), когда течение начинает терять симметрию (Рис. 15а), и на момент времени t = 700 (~23 оборота), когда течение подверглось значительной перестройке, и образовались отдельные несимметричные более крупные вихревые структуры. Отметим, что возникающая двуспиральная структура качественно схожа со структурой, показанной в параграфе 3.2, возникающей в результате развития локального возмущения во внешней области некеплеровского аккреционного диска.
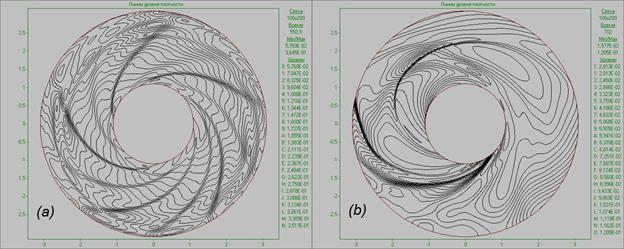
Рис. 15. Картины
течения в виде линий уровня плотности для кеплеровского диска
на моменты времени t = 18 оборотов диска (а) и t
= 23 оборота диска (b).
С момента потери течением симметрии (t ≈ 550, 18 оборотов) и началом роста вихревых структур начинает происходить отвод углового момента и вещества диска наружу через внешнюю границу. В результате этого сильно увеличивается темп внутренней аккреции, вещество начинает активно истекать через внутреннюю границу. Таким образом, крупные вихревые структуры являются механизмом отвода углового момента вещества диска наружу, что приводит к аккреции вещества сквозь внутреннюю границу расчетной области в направлении центрального гравитирующего тела.
Рассмотрим также задачу о возникновении локального возмущения в аккреционном звездном диске с кеплеровским распределением скорости. Такое возмущение запишется в виде:
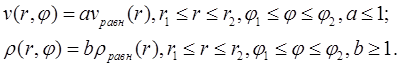
Параметры
возмущения для представленного расчета выбираются следующими: ![]() Область возмущения содержит
две ячейки по r и пять ячеек по φ.
Область возмущения содержит
две ячейки по r и пять ячеек по φ.
На Рис. 16 представлена анимация плотности течения с цветовой заливкой до момента времени, соответствующего одиннадцати оборотам диска. Из расчетов видно, что малое возмущение, эмулирующее попадание тяжелого тела в область диска и внесенное в равновесное состояние, развивается, и со временем происходит образование крупных вихревых структур, захватывающих значительную часть расчетной области и существующих на протяжении всего расчета. Возмущение приводит к перестройке течения во всей расчетной области, при этом образовавшееся течение качественно напоминает течение, возникшее в предыдущей задаче после потери течением симметрии (Рис. 15b), но здесь такое течение образовалось раньше, поскольку изначально не обладало симметрией.
Рис. 16. Анимация
плотности с цветовой заливкой для диска с кеплеровским
распределением скорости при задании локального возмущения до момента
времени, соответствующего одиннадцати оборотам диска.
Поведение углового момента качественно повторяет поведение углового момента для рассмотренной выше задачи, поэтому мы не будем приводить здесь анализ поведения углового момента. Отметим, что крупные вихревые структуры приводят к отводу углового момента через внешнюю границу и увеличению внутренней аккреции.
Таким образом, проведенные исследования и визуальный анализ подтверждают, что для Кеплеровского диска качественно верны полученные результаты для равновесного аккреционного диска с околокеплеровским распределением скорости.
Использование современных способов визуализации результатов научных расчетов позволило изучить свойства вихревых течений, возникающих в аккреционных звездных дисках в результате развития неустойчивости. Это, в свою очередь, позволило предложить механизм переноса углового момента к внешним частям диска образующимися в результате развития неустойчивости крупными вихревыми структурами. Отвод момента ведет к аккреции вещества на центральное гравитирующее тело и вызывает наблюдаемое излучение.
Работа выполнена при поддержке грантов РФФИ 12-01-00606, 12-02-00687, Программ Президиума РАН №15 и №21, ведущей научной школы России НШ-6061.2014.2.
1. Бондарев А.Е., Галактионов В.А., Чечеткин В.М.. Научная визуализация в задачах вычислительной механики жидкости и газа. – Научная визуализация, М.: 2010, т. 2, № 4, с. 1-26. URL: http://sv-journal.com/2010-4/01.php?lang=ru
2. Абакумов М.В., Луговский А.Ю.. О методах визуализации сеточных данных и их реализации в прикладной программе ClcView. – Научная визуализация, М.: 2014, т. 6, № 1, с. 68 - 105. URL: http://sv-journal.com/2014-1/05.php?lang=ru
3. Луговский А.Ю., Мухин С.И., Попов Ю.П., Чечеткин В.М.. Численные методы для моделирования развития турбулентности в аккреционных дисках. – Препринт. МАКС Пресс, М.: 2003.
4. Абакумов М.В., Мухин С.И., Попов Ю.П., Чечеткин В.М.. Сравнение результатов математического моделирования структуры аккреционного диска двойной звездной системы в двумерном и трехмерном приближении. – Астрономический журнал, М.:2003, т. 80, № 1, с. 14-22.
5. Абакумов М.В., Мухин С.И., Попов Ю.П., Чечеткин В.М.. Стационарные дисковые структуры около гравитирующих компактных объектов. – Астрономический журнал, М.: 1996, т. 73, № 3, с. 407-418.
6. Луговский А.Ю., Мухин С.И., Попов Ю.П., Чечеткин В.М.. Эволюция мелкомасштабных возмущений в аккреционных дисках. – Препринт. МАКС Пресс, М.: 2005.
7. Велихов Е.П., Луговский А.Ю., Мухин С.И., Попов Ю.П., Чечеткин В.М.. Роль крупномасштабной турбулентности в перераспределении углового момента в аккреционных звездных дисках. – Астрономический журнал, М.: 2007, т. 84, № 2, с. 177-184.
8. Луговский А.Ю., Мухин С.И., Попов Ю.П., Чечеткин В.М.. Развитие крупномасштабной неустойчивости в аккреционных звездных дисках и ее влияние на перераспределение углового момента. – Астрономический журнал, М.: 2008, т. 85, № 8, с. 901-905.
9. Луговский А.Ю., Чечеткин В.М.. Развитие крупномасштабной неустойчивости в Кеплеровских аккреционных звездных дисках. – Астрономический журнал, М.: 2012, т. 89, № 2, с. 120-127.
MATHEMATICAL
MODELING AND VISUALIZATION
OF MATTER FLOWS IN ACCRETION STELLAR DISKS
A. Lugovsky1,2, M. Abakumov3, V. Chechetkin1,2,4
1 Keldysh Institute for Applied Mathematics RAS, Moscow, Russian Federation
2 National Research Centre “Kurchatov Institute”, Moscow, Russian Federation
3 Lomonosov Moscow State University, Moscow, Russian Federation
4 National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Moscow, Russian Federation
alex_lugovsky@mail.ru, vmabk@yandex.ru, chechetv@gmail.com
Abstract
In recent years large amount of observational data on stellar accretion disks obtained. Numerical simulations are virtually the only way to a comprehensive study of such astrophysical objects. The calculations produced vast amounts of information, so their visualization is not only a way to look, but also research. The results of the simulation and study by using a visual representation of the structure of gasdynamic flows in these discs with gravity are shown. A new mechanism that defines and characterizes the accretion (fall) of the matter to the central body is proposed. The problem of the emergence and development of large-scale vortex motion in shear flow of the accretion disk is considered in the article. The mechanism of angular momentum transfer by large vortex structures arising from the initial development of small perturbations is investigated. Considered problems involve a huge amount of computational work so they carried out on multiprocessor computer systems. Visualization of the calculations in these problems is the method of research and study of the flows structure. Animation of the calculations allows to trace the evolution of flows. Comparison of flow patterns for different characteristics in the form of contour lines gives a visual representation of the vortex flow structure. Allocation of investigated subdomains and use special palettes as well as narrowing of the considered variation range of the flow characteristics provide an opportunity to study small-scale features of the flow.
Key words: visualization in astrophysics, accretion stellar disks, angular momentum, ClcView.
References
1. A. E. Bondarev, V. A. Galaktionov, V. M. Chechetkin. Scientific Visualization for Computational Fluid Dynamics. Scientific Visualization. vol. 2, no 4, 2010, pp. 1 - 26. Available at: http://sv-journal.com/2010-4/01.php
2. M. V. Abakumov, A. Yu. Lugovsky. About Visualization Methods of Grid Data and their Implementation in the Application Program ClcView. Scientific Visualization. vol. 6, no 1, 2014, pp. 68 - 105. Available at: http://sv-journal.com/2014-1/05.php
3. A. Yu. Lugovskii, S. I. Mukhin, Yu. P. Popov, V. M. Chechetkin. Chislennye metody dlya modelirovaniya razvitiya turbulentnosti v akkretsionnykh diskakh [Numerical Methods for Turbulence Modelling in Accretion Disks]. MAKS Press, Мoscow, 2003.
4. M. V. Abakumov, S. I. Mukhin, Yu. P. Popov, V. M. Chechetkin. Comparison B etween Two-and Three-Dimensional Modeling of the Structure of an Accretion Disk in a Binary System. Astronomy Reports, vol. 47, no 1, 2003, pp. 11-19.
5. M. V. Abakumov, S. I. Mukhin, Yu. P. Popov, V. M. Chechetkin. Studies of Equilibrium Configurations for a Gaseous Cloud Near a Gravitating Center. Astronomy Reports, vol. 40, no 3, 1996, pp. 366-377.
6. A. Yu. Lugovskii, S. I. Mukhin, Yu. P. Popov, V. M. Chechetkin. Evolyutsiya melkomasshtabnykh vozmuscheniy v akkretsionnykh diskakh [The Evolution of Small-Scale Perturbations in Accretion Disks], MAKS Press, Мoscow, 2005.
7. E. P. Velikhov, A. Yu. Lugovskii, S. I. Mukhin, et al. The Impact of Large-Scale Turbulence on the Redistribution of Angular Momentum in Stellar Accretion Disks. Astronomy Reports, vol. 51, no 2, 2007, pp. 154-160.
8. A. Yu. Lugovskii, S. I. Mukhin, Yu. P. Popov, V. M. Chechetkin. The Development of Large-Scale Instability in Stellar Accretion Disks and its Influence on the Redistribution of Angular Momentum. Astronomy Reports, vol. 52, no 10, 2008, pp. 811-814.
9. A. Yu. Lugovskii, V. M. Chechetkin. The Development of Large-Scale Instability in Keplerian Stellar Accretion Disks. Astronomy Reports, vol. 56, no 2, 2012, pp. 96-103.