Разработка
мультиплатформенной библиотеки
построения и визуализации диаграмм
К. Рябинин
ООО «Ньюлана», Пермь, Россия
Оглавление
4. Центрирование объектов в NChart3D
Статья посвящена вопросу разработки высокопроизводительной библиотеки построения диаграмм и графиков, совместимой с настольными компьютерами и мобильными устройствами.
Проведённое исследование рынка программного обеспечения показало, что на сегодняшний день существует довольно мало универсальных мультиплатформенных средств построения диаграмм, хотя этот вид наглядного представления данных является одним из самых популярных как в контексте научной визуализации, так и в контексте деловой графики. В российской IT-компании ООО «Ньюлана» (г. Пермь) была разработана библиотека NChart3D, отвечающая ряду концептуальных требований:
1) мультиплатформенность;
2) высокая производительность;
3) высокое визуальное качество генерируемого изображения;
4) независимость от предметной области;
5) расширяемость;
6) гибкий и удобный API.
Библиотека была успешно протестирована на настольных компьютерах под управлением Windows, GNU/Linux и OS X, а также на мобильных устройствах под управлением iOS и Android.
В статье рассматривается архитектура библиотеки и приводятся описания решений основных задач визуализации, в частности, задачи сглаживания границ объектов на изображении и задачи размещения диаграммы в некоторой области на экране. Кроме того, описываются особенности практического использования библиотеки прикладными программистами.
Ключевые слова: мобильные устройства, мультиплатформенная визуализация, диаграммы, графики, OpenGL, OpenGLES, Direct3D.
Построение диаграмм является одним из самых распространённых и востребованных способов визуализации числовых данных. В связи с этим существует большое количество различных библиотек, позволяющих программистам быстро встраивать в свои приложения компоненты отображения диаграмм и графиков. Однако на сегодняшний день ощущается острая нехватка мультиплатформенных решений для данного вида визуализации, то есть таких библиотек, которые можно было бы использовать одновременно и на настольных компьютерах, и на мобильных устройствах. При этом, ввиду широкой популярности и всё возрастающей вычислительной мощности мобильных устройств, вопрос мультиплатформенности становится всё более актуальным.
В ходе проведённого маркетингового исследования было выяснено, что библиотеки построения диаграмм пользуются спросом на рынке программного обеспечения, а потому большинство популярных решений являются платными. Для достижения мультиплатформенности, как правило, используется Web-ориентированный подход и соответствующие библиотеки реализованы с использованием JavaScript и Flash. Примерами таких библиотек являются Highcharts [1] и FusionCharts [2]. Однако на сегодняшний день Web-приложения ещё сильно уступают нативным в плане производительности, в особенности на мобильных устройствах. Так, например, на устройствах под управлением iOS в Web-приложениях невозможно использовать аппаратное ускорение графики средствами WebGL. Ввиду того, что в контексте научной визуализации производительность и возможность обрабатывать большие объёмы данных являются критичными аспектами, нативные приложения в общем случае оказываются более адекватны возникающим в науке задачам.
Также было выяснено, что в большинстве случаев создатели библиотек построения диаграмм концентрируют своё внимание на довольно простой бизнес-графике, обеспечивая поддержку лишь двумерной визуализации. При этом в задачах естественных наук или многомерного эконометрического анализа часто возникает потребность в трёхмерной графике, а иногда даже в графике высших порядков.
Наибольшую функциональность из проанализированных нами программных средств предоставляет коммерческий продукт Three D Charts [3]. Этот продукт можно назвать мультиплатформенным, так как он имеет пригодное для портирования на любую платформу ядро, написанное на C++, обёртку, написанную на Java, Web-версию на основе технологии Flex [4], версию, совместимую с Crystal Reports [5] и версию для iOS. Three D Charts предоставляет большое количество различных двумерных и трёхмерных видов диаграмм и графиков, может быть использован для решения широкого спектра задач, однако является достаточно тяжеловесным и сложным в изучении.
Свободным аналогом Three D Charts можно считать библиотеку MathGL [6]. Данная библиотека поддерживает более 50 различных типов диаграмм, включая специализированные, востребованные в естественных науках (например, типы для отображения векторных полей, потоков, изолиний и изоповерхностей). Она является кроссплатформенной, но при этом применяется лишь на платформах для настольных компьютеров. Единственным шагом к мультиплатформенности (потенциальной поддержке мобильных устройств) является наличие интерфейса на языке JavaScript. Однако подход на базе Web-приложений, как уже было отмечено, в общем случае плохо подходит для задач научной визуализации.
На основе проведённого маркетингового исследования был сделан вывод о том, что создание легковесной и высокопроизводительной мультиплатформенной библиотеки для построения диаграмм оказалось бы полезным в контексте научной визуализации и даже могло бы иметь определённый коммерческий успех.
Целью описываемой работы было создание библиотеки построения двумерных и трёхмерных диаграмм, отвечающей следующим требованиям:
1) мультиплатформенность;
2) высокая производительность;
3) высокое визуальное качество генерируемого изображения;
4) независимость от предметной области;
5) расширяемость;
6) гибкий и удобный API.
Библиотека, получившая название NChart3D, была реализована и внедрена в IT-компании ООО «Ньюлана» [7] (Россия, г. Пермь). Демонстрационный прототип NChart3D был успешно протестирован на мобильных устройствах под управлением операционных систем iOS, Android и на настольных компьютерах под управлением Windows, GNU/Linux и OS X. Версия для iOS на данный момент доведена до промышленного продукта [8].
Библиотека NChart3D является самостоятельным программным продуктом, но ввиду своей универсальности и пригодности для отображения разнородных данных была интегрирована в систему научной визуализации SciVi [9, 10].
Для достижения мультиплатформенности было принято решение использовать в качестве языка реализации C++, так как программы, написанные на этом языке, могут быть скомпилированы и скомпонованы под большую часть существующих операционных систем. В качестве наиболее приоритетных операционных систем были выбраны iOS и Android со стороны мобильных устройств и Windows, GNU/Linux и OS X со стороны настольных компьютеров. Такой выбор был сделан на основе анализа состояния рынка программного обеспечения. Библиотеки, написанные на C++, достаточно легко интегрируются в приложения на всех перечисленных платформах. Относительную сложность представляет лишь Android, так как там использование модулей, написанных на C++, возможно лишь посредством технологии JNI [11]. Однако данная проблема легко решается созданием обёртки на языке Java, инкапсулирующей в себе всю работу с JNI и предоставляющей пользователю API библиотеки в привычном для данной операционной системы виде.
Подсистема вывода графики была организована на основе стандартов визуализации OpenGL(ES) и Direct3D. OpenGL(ES) поддерживается на всех выбранных платформах и, кроме того, его использование обеспечивает высокую производительность рендеринга за счёт аппаратного ускорения графики. Однако на операционных системах семейства Windows ещё более эффективным оказывается использование нативного графического API Direct3D.
Высокой производительности при обработке данных удалось достичь путём низкоуровневых оптимизаций наиболее затратных по времени алгоритмов, а также участков кода, производящих работу с памятью. Благодаря использованию языка С++ такие оптимизации оказались возможными.
Высокое качество изображения достигнуто путём использования эффектов освещения, реализуемых посредством аппарата шейдеров, а также за счёт адаптивного и адаптируемого сглаживания границ объектов. Кроме того, была решена задача автоматической подгонки размера и положения диаграммы под заданную область на экране. Более подробно об этих двух методах рассказано в разделах 3 и 4 соответственно.
Независимость от предметной области достигнута за счёт использования в API библиотеки предельно общих понятий, таких как «источник данных», «график», «точка графика» и т. д. Таким образом, NChart3D является универсальным инструментом, пригодным для визуализации данных в различных предметных областях, например, в естественных науках, экономике, в задачах математической статистики и т. п.
Расширяемость NChart3D вытекает из использования принципов объектно-ориентированного программирования. При необходимости набор поддерживаемых типов диаграмм, способов отображения и настроек может быть расширен программистом путём добавления новых классов и переопределения методов.
Гибкость API и его удобство для прикладного разработчика, а также чёткость модульной структуры NChart3D достигаются путём использования паттерна проектирования Model-View-Controller. В соответствии с этим паттерном логика управления, запроса данных и отображения чётко разделяется и входит в состав библиотеки в виде самостоятельных модулей. Более подробно вопросы практического использования библиотеки рассматриваются в разделе 5.
Упрощённая диаграмма классов NChart3D приведена на рис. 1.
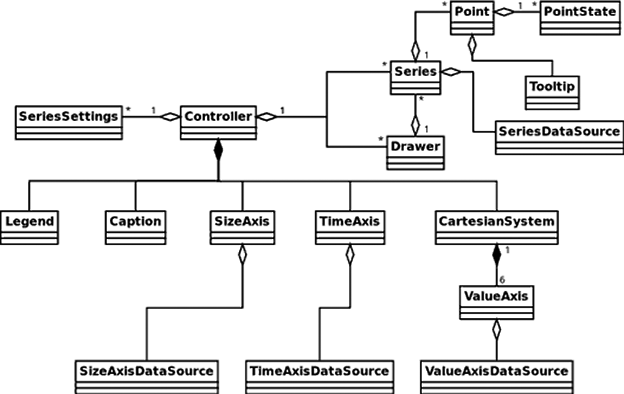
Рис. 1. UML-диаграмма классов NChart3D
Центральным классом иерархии является Controller, отвечающий за управление и агрегирующий в себе ссылки на все остальные модули NChart3D. Методы класса Controller позволяют программисту добавлять и удалять графики, управлять настройками, а также сообщать о командах, отданных пользователем. В своём конструкторе Controller создаёт все необходимые для функционирования библиотеки структуры данных, в частности экземпляры классов Legend, Caption, SizeAxis, TimeAxis и CartesianSystem.
Класс Legend отвечает за отображение легенды, предоставляя свойства и методы для её настройки. Легенда заполняется автоматически в процессе обновления данных. В неё попадают имена и пиктограммы всех графиков, добавленных в контроллер.
Класс Caption отвечает за заголовок диаграммы и может отображать произвольный текст.
Класс SizeAxis служит для настройки т. н. оси размера, которая используется для преобразования масштаба маркеров графика из заданных пользователем величин в пиксели экрана. Маркеры – это визуальное отображение точек графика. Их размер может нести смысловую нагрузку, будучи связанным через ось размера с числовыми значениями, хранящимися в точке. Например, в пузырьковой диаграмме размер пузырьков, как правило, отражает одно из измерений представляемых данных. Ось размера получает данные из специального источника, который может предоставить программист, реализовав интерфейс SizeAxisDataSource.
Класс TimeAxis содержит методы настройки оси времени. Данные для графиков могут содержать несколько временных срезов, и в этом случае при помощи оси времени можно будет осуществлять навигацию между ними. Ось времени представляет собой ползунок с нанесёнными на него от отметками, которые соответствуют временным срезам. Состояние графиков между соседними срезами вычисляется автоматически методом линейной интерполяции изменяющихся параметров. Данные для оси времени запрашиваются у класса, который реализует интерфейс TimeAxisDataSource.
Оси значений диаграммы объединены в класс CartesianSystem, олицетворяющий декартову систему координат. Этот класс содержит в себе 6 экземпляров класса ValueAxis, так как для каждой оси трёхмерного пространства имеется возможность использовать основной и дополнительный диапазоны значений. Каждый отображаемый график можно связывать с одним из диапазонов, и тем самым увеличивать читаемость диаграммы, отображающей одновременно несколько различных показателей. Данные для осей запрашиваются у класса, который реализует интерфейс ValueAxisDataSource.
Класс Series отвечает за конкретные графики. В NChart3D имеется отдельная иерархия различных типов графиков, которая может быть пополнена, в том числе, и прикладным программистом. Данные, которые будут отображены, запрашиваются у класса-источника, реализующего интерфейс SeriesDataSource, и по ним создаётся массив точек графика. Точки представляют собой экземпляры класса Point и содержат в себе массив временных срезов – экземпляров класса PointState. В том случае, если данные об изменении показателей во времени отсутствуют, временной срез полагается единственным. Временной срез описывает всё состояние отображаемого показателя в определённый момент времени. С ним могут быть связаны различные характеристики точки: внешний вид маркера точки (в роли маркеров могут быть использованы как простые геометрические формы, так и трёхмерные модели, загружаемые из файлов), цвет (или текстура), размер, углы поворота и положение в пространстве (относительно осей значений). С точкой также может быть связана всплывающая подсказка, представляющая собой экземпляр класса Tooltip и служащая для отображения контекстной информации. Отображаемой информацией управляет программист; например, он может выводить туда название показателя и интересующие значения из текущего временного среза.
Настройка внешнего вида графиков осуществляется двумя путями. Первый путь – это параметры, связанные с каждым графиком в отдельности. Их значения хранятся в полях классов этих графиков. Второй путь – это настройки, устанавливаемые одновременно для всех графиков одного типа. Их значения находятся в полях классов-потомков класса SeriesSettings. С каждым типом графика связан свой тип настроек.
Для оптимизации отрисовки графики одинаковых типов объединяются в более крупные структуры, за создание которых отвечают экземпляры класса Drawer. Drawer является корнем иерархии визуализаторов графиков. Создание экземпляров классов из этой иерархии происходит автоматически и работа с ними недоступна прикладному программисту. Однако если ему потребуется расширить библиотеку дополнительными типами графиков, он должен будет реализовать для них и соответствующие визуализаторы. Визуализатор хранит в себе ссылки на все графики того типа, на который он рассчитан и, используя все доступные настройки, создаёт структуры данных, необходимые для отображения. При этом автоматически происходят оптимизации по памяти, и структуры данных строятся таким образом, чтобы количество вызовов функций графического API для отрисовки оказалось минимальным. Это позволяет максимально увеличить производительность рендеринга.
NChart3D базируется на двух других фреймворках, также разработанных в компании ООО «Ньюлана»: NFoundation и NGraphics. NFoundation предоставляет уровень абстракции от операционной системы и набор инструментов, полезных для решения типовых задач. По своей архитектуре и функциональности он схож с Boost и Apple Foundation и включает в себя методы для:
•динамического распределения памяти (умные указатели и защищённое выделение памяти);
•работы с внешними ресурсами (независимые от операционной системы модули для чтения и записи файлов, потокового ввода-вывода, кодирования и декодирования изображений, разбора XML и т. д.);
•работы с сетью (сокеты, шифрование, http-запросы и т. д.);
•управления потоками (создание, настройка и синхронизация потоков, вызов функций из одного потока в другом);
•объявления функций обратного вызова и делегатов (структуры данных для организации функций обратного вызова, в том числе таких, которые выполнялись бы в главном потоке, будучи вызванными из второстепенного и абстрактные классы для организации интерфейсов);
•работы с контейнерами (динамические массивы, множества, словари и т. д.);
•вычисления математических функций и решения типовых задач (общая математика, тригонометрия, основные алгоритмы сортировки и оптимизации).
NGraphics используется в качестве подсистемы вывода графики, являясь обёрткой над низкоуровневыми функциями графического API. Он поддерживает:
• универсальную абстракцию от графического API, которая может использовать для построения изображений OpenGL, OpenGLES, Direct3D 9 и Direct3D 11;
• работу с вершинными и фрагментными шейдерами;
• потокобезопасность с возможностью размещать рендеринг и обработку системных событий в разных потоках;
• работу с графом сцены;
• аффинные преобразования на основе аппарата матриц и кватернионов;
• рендеринг в текстуру и постобработку полученного изображения;
• средства растеризации текста и векторных контуров.
В качестве платформы, под которую ведётся первичная разработка (реализация и отладка новых функций) была выбрана iOS, так как она поддерживает прозрачную интеграцию с кодом, написанным на C++ и, при этом, является мобильной платформой, а значит, на ней может быть выявлено большинство ограничений, присущих мобильным устройствам. К таким ограничениям можно отнести, например, меньший по сравнению с настольными компьютерами объём оперативной памяти, более низкую тактовую частоту процессора и необходимость минимизировать энергопотребление в процессе работы приложения.
Для снижения энергетических затрат (и, как следствие, избежания перегрева мобильного устройства) перерисовка сцены происходит «по требованию», то есть только в тех случаях, когда изменились визуальные характеристики объектов, такие как цвет, положение и т. д.
Пример диаграммы, построенной при помощи библиотеки NChart3D, приведён на рис. 2.
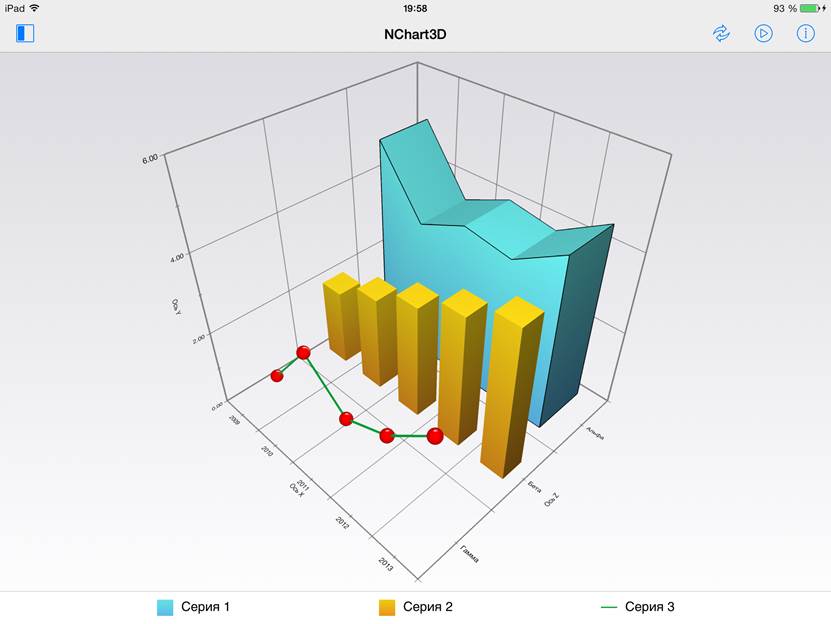
Рис. 2. Пример диаграммы, построенной при помощи NChart3D
Ступенчатость границ объектов, неизбежно возникающая на этапе растеризации сцены, заметно снижает визуальное качество результирующего изображения. В связи с этим, важным этапом в процессе визуализации является сглаживание границ (антиалиасинг), нивелирующее ступенчатость. Большинство современных платформ поддерживают антиалиасинг на аппаратном уровне. Чаще всего для этого используется алгоритм мультисемплинга (MSAA) [12], дающий высококачественный результат. Однако с использованием системного антиалиасинга связан ряд проблем:
1) падение производительности;
2) появление артефактов нежелательного размытия некоторых объектов;
3) нарушение мультиплатформенности.
Первая проблема является наиболее существенной. Нами было зарегистрировано в среднем трёхкратное снижение производительности при использовании системного антиалиасинга на мобильных устройствах. Так, например, сцена, состоящая из 1 600 000 треугольников на устройстве iPad 3 без антиалиасинга визуализируется со скоростью 15 FPS (что является достаточным для воспроизведения плавных анимаций), а со включенным системным антиалиасингом – со скоростью всего 5 FPS (что уже нарушает плавность движений). Данная проблема может быть частично решена выключением антиалиасинга на периоды воспроизведения анимаций, так как ступенчатость границ у движущихся объектов менее заметна. Однако включение и выключение системного антиалиасинга в общем случае занимает достаточно много времени – по нашим оценкам в худшем случае до 1000 миллисекунд. Такая задержка перед началом каждой анимации (включая изменение сцены в ответ на команды пользователя) является неприемлемой для графических систем реального времени.
Вторая проблема проявляется лишь в некоторых случаях. Так, например, линии, параллельные сторонам экрана, размываются, если координаты порождающих их вершин в результате преобразований оказываются дробными. Зачастую весьма нетривиально подобрать начальные значения координат такими, чтобы в результате преобразований сцены они становились целыми. При этом в условиях отображения диаграмм наличие строго вертикальных и строго горизонтальных линий является частой ситуацией (например, оси координат и линии сетки). Решением было бы исключение подобного рода объектов из того множества, которое подвергается антиалиасингу. Однако системный антиалиасинг воздействует на весь буфер кадра целиком, и применить его лишь к части сцены невозможно.
Третья проблема связана с тем, что системное сглаживание на разных платформах управляется по-разному. Таким образом, при его использовании увеличилось бы количество платформенно-зависимого кода.
Общим решением всех вышеперечисленных проблем является разработка собственного способа антиалиасинга, который не зависел бы от системного.
Нами было проанализировано достаточно большое количество различных алгоритмов и предложена следующая их классификация:
1) алгоритмы времени рендеринга (например, SSAA [13], MSAA [12] и CSAA [14]);
2) алгоритмы постобработки (например, MLAA [15] и FXAA [16]);
3) алгоритмы, использующие многопроходный рендеринг (например, DMSAA [17], TXAA [18]).
Было выяснено, что из списка изученных алгоритмов для использования на мобильных устройствах наиболее хорошо подходят SSAA и FXAA. Чтобы сохранить мультиплатформенность, было решено использовать именно их.
Принцип SSAA состоит в том, что сцена визуализируется в текстуру большего разрешения, чем итоговое изображение. Затем текстура накладывается на полноэкранный спрайт и в результате фильтрации (при уменьшении) ступенчатые границы объектов оказываются сглаженными.
Принцип FXAA состоит в том, что на этапе постобработки изображения происходит поиск ступенек на границах и их размытие в перпендикулярном им направлении. Данный алгоритм основывается на конволюции изображения и может быть реализован во фрагментном шейдере.
В классической реализации этих алгоритмов производительность SSAA на тестовой сцене (1 600 000 треугольников) на iPad 3 составила 4,5 FPS, а FXAA – 8 FPS. Однако по отдельности данные алгоритмы не обеспечивают достаточно высокого визуального качества результата. В связи с этим было принято решение использовать их суперпозицию.
Идея суперпозиции состоит в том, что сцена визуализируется с использованием SSAA, а затем результат подвергается постобработке при помощи FXAA, то есть сначала происходит рендеринг сцены в текстуру размера, превосходящего размер экрана, а затем эта текстура накладывается на полноэкранный спрайт с использованием шейдера FXAA.
Оба алгоритма были нами оптимизированы для более эффективной работы на мобильных устройствах. Эффективность работы на настольных компьютерах в результате произведённых изменений также возросла, однако там прирост производительности оказывается менее заметен ввиду большей вычислительной мощности оборудования. Для SSAA нами был введён переменный коэффициент суперсемплинга (увеличения текстуры по сравнению с итоговым изображением), автоматически корректирующийся в зависимости от максимального поддерживаемого размера текстуры. Это позволило сделать SSAA применимым на широком классе различных устройств. Для FXAA нами был произведён ряд оптимизаций кода шейдера с учётом аппаратных особенностей графических процессоров. В результате этого удалось увеличить скорость визулизации сцены с использованием FXAA с 8 до 10 FPS.
Теоретически было доказано,
что средняя сложность суперпозиции этих алгоритмов равна средней сложности SSAA
и может быть выражена как 
где n
– количество вершин на сцене, s – коэффициент суперсемплинга, w –
ширина и h – высота экрана. Этот результат был подтверждён на практике.
Так, например, скорость визуализации тестовой сцены с использованием
суперпозиции SSAA и FXAA составила 4.5 FPS. Изображение, полученное с
применением предложенного метода антиалиасинга приведено на рис. 3.
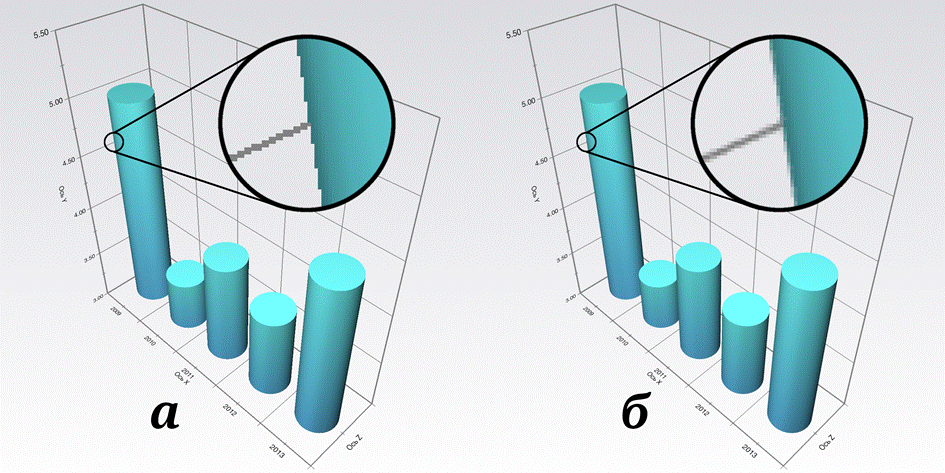
Рис. 3. Изображение без использования антиалиасинга (а) и
с использованием суперпозиции SSAA и FXAA (б)
Хотя производительность у предложенного метода антиалиасинга ниже, чем у системного, он может быть быстро отключен (на это требуется время, равное прорисовке одного кадра) и так же быстро включен вновь. Благодаря этому удалось добиться быстрого отклика системы визуализации на команды пользователя и иные события, вызывающие изменение сцены.
Адаптивность метода заключается в автоматической подстройке под особенности аппаратного обеспечения (подборе коэффициента суперсемплинга) и автоматическом отключении на периоды воспроизведения анимаций.
По визуальному качеству результата предложенный метод антиалиасинга не уступает системному, а в некоторых случаях даже превосходит его. Для того, чтобы можно было комбинировать объекты с антиалиасингом и без на одной сцене, был реализован метод послойного рендеринга: все объекты сцены объединяются программистом в группы (слои) и каждая группа может быть визуализирована либо напрямую на экран, либо через текстуру с применением предложенного метода антиалиасинга. Таким образом появляется возможность избежать нежелательного размытия объектов, чьи границы заведомо параллельны границам экрана и антиалиасинг становится адаптируемым.
Как уже отмечалось ранее, предложенный метод антиалиасинга является мультиплатформенным, так как работает и на настольных компьютерах, и на мобильных устройствах. Таким образом, он решает все проблемы, присущие системному антиалиасингу, сохраняя при этом высокое визуальное качество результирующего изображения.
4. Центрирование объектов в NChart3D
Визуализация всех элементов диаграммы, включая легенду, заголовок и все подписи осуществляется при помощи фреймворка NGraphics, который, в свою очередь, работает через низкоуровневое графическое API OpenGL(ES) или Direct3D. Такой подход обеспечивает высокое быстродействие (так как отсутствует переключение между различными графическими API в процессе отрисовки) и сохраняет мультиплатформенность (так как код отображения всех частей диаграммы оказывается единообразным и портируемым). Ввиду этого, с каждым из элементов диаграммы связаны свои матрицы преобразования и проекции.
Второстепенные элементы, такие как легенда, заголовок и подписи выводятся в виде спрайтов в ортогональной проекции, соответствующий параллелепипед видимости которой по ширине и высоте равняется экрану. Таким образом, сценические координаты спрайтов, отвечающих за отображение этих элементов, совпадают с экранными координатами элементов, и расположение их на экране является тривиальной задачей.
Для самой диаграммы преобразования устроены более сложно. С целью обеспечения единообразной работы двумерного и трёхмерного режима отображения, координаты вершин, из которых складываются полигоны графиков, задаются в интервале от 0 до 1.
В двумерном режиме используется ортогональная проекция с параллелепипедом видимости, центр которого находится в нуле, длина и ширина равны 2, а глубина равна 10. Значение глубины здесь задаётся с некоторым запасом на тот случай, если в качестве маркеров диаграммы будут использованы трёхмерные модели, имеющие определённую протяжённость по оси Z. Матрица камеры при этом формируется следующим образом:
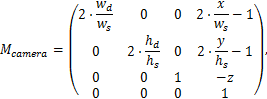
где 
– ширина и
высота экрана, 
– ширина и
высота области диаграммы в экранных координатах, 
– экранные координаты левого нижнего угла области
диаграммы, z – половина максимальной протяжённости по оси Z
использованных на диаграмме трёхмерных моделей. Данная матрица производит
смещение сцены в зону диаграммы и масштабирование сцены к размеру этой зоны. В
дальнейшем все преобразования для объектов диаграммы строятся по принципу
где 
– матрица
преобразования объекта в пространстве диаграммы. Во время отрисовки объектов
диаграммы в двумерном режиме включается блокировка буфера кадра для областей,
лежащих за пределами области диаграммы (scissor test). Таким образом, объекты
не могут быть отрисованы за пределами отведённого для них места.
В трёхмерном режиме по выбору
программиста может быть использована как ортогональная, так и перспективная
проекция. В обоих случаях область видимости (параллелепипед или усечённая
пирамида соответственно) имеет схожие характеристики (обозначения аналогичны
предыдущей формуле): её центр имеет координаты 
глубина
равна 10, а соотношение сторон равно 
Смещение
центра по приведённой формуле необходимо для совмещения центров области
видимости и области диаграммы. Если центр области видимости останется в нуле, а
смещение объектов диаграммы к центру области диаграммы будет организовано через
матрицу преобразования камеры, то при достаточно больших относительно размеров
экрана значениях смещений в перспективной проекции будут наблюдаться заметные
перспективные искажения. Данная ситуация продемонстрирована на рис. 4 (а). При
смещении центра области видимости искажений объектов не возникает, как показано
на рис. 4 (б).
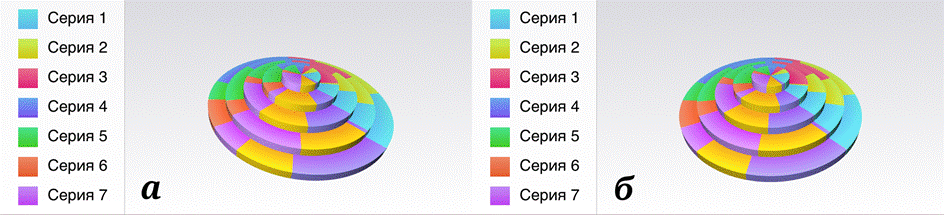
Рис. 4. Сцена со смещением объектов (а) и смещением проекции (б)
Формула для смещения выведена следующим образом. На рис. 5 представлена одна из возможных ситуаций расположения области диаграммы на экране.
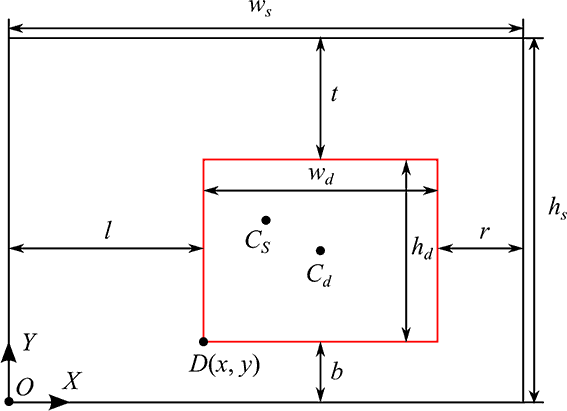
Рис. 5. Пример расположения области диаграммы на экране
Область диаграммы имеет
красный контур, а экран – чёрный, r, l, b, t –
расстояния от области диаграммы до границ экрана, – ширина и
высота экрана, – ширина и
высота области диаграммы, 
– центр
экрана, 
– центр
области диаграммы, 
–
левый нижний угол области диаграммы. Все координаты являются экранными, начало
экранной системы координат находится в левом нижнем углу экрана (это
обусловлено использованием низкоуровневого графического API OpenGL(ES) и
Direct3D). Для того, чтобы совместить точку с точкой 
необходимо
сместить область диаграммы на 
по оси X,
и на 
по оси Y.
Для расстояний r, l, b, t справедливы следующие
соотношения:
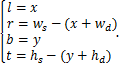
Смещение должно воздействовать на центр параллелепипеда (либо усечённой пирамиды видимости), который, в соответствии с использованным аппаратом проекций, задаётся в нормированных координатах устройства (NDC) [19]. Так как NDC представляет собой куб с центром в нуле и длиной стороны, равной 2, который отображается на экран, расстояния по осям X и Y могут быть переведены из экранных координат в NDC по формулам
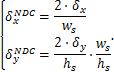
Следовательно, смещение в NDC имеет вид:
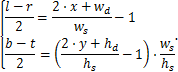
Преобразование камеры в трёхмерном режиме включает в себя дополнительное смещение объектов на сцене в плоскости XOZ (соответствующее перемещению диаграммы пользователем), масштаб и повороты вокруг осей X и Y.
При первом отображении для диаграммы по заданным начальным углам поворота автоматически вычисляются такие смещение и масштаб, чтобы она заняла максимальную площадь в отведённой ей области, но при этом не вышла за границы. Вычисление производится на основе бинарного поиска и эвристик. Диапазон поиска смещения вытекает из вида NDC: координаты x и z могут меняться от -1 до 1. Диапазон поиска масштаба является эвристикой: экспериментально было установлено, что в большинстве случаев нужный масштаб лежит в пределах от 0.1 до 3. Эвристикой также является порядок поиска значений. Было выяснено, что наиболее качественный результат с минимальным количеством «холостых» итераций (итераций поиска, не дающих визуального улучшения результата) достигается при следующем порядке поиска:
1) найти смещение по x и z, обеспечивающее центровку диаграммы;
2) найти масштаб, обеспечивающий максимальную близость диаграммы к границам области;
3) повторить шаг (1);
4) повторить шаг (2).
Для произведения бинарного поиска сначала определяется ограничивающий параллелепипед для множества объектов диаграммы. Затем, на каждой итерации поиска по текущим значениям углов поворота, смещения и масштаба строится матрица камеры – такая, которая использовалась бы для объектов диаграммы. Эта матрица перемножается с матрицей проекции, а результат последовательно умножается на координаты всех 8 вершин ограничивающего параллелепипеда. Таким образом определяются координаты этих вершин в NDC. Аппликаты полученных координат отбрасываются, а из нормированных абсцисс и ординат выбираются минимальные и максимальные.
Критерием для бинарного поиска смещения является равенство расстояний по осям X и Y от преобразованного ограничивающего параллелепипеда до границ области диаграммы, то есть
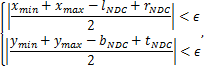
где 
и 
–
соответственно минимальные и максимальные координаты преобразованных вершин
ограничивающего параллелепипеда, 
–
расстояния от границ области диаграммы до границ экрана, приведённые к NDC, 
– эвристический параметр, отвечающий за точность
поиска.
Критерием для бинарного поиска масштаба является равенство размера преобразованного ограничивающего параллелепипеда размеру области диаграммы, то есть
Для обоих критериев
экспериментально было подобрано значение 
Максимальное количество итераций описанного алгоритма центрирования может быть выражено как
где 
– диапазоны
поиска смещения и масштаба соответственно. Таким образом, алгоритм имеет
логарифмическую сложность. С учётом указанных ранее числовых значений,
максимальное количество итераций поиска равно 32. Использование данного
алгоритма не наносит ущерба производительности, так как, во-первых, он
выполняется только один раз после обновления данных диаграммы (чтобы определить
начальные значения трансформации для первого показа), а во-вторых, в среднем
время его исполнения на устройстве iPad 3 составляет всего одну миллисекунду.
Описанный алгоритм позволяет определить оптимальные положения и размер для произвольной группы трёхмерных объектов, для которых заданы определённые углы поворота и определённая проекция. В совокупности с заданием соответствующих проекций и подбором начальных углов поворота, при помощи этого алгоритма удалось автоматизировать настройку первого показа элементов диаграммы – т. н. вида по умолчанию, состояния, в котором находится диаграмма до каких-либо навигационных действия со стороны пользователя.
Библиотека NChart3D предоставляет программисту возможность построения и визуализации двумерных и трёхмерных интерактивных диаграмм следующих типов:
1)вертикальные и горизонтальные колонки;
2)диаграммы с областями;
3)линейные диаграммы, ступенчатые диаграммы
и графики функций вида 
причём
f может иметь разрывы;
4)круговые и кольцевые диаграммы;
5)пузырьковые диаграммы;
6)диаграммы рассеивания;
7)японские свечи;
8)OHLC-диаграммы;
9)полосы;
10)диаграммы, отображающие последовательности элементов;
11)поверхности по функциям вида 
причём f может иметь разрывы.
Типы (1)-(6) можно считать универсальными, так как они применимы в различных предметных областях для отображения количеств, долей и зависимостей каких-либо показателей. Для типов (1)-(3) помимо обычной оси абсолютных значений доступны также ось с процентными значениями и ось с накоплением. В случае, если имеется несколько различных показателей, эти виды осей могут быть использованы для оценки вклада каждого из показателей в общую сумму (ось с процентными значениями), а также количественной оценки всей суммы (ось с накоплением). Кроме того, в случае большого количества показателей, значения которых лежат в сильно отличающихся диапазонах, имеется возможность добавить дополнительную ось значений, чтобы сделать диаграмму более удобной для восприятия.
Типы (7)-(9) предназначены для отображения эконометрических данных, а именно – изменения цен на какие-либо товары с течением времени.
Тип (10) может быть использован для отображения цепочек элементов некоторого вида, например, цепочек азотистых оснований в последовательности ДНК.
Тип (11) востребован, в основном, в физике и математике, например, для построения поверхностей уровня или отображения двумерных данных.
Диаграммы, построенные средствами NChart3D, являются интерактивными: пользователь может изменять масштаб, пролистывать диаграммы на экране, а также выделять отдельные точки и получать по ним контекстную информацию во всплывающих подсказках. В режиме трёхмерного отображения поддерживаются также вращения диаграмм в пространстве.
Кроме того, NChart3D поддерживает целый ряд «презентационных» возможностей, позволяющих осуществлять эффектные анимационные переходы между диаграммами и подсвечивать отдельные группы данных. При изменении набора входных данных анимационный переход от старого состояния диаграммы к новому может быть осуществлён всего одним вызовом функции, принимающей параметрами направление перехода (от старого состояния к новому, или от нового к старому) и продолжительность анимации в секундах. Для выделения отдельных точек на диаграмме могут быть использованы цвет и смещение, при этом API-функции позволяют собирать целые анимационные последовательности изменения этих параметров во времени. Программно могут быть изменены размер, положение диаграммы на экране, а для трёхмерного режима отображения – и её поворот. Эти настройки могут применяться как мгновенно, так и в течение заданного времени по заданному закону интерполяции от старого состояния к новому. Пример презентационных возможностей NChart3D представлен в рекламном видеоролике, размещённом на YouTube [20].
Внешний вид элементов диаграммы является полностью настраиваемым: существуют API-функции для изменения цветов, шрифтов, толщин линий, отступов между элементами и т. д.
Входными данными для диаграмм могут служить числа в любых диапазонах. NChart3D автоматически определяет минимум, максимум и шаг делений на осях так, чтобы эти значения смотрелись наиболее эффектно: минимум и максимум округляются так, чтобы иметь в младшем разряде 0 или 5, а шаг делений определяется таким, чтобы количество делений было равно 3, 4 или 5. Однако программист всегда может переопределить значения минимума, максимума и шага по своему желанию.
Версия NChart3D для iOS была доведена до промышленного продукта. Чтобы облегчить труд программистов, привыкших писать под iOS с использованием только традиционных для данной ОС средств, для NChart3D была создана оболочка на языке Objective-C, совместимая с UIKit [21].
Пример использования NChart3D на языке Objective-C представлен в листинге 1.
Листинг 1. Пример использования NChart3D для построения простой диаграммы со столбцами
- (void)loadView
{
// Create a chart view that will display the chart.
m_view = [[NChartView alloc] initWithFrame:CGRectZero];
// Paste your license key here.
m_view.chart.licenseKey = @"";
// Margin to ensure some free space for the iOS status bar.
m_view.chart.cartesianSystem.margin = NChartMarginMake(10.0f, 10.0f, 10.0f, 20.0f);
// Create series that will be displayed on the chart.
NChartColumnSeries *series = [[NChartColumnSeries new] autorelease];
// Set brush that will fill that series with color.
series.brush = [NChartSolidColorBrush solidColorBrushWithColor:[UIColor colorWithRed:0.38f green:0.8f blue:0.91f alpha:1.0f]];
// Set data source for the series.
series.dataSource = self;
// Add series to the chart.
[m_view.chart addSeries:series];
// Update data in the chart.
[m_view.chart updateData];
// Set chart view to the controller.
self.view = m_view;
}
- (NSArray *)seriesDataSourcePointsForSeries:(NChartSeries *)series
{
// Create points with some data for the series.
NSMutableArray *result = [NSMutableArray array];
for (int i = 0; i <= 10; ++i)
[result addObject:[NChartPoint pointWithState:[NChartPointState pointStateAlignedToXWithX:i Y:(rand() % 30) + 1] forSeries:series]];
return result;
}
- (NSString *)seriesDataSourceNameForSeries:(NChartSeries *)series
{
// Get name of the series.
return @"My series";
}
Более подробная информация об использовании NChart3D может быть найдена в документации [22], размещённой на официальном сайте проекта.
Результатом описанной работы является библиотека построения диаграмм NChart3D, отвечающая всем заявленным требованиям:
1)мультиплатформенность достигнута путём написания кода библиотеки на языке C++ и использования абстракции от графического API;
2)высокая производительность обеспечена использованием аппаратного ускорения графики и произведением низкоуровневых оптимизаций вычислений и работы с памятью;
3)высокое визуальное качество достигнуто за счёт использования эффектов освещения, реализованных на основе аппарата шейдеров, сглаживания границ объектов и автоматической подгонки элементов диаграммы под размер отведённой для неё области;
4)независимость от предметной области обусловлена использованием в API библиотеки предельно общих понятий, таких, как «источник данных», «график», «точка графика» и т. д.;
5)расширяемость вытекает из принципов ООП, на которых построена библиотека, так как иерархия классов может быть в любой момент дополнена новыми сущностями, если того потребуют конкретные задачи;
6)гибкий и удобный API, с одной стороны, также является следствием использования принципов ООП, а с другой – использованием паттерна проектирования Model-View-Controller.
Разработанная библиотека успешно протестирована под управлением операционных систем iOS, Android, Windows, GNU/Linux и OS X, что доказывает её мультиплатформенность.
Скорость визуализации на устройстве iPad 3 на сцене, содержащей 800 000 вершин, объединённых в 1 600 000 треугольников, составляет 15 FPS, что является достаточным для воспроизведения плавных анимаций. Однако указанную нагрузку можно считать пиковой, так как в среднем случае диаграммы включают в себя в 3-4 раза меньшее количество полигонов. Обработка массивов данных, состоящих из 20 000 значений для простых типов диаграмм (например, двумерные столбцы) занимает на iPad 3 менее секунды, для сложных графиков (например, поверхность) – порядка двух секунд.
За счёт поддержки большого количества различных типов диаграмм, библиотека NChart3D может быть использована в различных предметных областях, например, в бизнес-аналитике и эконометрике (чаще всего там используются линейные, столбиковые, круговые диаграммы, диаграммы с областями и японские свечи), математике (там могут быть использованы линейные диаграммы и поверхность) и биологии (там могут быть использованы последовательность для представления цепочек ДНК, а также линейные и столбиковые диаграммы для представления данных популяционной статистики).
В дальнейшем планируется расширять возможности NChart3D путём добавления новых типов диаграмм и организации новых способов обработки данных. Кроме того, планируется довести до стадии промышленного продукта версии библиотеки под остальные платформы, на которых на данный момент был протестирован лишь демонстрационный прототип.
1. Библиотека Highcharts. URL: http://www.highcharts.com/
2. Библиотека FusionCharts. URL: http://www.fusioncharts.com/
3. Библиотека Three D Charts. URL: http://www.threedgraphics.com
4. Технология Flex. URL: http://flex.apache.org/
5. Система CrystalReports. URL: http://www.crystalreports.com/
6. Библиотека MathGL. URL: http://mathgl.sourceforge.net/doc_en/Main.html
7. Официальный сайт ООО «Ньюлана». URL: http://nulana.com/
8. Библиотека NChart3D. URL: http://nchart3d.com/nchart/
9. К. Рябинин. Разработка адаптивного мультиплатформенного визуализтора результатов научных расчётов для высокопроизводительных вычислительных систем // Scientific Visualization, 2012, Quart. 4, Vol. 4, Num. 4, P. 17-29. URL: http://sv-journal.com/2012-4/03.php?lang=ru
10. K. Ryabinin, S. Chuprina. Adaptive Scientific Visualization System for Desktop Computers and Mobile Devices // Procedia Computer Science, Vol. 18, 2013, P. 722-731. URL: http://www.sciencedirect.com/science/article/pii/S1877050913003797
11. Технология JNI. URL: http://java.sun.com/docs/books/jni/
12. Multisampling Anti-Aliasing: A Closeup View. URL: http://alt.3dcenter.org/artikel/multisampling_anti-aliasing/index_e.php"
13. M. Carmen Juan Lizandra. Graphic libraries for Windows programming // Crossroads, the ACM Student Magazine (ACM), 2000, Volume 6 Issue 4, Pages 14-18.
14. Coverage Sampling Antialiasing. URL: https://developer.nvidia.com/csaa-coverage-sampling-antialiasing
15. A. Reshetov. Morphological Antialiasing. URL: http://visual-computing.intel-research.net/publications/papers/2009/mlaa/mlaa.pdf
16. T. Lottes. Fast Approximate Antialiasing. URL: http://developer.download.nvidia.com/assets/gamedev/files/sdk/11/FXAA_WhitePaper.pdf
17. M. Pettineo. Deferred MSAA. http://mynameismjp.wordpress.com/2010/08/16/deferred-msaa/
18. Temporal Antialiasing. URL: http://www.geforce.com/hardware/technology/txaa/technology
19. Р. Райт-мл., Б. Липчак. OpenGL Cуперкнига // М.: Вильямс, 2006. С. 177-203.
20. Рекламный видеоролик NChart3D. URL: http://www.youtube.com/watch?v=KPmIYTKa00A
21. Apple UIKit Framework. URL: https://developer.apple.com/library/ios/documentation/uikit/reference/UIKit_Framework/_index.html
22. Официальная документация NChart3D. URL: http://nchart3d.com/nchart-doc/index.html
DEVELOPMENT OF MULTIPLATFORM CHARTING LIBRARY
K. Ryabinin
"Nulana LTD", Perm, Russian Federation
Annotation
This paper is devoted to the development of high-performance charting library that can be used on the mobile devices as well as on the desktop computers.
The research of the software market showed up, that there are only a few versatile multiplatform charting tools, though this kind of data visualization is very popular in science and business intelligence. The charting library called NChart3D was developed by Russian IT-company Nulana LTD (Perm). It meets the following requirements:
1) multiplatform portability;
2) high performance;
3) high visual quality of generated image;
4) independence of application domain;
5) extensibility;
6) flexible and convenient API.
This library was successfully tested on the desktop computers under Windows, GNU/Linux, OS X and on the mobile devices under iOS and Android.
In this paper we describe the architecture of NChart3D, our solutions of most important visualization tasks and examples of NChart3D usage. The tasks about system-independent anti-aliasing and about fitting the chart to the specified area on the screen are emphasized.
Key words: mobile devices, multiplatform visualization, charting, OpenGL, OpenGLES, Direct3D.
References
1. Highcharts Library. Available at: http://www.highcharts.com/
2. FusionCharts Library. Available at: http://www.fusioncharts.com/
3. Three D Charts Library. Available at: http://www.threedgraphics.com
4. Flex. Available at: http://flex.apache.org/
5. CrystalReports Available at: System. http://www.crystalreports.com/
6. MathGL Library. Available at: http://mathgl.sourceforge.net/doc_en/Main.html
7. Nulana LTD Official Website. Available at: http://nulana.com/
8. NChart3D Library. Available at: http://nchart3d.com/nchart/
9. K. Ryabinin. Development Of The Adaptive Multiplatform Science Visualization Module For High-performance Computing Systems. Scientific Visualization, vol. 4, №. 4, 2012, pp. 17-29. Available at: http://sv-journal.com/2012-4/03.php?lang=en
10. K. Ryabinin, S. Chuprina. Adaptive Scientific Visualization System for Desktop Computers and Mobile Devices. Procedia Computer Science, vol. 18, 2013, pp. 722-731. Available at: http://www.sciencedirect.com/science/article/pii/S1877050913003797
11. JNI. Available at: http://java.sun.com/docs/books/jni/
12. Multisampling Anti-Aliasing: A Closeup View. Available at: http://alt.3dcenter.org/artikel/multisampling_anti-aliasing/index_e.php
13. M. Carmen Juan Lizandra. Graphic libraries for Windows
programming.
Crossroads, the ACM Student Magazine (ACM), vol. 6, № 4,
2000, pp. 14-18.
14. Coverage Sampling Antialiasing. Available at: https://developer.nvidia.com/csaa-coverage-sampling-antialiasing
15. A. Reshetov. Morphological Antialiasing. Available at: http://visual-computing.intel-research.net/publications/papers/2009/mlaa/mlaa.pdf
16. T. Lottes. Fast Approximate Antialiasing. Available at: http://developer.download.nvidia.com/assets/gamedev/files/sdk/11/FXAA_WhitePaper.pdf
17. M. Pettineo. Deferred MSAA. Available at: http://mynameismjp.wordpress.com/2010/08/16/deferred-msaa/
18. Temporal Antialiasing. Available at: http://www.geforce.com/hardware/technology/txaa/technology
19. R. Wright Jr., B. Lipchak. OpenGL Superbible, M.: Williams, 2006, pp. 177-203.
20. NChart3D Video Presentation. Available at: http://www.youtube.com/watch?v=KPmIYTKa00A
21. Apple UIKit Framework. Available at: https://developer.apple.com/library/ios/documentation/uikit/reference/UIKit_Framework/_index.html
22. NChart3D Official API Reference. Available at: http://nchart3d.com/nchart-doc/index.html