ВИЗУАЛИЗАЦИЯ
ИНФОРМАЦИИ
НА ОСНОВЕ ГРАФОВЫХ МОДЕЛЕЙ
В. Касьянов, Е. Касьянова
ИСИ СО РАН, НГУ, Новосибирск, Россия
kvn@iis.nsk.su, kev@iis.nsk.su
Оглавление
1. Задача визуализации графовых моделей
4. Визуализация больших графов
Визуализация – это процесс преобразования больших и сложных видов абстрактной информации в визуальную форму, усиливающую когнитивные способности пользователей и позволяющую им принять наиболее оптимальные решения. Графы являются наиболее абстрактными структурами, встречающимися в информатике, и широко используются для представления абстрактной информации. Любая система, состоящая из дискретных состояний (или мест) и связей между ними, может быть промоделирована с помощью графа.
Методы и средства визуализации графов широко используется во многих областях, таких как системное и прикладное программирование, биология, химия, искусственный интеллект, анализ финансовой информации, социология и многие другие.
В статье дается обзор основных существующих методов визуализации информации на основе графовых моделей.
Ключевые слова: визуализация информации, граф, графовая модель, дерево, рисование графов, рисование деревьев, система визуализации.
Визуализация ‑ это процесс преобразования больших и сложных видов абстрактной информации в интуитивно понятную визуальную форму. Универсальным средством такого представления структурированной информации являются графы. Графы применяются для представления любой информации, которую можно промоделировать в виде объектов и связей между объектами [3, 4]. Поэтому визуализация графовых моделей является ключевой компонентой во многих приложениях в науке и технике, а методы визуализации графов представляют собой теоретическую основу методов визуализации абстрактной информации. Методы и средства визуализации графов и графовых моделей широко используется в таких областях, как информационные системы и программное обеспечение, компьютерное обучение, биологические науки, искусственный интеллект, анализ финансовой информации, компьютерное моделирование и многие другие.
В зависимости от применения элементы (Здесь и ниже без определений используются стандартные термины теории графов (см., например, [1]).) (вершины и ребра) графа должны изображаться различными способами. Например, вершины могут быть нарисованы в виде точек, кругов, прямоугольников или других геометрических фигур, или представлены неявно – через имена, которыми вершины помечены. Аналогично имеется большое разнообразие рисования ребер: например, в виде отрезков прямых, ломаных линий или кривых.
Граф может рисоваться на плоскости или в трехмерном пространстве. Он может изображаться целиком, частично или иерархически, например, путем стягивания некоторых его подграфов в вершины, которые могут раскрываться по требованию. Изображения графа могут быть не только статическими, но и интерактивными, поддерживающими различные способы навигации, адекватные потребностям пользователя. Интерактивная визуализация может быть вызвана не только динамическим характером работы с визуальным представлением графа в приложении, но и большим размером визуализируемого графа. Если число элементов графа велико, его обработка может занимать неприемлемо большие ресурсы или даже достигать предельных возможностей используемой для визуализации платформы. Даже если возможно разместить и показать все элементы большого графа, часто возникают проблемы наглядности и удобства, поскольку на таком изображении графа становится невозможным различать его элементы (вершины и дуги). Интерактивная визуализация превращает статическую демонстрацию визуального представления информации в непрерывный процесс взаимодействия пользователя с информацией через её визуальное отображение и доступные ему навигации. Пользователь может исследовать, рассматривать, открывать, узнавать и манипулировать данными через визуальные метафоры.
Активная разработка методов и средств визуализации графов началась во второй половине 80-х годов прошлого столетия. Это было связано, с одной стороны, с возросшей потребностью оперировать с большими объемами информации и сложными структурами данных, которые достаточно естественным образом представляются графами, а с другой стороны, с существенным прогрессом в развитии аппаратных средств, позволившим сделать графический интерфейс и компьютерную графику удобным и эффективным средством общения человека с компьютером.
В настоящее время вопросам визуализации графов и графовых моделей посвящена обширная литература (см., например, [2 - 15]), а на рынке широко представлены наукоемкие программные продукты, использующие методы визуализации информации на основе графовых моделей.
Исследования в области визуализации графов и графовых моделей проводятся широким фронтом и имеют обширные и все более разнообразные сферы приложения. В работе [8] перечисляются в качестве основных источников, содержащих результаты этих исследований, такие журналы, как Journal of Graph Algorithms and Applications (JGAA), IEEE Transactions on Visualization and Computer Graphics, Computational Geometry: Theory and Applications и Algorithmica, а также труды таких регулярных конференций, как Graph Drawing Symposia (GD), ACM Conference on Human Factors in Computing Systems (CHI), ACM Symposium on User Interface Software and Technology (UIST), IEEE Information Visualization Conference (InfoVis), Eurographics Workshop on Scientific Computing. Такая разбросанность исследований по журналам и конференциям, относящимся к весьма разной тематике, усложняет поиск подходящих методов визуализации при создании систем, использующих визуализацию графовых моделей, а также затрудняет объединение полученных результатов в единую теорию и/или структурированное множество методологий.
В статье дается краткий обзор основных существующих методов визуализации структурированной информации на основе графовых моделей. Статья начинается с описания задачи визуализации графовых моделей, рассмотрения требований к изображениям графа и основных понятий (изобразительное соглашение, эстетичность и ограничение), связанных с формализацией понятия качественного способа рисования графа. Далее рассматриваются вопросы изображения деревьев, важного подкласса графов, широко используемого для представления различных иерархий, таких как генеалогические деревья, организационные схемы или поисковые деревья. Описываются основные методы, позволяющие получать удовлетворительные решения задач статической визуализации графов, такие как планаризация, использование физических аналогий, поуровневые (или Сугияма-подобные) и потоковые методы. Далее рассматриваются основные подходы к изображению графов большого размера, а также вопросы интерактивности и навигации при визуализации графов и графовых моделей. Статья завершается кратким описанием существующих систем визуализации графовых моделей и небольшим заключением.
1. Задача визуализации графовых моделей
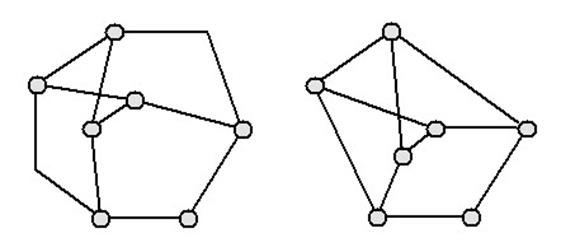
Изображение (drawing) (или, как иногда говорят, представление, рисунок, расположение, укладка или раскладка) графа на плоскости (или в пространстве) — это отображение вершин и ребер графа в множество точек плоскости (или пространства). Понятно, что один и тот же граф можно визуализировать разными способами (см., например, рис. 1 и 2), причем качество одного и того же изображения может по-разному оцениваться разными индивидуумами, а разные приложения могут требовать разные способы визуализации графа. Например, при работе с различными таксономиями часто желательно ортогональное расположение ребер и меток, так как взаимодействие с изображением должно облегчать чтение сопутствующей информации, а при визуализации карт дорог нужно, чтобы расположение вершин и ребер соответствовали географическим реалиям. Поэтому главным критерием оценки качества методов визуализации информации является адекватность изображения графовой модели заданному типу информации и характеру её использования.
Понятие качественного способа рисования графа формализуется с помощью таких понятий, как изобразительное соглашение, эстетический критерий и ограничение.
а) б)
в) г)
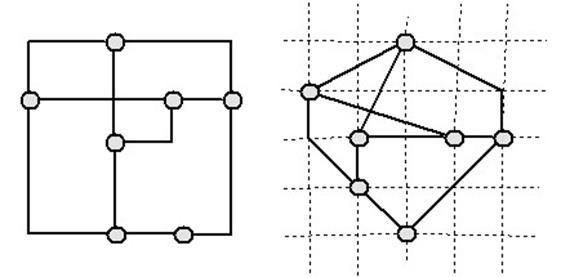
Рис. 1. Разнообразные изображения одного
графа:
а – полилинейное, б – прямолинейное, в – ортогональное, г – сетчатое
Изобразительное соглашение (drawing convention) — это одно из основных правил, которому должно удовлетворять изображение графа, чтобы быть допустимым. Например, при рисовании блок-схемного представления программ можно использовать соглашение о том, что все вершины должны изображаться прямоугольниками, а дуги — ломаными линиями, состоящими из вертикальных и горизонтальных звеньев. При этом, конкретный вид соглашения реального применения может быть достаточно сложен и включать много деталей, касающихся изображения.
Широко используются следующие изобразительные соглашения:
· полилинейное (polyline) изображение предполагает, что каждое ребро графа рисуется в виде ломаной линии (рис. 1, а),
· прямолинейное (straight-line) изображение характеризуется тем, что каждое ребро представляется с помощью отрезка прямой (рис. 1, б),
· ортогональное (orthogonal) изображение предполагает, что каждое ребро графа изображается в виде ломаной линии, состоящей из чередующихся горизонтальных и вертикальных сегментов (рис. 1, в),
· сетчатое (grid)изображение предполагает, что все вершины, а также все точки пересечения и сгибы ребер имеют целочисленные координаты, т.е. находятся в узлах координатной сетки, образованной прямыми, параллельными координатным осям и пересекающими их в точках с целочисленными координатами (рис. 1, г),
· плоское (planar)изображение предполагает отсутствие точек пересечения у линий, изображающих ребра (рис. 3, а),
· восходящее (upward) (соответственно нисходящее (downward)) изображение имеет смысл по отношению к ациклическому орграфу и предполагает, что каждая дуга изображается ориентированной линией, координаты точек которой монотонно изменяются в направлении снизу вверх (соответственно сверху вниз) и слева направо (рис. 3, б).
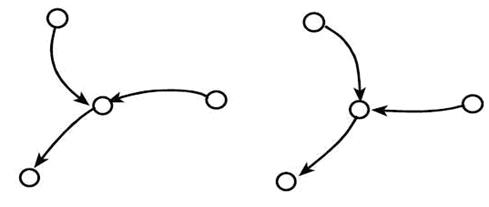
Рис. 2. Два
изображения одного и того же графа, различающиеся
только кривизной, которые выделяют
два разных пути в графе
Эстетические критерии (aesthetics) специфицируют такие свойства изображений, которые желательно применять в такой наибольшей степени, как только это возможно, чтобы повысить наглядность изображения. Широко используются следующие эстетические критерии:
· минимизация пересечений,
· минимизация сгибов,
· минимизация области размещения,
· максимизация разрешения,
· минимизация общей длины ребер,
· минимизация длины ребра,
· унификация длин ребер,
· минимизация числа сгибов на ребре,
· унификация сгибов,
· максимальная симметричность,
· минимизация коэффициента сторон.
Большинство из используемых эстетических критериев, как задачи оптимизации, являются сложными для решения с вычислительной точки зрения. Поэтому обычно при построении изображений используются различные эвристики и стратегии приближенных решений.
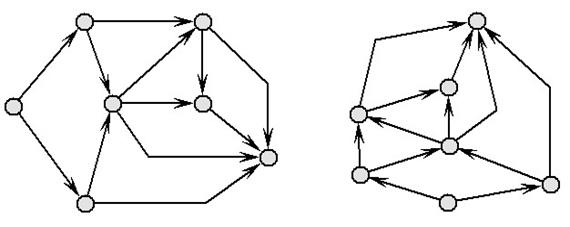
а) б)
Рис. 3. Разные полилинейные изображения одного графа:
а – плоское, б – строго восходящее
Ограничения (constraints). Если соглашения и эстетические критерии формулируются по отношению ко всему графу и его изображению, то ограничения относятся к отдельным подграфам и частям изображений.
Наиболее часто рассматриваются следующие ограничения:
· центр, когда требуется поместить заданную вершину ближе к центру изображения,
· внешность, когда требуется поместить заданную вершину на внешней границе изображения,
· кластер, когда требуется разместить заданную группу вершин рядом друг с другом,
· последовательность слева-направо (сверху-вниз), когда требуется нарисовать заданный путь горизонтально слева-направо (соответственно сверху-вниз).
Наиболее простым и широко используемым для решения задач визуализации информации подклассом графов являются деревья. Алгоритмы размещения деревьев имеют наименьшую сложность и являются наиболее простыми для реализации.
Корневые деревья часто используются для представления иерархий, таких как генеалогические деревья, организационные схемы или поисковые деревья.
К их изображениям часто применяют дополнительные соглашения, эстетические критерии и ограничения. Например, при соглашении включения (inclusion) вершины корневого дерева изображаются прямоугольниками, а отношения отец-сын представляются включением одного прямоугольника в другой, а соглашение опрокидывания (tip-over) подобно классическому соглашению нисходящего плоского изображения корневого дерева, однако допускает, чтобы сыновья некоторых вершин располагались не горизонтально, а вертикально (см., рис. 4).
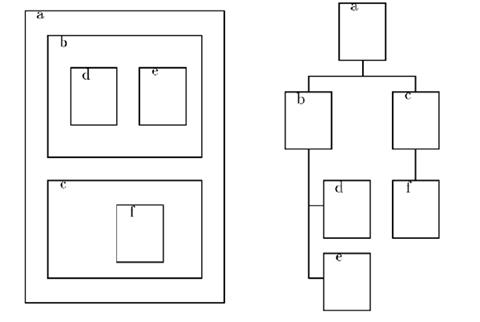
а) б)
Рис. 4. Разные изображения одного дерева:
а – включения, б – опрокидывания
Простой и эффективный метод построения нисходящего плоского изображения корневого дерева T состоит в использовании поуровневого расположения дерева, при котором вершины p глубины i имеют y-координату y(p'')=-i , а x-координаты присваиваются таким образом, чтобы разность x(p'')-x(p') имела тот же знак, что и разность x(отец(p''))-x(отец(p')).
Некоторой вариацией поуровневого изображения дерева является его радиальное расположение, в котором уровни имеют вид концентрических окружностей, а поддеревья занимают секторные сегменты (рис. 5).
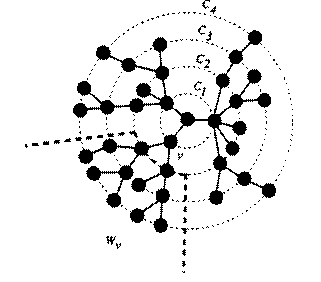
Рис. 5. Радиальное изображение дерева
"Свободные" деревья не представляют никакой иерархии и не имеют выделенного корня. Алгоритмы, применяемые к корневым деревьям, можно использовать для получения допустимых радиальных изображений свободных деревьев, размещая вершины свободного дерева на концентрических окружностях по уровням относительно теоретико-графового центра дерева.
Гиперболическое размещение деревьев (или других классов графов) является одной из таких форм раскладки, которая разрабатывалась под влиянием вопросов визуализации графов большого размера и интерактивности. Первыми статьями в этом направлении были статьи Лэмпинга и Мунзнера 1995-1996 годов. Оба проекта были связаны с разработкой браузеров, которые основывались на предложенных авторами новых технологиях. Гиперболические виды, которые могут быть реализованы как в 2D, так и в 3D, представляют собой искаженный вид деревьев (см. рис. 6). Этот способ изображения похож на эффект от использования линз рыбьего глаза при традиционном размещении деревьев. Такое искаженное изображение позволяет осуществлять визуализацию потенциально больших деревьев, делая их пригодными для приложений из реальной жизни. Другая пространственная природа гиперболической геометрии делает некоторые весьма простые алгоритмы укладки графов заметно более жизнеспособными.

Рис. 6. Гиперболический вид дерева в 3D-пространстве
Существует два канонических способа отображения гиперболической плоскости на внутренность круга евклидовой плоскости. В обоих случаях одна окрестность гиперболической плоскости находится в фокусе в центре круга, в то время как остальная часть гиперболической плоскости постепенно исчезает в перспективе по мере приближения к границе круга. Первая каноническая модель — это конформная модель Пуанкаре, которая сохраняет углы, но превращает линии гиперболического пространства в дуги единичного круга. Вторая каноническая модель — это проективное отображение или модель Клейна, которая отображает линии гиперболического пространства в прямые линии на плоскости, но зато искажает углы.
Метод визуализации, получивший название дерево-карта (tree-map), впервые был использован для визуализации распределения дискового пространства между файлами в иерархической структуре директорий в 1991 году, но постепенно получил широкое применение для визуализации иерархических (древовидных) структур во многих областях визуализации от финансовой информации до результатов спортивных состязаний.

Рис. 7. Пример изображения методом дерева-карты
Этот вид визуализаций дерева использует соглашение включения и является крайне эффективным при изображении численных атрибутов элементов (размер, стоимость, значение), организованных в большие иерархии.
Базовая идея метода состоит в том, чтобы изобразить дерево, каждая вершина которого имеет имя и значение численного атрибута, равного сумме значений атрибута всех ее сыновей, внутри прямоугольника заданного размера (рис. 7).
Для изображения поддеревьев обычно используется рекурсивная процедура разбиения прямоугольника, соответствующего всему дереву, на прямоугольники меньшей площади без незаполненных пространств и наложений. Для этого площадь прямоугольника разбивается горизонтальными и вертикальными линиями на прямоугольники, площадь которых пропорциональна значению данного атрибута. Такая разновидность метода называется методом продольно-поперечных разрезов (Slice-and-Dice).
Рассматриваются также различные модификации данного метода, использующие для изображения вершин графа геометрические фигуры, отличные от прямоугольников.
Например, деревья-карты Вороного (Voronoi treemaps) используют сечения Вороного для вычисления размещения произвольных многоугольников, заполняющих пространство экрана (рис. 8).
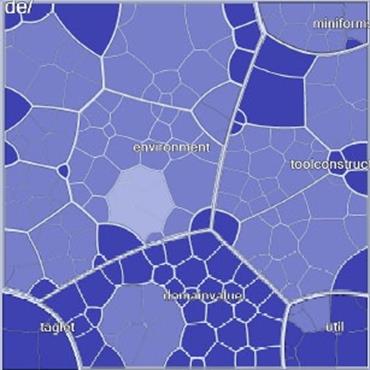
Рис. 8. Дерево-карта Вороного
Весьма популярны также круговые деревья-карты (circular treemaps). Хотя эти методы могут приводить к неполному заполнению больших кругов кругами меньшего радиуса (рис. 9), они позволяют строить изображения, хорошо показывающие вложенность, и поэтому используются для визуализации всевозможных иерархических структур, включая онтологии, тезаурусы, метрики программного обеспечения и т.д.

Рис. 9. Круговое дерево-карта
Большинство методологий рисования графа основывается на следующих двух простых наблюдениях: эстетические критерии часто противоречат друг другу и таким образом поиски компромиссов неизбежны; даже если эстетические критерии не конфликтуют, часто алгоритмически трудно удовлетворить всем им одновременно.
Тем не мене имеется ряд методов, которые позволяют получить удовлетворительные решения задач визуализации графов; основными среди них являются следующие.
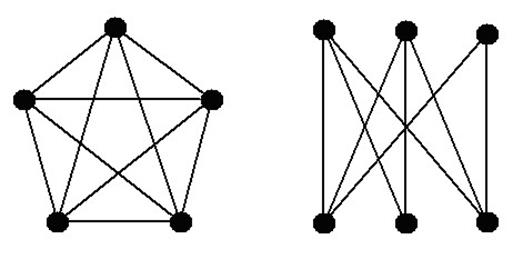
K5 K3,3
Рис. 10. Непланарные графы K5 и K3,3
Планаризация. Плоские расположения графов, т.е. без пересечений рёбер, обычно более привлекательны, чем неплоские. Например, они весьма важны в технологиях печатных плат с точки зрения минимизации размещения.
Существует целый ряд методов укладки планарных графов, которые опираются на специальные упорядочения вершин, часто называемые каноническими. В этих алгоритмах сначала вершины упорядочиваются, а затем по одной (или группами) вершины последовательно добавляются в соответствии с найденной упорядоченностью к структуре данных, описывающей представление графа.
Некоторые планарные графы можно нарисовать на плоскости таким образом, чтобы граница любой грани являлась выпуклым многоугольником. Такое представление возможно для графа только тогда, когда границы всех граней являются простыми циклами. Таким образом, граф, не являющийся двусвязным, не имеет выпуклого представления, а для любого 3-связного графа существует выпуклое представление (теорема Татта).
К сожалению, на практике многие графы не являются планарными, более того, почти все графы не являются планарными. Согласно теореме Понтрягина-Куратовского граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных K5 и K3,3 (рис. 10).
Можно пытаться сделать граф планарным, удаляя из него либо как можно меньше ребер (эта проблема является NP-полной), либо те ребра, чья вставка впоследствии может создать наименьшее число пересечений. Эта проблема минимизации пересечений является в общей постановке NP-трудной, но есть некоторые эвристики, которые позволяют получать вполне удовлетворительные результаты.
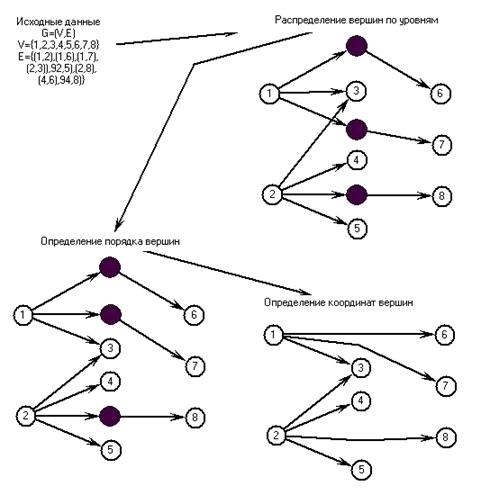
Рис. 11. Этапы построения поуровневого изображения
Использование физических аналогий. Эти методы интерпретируют граф при построении его изображения как физическую систему с силами между вершинами и пытаются минимизировать энергию системы для получения хорошего рисунка. Наиболее простой подход состоит в использовании комбинации пружин и электронных сил, когда каждое ребро рассматривается как пружина, а вершины считаются одинаково заряженными частицами, между которыми действуют силы отталкивания. Такого типа методы часто используются для рисования произвольных (разреженных) сетей, таких как блок-схемы, графы программного планирования, графы телефонных вызовов и т.п. Они также применяются для построения кластерных изображений.
В общем случае методы, основанные на использовании физических аналогий, дают хорошие результаты для относительно небольших графов, но не являются хорошо масштабируемыми. Большие графы часто приводят к тому, что функция энергии становится весьма трудной для достижения минимума. Более того, типичный алгоритм, реализующий данные методы, является итерационным. Во время каждой итерации позиции всех вершин переопределяются на основе результата предыдущей итерации, что вероятно требует O(n2 + m) времени, где n и m – количества вершин и ребер соответственно. Для достижения хорошей раскладки графа обычно требуется O(n) итераций. Следовательно, общая временная сложность итерационного алгоритма составляет O(n3) или даже O(n4). Кроме того, основанные на физических аналогиях алгоритмы раскладки не обладают предсказуемостью, и это означает, что один и тот же алгоритм, обрабатывая один и тот же граф, может получать совсем непохожие результаты. Отсутствие предсказуемости у данных алгоритмов может вызывать в некоторых случаях серьезные проблемы при их применении, поскольку навигация пользователя сильно зависит от визуального представления графов.
Рис. 12. Пример дерева (DOI-tree), в котором
изображения всех 400 вершин
разделены на три вида в зависимости от значений функции DOI степени
интереса
(degree of interest),
сопоставленных вершинам дерева
Поуровневые или Сугияма-подобные методы. Наиболее широко используемыми алгоритмами рисования являются алгоритмы, относящиеся к классу, предложенных Сугиямой. Они производят поуровневые (или иерархические) изображения для ациклических орграфов, пытаясь также минимизировать количество пересечений или размер области размещения.
Канонически метод поуровневого изображения состоит из трех основных последовательно применяющихся шагов, которые изображены на рис. 11.
Первый шаг ‑ это распределение вершин орграфа по уровням. Каждой вершине u присваивается число L(u), указывающее уровень этой вершины, так, чтобы все дуги, соединяющие вершины, следовали от меньшего номера к большему, при этом вершины одного уровня не должны быть связаны между собой. Подразумевается, что все вершины одного уровня будут расположены на одной прямой – вертикальной или горизонтальной – в зависимости от того, какое мы предпочитаем общее направление размещения: сверху вниз или слева направо.
Задача второго шага состоит в сортировке вершин на каждом из уровней. Порядок вершин определяет топологию конечного изображения и должен быть выбран с целью минимизации пересечений ребер графа. Следует отметить, что количество пересечения дуг в поуровневом графе не зависит от конечных координат вершин, а зависит только от их относительного положения внутри каждого уровня. Таким образом, задача данного этапа является не геометрической, а всего лишь комбинаторной. Однако эта задача является NP-полной уже для графа, имеющего всего лишь два уровня, и, более того, NP-полной эта задача остается, даже если есть всего лишь одна вершина со степенью, большей единицы на каждом из уровней.
На третьем шаге каждой вершине присваивается вертикальная координата (при размещении в горизонтальном направлении) так, чтобы сохранить порядок вершин на уровне, который был вычислен на предыдущем шаге. Координата выбирается с целью минимизации общей длины дуг и количества изломов. Наконец, конечное изображение получается представлением каждой дуги в виде прямолинейного отрезка и удалением фиктивных вершин. В этом случае длинные дуги оказываются изображенными в виде ломанных.
Выбор подкласса ациклических орграфов для рисования можно объяснить двумя причинами. Во-первых, преимущественное большинство реальных графов, встречающихся в программировании, являются ациклическими орграфами, а, во-вторых, любой ориентированный (и тем более неориентированный) граф может быть преобразован к ациклическому орграфу путем смены или задания ориентации у части его ребер. Методы, основанные на поуровневом размещении (иерархический подход), хотя и не являются лидерами по всем эстетическим критериям, однако значительно опережают конкурентов на больших графах, возникших в реальных приложениях.
Потоковые методы. Проблема минимизации числа сгибов может эффективно решаться путем сведения ее к задаче потока в сети, по крайней мере, в тех случаях, когда зафиксирована топология размещения. Те же самые методы могут применяться для максимизации углов между ребрами.
4. Визуализация больших графов
Размер визуализируемого графа является ключевой проблемой при визуализации графов. Большие графы ставят ряд сложных проблем. Если число элементов графа велико, его обработка может выходить за границы производительности или даже достигать предельных возможностей используемой для визуализации платформы. Даже если возможно разместить и показать все элементы большого графа, возникают проблемы наглядности и удобства, поскольку становится невозможным различать вершины и дуги. По существу, проблема удобства возникает даже раньше, чем проблема различия элементов. Хорошо известно, что охватывающий и детальный анализ данных в графовой структуре наиболее прост, когда размер демонстрируемого графа небольшой.
Вообще говоря, нет смысла проверять планарность графа, состоящего из нескольких сотен вершин, и пытаться минимизировать количество пересечений ребер. Часто более очевидным и практическим решением является простое размещение покрывающего дерева графа. Как известно, алгоритмы размещения деревьев имеют наименьшую сложность и являются наиболее простыми для реализации. При таком подходе проблема визуализации включает задачу нахождения покрывающего дерева. Он также предполагает построение изображения графа на основе уже построенного изображения дерева, которое содержит все вершины данного графа и перед этим было извлечено из него. При этом сам процесс построения сводится к добавлению некоторых дополнительных ребер к уже имеющемуся изображению дерева. Существенно, что, используя определенные изображения покрывающих деревьев для укладки графов, мы можем также получать размещения графа с определенными свойствами.
Другим популярным подходом к визуализации больших графов является переход от 2D к 3D изображению. Имеется громадное число методов представления графов на плоскости. Дополнительное третье измерение (переход от 2D к 3D изображению), однако, имеет ряд преимуществ. Оно позволяет более гибко размещать элементы графа и вообще обходиться без пересечений. С другой стороны, при использовании дополнительного измерения возникают новые проблемы, поскольку текущие устройства вывода являются двумерными по своей природе и поддерживают ограниченные разрешение и область визуализации. Поэтому результирующие изображения усложняются и становятся трудными для просмотра. Эти недостатки можно преодолеть с помощью таких навигационных операций как повороты, сдвиги и масштабирование. Указанные операции позволяют эффективно использовать область экрана и дают возможность пользователю разрешить неоднозначности для больших графов при сопровождении их общих абстрактных представлений. Возможность изменения точки зрения в 3D позволяет также снизить проблему пересечений ребер, связанную с двумерным изображением трехмерного графа на экране.
При работе с большими графами часто используются специальные методы, позволяющие уменьшать количество деталей, размещаемых одновременно. Вместо статического размещения также используются различные интерактивные методы с применением навигации и методов выделения (фокус+контекст), включающих геометрическую или семантическую деформацию, кластеризацию, агрегацию и другие техники.
В 1986 году Фурнас описал класс методов, в которых вершины иерархической структуры автоматически включаются или удаляются из изображения в соответствии с автоматически вычисляемой степенью пользовательского интереса, зависящей от априорной значимости данной вершины и её расстояния в дереве от вершины, выбранной пользователем в качестве фокуса. Он создал системы для просмотра и фильтрации структурированного программного кода, биологических таксономий и календарей, а также экспериментально продемонстрировал удобство этих динамических изображений для пользователя. Существует целый ряд методов и систем, использующих метрику Фурнаса для упрощения изображения путём фильтрации или кластеризации, а также для построения изображений, которые позволяют пользователю фокусироваться на некоторых деталях без потери контекста (см., например, рис. 12). В 1992 году Саркар и Браун обобщили данный подход на случай произвольного графа, предложив использовать в качестве функции расстояния до фокуса — евклидово расстояние между вершинами уже существующего изображения.
Кластеризация (clustering) в общем случае — это процесс разбиения заданной выборки объектов (ситуаций) на подмножества, называемые кластерами (clusters), так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались. Кластеризация позволяет уменьшать количество видимых элементов графа с сохранением при этом его глобальной структуры. Конкретным примером, где её применение весьма оправдано, являются так называемые графы малых миров (small-world graphs) — графы, которые имеют небольшой средний кратчайший путь между вершинами, но высокую степень кластеризации (по сравнению с усреднённым графом соответствующего размера). Это свойство присуще многим графам реальных приложений, таких как социальные сети, нейронные сети, программные системы, сети электроснабжения, базы знаний с перекрестными ссылками и Интернет.
Если кластеризация выполняется последовательным применением одного и того же процесса кластеризации к группам, обнаруженным на предыдущем шаге кластеризации, то говорят об иерархической кластеризации (hierarchical clustering). Результатом такой иерархической кластеризации является иерархия по включению, и по ней можно осуществлять навигацию как по дереву, в котором каждый кластер представлен в виде вершины. Следовательно, иерархическая кластеризация может быть использована для порождения иерархий в графах и построения на их основе так называемых иерархических графов (hierarchical graphs), ориентированных на поддержку визуализации сложных информационных моделей [2, 9 ‑ 13].
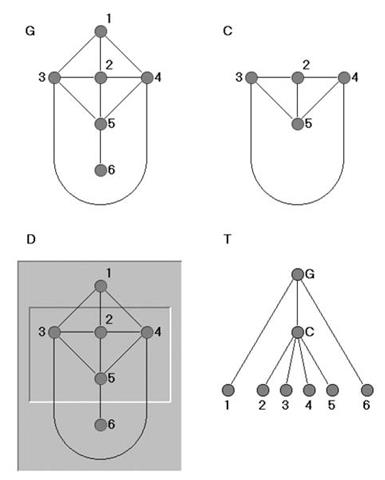
Рис. 13. Иерархический граф H=(G, T), в котором
C – единственный
нетривиальный фрагмент, отличный от G, и его изображение D на плоскости
Иерархический граф H – это пара (G, T), которая состоит из графа G и корневого дерева T, вершины которого соответствуют элементам некоторой иерархии фрагментов F графа G, а дуги отражают отношение их непосредственной вложенности. T называется деревом вложенности, а G – основным графом иерархического графа H (см. рис. 13).
В ряде случаев только за счет выбора подходящего способа изображения ребер можно уменьшить запутанность (clutter) изображения, что особенно важно для тех графов, чьи вершины должны иметь предопределенные позиции, как это, например, имеет место в геоинформационных приложениях. В частности, запутанность изображения можно уменьшить путем замены полилинейных линий, изображающих ребра, на гладкие кривые. Другие способы – это различные методы слияния изображений ребер (см., например, рис. 14) или их выборочного изображения.
Рассмотренные выше методы используются для рисования статических графов. Однако, есть ряд применений, требующих построения интерактивных изображений графов. Среди них: инструменты отладки, сохранение документов, модули отношений сущностей, схемы СБИС, а также Web-графы.
Средства навигации и интерактивности являются существенными также при визуализации информации большого объема. Сам алгоритм размещения графа не может преодолеть проблемы, вызванные громадными размерами визуализируемых графов, возникающих в различных приложениях. К тому же размещение внутри одного изображения большого количества элементов может лишь ухудшить понимаемость и наглядность графового изображения.
|
|

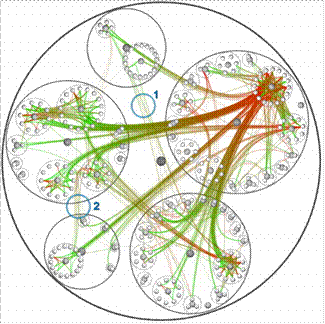
Рис. 14. Иерархические связки ребер
При разработке интерактивных визуализаций существенной становится временная сложность алгоритмов. Возникает необходимость в разработке алгоритмов, сложность которых близка к линейной. Также появляется новый критерий качества для динамических и интерактивных алгоритмов, называемый предсказуемостью (или сохранением ментальной карты). Этот критерий требует, чтобы два разных исполнения одного и того же алгоритма на одних и тех же или похожих данных давали похожий результат.
Обычно процесс создания интерактивной визуализации распадается на два последовательных этапа. Первый этап состоит в отображении исходных данных на геометрическую плоскость в виде статического графового изображения. Содержанием второго этапа является собственно навигация, обеспечивающая пошаговое изменение изображения и позволяющая достичь той формы представления информации, которая нужна пользователю в данный момент. Как правило, на этом этапе применяются различные методы поддержки взаимодействия пользователя с графовым изображением, построенном на первом этапе, но иногда реализация второго этапа — это многократное выполнение первого этапа с измененными требованиями к получаемому графовому изображению.
Приближение (zoom) и прокрутка (pan) — традиционные инструменты интерактивной визуализации. Они весьма необходимы, когда просматривается громадная графовая структура. Приближение путем увеличения масштаба изображения особенно хорошо подходит для графов, поскольку графические элементы, используемые для их изображения, обычно являются достаточно простыми (линии и простые геометрические формы). Это означает, что приближение может в большинстве случаев осуществляться не масштабированием пиксельного образа, а простыми настраивающими преобразованиями сцены и перерисовкой содержимого сцены по внутреннему представлению, при которой может изменяться видимая часть графа и показываться больше ее деталей.
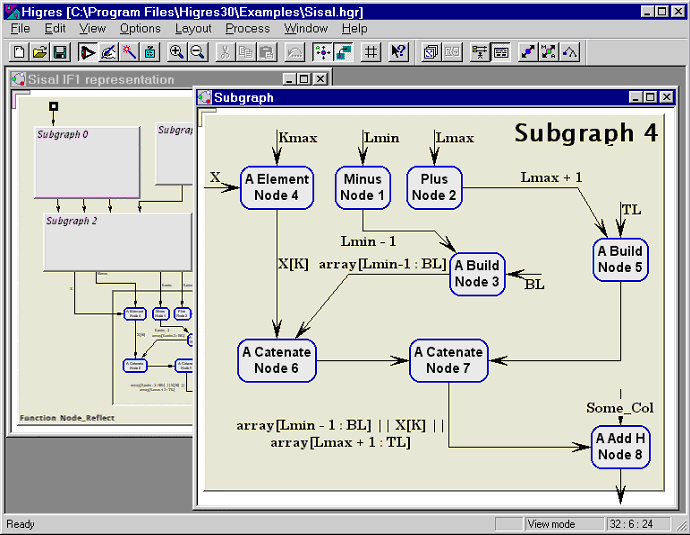
Рис. 15. Иерархический граф в системе Higres
Уже отмечалось, что во многих приложениях размер графов является основной проблемой при их визуализации. Имеются случаи, когда этот размер так велик, что делает вообще невозможным показать весь граф целиком; сеть Интернет является очевидным примером. Методы инкрементального просмотра (incremental exploration) хорошо подходят для таких ситуаций. Система демонстрирует только небольшую часть всего графа, а другие части графа демонстрируются по мере необходимости. Преимущество такого инкрементального подхода состоит в том, что в любой заданный момент на сцене может демонстрироваться только подграф ограниченного размера, и, следовательно, перестает быть критическим время, необходимое на построение изображения и осуществление взаимодействия с ним.
В процессе взаимодействия пользователь может иметь возможность открывать и закрывать новые окна для рассмотрения тех или других частей визуализируемого графа, а также осуществлять различные манипуляции с изображением, представленным в том или в другом окне. Часто оказывается полезным предоставлять пользователю отдельное окно для общего изображения большого графа с показом на нем частей графа, визуализируемым в других окнах.
При этом помимо стандартных методов навигации, таких как открытие (и закрытие) новых окон, масштабирование, прокрутка или инкрементальный просмотр, широко используются специальные методы взаимодействия с графовой информацией, такие как фильтрация, выделение, кластеризация и различные деформации.
Методы деформации фокус+контекст (focus+context) предназначены для взаимодействия с изображениями большого объема и позволяют совместить в одном изображении глобальный вид всей представленной структуры (графа, дерева, меню, календаря, таблицы и т.д.) и детали некоторого её фрагмента, находящегося в фокусе. Другой пример деформации — так называемая метафора резинового листа (rubber-sheet), при которой дисплей действует как резиновый лист с закреплёнными границами, в котором растягивание одних областей приводит к сморщиванию других.
Преимущества представления сложных структур и процессов графами становятся более ощутимыми при наличии хороших средств их визуализации. Поэтому неслучайно в последнее время в мире растет интерес к созданию и использованию систем визуализации информации на основе графовых моделей, которые условно можно разделить на два класса.
К первому (более широкому) классу относятся узкоспециальные системы, которые ориентированы на графовые модели с определенной семантикой и топологией.
Второй класс — это универсальные системы визуализации, такие как daVinci, GraphEd, Graphlet, GraVis, VCG, GLT, yEd [16], aiSee [17], Cytoscape [18], которые, как правило, являются зарубежными. Первой и, пожалуй, до сих пор единственной отечественной универсальной системой визуализации является созданная в ИСИ СО РАН система Higres [19], ориентированная на многооконную работу с иерархическими графами и графовыми моделями (рис. 15). Важным отличием системы Higres от других универсальных систем визуализации является ее способность сохранять во внутреннем представлении и визуализировать не только сам граф, но и его семантику, представленную в виде системы типов атрибутированных вершин, дуг и фрагментов графа, а также библиотеки алгоритмов обработки — так называемых внешних модулей. Причем пользователь системы может легко управлять методами визуализации графовой модели, а также корректировать и доопределять ее семантику. Такой подход обеспечивает, с одной стороны, универсальность системы Higres, с другой — возможность её специализации. Он также позволяет использовать систему как платформу для исполнения и анимации алгоритмов работы с иерархическими графами. Запустив внешний модуль, пользователь может регулировать параметры обработки графовой модели, прерывать алгоритм на любом шаге, просматривать в любую сторону последовательность изображений промежуточных результатов шагов работы алгоритма как в форме анимации, так и в покадровом режиме (см. рис. 16)
Наряду со специализированными и универсальными системами визуализации на основе графовых моделей широко распространены и используются различные библиотеки классов, такие как LEDA, ffGraph, Graph Drawing Server. Они позволят описывать семантику графовой модели путем создания производных классов с дополнительными атрибутами и обычно включают множество других полезных функций, связанных как с визуализацией графов, так и с выполнением на них различных теоретико-графовых алгоритмов и алгоритмов рисования.
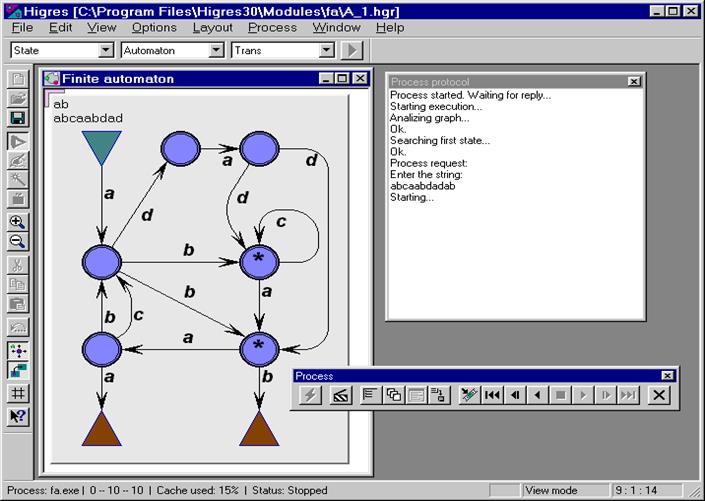
Рис. 16. Выполнение
алгоритма моделирования конечного автомата,
реализованного в виде внешнего модуля системы Higres
Визуализация информации на основе графовых моделей помогает пользователям понять глобальную и локальную структуры исходной абстрактной информации путем представления элементов взаимосвязанных данных, распределенных в пространстве, в интуитивно понятной визуальной графовой форме, поддерживающей удобные навигации. Исследования в области визуализации графов и графовых моделей, активно начатые в середине 80-х годов прошлого столетия, все эти годы проводятся широким фронтом, базируются на идеях таких интеллектуальных областей, как информатика, математика, психология, графика, картография и искусство, и имеют обширные и разнообразные сферы приложения, такие как системное и прикладное программирование, биологические науки, искусственный интеллект и многие другие. Результатам этих исследований посвящена обширная литература, а на рынке широко представлены наукоемкие программные продукты, использующие методы визуализации графовых моделей.
В данной небольшой статье мы лишь попытались рассмотреть основные идеи и существующие подходы, связанные с решением задач визуализации информации на основе графовых моделей. Те, кто желает углубить свои знания в данной области, могут обратиться к книгам [4 - 7, 14 - 15].
Работа выполнена при частичной финансовой поддержке Российского фонда фундаментальных исследований (грант РФФИ N 12-07-0091).
1. Евстигнеев В. А., Касьянов В. Н. Толковый словарь по теории графов в информатике и программировании. ‑ Новосибирск: Наука, 1999.
2. Касьянов В. Н. Иерархические графы и графовые модели: вопросы визуальной обработки // Проблемы систем информатики и программирования. ‑ Новосибирск: ИСИ СО РАН, 1999. ‑ С. 7-32.
3. Касьянов В. Н. Применение графов в программировании // Программирование. ‑ 2001. ‑ N 3. ‑ С. 51-70.
4. Касьянов В. Н., Евстигнеев В. А. Графы в программировании: обработка, визуализация и применение. ‑ СПб.: БХВ-Петербург, 2003.
5. Касьянов В. Н., Касьянова Е. В. Визуализация графов и графовых моделей. ‑ Новосибирск: Сибирское Научное Издательство, 2010.
6. Di Battista G., Eades P., Tamassia R., Tollis I. G. Graph Drawing: Algorithms for Vizualization of Graphs. ‑ Prentice Hall, 1999.
7. Drawing Graphs. Methods and Models. ‑ Berlin: Springer, 2001.
8. Herman I., Melancon G., Marshall M. S. Graph visualization and navigation in information visualization: a survey // IEEE Trans. on Visualization and Computer Graphics. ‑ 2000. ‑ Vol. 6. ‑ P. 24‑43.
9. Kasyanov V. N. Hierarchical graphs and visual processing // ICM 1998 International Congress of Mathematicians. Abstracts of Short Communications and Poster Sessions. ‑ Berlin, 1998. ‑ P. 292.
10. Kasyanov V. N., Lisitsyn I. A. Hierarchical graph models and visual processing // Proc. of Intern. Conf. on Software: Theory and Practice (ICS-2000). 16th World Computer Congress IFIP. ‑ Beijing, PHEI, 2000. ‑ P.179-182.
11. Kasyanov V. N. Methods and tools for structural information visualization // WSEAS Transactions on Computers. ‑ 2013. ‑ Vol. 12, Issue 7. ‑ P. 349-359.
12. Kasyanov V. N. Kasyanova E. V. Information visualization based on graph models // Enterprise Information Systems. ‑ 2013. ‑ Vol. 7, N 2. ‑ P. 187-197.
13. Lisitsyn I. A., Kasyanov V. N. Higres ‑ visualization system for clustered graphs and graph algorithms // Lecture Notes in Computer Science. ‑ 1999. ‑ Vol.1731. ‑ P.82-89.
14. Nishizeki T., Rahman M. Planar graph drawing. ‑ World Scientific. 2004.
15. Sugiyama K. Graph drawing and applications. For software and knowledge engineers. ‑ World Scientific. 2002.
16. yEd Graph Editor. URL: http://www.yworks.com/en/products_yed_about.html
17. aiSee — Graph Visualization. URL: http://www.absint.com/aisee/index.htm
18. Cytoscape. URL: http://www.cytoscape.org/index.html
19. Higres. URL: http://pco.iis.nsk.su/higres/
INFORMATION VISUALIZATION
ON THE BASE OF GRAPH MODELS
V. Kasyanov, E. Kasyanova
IIS, NSU, Novosibirsk, Russian Federation
kvn@iis.nsk.su, kev@iis.nsk.su
Abstract
Visualization is a process of transformation of large and complex abstract forms of information into visual form, strengthening user's cognitive abilities and allowing them to take the most optimal decisions. Graphs are the most common abstract structure encountered in computer science and are widely used for abstract information representation. Any system that consists of discrete states (or sites) and connections between them can be modeled by a graph.
Methods and tools for graph visualization are widely used in many applications, such as system and applied programming, biology, chemistry, artificial intellect, analysis of financial information, sociology and many others.
In the paper, a survey on main existent methods of information visualization on the base of graph models is given.
Key words: information visualization, graph, graph model, tree, graph drawing, tree drawing, visualization system.
References
1. Evstigneev V. A., Kasyanov V. N. Tolkovyy slovar po teorii grafov v informatike i programmirovanii [Explanatory Dictionary of Graph Theory in Computer Science and Programming]. Novosibirsk: Nauka Publ., 1999. (In Russian).
2. Kasyanov V. N. Ierarkhicheskie grafy i grafovye modeli: voprosy vizualnoy obrabotki [Hierarchical graphs and graph models: problems of visual processing]. Problemy sistem informatiki i programmirovaniya [Problems of Informatics Systems and Programming]. Novosibirsk: IIS, 1999, pp. 7–32. (in Russian).
3. Kasyanov V. N. Graph applications in programming. Programming and Computer Software, vol. 27, № 3, 2001, pp. 146–164.
4. Kasyanov V. N., Evstigneev V. A. Grafy v programmirovanii: obrabotka, vizualizatsiya i primenenie [Graphs in Programming: Processing, Visualization and Application]. St. Petersburg: BHV-Petersburg, 2003. (In Russian).
5. Kasyanov V. N., Kasyanova E. V. Vizualizatsiya grafov i grafovykh modeley [Visualization of Graphs and Graph Models]. Novosibirsk: Siberian Scientific Publ., 2010. (in Russian).
6. Di Battista G., Eades P., Tamassia R., Tollis I. G. Graph Drawing: Algorithms for Vizualization of Graphs. Prentice Hall, 1999.
7. Drawing Graphs. Methods and Models. Berlin: Springer, 2001.
8. Herman I., Melancon G., Marshall M. S. Graph visualization and navigation in information visualization: a survey. IEEE Trans. on Visualization and Computer Graphics, vol. 6, 2000, pp. 24–43.
9. Kasyanov V. N. Hierarchical graphs and visual processing. ICM 1998 International Congress of Mathematicians. Abstracts of Short Communications and Poster Sessions. Berlin. 1998. P. 292.
10. Kasyanov V. N., Lisitsyn I. A. Hierarchical graph models and visual processing Proc. of Intern. Conf. on Software: Theory and Practice (ICS-2000). 16th World Computer Congress IFIP. Beijing: PHEI, 2000, pp. 179–182.
11. Kasyanov V. N. Methods and tools for structural information visualization. WSEAS Transactions on Computers, vol. 12, № 7, 2013, pp. 349– 359.
12. Kasyanov V. N. Kasyanova E. V. Information visualization based on graph models. Enterprise Information Systems,. vol. 7, № 2, 2013, pp. 187–197.
13. Lisitsyn I. A., Kasyanov V. N. Higres – visualization system for clustered graphs and graph algorithms, Lecture Notes in Computer Science, vol. 1731, 1999, pp. 82–89.
14. Nishizeki T., Rahman M. Planar graph drawing. World Scientific, 2004.
15. Sugiyama K. Graph drawing and applications. For software and knowledge engineers. – World Scientific, 2002.
16. yEd Graph Editor. Available at: http://www.yworks.com/en/products_yed_about.html
17. aiSee — Graph Visualization. Available at: http://www.absint.com/aisee/index.htm
18. Cytoscape. Available at: http://www.cytoscape.org/index.html
19. Higres. Available at: http://pco.iis.nsk.su/higres/