ИСПОЛЬЗОВАНИЕ ТЕНЕВОГО
ФОНОВОГО МЕТОДА ДЛЯ ИССЛЕДОВАНИЯ
НЕСТАЦИОНАРНОГО ПОТОКА С УДАРНОЙ ВОЛНОЙ
Ф. Глазырин, И. Знаменская, Е. Коротеева, И. Мурсенкова, Н. Сысоев
Московский
государственный университет имени М.В. Ломоносова, Москва, Россия
glazyrin@phys.msu.ru, znamen@phys.msu.ru
Оглавление
Экспериментальные исследования
Аннотация
Проведены эксперименты по
визуализации структуры нестационарного
газодинамического потока с локальными сверхзвуковыми зонами теневым
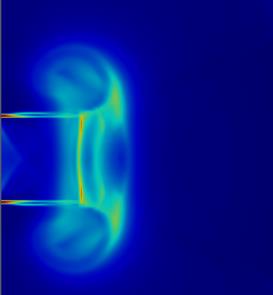
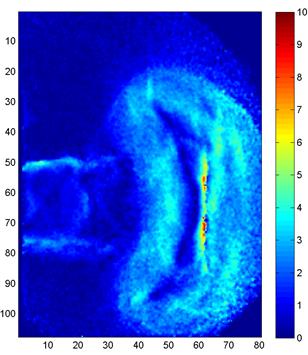
фоновым методом (ТФМ). Получены изображения последовательных стадий сложного
разрывного течения, возникающего после выхода ударной волны из прямоугольного
канала ударной трубы. Проанализированы
структурные особенности течения на основе полученных методом ТФМ полей сдвига.
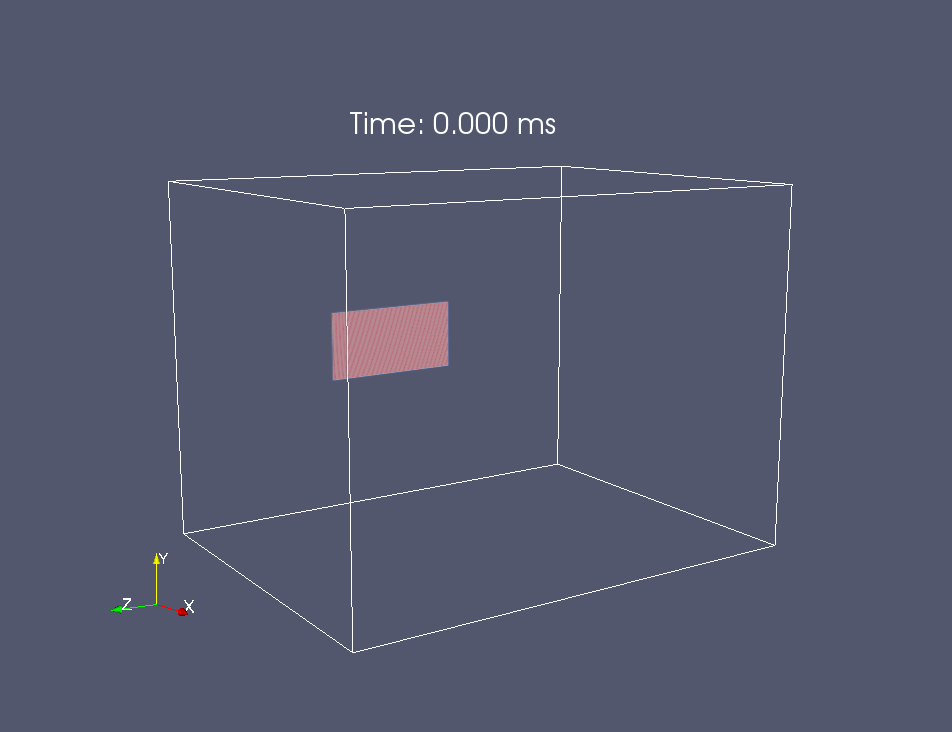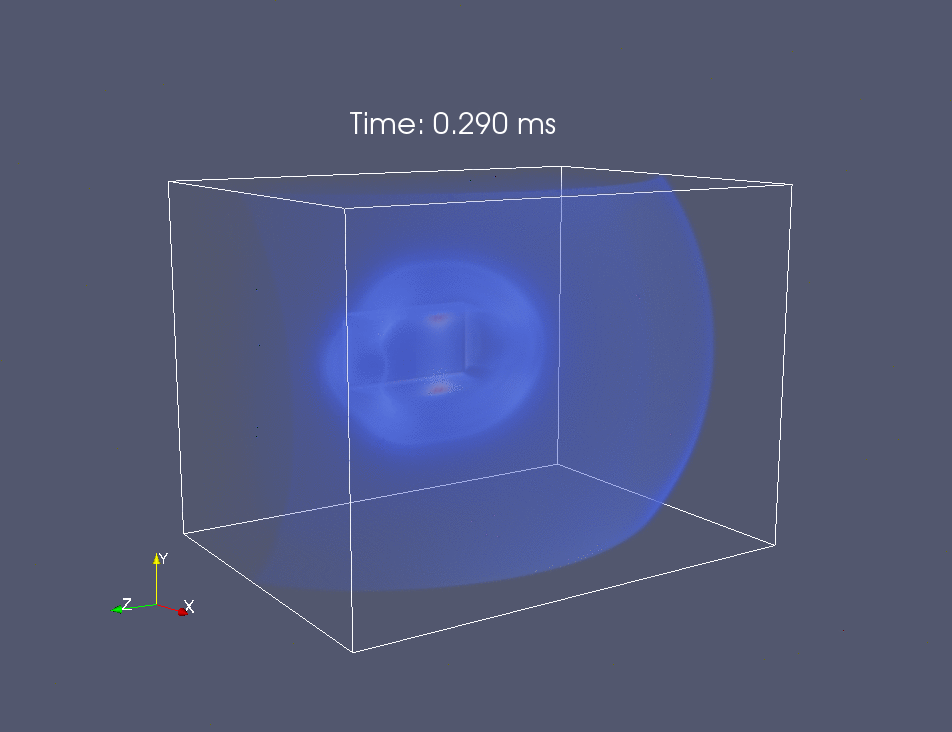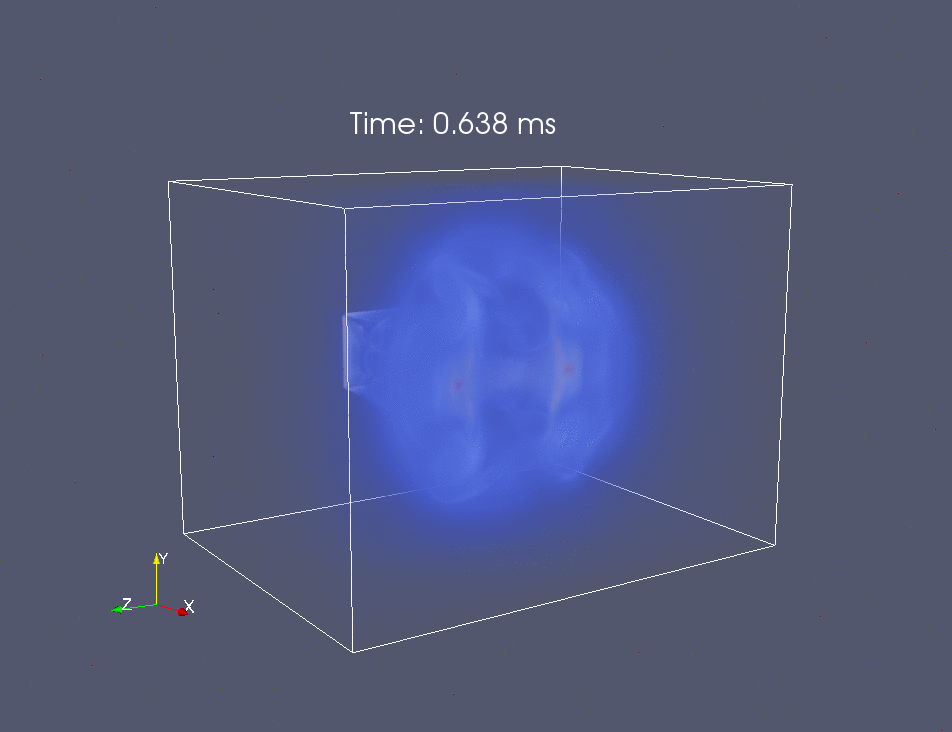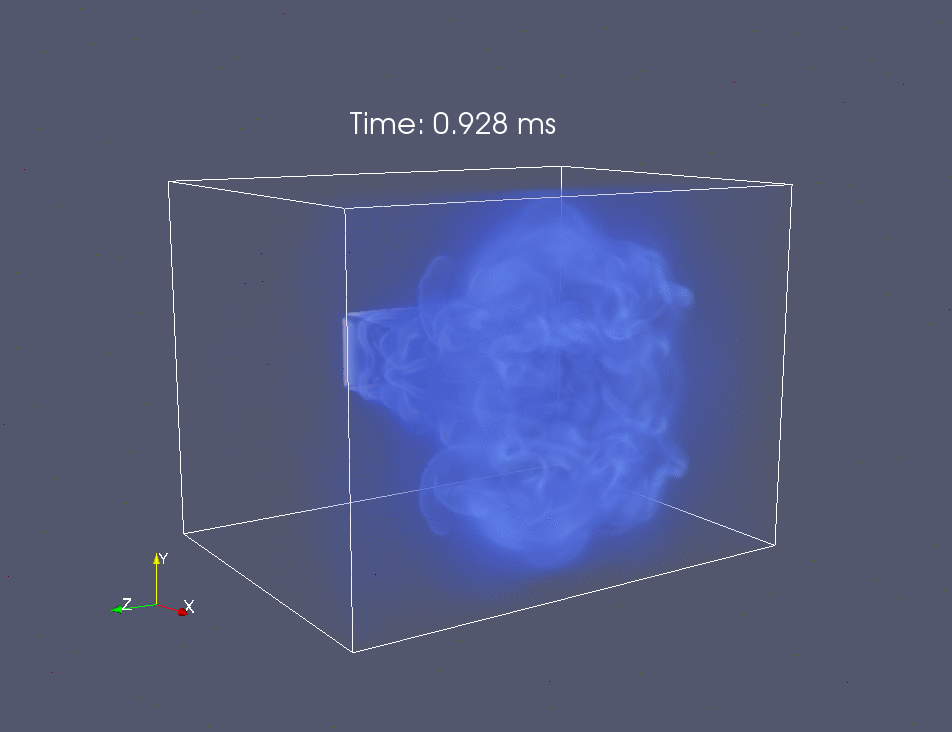
Проведено трехмерное численное моделирование процесса на основе уравнений
Эйлера. Продемонстрировано качественное совпадение расчетных и
экспериментальных картин эволюции течения, включая данные о положении его
характерных элементов, в том числе фронт ударной волны с числом Маха 1.5 и
динамику вихревого тороидального образования.
Ключевые слова: импульсное течение, дифракция ударной волны, теневой фоновый
метод (ТФМ/BOS), трёхмерное численное моделирование (3D CFD), вихревое кольцо.
Исследование импульсного процесса
выхода ударной волны из канала тесно связано с решением фундаментальной задачи о
нестационарной дифракции ударных волн. Интерес к данному явлению, возникший еще
в середине прошлого века [1], поддерживается большой ролью сверхзвуковых
импульсных течений в авиационной, ракетной и космической технике.
Выход ударной волны из канала в
атмосферу порождает спектр сложных газодинамических явлений: изменение формы
фронта ударной волны и скорости его движения, возникновение струйного течения
за фронтом, образование и взаимодействие пространственных вихрей, развитие
неустойчивости Кельвина-Гельмгольца и т.д. Возникающее осесимметричное либо
трехмерное нестационарное течение изучалось с помощью различных оптических
методов: теневого и шлирен-метода [2],
интерферометрии [3], интерферометрической томографии [4], цветного шлирен-метода [5], теневого фонового метода (ТФМ) [6].
За последнее десятилетие появился
ряд работ, в которых исследование выхода ударных волн из каналов различного (в
основном, осесимметричного) сечения проводилось
с использованием сравнительно нового метода диагностики потоков – метода
PIV (трассерной визуализации). В большинстве таких
работ основное внимание уделено изучению формирования и эволюции
крупномасштабных вихревых структур, возникающих в истекающем газе [7-8]. Приводятся данные по скорости
распространения и расширения вихревых колец, а также возникновении
вторичных вихрей и внутренних скачков уплотнения [9-10].
В данной работе исследовалась
дифракция плоской ударной волны при выходе из канала прямоугольного сечения.
Основной целью было изучение особенностей и применимости теневого фонового
метода для регистрации возникающего трехмерного течения. Проводилось сравнение
полученных данных по оптической визуализации с визуализированными результатами
численного моделирования.
Теневой фоновый метод визуализации
прозрачных неоднородностей основан на
известном оптическом явлении рефракции, но появление и внедрение ТФМ стали
возможны только в последнее десятилетие с производством цифровых камер высокого
разрешения, разработкой программ цифровой обработки изображений, доступностью
компьютеров с большим объемом памяти для обработки и хранения изображений и
фильмов [6, 11, 13-14]. Суть теневого фонового метода заключается в сравнении
двух изображений одного и того же фона, снятых при отсутствии и при наличии между
фотоаппаратом и фоном исследуемого прозрачного объекта с неоднородностями [13].
Изменение показателя преломления вдоль линии наблюдения в случае съемки фона
через течение приводит к несовпадению исходного (реперного) и «рабочего»
изображений (Рис. 1). Проанализировав смещение
характерных элементов фона на снимках, можно получить количественную информацию
об интегральных показателях преломления исследуемой среды вдоль оптического
луча.
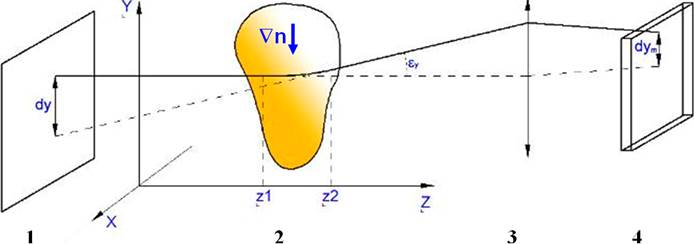
Рис. 1. Принципиальная оптическая схема
теневого фонового метода:
1 – фон, 2 – исследуемый объект, 3 – линза/объектив, 4 – CCD/CMOS матрица
Y-компонента отклонения луча,
идущего от фона, выражается из закона рефракции следующим образом:
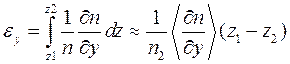
Тогда соответствующий элемент
фона будет смещён на рабочем изображении относительно реперного на величину:
![]()
Связь между плотностью
однородного газа и ее показателем преломления можно выразить соотношением Гладстона-Дейла:
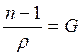 (1)
(1)
где G – постоянная Гладстона-Дейла,
характерная для данной среды. Таким образом, регистрируемое методом смещение
элемента фона прямо пропорционально градиенту плотности в плоскости,
перпендикулярной оптическому лучу схемы.
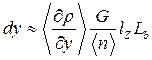
Здесь ![]() – расстояние от объекта до фона,
– расстояние от объекта до фона, ![]() - толщина исследуемого
течения вдоль оптической оси схемы. Данная формула приведена для одноракурсной ТФМ-схемы, когда съёмка течения производится
с одного направления. В этом случае на смещение изображения влияют все элементы
течения вдоль данного оптического луча – фактически, информация об исследуемом
потоке усредняется вдоль него. Восстановление непосредственно поля плотности из
результатов одноракурсного ТФМ возможно только для
двумерного течения (что крайне редко встречается в эксперименте), либо для
осесимметричного течения. В последнем случае можно использовать, например,
преобразование Абеля.
- толщина исследуемого
течения вдоль оптической оси схемы. Данная формула приведена для одноракурсной ТФМ-схемы, когда съёмка течения производится
с одного направления. В этом случае на смещение изображения влияют все элементы
течения вдоль данного оптического луча – фактически, информация об исследуемом
потоке усредняется вдоль него. Восстановление непосредственно поля плотности из
результатов одноракурсного ТФМ возможно только для
двумерного течения (что крайне редко встречается в эксперименте), либо для
осесимметричного течения. В последнем случае можно использовать, например,
преобразование Абеля.
Для получения количественных
значений поля плотности в сложных трёхмерных течениях необходима
многоракурсная ТФМ-съёмка с последующим
восстановлением трёхмерного поля из двумерных снимков различными методами томографической реконструкции. При этом съёмка производится
одновременно с нескольких (обычно не менее 6) ракурсов. Для стационарных
течений иногда съёмка производится последовательно с различных углов, одной и
той же камерой [11].
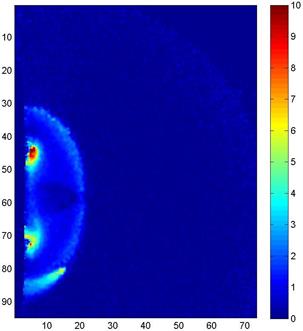
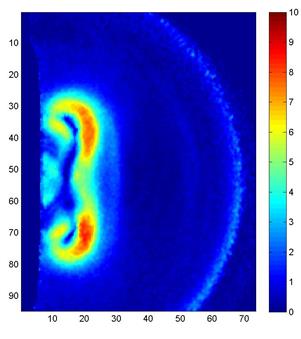
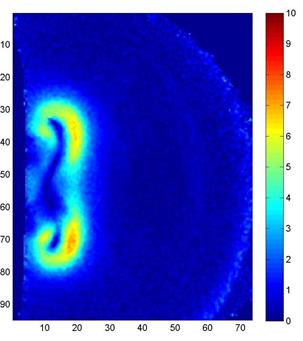
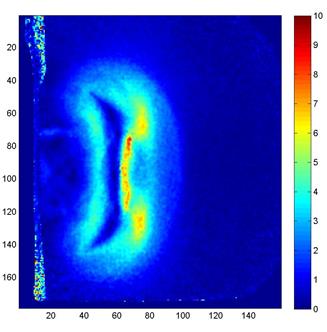
Однако даже без восстановления
поля плотности, результаты ТФМ могут служить полезным источником информации о
течении – например, данных о положении и границах характерных газодинамических
объектов в заданный момент времени.
Экспериментальные исследования
Эксперименты по исследованию течения, возникающего при выходе
ударной волны из канала,
проводились на ударной трубе диафрагменного типа (рис.
2). Секция низкого давления
длиной 200 мм и внутренним сечением 48´24 мм2 была открыта в атмосферу. Скорости ударных волн в канале измерялись базовым
методом по сигналам пьезоэлектрических датчиков давления PCB Piezoelectronics,
подключенных к цифровому осциллографу; с помощью этих сигналов также
осуществлялась синхронизация оптической системы с движением фронта
ударной волны в канале. Исследования проводились в воздухе
атмосферного давления, числа Маха ударных волн в канале 1.2-2.0.
Для ТФМ-визуализации использовался
цифровой фотоаппарат Canon 550D c объективом EF-S 18-55 mm. Фотоаппарат работал в режиме длинной выдержки в
затемнённом помещении. Фоновое изображение состояло из хаотически расположенных
точек. Масштаб изображения был подобран так, чтобы размер одной точки на снимке
составлял примерно 4-5 пк. Используемая для обработки
область фона составляла 1500´1800 пк
(полный кадр 5184´3156 пк).
Фон освещался вспышкой на базе импульсной лампы ИСШ-15. Длина светового
импульса составляла ≈2 мкс. Реперные кадры снимались непосредственно
перед запуском ударной трубы и сразу после него. В ходе обработки рабочий
снимок сравнивался с каждым из реперных, и результирующее поле смещений
усреднялось по всем парам сравниваемых кадров. Таким образом, в каждом эксперменте получалось одно ТФМ-изображение исследуемого
течения.
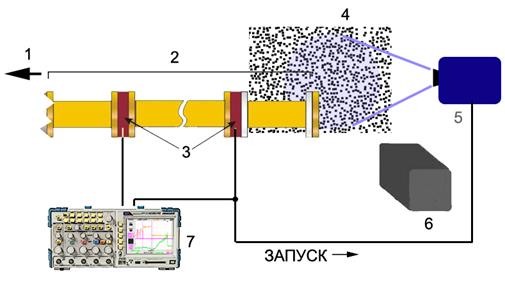
Рис. 2.
Схема эксперимента: 1 – камера высокого давления,
2 – канал ударной трубы, 3 – датчики давления в канале,
4 – фоновый экран, 5 – импульсная лампа-вспышка,
6 – фотоаппарат, 7 –осциллограф.
Запуск оптической схемы
осуществлялся от датчика давления, расположенного в конце канала ударной трубы.
Обработка полученных экспериментальных изображений производилась алгоритмом в
составе пакета DaVis 8.1 фирмы LaVision. Алгоритм использовал многопроходный вариант кросс-корреляционного метода, область опроса уменьшалась до
16 пк на последнем шаге. На всех шагах, кроме
последнего, применялась квадратная область опроса без перекрытия. Последняя
итерация метода проводилась на эллиптической области опроса с адаптивной формой
и 50% перекрытием. Между шагами кросс-корреляционного
метода к векторному полю применялся медианный фильтр с размером маски
3×3.
Было проведено численное
моделирование задачи выхода ударной волны из канала прямоугольного сечения на
основе решения нестационарных трехмерных уравнений газодинамики для сжимаемого
газа в декартовых координатах. Использовалась модель совершенного газа (воздух)
с показателем адиабаты 1.4 и числом Прандтля 0.72. Зависимость вязкости от
температуры описывалась формулой Сазерленда.
Численная конечно-объемная схема
представляла собой вариант метода Годунова повышенного порядка точности.
Конвективные потоки на гранях контрольных объемов рассчитывались с помощью
приближенного решения задачи Римана (HLLC). Для повышения пространственного
порядка схемы использовалась двумерная процедура восстановления параметров на
гранях и ограничитель minmod для сохранения
монотонности. Интегрирование по времени проводилось с помощью метода
Рунге-Кутты второго порядка.
Расчетная область представлена на
Рис. 3. В расчетах учитывалась
симметрия течения относительно двух плоскостей симметрии ударной трубы.
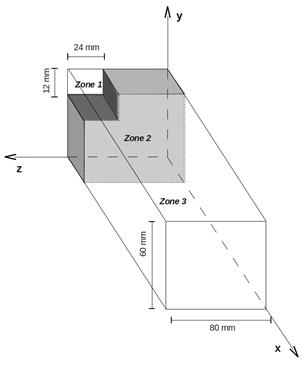
Рис. 3. Расчетная область.
Зона 1 – канал ударной трубы,
зона 2 – сплошная стенка, зона 3 – окружающий воздух при нормальных условиях.
Симметричные граничные условия были применены для плоскостей Y=Ymax и Z=Zmax. Остальные границы
были открытыми, на поверхности стенок использовались условия отсутствия
проскальзывания. Ударная волна (движется в положительном направлении оси x)
исходно находилась в зоне 1 в точке x=10 мм, с отношениями Рэнкина-Гюгонио на
фронте. Во всём объёме, кроме потока за исходной ударной волной, задавались
нормальные начальные условия. В работе [12], в случае осесимметричной геометрии истечения, было
показано, что моделирование в рамках уравнений Навье-Стокса отличается от Эйлеровского
только на поздних стадиях эволюции потока, когда начинают развиваться вихри,
порождаемые развитием неустойчивости Кельвина-Гельмгольца. В настоящем
исследовании основное внимание было направлено на первые 1000-1500 мкс после
дифракции ударной волны, когда вязкость существенно не влияет на структуру
течения. Поэтому, основная часть 3D-расчетов была выполнена для системы Эйлера,
с целью снижения вычислительных затрат.