ОБРАТНАЯ ЗАДАЧА АНАЛИЗА ПОВЕРХНОСТНОГО
ЭНЕРГОВКЛАДА НА ОСНОВЕ СРАВНЕНИЯ ЧИСЛЕННОЙ И
ЭКСПЕРИМЕНТАЛЬНОЙ ВИЗУАЛИЗАЦИИ ДВИЖЕНИЯ УДАРНОЙ
ВОЛНЫ ПО ВОЗМУЩЕННОЙ РАЗРЯДОМ ОБЛАСТИ
Е. Коротеева, И. Иванов
Московский государственный университет имении М.В. Ломоносова, Москва, Россия
koroteeva@physics.msu.ru
Оглавление
1. Экспериментальные результаты
2.1. Математическая модель и численный метод
2.2. Постановка расчетной задачи
3. Сравнение численной и экспериментальной визуализации
Аннотация
В данной статье рассмотрено воздействие зоны импульсного поверхностного энергоподвода на нестационарное течение с ударной волной в канале прямоугольного сечения. На примере анализа возникающего сверхзвукового пространственного течения проиллюстрирована эффективность взаимодействия экспериментальной теневой и численной визуализации.
В экспериментах теневым методом регистрировалось течение, образующееся при движении плоской ударной волны с числом Маха М=1.5-3.0 по области распределенного скользящего разряда наносекундной длительности («плазменного листа») через 40-500 мкс после его инициирования. Благодаря уникальной геометрии экспериментальной установки, газодинамическое течение в разрядной секции ударной трубы оказывалось в высокой степени двумерным. Это позволило выполнять и анализировать расчеты как в трехмерной, так и в двумерной постановке. Численное моделирование проводилось на основе решения уравнений Навье-Стокса и Эйлера для сжимаемого газа и модели мгновенного энерговклада.
Сравнение экспериментальных теневых снимков с результатами расчетной визуализации позволило восстановить всю динамику высокоскоростного процесса, а также решить обратную задачу – оценить энергетические параметры энерговклада в газ в начальный момент. Трехмерные численные расчеты выявили особенности пространственной структуры течения в зоне энерговыделения, недоступные для визуализации экспериментальным теневым методом, а также степень применимости двумерного приближения.
Ключевые слова: теневая визуализация, ударная волна, импульсный энерговклад, вычислительная газодинамика, расчетная CFD-визуализация.
Сопоставление численной и экспериментальной оптической визуализации течений - ключевой инструмент современных газодинамических исследований. Прежде всего, хорошее согласие численных и экспериментальных данных необходимо для подтверждения и интерпретации наблюдаемых в эксперименте физических явлений [1,2]. C другой стороны, сравнение с экспериментом позволяет проводить верификацию и тестирование используемых вычислительных алгоритмов и моделей.
Постоянное совершенствование высокопроизводительной компьютерной техники открывает широкие перспективы для развития вычислительной гидро- и газодинамики (CFD), в частности, благодаря появлению возможностей численного решения полной системы уравнений Навье-Стокса, а также обработки и визуализации больших массивов данных. Вместе с этим, возрастает и сложность процедур проверки численных результатов, особенно в случае нестационарных пространственных течений. Известно, что тестирование и валидацию численных алгоритмов предпочтительно проводить на модельных течениях, обладающих «упрощенной» пространственной геометрией (квазидвумерность, симметрия), но в то же время отражающих характерные черты изучаемого явления. В этой связи чрезвычайно важной оказывается возможность реализации модельного эксперимента и получения надежных экспериментальных данных о поле течения целом - с помощью метода, не вносящего возмущения в само течение.
В данной работе приводятся результаты сравнения экспериментальной теневой визуализации с визуализацией, полученной при решении уравнений численной газодинамики, для одного модельного нестационарного сверхзвукового течения.
Это течение представляет собой результат взаимодействия плоской ударной волны с неоднородным нагретым пристеночным слоем, образованным за счет локализованного поверхностного энерговложения в газ.
Интерес к подобного рода течениям (помимо исследования фундаментальной задачи о взаимодействии ударных волн с неоднородностями) обусловлен развитием плазменной аэродинамики и поисками методов активного управления высокоскоростными потоками с помощью внешнего энергетического воздействия [3]. Направленное воздействие на поток может быть обеспечено, в частности, инициированием на обтекаемой поверхности электрических разрядов (т.н. «плазменных актуаторов» [3-5]). При этом эффективным методом управления, особенно при сверхзвуковых скоростях, считается «мгновенное» (относительно характерных газодинамический времен) внесение энергии в среду, как при импульсном режиме инициирования разрядов.
В проведенных экспериментах источником импульсного энергоподвода служил распределенный скользящий разряд наносекундной длительности («плазменный лист»), развивающийся в слое толщиной порядка 1 мм на поверхности площадью 100х30 мм2. Рассматривалось течение, возникающее при движении плоской ударной волны по зоне разряда через 40-500 мкс после прекращения энерговклада.
Благодаря уникальной геометрии экспериментальной установки, газодинамическое течение в разрядной секции канала ударной трубы оказывалось в высокой степени двумерным. Это позволяло проводить и анализировать расчеты, в основном, в двумерной постановке (что накладывало меньшие требования к вычислительным ресурсам). Трехмерные численные расчеты выявили особенности пространственной структуры течения в зоне энерговыделения, недоступные для визуализации экспериментальным теневым методом, а также степень применимости двумерного приближения.
В ходе исследований была протестирована возможность осуществления визуализации массива данных двумерного и трехмерного газодинамического расчета с использованием ресурсов только персонального компьютера. Были изучены способы повышения производительности такой визуализации на примере применения пакета ParaView и языка программирования Python (для работы с файлами численных данных и их конвертации).
1. Экспериментальные результаты
Использованные в работе экспериментальные результаты были получены на установке УТРО-3, которая позволяет реализовывать и визуализировать модельные квазидвумерные, а также трехмерные течения газа и низкотемпературной плазмы. Установка представляет собой однодиафрагменную ударную трубу прямоугольного поперечного сечения высотой 24 мм и шириной 48 мм, в камеру низкого давления которой встроена разрядная (рабочая) секция того же внутреннего сечения. На нижней стенке разрядной секции в области размерами 100х30 мм2 возможно осуществить импульсный поверхностный энергоподвод в газ за счет инициирования особого типа газового разряда — сильноточного распределенного скользящего разряда наносекундной длительности («плазменного листа»). Конфигурация и свойства разряда представлены в [2,6].
В рассматриваемой серии экспериментов толкающим газом служил гелий, рабочим – воздух при комнатной температуре и давлении 20-80 Торр. Числа Маха ударных волн лежали в диапазоне 1.5-3.0.
Оптическая диагностика процессов в разрядной камере проводилась через плоскопараллельные кварцевые стекла, которыми были частично заменены две боковые стенки разрядной секции. Исследование структуры собственного свечения плазмы разряда проводилось интегральным методом с помощью цифровых фотоаппаратов и стробируемой камеры с наносекундным затвором. Газодинамическое течение с ударной волной в разрядной камере визуализировалось лазерным теневым методом. Были созданы однокадровая и двухкадровая теневые системы зондирования течения, которые позволяли получать только один или два кадра в течение всего процесса взаимодействия падающей ударной волны с результатом импульсного энерговклада в среду.
В ходе экспериментов «плазменный лист» инициировался в рабочей секции в неподвижном воздухе, и снималось его интегральное свечение. В результате интерференции взрывных ударных волн от отдельных каналов формировался квазиплоский фронт огибающей ударной волны, распространявшийся от зоны разряда.
Разряд инициировался не менее чем за 40-50 мкс до прихода плоской ударной волны в разрядную область. В момент, когда ударная волна находилась внутри разрядного промежутка, теневым методом регистрировалась определенная стадия ее взаимодействия с зоной разряда. При одних и тех же начальных условиях (числе Маха набегающей волны и давлении в разрядной камере) полученные в экспериментах газодинамические конфигурации различались в зависимости от времени после разряда, положения волны в разрядной секции, а также особенностей распределения энерговклада в газ.
2.1. Математическая модель и численный метод
Численное моделирование экспериментов по взаимодействию плоской ударной волны с зоной импульсного поверхностного энерговклада проводилось с помощью оригинальной программы расчета в рамках вычислительной газодинамики (CFD). Численная модель была построена на основе решения полной системы нестационарных уравнений Навье-Стокса и Эйлера для сжимаемого газа в двумерной и трехмерной постановке.
Для численной аппроксимации уравнений была применена явная квазимонотонная схема повышенного порядка точности, основанная на модификации метода Годунова. Конвективные потоки рассчитывались независимо по каждому направлению с помощью приближенного решения задачи Римана (HLLC). Повышение пространственного порядка точности схемы без потери монотонности алгоритма достигалось использованием двумерной процедуры восстановления с применением ограничителя MinMod. Вязкие потоки, в случае решения уравнений Навье-Стокса, вычислялись с помощью центральных разностей. Интегрирование по времени проводилось методом Рунге-Кутты второго или третьего порядка с неявной аппроксимацией источникового члена.
Использовалась модель совершенного газа (воздух) с постоянным показателем адиабаты (γ=1.4) и числом Прандтля Pr=0.72. Зависимость коэффициента вязкости от температуры описывалась формулой Сазерленда. Начальные параметры невозмущенного газа задавались в соответствии с экспериментальными условиями: p0=20-80 Торр, T=293 К. Программа численного расчета была написана на языке программирования Fortran90.
2.2. Постановка расчетной задачи
Расчетная область представляла собой часть канала ударной трубы размерами 120х24х48 мм3 (Рис. 1). Использовались следующие граничные условия: плоскости y=0 мм, y=24 мм и z=0 мм - «твердая стенка»; x=0 мм и x=120 мм - «свободная» граница. С учетом симметрии течения расчет выполнялся в области 0 ≤ z ≤ 24 мм, с плоскостью симметрии z=24 мм.
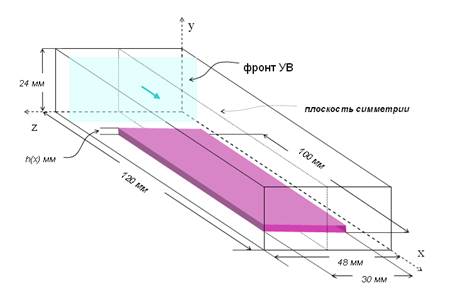
Рис. 1. Расчетная область для трехмерного численного моделирования –
часть
разрядной камеры с зоной разряда на нижней стенке.
Зона энерговклада занимала пространство 14 ≤ x ≤ 114 мм, 9 ≤ z ≤ 39 мм, 0 ≤ y ≤ h(x) мм, где значение h(x) варьировалось в численных экспериментах. Результат инициирования разряда моделировался как увеличение внутренней энергии газа в этой области на некоторое значение ∆W. Величина ∆W=K(x,y)W представляла собой долю всей вкладываемой в «плазменный лист» электрической энергии (W~0.33 Дж), мгновенно (с точки зрения газодинамических процессов) переходящую в тепло в субмиллиметровом приповерхностном слое [6]. Поскольку за время протекания тока разряда (сотни наносекунд) нагрева поверхности не происходило, на нижней границе расчетной области также поддерживалось постоянное значение температуры («изотермическая стенка»).
Набегающая ударная волна задавалась независимо от энерговклада с помощью соотношений Рэнкина-Гюгонио в точке с координатой x=4 мм, так, чтобы через определенное из эксперимента время (t) ее положение совпадало с наблюдаемым на соответствующем теневом снимке.
Поскольку задача решалась методом подбора (в расчетах варьировались параметры энерговклада — h(x) и K(x,y)), предварительные расчеты проводились на крупных сетках, а при достижении наилучшего совпадения с экспериментальными теневыми снимками расчеты повторялись на более мелкой сетке. Максимальное число ячеек расчетной сетки составляло 1000х200х200 для трехмерного и 1500х300 для двумерного расчета.
Для анализа численных данных были опробованы различные пакеты научной визуализации (TecPlot, Matlab, OpenDX, Vislt, ParaView).
К сожалению, большинство систем научной визуализации требуют представление результатов расчетов в определенном формате (например, .vtk, .plt, .tp). Кроме того, при работе с большими массивами данных (их хранении, визуализации и анализа) эффективнее использовать не текстовый (ASCII), а бинарный формат данных. Для повышения производительности в ходе численных экспериментов интересующие параметры течения на конкретном шаге по времени сохранялись в одном их форматов, и при необходимости исходные файлы конвертировались в нужный формат с помощью кода, написанного на языке программирования Python.
Среди опробованных систем визуализации на данном этапе был выбран пакет Paraview [7] за счет совокупности преимуществ: свободное распространение, кросс-платформенность, работа с различными форматами данных, удобный пользовательский интерфейс, потенциальная возможность использования параллельной версии при увеличении размеров численных массивов. В Paraview удобно реализована возможность применения различных фильтров для анализа данных и создания собственных; в том числе, имеется фильтр «отражения» данных относительно заданной плоскости.
Использование системы ParaView (совместно с Python-кодом для повышения эффективности работы с численными массивами) в данном исследовании позволило визуализировать в динамике большие массивы данных и проводить их графический анализ на основе ресурсов одного персонального компьютера.
3. Сравнение численной и экспериментальной визуализации
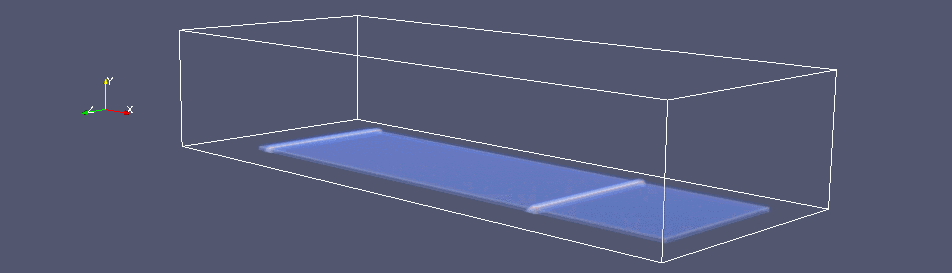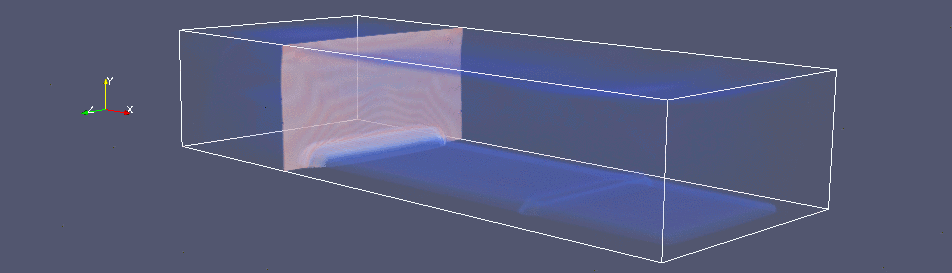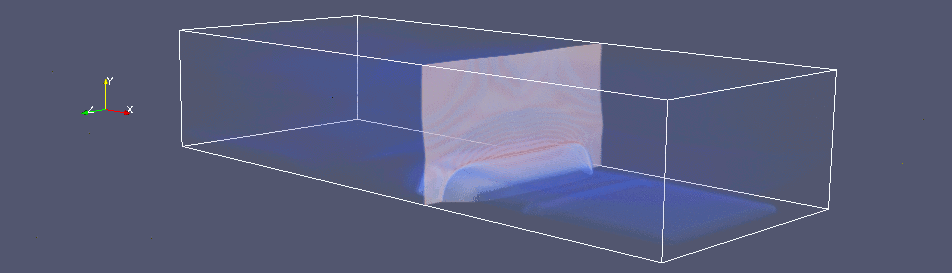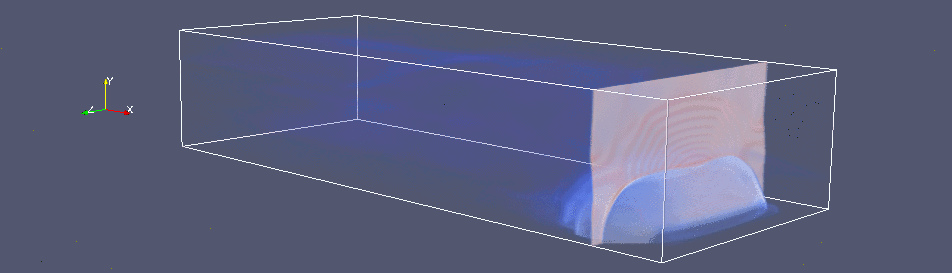
На Рис. 2 представлен пример восстановления течения в разрядной камере (при начальном давлении 25 Торр и числе Маха набегающей волны 2.5) по соответствующей картине свечения разряда (Рис. 2а) и экспериментальному теневому снимку (Рис. 2б). Параметры энерговклада в расчете: h(x)=3 мм и K(x,y)=15% за исключением «ярких каналов» (там коэффициент K меняется от 15 до 30 %, а h - от 3 до 6 мм). Результаты трехмерного расчета (Рис. 2в) представлены в виде изменения функции градиента плотности в течении (аналог шлирен-метода):
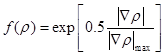 ,
,
где
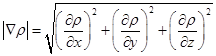
Трехмерная анимация расчетных данных дает наглядное представление о динамике течения в разрядной камере. Видно, что влияние импульсного энергоподвода на набегающую плоскую ударную волну выражается в незначительном искривлении фронта волны за счет взаимодействия с поперечной взрывной ударной волной от энерговклада, а также в эффекте «теплого слоя», приводящем к крупномасштабной перестройке течения [8].

(а)
(б)

(в)
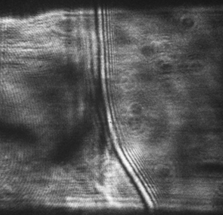
Рис. 2. (а) Фотография свечения разряда (0 мкс) и
(б) соответствующий теневой
снимок ударной волны в разрядной камере примерно через 120 мкс; (в) расчетная
визуализация изменения во времени градиента плотности в процессе.
Трехмерные расчеты показали высокую степень «двумерности» возникающего течения, а сечения численных картин в плоскости симметрии оказались близки к наблюдаемым на экспериментальных теневых снимках. На основе сравнения экспериментальной и численной двумерной визуализации была решена обратная задача — восстановление параметров энерговложения в газ от «плазменного листа» в начальный момент (доли электрической энергии, переходящей в тепло, и ее пространственного распределения).
Использование численных «шлирен»-изображений оказалось наиболее наглядным для визуального представления трехмерной структуры течения. Для имитации экспериментальных снимков, полученных теневым методом, и прямого сравнения с ними в двумерных численных расчетах визуализировалось распределение второй производной (лапласиана) плотности — расчетная «теневая» визуализация [9]:
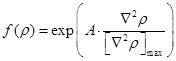
![]() ,
,
где коэффициент А лежал в диапазоне 0.5 < A < 1.5.
Теневая расчетная визуализация давала характерную темную полосу вблизи ударного скачка, свойственную теневому методу. Цветовая палитра численных изображений выбиралась с учетом особенностей экспериментальной оптической системы.
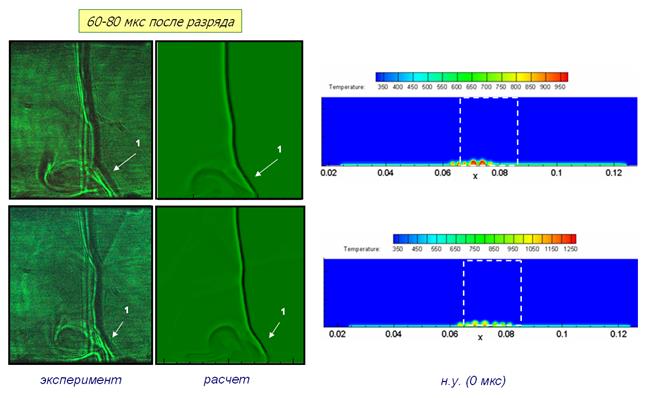
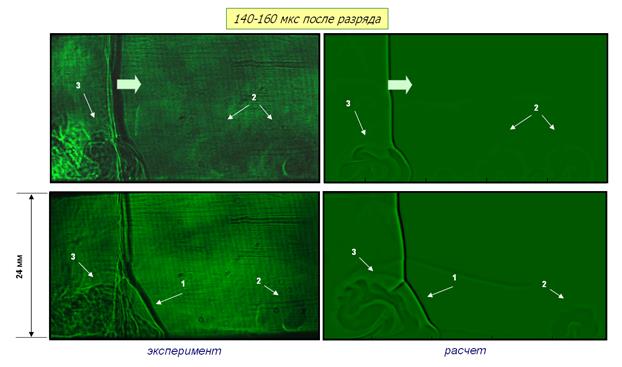
Задача восстановления параметров энерговклада решалась методом подбора, до достижения максимального совпадения экспериментальной и численной визуализации. При этом можно было говорить, что заданные параметры газа соответствовали реальному состоянию среды в результате воздействия поверхностного разряда (Рис. 3а). Кроме того, анализ картин течения выявил характерные особенности воздействия импульсного разряда на нестационарное течение с плоской ударной волной на различных временах после энерговклада. Так, на временах до 100-120 мкс после разряда (Рис. 3а) в течении отчетливо выделяется ударно-волновая структура с «предвестником», возникающая за счет образования вблизи поверхности разряда «теплого слоя» (слоя повышенной температуры и пониженной плотности, в котором фронт набегающей ударной волны распространяется с большей скоростью). При нестационарном взаимодействии ударной волны с «теплым слоем» размеры косого скачка - «предвестника» - растут с увеличением времени взаимодействия, как и характерное вихревое течение за фронтом. На временах, превышающих 100 мкс после разряда начинает проявляться влияние неоднородного распределения энерговклада от «плазменного листа» - течение за ударной волной в спутном потоке существенно турбулизуется, а вблизи зон с более интенсивным энерговкладом слабо визуализируются крупномасштабные неоднородные области типа «термика» (2 на Рис. 3б и 3в). Когда ударная волна проходит через эти области, неоднородности плотности усиливаются, и за фронтом возникают крупномасштабные вихревые структуры. Это хорошо видно на более поздних временах после разряда (Рис. 3в), когда на течение за ударной волной уже не влияет эффект «теплого слоя» (температура газа вблизи поверхности, в среднем, приближается к комнатной).
(a)
(б)

(в)
Рис. 3.
Пример сопоставления экспериментальных и численных двумерных
теневых картин на различных этапах после инициирования разряда: (а) 60-80 мкс
(с начальными условиями); (б) 140-160 мкс; (в) 300-320 мкс. 1 - предвестник, 2
-
неоднородность типа «термик», 3 - вихревое течение за фронтом ударной волны.
Трехмерная динамическая визуализация течения показывает, что отклонение от двумерности ударно-волновой структуры существенно лишь вблизи боковых стенок разрядной камеры, где плоский фронт ударной волны практически не искажается (Рис. 2). В экспериментах на ударной трубе при получении теневых изображений цифровой фотоаппарат фокусировался на центр разрядной камеры. В то же время на многих теневых снимках, помимо существенно возмущенного течения (искривленного фронта ударной волны и неоднородного течения за фронтом), регистрировался также и прямолинейный скачок уплотнения. На Рис. 4 представлены теневые снимки течений (числом Маха ударной волны 2.4), полученные через 134 и 176 мкс после инициирования разряда. Наилучшее совпадение численной и экспериментальной визуализации было достигнуто при наложении продольных срезов расчетных полей течения плоскостями z = 0 мм (стенка канала) и z=24 мм (плоскость симметрии). Сходство расчетных и экспериментальных данных в этом случае выявило наличие краевых эффектов у передней и задней стенки разрядной камеры.
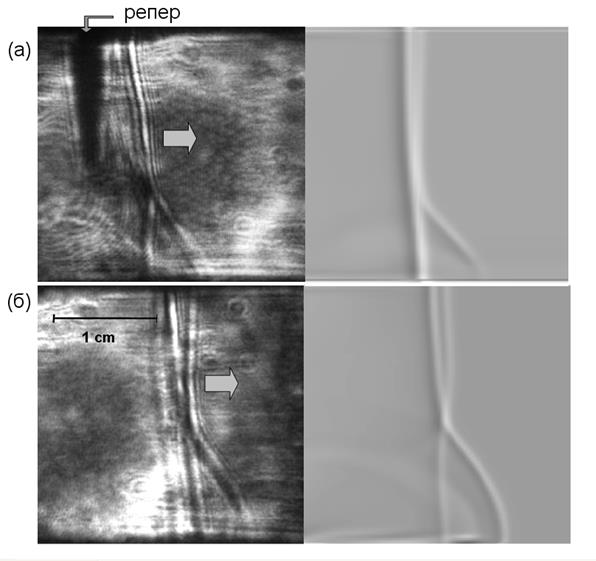
Рис. 4.
Сравнение теневых снимков (слева) и трехмерного численного
моделирования при визуализации продольных сечений плоскостями z=0 мм и
z=24 мм (справа) для двух экспериментов через 134 (а) и 176 мкс (б)
после разряда.
В работе продемонстрированы преимущества совместного использования экспериментальной оптической и численной визуализации на примере исследования модельного квазидвумерного сверхзвукового течения. Был рассмотрен процесс взаимодействия плоской ударной волны с неоднородной нагретой областью газа, сформированной вблизи поверхности через 40-500 мкс после инициирования импульсного скользящего разряда типа «плазменный лист».
Было проведено сравнение экспериментальной и численной теневой визуализации течения в разрядной камере при различных условиях, и на его основе была решена обратная задача — определение исходных параметров энерговклада в газ. Численное моделирование на основе уравнений газодинамики (CFD) дополнило представление о возникающем течении и его динамике.
Трехмерная численная визуализация позволила восстановить пространственную структуру фронта ударной волны в зоне энерговыделения, не доступную для регистрации экспериментальным теневым методом. Расчеты подтвердили, что благодаря геометрии эксперимента, в канале сечением высотой 24 и шириной 48 мм удается получать близкие к двумерным газодинамические течения; в задачах с поверхностным энерговыделением отклонение от двумерности происходит в небольших областях вблизи стенок канала ударной трубы.
Авторы выражают благодарность Знаменской И.А. за постановку задачи и Орлову Д.М. за предоставление результатов экспериментов.
Работа выполнена при финансовой поддержке РФФИ (грант 12-08-31293).
1. Znamenskaya I.A. The interaction of experimental and numerical visualization of flows with shock waves. The 15th International Symposium on Flow Visualization (15 ISFV), Minsk, Belarus, 2012, P. 180.
2. Ivanov I.E., Kryukov I.A., Orlov D.M., Znamenskaya I.A. Investigations of shock wave interaction with nanosecond surface discharge. Experiments in Fluids, 2009, V. 48, № 4, P. 607-613.
3. Proceedings of the 1-11th Workshops on Magneto-Plasma Aerodynamics for Aerospace Applications // Ed. by V.A.Bityurin. Moscow: IVTAN, 1999-2003, 2005, 2007, 2009-2012.
4. Cattafesta L.N., Sheplak M. Actuators for Active Flow Control // Annu. Rev. Fluid Mech. 2011. Vol. 43. P. 247–272.
5. Moreau E. Airflow control by non-thermal plasma actuators // J. Phys. D: Appl. Phys. 2007. Vol. 40. P. 605-636.
6. Знаменская И.А., Латфуллин Д.Ф., Луцкий А.Е., Мурсенкова И.В. Энерговклад в пристеночный слой газа при инициировании наносекундного скользящего поверхностного разряда // Письма в ЖТФ. 2010. Т. 36. № 17. С.35.
8. Бергельсон В.И., Немчинов И.В., Орлова Т.И., Смирнов В.А., Хазинс В.М. Автомодельное развитие предвестника перед ударной волной, взаимодействующей с теплым слоем // ДАН СССР. 1987. Т. 296. № 3. С. 554-557.
9. Hadjadj, A. and Kudryavtsev, A. Computation and flow visualization in high speed aerodynamics // J. Turbul. 2005, V. 6, i. 16, P. 33-81.
INVERSE PROBLEM OF SURFACE ENERGY DEPOSITION BASED
ON THE COMPARISON BETWEEN NUMERICAL AND EXPERIMENTAL
VISUALIZATION OF A SHOCK WAVE PROPAGATION ALONG THE
DISTURBED AREA
E. Koroteeva, I. Ivanov
Lomonosov Moscow State University, Moscow, Russian Federation
koroteeva@physics.msu.ru
Annotation
In this paper, the influence of pulsed surface energy deposition on the non-stationary flow with a shock wave in a rectangular channel was considered. Using the analysis of the arising spatial supersonic flow as an example, the effective interaction of experimental and numerical flow visualization was illustrated.
In the experiments, the propagation of a M=1.5-3.0 plane shock wave along the surface of a distributed sliding nanosecond-lasting discharge («plasma sheet») 40-500 µs after its initiation was recorded by the shadowgraph technique. Due to the unique experimental setup geometry, the gas-dynamic flow in the discharge chamber of the shock tube was highly two-dimensional.
It allowed performing and analyzing calculations not only in three- but also in two-dimensional formulations. The numerical simulations were carried out on the basis of Navier-Stokes and Euler equations for compressible flow and an instantaneous pulsed energy deposition model.
The comparison of the experimental shadow images with the numerical flow visualization results allowed restoring the whole dynamics of the high-speed process. The inverse problem — evaluation of the initial parameters of energy deposition in gas — was also solved. Three-dimensional simulations revealed all the spatial features of the flow in the discharge chamber which could not be captured solely by the shadowgraph method and demonstrated the validity of the two-dimensional approximation.
Key words: shadow visualization, shock wave, pulsed energy deposition, numerical CFD-visualization.
References
1. Znamenskaya I.A. The interaction of experimental and numerical visualization of flows with shock waves. The 15th International Symposium on Flow Visualization (15 ISFV), Minsk, Belarus, 2012, p. 180.
2. Ivanov I.E., Kryukov I.A., Orlov D.M., Znamenskaya I.A. Investigations of shock wave interaction with nanosecond surface discharge. Experiments in Fluids, 2009, vol. 48, no. 4, p. 607-613.
3. Proceedings of the 1-11th Workshops on Magneto-Plasma Aerodynamics for Aerospace Applications. Ed. by V.A. Bityurin. Moscow: IVTAN, 1999-2003, 2005, 2007, 2009-2012.
4. Cattafesta L.N., Sheplak M. Actuators for Active Flow Control. Annu. Rev. Fluid Mech. 2011. vol. 43. pp. 247–272.
5. Moreau E. Airflow control by non-thermal plasma actuators. J. Phys. D: Appl. Phys. 2007. vol. 40. pp. 605-636.
6. Znamenskaya I.A., Latfullin D.F., Lutskiy A.E., Mursenkova I.V. Energovklad v pristenochnyy sloy gaza pri initsiirovanii nanosekundnogo skolzyaschego poverkhnostnogo razryada [Energy deposition in boundary gas layer during initiation of nanosecond sliding surface discharge]. Technical Physics Letters. 2010. vol. 36, no. 9, p. 795.]
7. ParaView. Available at: http://www.paraview.org
8. Bergelson V.I., Nemchinov I.V., Orlova T.I., Smirnov V.A., KHazins V.M. Avtomodelnoe razvitie predvestnika pered udarnoy volnoy, vzaimodeystvuyuschey s teplym sloem [Self-similar development of a precursor in front of a shock wave interacting with a thermal layer]. Sov. Phys. Dokl., Engl. Transl., 32, pp. 691-692, 1987.
9. Hadjadj, A. and Kudryavtsev, A. Computation and flow visualization in high speed aerodynamics. J. Turbul, 2005, vol. 6, issue 16, pp. 33-81.