Взаимодействие численной и экспериментальной
визуализации при исследовании свойств разрядов методом
анализа ударно-волновых конфигураций
И. Знаменская1, А. Луцкий2, Я. Ханхасаева1, Ц. Цзинь1
1 Московский Государственный Университет имени М.В. Ломоносова, Москва, Россия
2 Институт прикладной математики им. М.В. Келдыша Российской академии наук, Москва, Россия
znamen@phys.msu.ru, allutsky@yandex.ru, hanhyana@mail.ru
Оглавление
Постановка экспериментальной задачи
Численное моделирование течения в условиях эксперимента
Особенности двумерного течения в условиях эксперимента
Аннотация
В работе развивается подход к анализу течения с энергоподводом на основе решения обратной задачи: метод предполагает численный эксперимент, позволяющий нахождение неизвестного параметра (в данном случае – пространственное распределение энергии локализованного энерговклада) путем сравнения численных и экспериментальных изображений с известными контролируемыми параметрами. Устранение различий в экспериментальной и численной визуализации газодинамического течения методом подбора приводит к нахождению правильного решения.
В рассмотренном случае вложение энергии в поток с ударной волной происходит в области комбинированного разряда - импульсного объемного разряда с предыонизацией ультрафиолетовым излучением от плазменных листов. Рассматриваемые течения представляют большой интерес с разных точек зрения. В них реализуется ряд интересных явлений, таких как взаимодействие ударной волны с прогретым приповерхностным слоем и неустойчивость тангенциального разрыва под действием ударной волны. Достаточно сложная конфигурация разрывов нестационарного течения предъявляет высокие требования к численным алгоритмам и, тем самым, стимулирует их дальнейшее совершенствование.
Одним из наиболее перспективных и уже достаточно широко используемых подходов при численном моделировании сверхзвуковых течений являются WENO (weighted essentially non-oscillatory) схемы. Такой алгоритм использовался при проведении представленных численных исследований.
В работе представлены результаты исследования пространственного распределения энергии импульсного комбинированного наносекундного разряда методом анализа динамики двумерных ударно-волновых конфигураций. Проведена численная 1D и 2D реализация двух вариантов задачи. Рассмотрена конфигурация и эволюция разрывов, возникающих при взаимодействии разряда с плоской ударной волной в канале. Учтена неравномерность распределения вложения энергии и то, каким образом она влияет на течение.
Ключевые слова: визуализация, численное моделирование, теневой метод, ударно-волновая конфигурация.
Важнейшей тенденцией последнего десятилетия в развитии научных исследований гидродинамических потоков является стремительное сближение визуализации результатов численного моделирования с визуализацией экспериментальной. Такое сближение стало возможным в связи с внедрением цифровых технологий в методы регистрации и анализа потоков с одной стороны, и способов представления результатов ЧМ с другой стороны.
Методы экспериментальной визуализации потоков опираются на физические явления, связанные с распространением электромагнитных волн (излучение, рассеяние, поглощение, отражение, рефракция, интерференция, люминесценция и.т.д.). Экспериментальные изображения могут быть получены непосредственно с различных типов цифровых камер, регистрирующих это излучение, в виде, готовом для сравнения и анализа (теневые методы), либо после дополнительной обработки, например на основе кросскорреляционных методов (ТФМ, PIV, LIF). Расчетные поля газодинамических параметров представляются при помощи соответствующих программных продуктов в виде, удобном для прямого сравнения с полями экспериментальными.
На основе сравнения с данными экспериментальной визуализации потоков проводится верификация моделей и алгоритмов численных расчетов. С другой стороны, результаты эксперимента расшифровываются и уточняются на основе данных численного эксперимента, упрощается решение обратных задач при определении физических полей. В связи с широкими возможностями такого взаимодействия встает проблема оптимизации экспериментальной и численной визуализации результатов.
Результаты, полученные теневыми и интерференционными методами, стали использоваться для прямого сравнения с расчетами в начале 90-х годов [1]. Сегодня большая часть результатов исследований сверхзвуковых 2D процессов представляется в виде численных теневых картин. Наиболее эффективно это происходит в структурированных течениях – с разрывами, выраженными неоднородностями, вихревыми структурами.
Специальной задачей является отработка средств визуализации данных, численных и экспериментальных, наиболее адекватных для получения максимальной информации о свойствах течения.
В данной работе развивается подход к анализу течения с энергоподводом на основе решения обратной задачи; метод предполагает численный эксперимент, позволяющий нахождение неизвестного параметра (в данном случае – пространственное распределение энергии локализованного энерговклада) путем сравнения численных и экспериментальных изображений с известными контролируемыми параметрами. Устранение различий в экспериментальной и численной визуализации газодинамического течения методом подбора приводит к нахождению правильного решения.
Одним из наиболее перспективных и уже достаточно широко используемых подходов при численном моделировании сверхзвуковых течений являются WENO (weighted essentially non-oscillatory) схемы [2-6]. Течения такого типа могут быть реализованы, в частности в экспериментах на ударных трубах [9,11]. В рассмотренном случае вложение энергии в поток с ударной волной происходит в области комбинированного разряда - импульсного объемного разряда с предионизацией ультрафиолетовым излучением от плазменных листов. Рассматриваемые течения представляют большой интерес с разных точек зрения. В них реализуется ряд интересных явлений, таких как взаимодействие ударной волны с прогретым приповерхностным слоем и неустойчивость тангенциального разрыва под действием ударной волны. Достаточно сложная конфигурация разрывов нестационарного течения предъявляет высокие требования к численным алгоритмам и, тем самым, стимулирует их дальнейшее совершенствование. Ряд указанных явлений ранее был исследован в работах [9,12]. При этом предполагалось, что область энерговыделения имеет резко очерченные границы и энергия выделяется равномерно по пространству. В настоящей работе предпринята попытка учесть неравномерность выделения энергии и ее влияние на возникающие ударно-волновые конфигурации.
Постановка экспериментальной задачи
Рассмотрим свойства течений, формирующихся в плоском канале при взаимодействии плоской ударной волны с областью вложения энергии конечных размеров. Схема экспериментальной реализации импульсного вложения энергии в сверхзвуковой поток представлена на рис. 1.
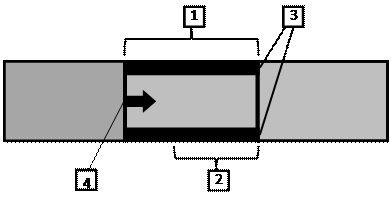
Рис. 1. Схема экспериментальной установки.
1-область между электродами; 2-область импульсного энерговклада перед УВ;
3-плазменные листы (область поверхностного энерговклада); 4-ударная волна.
В экспериментах использовалась установка [8-12], представляющая собой ударную трубу сечением 48х24мм, состоящую из камеры высокого давления, диафрагменной секции и разрядной секции. Рабочий газ - воздух, толкающий газ – гелий. Реализуется импульсный объемный разряд с предыонизацией ультрафиолетовым излучением от плазменных электродов на участке потока протяженностью 10 см в разрядной камере. Межэлектродное расстояние составляет 2.4 см. Разряд инициируется в заданный момент движения плоской ударной волны по каналу ударной трубы (разрядной секции) и протекает в два этапа: сначала в течение 60-100нс – на верхней и нижней поверхностях камеры горят плазменные листы – сильноточные разряды, скользящие по поверхности диэлектрика. Область плазменного листа представляет собой однородную зону приповерхностного импульсного энерговыделения на противоположных стенках прямоугольного канала. Скользящий разряд создаёт ультрафиолетовое излучение высокой интенсивности и ионизирует воздух в рабочей секции, подготавливая таким образом рабочий объём к созданию однородного импульсного объёмного разряда. Поверхностный разряд сопровождается возникновением ударных волн, распространяющихся в направлении, перпендикулярном направлению потока за падающей ударной волной в канале.
На втором этапе длительностью 100-200 нс происходит замыкание основного разрядного промежутка, и энергия вкладывается в межэлектродную область. Наличие неоднородностей плотности газа (ударной волны) в газодинамическом потоке приводит к пространственному перераспределению плазмы объемного разряда.
При наличии ударной волны в межэлектродном промежутке в момент инициирования разряда, область свечения и энерговклад локализуется перед её фронтом – в зоне низкого давления (Рис.2.б). Мгновенное повышение температуры и давления перед фронтом исходной ударной волны при интенсивном импульсном энергоподводе приводит к нарушению условий Ренкина-Гюгонио. Фронт исходной ударной волны в момент времени t_=_0 становится плоской границей раздела двух областей газа с различными, не связанными друг с другом, параметрами. Таким образом, создаются условия для распада разрыва. Исходный плоский разрыв распадается (в основном течении) на две ударные волны, между которыми образуется контактная поверхность. Эксперименты показывают, что свечение разряда и, возможно, энергия распределены в потоке перед волной не вполне равномерно. Основные неоднородности наблюдаются по краям области разряда (Рис. 2.б).
Численное моделирование течения в условиях эксперимента
Целью численного моделирования являлось уточнение распределения энергии разряда в момент t_=_0 на основе сравнения экспериментальных и расчетных изображений течения в различные моменты времени. Численное моделирование проводилось в рамках математической модели нестационарных 2D уравнений Эйлера с использованием описанного выше алгоритма. Область между электродами: 0 ≤ x ≤ 10. В начальный момент времени плоская ударная волна с числом Маха М=2.3 для первого варианта задачи располагается в сечении x0=6, для второй – x0=3. В эксперименте в объемную часть разряда x0 < x < 10, |y| < 1.1 (области 2-4 на рис. 2а) вкладывалось 0.4 Дж, в плазменные листы около стенок 1.1 < |y| < 1.2 (области 5 на рис. 2а) – по 0.1 Дж. На основании ранее проведенных исследований [8] предполагалось, что в поступательные степени свободы мгновенно переходит 50% вложенной энергии.
Вложение
энергии ![]() E/V в постоянный поток приводит
к росту давления на величину
E/V в постоянный поток приводит
к росту давления на величину ![]() при
сохранении плотности и скорости. В более ранних исследованиях [8, 9]
предполагалось, что вложение энергии в постоянный поток равномерно по времени и
пространству во всей области разряда, что соответствовало имевшимся на тот
момент экспериментальным данным. Анализ изображений (рис.2.б), полученных в
ходе новых экспериментов, показал отсутствие резкой границы справа, т.е. вместо
резкого скачка давления имеет место его плавный переход в невозмущенное
состояние.
при
сохранении плотности и скорости. В более ранних исследованиях [8, 9]
предполагалось, что вложение энергии в постоянный поток равномерно по времени и
пространству во всей области разряда, что соответствовало имевшимся на тот
момент экспериментальным данным. Анализ изображений (рис.2.б), полученных в
ходе новых экспериментов, показал отсутствие резкой границы справа, т.е. вместо
резкого скачка давления имеет место его плавный переход в невозмущенное
состояние.
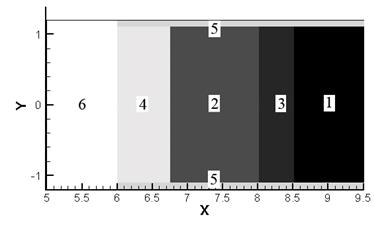
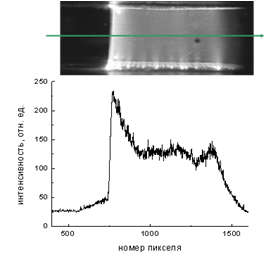
а б
Рис. 2.
Начальное распределение давления для 2D
расчета и график светимости вдоль трубы.
Также было рассмотрено влияние эффектов понижения параметров потока за фронтом ударной волны и неравномерности вложения энергии в область непосредственно перед фронтом ударной волны. В соответствие графику светимости (рис. 2) перед фронтом УВ имеется линейное увеличение кол-ва вложенной энергии. Общее кол-во вложенной в эту область энергии составляет 25%.
Для анализа этих фактов была проведена серия расчетов в упрощенной одномерной постановке. Поскольку большая часть энергии приходится на объемную часть разряда, можно ожидать, что в 1D течении, возникающем при отсутствии вложения энергии в плазменные листы, некоторые существенные детали реального 2D течения будут выявлены.
В расчетах плотность и давление были отнесены к величинам в невозмущенном газе – область 1 на рис. 2. При такой нормировке безразмерная единица времени соответствует 3.45*10-5 с.
В начальный момент времени существует 6 областей с постоянными (кроме областей 3 и 4) значениями газодинамических величин:
(1) невозмущенный неподвижный газ перед фронтом падающей ударной волны:
x > 9: r1=1, u1=0., v1=0., p1=1.
(2) объемная часть разряда:
x0 < x < 8, |y| < 1.1: r2=1, u2=0., v2=0., для x0=6 p2=1.7593, для x0=3 p2=1.3448.
(3) линейный спад давления в невозмущенный газ:
8 < x < 9, |y| < 1.1: r3=1, u3=0., v3=0., для x0=6 p3=1.7593 - 1, для x0=3 p3=1.3448 - 1.
(4) увеличение энергии разряда непосредственно перед фронтом УВ:
для x0=6 6 < x < 6.75, |y| < 1.1: r4=1, u4=0., v4=0., для x0=6 p4=3.3754 - 1.7593.
для x0=3 3 < x < 4.5, |y| < 1.1: r4=1, u4=0., v4=0., для x0=3 p4=2.1750 – 1.3448
(5) пристеночные области («плазменные листы»):
x0 < x < 10, |y| > 1.1: r5=1, u5=0., v5=0., для x0=6 p5=2.7365, для x0=3 p5=1.9923.
(6) область за фронтом падающей волны:
x < x0: r6=3.0845, u6=1.8391, v6=0., p6 =6.0050.
Эти величины подсчитываются с помощью следующих формул [7]
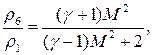
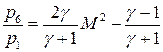
На границах (за исключением правой границы области объемного энерговложения) этих областей в начальный момент происходит распад разрывов с образованием волн разрежения, ударных волн и тангенциальных разрывов. В последующие моменты времени течение характеризуется достаточно сложным процессом движения и взаимодействия этих вторичных разрывов.
Для анализа динамики разрывов в основном течении была рассмотрена одномерная задача. Рассмотрим вариант течения, в котором ударная волна в момент зажигания разряда располагается в сечении x0=3. В результате распада разрыва в точке x0=3 формируются две ударные волны и тангенциальный разрыв (Рис. 3.а). Начальные интенсивности разрывов зависят от двух факторов – числа Маха падающей ударной волны и интенсивности вложенной энергии. Плавный переход на правой границе выражается в отсутствии на ней распада разрыва (Рис. 3.б). Наиболее наглядной характеристикой, по которой можно судить, отвечают ли результаты, полученные с помощью численного эксперимента, реальному, является расстояние между правой ударной волной и контактным разрывом. При численных экспериментах расстояния между правой УВ и контактным разрывом, соответствующие экспериментальным, получены лишь при существенном увеличении уровня вкладываемой энергии.
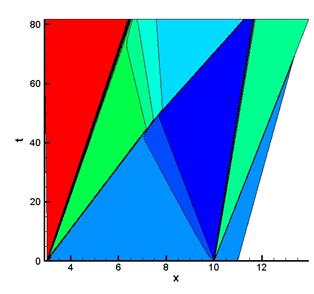
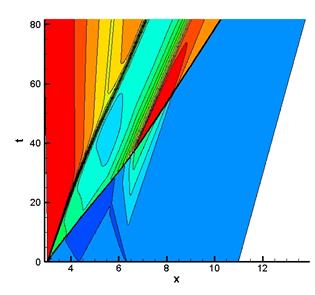
а б
Рис. 3.
Распределение плотности в 1D продольном течении, картинка
слева - резкий переход справа, картинка справа - плавный переход на правой
границе.
Особенности двумерного течения в условиях эксперимента
Расчеты 2D течения проводились на сетке, содержащих 1500*200 ячеек в полуплоскости y > 0 с учетом симметрии течения.
Первая задача: фронт ударной волны совпадает с сечением x0=6. Теневая лазерная фотография эксперимента, полученная на момент времени t=32 мкс, представлена на рис. 5а, на момент времени t=58 мкс на рис. 6а. Здесь показано развитие нестационарного ударно - волнового течения, возникшего после распада разрыва в результате импульсного локализованного энерговклада. Видно, что после разряда исходная ударная волна распалась на три разрыва: слева направо - ударную волну, контактную поверхность и еще одну ударную волну, движущуюся в том же направлении, что и исходная УВ – слева направо. Правая ударная волна и контактная поверхность движутся вперед с разными скоростями, ограничивая область неравновесного потока релаксирующей плазмы комбинированного разряда.
На рис. 4 б, в, 5 б, в показаны численные теневые фотографии, полученные с помощью WENO схемы.
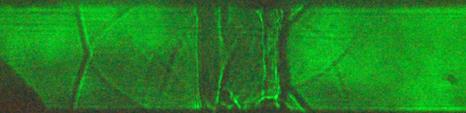
a)

б)

в)
Рис. 4. Течение
после распада разрыва, x0=6
см, t=32 мкс: а) теневой снимок,
б) численная теневая фотография, полученная при условии наличия плавного
убывания давления за фронтом УВ, в) при условии увеличения энергии
разряда непосредственно перед УВ.
Вторая задача: фронт ударной волны совпадает с сечением x0=3. Теневая фотография эксперимента, полученная на момент времени t=82 мкс, представлена на рис. 6. На рис. 7 показаны численные теневые фотографии, полученные с помощью WENO схемы.
Исходная плоская ударная волна после вхождения в область взаимодействовала с поперечными ударными волнами, неоднородной неравновесной средой в объеме камеры и значительным градиентом термодинамических параметров вблизи плазменных электродов (рис. 7). В зонах вблизи электродов, где было существенно влияние поверхностного разряда, плоская ударная волна выдвигалась вперед (эффект теплового слоя).
Рассмотрим эволюцию разрывов, образующихся в этом варианте задачи. Вблизи плоскости симметрии (у=0) течение близко к продольному одномерному. Слева направо можно наблюдать ударную волну и неустойчивый контактный разрыв. Однако, около стенок ударные волны и тангенциальные разрывы (рис. 7) движутся с более высокими скоростями. Кроме того, на границах плазменных листов в начальный момент образуются разрывы, распространяющиеся и взаимодействующие в поперечном направлении. Линии разрывов достаточно быстро оказываются искривленными в силу ускоренного движения вблизи стенок. Эти стадии течений изображены на рис. 7.
a)

б)
в)
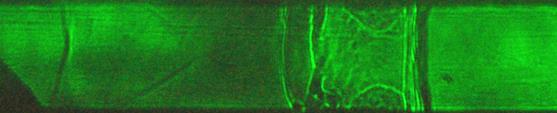
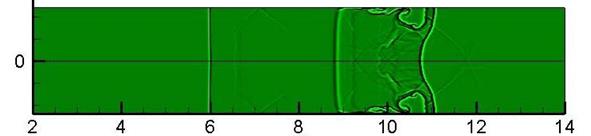
Рис. 5. Течение
после распада разрыва, x0=6
см, t=58 мкс: а) теневой снимок,
б) численная теневая фотография, полученная при условии наличия плавного
убывания давления за фронтом УВ, в) при условии увеличения энергии
разряда непосредственно перед УВ.

Рис. 6. Теневая фотография эксперимента, x0=3 см, t=82 мкс.
В случае первого варианта задачи получено совпадение с экспериментом расстояний между правой ударной волной и контактным разрывом, зафиксировано положение левого контактного разрыва. Также получены численно сложные характерные конфигурации разрывов и неустойчивость тангенциального разрыва в исследованном течении.
Понижение параметров потока за фронтом ударной волны выразилось в приобретении левой ударной волной отрицательной скорости (положительное направление – слева направо). Увеличение количества вложенной энергии в область непосредственно перед фронтом ударной волны выразилась в уменьшении расстояния между правыми ударной волной и контактным разрывом.
Таким образом, показано, что усиление интенсивности свечения объемного разряда в направлении к фронту УВ, в случае, если оно и сопровождается увеличением энерговклада, не влияет существенно на динамику ударно – волновых конфигураций при взаимодействии разряда с ударной волной. Определяющим является распад разрыва на фронте УВ, полная энергия разряда, соотношение поверхностного и объемного энерговклада. Эти параметры восстанавливаются путем решения обратной задачи.
a)
б)

в)
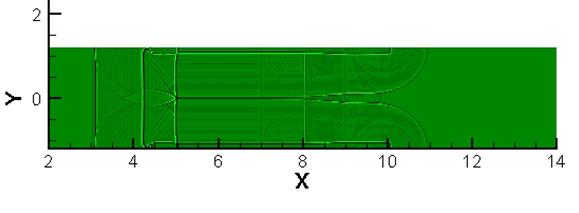
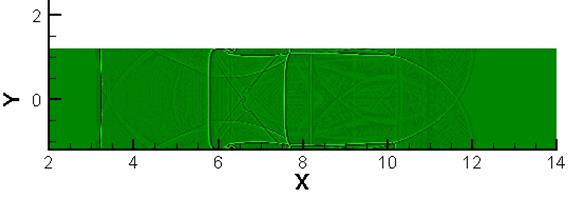
Рис. 7. Численные
теневые фотографии потока в
последовательные моменты времени, x0=3 см,
а) t=24 мкс, б) t=56 мкс, в) t=82 мкс.
На основе систематического сравнения результатов численной и теневой визуализации проведено исследование квазидвумерного нестационарного разрывного газодинамического течения, возникающего ври взаимодействии плоской ударной волны с импульсным комбинированным разрядом. Методом анализа динамики двумерных ударно-волновых конфигураций восстановлено пространственное распределение энергии разряда. Проведена численная 1D и 2D реализация двух вариантов задачи. Рассмотрены конфигурации и эволюция разрывов. Учтена неравномерность распределения вложения энергии и то, каким образом она влияет на течение.
Работа выполнена при поддержке грантов РФФИ 11-08-00297 и 11-08-00269.
Список обозначений
E – кол-во вложенной энергии.
V – объем.
γ – показатель адиабаты.
r – плотность.
p – давление.
u – продольная скорость.
v – поперечная скорость.
1. Y. Tamura and K. Fujii, Paper AIAA-90-3031 (1990).
2. A. A. Fursenko, D. M. Sharov, E. V. Timofeev and P. A. Voinovich, Numerical Simulation of Shock Wave Interactions with Channel Bends and Gas Nonunoformities. Computers Fluids Vol. 21, No. 3, pp. 377-396, 1992.
3. А.Н. Кудрявцев, Т.В. Поплавская, Д.В. Хотяновский, Применение схем высокого порядка точности при моделировании нестационарных сверхзвуковых течений, Математическое моделирование, 2007 г., том 19, номер 7, стр. 39-55.
4. G.-S. Jiang, C.-W. Shu, Efficient implementation of weighted ENO schemes, J. Comput. Phys. 126 (1996) 202-228.
5. X.D. Liu, S. Osher, T. Chan, Weighted essentially non-oscillatory schemes, J. Comput. Phys. 115 (1994) 200-212.
6. C.-W. Shu, High order ENO and WENO schemes for computational fluid dynamics, in High-Order Methods for Computational Physics. Ed. by T.J. Barth and H. Deconinck, Lecture Notes in Computational Science and Engineering, v. 9, Springer, 1999, p. 439-582.
7. C.-W. Shu, S. Osher, Efficient implementation of essentially non-oscillatory shock capturing schemes // J. Comput. Phys,, 1988, v. 77, p. 439-471.
8. Л.Д. Ландау, Е.М. Лифшиц. Теоретическая физика. Учебное пособие. В 10 Т. Т. VI Гидродинамика - 3-е изд., перераб. - М. Наука, 1986.-736 с.
9. И.А. Знаменская, Д.А. Коротеев, А.Е. Луцкий. Экспериментальная реализация двумерной задачи о распаде разрыва при импульсной ионизации потока с ударной волной //ДАН. 2008, Т. 420, № 5. С.619-622.
10. Е.Ю. Коротеева, И.Э. Иванов, И.А. Знаменская. Развитие турбулентности за фронтом ударной волны при ее движении по неоднородной области. Письма в ЖТФ, 2012, том 38, вып. 11.
11. I.A. Znamenskaya, D.A. Koroteev, A.E. Lutsky. Discontinuity breakdown on shock wave interaction with nanosecond discharge. Physics of Fluids. 2008. Vol. 20. P. 056101-1-056101-6.
12. И.А.Знаменская, А.Е.Луцкий. Исследование эволюции и взаимодействия разрывов течения в канале под действием импульсного вложения энергии. Препринт ИПМ им. М.В.Келдыша РАН № 88, 2005.
13. И.А. Знаменская, И.В. Мурсенкова, Д.М. Орлов, Н.Н. Сысоев. Локализация импульсного энерговкалада при инициировании поперечного поверхностного разряда в потоке с ударной волной. Письма в ЖТФ, 2007, том 33, вып. 13.
14. R. Liska, B. Wendroff, Comparison of several difference schemes on 1D and 2D test problems for the Euler equations, SIAM J. SCI. COMPUT. Vol. 25, No. 3, pp. 995–1017.
Interaction of
numerical and experimental
visualization at investigation of discharge properties
by means of shock wave configurations analysis
I. Znamenskaya1, A. Lutsky2, Y. Khankhasaeva1, J. Jin1
1 Lomonosov Moscow State University, Moscow, Russian Federation
2 Keldysh Institute of Applied Mathematic, Moscow, Russian Federation
znamen@phys.msu.ru, allutsky@yandex.ru, hanhyana@mail.ru
Abstract
An approach to the analysis of the flow with energy deposition on the basis of the inverse problem is considered. The method involves the numerical experiments targeting to find the unknown parameter (in case considered - the spatial distribution of the energy of the localized energy deposition) by comparing the numerical and experimental images with known controlled parameters. Eliminating differences in experimental and numerical visualization of gas-dynamic flow results is finding the right solutions.
In the case considered the energy deposition into the flow with a shock wave occurs in the combined discharge-the pulse volume discharge with preionization by ultraviolet radiation from the plasma sheet. These flows are of great interest from different points of view. They implemented a number of interesting phenomena, such as the interaction of a shockwave with the warmed surface layer rand the instability of the tangential discontinuity by a shock wave. Rather complex discontinuity configuration of the unsteady flow makes high demands on numerical algorithms and, thus, stimulates their further improvement.
One of the most promising and already wide used approaches for the numerical simulation of supersonic flows is the WENO (weighted essentially non-oscillatory) schemes. This is the algorithm used during the calculations presented.
The paper presents the results of the spatial distribution of the combined energy of the pulsed nanosecond discharge investigation by the method of analyzing the dynamics of two-dimensional shock-wave configurations. The numerical 1D and 2D implementation of two versions of the problem statement are presented. The configuration and evolution of the discontinuities arising from the interaction of the discharge with a plane shock wave in the channel are described. Taken into account the inhomogeneous distribution of energy input and the way in which it affects the course were considered.
Key words: visualization, CFD, the shadow method, shock-wave configurations.
Reference
1. Y. Tamura, K. Fujii. Visualization for computational fluid dynamics and the comparison with experiments. Paper AIAA-90-3031 (1990).
2. A. A. Fursenko, D. M. Sharov, E. V. Timofeev, P. A. Voinovich. Numerical Simulation of Shock Wave Interactions with Channel Bends and Gas Nonunoformities. Computers Fluids, vol. 21, no. 3, pp. 377-396, 1992.
3. A. N. Kudryavtsev, T. V. Poplavskaya, D. V. Khotyanovsky. Primenenie skhem vysokogo poryadka tochnosti pri modelirovanii nestatsionarnykh sverkhzvukovykh techeniy [Application of high-order accuracy schemes to numerical simulation of unsteady supersonic flows]. Matematicheskoe modelirovanie, vol 19, no. 7, pp. 39–55, 2007.
4. G.-S. Jiang, C.-W. Shu. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126 (1996), pp. 202-228.
5. X.D. Liu, S. Osher, T. Chan. Weighted essentially non-oscillatory schemes. J. Comput. Phys. 115 (1994), pp. 200-212.
6. C.-W. Shu. High order ENO and WENO schemes for computational fluid dynamics, in High-Order Methods for Computational Physics. Ed. by T.J. Barth and H. Deconinck, Lecture Notes in Computational Science and Engineering, v. 9, Springer, 1999, pp. 439-582.
7. C.-W. Shu, S. Osher. Efficient implementation of essentially non-oscillatory shock capturing schemes. J. Comput. Phys,, 1988, v. 77, p. 439-471.
8. L.D. Landau, E.M. Lifshitz, Course of Theoretical Physics. Fluid Mechanics. vol. 6, 3rd ed., M. Science, p. 736, 1986.
9. I.A. Znamenskaya, D.A. Koroteev, A.E. Lutsky. Eksperimentalnaya realizatsiya dvumernoy zadachi o raspade razryva pri impulsnoy ionizatsii potoka s udarnoy volnoy [Experimental realization of 2D discontinuity breakdown with pulse ionization of flow with a shock wave]. Doklady Akademii Nauk, 2008, vol. 420, no. 5, pp. 619-622.
10. E.Y. Koroteeva, I.E. Ivanov, I.A. Znamenskaya. Razvitie turbulentnosti za frontom udarnoy volny pri ee dvizhenii po neodnorodnoy oblasti [Development of turbulence behind the shock wave during its motion through the inhomogeneous field]. Pisma v Zhurnal Tekhnicheskoi Fiziki, vol. 38, issue 11, 2012.
11. I.A. Znamenskaya, D.A. Koroteev, A.E. Lutsky. Discontinuity breakdown on shock wave interaction with nanosecond discharge. Physics of Fluids. 2008. Vol. 20. P. 056101-1-056101-6.
12. I.A. Znamenskaya, A.E. Lutsky. Issledovanie evolyutsii i vzaimodeystviya razryvov techeniya v kanale pod deystviem impulsnogo vlozheniya energii [The evolution and interaction of channel flow discontinuities under the instant volume energy release influence], Keldysh Institute preprints, 2005, 088.
13. I.A. Znamenskaya, I.V. Mursenkova, D.M. Orlov, N.N. Sysoev. Lokalizatsiya impulsnogo energovkalada pri initsiirovanii poperechnogo poverkhnostnogo razryada v potoke s udarnoy volnoy [Localization of pulse energy input at the initiation of transversal surface discharge in a flow with a shock wave]. Pisma v Zhurnal Tekhnicheskoi Fiziki, vol. 33, issue 13, 2007.
14. R. Liska, B. Wendroff, Comparison of several difference schemes on 1D and 2D test problems for the Euler equations, SIAM J. SCI. COMPUT. Vol. 25, No. 3, pp. 995–1017.